Airborne SAR Imaging Algorithm for Ocean Waves Based on Optimum Focus Setting
Abstract
:1. Introduction
2. Theoretical Analysis of the Optimum Focus Setting for Different Targets
2.1. Analysis of the Optimum Focus Setting for Rigid Targets
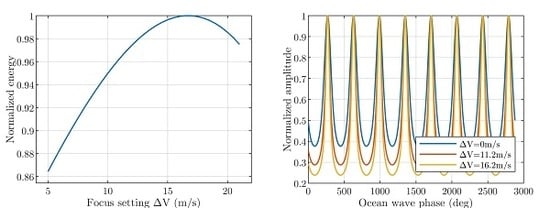
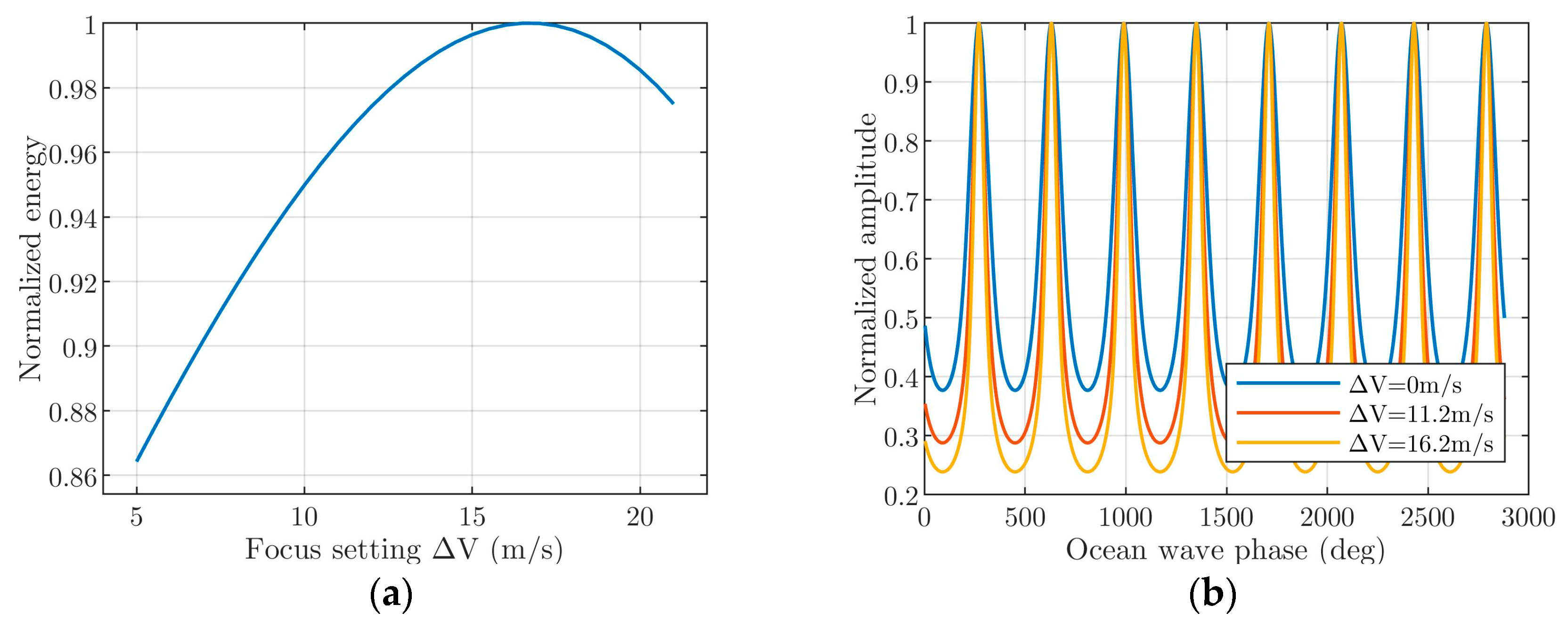
2.2. Analysis of the Optimum Focus Setting for Surface Waves
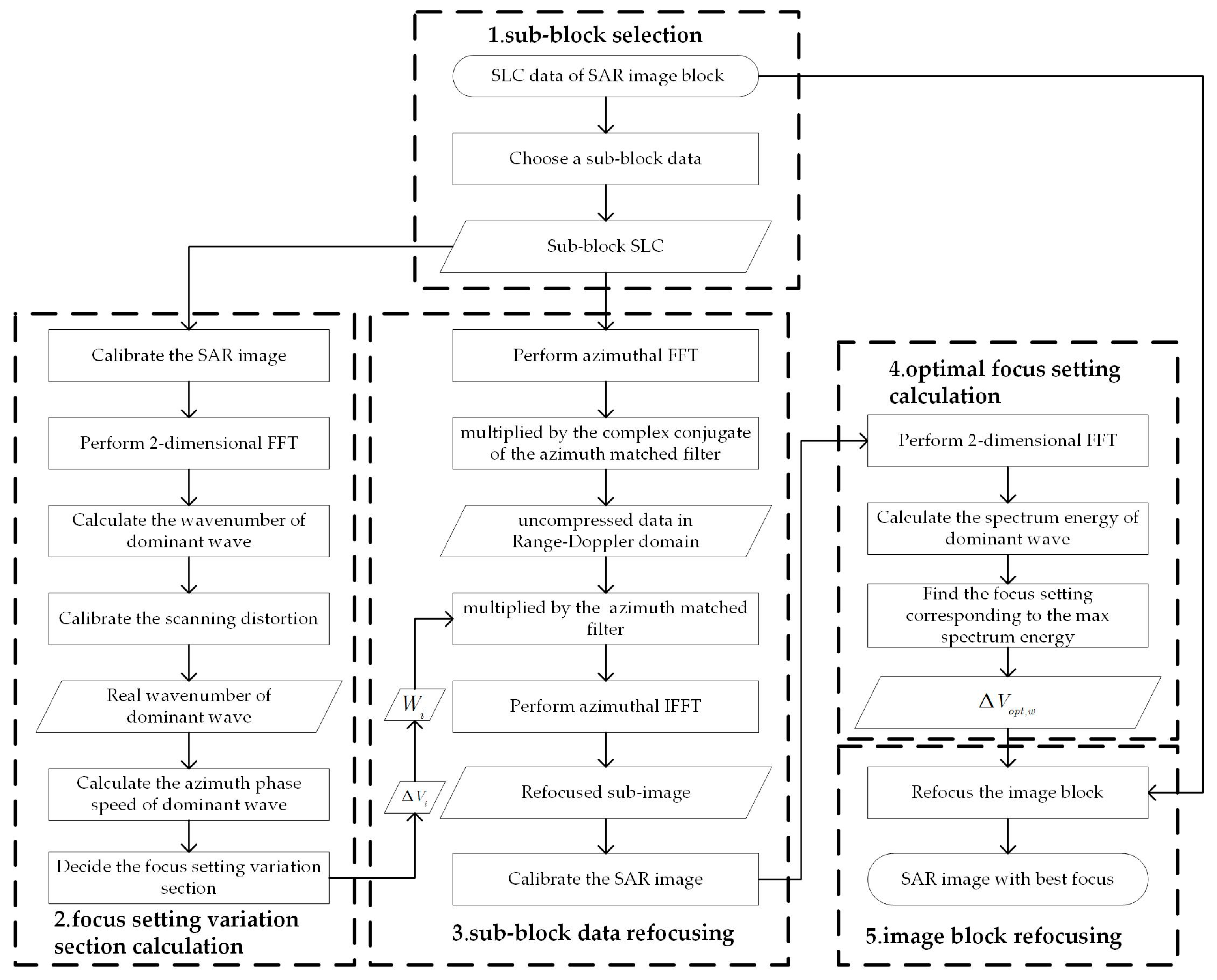
3. Airborne SAR Imaging Algorithm for Ocean Waves Based on Optimum Focus Setting
3.1. Selection of Sub-Block Data
3.2. Calculation of Focus Setting Variation Section
3.3. Sub-block Data Refocusing
3.4. Calculation of the Optimum Focus Setting
3.5. Image Block Refocusing
4. Validation of the Proposed Algorithm with Simulations and Field Data
4.1. Validation of the Algorithm with Simulations
4.1.1. Simulation Model
4.1.2. Simulation Results
4.2. Validation of the Proposed Algorithm with Field Data
4.2.1. Results of Field Data Processing
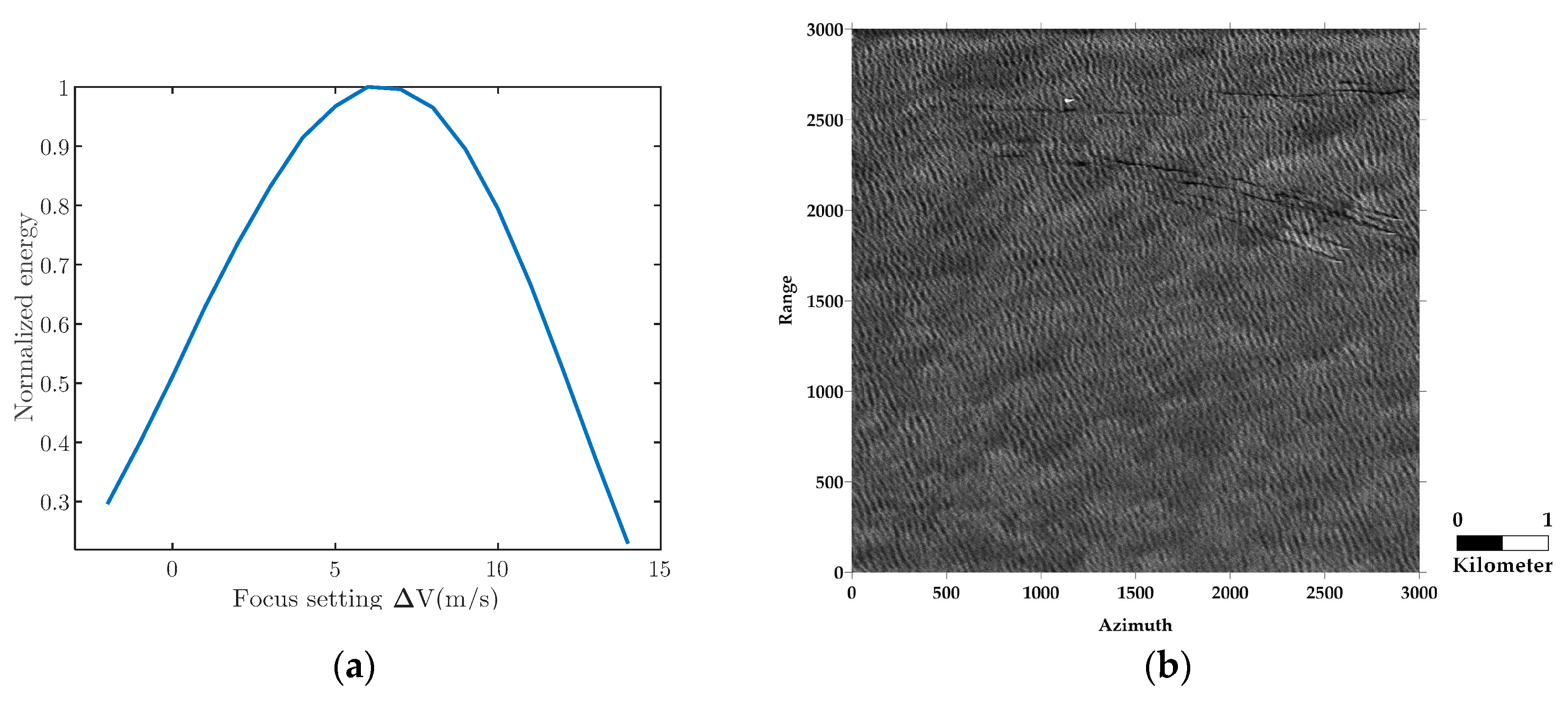
4.2.2. Quantitative Analysis of the Focus of Surface Waves
5. Discussion and Analysis
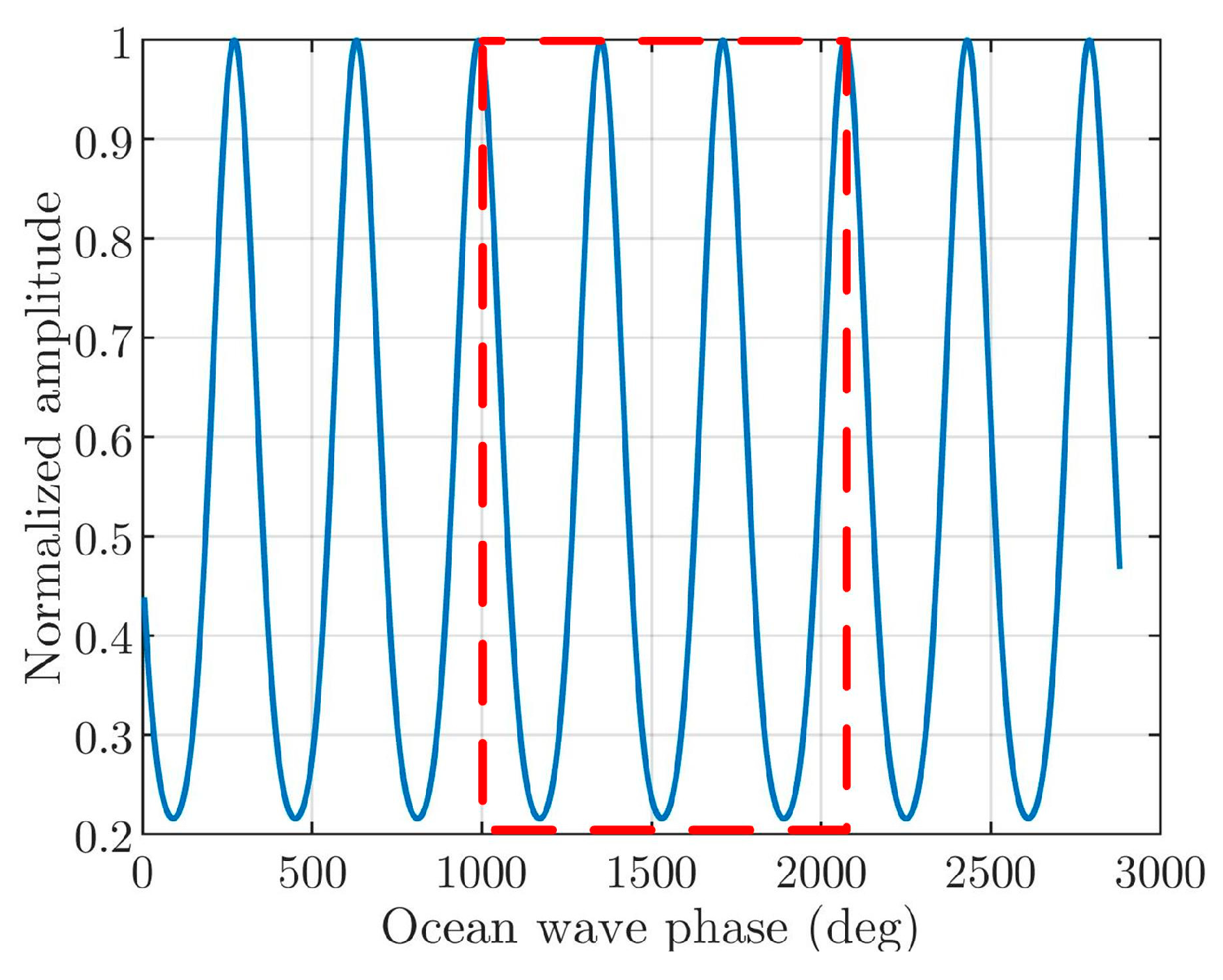
5.1. Analysis of the Selection of Focus Setting Variation Section
5.1.1. Analysis of the Selection of
5.1.2. Analysis of the Selection of
5.2. Analysis of the Applicability of the Proposed Algorithm
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tomiyasu, K. Tutorial review of synthetic-aperture radar (SAR) with applications to imaging of the ocean surface. Proc. IEEE 1978, 66, 563–583. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Raney, R.K. Synthetic Aperture Imaging Radar and Moving Targets. IEEE Trans. Aerosp. Electron. Syst. 1971, AES-7, 499–505. [Google Scholar] [CrossRef]
- Hayt, D.W.; Alpers, W.; Burning, C.; Dewitt, R.; Henyey, F.; Kasilingam, D.P.; Keller, W.C.; Lyzenga, D.R.; Plant, W.J.; Schult, R.L. Focusing simulations of synthetic aperture radar ocean images. J. Geophys. Res. Oceans 1990, 95, 16245–16261. [Google Scholar] [CrossRef]
- Kasilingam, D.P.; Hayt, D.W.; Shemdin, O.H. Focusing of synthetic aperture radar ocean images with long integration times. J. Geophys. Res. 1991, 96, 16935–16942. [Google Scholar] [CrossRef]
- Alpers, W.; Rufenach, C. The effect of orbital motions on synthetic aperture radar imagery of ocean waves. IEEE Trans. Antennas Propag. 1979, 27, 685–690. [Google Scholar] [CrossRef]
- Raney, R. Wave orbital velocity, fade, and SAR response to azimuth waves. IEEE J. Ocean. Eng. 1981, 6, 140–146. [Google Scholar] [CrossRef]
- Stopa, J.E.; Ardhuin, F.; Chapron, B.; Collard, F. Estimating wave orbital velocity through the azimuth cutoff from space-borne satellites. J. Geophys. Res. Oceans 2015, 120, 7616–7634. [Google Scholar] [CrossRef]
- Grieco, G.; Lin, W.; Migliaccio, M.; Nirchio, F.; Portabella, M. Dependency of the Sentinel-1 azimuth wavelength cut-off on significant wave height and wind speed. Int. J. Remote Sens. 2016, 37, 5086–5104. [Google Scholar] [CrossRef]
- Stopa, J.E.; Mouche, A. Significant wave heights from Sentinel-1 SAR: Validation and applications. J. Geophys. Res. Oceans 2017, 122, 1827–1848. [Google Scholar] [CrossRef]
- Ouchi, K. Recent Trend and Advance of Synthetic Aperture Radar with Selected Topics. Remote Sens. 2013, 5, 716–807. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.; Vachon, P.W.; Wolfe, J. Wind direction estimation from SAR images of the ocean using wavelet analysis. Can. J. Remote Sens. 2002, 28, 498–509. [Google Scholar] [CrossRef]
- Horstmann, J.; Koch, W. Measurement of Ocean Surface Winds Using Synthetic Aperture Radars. IEEE J. Ocean. Eng. 2006, 30, 508–515. [Google Scholar] [CrossRef]
- Schulz-Stellenfleth, J. Ocean Wave Measurements Using Complex Synthetic Aperture Radar Data; American Society of Civil Engineers: Reston, VA, USA, 2004. [Google Scholar]
- Kanevsky, M.B. Radar Imaging of the Ocean Waves; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Lyzenga, D.R. Numerical Simulation of Synthetic Aperture Radar Image Spectra for Ocean Waves. IEEE Trans. Geosci. Remote Sens. 1986, GE-24, 863–872. [Google Scholar] [CrossRef]
- Lyzenga, D.R. An analytic representation of the synthetic aperture radar image spectrum for ocean waves. J. Geophys. Res. Oceans 1988, 93, 13859–13865. [Google Scholar] [CrossRef]
- Kasilingam, D.P.; Shemdin, O.H. Theory for synthetic aperture radar imaging of the ocean surface: With application to the Tower Ocean Wave and Radar Dependence Experiment on focus, resolution, and wave height spectra. J. Geophys. Res. 1988, 93, 13837. [Google Scholar] [CrossRef]
- Raney, R.K.; Vachon, P.W. Synthetic aperture radar imaging of ocean waves from an airborne platform: Focus and tracking issues. J. Geophys. Res. Oceans 1988, 93, 12475–12486. [Google Scholar] [CrossRef]
- Vachon, P.W.; Raney, R.K.; Emergy, W.J. A simulation for spaceborne SAR imagery of a distributed, moving scene. IEEE Trans. Geosci. Remote Sens. 1989, 27, 67–78. [Google Scholar] [CrossRef]
- Shuchman, R.; Shemdin, O. Synthetic aperture radar imaging of ocean waves during the marineland experiment. IEEE J. Ocean. Eng. 1983, 8, 83–90. [Google Scholar] [CrossRef]
- Shemer, L. On the focusing of the ocean swell images produced by a regular and by an interferometric SAR. Int. J. Remote Sens. 1995, 16, 925–947. [Google Scholar] [CrossRef]
- Ouchi, K.; Burridge, D.A. Resolution of a controversy surrounding the focusing mechanisms of synthetic aperture radar images of ocean waves. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1004–1016. [Google Scholar] [CrossRef]
- Wei, X.; Wang, X.; Chong, J. Local region power spectrum-based unfocused ship detection method in synthetic aperture radar images. J. Appl. Remote Sens. 2018, 12, 016026. [Google Scholar] [CrossRef]
- Burridge, D.A.; Smith, R.W. Highly space-variant imaging system: Optical simulation of the synthetic-aperture radar. J. Opt. Soc. Am. A 1991, 8, 1195–1206. [Google Scholar] [CrossRef]
- Tajirian, E.K. Multifocus processing of L band synthetic aperture radar images of ocean waves obtained during the Tower Ocean Wave and Radar Dependence Experiment. J. Geophys. Res. Oceans 1988, 93, 13849–13857. [Google Scholar] [CrossRef]
- Vachon, P.; Krogstad, H.; Scottpaterson, J. Airborne and spaceborne synthetic aperture radar observations of ocean waves. Atmosphere 1994, 32, 83–112. [Google Scholar] [CrossRef] [Green Version]
- Hwang, P.A.; Toporkov, J.V.; Sletten, M.A.; Menk, S.P. Mapping Surface Currents and Waves with Interferometric Synthetic Aperture Radar in Coastal Waters: Observations of Wave Breaking in Swell-Dominant Conditions. J. Phys. Oceanogr. 2012, 43, 563–582. [Google Scholar] [CrossRef]
- Shemer, L. Interferometric SAR imagery of a monochromatic ocean wave in the presence of the real aperture radar modulation. Int. J. Remote Sens. 1993, 14, 3005–3019. [Google Scholar] [CrossRef]
- Shemer, L.; Kit, E. Simulation of an interferometric synthetic aperture radar imagery of an ocean system consisting of a current and a monochromatic wave. J. Geophys. Res. Oceans 1991, 96, 22063–22073. [Google Scholar] [CrossRef]
- Raney, R.K. SAR processing of partially coherent phenomena. Int. J. Remote Sens. 1980, 1, 29–51. [Google Scholar] [CrossRef]
- Hasselmann, K.; Hasselmann, S. On the nonlinear mapping of an ocean wave spectrum into a synthetic aperture radar image spectrum and its inversion. J. Geophys. Res. Oceans 1991, 96, 10713–10729. [Google Scholar] [CrossRef]
- Alpers, W.R.; Bruening, C. On the relative importance of motion-related contributions to the SAR imaging mechanism of ocean surface waves. IEEE Trans. Geosci. Remote Sens. 1986, GE-24, 873–885. [Google Scholar] [CrossRef]
- Shemer, L. An analytical presentation of the monochromatic ocean wave image by a regular or an interferometric synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1008–1013. [Google Scholar] [CrossRef]
- Jain, A.; Shemdin, O. L band SAR ocean wave observations during MARSEN. J. Geophys. Res. Oceans 1983, 88, 9792–9808. [Google Scholar] [CrossRef]












| Parametric Name | Parametric Symbol | Parametric Value |
|---|---|---|
| Radar Wavelength (m) | 0.25 | |
| Platform Speed (m/s) | 130 | |
| Slant Range (m) | 10,000 | |
| Integration Times (s) | 4 | |
| Coherence Time (s) | 0.14 | |
| Incidence Angle (deg) | 45 | |
| Wavelength of the wave (m) | 80 | |
| Amplitude of the wave (m) | 1.6 | |
| Propagation direction of the wave (deg) | 0, 30, 60 |
| Parametric Name | Parametric Symbol | Parametric Value |
|---|---|---|
| Radar wavelength(m) | 0.25 | |
| Pulse length(um) | 5.4 | |
| Radar bandwidth (MHz) | 125 | |
| Platform speed (m/s) | 130 | |
| Platform height (m) | 8100 | |
| Squint angle (deg) | 0 | |
| PRF(Hz) | 900 | |
| Antenna length (m) | 4 | |
| Polarization mode | / | VV |
| Data 1 | Data 2 | Data 3 | |
|---|---|---|---|
| Date | September 13 | September 14 | September 18 |
| Wind speed (m/s) | 10 | 11 | 8 |
| Wind direction (deg) | 5 | 25 | 65 |
| Significant wave height (m) | 1.5 | 1.3 | 1.2 |
| Mean wave period (s) | 7.2 | 7.9 | 7.3 |
| Peak wave period (s) | 8 | 8.6 | 8.1 |
| Mean wave direction (deg) | 5 | 25 | 65 |
| Focus Setting | ||||
|---|---|---|---|---|
| SD | sub-block data 1 | 40.09 | 42.45 | 42.49 |
| sub-block data 2 | 33.89 | 36.67 | 37.73 | |
| sub-block data 3 | 41.76 | 43.53 | 45.79 | |
| PBR | sub-block data 1 | 6.03 | 11.06 | 11.61 |
| sub-block data 2 | 17.22 | 25.37 | 30.23 | |
| sub-block data 3 | 24.74 | 33.78 | 43.56 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Chong, J.; Zhao, Y.; Li, Y.; Yao, X. Airborne SAR Imaging Algorithm for Ocean Waves Based on Optimum Focus Setting. Remote Sens. 2019, 11, 564. https://doi.org/10.3390/rs11050564
Wei X, Chong J, Zhao Y, Li Y, Yao X. Airborne SAR Imaging Algorithm for Ocean Waves Based on Optimum Focus Setting. Remote Sensing. 2019; 11(5):564. https://doi.org/10.3390/rs11050564
Chicago/Turabian StyleWei, Xiangfei, Jinsong Chong, Yawei Zhao, Yan Li, and Xiaonan Yao. 2019. "Airborne SAR Imaging Algorithm for Ocean Waves Based on Optimum Focus Setting" Remote Sensing 11, no. 5: 564. https://doi.org/10.3390/rs11050564
APA StyleWei, X., Chong, J., Zhao, Y., Li, Y., & Yao, X. (2019). Airborne SAR Imaging Algorithm for Ocean Waves Based on Optimum Focus Setting. Remote Sensing, 11(5), 564. https://doi.org/10.3390/rs11050564