A Concave Hull Methodology for Calculating the Crown Volume of Individual Trees Based on Vehicle-Borne LiDAR Data
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Field Data Collection
3.2. Calculating Crown Volume Using VLS Data
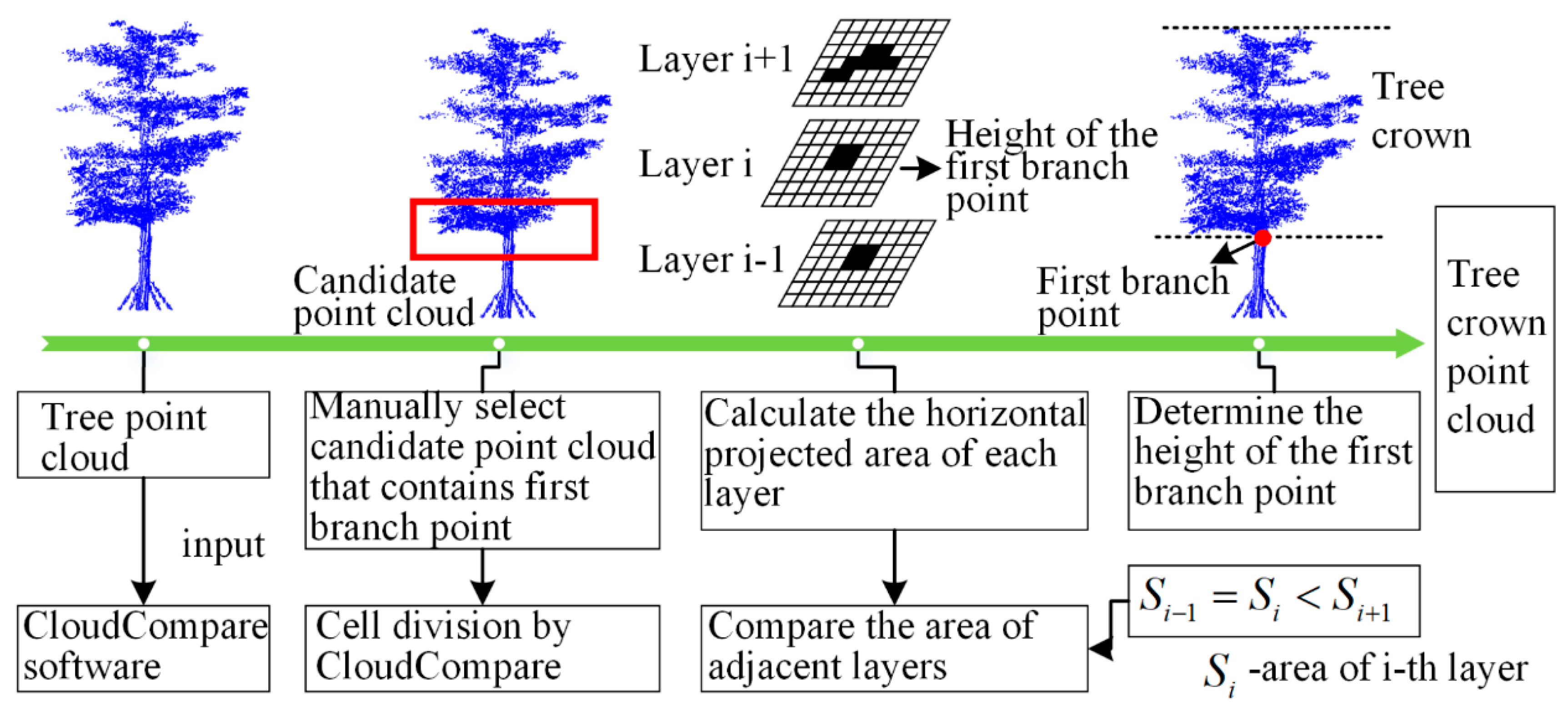
3.2.1. Tree Crown Extraction
3.2.2. Slice Area Calculation Using Concave Hull Algorithm
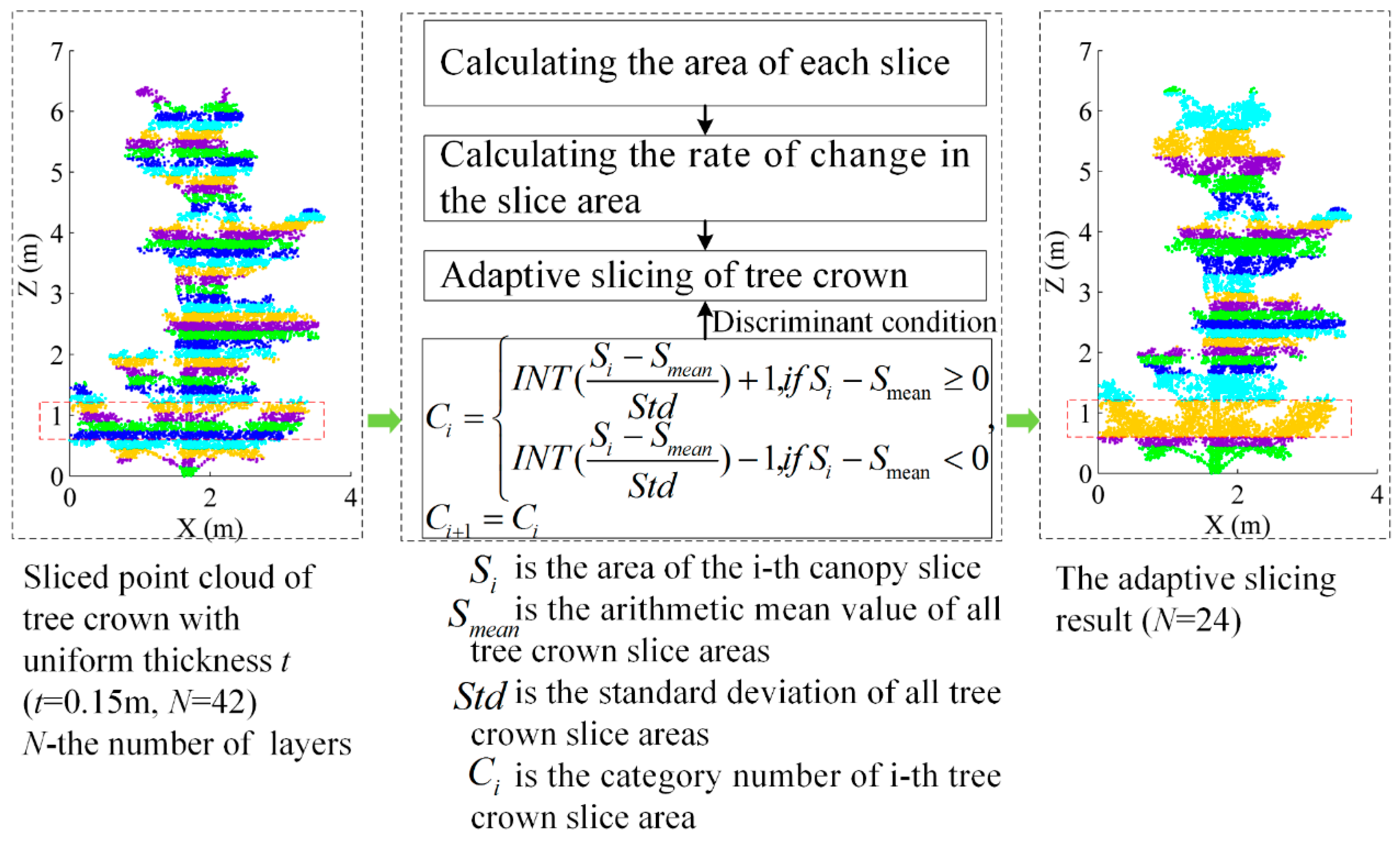
3.2.3. Adaptive Slicing of Tree Crown
3.2.4. Tree Crown Volume Calculation
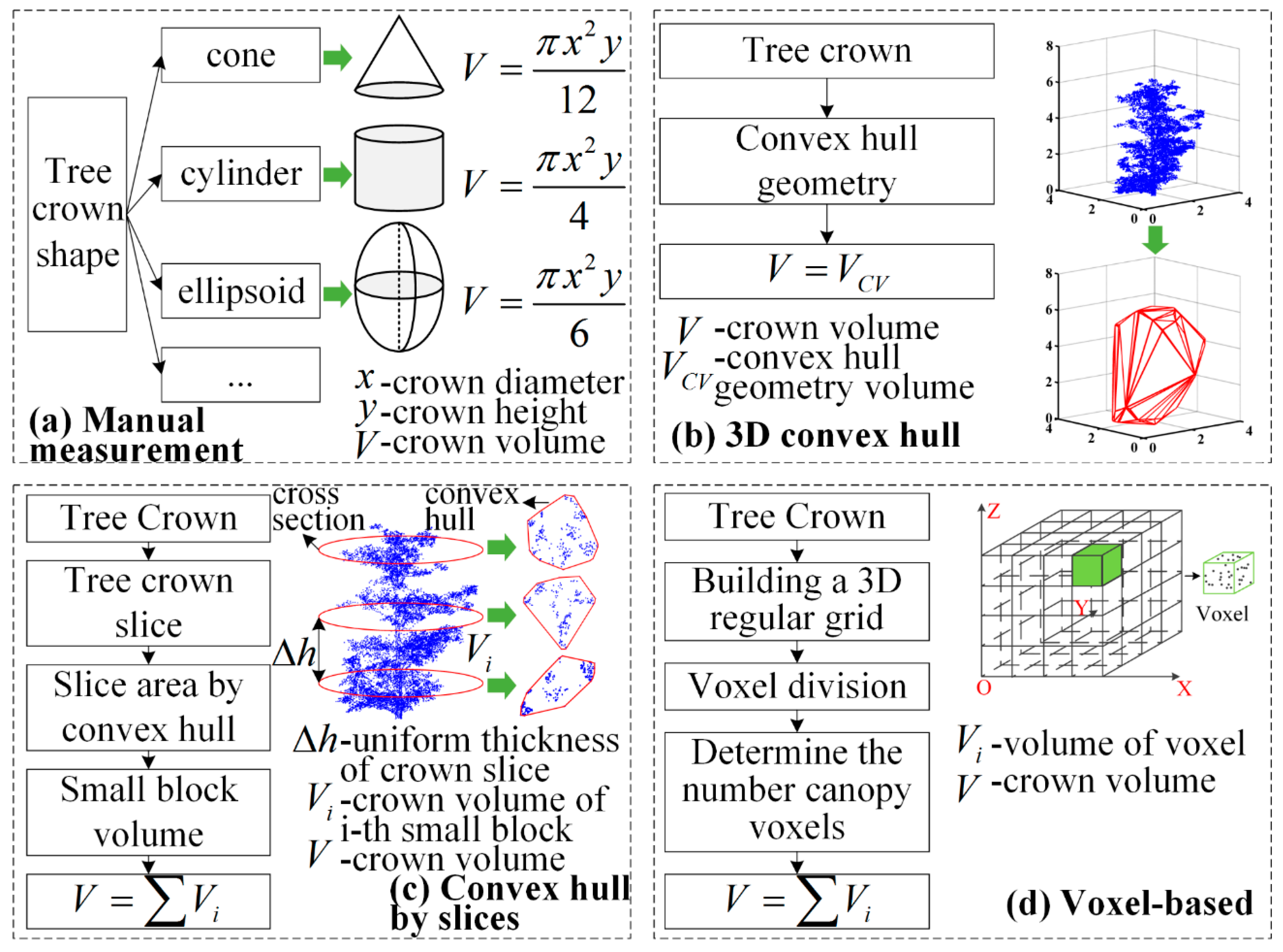
3.3. Comparison of Five Crown Volume Calculation Methods
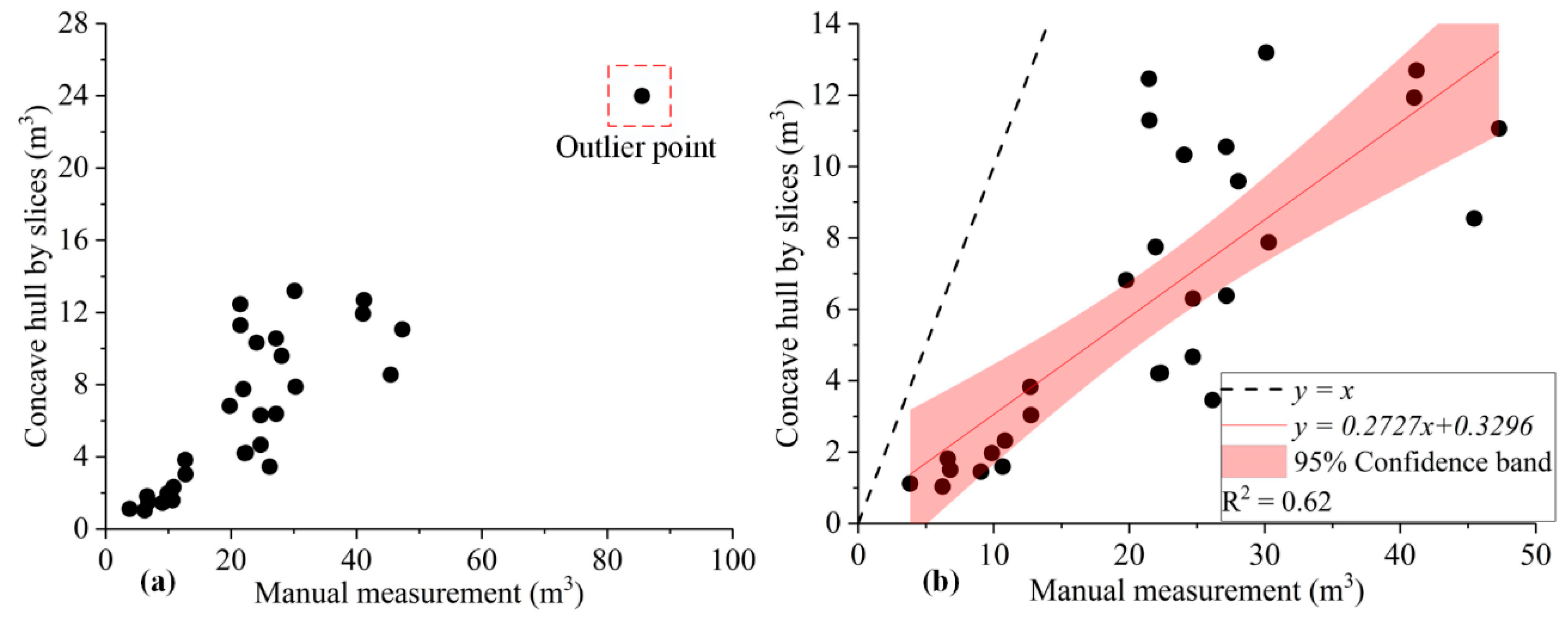
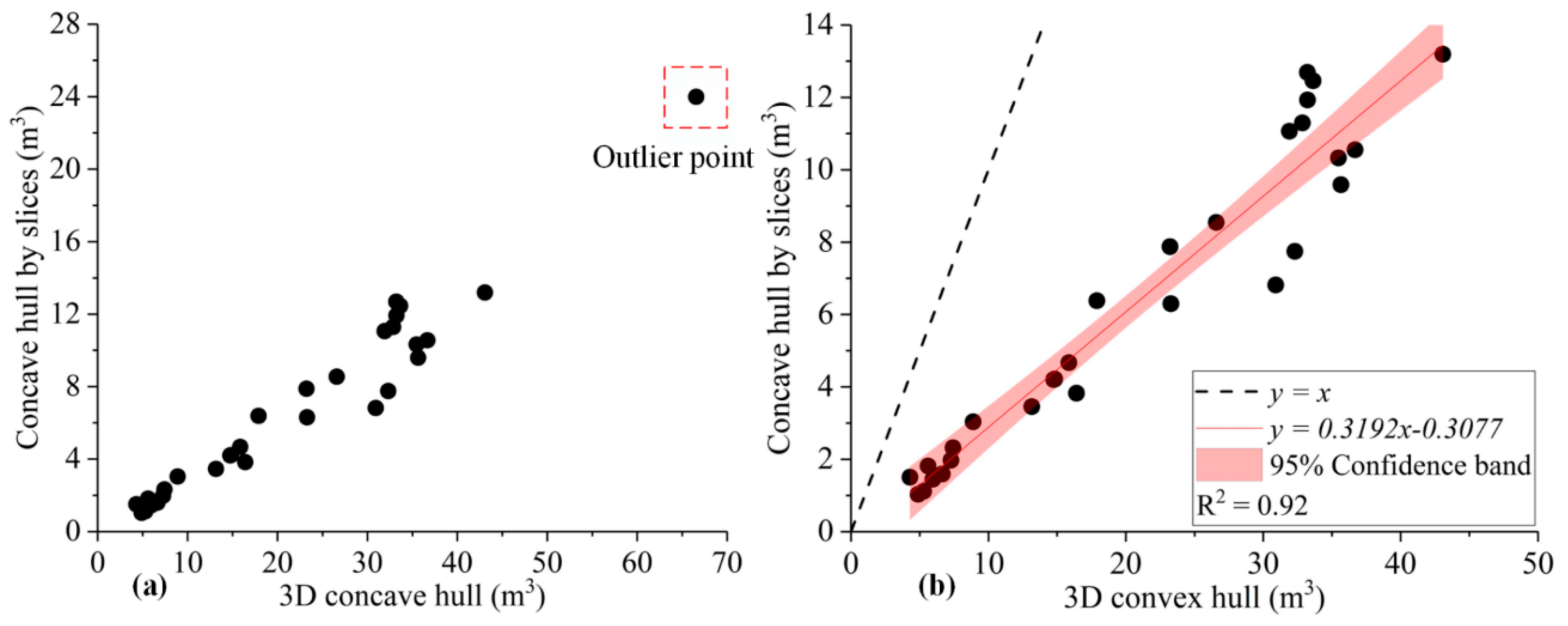
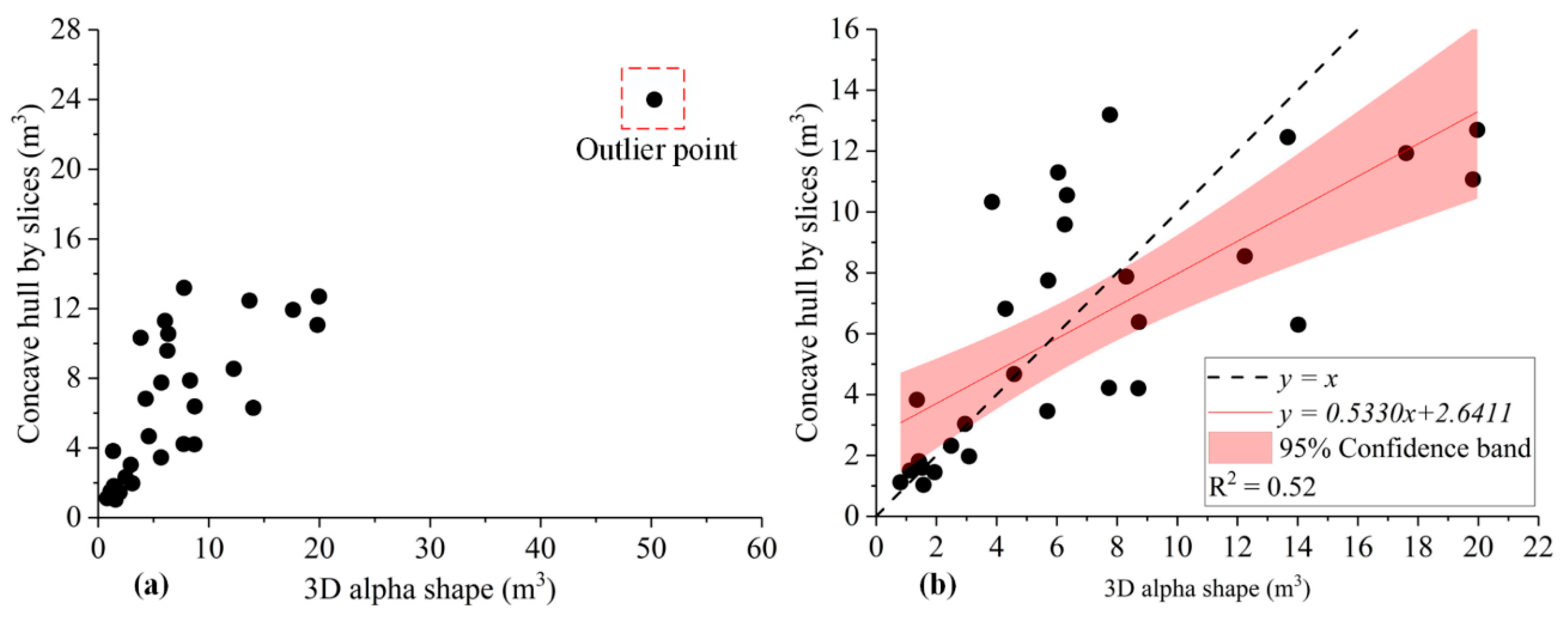
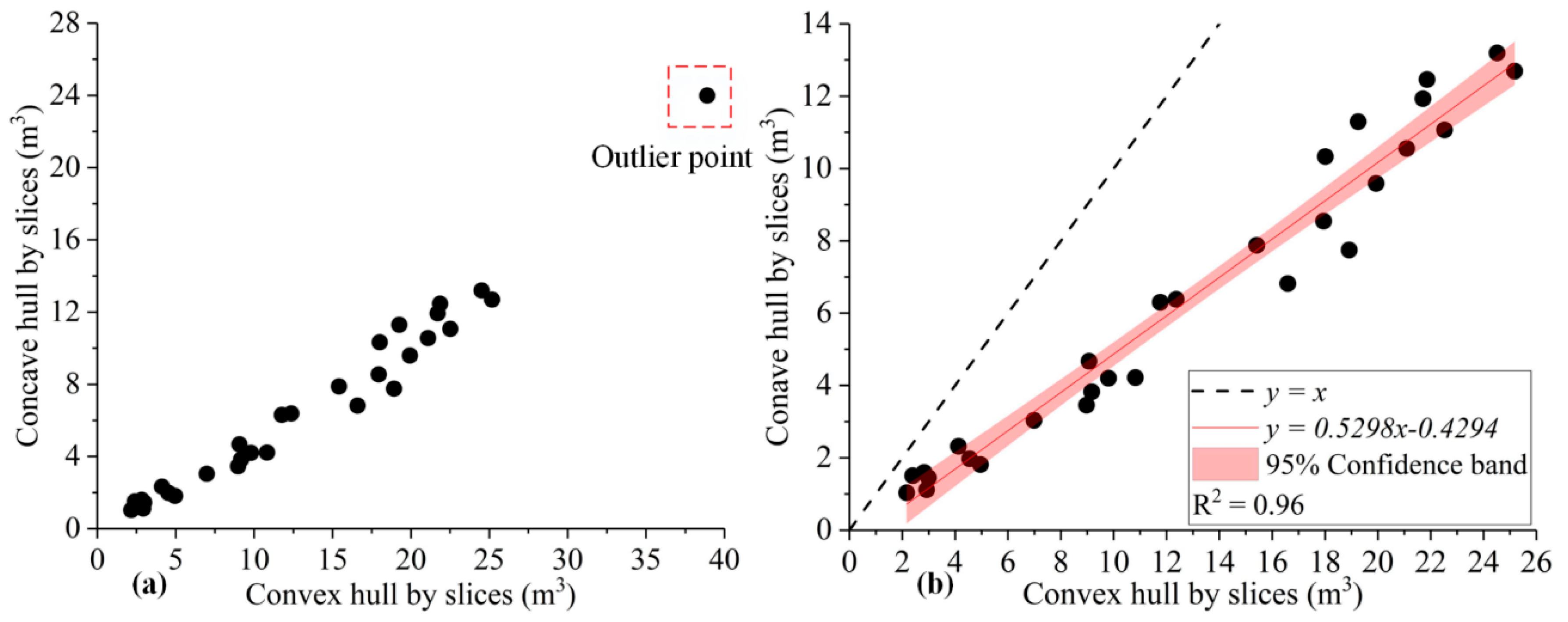
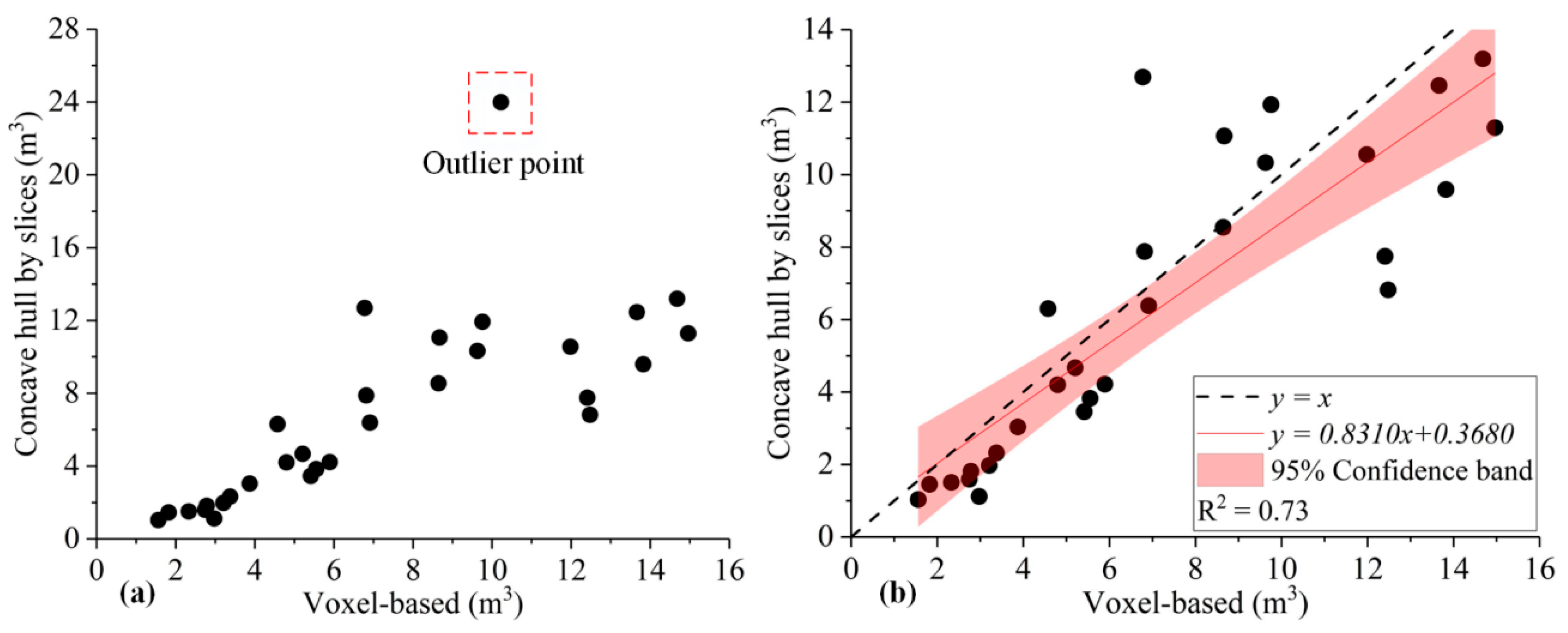
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bao, Y.; Tian, Q.; Chen, M.; Lin, H. An automatic extraction method for individual tree crowns based on self-adaptive mutual information and tile computing. Int. J. Digit. Earth 2014, 8, 495–516. [Google Scholar] [CrossRef]
- Newbold, T.; Hudson, L.N.; Hill, S.L.; Contu, S.; Lysenko, I.; Senior, R.A.; Borger, L.; Bennett, D.J.; Choimes, A.; Collen, B.; et al. Global effects of land use on local terrestrial biodiversity. Nature 2015, 520, 45–50. [Google Scholar] [CrossRef] [Green Version]
- Fang, F.; Im, J.; Lee, J.; Kim, K. An improved tree crown delineation method based on live crown ratios from airborne LiDAR data. GISci. Remote Sens. 2016, 53, 402–419. [Google Scholar] [CrossRef]
- Alexander, C.; Korstjens, A.H.; Hill, R.A. Influence of micro-topography and crown characteristics on tree height estimations in tropical forests based on LiDAR canopy height models. Int. J. Appl. Earth Obs. Geoinf. 2018, 65, 105–113. [Google Scholar] [CrossRef]
- Dalponte, M.; Frizzera, L.; Ørka, H.O.; Gobakken, T.; Næsset, E.; Gianelle, D. Predicting stem diameters and aboveground biomass of individual trees using remote sensing data. Ecol. Indic. 2018, 85, 367–376. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Wu, Q.; Huang, Y.; Chen, Z.; Wu, J. Individual tree crown delineation using localized contour tree method and airborne LiDAR data in coniferous forests. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 82–94. [Google Scholar] [CrossRef]
- Xu, W.H.; Feng, Z.K.; Su, Z.F.; Xu, H.; Jiao, Y.Q.; Deng, O. An automatic extraction algorithm for individual tree crown projection area and volume based on 3D point cloud data. Spectrosc. Spectr. Anal. 2014, 34, 465–471. [Google Scholar]
- Phattaralerphong, J.; Sinoquet, H. A method for 3D reconstruction of tree crown volume from photographs: Assessment with 3D-digitized plants. Tree Physiol. 2005, 25, 1229–1242. [Google Scholar] [CrossRef]
- Fernández-Sarría, A.; Martínez, L.; Velázquez-Martí, B.; Sajdak, M.; Estornell, J.; Recio, J.A. Different methodologies for calculating crown volumes of Platanus hispanica trees using terrestrial laser scanner and a comparison with classical dendrometric measurements. Comput. Electron. Agric. 2013, 90, 176–185. [Google Scholar] [CrossRef] [Green Version]
- Korhonen, L.; Vauhkonen, J.; Virolainen, A.; Hovi, A.; Korpela, I. Estimation of tree crown volume from airborne lidar data using computational geometry. Int. J. Remote Sens. 2013, 34, 7236–7248. [Google Scholar] [CrossRef]
- Lin, W.; Meng, Y.; Qiu, Z.; Zhang, S.; Wu, J. Measurement and calculation of crown projection area and crown volume of individual trees based on 3D laser-scanned point-cloud data. Int. J. Remote Sens. 2017, 38, 1083–1100. [Google Scholar] [CrossRef]
- Lin, Y.; Jaakkola, A.; Hyyppä, J.; Kaartinen, H. From TLS to VLS: Biomass Estimation at Individual Tree Level. Remote Sens. 2010, 2, 1864–1879. [Google Scholar] [CrossRef] [Green Version]
- Rautiainen, M.; Mõttus, M.; Stenberg, P.; Ervasti, S. Crown Envelope Shape Measurements and Models. Silva Fenn. 2008, 42, 19–33. [Google Scholar] [CrossRef]
- Paris, C.; Kelbe, D.; Aardt, J.V.; Bruzzone, L. A Novel Automatic Method for the Fusion of ALS and TLS LiDAR Data for Robust Assessment of Tree Crown Structure. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1–15. [Google Scholar] [CrossRef]
- Jing, L.; Hu, B.; Noland, T.; Li, J. An individual tree crown delineation method based on multi-scale segmentation of imagery. ISPRS J. Photogramm. Remote Sens. 2012, 70, 88–98. [Google Scholar] [CrossRef]
- Yin, W.; Yang, J.; Yamamoto, H.; Li, C. Object-based larch tree-crown delineation using high-resolution satellite imagery. Int. J. Remote Sens. 2015, 36, 822–844. [Google Scholar] [CrossRef]
- Varekamp, C.; Hoekman, D.H. High-resolution InSAR image simulation for forest canopies. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1648–1655. [Google Scholar] [CrossRef]
- Dalponte, M.; Ene, L.T.; Marconcini, M.; Gobakken, T.; Næsset, E. Semi-supervised SVM for individual tree crown species classification. ISPRS J. Photogramm. Remote Sens. 2015, 110, 77–87. [Google Scholar] [CrossRef]
- Liu, T.; Im, J.; Quackenbush, L.J. A novel transferable individual tree crown delineation model based on Fishing Net Dragging and boundary classification. ISPRS J. Photogramm. Remote Sens. 2015, 110, 34–47. [Google Scholar] [CrossRef]
- Tochon, G.; Féret, J.B.; Valero, S.; Martin, R.E.; Knapp, D.E.; Salembier, P.; Chanussot, J.; Asner, G.P. On the use of binary partition trees for the tree crown segmentation of tropical rainforest hyperspectral images. Remote Sens. Environ. 2015, 159, 318–331. [Google Scholar] [CrossRef] [Green Version]
- Strîmbu, V.F.; Strîmbu, B.M. A graph-based segmentation algorithm for tree crown extraction using airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2015, 104, 30–43. [Google Scholar] [CrossRef] [Green Version]
- Leckie, D.G.; Walsworth, N.; Gougeon, F.A. Identifying tree crown delineation shapes and need for remediation on high resolution imagery using an evidence based approach. ISPRS J. Photogramm. Remote Sens. 2016, 114, 206–227. [Google Scholar] [CrossRef]
- Kukunda, C.B.; Duque-Lazo, J.; González-Ferreiro, E.; Thaden, H.; Kleinn, C. Ensemble classification of individual Pinus crowns from multispectral satellite imagery and airborne LiDAR. Int. J. Appl. Earth Obs. Geoinf. 2018, 65, 12–23. [Google Scholar] [CrossRef]
- Kato, A.; Moskal, L.M.; Schiess, P.; Swanson, M.E.; Calhoun, D.; Stuetzle, W. Capturing tree crown formation through implicit surface reconstruction using airborne lidar data. Remote Sens. Environ. 2009, 113, 1148–1162. [Google Scholar] [CrossRef]
- Lecigne, B.; Delagrange, S.; Messier, C. Exploring trees in three dimensions: VoxR, a novel voxel-based R package dedicated to analysing the complex arrangement of tree crowns. Ann. Bot. 2018, 121, 589–601. [Google Scholar] [CrossRef]
- Miranda-Fuentes, A.; Llorens, J.; Gamarra-Diezma, J.L.; Gil-Ribes, J.A.; Gil, E. Towards an optimized method of olive tree crown volume measurement. Sensors 2015, 15, 3671–3687. [Google Scholar] [CrossRef]
- Gong, Y.X.; Fei, Y.; Feng, Z.K.; Liu, Y.F.; Xue, W.X.; Fei, X.; University, B.F. Extraction of crown volume using triangulated irregular network algorithm based on LiDAR. J. Infrared Millim. Waves 2016, 35, 177–183. [Google Scholar]
- Cabo, C.; Ordoñez, C.; García-Cortés, S.; Martínez, J. An algorithm for automatic detection of pole-like street furniture objects from Mobile Laser Scanner point clouds. ISPRS J. Photogramm. Remote Sens. 2014, 87, 47–56. [Google Scholar] [CrossRef]
- Yang, B.; Dong, Z.; Liu, Y.; Liang, F.; Wang, Y. Computing multiple aggregation levels and contextual features for road facilities recognition using mobile laser scanning data. ISPRS J. Photogramm. Remote Sens. 2017, 126, 180–194. [Google Scholar] [CrossRef]
- Wang, J.; Lindenbergh, R.; Menenti, M. SigVox—A 3D feature matching algorithm for automatic street object recognition in mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 128, 111–129. [Google Scholar] [CrossRef]
- Li, L.; Li, D.; Zhu, H.; Li, Y. A dual growing method for the automatic extraction of individual trees from mobile laser scanning data. ISPRS J. Photogramm. Remote Sens. 2016, 120, 37–52. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, L.; Chen, Y.; Wu, Y.; Li, M. Building Point Detection from Vehicle-Borne LiDAR Data Based on Voxel Group and Horizontal Hollow Analysis. Remote Sens. 2016, 8, 419. [Google Scholar] [CrossRef]
- Kukko, A.; Kaartinen, H.; Hyyppä, J.; Chen, Y. Multiplatform Mobile Laser Scanning: Usability and Performance. Sensors 2012, 12, 11712–11733. [Google Scholar] [CrossRef] [Green Version]
- Haala, N.; Peter, M.; Kremer, J.; Hunter, G. Mobile LiDAR mapping for 3D point cloud collection in urban areas—A performance test. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2008, 37, 1119–1127. [Google Scholar]
- Wu, B.; Yu, B.; Yue, W.; Shu, S.; Tan, W.; Hu, C.; Huang, Y.; Wu, J.; Liu, H. A Voxel-Based Method for Automated Identification and Morphological Parameters Estimation of Individual Street Trees from Mobile Laser Scanning Data. Remote Sens. 2013, 5, 584–611. [Google Scholar] [CrossRef] [Green Version]
- Schumann, A.W. Performance of an Ultrasonic Tree Volume Measurement System in Commercial Citrus Groves. Precis. Agric. 2005, 6, 467–480. [Google Scholar]
- Gupta, S.; Weinacker, H.; Koch, B. Comparative Analysis of Clustering-Based Approaches for 3-D Single Tree Detection Using Airborne Fullwave Lidar Data. Remote Sens. 2010, 2, 968–989. [Google Scholar] [CrossRef] [Green Version]
- Olsoy, P.J.; Glenn, N.F.; Clark, P.E.; Derryberry, D.R. Aboveground total and green biomass of dryland shrub derived from terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2014, 88, 166–173. [Google Scholar] [CrossRef] [Green Version]
- Vauhkonen, J.; Tokola, T.; Packalén, P.; Maltamo, M. Identification of Scandinavian commercial species of individual trees from airborne laser scanning data using alpha shape metrics. For. Sci. 2009, 55, 37–47. [Google Scholar]
- Vauhkonen, J.; Korpela, I.; Maltamo, M.; Tokola, T. Imputation of single-tree attributes using airborne laser scanning-based height, intensity, and alpha shape metrics. Remote Sens. Environ. 2010, 114, 1263–1276. [Google Scholar] [CrossRef]
- Yao, W.; Krzystek, P.; Heurich, M. Tree species classification and estimation of stem volume and DBH based on single tree extraction by exploiting airborne full-waveform LiDAR data. Remote Sens. Environ. 2012, 123, 368–380. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Seppänen, A.; Packalén, P.; Tokola, T. Improving species-specific plot volume estimates based on airborne laser scanning and image data using alpha shape metrics and balanced field data. Remote Sens. Environ. 2012, 124, 534–541. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.; Zhang, L. Trends in Automatic Individual Tree Crown Detection and Delineation—Evolution of LiDAR Data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Tokola, T.; Maltamo, M.; Packalén, P. Effects of pulse density on predicting characteristics of individual trees of Scandinavian commercial species using alpha shape metrics based on airborne laser scanning data. Can. J. Remote Sens. 2014, 34, S441–S459. [Google Scholar] [CrossRef]
- Popescu, S.C.; Zhao, K. A voxel-based lidar method for estimating crown base height for deciduous and pine trees. Remote Sens. Environ. 2008, 112, 767–781. [Google Scholar] [CrossRef]
- Hosoi, F.; Omasa, K. Voxel-Based 3-D Modeling of Individual Trees for Estimating Leaf Area Density Using High-Resolution Portable Scanning Lidar. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3610–3618. [Google Scholar] [CrossRef]
- Hyyppa, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners. IEEE Trans. Geosci. Remote Sens. 2001, 39, 969–975. [Google Scholar] [CrossRef]
- Moreira, A.J.C.; Santos, M.Y. Concave hull: A k-nearest neighbours approach for the computation of the region occupied by a set of points. In Proceedings of the Second International Conference on Computer Graphics Theory and Applications (GRAPP 2007), Barcelona, Spain, 8–11 March 2007; Volume GM/R, pp. 61–68. [Google Scholar]
- Zhong, L.; Cheng, L.; Xu, H.; Wu, Y.; Chen, Y.; Li, M. Segmentation of Individual Trees from TLS and MLS Data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 774–787. [Google Scholar] [CrossRef]
- Pourkhabbaz, A.; Rastin, N.; Olbrich, A.; Langenfeld-Heyser, R.; Polle, A. Influence of environmental pollution on leaf properties of urban plane trees, Platanus orientalis L. Bull. Environ. Contam. Toxicol. 2010, 85, 251–255. [Google Scholar] [CrossRef]
- Guan, R.; Zhao, Y.; Zhang, H.; Fan, G.; Liu, X.; Zhou, W.; Shi, C.; Wang, J.; Liu, W.; Liang, X.; et al. Draft genome of the living fossil Ginkgo biloba. GigaScience 2016, 5, 49. [Google Scholar] [CrossRef]
- Yin, S.; Shen, Z.; Zhou, P.; Zou, X.; Che, S.; Wang, W. Quantifying air pollution attenuation within urban parks: An experimental approach in Shanghai, China. Environ. Pollut. 2011, 159, 2155–2163. [Google Scholar] [CrossRef]
- CloudCompare. CloudCompare (Version 2.8). 2017. Available online: http://www.cloudcompare.org/ (accessed on 12 May 2018).
- Dewez, T.J.B.; Girardeau-Montaut, D.; Allanic, C.; Rohmer, J. Facets: A Cloudcompare Plugin to Extract Geological Planes from Unstructured 3d Point Clouds. ISPRS Arch. 2016, XLI-B5, 799–804. [Google Scholar]
- Stovall, A.E.L.; Vorster, A.G.; Anderson, R.S.; Evangelista, P.H.; Shugart, H.H. Non-destructive aboveground biomass estimation of coniferous trees using terrestrial LiDAR. Remote Sens. Environ. 2017, 200, 31–42. [Google Scholar] [CrossRef]
- Park, J.S.; Oh, S.J. A New Concave Hull Algorithm and Concaveness Measure for n-dimensional Datasets. J. Inf. Sci. Eng. 2013, 29, 587–600. [Google Scholar]
- Asaeedi, S.; Didehvar, F.; Mohades, A. α-Concave hull, a generalization of convex hull. Theor. Comput. Sci. 2017, 702, 48–59. [Google Scholar] [CrossRef]
- Cheng, L.; Wu, Y.; Chen, S.; Zong, W.; Yuan, Y.; Sun, Y.; Zhuang, Q.; Li, M. A symmetry-based method for Lidar point registration. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 285–299. [Google Scholar] [CrossRef]
- Hosoi, F.; Nakai, Y.; Omasa, K. 3-D voxel-based solid modeling of a broad-leaved tree for accurate volume estimation using portable scanning lidar. ISPRS J. Photogramm. Remote Sens. 2013, 82, 41–48. [Google Scholar] [CrossRef]





| Indicator | Value |
|---|---|
| Scanning distance | ≤130 m |
| Angle of field of view | Vertical angle 305° |
| Horizontal angle 360° | |
| Accuracy of measurement | ±2 mm accuracy of measurement at a scanning distance of 25 m |
| Angle resolution | Vertical resolution 0.009° |
| Horizontal resolution 0.009° | |
| Line frequency | 97 Hz |
| Scanning rate | 976,000 points/s |
| Tree Number | Tree Species | CD (m) | CH (m) | Crown Volume (m3) | |||||
|---|---|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | M6 | ||||
| 1 | G. biloba | 2.13 | 3.23 | 3.84 | 5.29 | 0.81 | 2.92 | 2.98 | 1.12 |
| 2 | G. biloba | 4.16 | 6.18 | 28.05 | 35.65 | 6.26 | 19.93 | 13.82 | 9.59 |
| 3 | G. biloba | 3.87 | 5.60 | 21.95 | 32.31 | 5.71 | 18.92 | 12.41 | 7.75 |
| 4 | G. biloba | 3.82 | 5.61 | 21.48 | 32.85 | 6.04 | 19.25 | 14.96 | 11.30 |
| 5 | G. biloba | 3.43 | 6.41 | 19.77 | 30.92 | 4.29 | 16.59 | 12.48 | 6.82 |
| 6 | G. biloba | 3.02 | 5.32 | 12.69 | 16.41 | 1.35 | 9.17 | 5.55 | 3.83 |
| 7 | G. biloba | 4.21 | 6.48 | 30.11 | 43.07 | 7.76 | 24.51 | 14.68 | 13.19 |
| 8 | G. biloba | 3.61 | 6.29 | 21.46 | 33.63 | 13.67 | 21.86 | 13.66 | 12.46 |
| 9 | G. biloba | 4.10 | 5.46 | 24.06 | 35.47 | 3.85 | 18.01 | 9.63 | 10.33 |
| 10 | G. biloba | 3.82 | 7.12 | 27.16 | 36.69 | 6.33 | 21.09 | 11.98 | 10.55 |
| 11 | P. orientalis | 2.11 | 2.85 | 6.61 | 5.61 | 1.42 | 4.96 | 2.78 | 1.81 |
| 12 | P. orientalis | 3.49 | 4.27 | 27.18 | 17.89 | 8.73 | 12.36 | 6.91 | 6.38 |
| 13 | P. orientalis | 2.38 | 3.64 | 10.83 | 7.43 | 2.49 | 4.13 | 3.38 | 2.32 |
| 14 | P. orientalis | 3.20 | 4.17 | 22.35 | 14.83 | 7.73 | 10.82 | 5.90 | 4.22 |
| 15 | P. orientalis | 4.34 | 4.17 | 41.19 | 33.21 | 19.96 | 25.18 | 6.78 | 12.69 |
| 16 | P. orientalis | 3.94 | 5.59 | 45.46 | 26.58 | 12.24 | 17.95 | 8.65 | 8.54 |
| 17 | P. orientalis | 2.40 | 2.99 | 9.05 | 5.97 | 1.94 | 2.99 | 1.82 | 1.45 |
| 18 | P. orientalis | 3.40 | 3.67 | 22.16 | 14.75 | 8.70 | 9.80 | 4.80 | 4.20 |
| 19 | P. orientalis | 3.37 | 4.39 | 26.15 | 13.16 | 5.68 | 8.98 | 5.42 | 3.46 |
| 20 | P. orientalis | 2.60 | 3.60 | 12.74 | 8.90 | 2.95 | 6.99 | 3.87 | 3.03 |
| 21 | P. orientalis | 1.89 | 3.34 | 6.22 | 4.89 | 1.57 | 2.17 | 1.56 | 1.03 |
| 22 | P. orientalis | 2.84 | 5.85 | 24.71 | 23.28 | 14.02 | 11.76 | 4.58 | 6.30 |
| 23 | P. orientalis | 2.23 | 3.78 | 9.87 | 7.27 | 3.08 | 4.55 | 3.21 | 1.97 |
| 24 | P. orientalis | 2.31 | 3.82 | 10.66 | 6.65 | 1.53 | 2.83 | 2.74 | 1.59 |
| 25 | P. orientalis | 3.22 | 4.55 | 24.69 | 15.86 | 4.58 | 9.07 | 5.21 | 4.67 |
| 26 | P. orientalis | 4.08 | 5.42 | 47.29 | 31.91 | 19.82 | 22.52 | 8.67 | 11.07 |
| 27 | P. orientalis | 1.94 | 3.45 | 6.79 | 4.30 | 1.12 | 2.40 | 2.33 | 1.50 |
| 28 | P. orientalis | 3.80 | 5.42 | 41.03 | 33.23 | 17.60 | 21.71 | 9.76 | 11.93 |
| 29 | P. orientalis | 3.59 | 4.48 | 30.29 | 23.22 | 8.31 | 15.42 | 6.82 | 7.87 |
| 30 | P. orientalis | 4.96 | 6.64 | 85.54 | 66.58 | 50.28 | 38.90 | 10.22 | 23.99 |
| Max (m3) | 85.54 | 66.58 | 50.28 | 38.90 | 14.96 | 23.99 | |||
| Min (m3) | 3.84 | 4.30 | 0.81 | 2.17 | 1.56 | 1.03 | |||
| Mean (m3) | 24.05 | 22.26 | 8.33 | 13.59 | 7.25 | 6.90 | |||
| Stand. Dev. (m3) | 16.21 | 14.54 | 9.48 | 8.74 | 4.14 | 5.09 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Z.; Liu, R.; Cheng, L.; Zhou, X.; Ruan, X.; Xiao, Y. A Concave Hull Methodology for Calculating the Crown Volume of Individual Trees Based on Vehicle-Borne LiDAR Data. Remote Sens. 2019, 11, 623. https://doi.org/10.3390/rs11060623
Yan Z, Liu R, Cheng L, Zhou X, Ruan X, Xiao Y. A Concave Hull Methodology for Calculating the Crown Volume of Individual Trees Based on Vehicle-Borne LiDAR Data. Remote Sensing. 2019; 11(6):623. https://doi.org/10.3390/rs11060623
Chicago/Turabian StyleYan, Zhaojin, Rufei Liu, Liang Cheng, Xiao Zhou, Xiaoguang Ruan, and Yijia Xiao. 2019. "A Concave Hull Methodology for Calculating the Crown Volume of Individual Trees Based on Vehicle-Borne LiDAR Data" Remote Sensing 11, no. 6: 623. https://doi.org/10.3390/rs11060623
APA StyleYan, Z., Liu, R., Cheng, L., Zhou, X., Ruan, X., & Xiao, Y. (2019). A Concave Hull Methodology for Calculating the Crown Volume of Individual Trees Based on Vehicle-Borne LiDAR Data. Remote Sensing, 11(6), 623. https://doi.org/10.3390/rs11060623







