Improving an Extreme Rainfall Detection System with GPM IMERG data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Analysis of the Accuracy of the Input Data
- n is the total number of time instants;
- t is time;
- RSATELLITE is the average rainfall intensity measured by satellite in the time interval t (expressed in mm/h);
- RGAUGE is the average rainfall intensity measured by rain gauge in the same time interval t (expressed in mm/h).
- both rain gauge and satellite data are null (case A, correct negatives);
- nonzero rain gauge data and zero satellite data (case B, misses);
- zero rain gauge data and non-null satellite data (case C, false alarms);
- both rain gauge and satellite data are non-null (case D, hits).
2.2. Development of an Extreme Rainfall Detection Methodology
- the number of “false alarms” (a false alarm is a condition that occurs if, at least in one cell of the examined country, the accumulated rainfall exceeds the threshold but, in that day, no disaster is reported in the database for the examined country);
- the number of “missed alarms” (a missed alarm is a condition that happens if, on the day a disaster has occurred in the examined country, in any cell of the country, the amount of rainfall does not exceed the threshold);
- the number of “hits events” (a hit event is a condition that happens if, on the day a disaster has occurred, the accumulated rainfall exceeds the threshold in at least one cell of the examined country).
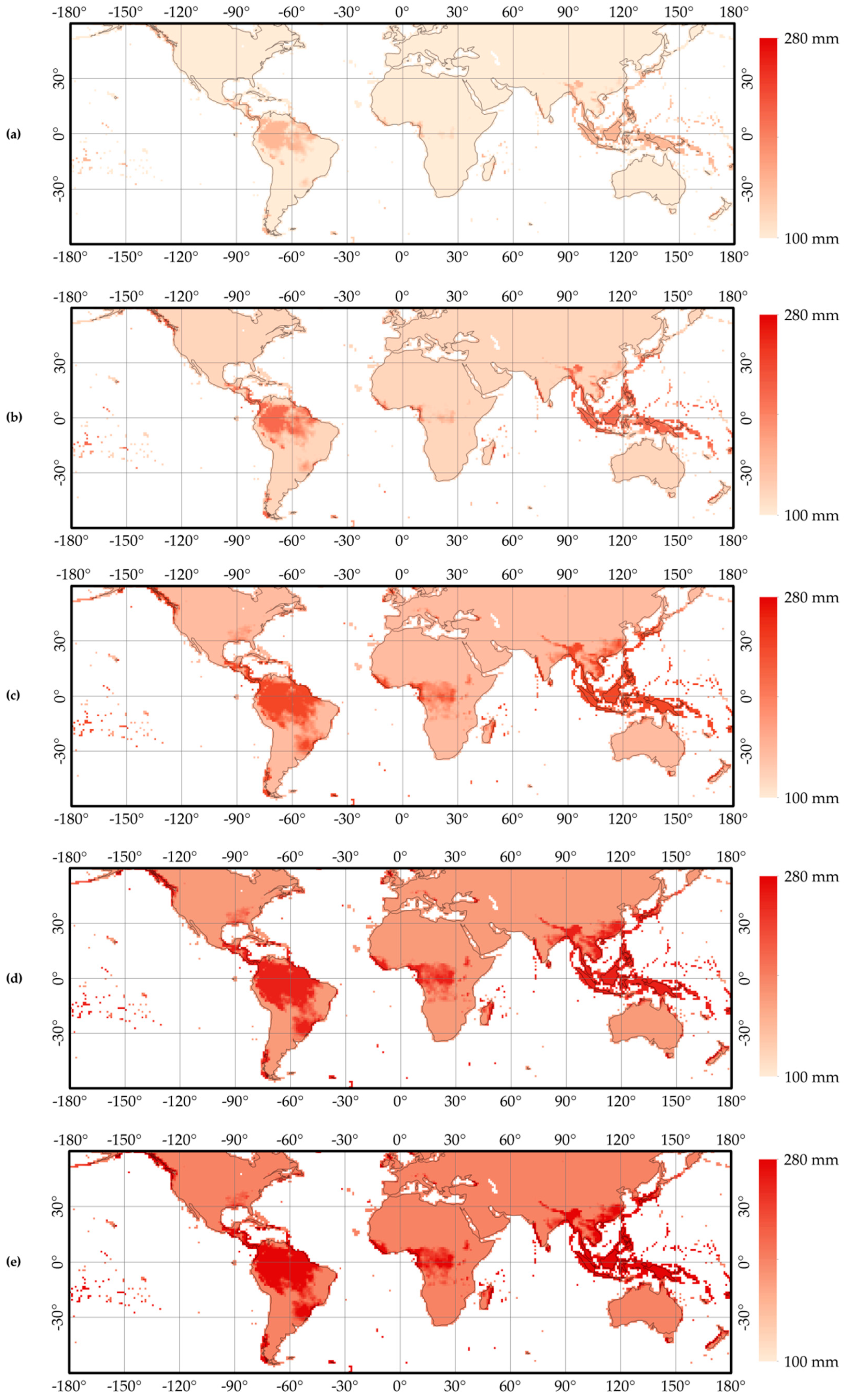
- for the aggregation of 12, 24 and 48 h, an interval ranging from 4 days before the start date of the disaster to the following 2 days;
- for the aggregation of 72 h, an interval ranging from 4 days before the start date of the disaster to the following 3 days;
- for the aggregation of 96 h, an interval ranging from 4 days before the start date of the disaster to the following 4 days.
- TOTAL COSTT(i) is the total cost of threshold T related to the aggregation interval i;
- n F.A. (T(i)) is the number of false alarms related to thresholds T and aggregation interval i;
- n M.A. (T(i)) is the number of missed alarms related to threshold T and aggregation interval i;
- C F.A. is the false alarm cost;
- C M.A. is the missed alarm cost.
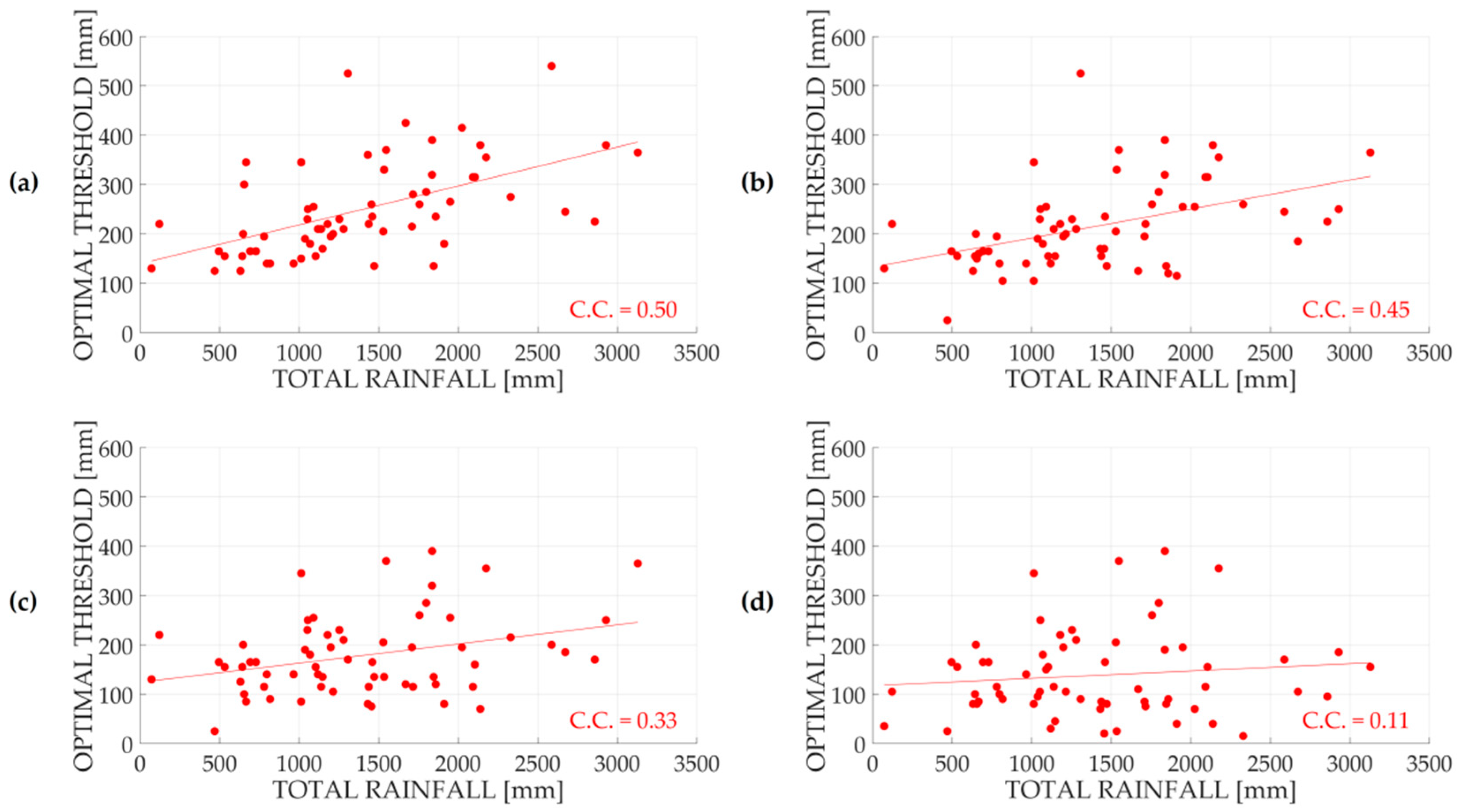
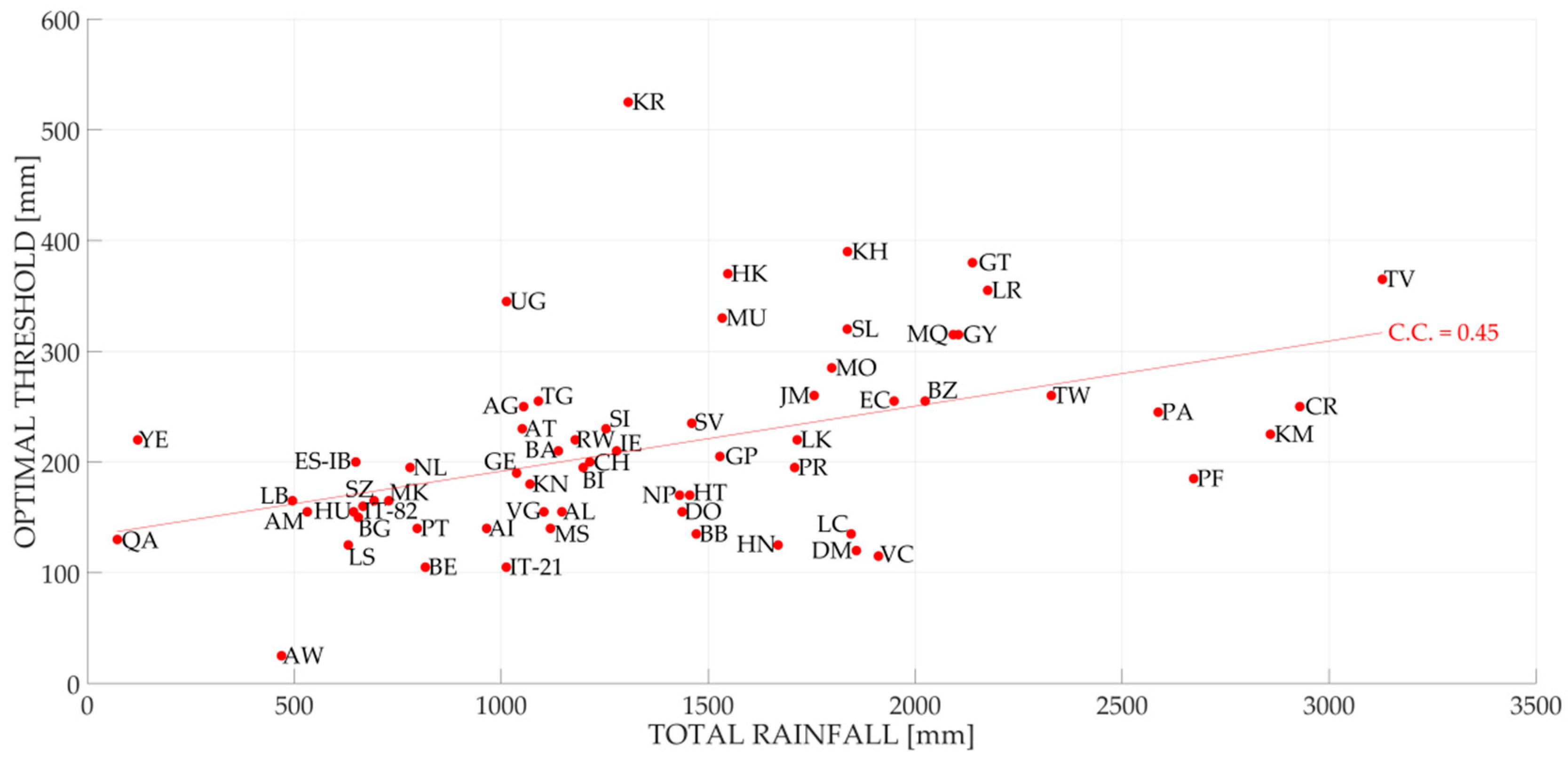
- T represents the threshold;
- T.R. represents the total rainfall (i.e., the mean annual rainfall calculated using 10 years of GPCC data);
- is a parameter representing the fraction of the total rainfall leading to the extreme event identification.
3. Results
3.1. Analysis of the Temporal and Spatial Influence of Missing Data
3.2. GPM IMERG Accuracy Evaluation
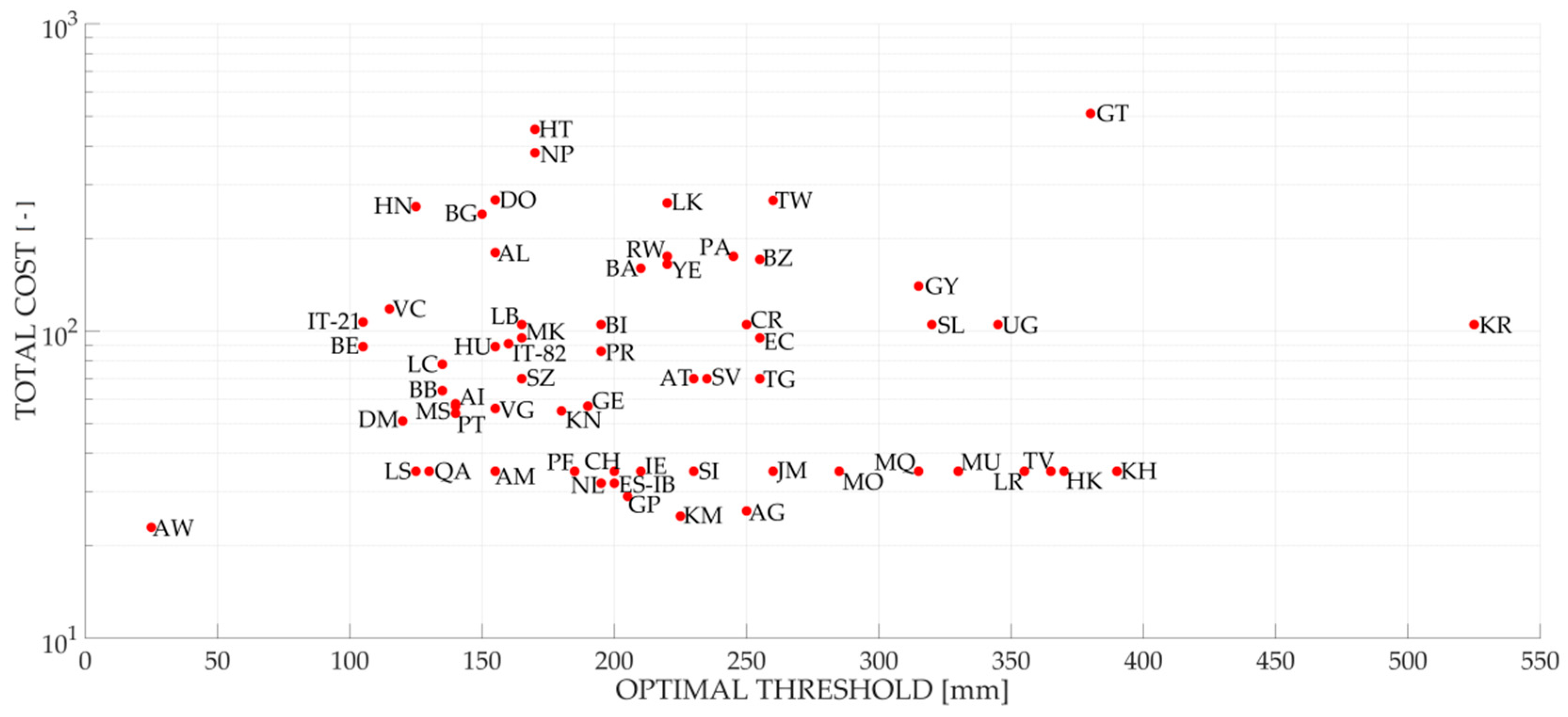
3.3. Development and Test of a New Extreme Rainfall Detection Methodology
- the introduction of too many false alarms in areas with a higher value of optimal threshold and
- a high number of missed events in areas with a lower value of optimal threshold.
3.4. Implementation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A






Appendix B

| 24 h | 48 h | 72 h | 96 h | 120 h | 144 h | |
|---|---|---|---|---|---|---|
| Threshold Alert Level 1 (mm) | 150 | 230 | 310 | 390 | 470 | 500 |
| Threshold Alert Level 2 (mm) | 210 | 290 | 370 | 450 | 530 | 560 |
| Threshold Alert Level 3 (mm) | 270 | 350 | 430 | 510 | 590 | 620 |
References
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. IPCC, Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1454. [Google Scholar]
- Mazzoglio, P.; Boccardo, P.; Laio, F.; Balbo, S.; Disabato, F. ERDS: A satellite-based approach in the extreme rainfall detection field. In Proceedings of the AIT 2018 Conference Abstract, Firenze, Italy, 4–6 July 2018; p. 137. Available online: https://aitonline.files.wordpress.com/2018/07/abstract_book1.pdf (accessed on 11 January 2019).
- EFAS. Available online: www.efas.eu (accessed on 11 January 2019).
- Global Flood Monitoring System. Available online: http://flood.umd.edu (accessed on 11 January 2019).
- Dartmouth Flood Observatory (DFO). Available online: http://floodobservatory.colorado.edu (accessed on 11 January 2019).
- Alfieri, L.; Cohen, S.; Galantowicz, J.; Schumann, G.J.P.; Trigg, M.A.; Zsoter, E.; Prudhomme, C.; Kruczkiewicz, A.; Coughlan de Perez, E.; Flamig, Z.; et al. A global network for operational flood risk reduction. Environ. Sci. Policy 2018, 84, 149–158. [Google Scholar] [CrossRef]
- Salamon, P.; Kettner, A.; Coughlan de Perez, E.; Rudari, R.; Trigg, M.; Weerts, A.; Cohen, S.; Prados, A.; Wu, H.; Schumann, G.J.P.; et al. The Global Flood Partnership Annual Meeting 2018–Bridging the Gap between Science and Users; PUBSY No. JRC113100; European Commission: Ispra, Italy, 2018; ISBN 978-92-79-93665-4. [Google Scholar] [CrossRef]
- ITHACA—Information Technology for Humanitarian Assistance, Cooperation and Action. Available online: www.ithacaweb.org (accessed on 11 January 2019).
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. Integrated Multi-satellitE Retrievals for GPM (IMERG) Technical Documentation. 2018. Available online: https://pmm.nasa.gov/sites/default/files/document_files/IMERG_doc_180207.pdf (accessed on 11 January 2019).
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG) Algorithm Theoretical Basis Document (ATBD) Version 5.2. 2018. Available online: https://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V5.2.pdf (accessed on 11 January 2019).
- GPM Data Downloads. Available online: https://pmm.nasa.gov/data-access/downloads/gpm (accessed on 11 January 2019).
- Huffman, G.J. GPM IMERG Early Precipitation L3 Half Hourly 0.1 Degree x 0.1 Degree V04; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2015.
- Huffman, G.J. GPM IMERG Late Precipitation L3 Half Hourly 0.1 Degree x 0.1 Degree V04; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2015.
- Khodadoust Siuki, S.; Saghafian, B.; Moazami, S. Comprehensive evaluation of 3-hourly TRMM and half-hourly GPM-IMERG satellite precipitation products. Int. J. Remote Sens. 2016, 38, 558–571. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of Integrated Multi-satellite Retrievals for Global Precipitation Measurement over China. Atmos. Res. 2016, 176–177, 121–133. [Google Scholar] [CrossRef]
- Gaona, M.F.; Overeem, A.; Leijnse, H.; Uijlenhoet, R. First-year evaluation of GPM rainfall over the Netherlands: IMERG day 1 final run (V03D). J. Hydrometeorol. 2016, 17, 2799–2814. [Google Scholar] [CrossRef]
- Sahlu, D.; Nikolopoulos, E.I.; Moges, S.A.; Anagnostou, E.N.; Hailu, D. First evaluation of the day-1 IMERG over the upper Blue Nile Basin. J. Hydrometeorol. 2016, 17, 2875–2882. [Google Scholar] [CrossRef]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Assessment of GPM-IMERG and other precipitation products against gauge data under different topographic and climatic conditions in Iran: Preliminary results. Remote Sens. 2016, 8, 135. [Google Scholar] [CrossRef]
- Kim, K.; Park, J.; Baik, J.; Choi, M. Evaluation of topographical and seasonal feature using GPM IMERG and TRMM 3B42 over Far-East Asia. Atmos. Res. 2017, 187, 95–105. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Pai, D.S.; AghaKouchak, A. From TRMM to GPM: How well can heavy rainfall be detected from space? Adv. Water Resour. 2016, 88, 1–7. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Q.; Duan, Z.; Zhang, J.; Mo, K.; Li, Z.; Tang, G. Multiscale comparative evaluation of the GPM IMERG v5 and TRMM 3B42 v7 precipitation products from 2015 to 2017 over a climate transition area of China. Remote Sens. 2018, 10, 944. [Google Scholar] [CrossRef]
- Local Climatological Data (LCD). Available online: www.ncdc.noaa.gov/cdo-web/datatools/lcd (accessed on 11 January 2019).
- Klimadatendeutschland. Available online: https://rcc.dwd.de/DE/leistungen/klimadatendeutschland/klarchivstunden.html%5Enn=561158 (accessed on 11 January 2019).
- Nurmi, P. Recommendations on the Verification of Local Weather Forecasts. ECMWF Technical Memorandum n° 430. 2003. Available online: www.ecmwf.int/en/elibrary/11401-recommendations-verification-local-weather-forecasts (accessed on 11 January 2019).
- EM-DAT: The Emergency Events Database–Université catholique de Louvain (UCL)–CRED, D. Guha-Sapir. Brussels, Belgium. Available online: www.emdat.be (accessed on 11 January 2019).
- Reliefweb. Available online: https://reliefweb.int (accessed on 11 January 2019).
- Floodlist. Available online: http://floodlist.com (accessed on 11 January 2019).
- Simmons, K.M.; Sutter, D. False alarms, tornado warnings, and tornado casualties. Weather Clim. Soc. 2009, 1, 38–53. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Ziese, M. GPCC Monitoring Product: Near Real-Time Monthly Land-Surface Precipitation from Rain-Gauges based on SYNOP and CLIMAT Data; GPCC: Ahmedabad, India, 2011. [CrossRef]
- European Civil Protection and Humanitarian Aid Operations. Available online: https://ec.europa.eu/echo/printpdf/what/humanitarian-aid/disaster_preparedness_en (accessed on 11 January 2019).
- Schröter, K.; Ostrowski, M.; Velasco, C.; Sempere-Torres, D.; Nachtnebel, H.; Kahl, B.; Beyene, M.; Rubin, C.; Gocht, M. Effectiveness and Efficiency of Early Warning Systems for Flash-Floods (EWASE). CRUE Research Report No I-5. Available online: www.researchgate.net/publication/255947664_Effectiveness_and_Efficiency_of_Early_Warning_Systems_for_Flash-Floods_EWASE (accessed on 11 January 2019).
- Hugenbusch, D.; Neumann, T.; Neumann, T. Cost-Benefit Analysis of Disaster Risk Reduction. Aktion Deutschland Hilft e.V GERMANY. 2016. Available online: www.aktion-deutschland-hilft.de/fileadmin/fm-dam/pdf/publikationen/aktion-deutschland-hilft-studie-zur-katastrophenvorsorge-englische-version-english-version.pdf (accessed on 11 January 2019).
- Gpm-accumul. Available online: https://github.com/ITHACA-org/gpm-accumul (accessed on 11 January 2019).
- Erds-web. Available online: https://github.com/ITHACA-org/erds-web (accessed on 11 January 2019).
- GPM IMERG Data. Available online: ftp://jsimpson.pps.eosdis.nasa.gov/NRTPUB/imerg/early (accessed on 11 January 2019).
- Surfrac0.1.PPS. Available online: https://pmm.nasa.gov/sites/default/files/downloads/surfrac0.1.PPS.gz (accessed on 11 January 2019).
- Tiepolo, M.; Cristofori, E.; Albanese, A.; Boccardo, P. 8. Early Warning Systems & Geomatics: Value-added Information in the Absence of High Resolution Data. In Planning to Cope with Tropical and Subtropical Climate Change; De Gruyter Open: Warsaw, Poland, 2016; pp. 141–153. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beckc, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]






| Rain Gauge | ||||
|---|---|---|---|---|
| = 0 mm/h | >0 mm/h | |||
| Satellite | = 0 mm/h | Correct Negatives (A) | Misses (B) | Estimated Non events |
| >0 mm/h | False Alarms (C) | Hits (D) | Estimated Events | |
| Observed Non events | Observed Events | |||
| 1 h | 2 h | 3 h | 6 h | 12 h | 24 h | 48 h | 72 h | 96 h | 120 h | 144 h | 168 h | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BIAS | E | −0.51 | −0.39 | −0.33 | −0.24 | −0.17 | −0.13 | −0.09 | −0.08 | −0.07 | −0.07 | −0.07 | −0.07 |
| L | −0.53 | −0.41 | −0.35 | −0.26 | −0.19 | −0.13 | −0.10 | −0.09 | −0.08 | −0.07 | −0.07 | −0.07 | |
| MAE | E | 2.19 | 1.58 | 1.28 | 0.87 | 0.59 | 0.40 | 0.28 | 0.23 | 0.20 | 0.19 | 0.18 | 0.17 |
| L | 2.11 | 1.55 | 1.26 | 0.87 | 0.59 | 0.40 | 0.28 | 0.23 | 0.20 | 0.19 | 0.18 | 0.17 |
| 1 h | 2 h | 3 h | 6 h | 12 h | 24 h | 48 h | 72 h | 96 h | 120 h | 144 h | 168 h | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FAR | E | 0.58 | 0.56 | 0.55 | 0.51 | 0.46 | 0.40 | 0.32 | 0.27 | 0.23 | 0.19 | 0.17 | 0.14 |
| L | 0.56 | 0.54 | 0.52 | 0.48 | 0.44 | 0.37 | 0.30 | 0.25 | 0.22 | 0.18 | 0.16 | 0.14 | |
| POD | E | 0.47 | 0.53 | 0.57 | 0.64 | 0.71 | 0.78 | 0.85 | 0.88 | 0.91 | 0.93 | 0.94 | 0.95 |
| L | 0.51 | 0.56 | 0.59 | 0.65 | 0.71 | 0.78 | 0.84 | 0.88 | 0.90 | 0.92 | 0.93 | 0.94 | |
| CSI | E | 0.28 | 0.31 | 0.33 | 0.38 | 0.43 | 0.51 | 0.60 | 0.67 | 0.72 | 0.76 | 0.79 | 0.82 |
| L | 0.30 | 0.33 | 0.35 | 0.40 | 0.45 | 0.53 | 0.61 | 0.67 | 0.72 | 0.76 | 0.80 | 0.82 |
| 1 h | 2 h | 3 h | 6 h | 12 h | 24 h | 48 h | 72 h | 96 h | 120 h | 144 h | 168 h | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BIAS | E | −10.35 | −9.01 | −8.02 | −6.21 | −4.59 | −3.18 | −2.16 | −1.72 | −1.50 | −1.31 | −1.19 | −1.08 |
| L | −10.02 | −8.71 | −7.76 | −6.03 | −4.48 | −3.10 | −2.11 | −1.68 | −1.47 | −1.29 | −1.17 | −1.06 | |
| MAE | E | 11.88 | 10.31 | 9.18 | 7.10 | 5.17 | 3.57 | 2.41 | 1.89 | 1.63 | 1.41 | 1.26 | 1.13 |
| L | 11.58 | 10.07 | 8.97 | 6.96 | 5.07 | 3.49 | 2.36 | 1.84 | 1.60 | 1.39 | 1.24 | 1.11 |
| Aggregation Interval (hours) | (%) | Lower Bound (mm) | Upper Bound (mm) |
|---|---|---|---|
| 12 | 6 | 100 | 150 |
| 24 | 8 | 120 | 210 |
| 48 | 12 | 140 | 240 |
| 72 | 15 | 170 | 260 |
| 96 | 16 | 190 | 280 |
| Previous Thresholds | Current Thresholds | |
|---|---|---|
| 12-h Aggregation Interval | - | 150 * |
| 24-h Aggregation Interval | 131 * | 137 * |
| 48-h Aggregation Interval | 85 * | 120 * |
| 72-h Aggregation Interval | 48 * | 112 * |
| 96-h Aggregation Interval | 39 * | 118 * |
| Total Number of Identified Events | 135 * | 162 * |
| % of Identified Events | 64% | 76.8% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazzoglio, P.; Laio, F.; Balbo, S.; Boccardo, P.; Disabato, F. Improving an Extreme Rainfall Detection System with GPM IMERG data. Remote Sens. 2019, 11, 677. https://doi.org/10.3390/rs11060677
Mazzoglio P, Laio F, Balbo S, Boccardo P, Disabato F. Improving an Extreme Rainfall Detection System with GPM IMERG data. Remote Sensing. 2019; 11(6):677. https://doi.org/10.3390/rs11060677
Chicago/Turabian StyleMazzoglio, Paola, Francesco Laio, Simone Balbo, Piero Boccardo, and Franca Disabato. 2019. "Improving an Extreme Rainfall Detection System with GPM IMERG data" Remote Sensing 11, no. 6: 677. https://doi.org/10.3390/rs11060677
APA StyleMazzoglio, P., Laio, F., Balbo, S., Boccardo, P., & Disabato, F. (2019). Improving an Extreme Rainfall Detection System with GPM IMERG data. Remote Sensing, 11(6), 677. https://doi.org/10.3390/rs11060677







