Optimization Performance Comparison of Three Different Group Intelligence Algorithms on a SVM for Hyperspectral Imagery Classification
Abstract
1. Introduction
2. Method
2.1. Artificial Bee Colony Algorithm
- Step 1.
- Randomly generate potential solutions for initialization in the D-dimensional hyperspace, .
- Step 2.
- Employed bees find new solutions, , near their old solutions, , according to , where and , and k and j are generated randomly. The parameter is the new value of the j-th parameter for the i-th employed bee. is a random number in the interval [−1,1], and v.
- Step 3.
- Each unemployed bee chooses an employed bee according to , where is the probability of the i-th employed bee being selected by the unemployed bees and is the fitness of the m-th employed bee.
- Step 4.
- If the solutions of the employed or unemployed bees are not optimized after iterations, they will abandon their solutions and they’ll become scouts to generate new solutions (same as step 1). This procedure can make bee colony avoid falling into a local optimum.
- Step 5.
- An iteration is terminated if the number of iteration reaches the pre-determined maximum number of iterations, MaxCycle. Otherwise, return to step two.
2.2. Genetic Algorithm
- Step 1.
- Code the parameters of the problem to be solved.
- Step 2.
- Randomly generate the initial population, . Each chromosome represents a potential solution, whose dimension is .
- Step 3.
- Estimate the fitness value of each chromosome in the population according to a fitness function.
- Step 4.
- Perform the genetic operations including crossover, mutations, selection etc.
- Step 5.
- The iteration is terminated if the number of iteration reaches the pre-determined maximum number of iterations, MaxCycle. Otherwise, return to step two.
2.3. Particle Swarm Optimization
- Step 1.
- Randomly generate an initial particle swarm of size .
- Step 2.
- Set the velocity vectors, , and position vectors, , of each particle (), and measure the fitness of each particle in the population.
- Step 3.
- Choose the best position of each particle that it experienced according to its fitness. (,)
- Step 4.
- Set the best position of entire swarm, according to the fitness function.
- Step 5.
- Compute the new velocity of each particle, , with equation, , , c1 and c2 are positive random numbers between 0.0 and 1.0
- Step 6.
- For each particle, move to the next position according to ,.
- Step 7.
- The iteration is terminated if the number of iteration reaches the pre-determined maximum number of iterations, MaxCycle. Otherwise, go to step three.
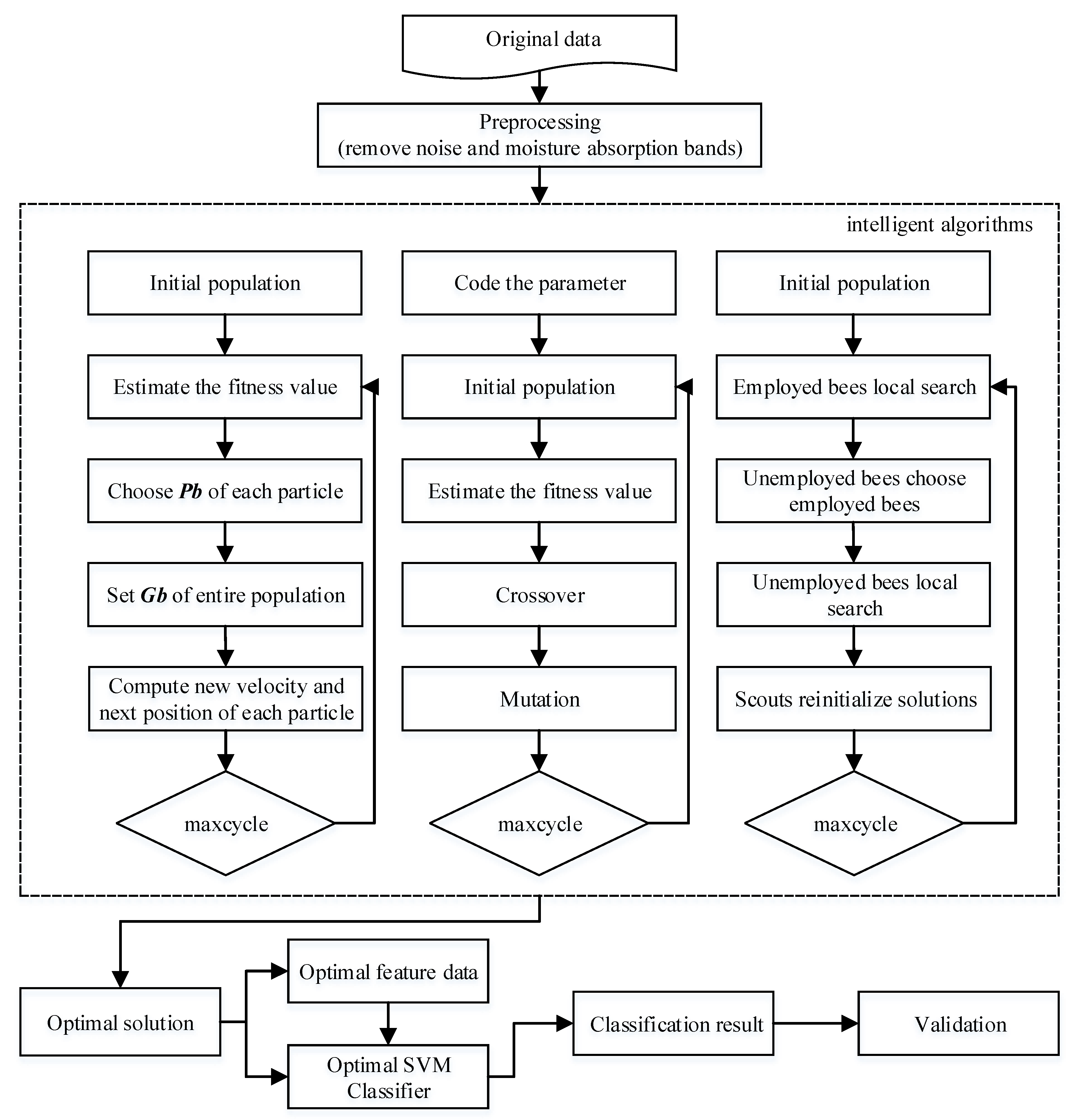
2.4. SVM Optimized with the GI Algorithms
3. Data and Experiments
3.1. Data
3.1.1. University of Pavia Image
3.1.2. Indian Pines Image
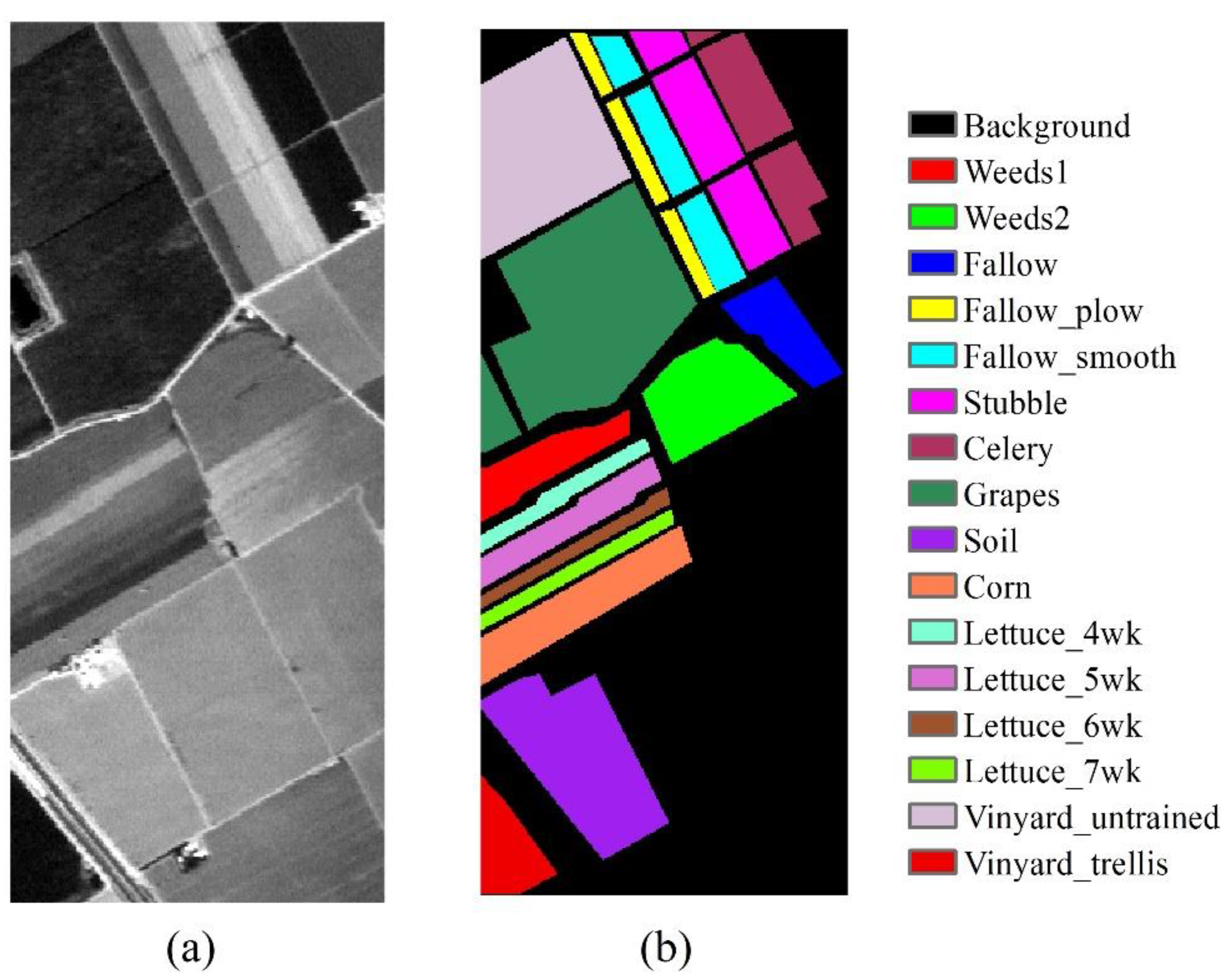
3.1.3. Salinas Image
3.2. Experiment Design
4. Results
4.1. Classification Results of the Three Hyperspectral Remote Sensing Datasets
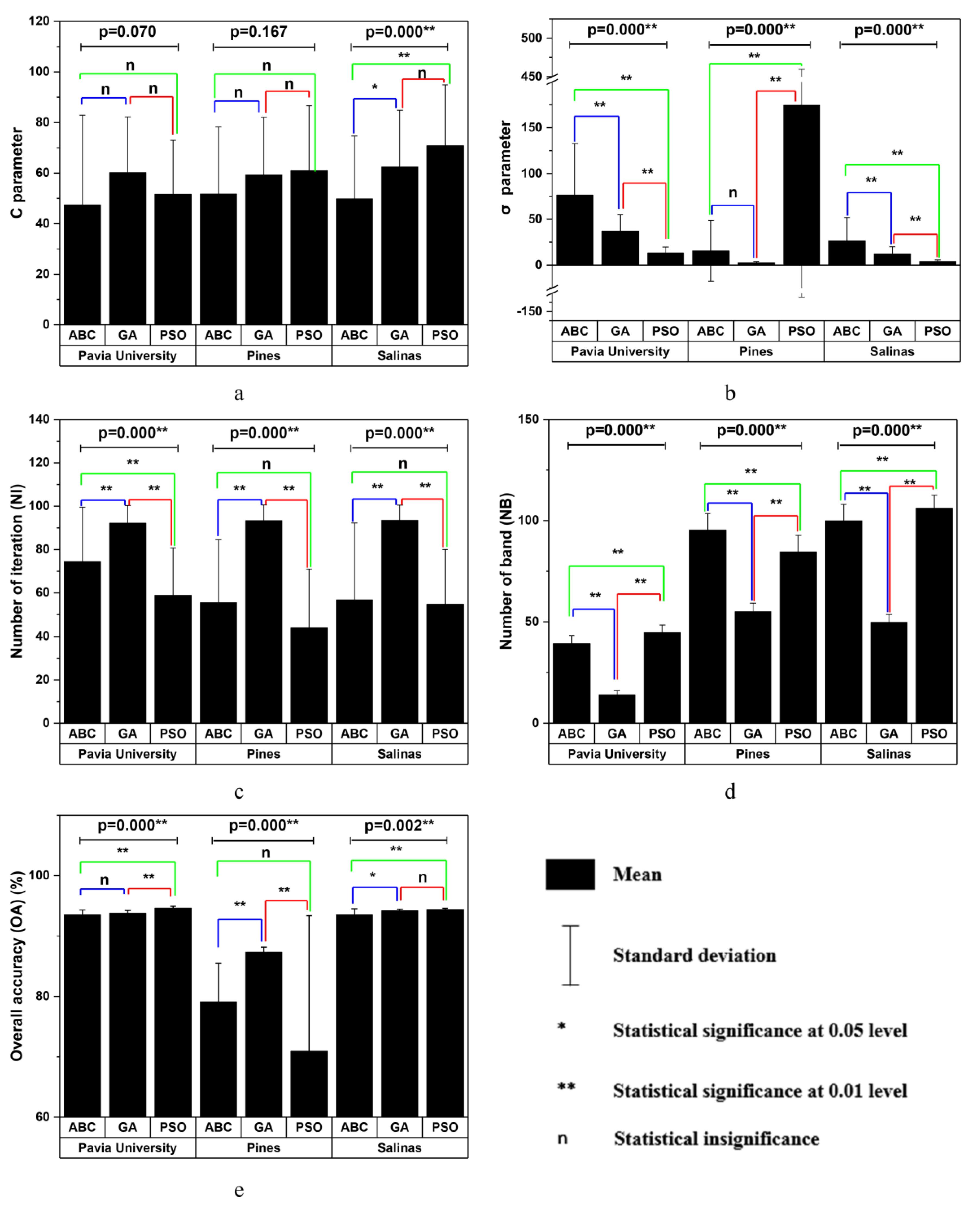
4.2. GI Algorithm Performance Comparison
4.3. The Impact of Sample Size on GI Algorithms’ Performance
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chapelle, O.; Vapnik, V.; Bousquet, O.; Mukherjee, S. Choosing multiple parameters for support vector machines. Mach. Learn. 2002, 46, 131–159. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Fusion of hyperspectral and lidar remote sensing data for classification of complex forest areas. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1416–1427. [Google Scholar] [CrossRef]
- Kuemmerle, T.; Chaskovskyy, O.; Knorn, J.; Radeloff, V.C.; Kruhlov, I.; Keeton, W.S.; Hostert, P. Forest cover change and illegal logging in the ukrainian carpathians in the transition period from 1988 to 2007. Remote Sens. Environ. 2009, 113, 1194–1207. [Google Scholar] [CrossRef]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and spatial classification of hyperspectral data using svms and morphological profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef]
- Cao, X.; Chen, J.; Imura, H.; Higashi, O. A svm-based method to extract urban areas from dmsp-ols and spot vgt data. Remote Sens. Environ. 2009, 113, 2205–2209. [Google Scholar] [CrossRef]
- Ma, X.; Tong, X.; Liu, S.; Luo, X.; Xie, H.; Li, C. Optimized sample selection in svm classification by combining with dmsp-ols, landsat ndvi and globeland30 products for extracting urban built-up areas. Remote Sens. 2017, 9, 236. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.; Wu, J.; Qi, J.; Salas, W.A. Mapping paddy rice with multitemporal alos/palsar imagery in southeast china. Int. J. Remote Sens. 2009, 30, 6301–6315. [Google Scholar] [CrossRef]
- Löw, F.; Michel, U.; Dech, S.; Conrad, C. Impact of feature selection on the accuracy and spatial uncertainty of per-field crop classification using support vector machines. ISPRS J. Photogramm. Remote Sens. 2013, 85, 102–119. [Google Scholar] [CrossRef]
- Hurni, K.; Schneider, A.; Heinimann, A.; Nong, D.H.; Fox, J. Mapping the expansion of boom crops in mainland southeast asia using dense time stacks of landsat data. Remote Sens. 2017, 9, 320. [Google Scholar] [CrossRef]
- Han, X.; Chen, X.; Feng, L. Four decades of winter wetland changes in poyang lake based on landsat observations between 1973 and 2013. Remote Sens. Environ. 2015, 156, 426–437. [Google Scholar] [CrossRef]
- Foody, G.M.; Mathur, A.; Sanchez-Hernandez, C.; Boyd, D.S. Training set size requirements for the classification of a specific class. Remote Sens. Environ. 2006, 104, 1–14. [Google Scholar] [CrossRef]
- Huang, C.; Davis, L.S.; Townshend, J.R.G. An assessment of support vector machines for land cover classification. Int. J. Remote Sens. 2002, 23, 725–749. [Google Scholar] [CrossRef]
- Zhu, X.; Pan, Y.; Jinshui, Z.; Wang, S.; Gu, X.; Xu, C. The effects of training samples on the wheat planting area measure accuracy in tm scale(i): The accuracy response of different classifiers to training samples. J. Remote Sens. 2007, 11, 826–837. [Google Scholar] [CrossRef]
- Foody, G.M.; Mathur, A. Toward intelligent training of supervised image classifications: Directing training data acquisition for svm classification. Remote Sens. Environ. 2004, 93, 107–117. [Google Scholar] [CrossRef]
- Foody, G.M.; Mathur, A. The use of small training sets containing mixed pixels for accurate hard image classification: Training on mixed spectral responses for classification by a svm. Remote Sens. Environ. 2006, 103, 179–189. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Pal, M.; Foody, G.M. Feature selection for classification of hyperspectral data by svm. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2297–2307. [Google Scholar] [CrossRef]
- Pal, M.; Mather, P.M. Support vector machines for classification in remote sensing. Int. J. Remote Sens. 2005, 26, 1007–1011. [Google Scholar] [CrossRef]
- Inglada, J. Automatic recognition of man-made objects in high resolution optical remote sensing images by svm classification of geometric image features. ISPRS J. Photogramm. Remote Sens. 2007, 62, 236–248. [Google Scholar] [CrossRef]
- Dash, J.; Mathur, A.; Foody, G.M.; Curran, P.J.; Chipman, J.W.; Lillesand, T.M. Land cover classification using multi-temporal meris vegetation indices. Int. J. Remote Sens. 2007, 28, 1137–1159. [Google Scholar] [CrossRef]
- Waske, B.; Linden, S.v.d.; Benediktsson, J.A.; Rabe, A.; Hostert, P. Sensitivity of support vector machines to random feature selection in classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2880–2889. [Google Scholar] [CrossRef]
- Foody, G.M. Rvm-based multi-class classification of remotely sensed data. Int. J. Remote Sens. 2008, 29, 1817–1823. [Google Scholar] [CrossRef]
- Ben-Hur, A.; Weston, J. A User’s Guide to Support Vector Machines. In Data Mining Techniques for the Life Sciences; Springer: New York, NY, USA, 2010; pp. 223–239. [Google Scholar]
- Cawley, G.C.; Talbot, N.L. On over-fitting in model selection and subsequent selection bias in performance evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Devos, O.; Ruckebusch, C.; Durand, A.; Duponchel, L.; Huvenne, J.-P. Support vector machines (svm) in near infrared (nir) spectroscopy: Focus on parameters optimization and model interpretation. Chemom. Intell. Lab. Syst. 2009, 96, 27–33. [Google Scholar] [CrossRef]
- Guo, B.; Gunn, S.R.; Damper, R.I.; Nelson, J.D.B. Customizing kernel functions for svm-based hyperspectral image classification. IEEE Trans. Image Process. 2008, 17, 622–629. [Google Scholar] [CrossRef] [PubMed]
- Tuia, D.; Camps-Valls, G.; Matasci, G.; Kanevski, M. Learning relevant image features with multiple-kernel classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3780–3791. [Google Scholar] [CrossRef]
- Samadzadegan, F.; Hasani, H.; Schenk, T. Simultaneous feature selection and svm parameter determination in classification of hyperspectral imagery using ant colony optimization. Can. J. Remote Sens. 2012, 38, 139–156. [Google Scholar] [CrossRef]
- Bazi, Y.; Melgani, F. Toward an optimal svm classification system for hyperspectral remote sensing images. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3374–3385. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Peng, X.; Li, H.; He, J. Swarm intelligence for classification of remote sensing data. Sci. China Ser. D Earth Sci. 2008, 51, 79–87. [Google Scholar] [CrossRef]
- Li, N.; Zhu, X.; Pan, Y.; Zhan, P. Optimized svm based on artificial bee colony algorithm for remote sensing image classification. J. Remote Sens. 2018, 22, 559–569. [Google Scholar] [CrossRef]
- Jayanth, J.; Ashok Kumar, T.; Koliwad, S.; Krishnashastry, S. Identification of land cover changes in the coastal area of dakshina kannada district, south india during the year 2004–2008. Egypt. J. Remote Sens. Space Sci. 2016, 19, 73–93. [Google Scholar] [CrossRef]
- Xue, Z.; Du, P.; Su, H. Harmonic analysis for hyperspectral image classification integrated with pso optimized svm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2131–2146. [Google Scholar] [CrossRef]
- Kuo, R.-J.; Huang, S.L.; Zulvia, F.E.; Liao, T.W. Artificial bee colony-based support vector machines with feature selection and parameter optimization for rule extraction. Knowl. Inf. Syst. 2018, 55, 253–274. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Pal, M. Support vector machine-based feature selection for land cover classification: A case study with dais hyperspectral data. Int. J. Remote Sens. 2006, 27, 2877–2894. [Google Scholar] [CrossRef]
- Bradley, P.E.; Keller, S.; Weinmann, M. Unsupervised feature selection based on ultrametricity and sparse training data: A case study for the classification of high-dimensional hyperspectral data. Remote Sens. 2018, 10, 1564. [Google Scholar] [CrossRef]
- Li, S.; Wu, H.; Wan, D.; Zhu, J. An effective feature selection method for hyperspectral image classification based on genetic algorithm and support vector machine. Knowl. Based Syst. 2011, 24, 40–48. [Google Scholar] [CrossRef]
- Ghamisi, P.; Benediktsson, J.A. Feature selection based on hybridization of genetic algorithm and particle swarm optimization. IEEE Geosci. Remote Sens. Lett. 2015, 12, 309–313. [Google Scholar] [CrossRef]
- Sukawattanavijit, C.; Chen, J.; Zhang, H. Ga-svm algorithm for improving land-cover classification using sar and optical remote sensing data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 284–288. [Google Scholar] [CrossRef]
- Wang, M.; Wan, Y.; Ye, Z.; Lai, X. Remote sensing image classification based on the optimal support vector machine and modified binary coded ant colony optimization algorithm. Inf. Sci. 2017, 402, 50–68. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization. Technical Report-tr06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In MHS’95, Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 39–43. [Google Scholar]
- Stone, M. Cross-validatory choice and assessment of statistical predictions. J. R. Stat. Society Ser. B (Methodol.) 1974, 36, 111–147. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Tuia, D.; Bruzzone, L.; Benediktsson, J.A. Advances in hyperspectral image classification: Earth monitoring with statistical learning methods. IEEE Signal Process. Mag. 2014, 31, 45–54. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. Libsvm: A library for support vector machines. Acm Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Samsudin, S.H.; Shafri, H.Z.; Hamedianfar, A.; Mansor, S. Spectral feature selection and classification of roofing materials using field spectroscopy data. J. Appl. Remote Sens. 2015, 9, 095079. [Google Scholar] [CrossRef]
- Tamimi, E.; Ebadi, H.; Kiani, A. Evaluation of different metaheuristic optimization algorithms in feature selection and parameter determination in svm classification. Arab. J. Geosci. 2017, 10, 478. [Google Scholar] [CrossRef]
- Ghoggali, N.; Melgani, F. Genetic svm approach to semisupervised multitemporal classification. IEEE Geosci. Remote Sens. Lett. 2008, 5, 212–216. [Google Scholar] [CrossRef]
- Silva, R.; Gomes, V.; Mendes-Faia, A.; Melo-Pinto, P. Using support vector regression and hyperspectral imaging for the prediction of oenological parameters on different vintages and varieties of wine grape berries. Remote Sens. 2018, 10, 312. [Google Scholar] [CrossRef]





| Method | Parameters/Performance | Sample Size | Mean | |||||
|---|---|---|---|---|---|---|---|---|
| 5% | 10% | 15% | 20% | 25% | ||||
| ABC | C | Mean | 49.20 | 34.67 | 51.65 | 44.76 | 57.11 | 47.48 |
| SD | 38.91 | 32.30 | 28.22 | 28.66 | 48.95 | 35.41 | ||
| σ | Mean | 78.44 | 68.77 | 47.09 | 92.89 | 94.61 | 76.36 | |
| SD | 65.75 | 57.10 | 39.73 | 60.53 | 58.53 | 56.33 | ||
| Number of iterations (NI) | Mean | 63.00 | 82.80 | 79.80 | 81.50 | 65.00 | 74.42 | |
| SD | 38.49 | 20.31 | 21.51 | 21.95 | 23.35 | 25.12 | ||
| Number of band (NB) | Mean | 40.90 | 40.10 | 40.70 | 37.80 | 37.10 | 39.32 | |
| SD | 4.61 | 4.82 | 3.06 | 4.08 | 3.38 | 3.99 | ||
| overall accuracy (OA) | Mean | 91.31% | 93.05% | 94.21% | 94.32% | 94.94% | 93.56% | |
| SD | 1.15 | 1.01 | 0.67 | 0.83 | 0.38 | 0.81 | ||
| GA | C | Mean | 77.61 | 53.74 | 54.44 | 68.02 | 47.20 | 60.20 |
| SD | 16.89 | 18.91 | 27.25 | 16.94 | 30.16 | 22.03 | ||
| σ | Mean | 17.76 | 39.34 | 37.23 | 51.23 | 40.50 | 37.21 | |
| SD | 10.24 | 10.81 | 22.01 | 26.67 | 18.21 | 17.59 | ||
| Number of iterations (NI) | Mean | 92.60 | 91.50 | 90.80 | 93.70 | 92.20 | 92.16 | |
| SD | 7.88 | 7.31 | 9.37 | 7.53 | 8.70 | 8.16 | ||
| Number of band (NB) | Mean | 15.40 | 13.60 | 14.10 | 13.60 | 13.30 | 14.00 | |
| SD | 2.63 | 1.65 | 2.77 | 1.51 | 1.83 | 2.08 | ||
| overall accuracy (OA) | Mean | 92.52% | 93.51% | 94.00% | 94.39% | 94.57% | 93.80% | |
| SD | 0.56 | 0.40 | 0.42 | 0.40 | 0.44 | 0.45 | ||
| PSO | C | Mean | 59.12 | 50.36 | 56.91 | 43.78 | 47.87 | 51.61 |
| SD | 25.69 | 23.71 | 21.39 | 20.66 | 15.27 | 21.35 | ||
| σ | Mean | 9.14 | 11.69 | 13.13 | 18.23 | 14.73 | 13.38 | |
| SD | 7.35 | 6.34 | 4.13 | 10.93 | 2.86 | 6.32 | ||
| Number of iterations (NI) | Mean | 57.20 | 67.70 | 61.70 | 47.80 | 60.00 | 58.88 | |
| SD | 22.53 | 19.53 | 24.87 | 20.47 | 21.76 | 21.83 | ||
| Number of band (NB) | Mean | 45.20 | 46.90 | 46.40 | 43.20 | 42.90 | 44.92 | |
| SD | 4.61 | 3.57 | 3.50 | 3.33 | 2.42 | 3.49 | ||
| overall accuracy (OA) | Mean | 92.99% | 94.35% | 95.12% | 95.37% | 95.34% | 94.63% | |
| SD | 0.41 | 0.24 | 0.19 | 0.25 | 0.39 | 0.30 | ||
| Method | Parameters/Performance | Sample Size | Mean | |||||
|---|---|---|---|---|---|---|---|---|
| 5% | 10% | 15% | 20% | 25% | ||||
| ABC | C | Mean | 59.55 | 35.26 | 60.13 | 42.60 | 60.84 | 51.68 |
| SD | 23.29 | 30.48 | 23.22 | 25.04 | 30.78 | 26.56 | ||
| σ | Mean | 51.31 | 7.79 | 6.98 | 5.71 | 5.20 | 15.40 | |
| SD | 139.17 | 8.60 | 5.64 | 6.40 | 6.46 | 33.25 | ||
| Number of iterations (NI) | Mean | 55.30 | 55.70 | 53.20 | 66.10 | 47.10 | 55.48 | |
| SD | 38.75 | 32.35 | 24.43 | 21.16 | 28.63 | 29.06 | ||
| Number of band (NB) | Mean | 95.60 | 97.50 | 97.30 | 93.20 | 93.20 | 95.36 | |
| SD | 11.88 | 3.54 | 9.73 | 8.83 | 6.71 | 8.14 | ||
| overall accuracy (OA) | Mean | 65.72% | 77.06% | 81.79% | 85.04% | 85.95% | 79.11% | |
| SD | 15.41 | 7.13 | 3.85 | 3.05 | 2.39 | 6.36 | ||
| GA | C | Mean | 69.90 | 49.90 | 65.94 | 65.41 | 45.25 | 59.28 |
| SD | 15.41 | 20.63 | 21.20 | 31.67 | 24.99 | 22.78 | ||
| σ | Mean | 1.11 | 2.94 | 2.27 | 1.83 | 3.74 | 2.38 | |
| SD | 0.62 | 2.16 | 1.22 | 0.54 | 3.28 | 1.56 | ||
| Number of iterations (NI) | Mean | 93.40 | 91.50 | 95.10 | 92.60 | 94.10 | 93.34 | |
| SD | 10.39 | 7.85 | 4.51 | 6.83 | 6.54 | 7.23 | ||
| Number of band (NB) | Mean | 59.40 | 56.00 | 55.80 | 52.40 | 51.40 | 55.00 | |
| SD | 2.50 | 4.85 | 5.69 | 3.95 | 4.06 | 4.21 | ||
| overall accuracy (OA) | Mean | 81.90% | 85.09% | 88.80% | 90.12% | 90.78% | 87.34% | |
| SD | 0.80 | 1.70 | 0.57 | 0.64 | 0.41 | 0.82 | ||
| PSO | C | Mean | 60.71 | 62.36 | 66.19 | 63.64 | 51.87 | 60.95 |
| SD | 27.96 | 29.12 | 21.45 | 19.05 | 30.85 | 25.68 | ||
| σ | Mean | 66.47 | 187.83 | 169.36 | 111.20 | 337.33 | 174.44 | |
| SD | 209.37 | 317.16 | 272.96 | 233.01 | 393.60 | 285.22 | ||
| Number of iterations (NI) | Mean | 57.40 | 41.40 | 45.20 | 40.90 | 34.50 | 43.88 | |
| SD | 33.02 | 24.45 | 30.53 | 23.76 | 23.81 | 27.11 | ||
| Number of band (NB) | Mean | 84.00 | 84.60 | 87.40 | 84.60 | 82.10 | 84.54 | |
| SD | 7.69 | 7.59 | 8.55 | 7.69 | 9.36 | 8.18 | ||
| overall accuracy (OA) | Mean | 70.80% | 68.04% | 71.16% | 78.71% | 65.89% | 70.92% | |
| SD | 16.92 | 25.30 | 24.82 | 20.91 | 24.27 | 22.45 | ||
| Method | Parameters/Performance | Sample Size | Mean | |||||
|---|---|---|---|---|---|---|---|---|
| 5% | 10% | 15% | 20% | 25% | ||||
| ABC | C | Mean | 46.48 | 56.03 | 61.24 | 47.48 | 37.82 | 49.81 |
| SD | 31.83 | 23.52 | 23.93 | 26.35 | 18.58 | 24.84 | ||
| σ | Mean | 13.16 | 22.83 | 6.13 | 43.13 | 46.39 | 26.33 | |
| SD | 12.28 | 19.74 | 6.06 | 51.20 | 38.77 | 25.61 | ||
| Number of iterations (NI) | Mean | 53.50 | 55.70 | 58.00 | 49.90 | 66.80 | 56.78 | |
| SD | 33.49 | 40.50 | 31.72 | 39.53 | 32.10 | 35.47 | ||
| Number of band (NB) | Mean | 101.70 | 99.60 | 99.50 | 100.10 | 98.70 | 99.92 | |
| SD | 7.29 | 10.65 | 8.49 | 7.25 | 6.93 | 8.12 | ||
| overall accuracy (OA) | Mean | 91.67% | 93.14% | 93.32% | 94.16% | 95.21% | 93.50% | |
| SD | 1.06% | 0.98% | 1.39% | 1.19% | 0.47% | 1.02% | ||
| GA | C | Mean | 69.06 | 62.05 | 72.60 | 43.94 | 64.19 | 62.37 |
| SD | 11.02 | 26.17 | 27.05 | 27.68 | 20.37 | 22.46 | ||
| σ | Mean | 4.55 | 10.41 | 10.62 | 20.25 | 13.90 | 11.95 | |
| SD | 1.67 | 5.22 | 5.34 | 17.03 | 11.12 | 8.07 | ||
| Number of iterations (NI) | Mean | 97.40 | 92.20 | 95.10 | 88.60 | 94.10 | 93.48 | |
| SD | 2.32 | 9.59 | 5.22 | 10.55 | 7.42 | 7.02 | ||
| Number of band (NB) | Mean | 52.90 | 49.00 | 49.40 | 48.20 | 49.20 | 49.74 | |
| SD | 3.90 | 3.92 | 3.17 | 2.82 | 5.53 | 3.87 | ||
| overall accuracy (OA) | Mean | 93.00% | 93.92% | 94.35% | 94.60% | 94.98% | 94.17% | |
| SD | 0.24% | 0.34% | 0.22% | 0.30% | 0.28% | 0.28% | ||
| PSO | C | Mean | 59.44 | 83.92 | 73.99 | 69.87 | 66.92 | 70.83 |
| SD | 29.84 | 12.37 | 23.63 | 26.17 | 28.36 | 24.07 | ||
| σ | Mean | 2.28 | 2.48 | 4.08 | 5.86 | 5.61 | 4.06 | |
| SD | 0.88 | 0.53 | 1.19 | 2.74 | 2.56 | 1.58 | ||
| Number of iterations (NI) | Mean | 54.00 | 50.60 | 53.40 | 60.30 | 55.70 | 54.80 | |
| SD | 26.20 | 25.68 | 17.75 | 28.67 | 27.84 | 25.23 | ||
| Number of bands (NB) | Mean | 108.50 | 106.00 | 109.20 | 105.80 | 101.20 | 106.14 | |
| SD | 8.29 | 6.22 | 6.29 | 5.27 | 6.14 | 6.44 | ||
| overall accuracy (OA) | Mean | 93.14% | 94.11% | 94.65% | 94.89% | 95.23% | 94.40% | |
| SD | 0.23% | 0.12% | 0.23% | 0.20% | 0.22% | 0.20% | ||
| Datasets | ABC | GA | PSO | |||
|---|---|---|---|---|---|---|
| [0.1,300] | [300,600] | [0.1,300] | [300,600] | [0.1,300] | [300,600] | |
| Pavia University | 95.31% | 91.02% | 94.17% | 95.31% | 95.31% | 94.79% |
| Pine | 89.43% | 42.89% | 91.29% | 53.57% | 89.22% | 42.89% |
| Salinas | 94.95% | 87.35% | 94.90% | 94.22% | 95.37% | 90.58% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Li, N.; Pan, Y. Optimization Performance Comparison of Three Different Group Intelligence Algorithms on a SVM for Hyperspectral Imagery Classification. Remote Sens. 2019, 11, 734. https://doi.org/10.3390/rs11060734
Zhu X, Li N, Pan Y. Optimization Performance Comparison of Three Different Group Intelligence Algorithms on a SVM for Hyperspectral Imagery Classification. Remote Sensing. 2019; 11(6):734. https://doi.org/10.3390/rs11060734
Chicago/Turabian StyleZhu, Xiufang, Nan Li, and Yaozhong Pan. 2019. "Optimization Performance Comparison of Three Different Group Intelligence Algorithms on a SVM for Hyperspectral Imagery Classification" Remote Sensing 11, no. 6: 734. https://doi.org/10.3390/rs11060734
APA StyleZhu, X., Li, N., & Pan, Y. (2019). Optimization Performance Comparison of Three Different Group Intelligence Algorithms on a SVM for Hyperspectral Imagery Classification. Remote Sensing, 11(6), 734. https://doi.org/10.3390/rs11060734





