Multispectral Transforms Using Convolution Neural Networks for Remote Sensing Multispectral Image Compression
Abstract
:1. Introduction
2. Materials and Methods
2.1. NTD for Multispectral Compression
| Algorithm 1 [43,44]: |
| 1: Input: a given tensor , its size is ; |
| The core tensor size is . |
| 2: Output: a core tensor , |
| N factors . |
| 3: Begin |
| 4: Initializing and all . |
| 5: Normalizing all for n = 1, 2, …, N to unit length. |
| 6: Calculating the residual tensor as . |
| 7: Repeat |
| 8: for n = 1 to N do |
| 9: for jn = 1 to jn = Jn do |
| 10: Calculate prediction tensor: |
| 11: Update factors: |
| 12: Normalizing factors: |
| 13: Update errors: |
| 14: End |
| 15: End |
| 16: Update core tensor: |
| 17: For each j1 = 1, …, J1, j2 = 1, …, J2, …, jN = 1, …, JN do |
| 18: Calculate core tensor: |
| 19: Calculate error tensor: |
| 20: End |
| 21: Until the converge condition is achieved. |
| 22: End |
| 23: Return G and . |
2.2. Proposed Multispectral Tensor with CNNs
| Algorithm 2: Spectral tensor transform using two CNNs |
| 1: Input: The original spectral tensor, denoted by X; |
| 2: Output: The learnable parameters of two CNNs , . The best small-3: scale spectral tensor |
| 3: Initialization: initial learnable parameters, , for two CNNs, alternate iteration number k = 0. |
| 4: While do { |
| 5: k = k + 1; |
| 6: Step 1: |
| 7: |
| 8: Update by training the backward CNN to compute Equation (14). |
| 9: Step 2: |
| 10: |
| 11: Update by training the forward CNN to compute Equation (13). |
| 12: Until iteration condition is met, here, the iteration condition is k = K. |
| 13: Return: |
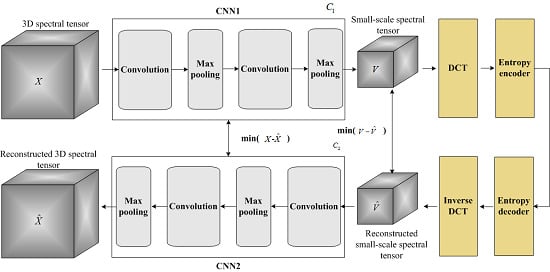
2.3. Proposed Multispectral Compression Scheme with CNNs
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| TD | Tensor decomposition |
| NTD | Nonnegative Tucker Decomposition |
| CNNs | Convolution neural networks |
| DCT | Discrete Cosine Transformation |
| LUT | Look-Up Table |
| CCSDS-IDC | Consultative Committee for Space Data Systems—Image Data Compression |
| DPCM | Differential pulse-code modulation |
| DWT | Discrete wavelet transform |
| KLT | Karhunen–Loeve Transform |
| PCA | Principal Components Analysis |
| SPECK | Set Partitioned Embedded Block Coder |
| DSC | Distributed source coding |
Appendix A. Two-Step Calculation Function
References
- Smith, M.O.; Ustin, S.L.; Adams, J.B.; Gillespie, A.R. Vegetation in deserts. I. A regional measure of abundance from multispectral images. Remote Sens. Environ. 1990, 31, 1–26. [Google Scholar] [CrossRef]
- Chavez, P.S., Jr. Radiometric calibration of Landsat Thematic Mapper multispectral images. Photogramm. Eng. Remote Sens. 1989, 55, 1285–1294. [Google Scholar]
- Zeng, Y.; Huang, W.; Liu, M.; Zhang, H.; Zou, B. Fusion of satellite images in urban area: Assessing the quality of resulting images. In Proceedings of the Geoinformatics of 2010 18th IEEE International Conference, Beijing, China, 18–20 June 2010; pp. 1–4. [Google Scholar]
- Franklin, S.E.; Hall, R.J.; Moskal, L.M.; Maudie, A.J.; Lavigne, M.B. Incorporating texture into classification of forest species composition from airborne multispectral images. Int. J. Remote Sens. 2000, 21, 61–79. [Google Scholar] [CrossRef]
- Rowan, L.C.; Goetz, A.F.; Ashley, R.P. Discrimination of hydrothermally altered and unaltered rocks in visible and near infrared multispectral images. Geophysics 1977, 42, 522–535. [Google Scholar] [CrossRef]
- Hahn, J.; Debes, C.; Leigsnering, M.; Zoubir, A.M. Compressive sensing and adaptive direct sampling in hyperspectral imaging. Digit. Signal Process. 2014, 26, 113–126. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, C.; Li, D.; Li, J. Semisupervised classification for hyperspectral imagery with transductive multiple-kernel learning. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1991–1995. [Google Scholar]
- Li, J. A highly reliable and super-speed optical fiber transmission for hyper-spectral SCMOS camera. Opt. Int. J. Light Electron Opt. 2016, 127, 1532–1545. [Google Scholar] [CrossRef]
- Imai, F.H.; Berns, R.S. High-resolution multi-spectral image archives: A hybrid approach. In Proceedings of the Color and Imaging Conference, Scottsdale, AZ, USA, 17–20 November 1998; pp. 224–227. [Google Scholar]
- Pu, H.; Chen, Z.; Wang, B.; Jiang, G.M. A novel spatial–spectral similarity measure for dimensionality reduction and classification of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7008–7022. [Google Scholar]
- Valsesia, D.; Magli, E. A novel rate control algorithm for onboard predictive coding of multispectral and hyperspectral images. Ieee Trans. Geosci. Remote Sens. 2014, 52, 6341–6355. [Google Scholar] [CrossRef]
- Li, J.; Jin, L.X.; Han, S.L.; Li, G.N.; Wang, W.H. Reliability of space image recorder based on NAND flash memory. Guangxue Jingmi Gongcheng (Opt. Precis. Eng.) 2012, 20, 1090–1101. [Google Scholar]
- Lee, Y.; Hirakawa, K.; Nguyen, T.Q. Camera-Aware Multi-Resolution Analysis for Raw Image Sensor Data Compression. IEEE Trans. Image Process. 2018, 27, 2806–2817. [Google Scholar] [CrossRef] [PubMed]
- Zemliachenko, A.N.; Kozhemiakin, R.A.; Abramov, S.K.; Lukin, V.V.; Vozel, B.; Chehdi, K.; Egiazarian, K.O. Prediction of Compression Ratio for DCT-Based Coders With Application to Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 257–270. [Google Scholar] [CrossRef]
- Li, J.; Liu, Z.; Liu, F. Compressive sampling based on frequency saliency for remote sensing imaging. Sci. Rep. 2017, 7, 6539. [Google Scholar] [CrossRef]
- Li, J.; Zhang, K. Application of ADV212 to the large field of view multi-spectral TDICCD space camera. Spectrosc. Spectr. Anal. 2012, 32, 1700–1707. [Google Scholar]
- Wei, Y.; Zhao, Z.; Song, J. Urban building extraction from high-resolution satellite panchromatic image using clustering and edge detection. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; pp. 2008–2010. [Google Scholar]
- Cetin, M.; Musaoglu, N. Merging hyperspectral and panchromatic image data: Qualitative and quantitative analysis. Int. J. Remote Sens. 2009, 30, 1779–1804. [Google Scholar] [CrossRef]
- Carper, W.; Lillesand, T.; Kiefer, R. The use of intensity-hue-saturation transformations for merging SPOT panchromatic and multispectral image data. Photogramm. Eng. Remote Sens. 1990, 56, 459–467. [Google Scholar]
- Dong, L.; Yang, Q.; Wu, H.; Xiao, H.; Xu, M. High quality multi-spectral and panchromatic image fusion technologies based on Curvelet transform. Neurocomputing 2015, 159, 268–274. [Google Scholar] [CrossRef]
- Vaughn, V.D.; Wilkinson, T.S. System considerations for multispectral image compression designs. IEEE Signal Process. Mag. 1995, 12, 19–31. [Google Scholar] [CrossRef]
- Kaarna, A.; Zemcik, P.; Kalviainen, H.; Parkkinen, J. Compression of multispectral remote sensing images using clustering and spectral reduction. Ieee Trans. Geosci. Remote Sens. 2000, 38, 1073–1082. [Google Scholar] [CrossRef]
- Li, J.; Liu, F.; Liu, Z. Efficient multi-bands image compression method for remote cameras. Chin. Opt. Lett. 2017, 15, 022801. [Google Scholar]
- Li, J.; Xing, F.; Sun, T.; You, Z. Multispectral image compression based on DSC combined with CCSDS-IDC. Sci. World J. 2014, 2014, 738735. [Google Scholar] [CrossRef]
- Li, J.; Jin, L.; Zhang, R. An image compression method for space multispectral time delay and integration charge coupled device camera. Chin. Phys. B 2013, 22, 064203. [Google Scholar] [CrossRef]
- Markas, T.; Reif, J. Multispectral image compression algorithms. In Proceedings of the Data Compression of IEEE Conference, Snowbird, UT, USA, 30 March–2 April 1993; pp. 391–400. [Google Scholar]
- Schowengerdt, R.A. Reconstruction of multispatial, multispectral image data using spatial frequency content. Photogramm. Eng. Remote Sens. 1980, 46, 1325–1334. [Google Scholar]
- Epstein, B.R.; Hingorani, R.; Shapiro, J.M.; Czigler, M. Multispectral KLT-wavelet data compression for Landsat thematic mapper images. In Proceedings of the 1992 Data Compression IEEE Conference, Snowbird, UT, USA, 24–27 March 1992; pp. 200–208. [Google Scholar]
- Chang, L. Multispectral image compression using eigenregion-based segmentation. Pattern Recognit. 2004, 37, 1233–1243. [Google Scholar] [CrossRef]
- Ricci, M.; Magli, E. Predictor analysis for onboard lossy predictive compression of multispectral and hyperspectral images. J. Appl. Remote Sens. 2013, 7, 074591. [Google Scholar] [CrossRef]
- Wang, Z.; Nasrabadi, N.M.; Huang, T.S. Spatial–spectral classification of hyperspectral images using discriminative dictionary designed by learning vector quantization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4808–4822. [Google Scholar] [CrossRef]
- Cheng, K.J.; Dill, J. Lossless to lossy compression for hyperspectral imagery based on wavelet and integer KLT transforms with 3D binary EZW. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery of International Society for Optics and Photonics, Proceedings of the SPIE Defense, Security, and Sensing, Baltimore, MD, USA, 29 April–3 May 2013; SPIE: Bellingham, WA, USA, 2013; p. 87430U. [Google Scholar]
- Aulí-Llinàs, F.; Marcellin, M.W.; Serra-Sagrista, J.; Bartrina-Rapesta, J. Lossy-to-lossless 3D image coding through prior coefficient lookup tables. Inf. Sci. 2013, 239, 266–282. [Google Scholar] [CrossRef]
- Augé, E.; Sánchez, J.E.; Kiely, A.B.; Blanes, I.; Serra-Sagristà, J. Performance impact of parameter tuning on the CCSDS-123 lossless multi-and hyperspectral image compression standard. J. Appl. Remote Sens. 2013, 7, 074594. [Google Scholar] [CrossRef]
- Karami, A.; Yazdi, M.; Asli, A.Z. Hyperspectral image compression based on tucker decomposition and discrete cosine transform. In Proceedings of the 2nd International Conference on Image Processing Theory, Tools and Applications, Paris, France, 7–10 July 2010; pp. 122–125. [Google Scholar]
- Karami, A.; Yazdi, M.; Mercier, G. Compression of hyperspectral images using discerete wavelet transform and tucker decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 444–450. [Google Scholar] [CrossRef]
- Sidiropoulos, N.D.; Kyrillidis, A. Multi-way compressed sensing for sparse low-rank tensors. IEEE Signal Process. Lett. 2012, 19, 757–760. [Google Scholar] [CrossRef]
- Li, N.; Li, B. Tensor completion for on-board compression of hyperspectral images. In Proceedings of the IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 517–520. [Google Scholar]
- Zhang, L.; Zhang, L.; Tao, D.; Huang, X.; Du, B. Compression of hyperspectral remote sensing images by tensor approach. Neurocomputing 2015, 147, 358–363. [Google Scholar] [CrossRef]
- Li, J.; Liu, Z. Compression of hyper-spectral images using an accelerated nonnegative tensor decomposition. Open Phys. 2017, 15, 992–996. [Google Scholar] [CrossRef]
- Li, J.; Xing, F.; You, Z. Compression of multispectral images with comparatively few bands using posttransform Tucker decomposition. Math. Probl. Eng. 2014, 2014, 296474. [Google Scholar] [CrossRef]
- Tucker, L.R. Some mathematical notes on three-mode factor analysis. Psychometrika 1966, 31, 279–311. [Google Scholar] [CrossRef] [PubMed]
- Phan, A.H.; Cichocki, A. Extended HALS algorithm for nonnegative Tucker decomposition and its applications for multiway analysis and classification. Neurocomputing 2011, 74, 1956–1969. [Google Scholar] [CrossRef]
- Cichocki, A.; Zdunek, R.; Phan, A.H.; Amari, S.I. Nonnegative Matrix and Tensor Factorizations; Wiley: Chichester, UK, 2009. [Google Scholar]
- Khelifi, F.; Bouridane, A.; Kurugollu, F. Joined spectral trees for scalable SPIHT-based multispectral image compression. IEEE Trans. Multimed. 2008, 10, 316–329. [Google Scholar] [CrossRef]
- Gonzalez-Conejero, J.; Bartrina-Rapesta, J.; Serra-Sagrista, J. JPEG2000 encoding of remote sensing multispectral images with no-data regions. IEEE Geosci. Remote Sens. Lett. 2010, 7, 251–255. [Google Scholar] [CrossRef]
- Blanes, I.; Serra-Sagristà, J. Pairwise orthogonal transform for spectral image coding. IEEE Trans. Geosci. Remote Sens. 2011, 49, 961–972. [Google Scholar] [CrossRef]
- Yu, G.; Vladimirova, T.; Sweeting, M.N. Image compression systems on board satellites. Acta Astronaut. 2009, 64, 988–1005. [Google Scholar] [CrossRef]
- Nebiker, S.; Annen, A.; Scherrer, M.; Oesch, D. A light-weight multispectral sensor for micro UAV—Opportunities for very high resolution airborne remote sensing. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1193–1199. [Google Scholar]
- Sankaran, S.; Khot, L.R.; Espinoza, C.Z.; Jarolmasjed, S.; Sathuvalli, V.R.; Vandemark, G.J.; Miklas, P.N.; Carter, A.H.; Pumphrey, O.M.; Pavek, M.J.; et al. Low-altitude, high-resolution aerial imaging systems for row and field crop phenotyping: A review. Eur. J. Agron. 2015, 70, 112–123. [Google Scholar] [CrossRef]
- Li, J.; Fu, B.; Liu, Z. Panchromatic image compression based on improved post-transform for space optical remote sensors. Signal Process. 2019, 159, 72–88. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J.C.W. Nonlocal Tensor Sparse Representation and Low-Rank Regularization for Hyperspectral Image Compressive Sensing Reconstruction. Remote Sens. 2019, 11, 193. [Google Scholar] [CrossRef]











| Categories | Methods | Main Advantages | Main Disadvantages |
|---|---|---|---|
| Prediction-based approaches | DPCM, LUT, CCSDS-MDC, etc. | Low-complexity | Low compression performance Weak fault-tolerance ability |
| Vector quantization approaches | Grouping vectors, quantizing vector, etc. | Moderate compression performance | Without fast algorithm |
| transform-based approaches | KLT + 2DWT, KLT + 2DCT, KLT + post wavelet transform, etc. | High compression performance | High-order dependencies still exists |
| Tensor decomposition-based approaches | NTD + DWT, NTD + DCT, etc. | High compression performance | Without high-order dependencies High computation complexity |
| Notation | Description |
|---|---|
| n-dimensional real vector space | |
| Outer product | |
| n-mode product of a tensor by matrix | |
| n-mode matrix in Tucker model | |
| Product operator |
| Notation | Description |
|---|---|
| Hadamard product | |
| Element-wise division | |
| Kronecker product | |
| p-norm (length) of the vector x, where p = 1, 2 |
| Methods | 0.25 bpp (dB) | 0.5 bpp (dB) | 1 bpp (dB) | 2 bpp (dB) |
|---|---|---|---|---|
| POT | 38.17 | 43.10 | 46.23 | 51.67 |
| PCA | 38.88 | 43.60 | 46.62 | 51.91 |
| SPIHT + 2D-DWT with KLT | 39.78 | 44.35 | 47.34 | 52.47 |
| SPECK + 2D-DWT with KLT | 40.79 | 44.88 | 47.79 | 52.63 |
| CNN | 41.41 | 45.65 | 48.12 | 52.93 |
| Contents | NTD + DWT | Our Methods | Improvement |
|---|---|---|---|
| Average compression times | 10.1990 s | 4.3829 s | 49.66% |
| Average PSNR | 41.8497 dB | 41.5128 | −0.3369 |
| Contents | Evaluation | Analysis |
|---|---|---|
| Compression performance | Slightly lower than conventional NTD | CNN achieves a compression tensor NTD does not involve the CNN Fast multilevel NTD is used to surface |
| Complexity | Higher computation efficiency | Small-scale NTD decomposition Fast multilevel NTD |
| Hardmard Transform in CNN | Lower PSNR than DCT-CNN | In the convolution neural learning network, transform method is different from one used in compression link. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liu, Z. Multispectral Transforms Using Convolution Neural Networks for Remote Sensing Multispectral Image Compression. Remote Sens. 2019, 11, 759. https://doi.org/10.3390/rs11070759
Li J, Liu Z. Multispectral Transforms Using Convolution Neural Networks for Remote Sensing Multispectral Image Compression. Remote Sensing. 2019; 11(7):759. https://doi.org/10.3390/rs11070759
Chicago/Turabian StyleLi, Jin, and Zilong Liu. 2019. "Multispectral Transforms Using Convolution Neural Networks for Remote Sensing Multispectral Image Compression" Remote Sensing 11, no. 7: 759. https://doi.org/10.3390/rs11070759
APA StyleLi, J., & Liu, Z. (2019). Multispectral Transforms Using Convolution Neural Networks for Remote Sensing Multispectral Image Compression. Remote Sensing, 11(7), 759. https://doi.org/10.3390/rs11070759