Next Article in Journal
Accounting for Surface Roughness Scattering in the Characterization of Forest Litter with Ground-Penetrating Radar
Previous Article in Journal
A Random Forest Method to Forecast Downbursts Based on Dual-Polarization Radar Signatures
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 11
Issue 7
10.3390/rs11070827
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Monitoring Reservoir Drought Dynamics with Landsat and Radar/Lidar Altimetry Time Series in Persistently Cloudy Eastern Brazil

by
Jamon Van Den Hoek
1,*,
Augusto Getirana
2,3,
Hahn Chul Jung
3,4,
Modurodoluwa A. Okeowo
5 and
Hyongki Lee
5
1
Geography Program, College of Earth, Ocean, and Atmospheric Sciences, Oregon State University, Corvallis, OR 97331, USA
2
Earth System Science Interdisciplinary Center, University of Maryland, College Park, MD 20740, USA
3
Hydrological Sciences Laboratory, NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
4
Science Systems and Applications, Inc., Lanham, MD 20706, USA
5
Department of Civil and Environmental Engineering, University of Houston, Houston, TX 77005, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2019, 11(7), 827; https://doi.org/10.3390/rs11070827
Submission received: 5 March 2019 / Revised: 1 April 2019 / Accepted: 4 April 2019 / Published: 6 April 2019
Browse Figures
Versions Notes

Abstract

:
Tropical reservoirs are critical infrastructure for managing drinking and irrigation water and generating hydroelectric power. However, long-term spaceborne monitoring of reservoir storage is challenged by data scarcity from near-persistent cloud cover and drought, which may reduce volumes below those in the observational record. In evaluating our ability to accurately monitor long-term reservoir volume dynamics using spaceborne data and overcome such observational challenges, we integrated optical, lidar, and radar time series to estimate reservoir volume dynamics across 13 reservoirs in eastern Brazil over a 12-year (2003–2014) period affected by historic drought. We (i) used 1560 Landsat images to measure reservoir surface area; (ii) built reservoir-specific regression models relating surface area and elevation from ICESat GLAS and Envisat RA-2 data; (iii) modeled volume changes for each reservoir; and (iv) compared modeled and in situ reservoir volume changes. Regression models had high goodness-of-fit (median RMSE = 0.89 m and r = 0.88) across reservoirs. Even though 88% of an average reservoir’s volume time series was based on modeled area–elevation relationships, we found exceptional agreement (RMSE = 0.31 km3 and r = 0.95) with in situ volume time series, and accurately captured seasonal recharge/depletion dynamics and the drought’s prolonged drawdown. Disagreements in volume dynamics were neither driven by wet/dry season conditions nor reservoir capacity, indicating analytical efficacy across a range of monitoring scenarios.

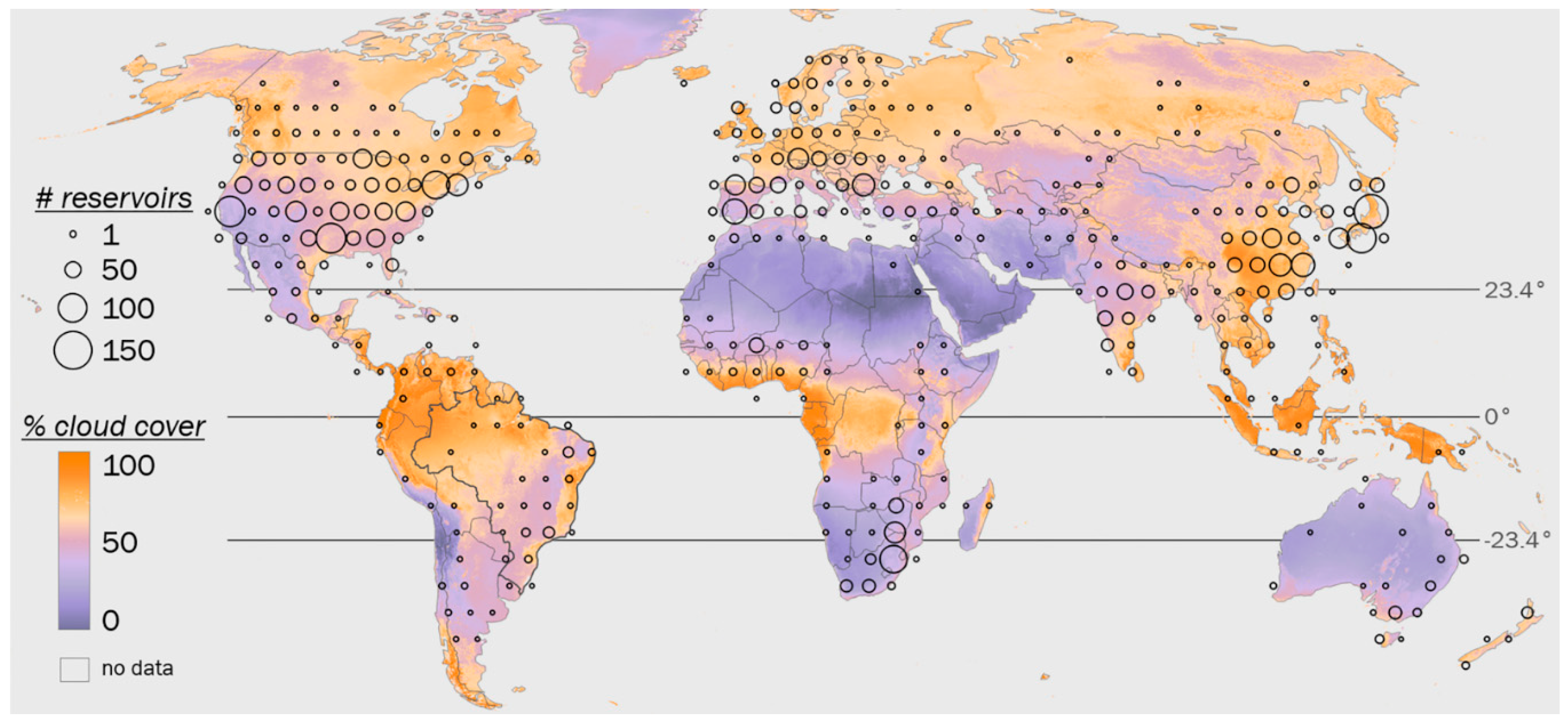
1. Introduction

Reservoirs are critical global infrastructure that occupy at least 26 × 104 km2 (0.2%) of global land surface area and contribute 6 × 103 km3 (0.0004%) of global freshwater storage [1]. The freshwater held by reservoirs is essential for meeting global demand for drinking water, irrigation water for agriculture [2,3], and hydroelectric power generation [4]. Recent research has identified the dual roles of reservoirs in atmospheric carbon dynamics being large-scale sites of both carbon sequestration as well as greenhouse gas emission [5,6,7,8,9,10,11]. Tropical reservoirs only make up 15% (1040) of the 6824 Global Reservoir and Dam (GRanD) Database reservoirs [12] but play a relatively outsized role in atmospheric carbon flux compared to temperate reservoirs [13,14,15,16,17,18]. Consistent, systematic, and long-term monitoring of reservoir storage throughout drought as well as high precipitation periods is essential to understanding the role of tropical reservoirs on society and environment [8,16]).
Reservoir storage is temporally dynamic and satellite remote sensing time series from optical (e.g., Landsat, MODIS, Sentinel-2) and radar or lidar (e.g., Envisat, GLAS/ICESat) systems support systematic monitoring of changes in reservoir volume at low cost per reservoir [19,20,21,22,23,24,25,26,27]. Spaceborne observation of reservoir dynamics are especially valuable for geographically remote or high-elevation reservoirs where consistent and long-term monitoring are a challenge, or in regions where the cost of constructing or maintaining a hydrologic gauge network is prohibitively expensive [28,29,30]. However, optical remote sensing of tropical reservoir dynamics is complicated by persistent cloud cover [31,32,33]. Indeed, as shown in Figure 1, the 178 Brazilian reservoirs included in GRanD are on average obscured by clouds 54% of days between 2003 and 2014.
In addition to the challenges of persistent cloud cover, monitoring long-term tropical reservoir dynamics is complicated by sensor spatial resolution, satellite revisit period, and, in some cases, a limited observational record. MODIS has regularly been used to monitor reservoir dynamics at sub-monthly time scales (e.g., [23,25,35]). While spectral unmixing of MODIS imagery has been effective at measuring sub-pixel fractional water area [36,37], the relatively coarse 250 m spatial resolution impedes detection of the reservoir edge and quantification of fine-scale surface area changes (e.g., [38]) with heightened consequences for reservoirs with shallow sloped near-surface bathymetry [25]. Landsat’s 30 m spatial resolution, over 40 years of global coverage makes it well suited for long-term, high spatial resolution monitoring of reservoir surface water dynamics [39,40,41,42,43]. Unfortunately, Landsat’s 16-day revisit period limits the opportunities to mitigate cloud cover or haze compared to 8- or 16-day MODIS temporal composites [44], which further restricts opportunities for pairing surface area estimates with concurrent altimetry elevation observations. While spaceborne radar is broadly robust to atmospheric effects, altimeters on TOPEX/Poseidon and Jason-1, 2, and 3 satellites with 3–10 km spatial resolutions are not well suited for monitoring smaller reservoirs [45,46]. More recent platforms such as and Cryosat-2 and Sentinel 3 have higher spatial resolution but lack long-term coverage [24,47,48]. However, Envisat RA-2 (Radar Altimeter 2) radar (2002–2012) and ICESat GLAS (Geoscience Laser Altimeter System) lidar (2003–2010) altimeters lend themselves to reservoir monitoring applications given their sub-kilometer resolution and many years of coverage [28,35,49,50,51,52].
Using a case study of 13 reservoirs in eastern Brazil, the goal of this study is to accurately model tropical reservoir volume dynamics from 2003 to 2014 despite near-persistent cloud cover and reservoir depletion due to a historic drought in 2014. To achieve our goal, we estimated surface area and elevation across study reservoirs by integrating Landsat, Envisat RA-2, and ICESat GLAS time series, modeling surface area–elevation relationship, calculating volume changes over the study period, and assessing agreement between modeled and in situ volume time series data per date, month, and year with attention to differences in agreement before and during the drought.

2. Materials and Methods

2.1. Study Area

Brazil is the largest (8.5 million km2) and most populous country (approximately 209 million residents in 2017) in South America. The country is dominated by tropical rain forest in its west and north, has tropical semideciduous forest along its southeastern Atlantic coast with tropical savannas (cerrado) stretching between the Brazilian Highlands to the Mato Grosso Plateau, and is home to major urban population centers including São Paulo, Rio de Janeiro, and the capital, Brasilia, in the eastern half of the country. Brazil has the largest reserve of renewable surface water in the world, approximately 32% of which is used for agricultural production [53]. Beginning in 2012, changing atmospheric circulation patterns, declining rainfall, and increased temperatures culminated in the summer of 2014 being the warmest and driest since 1951 [54] and a series of historically intense droughts that parched extensive cropland, dwindled drinking water supply, and shrank Brazil’s rivers and reservoirs [55,56].
During the peak of the drought in the summer of 2014, national hydroelectric production declined by approximately 20% compared to average 2000–2010 levels, and the Cantareira reservoir system relied upon by São Paulo saw nearly 11% reduction in its total capacity [53]. Over half of Brazil’s largest reservoirs (by hydroelectric production) are located in the drought-affected eastern region of the country. Thirteen reservoirs were included in this study that span southeast Brazil (Figure 2) with at least three dates of observation between Envisat and GLAS. Four study reservoirs–Agua Vermelha, Furnas, Marimbondo, and Tres Marias—with a range in nominal storage capacity from 1.3 to 34.1 km3 and a diversity of inter-annual storage dynamics were selected for focused data presentation below with the remaining reservoirs’ data included in the Appendix A.

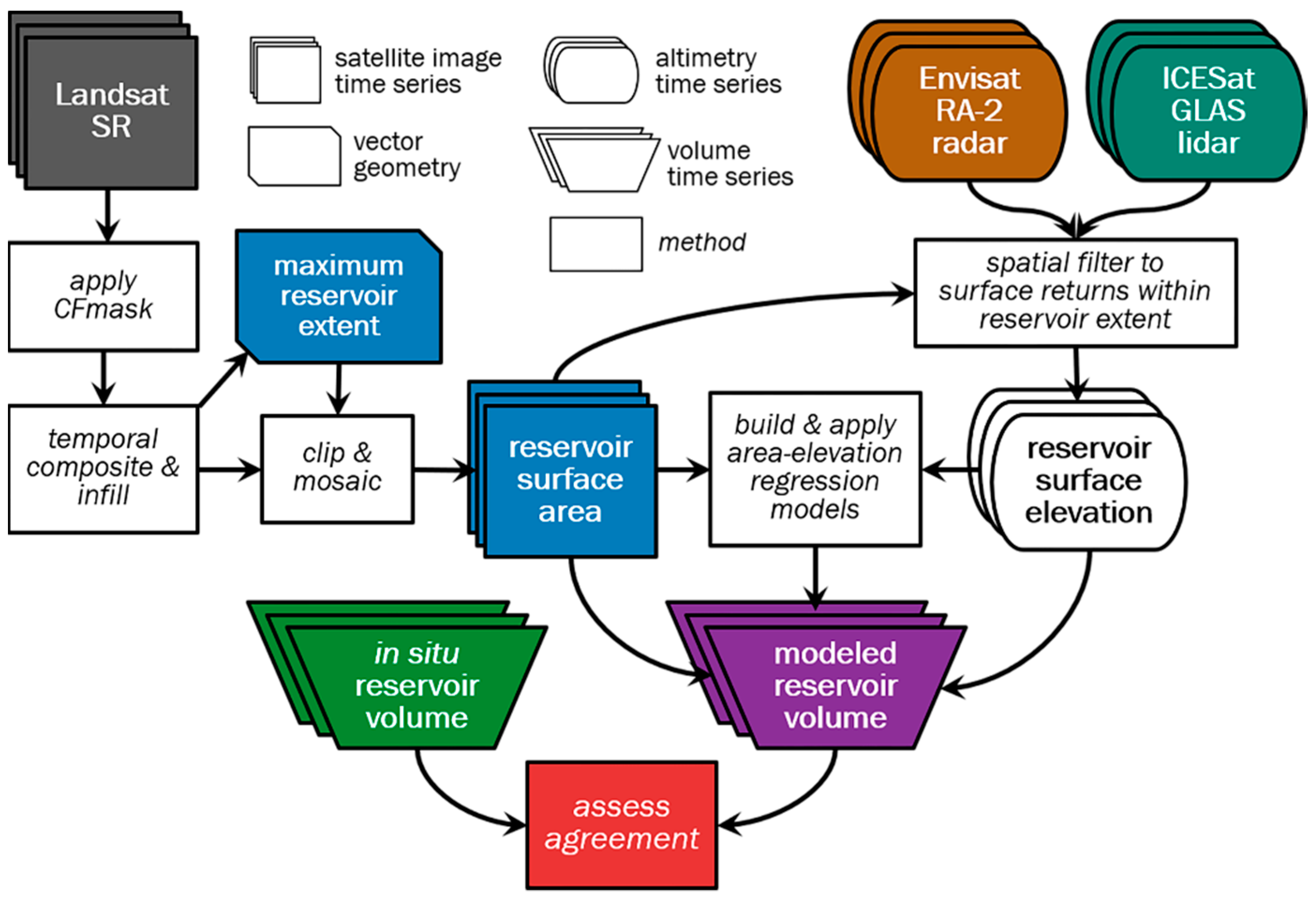
2.2. Modeling Framework

The volumetric modeling framework (Figure 3) for a given reservoir comprised five main objectives: (1) generate reservoir surface area time series; (2) generate surface elevation time series; (3) build and apply a linear regression model relating surface area and elevation; (4) estimate volumetric change over the study period; and (5) assess agreement between modeled and in situ volumes.

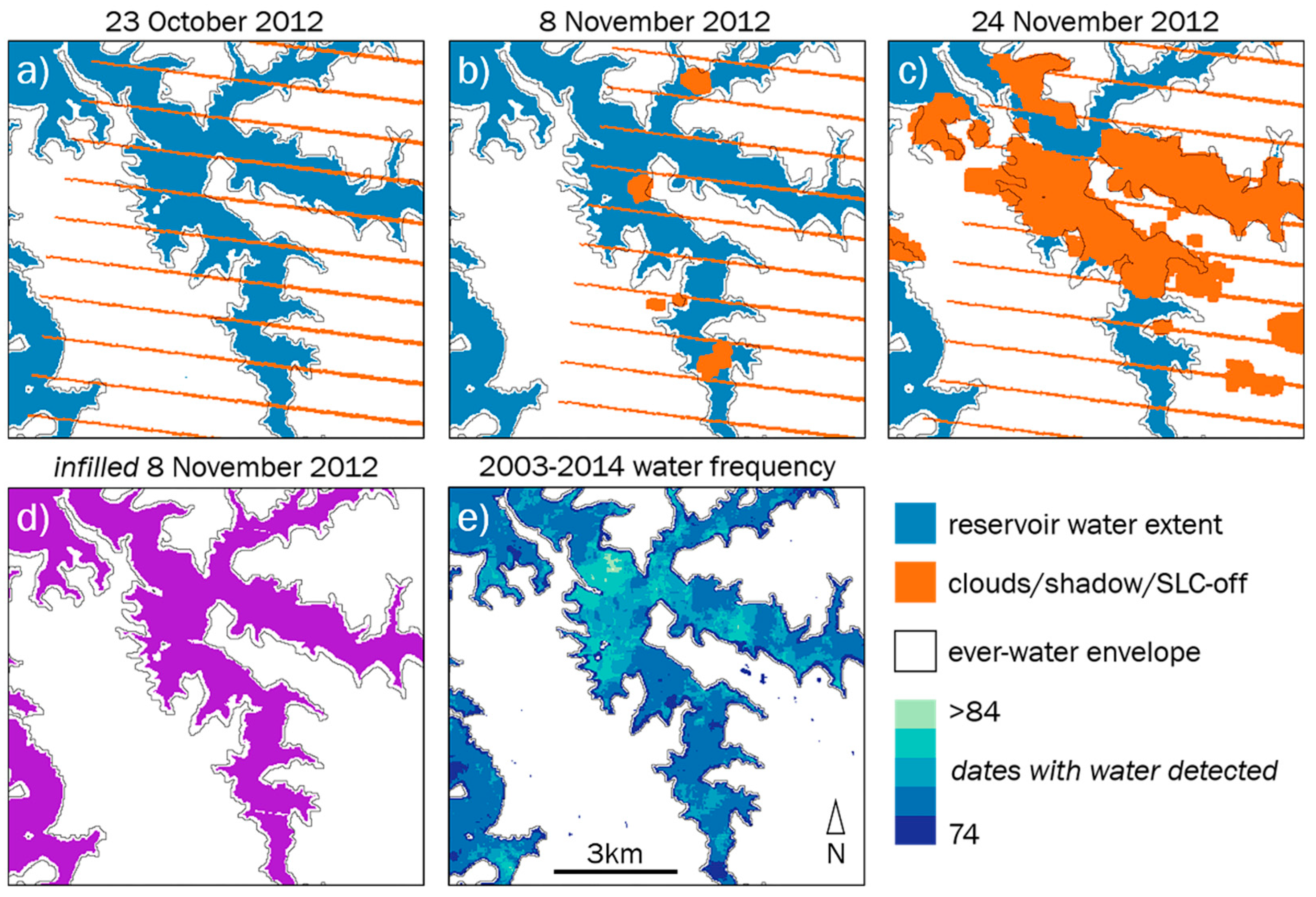
2.3. Surface Area Time Series Generation

The 13 study reservoirs collectively span 15 Landsat WRS-2 path-row footprints, with three reservoirs stretching across 2–4 footprints, respectively. A total of 1460 Landsat 5, 7, and 8 surface reflectance (SR)-corrected scenes with 20% or less cloud cover were collected from 2003 through 2014; this cloud cover threshold reduced the likelihood of missing data due to cloud cover while still supporting an intra-annually dense time series. We measured surface water time series with the commonly used Modified Normalized Difference Water Index (MNDWI), which is effective at discriminating water from non-water features [57]. We included all pixels that have a MDWI value larger than 0.1 as ‘water’ for each image date. Missing pixels associated with clouds, shadows, and Landsat 7’s Scan Line Corrector (SLC) Error data gaps were identified and removed using Landsat’s CFmask product. For each image’s missing pixels, pixels from images collected within a 36-day window before/after (e.g., Figure 4a–c) were infilled into the image, prioritized by the nearest date of observation (e.g., Figure 4d). Infilling using a 36-day temporal window ensured inclusion of images from up to two along-track (every 16 days) and up to four across-track (7 or 9 days) observations and reduced the amount of missing data within an average reservoir from 8.6% to 1.2% (Figure 5). On some dates, an image’s missing pixels could not be directly infilled through temporal compositing; in this case, if these missing pixels were in locations classified as ‘water’ on at least the median frequency for a given reservoir, the missing pixels were automatically included in the surface water extent. A reservoir’s water frequency map showing the total number of days when ‘water’ was detected (Figure 4e) was also used to generate a consistent spatial extent within which surface water area was measured: pixels classified as ‘water’ on at least two dates made up an ‘ever-water’ envelope for this purpose (shown in Figure 4). Finally, each reservoir’s surface area time series was clipped by an integrated (i.e., upstream to dam wall) reservoir region that was visually interpreted using very high-resolution imagery hosted by Google Earth.

2.4. Surface Elevation Time Series Generation

Separate surface water elevation time series were built using Envisat RA-2 (2002–2010) and ICESat GLAS (2003–2009) altimetry data, respectively. The long wavelength of Envisat’s RA-2 (Ku-band) radar altimetry provides resilience to cloud cover effects while the vertical profiling capabilities of ICESat’s GLAS support the discrimination of ground-level conditions in all but the densest cloud cover [31,58]. Both RA-2 and GLAS datasets are suitable for reservoir monitoring with along-track sampling distances of approximately 350 and 172 m, nominal footprint sizes of approximately 2 km and 70 m, and vertical accuracies (i.e., RMSE) of approximately 50 and 15 cm [59], respectively. Envisat altimetry has often been used for measuring freshwater surface elevation changes (e.g., [60,61,62,63,64,65,66,67] though ICESat has been used less often for monitoring surface water dynamics due to its erratic operational history of premature laser failures see [68] with notable exceptions (e.g., [69,70,71,72,73]).
The Envisat RA-2 surface elevation time series was generated using an automated return clustering algorithm detailed in [74], which yielded an average RMSE of 48.9 cm compared to in situ gauge observation data across study reservoirs. ICESat GLAS GLA14 product (Level-2 Global Land Surface Altimetry; [75]) data were filtered to single Gaussian peak returns typical of surface water, saturated returns were corrected or removed using the saturation index, and surface elevation was calculated at the centroid of the single Gaussian peak. All RA-2 and GLAS surface returns collected within 15 days of a Landsat surface area measurement were spatially filtered by the surface area perimeter buffered inwards by 100 m to eliminate potential measurement of near-surface topography. The median elevation over a reservoir’s extent on a given date was measured and used to generate reservoir elevation and volume time series. Since GLAS’ reference ellipsoid (equatorial radius = 6378.1363 km; flattening coefficient = 1/298.257) is offset 70 cm from RA-2’s WGS 84 ellipsoid, GLAS elevation data were adjusted to fit the WGS 84 vertical datum following [76].

2.5. Surface Area–Elevation Model Generation

Surface area and elevation time series were used to estimate changes in reservoir volumes. However, since the vast majority of surface area measurements lacked same-day measurements of surface elevation, regression models were built for each reservoir to relate surface area measurements to altimeter elevations collected within 15 days of the surface area measurement; linear regression was used following successful regional application (e.g., [23,25,49]). Modeled surface elevation values based on measured surface areas were used to build an elevation time series with the same temporal sampling as the surface area time series. The goodness-of-fit of each reservoir’s area-elevation model was measured using the Pearson correlation coefficient (r) and the root mean square error (RMSE).

2.6. Volume Time Series Generation

As the volume of a reservoir with unknown bathymetry cannot be remotely measured, the reservoir was rather conceived as a circular cone with a series of water layers as detailed in [77]. Reservoir volume on a given date, t, was based on changes in surface area and elevation time series data measured relative to the median 2003–2011 volume (before the drought):
V m e d − t = 1 3 ( z t − z m e d ) ∗ ( A m e d + A t + ( A m e d ∗ A t ) )
where, Vmed-t represents the relative difference in volume, Amed and At and zmed and zt represent surface areas and elevations based on median 2003–2011 values and the date of observation, respectively. The median 2003–2011 in situ volume was measured for each reservoir to serve as a pre-drought baseline, and the relative volume difference for each date of in situ observation was measured.

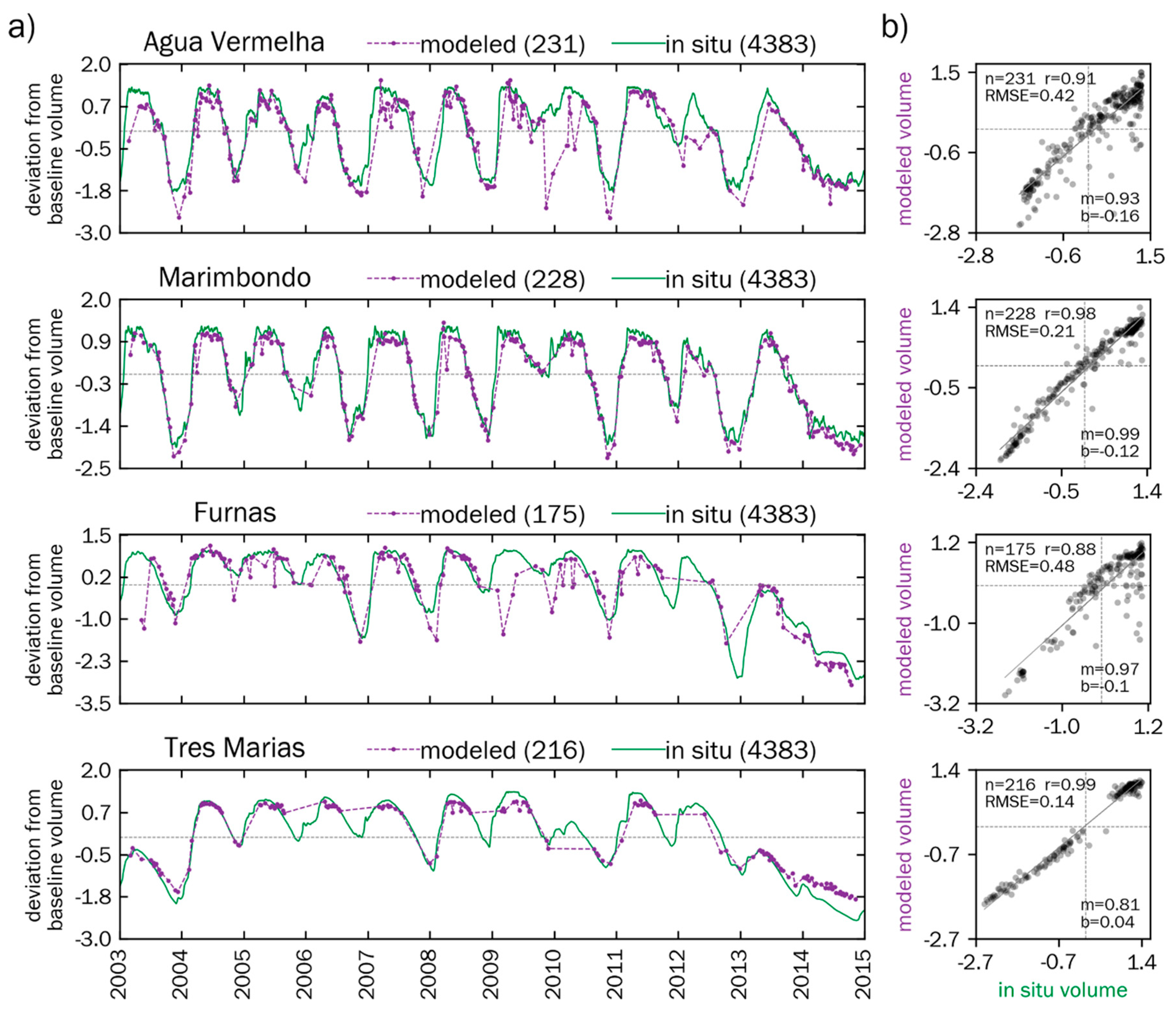
2.7. Comparison between In Situ and Modeled Volumetric Time Series

Changes in modeled reservoir volumes were compared to a median 4383 daily in situ reservoir volume measurements collected from 2003–2014 by the Brazilian Electric Sector available at http://www.ons.org.br/. However, study reservoir boundaries deviated from (unavailable) management boundaries used by the Brazilian Electric Sector to collect in situ volume and modeled and in situ volume time series could not be directly compared. To mitigate this disparity, both time series were standardized to preserve relative variations with the following equation:
S t = ( V t − V ¯ ) σ
where St and Vt are standardized and modeled volume changes for a given reservoir on date, t, respectively, and V ¯ and σ are the mean and standard deviation of modeled volume changes over the full time series, respectively. Using standardized (unitless) values, the agreement between modeled and in situ volume dynamics time series were assessed using linear regression, r, and RMSE, and annual and monthly agreement between modeled and in situ data were evaluated.

3. Results

3.1. Surface Area and Elevation Time Series

Over the 12-year study period, a median 216 Landsat image dates were used to generate each reservoir surface area time series (Figure 6 and Figure A1). Prior to the drought’s intensification in 2014, reservoirs typically reached their lowest extent in December or January before recharging to the maximum surface area between March and June following the end of the rainy season. Surface water expansion and contraction was highly dynamic with a median annual range (i.e., difference between maximum and minimum) of reservoir surface areas representing 31.3% of the maximum surface area in the pre-drought 2003–2011 period. During the drought period (2012–2014), this range was nominally consistent at 30.7% though the minimum and maximum surface areas declined relative to the pre-drought period by median 4.5% and 3.6%, respectively. Seasonal dynamics shifted under the drought, as well, as early year recharge was typically reduced in 2012 and 2013 and absent by 2014. Reservoirs such as Furnas and Tres Marias contracted during the drought so much that low surface areas (below 900 km2 and 350 km2, respectively) were without precedent in the pre-drought time series.
While each reservoir’s seasonal dynamics are apparent, there was often a disproportionate exclusion of cloudy wet season imagery (October–March; Figure 7a and Figure A2). Conversely, since cloud-free observations are more likely in eastern Brazil during winter months, there is a relative abundance of imagery available in July and August when reservoirs tend to be near capacity. Fewer images and generally more cloud cover during the wet season meant fewer near-date images for infilling and compositing, which may yield a larger amount of residual missing data and low biased surface area estimates [33], as well as fewer surface area measurements with which to couple elevation data. While the collection of surface elevation values was not affected by atmospheric conditions in the same way as surface area measurements, having a larger surface area (unobstructed by clouds) meant that more altimetric returns could be collected over the reservoir body (Figure 7b and Figure A3).

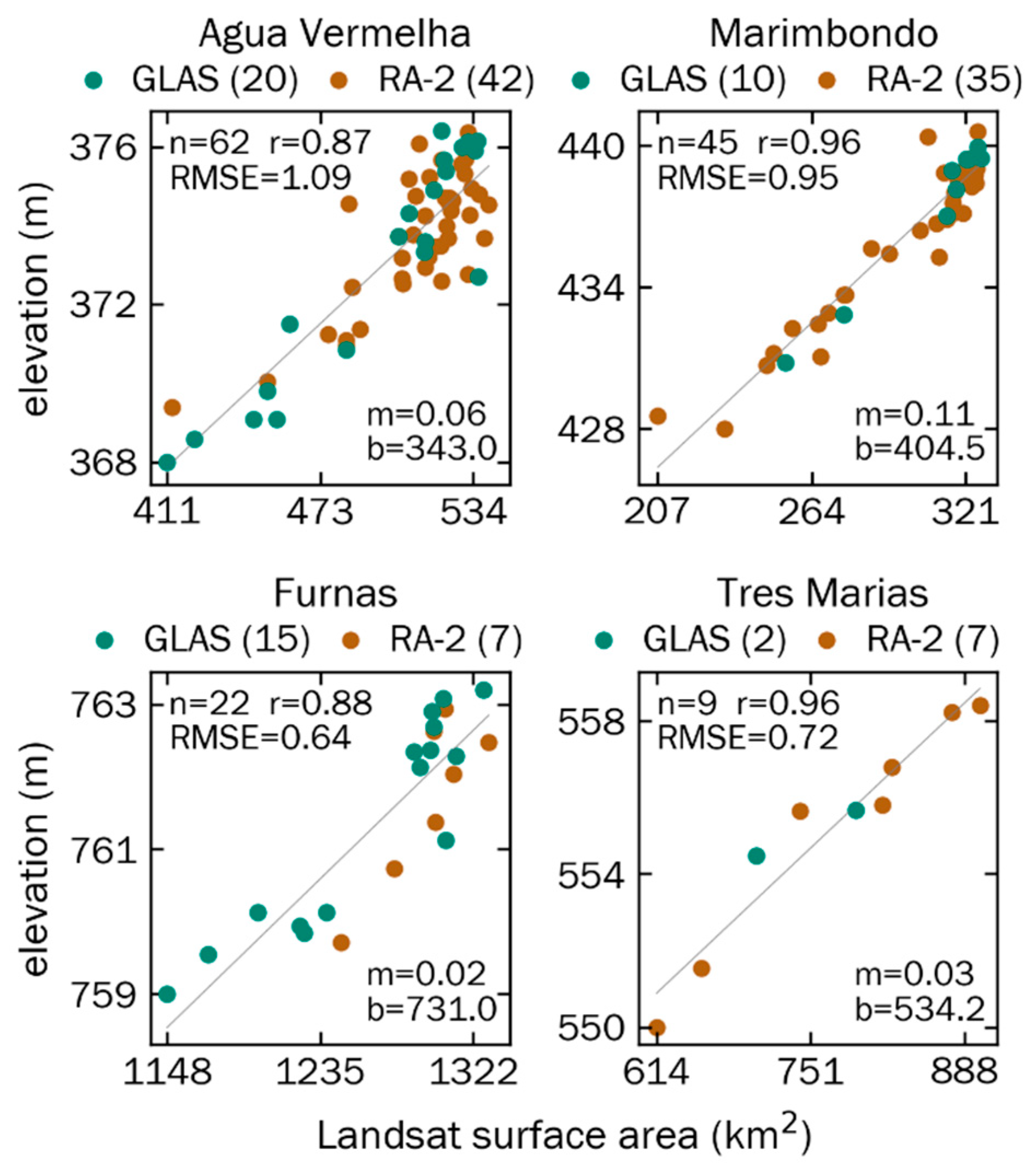
3.2. Modeled Surface Area–Elevation Relationships

Linear regression models relating Landsat-derived surface area and altimeter-derived surface elevation measurements were built for the 13 study reservoirs (Figure 8 and Figure A4). The median number of area–elevation pairs for “combined” regression models was 21, with 13 and 17 measurements for GLAS- and RA-2-specific models, respectively. Combined linear models showed high goodness-of-fit with a median RMSE of 0.89 m and r of 0.88 across reservoirs. A poor model may reflect a combination of seasonal variation in surface area and elevation, differences in Landsat and altimetry acquisition dates, variation in bathymetric slope along a reservoir’s perimeter and across its depth, as well as lingering cloud cover effects. Though GLAS and RA-2 elevations span a median 74.9% of reservoir surface area range (highlighted in grey in Figure 6 and Figure A1), the elevation distribution is often skewed towards including higher elevations. This skew is most pronounced for reservoirs with fewer dates of observation during the wet season as well as those with a smaller surface area, which limits the area within which altimetry data could be collected. The contraction of surface areas during the drought also limited potential for coupling surface area-elevation values as very low surface areas during the drought had no paired elevation values.
GLAS-specific models provided a slightly better fit with median RMSE = 0.68 m and r = 0.94 compared to RA-2’s RMSE = 0.94 m and r = 0.90 (see Table A1). The better fit provided by GLAS is expected given its higher vertical accuracy and smaller footprint. For the 8 of 11 reservoirs with both GLAS and RA-2 coverage over the study period, GLAS also captured a larger surface area range despite GLAS having fewer samples for these reservoirs (see Figure A4). Further, GLAS alone provided coverage for two reservoirs, Ilha Solteira and Sao Simao. Despite the driving role of GLAS data in shaping surface area–elevation models, there remains considerable value in combining altimeter measurements into a single area–elevation model. Since GLAS and RA-2 captured reservoirs at different stages over the time series, combining altimetric observations in a single model expanded the seasonality of coverage, which helped compensate for irregularity of observations at a given reservoir. Combining altimetric data also increased the average range of observed surface elevations across reservoirs by at least 1.3 m compared to the elevation range observed by either GLAS or RA-2 alone. This expanded range supports characterizing reservoir dynamics from the drawdown through recharge conditions, which is especially valuable for reservoirs with a large annual range, e.g., Agua Vermelha. 3.3. Volume Time Series and In Situ Comparison.
Across reservoirs, the median modeled volume time series is composed of 216 time steps (Figure 9a and Figure A5a). Of these, 88% of time series values were based on reservoir-specific surface area–elevation regression models (i.e., Figure 8) while the remaining 12% were based on direct observations. While some reservoirs such as Agua Vermelha have a clear, consistent seasonality with a pronounced annual recharge and depletion, other reservoirs such as Chavantes or Sao Simao (see Figure A5) are much less dynamic. Linear regression models showed exceptionally high agreement between modeled and in situ volumetric changes with median RMSE = 0.31 km3 and r = 0.95 (Figure 9b). The low median bias of 0.11 km3 indicates an underestimation of in situ volume, and, indeed, each reservoir’s maximum modeled volume was consistently less than the maximum in situ volume. This divergence likely results from the mismatch between reservoir boundaries used to generate modeled values and boundaries considered in in situ data collection, differing 2003–2011 reference volumes, and spuriously low modeled volumes that most often occur during the wet season.
To examine intra-annual variation in agreement, the mean absolute difference between modeled and in situ volumetric change was estimated for each month (Figure 10 and Figure A6). Wet season months (October–March) showed higher disagreement than winter months (July–August) in 5 of 13 study reservoirs. Since reservoirs tend to have their lowest volumes during wet months of November–January, accurately modeling reservoir volumes during these low volume months would improve modeling of anomalously low volumes during drought periods. Considering inter-annual variation, the mean annual flux (i.e., the range of standardized volumes within a calendar year) of modeled and in situ time series only differed between 0.004 and 0.041 in 2003–2010 across reservoirs (Figure 11). With the drought came a larger disagreement of 0.62 in 2012 but was reduced to a very low disagreement of only 0.04 in 2014. The divergence between modeled and in situ flux in 2011–2013 was likely influenced by fewer Landsat images being collected after Landsat 5 operational imaging ended in November 2011, 17 months before Landsat 8’s operational imaging began in April 2013. The agreement in 2014 benefitted from Landsat 8’s data collection, a low annual flux due to the drought, and good fitting area–elevation regression models that allowed for estimating elevations beyond the range of historical direct observation.

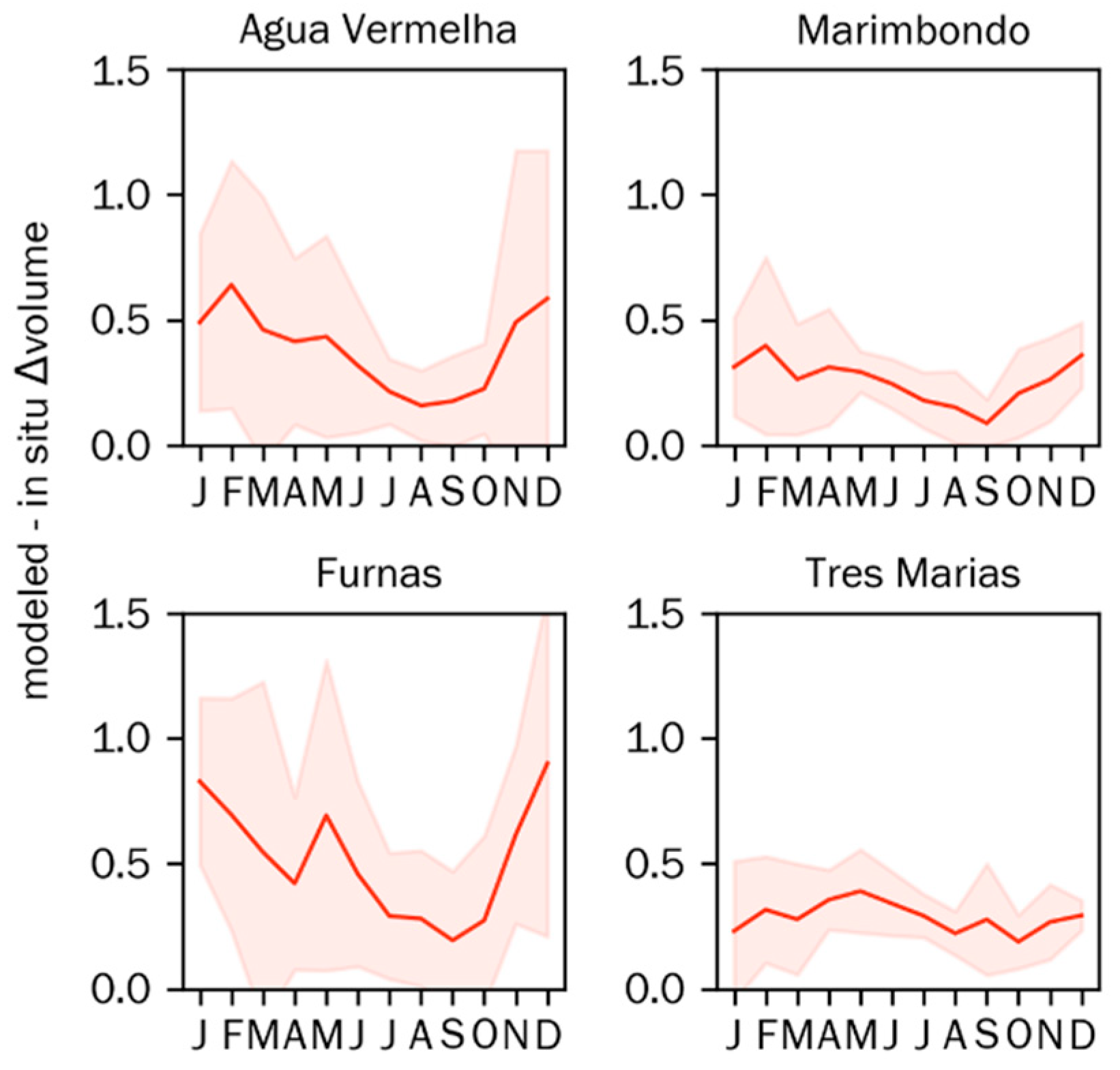
4. Discussion

Accurate long-term monitoring of reservoir dynamics achieved by this study is of paramount interest for assessing United Nations Development Program Sustainable Development Goal (SDG) 6 (Clean Water and Sanitation) and 7 (Affordable and Clean Energy) [78], managing national-level water resources, examining reservoir dynamics and hydroelectric power generation (e.g., [3]), assessing the impact of changing precipitation and temperature regimes on reservoir storage [54,56,79,80], and as input to or validation of hydrodynamic models (e.g., [81,82,83]. This study’s high agreement between remote sensing and in situ volumetric flux (i.e., RMSE = 0.31 km3) illustrates the potential for effective monitoring in tropical regions with persistent cloud cover or even those affected by historic drought.
Volumetric modeling is an essential tool in monitoring climate effects on global surface water dynamics especially in regions with unavailable or scarce in situ data [43]. This study builds on research by [19,20,22,23,24,25,65,84,85] in pursuing remote sensing-based estimation of reservoir volume dynamics. However, this research alongside [49] extends previous efforts by maintaining high accuracy in modeled volume changes outside the historical range of altimetric observations, in this case due to historic drought. Though the drought began in 2012, the reduction of reservoir surface areas, elevations, and volumes was broadly delayed across study reservoirs until 2013 as is evident in modeled and in situ volumetric change time series (e.g., Figure A5). In 2013, surface elevations at eight of the study reservoirs fell below the observed minimum surface elevation from 2000–2009; by 2014, 12 of the 13 study reservoirs had done so. Despite extrapolating surface area–elevation relationships to capture volumetric change in 2013–2014, the mean standardized modeled and in situ volumetric fluxes (e.g., Figure 11) were in agreement, thereby demonstrating the effectiveness of monitoring. Volume estimate accuracies for Tres Marias, Marimbondo, and others are comparable to those achieved by [19] (i.e., r = 0.99) despite this study’s challenges of persistent cloud cover and extreme volumetric loss.
Limited observational frequency remained a challenge in this study. The largest difference between mean annual standardized modeled and in situ volumetric fluxes was 0.62 (unitless) and measured in 2012. This did not result from drought-induced depletion but was rather associated with reduced surface area measurements since only Landsat 7 was operational in 2012. Nonetheless, despite intra-annual variability of surface area measurements, limited observational data, and drought-induced depletion of reservoir volume beyond the range of observations, agreement between modeled and in situ volume dynamics was high. This is perhaps best exemplified by Tres Marias, which lacked any altimetry observations for six months of the calendar year yet shows better agreement with in situ volume data (i.e., RMSE = 0.14 km3) than any other reservoir. Future volumetric modeling efforts will benefit from the increased observational frequency by including additional surface area time series from Sentinel-1, Sentinel-2, as well as the upcoming Surface Water and Ocean Topography (SWOT) mission [86]. Similarly, while no current hydrodynamic models accurately simulates reservoirs and lakes, recent developments on hydrological modeling have taken into account reservoir operation (e.g., [87,88,89]). Results presented in this study can therefore be used for further model evaluation and improvement of model parameters to better model human activities.
Errors inherent to the volumetric modeling approach include Landsat-derived surface area resolution, altimetry-derived vertical resolution, area–elevation linear regression modeling, and unavailable reservoir boundaries used for in situ data collection. Moreover, referencing the median water frequency coverage for infilling remaining pixels that could not be directly infilled with temporal compositing lead to overestimating surface area and volume on low volume days and underestimating surface area and volume on high volume days; this, in turn, degraded surface area-elevation correlations. While a linear area–elevation relationship that assumes a consistent bathymetric (i.e., hypsographic) profile across all depths and along the entire boundary of a given shoreline has been used effectively by other researchers (e.g., [23]), non-linear models have also been used to model sections or the entirety of a reservoir’s hypsographic profile (e.g., [36,85]). A more extensive examination of the relationship between reservoir dynamics and bathymetry would have added valuable information. Unfortunately, there were no available reference bathymetry datasets with which to evaluate this relationship, nor were there surface area validation time series data with which to evaluate the accuracy of surface area dynamics for any reservoir in the study. Including information from a high-resolution bathymetric model would have improved volumetric modeling effort [84].
There are several opportunities for improving the water classification through use of a more advanced classification approach sensitive to reservoir-specific hydrologic conditions such as clarity, turbidity, and bathymetry, e.g., [90]. The results of this study point towards more effective monitoring using recently launched sensors such as Sentinel 1 and 2 [91,92,93]. The use of 20 m spatial resolution Sentinel 2A and 2B time series data with a nominal 5-day temporal resolution rather than 30 m, 16-day repeat Landsat data have the potential to estimate much more detailed volumetric changes, especially for reservoirs with complex shorelines that cannot be readily captured with Landsat, let alone MODIS imagery. Use of imaging radars such Sentinel 1, SWOT, and RADARSAT-2 [94] with <100 m horizontal resolution and <10 cm vertical resolution as well as passive microwave sensors [95] offer data fusion opportunities that make the most of available optical and passive time series data.

5. Conclusions

This study presented a remote sensing-based approach for monitoring reservoir dynamics over a 12-year period (2003–2014), which included a historic two-year long drought. Using the case study of regularly clouded eastern Brazil, Landsat 5, 7, 8, ICESat GLAS, and Envisat RA-2 time series data were used to measure surface area, elevation, and volume time series for 13 study reservoirs of varying size and intra- and inter-annual dynamics. Volumetric changes have high overall agreement with in situ volumetric time series data as well as intra- and inter-annual agreement throughout the study period including the drought. The high agreement despite regular cloud obfuscation and drought depletion points the way towards routine, very high-resolution monitoring of reservoir dynamics in regions that lack existing or available in situ monitoring. While this study benefits from reservoir management data, anticipated applications extend to regularly clouded regions without existing or otherwise inaccessible data on reservoir dynamics.

Author Contributions

Conceptualization, J.V.D.H., A.G., and H.C.J.; Formal analysis, J.V.D.H., M.O., and H.L.; Methodology, J.V.D.H., A.G., and H.C.J.; Visualization, J.V.D.H.; Writing—original draft, J.V.D.H.; Writing—review & editing, J.V.D.H.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Remotesensing 11 00827 g0a1 550
Figure A1. Landsat-derived surface area time series for all 13 study reservoirs with dates of ICESat GLAS (green dot) and Envisat RA-2 (red dot) measurement. The gray background indicates the range of surface areas measured on altimetry data collection dates. Time series for select four reservoirs are shown in Figure 6.
Figure A1. Landsat-derived surface area time series for all 13 study reservoirs with dates of ICESat GLAS (green dot) and Envisat RA-2 (red dot) measurement. The gray background indicates the range of surface areas measured on altimetry data collection dates. Time series for select four reservoirs are shown in Figure 6.
Remotesensing 11 00827 g0a1
Remotesensing 11 00827 g0a2 550
Figure A2. Stacked monthly frequency of Landsat images for all 13 study reservoirs. Monthly frequency information for four selected reservoirs is in Figure 7.
Figure A2. Stacked monthly frequency of Landsat images for all 13 study reservoirs. Monthly frequency information for four selected reservoirs is in Figure 7.
Remotesensing 11 00827 g0a2
Remotesensing 11 00827 g0a3 550
Figure A3. Stacked monthly frequency of GLAS and RA-2 surface elevation observations for all 13 study reservoirs. Monthly frequency information for four selected reservoirs is in Figure 7.
Figure A3. Stacked monthly frequency of GLAS and RA-2 surface elevation observations for all 13 study reservoirs. Monthly frequency information for four selected reservoirs is in Figure 7.
Remotesensing 11 00827 g0a3
Remotesensing 11 00827 g0a4 550
Figure A4. Derived surface area–elevation linear regressions for all 13 study reservoirs based on Landsat surface area and combined GLAS and RA-2 elevation data. n = number of area–elevation pairs, r = Pearson correlation coefficient, RMSE = root mean square error, m = linear slope, and b = linear intercept. Area–elevation models for select four reservoirs are in Figure 8.
Figure A4. Derived surface area–elevation linear regressions for all 13 study reservoirs based on Landsat surface area and combined GLAS and RA-2 elevation data. n = number of area–elevation pairs, r = Pearson correlation coefficient, RMSE = root mean square error, m = linear slope, and b = linear intercept. Area–elevation models for select four reservoirs are in Figure 8.
Remotesensing 11 00827 g0a4
Table
Table A1. List of reservoir-specific linear regression model parameters and goodness-of-fit values for GLAS- or RA-2-specific models as well as ‘combined’ models. n = number of altimeter surface elevation measurements, m = linear slope, b = linear intercept, r = Pearson correlation coefficient, and RMSE = root mean square error.
Table A1. List of reservoir-specific linear regression model parameters and goodness-of-fit values for GLAS- or RA-2-specific models as well as ‘combined’ models. n = number of altimeter surface elevation measurements, m = linear slope, b = linear intercept, r = Pearson correlation coefficient, and RMSE = root mean square error.
Reservoir NameAltimeternmbrRMSE
Agua VermelhaGLAS200.070339.100.9331.054
RA-2420.054347.030.7771.055
combined620.062343.010.8671.088
Barra BonitaGLAS130.109419.130.8840.683
RA-220.097422.630.8390.745
combined150.100421.210.8550.710
CapivaraGLAS190.063295.130.9370.864
RA-2320.075288.460.7730.979
combined510.064294.410.8620.982
ChavantesGLAS90.077443.260.5480.799
RA-2120.087439.300.6810.902
combined210.082441.210.6220.887
EmborcacaoGLAS0--------
RA-2170.074615.690.9511.534
combined170.074615.690.9511.534
FurnasGLAS150.024730.670.9210.567
RA-270.038712.250.8630.559
combined220.024731.000.8830.641
Ilha SolteiraGLAS160.039275.780.8630.362
RA-20--------
combined160.039275.780.8630.362
ItumbiraGLAS160.054471.900.9770.861
RA-2450.045478.620.8401.994
combined610.048476.730.8721.869
MarimbondoGLAS100.127398.200.9850.504
RA-2350.102405.620.9540.995
combined450.106404.510.9580.947
Nova PonteGLAS80.129757.660.9681.210
RA-2240.113762.890.9420.887
combined320.119760.860.9521.028
Sao SimaoGLAS130.057358.410.9550.612
RA-20--------
combined130.057358.410.9550.612
SobradinhoGLAS100.004364.810.9630.544
RA-250.003367.010.9740.370
combined150.004366.130.9250.729
Tres MariasGLAS20.029535.310.9630.743
RA-270.029533.100.9770.658
combined90.028534.180.9640.719
Remotesensing 11 00827 g0a5 550
Figure A5. (a) Time series of difference between standardized reservoir volumes and each reservoir’s baseline, pre-drought (i.e., median 2003-2011) volume for modeled (purple) and in situ (green) data, respectively; for dates without altimetry data, regression-based elevation values are used in modeling volume. (b) Linear regressions relating standardized in situ and modeled volumes on dates of mutual observation. Light grey lines in (a) and (b) indicate zero values on respective axes. All volume values are in km3. Time series and regressions for four select reservoirs are in Figure 9.
Figure A5. (a) Time series of difference between standardized reservoir volumes and each reservoir’s baseline, pre-drought (i.e., median 2003-2011) volume for modeled (purple) and in situ (green) data, respectively; for dates without altimetry data, regression-based elevation values are used in modeling volume. (b) Linear regressions relating standardized in situ and modeled volumes on dates of mutual observation. Light grey lines in (a) and (b) indicate zero values on respective axes. All volume values are in km3. Time series and regressions for four select reservoirs are in Figure 9.
Remotesensing 11 00827 g0a5
Remotesensing 11 00827 g0a6 550
Figure A6. Mean monthly absolute difference between modeled and in situ standardized (unitless) volume changes (2003–2014; red line) with standard deviation range depicted (red field). Monthly comparisons for four select study reservoirs are in Figure 10.
Figure A6. Mean monthly absolute difference between modeled and in situ standardized (unitless) volume changes (2003–2014; red line) with standard deviation range depicted (red field). Monthly comparisons for four select study reservoirs are in Figure 10.
Remotesensing 11 00827 g0a6

References

  1. Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the volume and age of water stored in global lakes using a geo-statistical approach. Nat. Commun. 2016, 7, 13603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. García, L.; Rodríguez, D.; Wijnen, M.; Pakulski, I. (Eds.) Earth Observation for Water Resources Management: Current Use and Future Opportunities for the Water Sector; The World Bank: Washington, DC, USA, 2016; ISBN 978-1-4648-0475-5. [Google Scholar]
  3. Vörösmarty, C.J.; Sahagian, D. Anthropogenic Disturbance of the Terrestrial Water Cycle. Bioscience 2006, 50, 753. [Google Scholar] [CrossRef]
  4. Zambon, R.C.; Barros, M.T.L.; Yeh, W.W.G. Impacts of the 2012–2015 Drought on the Brazilian Hydropower System. In Proceedings of the World Environmental and Water Resources Congress 2016, West Palm Beach, FL, USA, 22–26 May 2016; American Society of Civil Engineers: Reston, VA, USA, 2016; pp. 82–91. [Google Scholar]
  5. Bastviken, D.; Tranvik, L.J.; Downing, J.A.; Crill, P.M.; Enrich-Prast, A. Freshwater methane emissions offset the continental carbon sink. Science 2011, 331. [Google Scholar] [CrossRef] [PubMed]
  6. Fearnside, P.M. Do hydroelectric dams mitigate global warming? The case of Brazil’s Curuá-Una Dam. Mitig. Adapt. Strateg. Glob. Chang. 2005, 10, 675–691. [Google Scholar] [CrossRef]
  7. Kosten, S.; van den Berg, S.; Mendonça, R.; Paranaíba, J.R.; Roland, F.; Sobek, S.; Van Den Hoek, J.; Barros, N. Extreme drought boosts CO2 and CH4 emissions from reservoir drawdown areas. Inland Waters 2018, 8, 329–340. [Google Scholar] [CrossRef]
  8. Mendonça, R.; Kosten, S.; Sobek, S.; Barros, N.; Cole, J.J.; Tranvik, L.; Roland, F. Hydroelectric carbon sequestration. Nat. Geosci. 2012, 5, 838–840. [Google Scholar] [CrossRef] [Green Version]
  9. Rudd, J.W.M.; Hecky, R.E.; Harris, R.; Kelly, C.A. Are hydroelectric reservoirs significant sources of greenhouse gases. Ambio 1993, 22, 246–248. [Google Scholar]
  10. Duchemin, É.; Rudd, J.W.M.; St. Louis, V.L.; Kelly, C.A.; Rosenberg, D.M. Reservoir Surfaces as Sources of Greenhouse Gases to the Atmosphere: A Global Estimate. Bioscience 2006, 50, 766. [Google Scholar]
  11. Knoll, L.B.; McKnight, D.M.; Larsen, S.; Dillon, P.; Fortino, K.; Cotner, J.B.; Striegl, R.G.; Prairie, Y.; Finlay, K.; Sherman, B.S.; et al. Lakes and reservoirs as regulators of carbon cycling and climate. Limnol. Oceanogr. 2011, 54, 2298–2314. [Google Scholar]
  12. Lehner, B.; Liermann, C.R.; Revenga, C.; Vörömsmarty, C.; Fekete, B.; Crouzet, P.; Döll, P.; Endejan, M.; Frenken, K.; Magome, J.; et al. High-resolution mapping of the world’s reservoirs and dams for sustainable river-flow management. Front. Ecol. Environ. 2011, 9, 494–502. [Google Scholar] [CrossRef]
  13. Barros, N.; Cole, J.J.; Tranvik, L.J.; Prairie, Y.T.; Bastviken, D.; Huszar, V.L.M.; del Giorgio, P.; Roland, F. Carbon emission from hydroelectric reservoirs linked to reservoir age and latitude. Nat. Geosci. 2011, 4, 593–596. [Google Scholar] [CrossRef]
  14. Deshmukh, C.; Serça, D.; Delon, C.; Tardif, R.; Demarty, M.; Jarnot, C.; Meyerfeld, Y.; Chanudet, V.; Guédant, P.; Rode, W.; et al. Physical controls on CH4 emissions from a newly flooded subtropical freshwater hydroelectric reservoir: Nam Theun 2. Biogeosciences 2014, 11, 4251–4269. [Google Scholar] [CrossRef]
  15. Fearnside, P.M. Greenhouse gas emissions from a hydroelectric reservoir (Brazil’s Tucuruídam) and the energy policy implications. Water Air Soil Pollut. 2002, 133, 69–96. [Google Scholar] [CrossRef]
  16. Galy-Lacaux, C.; Delmas, R.; Kouadio, G.; Richard, S.; Gosse, P. Long-term greenhouse gas emissions from hydroelectric reservoirs in tropical forest regions. Glob. Biogeochem. Cycles 1999, 13, 503–517. [Google Scholar] [CrossRef] [Green Version]
  17. Lima, I.B.T.; Ramos, F.M.; Bambace, L.A.W.; Rosa, R.R. Methane emissions from large dams as renewable energy resources: A developing nation perspective. Mitig. Adapt. Strateg. Glob. Chang. 2008, 13, 193–206. [Google Scholar] [CrossRef]
  18. Deemer, B.R.; Harrison, J.A.; Li, S.; Beaulieu, J.J.; DelSontro, T.; Barros, N.; Bezerra-Neto, J.F.; Powers, S.M.; dos Santos, M.A.; Arie Vonk, J. Greenhouse Gas Emissions from Reservoir Water Surfaces: A New Global Synthesis. Bioscience 2016, 66, 949–964. [Google Scholar] [CrossRef] [Green Version]
  19. Baup, F.; Frappart, F.; Maubant, J. Combining high-resolution satellite images and altimetry to estimate the volume of small lakes. Hydrol. Earth Syst. Sci. 2014, 18, 2007–2020. [Google Scholar] [CrossRef] [Green Version]
  20. Crétaux, J.F.; Jelinski, W.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.C.; Nino, F.; Abarca Del Rio, R.; Cazenave, A.; et al. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
  21. Ding, X.W.; Li, X.F. Monitoring of the water-area variations of Lake Dongting in China with ENVISAT ASAR images. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 894–901. [Google Scholar] [CrossRef]
  22. Duan, Z.; Bastiaanssen, W.G.M. Estimating water volume variations in lakes and reservoirs from four operational satellite altimetry databases and satellite imagery data. Remote Sens. Environ. 2013, 134, 403–416. [Google Scholar] [CrossRef]
  23. Gao, H.; Birkett, C.; Lettenmaier, D.P. Global monitoring of large reservoir storage from satellite remote sensing. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
  24. Jiang, L.; Nielsen, K.; Andersen, O.B.; Bauer-Gottwein, P. CryoSat-2 radar altimetry for monitoring freshwater resources of China. Remote Sens. Environ. 2017, 200, 125–139. [Google Scholar] [CrossRef]
  25. Smith, L.C.; Pavelsky, T.M. Remote sensing of volumetric storage changes in lakes. Earth Surf. Process. Landf. 2009, 34, 1353–1358. [Google Scholar] [CrossRef]
  26. Tseng, K.H.; Shum, C.K.; Kim, J.W.; Wang, X.; Zhu, K.; Cheng, X. Integrating Landsat Imageries and Digital Elevation Models to Infer Water Level Change in Hoover Dam. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1696–1709. [Google Scholar] [CrossRef]
  27. Zhang, J.; Xu, K.; Yang, Y.; Qi, L.; Hayashi, S.; Watanabe, M. Measuring Water Storage Fluctuations in Lake Dongting, China, by Topex/Poseidon Satellite Altimetry. Environ. Monit. Assess. 2006, 115, 23–37. [Google Scholar] [CrossRef]
  28. Liebe, J.; van de Giesen, N.; Andreini, M. Estimation of small reservoir storage capacities in a semi-arid environment. Phys. Chem. Earth 2005, 30, 448–454. [Google Scholar] [CrossRef]
  29. Ogilvie, A.; Belaud, G.; Massuel, S.; Mulligan, M.; Le Goulven, P.; Calvez, R.; Ogilvie, A.; Belaud, G.; Massuel, S.; Mulligan, M.; et al. Assessing Floods and Droughts in Ungauged Small Reservoirs with Long-Term Landsat Imagery. Geosciences 2016, 6, 42. [Google Scholar] [CrossRef]
  30. Singh, A.; Kumar, U.; Seitz, F. Remote Sensing of Storage Fluctuations of Poorly Gauged Reservoirs and State Space Model (SSM)-Based Estimation. Remote Sens. 2015, 7, 17113–17134. [Google Scholar] [CrossRef] [Green Version]
  31. Wang, L.; Dessler, A.E. Instantaneous cloud overlap statistics in the tropical area revealed by ICESat/GLAS data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
  32. Rodrigues, L.N.; Sano, E.E.; Steenhuis, T.S.; Passo, D.P. Estimation of small reservoir storage capacities with remote sensing in the Brazilian Savannah region. Water Resour. Manag. 2012, 26, 873–882. [Google Scholar] [CrossRef]
  33. Sano, E.E.; Ferreira, L.G.; Asner, G.P.; Steinke, E.T. Spatial and temporal probabilities of obtaining cloud-free Landsat images over the Brazilian tropical savanna. Int. J. Remote Sens. 2007, 28, 2739–2752. [Google Scholar] [CrossRef]
  34. Vermote, E.; Wolfe, R. MOD09GA MODIS/Terra Surface Reflectance Daily L2G Global 1kmand 500m SIN Grid V006 [Data set]; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2015.
  35. Zhang, S.; Gao, H.; Naz, B.S. Monitoring reservoir storage in South Asia from multisatellite remote sensing. Water Resour. Res. 2014, 50, 8927–8943. [Google Scholar] [CrossRef] [Green Version]
  36. Chipman, J.W. A Multisensor Approach to Satellite Monitoring of Trends in Lake Area, Water Level, and Volume. Remote Sens. 2019, 11, 158. [Google Scholar] [CrossRef]
  37. Hamilton, S.K.; Sippel, S.J.; Melack, J.M. Seasonal inundation patterns in two large savanna floodplains of South America: The Llanos de Moxos (Bolivia) and the Llanos del Orinoco (Venezuela and Colombia). Hydrol. Proc. 2004, 18, 2103–2116. [Google Scholar] [CrossRef]
  38. Kang, S.; Hong, S.Y. Assessing Seasonal and Inter-Annual Variations of Lake Surface Areas in Mongolia during 2000-2011 Using Minimum Composite MODIS NDVI. PLoS ONE 2016, 11, e0151395. [Google Scholar] [CrossRef]
  39. Donchyts, G.; Baart, F.; Winsemius, H.; Gorelick, N.; Kwadijk, J.; Van De Giesen, N. Earth’s surface water change over the past 30 years. Nat. Clim. Chang. 2016, 6, 810–813. [Google Scholar] [CrossRef]
  40. Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
  41. Feng, M.; Sexton, J.O.; Channan, S.; Townshend, J.R. A global, high-resolution (30-m) inland water body dataset for 2000: First results of a topographic–spectral classification algorithm. Int. J. Digit. Earth 2016, 9, 113–133. [Google Scholar] [CrossRef]
  42. Mueller, N.; Lewis, A.; Roberts, D.; Ring, S.; Melrose, R.; Sixsmith, J.; Lymburner, L.; McIntyre, A.; Tan, P.; Curnow, S.; et al. Water observations from space: Mapping surface water from 25years of Landsat imagery across Australia. Remote Sens. Environ. 2016, 174, 341–352. [Google Scholar] [CrossRef]
  43. Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
  44. Alsdorf, D.E.; Rodríguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef] [Green Version]
  45. Avisse, N.; Tilmant, A.; François Müller, M.; Zhang, H. Monitoring small reservoirs’ storage with satellite remote sensing in inaccessible areas. Hydrol. Earth Syst. Sci. 2017, 21, 6445–6459. [Google Scholar] [CrossRef]
  46. Uebbing, B.; Kusche, J.; Forootan, E. Waveform retracking for improving level estimations from TOPEX/Poseidon, Jason-1, and Jason-2 altimetry observations over African lakes. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2211–2224. [Google Scholar] [CrossRef]
  47. Jiang, L.; Schneider, R.; Andersen, O.B.; Bauer-Gottwein, P. CryoSat-2 altimetry applications over rivers and lakes. Water 2017, 9, 211. [Google Scholar] [CrossRef]
  48. Politi, E.; MacCallum, S.; Cutler, M.E.J.; Merchant, C.J.; Rowan, J.S.; Dawson, T.P. Selection of a network of large lakes and reservoirs suitable for global environmental change analysis using Earth Observation. Int. J. Remote Sens. 2016, 37, 3042–3060. [Google Scholar] [CrossRef] [Green Version]
  49. Busker, T.; de Roo, A.; Gelati, E.; Schwatke, C.; Adamovic, M.; Bisselink, B.; Pekel, J.F.; Cottam, A. A global lake and reservoir volume analysis using a surface water dataset and satellite altimetry. Hydrol. Earth Syst. Sci. 2019, 23, 669–690. [Google Scholar] [CrossRef]
  50. Narasimha Rao, P.V.; Sesha Sai, M.V.R. Cover: Clouds over land in Envisat ASAR C-band image. Int. J. Remote Sens. 2006, 27, 833–834. [Google Scholar] [CrossRef]
  51. Pipitone, C.; Maltese, A.; Dardanelli, G.; Brutto, M.L.; Loggia, G.L. Monitoring water surface and level of a reservoir using different remote sensing approaches and comparison with dam displacements evaluated via GNSS. Remote Sens. 2018, 10, 71. [Google Scholar] [CrossRef]
  52. Ye, Z.; Liu, H.; Chen, Y.; Shu, S.; Wu, Q.; Wang, S. Analysis of water level variation of lakes and reservoirs in Xinjiang, China using ICESat laser altimetry data (2003–2009). PLoS ONE 2017, 12, e0183800. [Google Scholar] [CrossRef]
  53. Getirana, A. Extreme Water Deficit in Brazil Detected from Space. J. Hydrometeorol. 2016, 17, 591–599. [Google Scholar] [CrossRef]
  54. Nobre, C.A.; Marengo, J.A.; Seluchi, M.E.; Cuartas, L.A.; Alves, L.M. Some Characteristics and Impacts of the Drought and Water Crisis in Southeastern Brazil during 2014 and 2015. J. Water Resour. Prot. 2016, 08, 252–262. [Google Scholar] [CrossRef]
  55. Marengo, J.A.; Alves, L.M.; Soares, W.R.; Rodriguez, D.A. Two Contrasting Severe Seasonal Extremes in Tropical South America in 2012: Flood in Amazonia and Drought in Northeast Brazil. J. Clim. 2013, 26, 9137–9154. [Google Scholar] [CrossRef]
  56. Marengo, J.A.; Torres, R.R.; Alves, L.M. Drought in Northeast Brazil—Past, present, and future. Theor. Appl. Climatol. 2017, 129, 1189–1200. [Google Scholar] [CrossRef]
  57. Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
  58. Wang, X.; Cheng, X.; Gong, P.; Huang, H.; Li, Z.; Li, X. Earth science applications of ICESat/GLAS: A review. Int. J. Remote Sens. 2011, 32, 8837–8864. [Google Scholar] [CrossRef]
  59. Phan, V.H.; Lindenbergh, R.; Menenti, M. ICESat derived elevation changes of Tibetan lakes between 2003 and 2009. Int. J. Appl. Earth Obs. Geoinf. 2012, 17, 12–22. [Google Scholar] [CrossRef]
  60. Birkett, C.; Reynolds, C.; Beckley, B.; Doorn, B. From research to operations: The USDA global reservoir and lake monitor. In Coastal Altimetry; Springer-Verlag Berlin Heidelberg: Berlin, Germany, 2011; pp. 19–50. ISBN 9783642127953. [Google Scholar]
  61. da Silva, J.S.; Calmant, S.; Seyler, F.; Rotunno Filho, O.C.; Cochonneau, G.; Mansur, W.J. Water levels in the Amazon basin derived from the ERS 2 and ENVISAT radar altimetry missions. Remote Sens. Environ. 2010, 114, 2160–2181. [Google Scholar] [CrossRef]
  62. Frappart, F.; Calmant, S.; Cauhopé, M.; Seyler, F.; Cazenave, A. Preliminary results of ENVISAT RA-2-derived water levels validation over the Amazon basin. Remote Sens. Environ. 2006, 100, 252–264. [Google Scholar] [CrossRef] [Green Version]
  63. Lee, H.; Shum, C.K.; Tseng, K.H.; Guo, J.Y.; Kuo, C.Y. Present-day lake level variation from envisat altimetry over the northeastern qinghai-tibetan plateau: Links with precipitation and temperature. Terr. Atmos. Ocean. Sci. 2011, 22, 169–175. [Google Scholar] [CrossRef]
  64. Medina, C.E.; Gomez-Enri, J.; Alonso, J.J.; Villares, P. Water level fluctuations derived from ENVISAT Radar Altimeter (RA-2) and in-situ measurements in a subtropical waterbody: Lake Izabal (Guatemala). Remote Sens. Environ. 2008, 112, 3604–3617. [Google Scholar] [CrossRef]
  65. Medina, C.; Gomez-Enri, J.; Alonso, J.J.; Villares, P. Water volume variations in Lake Izabal (Guatemala) from in situ measurements and ENVISAT Radar Altimeter (RA-2) and Advanced Synthetic Aperture Radar (ASAR) data products. J. Hydrol. 2010, 382, 34–48. [Google Scholar] [CrossRef]
  66. Schwatke, C.; Dettmering, D.; Bosch, W.; Seitz, F. DAHITI—An innovative approach for estimating water level time series over inland waters using multi-mission satellite altimetry. Hydrol. Earth Syst. Sci. 2015, 19, 4345–4364. [Google Scholar] [CrossRef]
  67. Siddique-E-Akbor, A.H.M.; Hossain, F.; Lee, H.; Shum, C.K. Inter-comparison study of water level estimates derived from hydrodynamic-hydrologic model and satellite altimetry for a complex deltaic environment. Remote Sens. Environ. 2011, 115, 1522–1531. [Google Scholar] [CrossRef]
  68. Abshire, J.B.; Sun, X.; Riris, H.; Sirota, J.M.; McGarry, J.F.; Liiva, P.; Palm, S.; Yi, D. Geoscience Laser Altimeter System (GLAS) on the ICESat Mission: On-orbit measurement performance. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
  69. Hall, A.C.; Schumann, G.J.P.; Bamber, J.L.; Bates, P.D.; Trigg, M.A. Geodetic corrections to Amazon River water level gauges using ICESat altimetry. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
  70. O’Loughlin, F.E.; Neal, J.; Yamazaki, D.; Bates, P.D. ICESat-derived inland water surface spot heights. Water Resour. Res. 2016, 52, 3276–3284. [Google Scholar] [CrossRef] [Green Version]
  71. Swenson, S.; Wahr, J. Monitoring the water balance of Lake Victoria, East Africa, from space. J. Hydrol. 2009, 370, 163–176. [Google Scholar] [CrossRef]
  72. Wang, X.; Cheng, X.; Li, Z.; Huang, H.; Niu, Z.; Li, X.; Gong, P. Lake water footprint identification from time-series ICESat/GLAS data. IEEE Geosci. Remote Sens. Lett. 2012, 9, 333–337. [Google Scholar] [CrossRef]
  73. Zhang, G.Q.; Xie, H.J.; Yao, T.D.; Kang, S.C. Water balance estimates of ten greatest lakes in China using ICESat and Landsat data. Chin. Sci. Bull. 2013, 58, 3815–3829. [Google Scholar] [CrossRef] [Green Version]
  74. Okeowo, M.A.; Lee, H.; Hossain, F.; Getirana, A. Automated Generation of Lakes and Reservoirs Water Elevation Changes from Satellite Radar Altimetry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3465–3481. [Google Scholar] [CrossRef]
  75. Zwally, H.J.; Schutz, R.; Bentley, C.; Bufton, J.; Herring, T.; Minster, J.; Spinhirne, J.; Thomas, R. GLAS/ICESat L2 Global Land Surface Altimetry Data, Version 34. [GLA14]; NASA National Snow and Ice Data Center: Boulder, CO, USA, 2014. [CrossRef]
  76. Frequently Asked Questions. Available online: https://nsidc.org/data/icesat/faq.html#alt7 (accessed on 18 May 2018).
  77. Taube, C.M. Three Methods for Computing the Volume of a Lake. In Manual of Fisheries Survey Methods II: With Periodic Updates; Schneider, J.C., Ed.; Michigan Department of Natural Resources: Lansing, MI, USA, 2000. [Google Scholar]
  78. Ait-Kadi, M. Water for Development and Development for Water: Realizing the Sustainable Development Goals (SDGs) Vision. Aquat. Procedia 2016, 6, 106–110. [Google Scholar] [CrossRef]
  79. Chadwick, R.; Good, P.; Martin, G.; Rowell, D.P. Large rainfall changes consistently projected over substantial areas of tropical land. Nat. Clim. Chang. 2016, 6, 177–181. [Google Scholar] [CrossRef]
  80. Feng, X.; Porporato, A.; Rodriguez-Iturbe, I. Changes in rainfall seasonality in the tropics. Nat. Clim. Chang. 2013, 3, 811–815. [Google Scholar] [CrossRef]
  81. De Paiva, R.C.D.; Collischonn, W.; Calmant, S.; Bulhões Mendes, C.A.; Bonnet, M.P.; Frappart, F.; Buarque, D.C. Large-scale hydrologic and hydrodynamic modeling of the Amazon River basin. Water Resour. Res. 2013, 49, 1226–1243. [Google Scholar] [CrossRef] [Green Version]
  82. Getirana, A.C.; Boone, A.; Yamazaki, D.; Decharme, B.; Papa, F.; Mognard, N. The Hydrological Modeling and Analysis Platform (HyMAP): Evaluation in the Amazon Basin. J. Hydrometeorol. 2012, 13, 1641–1665. [Google Scholar] [CrossRef] [Green Version]
  83. Jarihani, A.A.; Callow, J.N.; McVicar, T.R.; Van Niel, T.G.; Larsen, J.R. Satellite-derived Digital Elevation Model (DEM) selection, preparation and correction for hydrodynamic modelling in large, low-gradient and data-sparse catchments. J. Hydrol. 2015, 524, 489–506. [Google Scholar] [CrossRef]
  84. Lu, S.; Ouyang, N.; Wu, B.; Wei, Y.; Tesemma, Z. Lake water volume calculation with time series remote-sensing images. Int. J. Remote Sens. 2013, 34, 7962–7973. [Google Scholar] [CrossRef]
  85. Pillco Zolá, R.; Bengtsson, L. Three methods for determining the area-depth relationship of Lake Poopó, a large shallow lake in Bolivia. Lakes Reserv. 2007, 12, 275–284. [Google Scholar] [CrossRef]
  86. Solander, K.C.; Reager, J.T.; Famiglietti, J.S. How well will the Surface Water and Ocean Topography (SWOT) mission observe global reservoirs? Water Resour. Res. 2016, 52, 2123–2140. [Google Scholar] [CrossRef] [Green Version]
  87. Doll, P.; Fiedler, K.; Zhang, J. Global-scale analysis of river flow alterations due to water withdrawals and reservoirs. Hydrol. Earth Syst. Sci. 2009, 13, 2413–2432. [Google Scholar] [CrossRef] [Green Version]
  88. Haddeland, I.; Skaugen, T.; Lettenmaier, D.P. Anthropogenic impacts on continental surface water fluxes. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
  89. Mateo, C.M.; Hanasaki, N.; Komori, D.; Tanaka, K.; Kiguchi, M.; Champathong, A.; Sukhapunnaphan, T.; Yamazaki, D.; Oki, T. Assessing the impacts of reservoir operation to floodplain inundation by combining hydrological, reservoir management, and hydrodynamic models. Water Resour. Res. 2014, 50, 7245–7266. [Google Scholar] [CrossRef] [Green Version]
  90. Ji, L.; Zhang, L.; Wylie, B. Analysis of Dynamic Thresholds for the Normalized Difference Water Index. Photogramm. Eng. Remote Sens. 2013, 75, 1307–1317. [Google Scholar] [CrossRef]
  91. Amitrano, D.; di Martino, G.; Iodice, A.; Mitidieri, F.; Papa, M.N.; Riccio, D.; Ruello, G. Sentinel-1 for monitoring reservoirs: A performance analysis. Remote Sens. 2014, 6, 10676–10693. [Google Scholar] [CrossRef]
  92. Du, Y.; Zhang, Y.; Ling, F.; Wang, Q.; Li, W.; Li, X. Water bodies’ mapping from Sentinel-2 imagery with Modified Normalized Difference Water Index at 10-m spatial resolution produced by sharpening the swir band. Remote Sens. 2016, 8, 354. [Google Scholar] [CrossRef]
  93. Rucci, A.; Ferretti, A.; Monti Guarnieri, A.; Rocca, F. Sentinel 1 SAR interferometry applications: The outlook for sub millimeter measurements. Remote Sens. Environ. 2012, 120, 156–163. [Google Scholar] [CrossRef]
  94. Eilander, D.; Annor, F.O.; Iannini, L.; van de Giesen, N. Remotely sensed monitoring of small reservoir dynamics: A Bayesian approach. Remote Sens. 2014, 6, 1191–1210. [Google Scholar] [CrossRef]
  95. Sippel, S.J.; Hamilton, S.K.; Melack, J.M.; Novo, E.M.M. Passive microwave observations of inundation area and the area/stage relation in the Amazon River floodplain. Int. J. Remote Sens. 1998, 19, 3055–3074. [Google Scholar] [CrossRef] [Green Version]
Remotesensing 11 00827 g001 550
Figure 1. Global distribution of Global Reservoir and Dam (GRanD) Database reservoirs [12]. Reservoir counts are summarized at 5° resolution), and percent daily cloud cover is based on MODIS MOD09GA [34] (2003–2014, 1 km resolution, Robinson projection).
Figure 1. Global distribution of Global Reservoir and Dam (GRanD) Database reservoirs [12]. Reservoir counts are summarized at 5° resolution), and percent daily cloud cover is based on MODIS MOD09GA [34] (2003–2014, 1 km resolution, Robinson projection).
Remotesensing 11 00827 g001
Remotesensing 11 00827 g002 550
Figure 2. Geographic distribution and storage capacities (km3) of study reservoirs in eastern Brazil [12]. Four focus reservoirs whose volume dynamics are illustrated in the manuscript text are identified with a black point on the map and an asterisk (*) in the reservoir list; all reservoirs’ dynamics are illustrated in Appendix A.
Figure 2. Geographic distribution and storage capacities (km3) of study reservoirs in eastern Brazil [12]. Four focus reservoirs whose volume dynamics are illustrated in the manuscript text are identified with a black point on the map and an asterisk (*) in the reservoir list; all reservoirs’ dynamics are illustrated in Appendix A.
Remotesensing 11 00827 g002
Remotesensing 11 00827 g003 550
Figure 3. Overview of analytical framework to generate surface area, elevation, and volumetric time series for a given reservoir. Colors shown for each dataset are consistent throughout all figures.
Figure 3. Overview of analytical framework to generate surface area, elevation, and volumetric time series for a given reservoir. Colors shown for each dataset are consistent throughout all figures.
Remotesensing 11 00827 g003
Remotesensing 11 00827 g004 550
Figure 4. Example generation of temporally composited, infilled surface water extent maps showing southeastern Chavantes reservoir. (a–c) Surface water coverage from three near-date images (23 October, 8 November, and 24 November 2012) with data gaps. (d) Coverage maps are composited to create an infilled surface water map for 8 November 2012. (e) A time series of infilled water maps are used to generate a water frequency map for 2003–2014.
Figure 4. Example generation of temporally composited, infilled surface water extent maps showing southeastern Chavantes reservoir. (a–c) Surface water coverage from three near-date images (23 October, 8 November, and 24 November 2012) with data gaps. (d) Coverage maps are composited to create an infilled surface water map for 8 November 2012. (e) A time series of infilled water maps are used to generate a water frequency map for 2003–2014.
Remotesensing 11 00827 g004
Remotesensing 11 00827 g005 550
Figure 5. Reductions in average percentage of missing data across all image dates and reservoirs after infilling.
Figure 5. Reductions in average percentage of missing data across all image dates and reservoirs after infilling.
Remotesensing 11 00827 g005
Remotesensing 11 00827 g006 550
Figure 6. Landsat-derived surface area time series for four reservoirs with dates of ICESat GLAS (green dot) and Envisat RA-2 (red dot) measurement. The gray background indicates the range of surface areas measured on altimetry data collection dates. Time series for all 13 reservoirs are shown in Figure A1.
Figure 6. Landsat-derived surface area time series for four reservoirs with dates of ICESat GLAS (green dot) and Envisat RA-2 (red dot) measurement. The gray background indicates the range of surface areas measured on altimetry data collection dates. Time series for all 13 reservoirs are shown in Figure A1.
Remotesensing 11 00827 g006
Remotesensing 11 00827 g007 550
Figure 7. Monthly frequency of (a) Landsat images and (b) GLAS and RA-2 surface elevation observations for four selected reservoirs from 2003–2014. Monthly frequency of Landsat images and surface elevation observations for all 13 reservoirs are shown in Figure A2 and Figure A3, respectively.
Figure 7. Monthly frequency of (a) Landsat images and (b) GLAS and RA-2 surface elevation observations for four selected reservoirs from 2003–2014. Monthly frequency of Landsat images and surface elevation observations for all 13 reservoirs are shown in Figure A2 and Figure A3, respectively.
Remotesensing 11 00827 g007
Remotesensing 11 00827 g008 550
Figure 8. Derived surface area–elevation linear regressions for four selected reservoirs based on Landsat surface area and combined GLAS and RA-2 elevation data. n = number of area–elevation pairs, r = Pearson correlation coefficient, RMSE = root mean square error, m = linear slope, and b = linear intercept. Area-elevation models for all 13 reservoirs are in Figure A4.
Figure 8. Derived surface area–elevation linear regressions for four selected reservoirs based on Landsat surface area and combined GLAS and RA-2 elevation data. n = number of area–elevation pairs, r = Pearson correlation coefficient, RMSE = root mean square error, m = linear slope, and b = linear intercept. Area-elevation models for all 13 reservoirs are in Figure A4.
Remotesensing 11 00827 g008
Remotesensing 11 00827 g009 550
Figure 9. (a) Time series of difference between standardized reservoir volumes and each reservoir’s baseline, pre-drought (i.e., median 2003–2011) volume for modeled (purple) and in situ (green) data, respectively; for dates without altimetry data, regression-based elevation values are used in modeling volume. (b) Linear regressions relating standardized in situ and modeled volumes on dates of mutual observation. Light grey lines in (a) and (b) indicate zero values on respective axes. All volume values are in km3. Time series and regressions for all 13 reservoirs are in Figure A5.
Figure 9. (a) Time series of difference between standardized reservoir volumes and each reservoir’s baseline, pre-drought (i.e., median 2003–2011) volume for modeled (purple) and in situ (green) data, respectively; for dates without altimetry data, regression-based elevation values are used in modeling volume. (b) Linear regressions relating standardized in situ and modeled volumes on dates of mutual observation. Light grey lines in (a) and (b) indicate zero values on respective axes. All volume values are in km3. Time series and regressions for all 13 reservoirs are in Figure A5.
Remotesensing 11 00827 g009
Remotesensing 11 00827 g010 550
Figure 10. Mean monthly absolute difference between modeled and in situ standardized (unitless) volume changes (2003–2014; red line) with standard deviation range (red field). Monthly comparisons for all 13 reservoirs are in Figure A6.
Figure 10. Mean monthly absolute difference between modeled and in situ standardized (unitless) volume changes (2003–2014; red line) with standard deviation range (red field). Monthly comparisons for all 13 reservoirs are in Figure A6.
Remotesensing 11 00827 g010
Remotesensing 11 00827 g011 550
Figure 11. Comparison between mean annual flux of standardized (unitless) modeled (purple line) and in situ (green line) volume dynamics across all study reservoirs with ±1 standard deviation ranges (purple and green fields, respectively).
Figure 11. Comparison between mean annual flux of standardized (unitless) modeled (purple line) and in situ (green line) volume dynamics across all study reservoirs with ±1 standard deviation ranges (purple and green fields, respectively).
Remotesensing 11 00827 g011

Share and Cite

MDPI and ACS Style

Van Den Hoek, J.; Getirana, A.; Jung, H.C.; Okeowo, M.A.; Lee, H. Monitoring Reservoir Drought Dynamics with Landsat and Radar/Lidar Altimetry Time Series in Persistently Cloudy Eastern Brazil. Remote Sens. 2019, 11, 827. https://doi.org/10.3390/rs11070827

AMA Style

Van Den Hoek J, Getirana A, Jung HC, Okeowo MA, Lee H. Monitoring Reservoir Drought Dynamics with Landsat and Radar/Lidar Altimetry Time Series in Persistently Cloudy Eastern Brazil. Remote Sensing. 2019; 11(7):827. https://doi.org/10.3390/rs11070827

Chicago/Turabian Style

Van Den Hoek, Jamon, Augusto Getirana, Hahn Chul Jung, Modurodoluwa A. Okeowo, and Hyongki Lee. 2019. "Monitoring Reservoir Drought Dynamics with Landsat and Radar/Lidar Altimetry Time Series in Persistently Cloudy Eastern Brazil" Remote Sensing 11, no. 7: 827. https://doi.org/10.3390/rs11070827

APA Style

Van Den Hoek, J., Getirana, A., Jung, H. C., Okeowo, M. A., & Lee, H. (2019). Monitoring Reservoir Drought Dynamics with Landsat and Radar/Lidar Altimetry Time Series in Persistently Cloudy Eastern Brazil. Remote Sensing, 11(7), 827. https://doi.org/10.3390/rs11070827

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop