IMU/Magnetometer/Barometer/Mass-Flow Sensor Integrated Indoor Quadrotor UAV Localization with Robust Velocity Updates
Abstract
:1. Introduction
- The candidate sensors include vision sensors (e.g., camera, lidar, and optical flow sensor), motion sensors (e.g., IMU, mass flow sensor, and the Hall-effect sensor), wireless sensors (e.g., UWB, ultrasonic, radar, WiFi, Bluetooth low energy (BLE), and radio frequency identification (RFID)), and environmental sensors (e.g., magnetometer and barometer).
- Different types of sensors typically provide various localization accuracies and meanwhile have different costs and coverage areas. Thus, there is a trade-off between performance and cost/coverage.
- High-precision wireless technologies (e.g., UWB and ultrasonic) can provide high localization accuracy (e.g., decimeter or even centimeter level). However, although the prices for low-cost commercial UWB and ultrasonic development kits have been reduced to the hundreds of dollars level, such systems have limited ranges (e.g., 30 m between nodes and anchors). Thus, other technologies are required to bridge their signal outages in wide-area applications. Meanwhile, for wireless ranging systems, there are inherent issues such as signal obstruction and multipath [36]. Thus, other technologies are needed to ensure localization reliability and integrity.
- Cameras and lidars can also provide high location accuracy when loop closures are correctly detected. Furthermore, some previous issues, such as heavy computational load, are being eliminated because of the development of modern processors and wireless data transmission technologies. However, the performance of vision-based localization systems is highly dependent on whether the measured features are distinct in space and stable over time. For database matching, any inconsistency between the measured data and the database may cause mismatches [37]. For mobile mapping, it is possible to add updates and loop closures to control errors. However, real-world localization conditions are complex and unpredictable; thus, it is difficult to maintain accuracy in challenging environments (e.g., areas with glass or solid-color walls). Therefore, external technologies may be needed to bridge such task periods as well as detect the outliers in vision sensor measurements.
- Dead-reckoning (DR) solutions from IMUs have been widely used to bridge other localization technologies’ signal outages and integrate with them to provide smoother and more robust solutions [38]. However, traditional navigation- or tactical-grade IMUs are heavy and costly and thus are not suitable for consumer-level UAVs. Micro-electro-mechanical systems (MEMS) IMUs are light and low-cost, which have made them suitable for low-cost indoor localization. However, low-cost MEMS IMUs suffer from significant run-to-run biases and thermal drifts [39], which are issues inherent to MEMS sensors. Therefore, standalone IMU-based DR solutions will drift over time. Magnetometer measurements can be used to derive an absolute heading update. However, the indoor magnetic declination angle becomes unknown, which makes the magnetometer heading unreliable [40]. Thus, it is still important to implement periodical updates to correct DR solutions.
- Vehicle motion model updates can be used to enhance the navigation system observability [41], especially when there are significant vehicle dynamics (e.g., accelerating or turning). Sensors such as the mass flow and Hall-effect sensors can measure the forward velocity. Meanwhile, it is assumed that the lateral and vertical velocity components are zeroes plus noises when the UAV is being controlled to move horizontally, i.e., the non-holonomic constraint (NHC) [42]. Accordingly, 3D velocity updates can be applied. Furthermore, there are other updates, such as the zero velocity update (ZUPT) and zero angular rate update (ZARU) when the UAV is hovering in a quasi-static mode [43]. These updates are effective when the actual UAV motion meets the assumption. However, in contrast to land vehicles that are constrained by the road surface, UAVs may suffer from vertical velocity passively during task periods, which degrades the NHC performance. Meanwhile, UAVs may have a pitch angle when moving horizontally, which pollutes the forward velocity measurements. Therefore, some updates are needed to better use the velocity updates.
- Velocity updates have been proven to be effective in constraining DR errors. However, it is observed that the quadrotor UAV may have vertical velocity even when it is controlled to move horizontally. Therefore, the barometer data are utilized to detect height changes and thus determine the weight for the vertical velocity update.
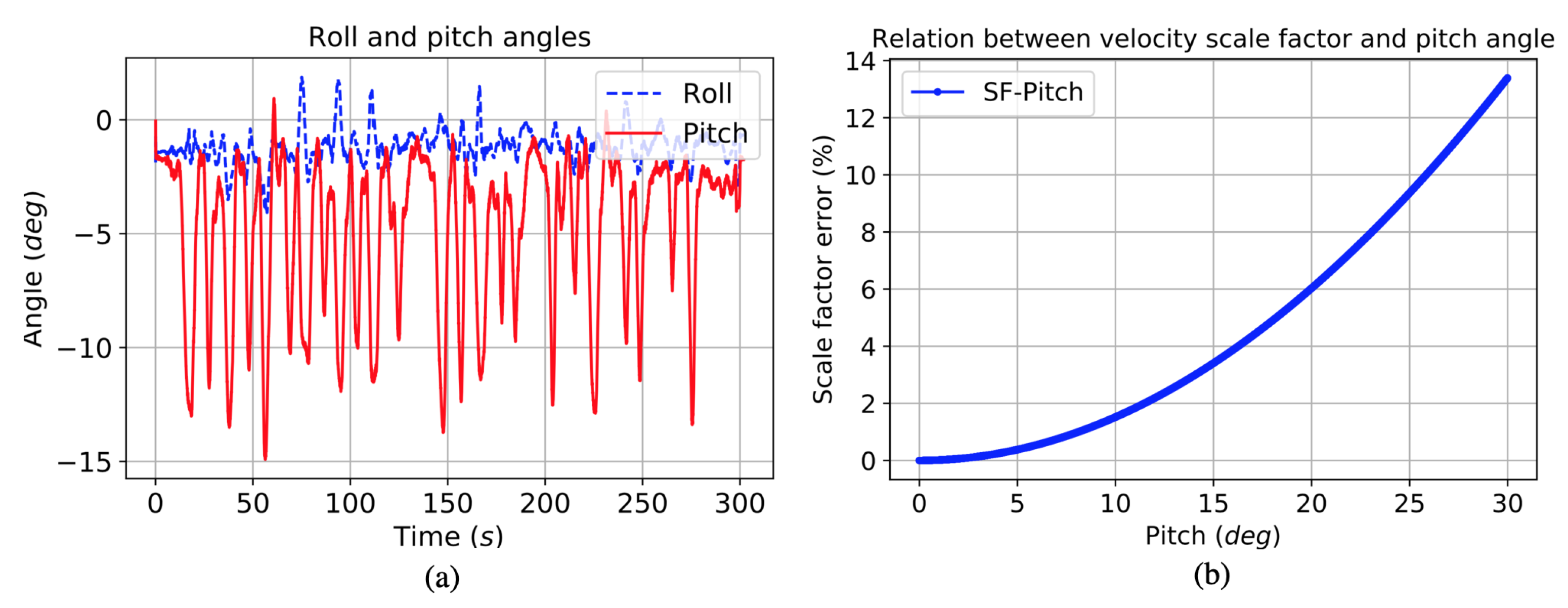
- According to the fact that the quadrotor may have a pitch angle when moving horizontally, the pitch angle, which is obtained from IMU and magnetometer data fusion, is used to set the weight of the forward velocity update.
- It is observed that the mass flow sensor may suffer from significant sensor errors, especially the scale factor error. Thus, a specific mass flow sensor calibration module is introduced.
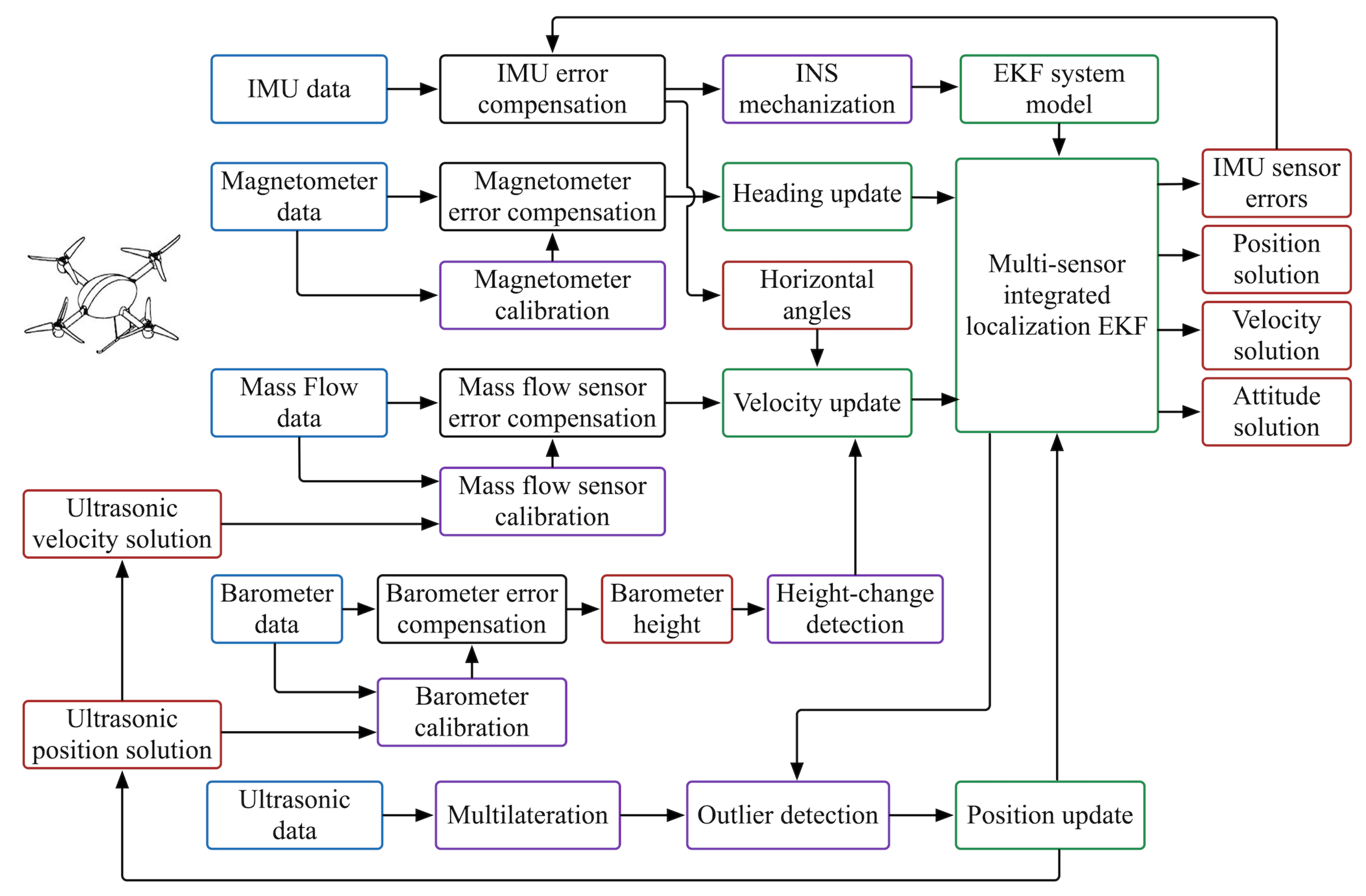
2. Methodology
2.1. EKF System Model
2.2. Magnetometer Heading Update
2.3. Velocity Update
2.3.1. Velocity Update for Multi-Sensor Localization EKF
2.3.2. Mass Flow Sensor Calibration
2.3.3. Availability for the Velocity Update
2.4. Position Update
2.4.1. Ultrasonic Multilateration
2.4.2. Position Update for Multi-Sensor Localization EKF
2.4.3. Ultrasonic Position Outlier Detection
3. Tests and Results
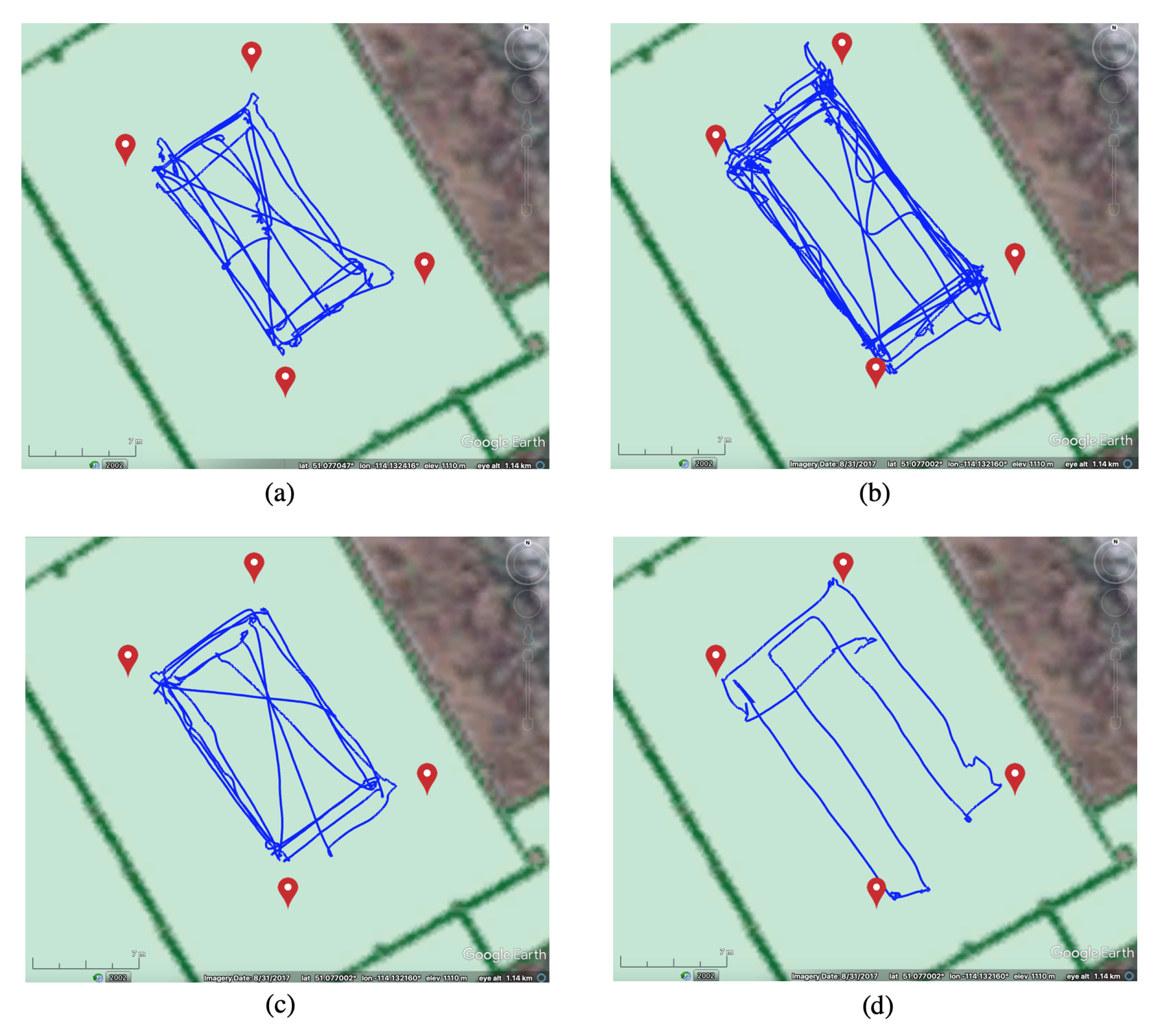
3.1. Test Description
3.2. Impact of Velocity Solutions
3.2.1. Velocity Solutions (Mass Flow-Based)
3.2.2. Height-Change Detection (Barometer-Based)
3.2.3. Impact of Pitch Angle on Velocity
3.2.4. AHRS/INS/Velocity Integrated Solutions with Various Velocity Strategies
- AHRS/INS: integration of AHRS heading and INS mechanization, without using any velocity update.
- AHRS/INS/Flow(Raw): using raw mass flow sensor data (i.e., 1D velocity) as the update in the MSL EKF.
- AHRS/INS/Vel(Raw): using raw mass flow sensor data and NHC for 3D velocity updates in the MSL EKF.
- AHRS/INS/Vel(Cali): using calibrated mass flow sensor data and NHC (i.e., 3D velocity) in the MSL EKF.
- AHRS/INS/Vel(Cali,QC): using mass flow sensor data that were calibrated and had QC based on height-change and pitch-angle detection, as well as NHC (i.e., 3D velocity) in the MSL EKF.
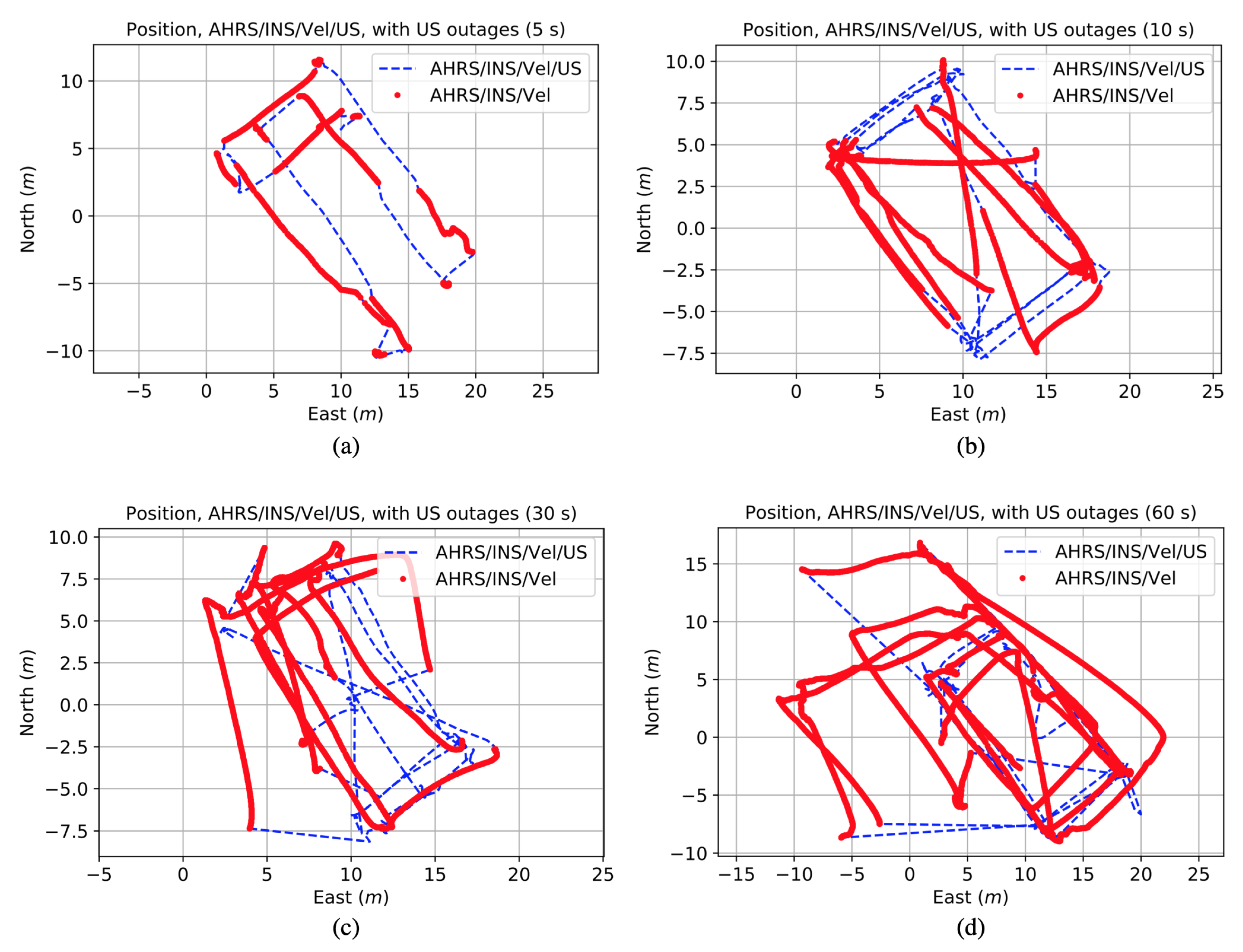
3.3. Integrated Localization Solutions during Ultrasonic Positioning Signal Outages
3.3.1. Use of Ultrasonic Positioning
3.3.2. AHRS/INS/Velocity/Ultrasonic Integrated Solution
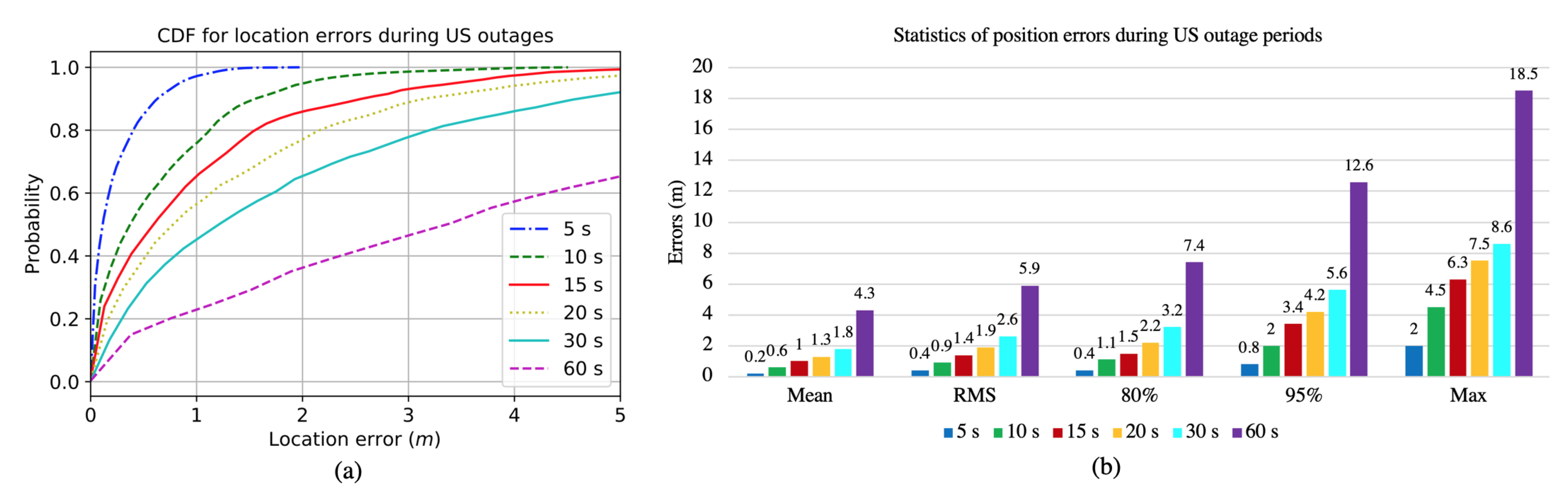
3.3.3. AHRS/INS/Velocity Integrated Solution during US Outages
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AoA | angle-of-arrival |
| AP | access point |
| BLE | Bluetooth low energy |
| CDF | cumulative distribution function |
| CNN | convolution neural network |
| CPN | counter propagation neural network |
| DCM | direction cosine matrix |
| DR | dead-reckoning |
| EKF | extended Kalman filter |
| GNSS | global navigation satellite systems |
| IGRF | international geomagnetic reference field |
| IMU | inertial measurement unit |
| INS | inertial navigation system |
| KF | Kalman filter |
| LED | light-emitting diode |
| MEMS | micro-electro-mechanical systems |
| MSL | multi-sensor integrated localization |
| M/A | not provided |
| NHC | non-holonomic constraint |
| NLoS | non-line-of-sight |
| PF | particle filter |
| PPP | precise point positioning |
| QC | quality control |
| RFID | radio frequency identification |
| RGB-D | red-green-blue-depth |
| RMS | root mean squares |
| RSS | received signal strength |
| RTK | real-time kinematic |
| SLAM | simultaneous localization and mapping |
| STD | standard deviation |
| TDoA | time-difference-of-arrival |
| ToA | time-of-arrival |
| UAV | unmanned aerial vehicle |
| US | ultrasonic |
| UWB | ultra-wide-band |
| WiFi | wireless fidelity |
| ZARU | zero angular rate update |
| ZUPT | zero velocity update |
| 1D/2D/3D | one/two/three-dimensional |
References
- Feng, Q.; Liu, J.; Gong, J. UAV Remote Sensing for Urban Vegetation Mapping Using Random Forest and Texture Analysis. Remote Sens. 2015, 7, 1074–1094. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Guo, S.; Li, Y. Real-time tracking a ground moving target in complex indoor and outdoor environments with UAV. In Proceedings of the IEEE International Conference on Information and Automation (ICIA), Ningbo, China, 1–3 August 2016; pp. 362–367. [Google Scholar]
- Kobayashi, T.; Seimiya, S.; Harada, K.; Noi, M.; Barker, Z.; Woodward, G.; Willig, A.; Kohno, R. Wireless technologies to assist search and localization of victims of wide-scale natural disasters by unmanned aerial vehicles. In Proceedings of the International Symposium on Wireless Personal Multimedia Communications (WPMC), Bali, Indonesia, 17–20 December 2017; pp. 404–410. [Google Scholar]
- Wu, K.; Gregory, T.; Moore, J.; Hooper, B.; Lewis, D.; Tse, Z. Development of an indoor guidance system for unmanned aerial vehicles with power industry applications. IET Radar Sonar Navig. 2017, 11, 212–218. [Google Scholar] [CrossRef]
- Gao, Z.; Li, Y.; Zhuang, Y.; Yang, H.; Pan, Y.; Zhang, H. Robust Kalman Filter Aided GEO/IGSO/GPS Raw-PPP/INS Tight Integration. Sensors 2019, 19, 417. [Google Scholar] [CrossRef] [PubMed]
- Burdziakowski, P. Towards Precise Visual Navigation and Direct Georeferencing for MAV Using ORB-SLAM2. In Proceedings of the Baltic Geodetic Congress (BGC Geomatics), Gdansk, Poland, 22–25 June 2017; pp. 394–398. [Google Scholar]
- Valenti, F.; Giaquinto, D.; Musto, L.; Zinelli, A.; Bertozzi, M.; Broggi, A. Enabling Computer Vision-Based Autonomous Navigation for Unmanned Aerial Vehicles in Cluttered GPS-Denied Environments. In Proceedings of the IEEE International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, C.; Wang, H.; Ma, Y.; Liang, G.; Wu, X. Heterogeneous Sensor Information Fusion based on Kernel Adaptive Filtering for UAVs’ Localization. In Proceedings of the IEEE International Conference on Information and Automation (ICIA), Macau, China, 18–20 July 2017; pp. 171–176. [Google Scholar]
- Bulunseechart, T.; Smithmaitrie, P. A method for UAV multi-sensor fusion 3D-localization under degraded or denied GPS situation. J. Unmanned Veh. Syst. 2018, 6, 155–176. [Google Scholar] [CrossRef]
- Nahangi, M.; Heins, A.; McCabe, B.; Schoellig, A.P. Automated Localization of UAVs in GPS-Denied Indoor Construction Environments Using Fiducial Markers. In Proceedings of the 35th ISARC, Berlin, Germany, 20–25 July 2018; pp. 88–94. [Google Scholar]
- Santos, M.; Santana, L.; Brandão, A.; Sarcinelli-Filhod, M.; Carellie, R. Indoor low-cost localization system for controlling aerial robots. Control Eng. Pract. 2017, 61, 93–111. [Google Scholar] [CrossRef]
- Qi, J.; Yu, N.; Lu, X. A UAV positioning strategy based on optical flow sensor and inertial navigation. In Proceedings of the IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 27–29 October 2017; pp. 81–87. [Google Scholar]
- Walter, V.; Saska, M.; Franchi, A. Fast Mutual Relative Localization of UAVs using Ultraviolet LED markers. In Proceedings of the International Conference on Unmanned Aircraft Systems, Dallas, TX, USA, 12–15 June 2018; pp. 1217–1226. [Google Scholar]
- Li, K.; Wang, C.; Huang, S.; Liang, G.; Wu, X.; Liao, Y. Self-positioning for UAV indoor navigation based on 3D laser scanner, UWB and INS. In Proceedings of the IEEE International Conference on Information and Automation (ICIA), Ningbo, China, 1–3 August 2016; pp. 498–503. [Google Scholar]
- Li, J.; Zhan, H.; Chen, B.; Reid, I.; Lee, G. Deep learning for 2D scan matching and loop closure. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 763–768. [Google Scholar]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M.; Savvaris, A. Lidar-inertial integration for UAV localization and mapping in complex environments. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 649–656. [Google Scholar]
- Yuan, C.; Lai, J.; Zhang, J.; Lyu, P. Research on an autonomously tightly integrated positioning method for UAV in sparse-feature indoor environment. In Proceedings of the International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 9–13 January 2018; pp. 318–324. [Google Scholar]
- Bavle, H.; Sanchez-Lopez, J.; Rodriguez-Ramos, A.; Sampedro, C.; Campoy, P. A flight altitude estimator for multirotor UAVs in dynamic and unstructured indoor environments. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1044–1051. [Google Scholar]
- Scannapieco, A.; Renga, A.; Fasano, G.; Moccia, A. Experimental Analysis of Radar Odometry by Commercial Ultralight Radar Sensor for Miniaturized UAS. J. Intell. Robot. Syst. 2018, 90, 485–503. [Google Scholar] [CrossRef]
- Zahran, S.; Mostafa, M.; Masiero, A.; Moussa, A.; Vettore, A.; El-Sheimy, N. Micro-radar and uwb aided uav navigation in gnss denied environment, Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 469–476. [Google Scholar]
- Cisek, K.; Zolich, A.; Klausen, K.; Johansen, T. Ultra-wide band Real time Location Systems: Practical implementation and UAV performance evaluation. In Proceedings of the Workshop on Research, Education and Development of Unmanned Aerial Systems (RED-UAS), Linkoping, Sweden, 3–5 October 2017; pp. 204–209. [Google Scholar]
- Tiemann, J.; Wietfeld, C. Scalable and precise multi-UAV indoor navigation using TDOA-based UWB localization. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; pp. 1–7. [Google Scholar]
- Miraglia, G.; Maleki, K.; Hook, L. Comparison of two sensor data fusion methods in a tightly coupled UWB/IMU 3-D localization system. In Proceedings of the International Conference on Engineering, Technology and Innovation (ICE/ITMC), Funchal, Portugal, 27–29 June 2017; pp. 611–618. [Google Scholar]
- Tiemann, J.; Ramsey, A.; Wietfeld, C. Enhanced UAV Indoor Navigation through SLAM-Augmented UWB Localization. In Proceedings of the IEEE International Conference on Communications Workshops (ICC Workshops), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Perez-Grau, F.; Caballero, F.; Merino, L.; Viguria, A. Multi-modal mapping and localization of unmanned aerial robots based on ultra-wideband and RGB-D sensing. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 3495–3502. [Google Scholar]
- Kapoor, R.; Ramasamy, S.; Gardi, A.; Sabatini, R. Indoor navigation using distributed ultrasonic beacons. In Proceedings of the 17th Australian International Aerospace Congress (AIAC17), Melbourne, Australia, 26–28 February 2017; pp. 551–556. [Google Scholar]
- Kang, D.; Cha, Y. Autonomous UAVs for Structural Health Monitoring Using Deep Learning and an Ultrasonic Beacon System with Geo-Tagging. Comput.-Aided Civ. Infrastruct. Eng. 2018, 33, 885–902. [Google Scholar] [CrossRef]
- Paredes, J.A.; Alvarez, F.J.; Aguilera, T.; Villadangos, J.M. 3D Indoor Positioning of UAVs with Spread Spectrum Ultrasound and Time-of-Flight Cameras. Sensors 2018, 18, 89. [Google Scholar] [CrossRef]
- Zou, H.; Jin, M.; Jiang, H.; Xie, L.; Spanos, C. WinIPS: WiFi-Based Non-Intrusive Indoor Positioning System With Online Radio Map Construction and Adaptation. IEEE Trans. Wirel. Commun. 2017, 16, 8118–8130. [Google Scholar] [CrossRef]
- Tian, X.; Song, Z.; Jiang, B.; Zhang, Y.; Yu, T.; Wang, X. HiQuadLoc: A RSS Fingerprinting Based Indoor Localization System for Quadrotors. IEEE Trans. Mob. Comput. 2017, 16, 2545–2559. [Google Scholar] [CrossRef]
- Zhou, M.; Lin, J.; Liang, S.; Du, W.; Cheng, L. A UAV patrol system based on Bluetooth localization. In Proceedings of the Asia-Pacific Conference on Intelligent Robot Systems (ACIRS), Wuhan, China, 16–18 June 2017; pp. 205–209. [Google Scholar]
- Won, D.; Park, M.; Chi, S. Construction Resource Localization Based on UAV-RFID Platform Using Machine Learning Algorithm. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018; pp. 1086–1090. [Google Scholar] [CrossRef]
- Brzozowski, B.; Kaźmierczak, K.; Rochala, Z.; Wojda, M.; Wojtowicz, K. A concept of UAV indoor navigation system based on magnetic field measurements. Proceedngs of the IEEE Metrology for Aerospace (MetroAeroSpace), Florence, Italy, 22–23 June 2016; pp. 636–640. [Google Scholar]
- Zahran, S.; Moussa, A.; Sesay, A.; El-Sheimy, A. A New Velocity Meter based on Hall Effect Sensors for UAV Indoor Navigation. IEEE Sens. J. 2018. [Google Scholar] [CrossRef]
- Xiao, X.; Fan, Y.; Dufek, J.; Murphy, R. Indoor UAV Localization Using a Tether. In Proceedings of the IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Philadelphia, PA, USA, 6–8 August 2018; pp. 1–6. [Google Scholar]
- He, Z.; Renaudin, V.; Petovello, M.G.; Lachapelle, G. Use of High Sensitivity GNSS Receiver Doppler Measurements for Indoor Pedestrian Dead Reckoning. Sensors 2013, 13, 4303–4326. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; He, Z.; Gao, Z.; Zhuang, Y.; Shi, C.; El-Sheimy, N. Towards Robust Crowdsourcing-Based Localization: A Fingerprinting Accuracy Indicator Enhanced Wireless/Magnetic/Inertial Integration Approach. IEEE Internet Things J. 2018. [Google Scholar] [CrossRef]
- Li, Y.; Zhuang, Y.; Zhang, P.; Lan, H.; Niu, X.; El-Sheimy, N. An improved inertial/wifi/magnetic fusion structure for indoor navigation. Inf. Fusion 2017, 34, 101–119. [Google Scholar] [CrossRef]
- Li, Y.; Georgy, J.; Niu, X.; Li, Q.; El-Sheimy, N. Autonomous Calibration of MEMS Gyros in Consumer Portable Devices. IEEE Sens. J. 2015, 15, 4062–4072. [Google Scholar] [CrossRef]
- Li, Y.; Zhuang, Y.; Lan, H.; Zhang, P.; Niu, X.; El-Sheimy, N. Self-Contained Indoor Pedestrian Navigation Using Smartphone Sensors and Magnetic Features. IEEE Sens. J. 2016, 16, 7173–7182. [Google Scholar] [CrossRef]
- Li, Y.; Niu, X.; Cheng, Y.; Shi, C.; El-Sheimy, N. The Impact of Vehicle Maneuvers on the Attitude Estimation of GNSS/INS for Mobile Mapping. J. Appl. Geod. 2015, 9, 183–197. [Google Scholar] [CrossRef]
- Li, Y.; Niu, X.; Zhang, Q.; Cheng, Y.; Shi, C. Observability Analysis of Non-Holonomic Constraints for Land-Vehicle Navigation Systems. In Proceedings of the 25th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012; pp. 1521–1529. [Google Scholar]
- Lin, C.; Chiang, K.; Kuo, C. Development of INS/GNSS UAV-Borne Vector Gravimetry System. IEEE Geosci. Remote Sens. Lett. 2017, 14, 759–763. [Google Scholar] [CrossRef]
- Titterton, D.; Weston, J. Strapdown Inertial Navigation Technology; Institution of Electrical Engineers: London, UK, 1997. [Google Scholar]
- Shin, E.H. Estimation Techniques for Low-Cost Inertial Navigation; UCGE Reports Number 20219; The University of Calgary: Calgary, AB, Canada, 2005. [Google Scholar]
- Gebre-Egziabher, D.; Elkaim, G.; Powell, D.; Parkinson, B. Calibration of Strapdown Magnetometers in Magnetic Field Domain. J. Aerosp. Eng. 2006, 19, 1–45. [Google Scholar] [CrossRef]
- Li, Y. Integration of MEMS Sensors, WiFi, and Magnetic Features for Indoor Pedestrian Navigation with Consumer Portable Devices; UCGE Reports Number 22455; The University of Calgary: Calgary, AB, Canada, 2015. [Google Scholar]
- Han, S.; Wang, J. A Novel Method to Integrate IMU and Magnetometers in Attitude and Heading Reference Systems. J. Navig. 2011, 64, 727–738. [Google Scholar] [CrossRef]
- Syed, Z.; Aggarwal, P.; Niu, X.; El-Sheimy, N. Civilian Vehicle Navigation: Required Alignment of the Inertial Sensors for Acceptable Navigation Accuracies. IEEE Trans. Veh. Technol. 2008, 57, 3402–3412. [Google Scholar] [CrossRef]
- YLi, Y.; Gao, Z.; He, Z.; Zhang, P.; Chen, R.; El-Sheimy, N. Multi-Sensor Multi-Floor 3D Localization with Robust Floor Detection. IEEE Access 2018, 6, 76689–76699. [Google Scholar]
- Teunissen, P.J. The 1990’s—A Decade of Excellence in the Navigation Sciences. In Proceedings of the IEEE Symposium on Position Location and Navigation. A Decade of Excellence in the Navigation Sciences, Las Vegas, NV, USA, 20–23 March 1990. [Google Scholar] [CrossRef]
- 3DR. SOLO User Manual. 2017. Available online: https://3dr.com/wp-content/uploads/2017/03/v9_02_25_16.pdf (accessed on 1 February 2019).
- Marvelmind. Marvelmind Indoor Navigation System Operating Manual. Available online: https://marvelmind.com/pics/marvelmind_navigation_system_manual.pdf (accessed on 1 February 2019).
- InvenSense. MPU-6000 and MPU-6050 Product Specification. Available online: https://www.invensense.com/wp-content/uploads/2015/02/MPU-6000-Datasheet1.pdf (accessed on 1 February 2019).
- Honeywell. 3-Axis Digital Compass IC HMC5983. Available online: https://www.sparkfun.com/datasheets/Sensors/Magneto/HMC5843.pdf (accessed on 1 February 2019).
- TE. MS5611-01BA03 Barometric Pressure Sensor. Available online: https://www.te.com/usa-en/product-CAT-BLPS0036.html (accessed on 1 February 2019).
- Sensirion. Mass Flow Meter SFM3000. Available online: https://www.sensirion.com/en/flow-sensors/ (accessed on 1 February 2019).
- LattePanda. LattePanda Single Board Computer. Available online: https://www.lattepanda.com (accessed on 1 February 2019).








| Method | Sensors | Algorithm | Test Area | Accuracy |
|---|---|---|---|---|
| [6] | Stereo camera | SLAM | 200 m * 300 m | Meter level |
| [7] | Stereo camera, IMU | SLAM | 16 m * 16 m | Meter level |
| [8] | Monocular camera, IMU | Kernel adaptive filtering | N/A | Decimeter level |
| [9] | Monocular camera, optical flow sensor, IMU, barometer | Indirect EKF | 50 m * 20 m | Meter level |
| [10] | Monocular camera, fiducial markers | Relative pose identification | 5 m * 5 m | Decimeter level |
| [11] | RGB-D camera, IMU, ultrasonic, optical flow sensor | Decentralized information filter | 3 m * 2 m | Decimeter level |
| [12] | Optical flow sensor, IMU | EKF | 6 m * 6 m | 0.3 m in mean |
| [13] | Ultraviolet LED makers | Mutual relative localization | 10 m distance | Meter level |
| [14] | 3D lidar, UWB, IMU | EKF | Simulation | Decimeter level |
| [15] | 2D lidar | CNN | 4 m * 4 m | Decimeter level |
| [16] | 2D lidar, IMU | SLAM | 8 m * 8 m | 1.0 m for 26 s, 0.5 m for 10 s |
| [17] | 2D lidar, IMU | Tightly coupled SLAM | 60 m corridor | Meter level |
| [18] | 1D laser, IMU, barometer | EKF | 5 m * 9 m | 0.1 m height accuracy in mean |
| [19] | Radar | Radar odometry | 80 m * 10 m | 3.3 m in mean |
| [20] | Radar, UWB, IMU | EKF | 40 m * 40 m | 0.8 m in RMS |
| [21] | UWB | Multilateration | 20 m * 30 m, 4 AP | 2.0 m in mean |
| [22] | UWB | TDoA | 4 m * 2 m, 4 AP | 0.1 m in 75 % |
| [23] | UWB, IMU | Tightly coupled EKF | 19 m * 13 m | 0.15 m in mean |
| [24] | UWB, monocular camera | SLAM | 8 m * 8 m | 0.23 m in 75 % |
| [25] | UWB, RGB-D camera | Monte Carlo localization | 15 m * 15 m | 0.2 m in RMS |
| [26] | Ultrasonic | Multilateration | 4 m * 3 m, 6 AP | 0.16 m in RMS |
| [27] | Ultrasonic | CNN | 10 m * 4 m | Decimeter level |
| [28] | Ultrasonic, time-of-flight camera | Multilateration | 0.7 m * 0.7 m, 5 AP | 0.17 m in median |
| [29] | WiFi | Fingerprinting | 36 m * 17 m, 10 APs | 1.7 m in mean |
| [30] | WiFi | Fingerprinting with RSS interpolation | 9 m * 9 m, 4 APs | 2.2 m in mean |
| [31] | BLE | Multilateration | 4 m * 4 m | Meter level |
| [32] | RFID, GNSS (RTK) | K-nearest neighbors | 30 m * 30 m, 9 tags | 0.18 m in RMS |
| [33] | Magnetometers | Magnetic matching | 24 m * 2 m | Sub-meter level |
| [34] | Hall-effect sensor, IMU | EKF | 30 m * 30 m | 2.15 m in 54 s |
| [35] | A quasi-taut tether | Angle and range-based | 2.5 m * 2.5 m | 0.37 m in mean |
| Strategy | Mean | RMS | 80% | 95% | Max |
|---|---|---|---|---|---|
| AHRS/INS (m) | 415.6 | 475.7 | 632.6 | 792.9 | 966.0 |
| AHRS/INS/Flow(Raw) (m) | 20.2 | 22.4 | 27.6 | 38.4 | 58.4 |
| AHRS/INS/Vel(Raw) (m) | 15.9 | 18.1 | 21.6 | 32.9 | 44.3 |
| AHRS/INS/Vel(Cali) (m) | 10.6 | 12.1 | 15.5 | 23.8 | 28.9 |
| AHRS/INS/Vel(Cali,QC) (m) | 9.4 | 11.0 | 14.8 | 22.4 | 26.8 |
| 95.1% | 95.3% | 95.6% | 95.2% | 94.0% | |
| 21.3% | 19.2% | 21.7% | 14.3% | 24.1% | |
| 33.3% | 33.1% | 28.2% | 27.7% | 34.7% | |
| 11.3% | 9.1% | 4.5% | 5.9% | 7.3% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zahran, S.; Zhuang, Y.; Gao, Z.; Luo, Y.; He, Z.; Pei, L.; Chen, R.; El-Sheimy, N. IMU/Magnetometer/Barometer/Mass-Flow Sensor Integrated Indoor Quadrotor UAV Localization with Robust Velocity Updates. Remote Sens. 2019, 11, 838. https://doi.org/10.3390/rs11070838
Li Y, Zahran S, Zhuang Y, Gao Z, Luo Y, He Z, Pei L, Chen R, El-Sheimy N. IMU/Magnetometer/Barometer/Mass-Flow Sensor Integrated Indoor Quadrotor UAV Localization with Robust Velocity Updates. Remote Sensing. 2019; 11(7):838. https://doi.org/10.3390/rs11070838
Chicago/Turabian StyleLi, You, Shady Zahran, Yuan Zhuang, Zhouzheng Gao, Yiran Luo, Zhe He, Ling Pei, Ruizhi Chen, and Naser El-Sheimy. 2019. "IMU/Magnetometer/Barometer/Mass-Flow Sensor Integrated Indoor Quadrotor UAV Localization with Robust Velocity Updates" Remote Sensing 11, no. 7: 838. https://doi.org/10.3390/rs11070838
APA StyleLi, Y., Zahran, S., Zhuang, Y., Gao, Z., Luo, Y., He, Z., Pei, L., Chen, R., & El-Sheimy, N. (2019). IMU/Magnetometer/Barometer/Mass-Flow Sensor Integrated Indoor Quadrotor UAV Localization with Robust Velocity Updates. Remote Sensing, 11(7), 838. https://doi.org/10.3390/rs11070838






