Potential of Forest Parameter Estimation Using Metrics from Photon Counting LiDAR Data in Howland Research Forest
Abstract
:1. Introduction
2. Study Site and Data
2.1. Study Site
2.2. Photon Counting LiDAR Data from SIMPL
2.3. Airborne LiDAR Data from G-LiHT
2.4. Field Measurement
3. Methods
3.1. Overview
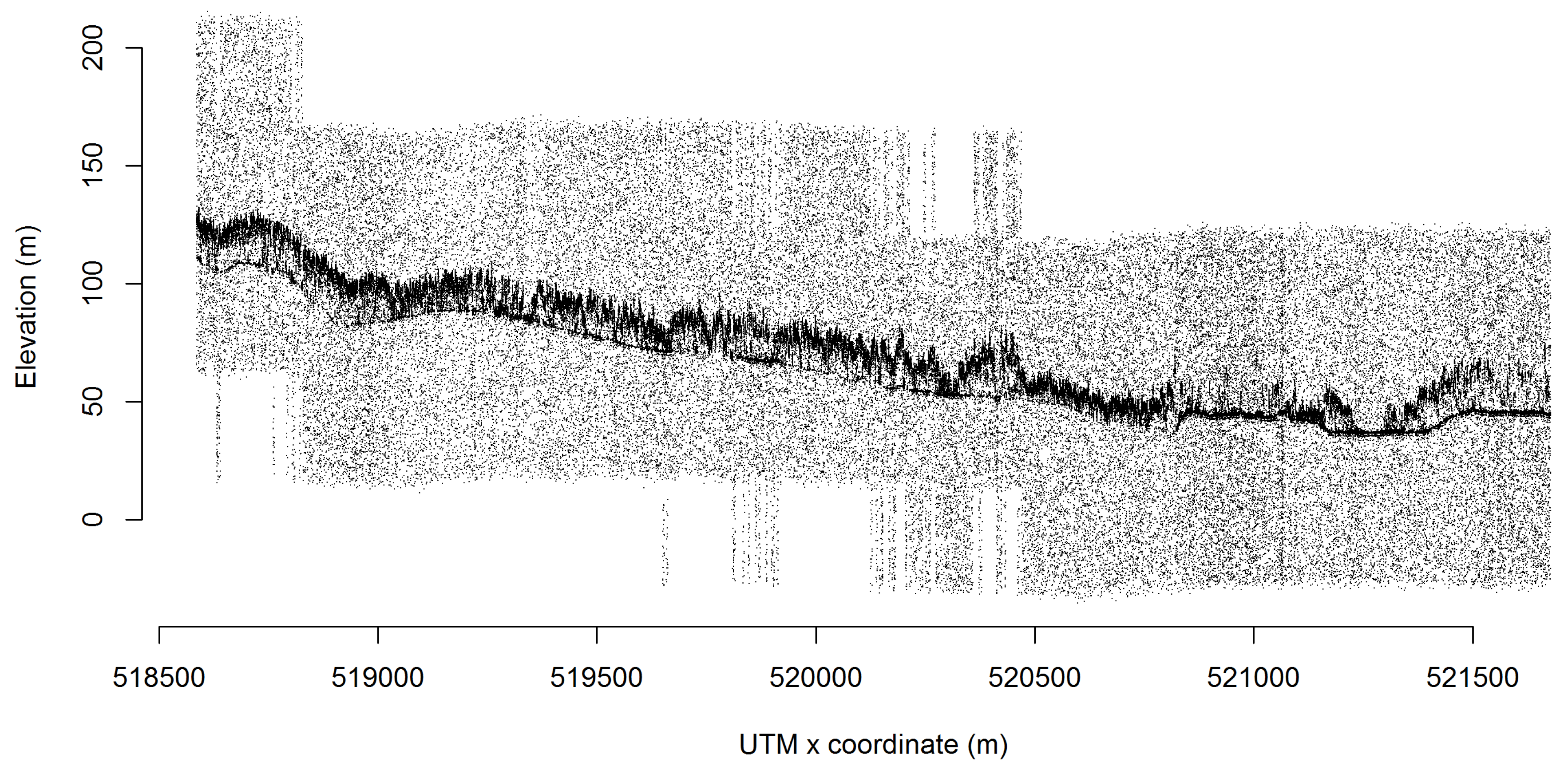
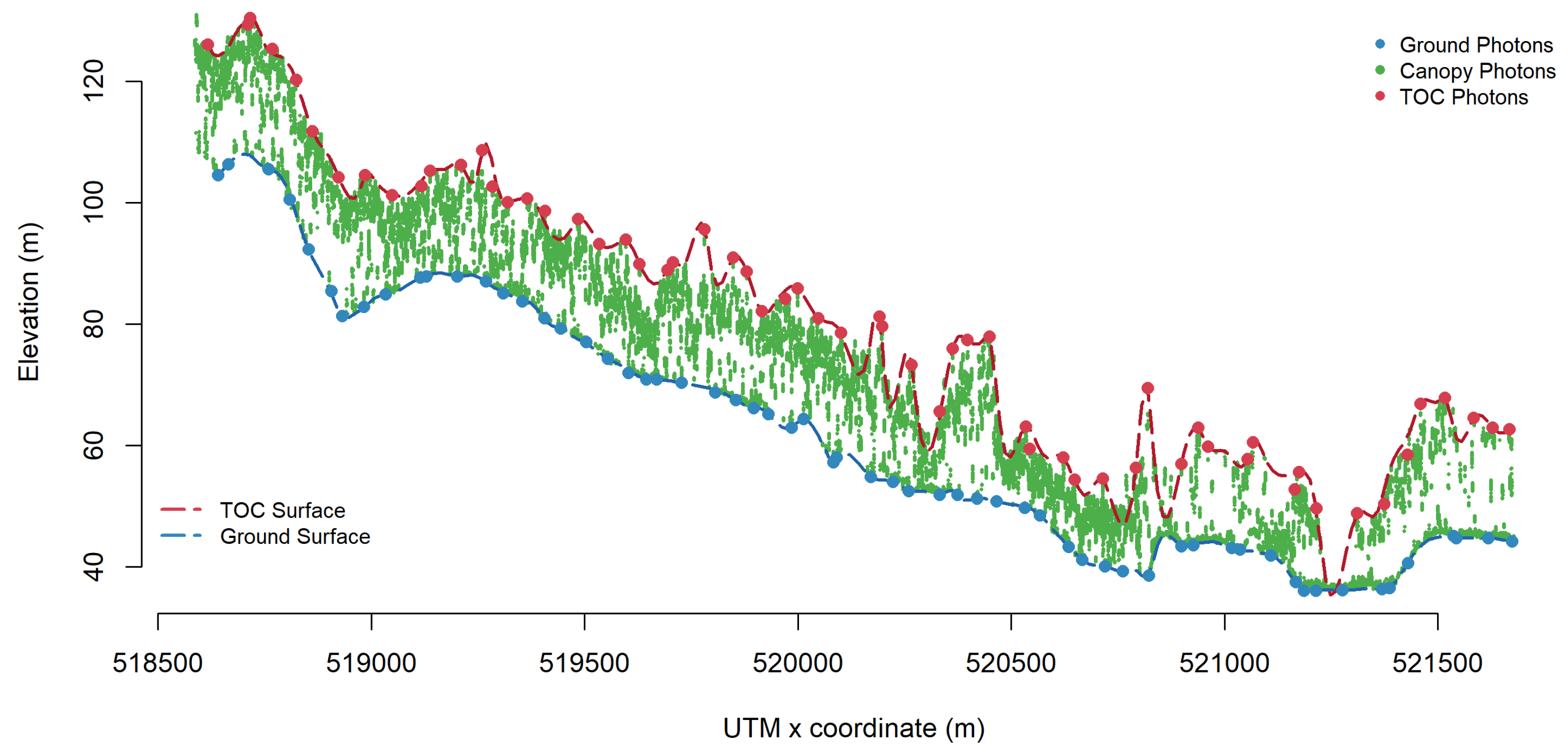
3.2. Extraction of Ground and Canopy Surface
3.3. Co-Registration between SIMPL and G-LiHT Data
3.4. Metrics and Accuracy Assessment
4. Results
4.1. Results of Extraction of Ground and Canopy Surface
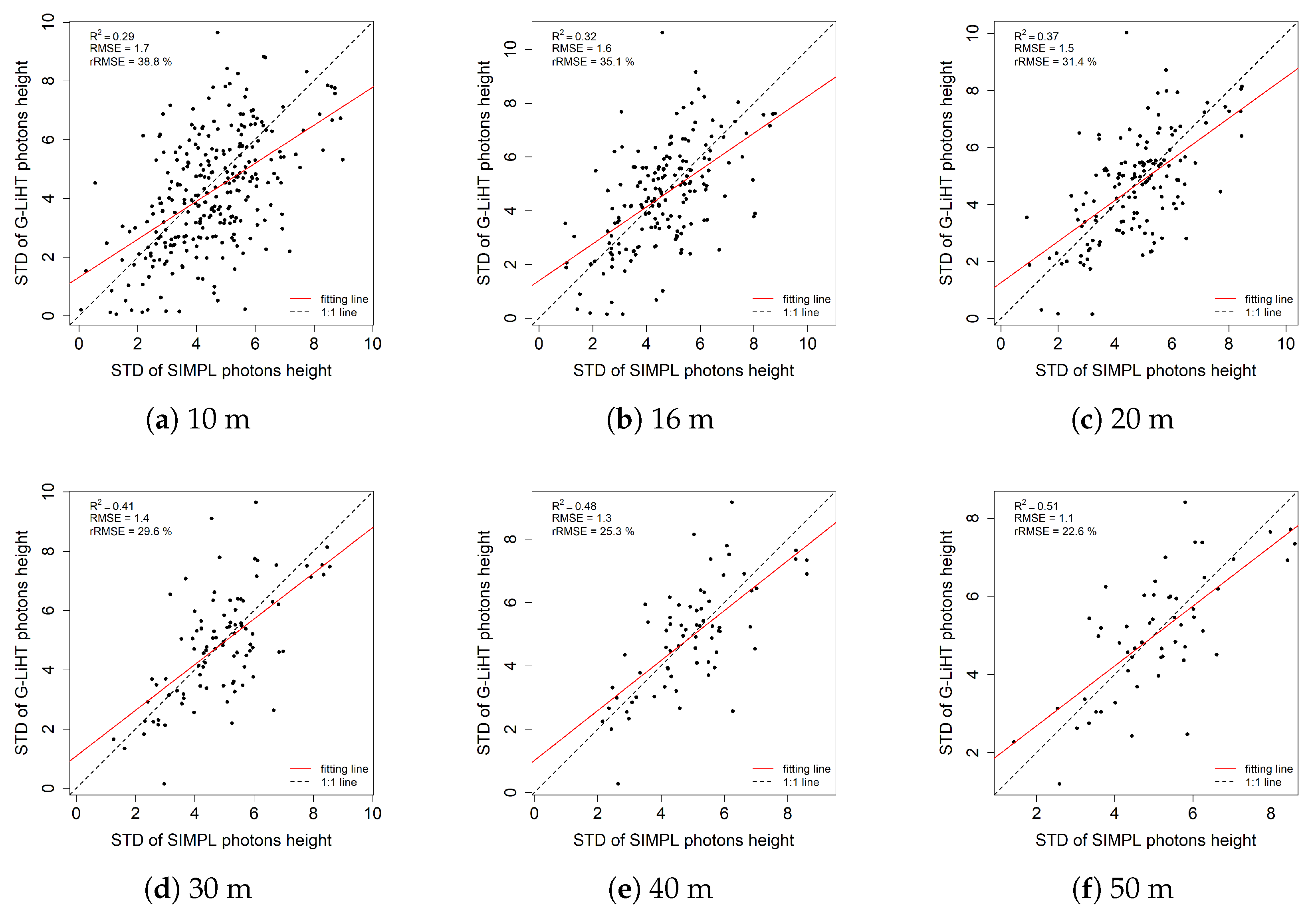
4.2. Results of Co-Registration between SIMPL and G-LiHT Data
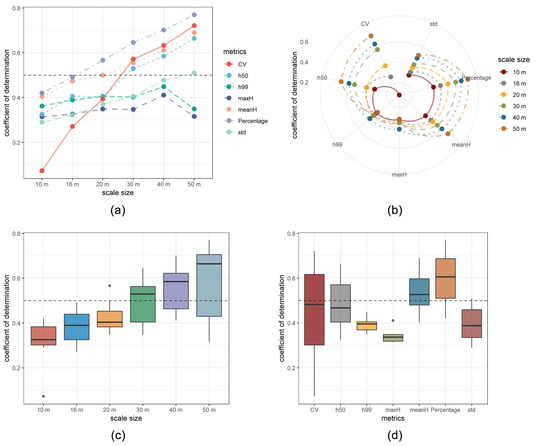
4.3. Results of Metrics from SIMPL Data
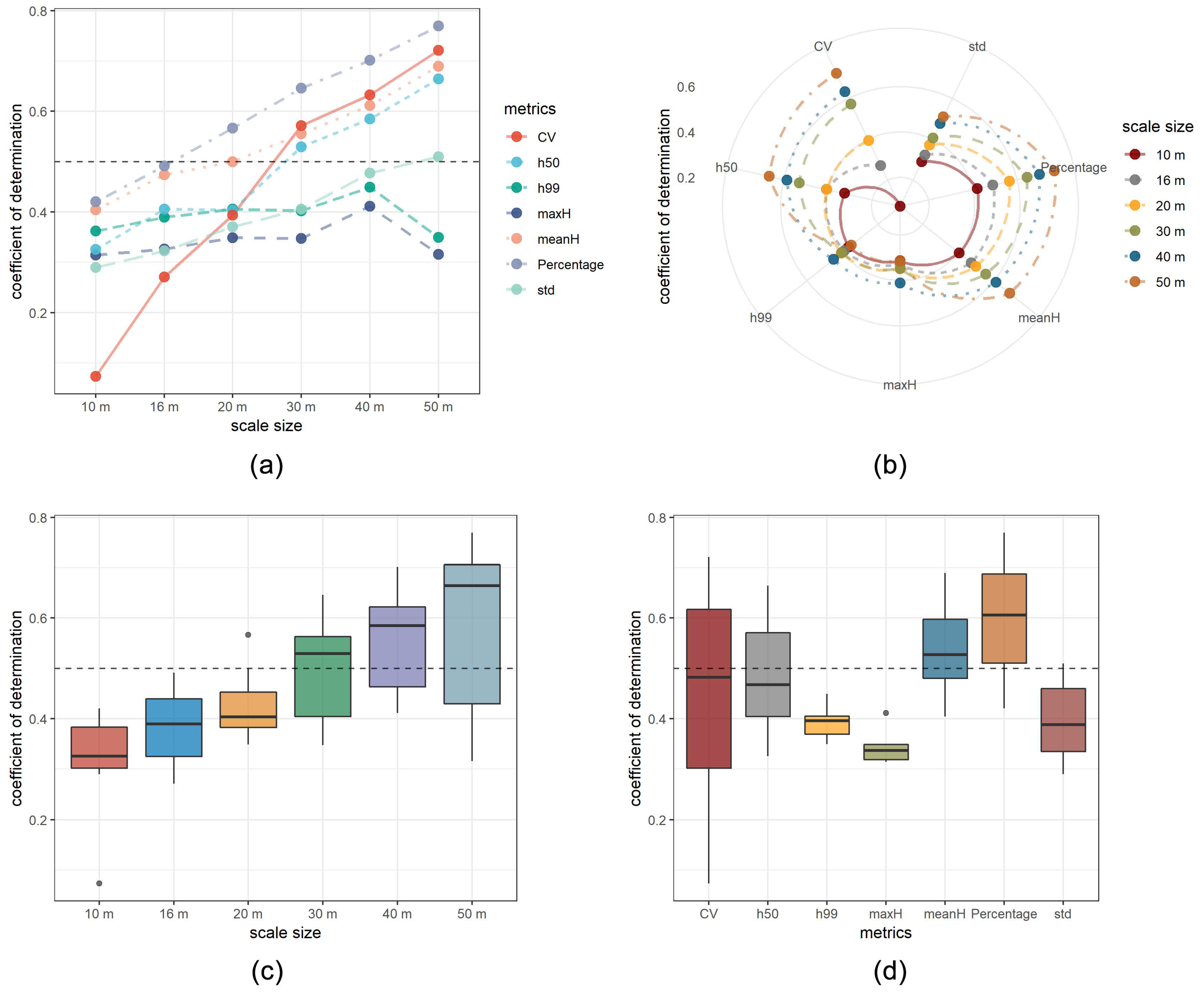
4.4. Validation with Field Measurements
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shevliakova, E.; Pacala, S.W.; Malyshev, S.; Hurtt, G.C.; Milly, P.; Caspersen, J.P.; Sentman, L.T.; Fisk, J.P.; Wirth, C.; Crevoisier, C. Carbon cycling under 300 years of land use change: Importance of the secondary vegetation sink. Glob. Biogeochem. Cycles 2009, 23. [Google Scholar] [CrossRef]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Reese, H.; Nilsson, M.; Sandström, P.; Olsson, H. Applications using estimates of forest parameters derived from satellite and forest inventory data. Comput. Electron. Agric. 2002, 37, 37–55. [Google Scholar] [CrossRef]
- Kindermann, G.; McCallum, I.; Fritz, S.; Obersteiner, M. A global forest growing stock, biomass and carbon map based on FAO statistics. Silva Fennica 2008, 42, 387–396. [Google Scholar] [CrossRef]
- Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar]
- Dubayah, R.O.; Drake, J.B. Lidar remote sensing for forestry. J. For. 2000, 98, 44–46. [Google Scholar]
- Koetz, B.; Morsdorf, F.; Sun, G.; Ranson, K.J.; Itten, K.; Allgower, B. Inversion of a lidar waveform model for forest biophysical parameter estimation. IEEE Geosci. Remote Sens. Lett. 2006, 3, 49–53. [Google Scholar] [CrossRef]
- Rosette, J.; Suárez, J.; North, P.; Los, S. Forestry applications for satellite LiDAR remote sensing. Photogramm. Eng. Remote Sens. 2011, 77, 271–279. [Google Scholar] [CrossRef]
- Rosette, J.; Cook, B.; Nelson, R.; Huang, C.; Masek, J.; Tucker, C.; Sun, G.; Huang, W.; Montesano, P.; Rubio-Gil, J.; et al. Sensor Compatibility for Biomass Change Estimation Using Remote Sensing Data Sets: Part of NASA’s Carbon Monitoring System Initiative. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1511–1515. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Del Bom Espirito-Santo, F.; Hunter, M.O.; de Oliveira, R. Estimates of forest canopy height and aboveground biomass using ICESat. Geophys. Res. Lett. 2005, 32, L22S02. [Google Scholar] [CrossRef]
- Keller, M. Revised method for forest canopy height estimation from Geoscience Laser Altimeter System waveforms. J. Appl. Remote Sens. 2007, 1, 013537. [Google Scholar] [CrossRef]
- Duncanson, L.I.; Niemann, K.O.; Wulder, M.A. Estimating forest canopy height and terrain relief from GLAS waveform metrics. Remote Sens. Environ. 2010, 114, 138–154. [Google Scholar] [CrossRef]
- Bye, I.; North, P.R.; Los, S.; Kljun, N.; Rosette, J.; Hopkinson, C.; Chasmer, L.; Mahoney, C. Estimating forest canopy parameters from satellite waveform LiDAR by inversion of the FLIGHT three-dimensional radiative transfer model. Remote Sens. Environ. 2017, 188, 177–189. [Google Scholar] [CrossRef]
- Lefsky, M.; Keller, M.; Harding, D.; Pang, Y. A Global Forest Canopy Height and Vertical Structure Product from the Geoscience Laser Altimeter System. In AGU Fall Meeting Abstracts; American Geophysical Union: San Francisco, CA, USA, 2006. [Google Scholar]
- Los, S.; Rosette, J.; Kljun, N.; North, P.; Chasmer, L.; Suárez, J.; Hopkinson, C.; Hill, R.; Van Gorsel, E.; Mahoney, C.; et al. Vegetation height products between 60 S and 60 N from ICESat GLAS data. Geosci. Model Dev. 2012, 5, 413–432. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Leigh, H.W.; Magruder, L.A.; Carabajal, C.C.; Saba, J.L.; McGarry, J.F. Development of Onboard Digital Elevation and Relief Databases for ICESat-2. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2011–2020. [Google Scholar] [CrossRef]
- Troupaki, E.; Denny, Z.H.; Wu, S.; Bradshaw, H.N.; Smith, K.A.; Hults, J.A.; Ramos-Izquierdo, L.A.; Cook, W.B. Space qualification of the optical filter assemblies for the ICESat-2/ATLAS instrument. In Proceedings of the Components and Packaging for Laser Systems. International Society for Optics and Photonics, San Francisco, CA, USA, 20 February 2015; Volume 9346, p. 93460H. [Google Scholar]
- Anthony, W.Y.; Harding, D.J.; Dabney, P.W. Laser transmitter design and performance for the slope imaging multi-polarization photon-counting lidar (SIMPL) instrument. In Proceedings of the Solid State Lasers XXV: Technology and Devices. International Society for Optics and Photonics, San Francisco, CA, USA, 16 March 2016; Volume 9726, p. 97260J. [Google Scholar]
- Brunt, K.; Neumann, T.; Markus, T.; Cook, W.; Hart, W.; Webb, C.; Dimarzio, J.; Hancock, D.; Lee, J.; Bhardwaj, S.; et al. MABEL photon-counting altimetry data for ICESat-2 simulations. In AGU Fall Meeting Abstracts; American Geophysical Union: San Francisco, CA, USA, 2011. [Google Scholar]
- McGill, M.; Markus, T.; Scott, S.S.; Neumann, T. The multiple altimeter beam experimental lidar (MABEL): An airborne simulator for the ICESat-2 mission. J. Atmos. Ocean. Technol. 2013, 30, 345–352. [Google Scholar] [CrossRef]
- Brunt, K.M.; Neumann, T.A.; Amundson, J.M.; Kavanaugh, J.L.; Moussavi, M.S.; Walsh, K.M.; Cook, W.B.; Markus, T. MABEL photon-counting laser altimetry data in Alaska for ICESat-2 simulations and development. Cryosphere 2016, 10. [Google Scholar] [CrossRef]
- Rosette, J.; Field, C.; Nelson, R.; Decola, P.; Cook, B.; Degnan, J. Single-Photon LiDAR for Vegetation Analysis. In AGU Fall Meeting Abstracts; American Geophysical Union: San Francisco, CA, USA, 2011. [Google Scholar]
- Magruder, L.A.; Brunt, K.M. Performance Analysis of Airborne Photon-Counting Lidar Data in Preparation for the ICESat-2 Mission. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2911–2918. [Google Scholar] [CrossRef]
- Brunt, K.M.; Neumann, T.A.; Walsh, K.M.; Markus, T. Determination of Local Slope on the Greenland Ice Sheet Using a Multibeam Photon-Counting Lidar in Preparation for the ICESat-2 Mission. IEEE Geosci. Remote Sens. Lett. 2014, 11, 935–939. [Google Scholar] [CrossRef]
- Herzfeld, U.C.; McDonald, B.W.; Wallin, B.F.; Neumann, T.A.; Markus, T.; Brenner, A.; Field, C. Algorithm for Detection of Ground and Canopy Cover in Micropulse Photon-Counting Lidar Altimeter Data in Preparation for the ICESat-2 Mission. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2109–2125. [Google Scholar] [CrossRef]
- Zhang, J.; Kerekes, J. An Adaptive Density-Based Model for Extracting Surface Returns from Photon-Counting Laser Altimeter Data. IEEE Geosci. Remote Sens. Lett. 2015, 12, 726–730. [Google Scholar] [CrossRef]
- Gwenzi, D.; Lefsky, M.A.; Suchdeo, V.P.; Harding, D.J. Prospects of the ICESat-2 laser altimetry mission for savanna ecosystem structural studies based on airborne simulation data. ISPRS J. Photogramm. Remote Sens. 2016, 118, 68–82. [Google Scholar] [CrossRef]
- Popescu, S.; Zhou, T.; Nelson, R.; Neuenschwander, A.; Sheridan, R.; Narine, L.; Walsh, K. Photon counting LiDAR: An adaptive ground and canopy height retrieval algorithm for ICESat-2 data. Remote Sens. Environ. 2018, 208, 154–170. [Google Scholar] [CrossRef]
- Brown, M.E.; Arias, S.D.; Neumann, T.; Jasinski, M.F.; Posey, P.; Babonis, G.; Glenn, N.F.; Birkett, C.M.; Escobar, V.M.; Markus, T. Applications for ICESat-2 Data: From NASA’s Early Adopter Program. IEEE Geosci. Remote Sens. Mag. 2016, 4, 24–37. [Google Scholar] [CrossRef]
- Neuenschwander, A.L.; Magruder, L.A. The potential impact of vertical sampling uncertainty on ICESat-2/ATLAS terrain and canopy height retrievals for multiple ecosystems. Remote Sens. 2016, 8, 1039. [Google Scholar] [CrossRef]
- Swatantran, A.; Tang, H.; Barrett, T.; DeCola, P.; Dubayah, R. Rapid, high-resolution forest structure and terrain mapping over large areas using single photon lidar. Sci. Rep. 2016, 6, 28277. [Google Scholar] [CrossRef]
- Kwok, R.; Markus, T. Potential basin-scale estimates of Arctic snow depth with sea ice freeboards from CryoSat-2 and ICESat-2: An exploratory analysis. Adv. Space Res. 2017, 62, 1243–1250. [Google Scholar] [CrossRef]
- Glenn, N.F.; Neuenschwander, A.; Vierling, L.A.; Spaete, L.; Li, A.; Shinneman, D.J.; Pilliod, D.S.; Arkle, R.S.; McIlroy, S.K. Landsat 8 and ICESat-2: Performance and potential synergies for quantifying dryland ecosystem vegetation cover and biomass. Remote Sens. Environ. 2016, 185, 233–242. [Google Scholar] [CrossRef]
- Gwenzi, D.; Lefsky, M. Prospects of photon counting lidar for savanna ecosystem structural studies. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing & Spatial Information Sciences, Denver, CO, USA, 7–20 November 2014. [Google Scholar]
- Nie, S.; Wang, C.; Xi, X.; Luo, S.; Li, G.; Tian, J.; Wang, H. Estimating the vegetation canopy height using micro-pulse photon-counting LiDAR data. Opt. Express 2018, 26, A520–A540. [Google Scholar] [CrossRef]
- Montesano, P.; Rosette, J.; Sun, G.; North, P.; Nelson, R.; Dubayah, R.; Ranson, K.; Kharuk, V. The uncertainty of biomass estimates from modeled ICESat-2 returns across a boreal forest gradient. Remote Sens. Environ. 2015, 158, 95–109. [Google Scholar] [CrossRef]
- Cook, B.D.; Corp, L.A.; Nelson, R.F.; Middleton, E.M.; Morton, D.C.; McCorkel, J.T.; Masek, J.G.; Ranson, K.J.; Ly, V.; Montesano, P.M. NASA Goddard’s LiDAR, hyperspectral and thermal (G-LiHT) airborne imager. Remote Sens. 2013, 5, 4045–4066. [Google Scholar] [CrossRef]
- Chen, B.; Pang, Y.; Li, Z.; Lu, H.; Liu, L.; North, P.; Rosette, J. Ground and Top of Canopy Extraction from Photon Counting LiDAR Data Using Local Outlier Factor with Ellipse Searching Area. IEEE Geosci. Remote Sens. Lett. 2019, in press. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. Sigmod Record 2000, 29, 93–104. [Google Scholar] [CrossRef]
- Drake, J.B.; Dubayah, R.O.; Knox, R.G.; Clark, D.B.; Blair, J.B. Sensitivity of large-footprint lidar to canopy structure and biomass in a neotropical rainforest. Remote Sens. Environ. 2002, 81, 378–392. [Google Scholar] [CrossRef]
- Anderson, J.; Martin, M.; Smith, M.; Dubayah, R.; Hofton, M.; Hyde, P.; Peterson, B.; Blair, J.; Knox, R. The use of waveform lidar to measure northern temperate mixed conifer and deciduous forest structure in New Hampshire. Remote Sens. Environ. 2006, 105, 248–261. [Google Scholar] [CrossRef]
- Pang, Y.; Lefsky, M.; Sun, G.; Ranson, J. Impact of footprint diameter and off-nadir pointing on the precision of canopy height estimates from spaceborne lidar. Remote Sens. Environ. 2011, 115, 2798–2809. [Google Scholar] [CrossRef]













| Species | No. of Trees | Statistics | Height (m) | DBH (cm) | d-East-West (m) | d-North-South (m) |
|---|---|---|---|---|---|---|
| Hemlock | 7239 | Min | 3.17 | 2.90 | 0.21 | 1.10 |
| Max | 37.99 | 60.90 | 6.91 | 13.21 | ||
| Mean | 12.94 | 12.12 | 1.19 | 4.5 | ||
| SD | 7.91 | 8.10 | 0.53 | 2.75 | ||
| Aspen | 750 | Min | 4.36 | 3.0 | 0.23 | 1.05 |
| Max | 46.47 | 61.8 | 2.66 | 11.22 | ||
| Mean | 15.47 | 10.9 | 1.12 | 3.74 | ||
| SD | 9.49 | 7.37 | 0.43 | 2.29 | ||
| All | 7989 | Min | 3.17 | 2.9 | 0.21 | 1.05 |
| Max | 46.47 | 61.8 | 6.91 | 13.21 | ||
| Mean | 12.83 | 12.0 | 1.19 | 4.43 | ||
| SD | 7.86 | 8.04 | 0.52 | 2.72 |
| Source of Data | Name of the Metrics | Description |
|---|---|---|
| Metrics from SIMPL | SmaxH | Max value of all photon heights |
| SmeanH | Mean value of all photon heights | |
| Sh99 | 99th percentile of all photon heights | |
| Sh50 | 50th percentile of all photon heights | |
| SPercentage | Fraction of the number of photons above 1.3 m | |
| SSTD | Standard deviation of all photon heights | |
| SCV | Coefficient of variation of all photon heights | |
| Metrics from G-LiHT | GmaxH | Max value of all return heights |
| GmeanH | Mean value of all return heights | |
| Gh99 | 99th percentile of all return heights | |
| Gh50 | 50th percentile of all return heights | |
| GPercentage | Fraction of the number of points above 1.3 m | |
| GSTD | Standard deviation of all return heights | |
| GCV | Coefficient of variation of all return heights |
| Data Source | Scale Size | MAE (m) | SD (m) | RMSE (m) |
|---|---|---|---|---|
| G-LiHT | 10 m | 2.9 | 3.9 | 3.6 |
| 16 m | 2.4 | 1.7 | 2.1 | |
| 20 m | 1.7 | 1.8 | 2.1 | |
| 30 m | 1.2 | 2.1 | 1.9 | |
| Mean value | 2.1 | 2.4 | 2.4 | |
| SIMPL | 10 m | 3.5 | 4.6 | 4.5 |
| 16 m | 2.7 | 5.7 | 5.3 | |
| 20 m | 3 | 5.4 | 5 | |
| 30 m | 2.4 | 5.3 | 4.9 | |
| Mean value | 2.9 | 5.3 | 4.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Pang, Y.; Li, Z.; North, P.; Rosette, J.; Sun, G.; Suárez, J.; Bye, I.; Lu, H. Potential of Forest Parameter Estimation Using Metrics from Photon Counting LiDAR Data in Howland Research Forest. Remote Sens. 2019, 11, 856. https://doi.org/10.3390/rs11070856
Chen B, Pang Y, Li Z, North P, Rosette J, Sun G, Suárez J, Bye I, Lu H. Potential of Forest Parameter Estimation Using Metrics from Photon Counting LiDAR Data in Howland Research Forest. Remote Sensing. 2019; 11(7):856. https://doi.org/10.3390/rs11070856
Chicago/Turabian StyleChen, Bowei, Yong Pang, Zengyuan Li, Peter North, Jacqueline Rosette, Guoqing Sun, Juan Suárez, Iain Bye, and Hao Lu. 2019. "Potential of Forest Parameter Estimation Using Metrics from Photon Counting LiDAR Data in Howland Research Forest" Remote Sensing 11, no. 7: 856. https://doi.org/10.3390/rs11070856
APA StyleChen, B., Pang, Y., Li, Z., North, P., Rosette, J., Sun, G., Suárez, J., Bye, I., & Lu, H. (2019). Potential of Forest Parameter Estimation Using Metrics from Photon Counting LiDAR Data in Howland Research Forest. Remote Sensing, 11(7), 856. https://doi.org/10.3390/rs11070856