Combining MODIS and National Land Resource Products to Model Land Cover-Dependent Surface Albedo for Norway
Abstract
:1. Introduction
2. Materials and Methods
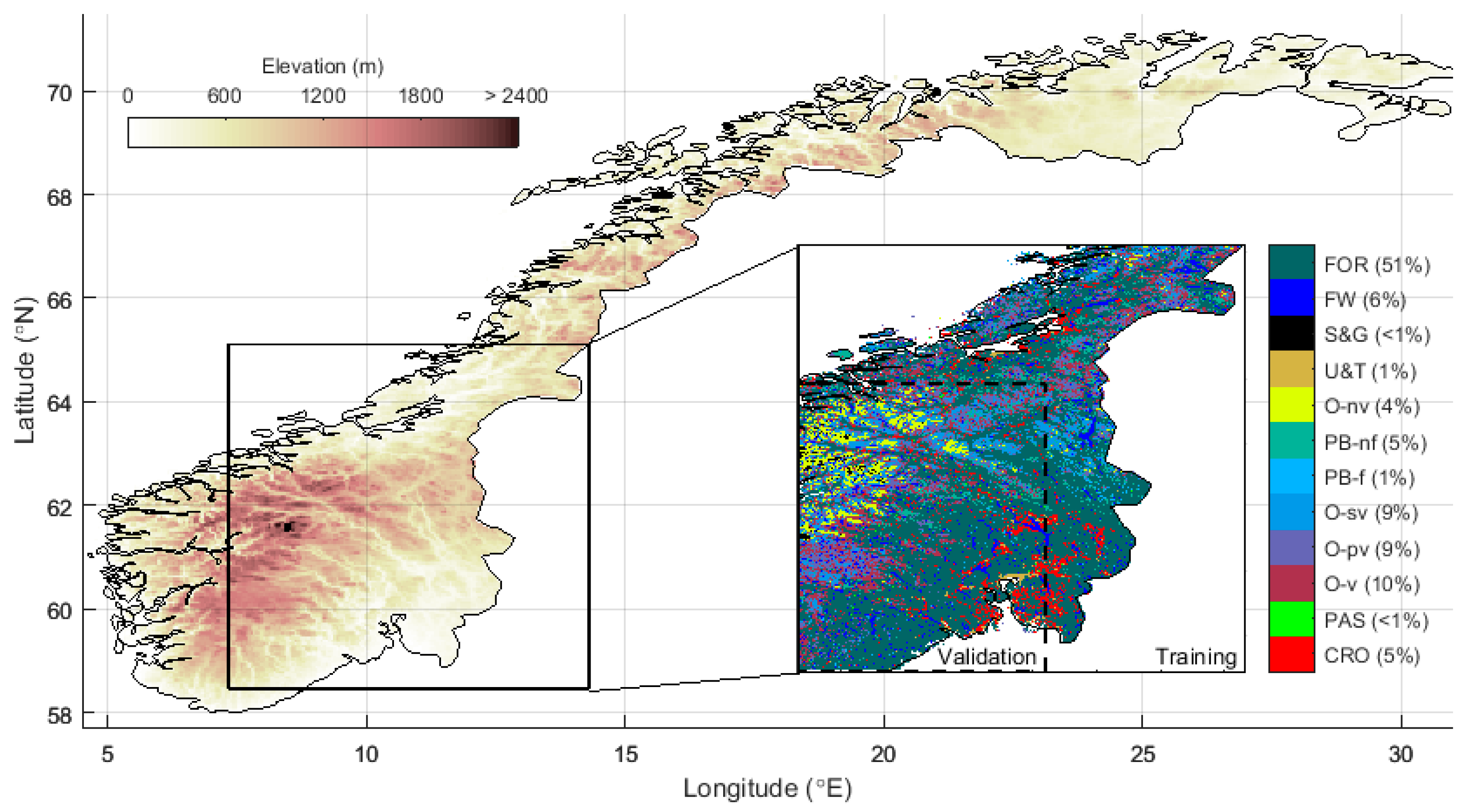
2.1. Study Region
2.2. Spectral Unmixing Regression Analysis
2.3. Land Cover Data
2.4. Forest Cover and Structure Data
2.5. Albedo Data
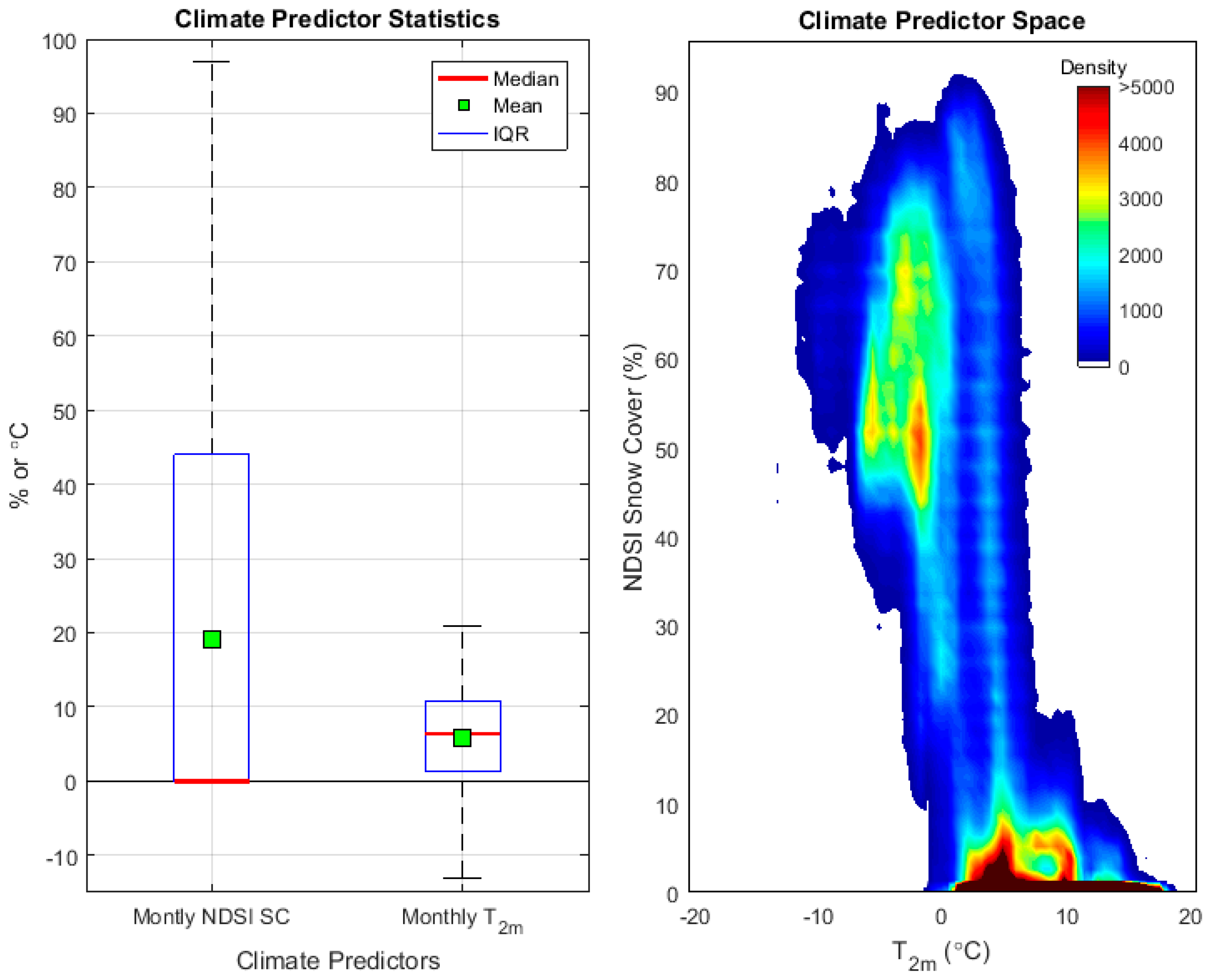
2.6. Snow Cover Data
2.7. Temperature Data
2.8. Endmember Data Processing
2.9. Model Validation
3. Results
3.1. Fit Statistics
3.2. Model Parameters
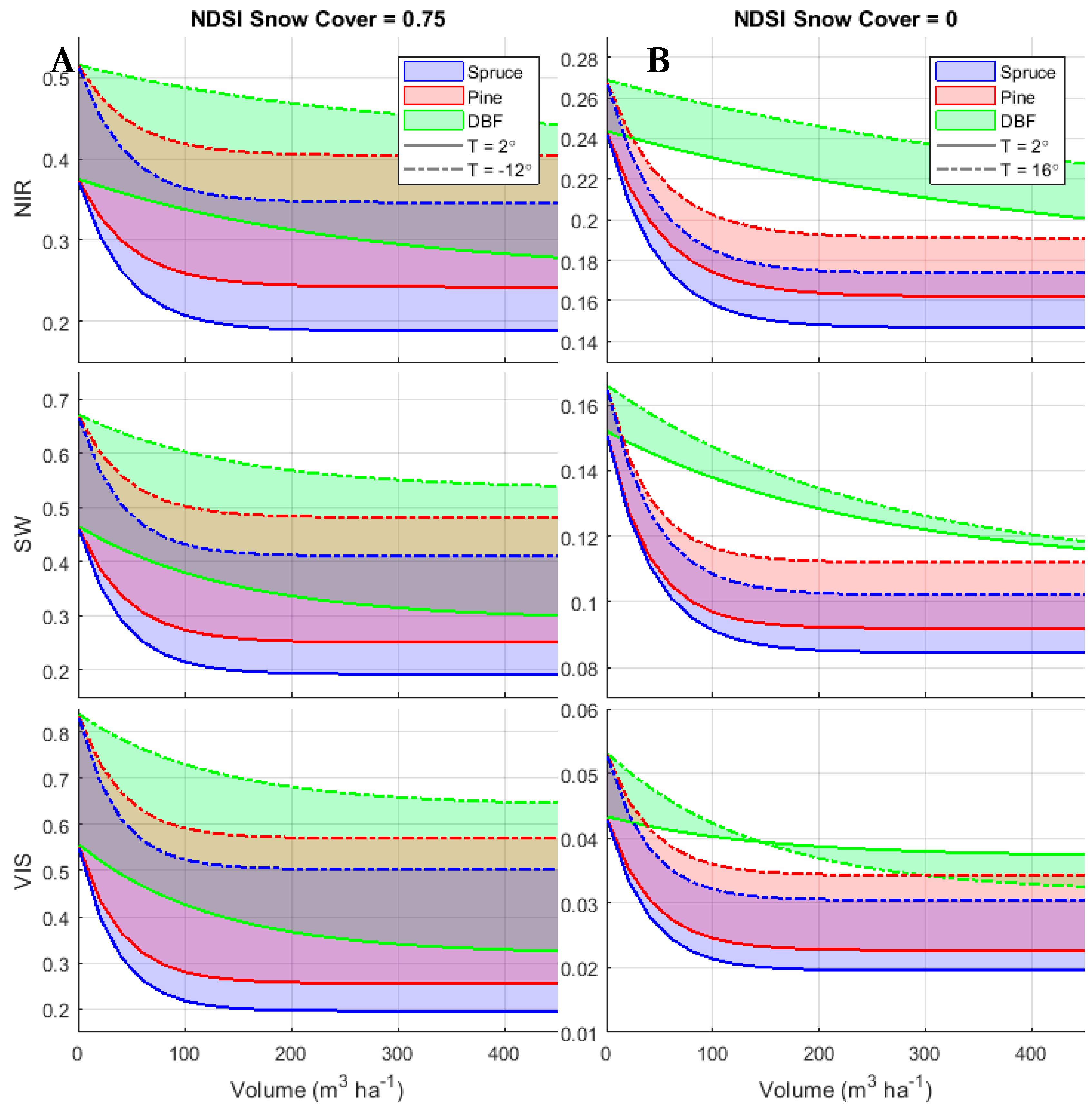
3.3. Model Behavior in Forests
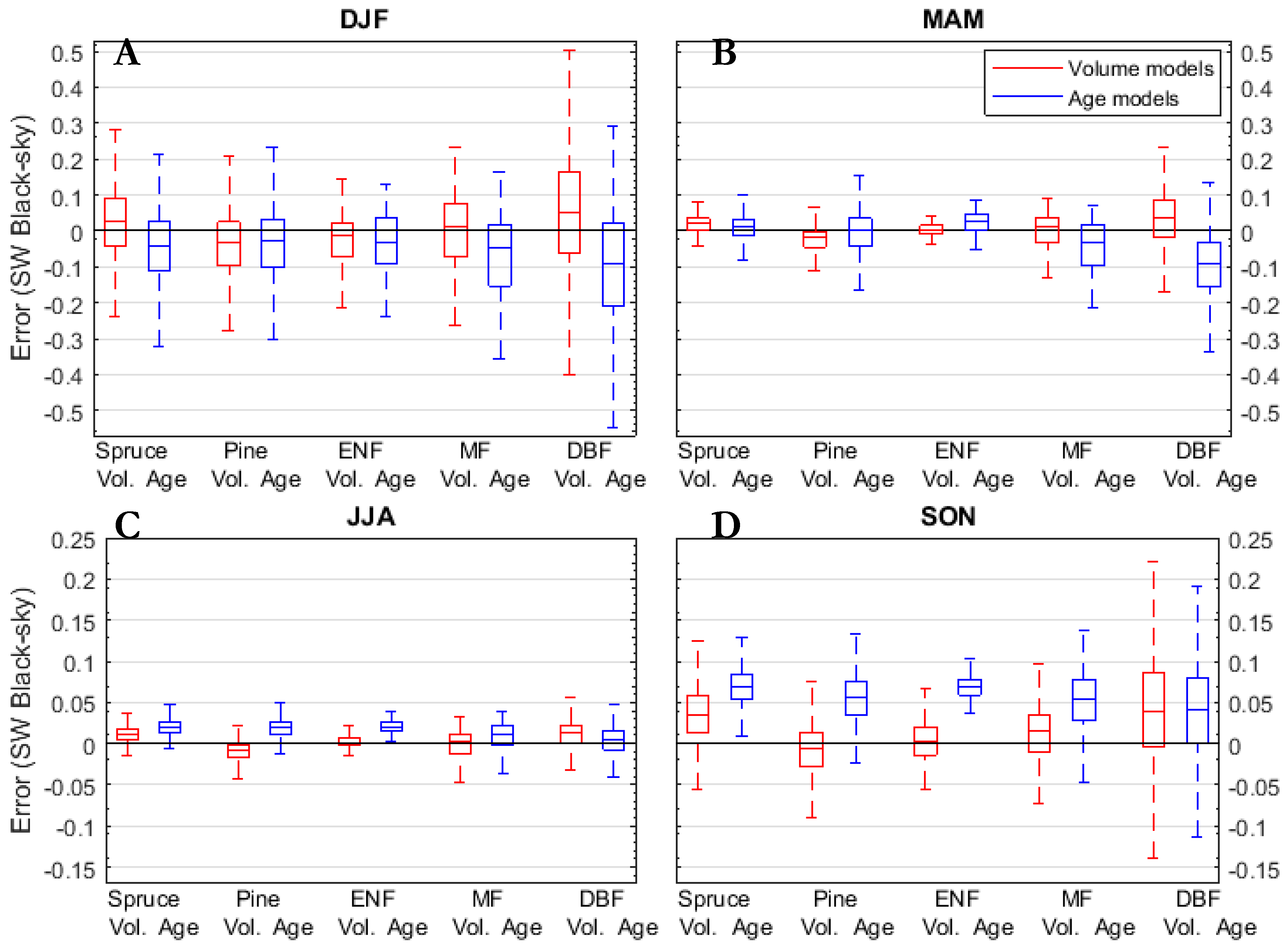
3.4. Model Benchmarking and Validation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Mahmood, R.; Quintanar, A.I.; Conner, G.; Leeper, R.; Dobler, S.; Pielke, R.A.; Bonan, G.; Chase, T.; McNider, R.; McAlpine, C.; et al. Impacts of Land Use/Land Cover Change on Climate and Future Research Priorities. Bull. Am. Meteorol. Soc. 2010, 91, 37–46. [Google Scholar] [CrossRef] [Green Version]
- Mahmood, R.; Pielke, R.A.; Loveland, T.R.; McAlpine, C.A. Climate Relevant Land Use and Land Cover Change Policies. Bull. Am. Meteorol. Soc. 2016, 97, 195–202. [Google Scholar] [CrossRef]
- Stephens, G.L.; O’Brien, D.; Webster, P.J.; Pilewski, P.; Kato, S.; Li, J. The albedo of Earth. Rev. Geophys. 2015, 53, 141–163. [Google Scholar] [CrossRef] [Green Version]
- Jackson, R.B.; Randerson, J.T.; Canadell, J.G.; Anderson, R.G.; Avissar, R.; Baldocchi, D.D.; Bonan, G.B.; Caldeira, K.; Diffenbaugh, N.S.; Field, C.B.; et al. Protecting climate with forests. Environ. Res. Lett. 2008, 3, 044006. [Google Scholar] [CrossRef] [Green Version]
- Pielke, R.A., Sr.; Marland, G.; Betts, R.A.; Chase, T.N.; Eastman, J.L.; Niles, J.O.; Niyogi, D.d.S.; Running, S.W. The influence of land-use change and landscape dynamics on the climate system: Relevance to climate-change policy beyond the radiative effect of greenhouse gases. Phil. Trans. R. Soc. Lond. A 2002, 360, 1705–1719. [Google Scholar] [CrossRef] [PubMed]
- Lutz, D.A.; Howarth, R. Valuing albedo as an ecosystem service: Implications for forest management. Clim. Chang. 2014, 124, 53–63. [Google Scholar] [CrossRef]
- Lutz, D.A.; Burakowski, E.A.; Murphy, M.B.; Borsuk, M.E.; Niemiec, R.M.; Howarth, R.B.; Burakowski, E. Tradeoffs between three forest ecosystem services across the state of New Hampshire, USA: Timber, carbon, and albedo. Ecol. Appl. 2015, 26, 146–161. [Google Scholar] [CrossRef]
- Favero, A.; Sohngen, B.; Huang, Y.; Jin, Y. Global cost estimates of forest climate mitigation with albedo: A new integrative policy approach. Environ. Res. Lett. 2018, 13, 125002. [Google Scholar] [CrossRef]
- Thompson, M.P.; Adams, D.; Sessions, J. Radiative forcing and the optimal rotation age. Ecol. Econ. 2009, 68, 2713–2720. [Google Scholar] [CrossRef]
- Matthies, B.D.; Valsta, L.T. Optimal forest species mixture with carbon storage and albedo effect for climate change mitigation. Ecol. Econ. 2016, 123, 95–105. [Google Scholar] [CrossRef]
- He, T.; Liang, S.; Song, D.-X. Analysis of global land surface albedo climatology and spatial-temporal variation during 1981–2010 from multiple satellite products. J. Geophys. Res. Atmos. 2014, 119, 10281–10298. [Google Scholar] [CrossRef]
- Gao, F.; He, T.; Wang, Z.; Ghimire, B.; Shuai, Y.; Masek, J.; Schaaf, C.; Williams, C. Multi-scale climatological albedo look-up maps derived from MODIS BRDF/albedo products. J. Appl. Remote Sens. 2014, 8, 083532-1. [Google Scholar] [CrossRef]
- Gao, F.; Schaaf, C.B.; Strahler, A.H.; Roesch, A.; Lucht, W.; Dickinson, R. MODIS bidirectional reflectance distribution function and albedo Climate Modeling Grid products and the variablility of albedo for major global vegetation types. J. Geophys. Res. 2005, 110, 1–13. [Google Scholar] [CrossRef]
- Zhao, K.; Jackson, R.B. Biophysical forcings of land-use changes from potential forestry activities in North America. Ecol. Monogr. 2014, 84, 329–353. [Google Scholar] [CrossRef]
- Román, M.O.; Schaaf, C.B.; Woodcock, C.E.; Strahler, A.H.; Yang, X.; Braswell, R.H.; Curtis, P.S.; Davis, K.J.; Dragoni, D.; Goulden, M.L. The MODIS (Collection V005) BRDF/albedo product: Assessment of spatial representativeness over forested landscapes. Remote. Sens. Environ. 2009, 113, 2476–2498. [Google Scholar] [CrossRef] [Green Version]
- Ni, W.; Woodcock, C.E. Effect of canopy structure and the presence of snow on the albedo of boreal conifer forests. J. Geophys. Res. Phys. 2000, 105, 11879–11888. [Google Scholar] [CrossRef] [Green Version]
- Kung, E.C.; Bryson, R.A.; Lenschow, D.H. Study of a continental surface albedo on the basis of flight measurements and structure of the earth’s surface cover over north america. Mon. Weather. Rev. 1964, 92, 543–564. [Google Scholar] [CrossRef]
- Betts, A.K.; Ball, J.H. Albedo over the boreal forest. J. Geophys. Res. 1997, 102, 28901–28909. [Google Scholar] [CrossRef] [Green Version]
- Richardson, A.D.; Black, T.A.; Ciais, P.; Delbart, N.; Friedl, M.A.; Gobron, N.; Hollinger, D.Y.; Kutsch, W.L.; Longdoz, B.; Luyssaert, S.; et al. Influence of spring and autumn phenological transitions on forest ecosystem productivity. Philos. Trans. R. Soc. B Boil. Sci. 2010, 365, 3227–3246. [Google Scholar] [CrossRef] [Green Version]
- Ollinger, S.V.; Richardson, A.D.; Martín, M.E.; Hollinger, D.Y.; Frolking, S.E.; Reich, P.B.; Plourde, L.C.; Katul, G.G.; Munger, J.W.; Oren, R.; et al. Canopy nitrogen, carbon assimilation, and albedo in temperate and boreal forests: Functional relations and potential climate feedbacks. Proc. Natl. Acad. Sci. USA 2008, 105, 19336–19341. [Google Scholar] [CrossRef] [Green Version]
- Duveiller, G.; Hooker, J.; Cescatti, A. A dataset mapping the potential biophysical effects of vegetation cover change. Sci. Data 2018, 5, 180014. [Google Scholar] [CrossRef]
- Duveiller, G.; Hooker, J.; Cescatti, A. The mark of vegetation change on Earth’s surface energy balance. Nat. Commun. 2018, 9, 679. [Google Scholar] [CrossRef] [PubMed]
- Seneviratne, S.I.; Phipps, S.J.; Pitman, A.J.; Hirsch, A.L.; Davin, E.L.; Donat, M.G.; Hirschi, M.; Lenton, A.; Wilhelm, M.; Kravitz, B. Land radiative management as contributor to regional-scale climate adaptation and mitigation. Nat. Geosci. 2018, 11, 88–96. [Google Scholar] [CrossRef]
- Miller, J.N.; Vanloocke, A.; Gomez-Casanovas, N.; Bernacchi, C.J.; Gomez-Casanovas, N. Candidate perennial bioenergy grasses have a higher albedo than annual row crops. GCB Bioenergy 2015, 8, 818–825. [Google Scholar] [CrossRef] [Green Version]
- Wickham, J.; Barnes, C.; Nash, M.; Wade, T. Combining NLCD and MODIS to create a land cover-albedo database for the continental United States. Remote. Sens. Environ. 2015, 170, 143–152. [Google Scholar] [CrossRef]
- Leonardi, S.; Magnani, F.; Nolè, A.; Van Noije, T.; Borghetti, M. A global assessment of forest surface albedo and its relationships with climate and atmospheric nitrogen deposition. Glob. Chang. Boil. 2014, 21, 287–298. [Google Scholar] [CrossRef]
- Bright, R.M.; Astrup, R.; Strømman, A.H. Empirical models of monthly and annual albedo in managed boreal forests of interior Norway. Clim. Chang. 2013, 120, 183–196. [Google Scholar] [CrossRef]
- Rechid, D.; Raddatz, T.J.; Jacob, D. Parameterization of snow-free land surface albedo as a function of vegetation phenology based on MODIS data and applied in climate modelling. Theor. Appl. Climatol. 2009, 95, 245–255. [Google Scholar] [CrossRef]
- Song, J. Phenological influences on the albedo of prairie grassland and crop fields. Int. J. Biometeorol. 1999, 42, 153–157. [Google Scholar] [CrossRef]
- Granhus, A.; Hylen, G.; Nilsen, J.-E.Ø. Statistics of Forest Conditions and Resources in Norway, in Ressursoversikt fra Skog og Landskap 03/12; Norwegian Forest and Landscape Institute: Ås, Norway, 2012. [Google Scholar]
- Larsson, J.Y.; Hylen, G. Skogen i Norge: Statistikk over Skogforhold og Skogressurser i Norge Registrert i Perioden 2000–2004 [Forest in Norway: Forest Resource Statistics for the Period 2000–2004]. Norwegian Forest and Landscape Institute: Ås, Norway, 2007; p. 95. Available online: https://brage.bibsys.no/xmlui/bitstream/handle/11250/2508185/SoL-Viten-2007-01.pdf?sequence=1&isAllowed=y (accessed on 21 October 2018).
- Kuusinen, N.; Tomppo, E.; Berninger, F. Linear unmixing of MODIS albedo composites to infer subpixel land cover type albedos. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 324–333. [Google Scholar] [CrossRef]
- Kuusinen, N.; Tomppo, E.; Shuai, Y.; Berninger, F. Effects of forest age on albedo in boreal forests estimated from MODIS and Landsat albedo retrievals. Remote. Sens. Environ. 2014, 145, 145–153. [Google Scholar] [CrossRef]
- Bright, R.M.; Eisner, S.; Lund, M.T.; Majasalmi, T.; Myhre, G.; Astrup, R. Inferring Surface Albedo Prediction Error Linked to Forest Structure at High Latitudes. J. Geophys. Res. Atmos. 2018, 123, 4910–4925. [Google Scholar] [CrossRef] [Green Version]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral Unmixing Overview: Geometrical, Statistical, and Sparse Regression-Based Approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef] [Green Version]
- Qu, X.; Hall, A. On the persistent spread in snow-albedo feedback. Clim. Dyn. 2014, 42, 69–81. [Google Scholar] [CrossRef]
- Essery, R. Large-scale simulations of snow albedo masking by forests. Geophys. Res. Lett. 2013, 40, 5521–5525. [Google Scholar] [CrossRef] [Green Version]
- Lukeš, P.; Stenberg, P.; Rautiainen, M. Relationship between forest density and albedo in the boreal zone. Ecol. Model. 2013, 261, 74–79. [Google Scholar] [CrossRef]
- Bright, R.M.; Myhre, G.; Astrup, R.; Antón-Fernández, C.; Strømman, A.H. Radiative forcing bias of simulated surface albedo modifications linked to forest cover changes at northern latitudes. Biogeosciences 2015, 12, 2195–2205. [Google Scholar] [CrossRef]
- Lukeš, P.; Rautiainen, M.; Manninen, T.; Stenberg, P.; Mõttus, M. Geographical gradients in boreal forest albedo and structure in Finland. Remote. Sens. Environ. 2014, 152, 526–535. [Google Scholar] [CrossRef] [Green Version]
- Kuusinen, N.; Stenberg, P.; Korhonen, L.; Rautiainen, M.; Tomppo, E. Structural factors driving boreal forest albedo in Finland. Remote. Sens. Environ. 2016, 175, 43–51. [Google Scholar] [CrossRef]
- Loranty, M.M.; Berner, L.T.; Goetz, S.J.; Jin, Y.; Randerson, J.T. Vegetation controls on northern high latitude snow-albedo feedback: Observations and CMIP5 model simulations. Glob. Chang. Biol. 2014, 20, 594–606. [Google Scholar] [CrossRef] [PubMed]
- Kuusinen, N.; Kolari, P.; Levula, J.; Porcar-Castell, A.; Stenberg, P.; Berninger, F. Seasonal variation in boreal pine forest albedo and effects of canopy snow on forest reflectance. Agric. For. Meteorol. 2012, 164, 53–60. [Google Scholar] [CrossRef]
- Pomeroy, J.W.; Parviainen, J.; Hedstrom, N.; Gray, D.M. Coupled modelling of forest snow interception and sublimation. Hydrol. Process. 1998, 12, 2317–2337. [Google Scholar] [CrossRef]
- Hedstrom, N.R.; Pomeroy, J.W. Measurements and modelling of snow interception in the boreal forest. Hydrol. Process. 1998, 12, 1611–1625. [Google Scholar] [CrossRef]
- Wiscombe, W.J.; Warren, S.G. A model for the spectral albedo of snow. I. Pure Snow. J. Atmos. Sci. 1980, 37, 2712–2733. [Google Scholar] [CrossRef]
- Aoki, T.; Hachikubo, A.; Hori, M. Effects of snow physical parameters on shortwave broadband albedos. J. Geophys. Res. Phys. 2003, 108, 4616. [Google Scholar] [CrossRef]
- Brun, E. Investigation on Wet-Snow Metamorphism in Respect of Liquid-Water Content. Ann. Glaciol. 1989, 13, 22–26. [Google Scholar] [CrossRef]
- Painter, T.H.; Rittger, K.; McKenzie, C.; Slaughter, P.; Davis, R.E.; Dozier, J. Retrieval of subpixel snow covered area, grain size, and albedo from MODIS. Remote. Sens. Environ. 2009, 113, 868–879. [Google Scholar] [CrossRef] [Green Version]
- Essery, R.; Morin, S.; Lejeune, Y.; Ménard, C.B. A comparison of 1701 snow models using observations from an alpine site. Adv. Resour. 2013, 55, 131–148. [Google Scholar] [CrossRef]
- Pedersen, C.A.; Winther, J.-G. Intercomparison and validation of snow albedo parameterization schemes in climate models. Clim. Dyn. 2005, 25, 351–362. [Google Scholar] [CrossRef] [Green Version]
- Olsson, C.; Jönsson, A.M. Process-based models not always better than empirical models for simulating budburst of Norway spruce and birch in Europe. Glob. Chang. Boil. 2014, 20, 3492–3507. [Google Scholar] [CrossRef] [PubMed]
- Zohner, C.M.; Benito, B.M.; Svenning, J.-C.; Renner, S.S. Day length unlikely to constrain climate-driven shifts in leaf-out times of northern woody plants. Nat. Clim. Chang. 2016, 6, 1120–1123. [Google Scholar] [CrossRef] [Green Version]
- Rutter, N.; Essery, R.; Pomeroy, J.; Altimir, N.; Andreadis, K.; Baker, I.; Barr, A.; Bartlett, P.; Boone, A.; Deng, H.; et al. Evaluation of forest snow processes models (SnowMIP2). J. Geophys. Res. Phys. 2009, 114, 06111. [Google Scholar] [CrossRef]
- Bjørdal, I.; Bjørkelo, K. AR5 Klassifikasjonssystem—Klassifikasjon av arealressurser, in Håndbok fra Skog og Landskap—01/2006; Norwegian Forest and Landscape Institute: Ås, Norway, 2006; p. 26. [Google Scholar]
- Gjertsen, A.K.; Angeloff, M.; Strand, G.-H. Arealressurskart over fjellområdene. Kart og Plan 2012, 71, 45–51. [Google Scholar]
- Mathiesen, H.F. Arealstatistikk—Fulldyrka Jord og Dyrkbar Jord; Norwegian Forest and Landscape Institute: Ås, Norway, 2014; p. 43. [Google Scholar]
- Astrup, R.; Rahlf, J.; Bjørkelo, K.; Debella-Gilo, M.; Gjertsen, Ar.; Breidenbach, J. Forest information at multiple scales: Development, evaluation and application of the Norwegian Forest Resources Map. Scand. J. For. Res. 2018. under review. [Google Scholar] [CrossRef]
- Blaschke, T.; Lang, S.; Hay, G.J. Object-Based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Gjertsen, A. Accuracy of forest mapping based on Landsat TM data and a kNN-based method. Remote. Sens. Environ. 2007, 110, 420–430. [Google Scholar] [CrossRef]
- Gjertsen, A.K.; Nilsen, J.-E.Ø. SAT-SKOG: Et skogkart basert på tolking av Satellittbilder [SAT-SKOG: A Forest Map Based on Interpretation of Satellite Imagery]; Norwegian Forest and Landscape Institute: Ås, Norway, 2012; p. 54. Available online: http://www.skogoglandskap.no/filearchive/rapport_23_12_sat_skog_skogkart_basert_pa_tolking_av_satellittbilder.pdf (accessed on 11 February 2014). (In Norwegian)
- Kotchenova, S.Y.; Vermote, E.F.; Matarrese, R.; Klemm, J.F.J. Validation of a vector version of the 6S radiative transfer code for atmospheric correction of satellite data Part I: Path radiance. Appl. Opt. 2006, 45, 6762. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kotchenova, S.Y.; Vermote, E.F. Validation of a vector version of the 6S radiative transfer code for atmospheric correction of satellite data. Part II. Homogeneous Lambertian and anisotropic surfaces. Appl. Opt. 2007, 46, 4455–4464. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.-P.; et al. First operational BRDF, albedo nadir reflectance products from MODIS. Remote. Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef] [Green Version]
- Lucht, W.; Lewis, P. Theoretical noise sensitivity of BRDF and albedo retrieval from the EOS-MODIS and MISR sensors with respect to angular sampling. Int. J. Remote. Sens. 2000, 21, 81–98. [Google Scholar] [CrossRef]
- Schaaf, C.; Strahler, A.; Lucht, W. An algorithm for the retrieval of albedo from space using semiempirical BRDF models. IEEE Trans. Geosci. Remote. Sens. 2000, 38, 977–998. [Google Scholar]
- Schaaf, C.; Wang, Z. MCD43A3 MODIS/Terra + Aqua BRDF/Albedo Daily L3 Global—500m V006 [Data set]; NASA EOSDIS LP DAAC: Sioux Falls, SD, USA, 2015. [Google Scholar] [CrossRef]
- Wang, Z.; Schaaf, C.B.; Strahler, A.H.; Chopping, M.J.; Román, M.O.; Shuai, Y.; Woodcock, C.E.; Hollinger, D.Y.; Fitzjarrald, D.R. Evaluation of MODIS albedo product (MCD43A) over grassland, agriculture and forest surface types during dormant and snow-covered periods. Remote. Sens. Environ. 2014, 140, 60–77. [Google Scholar] [CrossRef]
- Wang, Z.; Schaaf, C.B.; Sun, Q.; Shuai, Y.; Román, M.O. Capturing rapid land surface dynamics with Collection V006 MODIS BRDF/NBAR/Albedo (MCD43) products. Remote. Sens. Environ. 2018, 207, 50–64. [Google Scholar] [CrossRef]
- Schaaf, C.; Wang, Z. MCD43A2 MODIS/Terra+Aqua BRDF/Albedo Quality Daily L3 Global—500m V006 [Data set]; NASA LP DAAC: Sioux Falls, SD, USA, 2015. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. MODIS/Terra Snow Cover Daily L3 Global 500m Grid, Version 6 [Data set]. Available online: https://doi.org/10.5067/MODIS/MOD10A1.006 (accessed on 5 November 2018).
- Salomonson, V.; Appel, I. Estimating fractional snow cover from MODIS using the normalized difference snow index. Remote. Sens. Environ. 2004, 89, 351–360. [Google Scholar] [CrossRef]
- Riggs, G.A.; Hall, D.K.; Román, M.O. MODIS Snow Products Collection 6 User Guide (Version 1.0). Available online: https://modis-snow-ice.gsfc.nasa.gov/?c=userguides 2016 (accessed on 7 October 2018).
- Riggs, G.A.; Hall, D.K.; Román, M.O. Overview of NASA’s MODIS and Visible Infrared Imaging Radiometer Suite (VIIRS) snow-cover Earth System Data Records. Earth Syst. Sci. Data 2017, 9, 765–777. [Google Scholar] [CrossRef]
- Masson, T.; Dumont, M.; Mura, M.; Sirguey, P.; Gascoin, S.; Dedieu, J.-P.; Chanussot, J. An Assessment of Existing Methodologies to Retrieve Snow Cover Fraction from MODIS Data. Remote Sens. 2018, 10, 619. [Google Scholar] [CrossRef]
- Dong, J.; Ek, M.; Hall, D.; Peters-Lidard, C.; Cosgrove, B.; Miller, J.; Riggs, G.; Xia, Y. Using Air Temperature to Quantitatively Predict the MODIS Fractional Snow Cover Retrieval Errors over the Continental United States. J. Hydrometeorol. 2013, 15, 551–562. [Google Scholar] [CrossRef]
- Lussana, C.; Tveito, O.E.; Uboldi, F. Three-dimensional spatial interpolation of 2 m temperature over Norway. Q. J. R. Meteorol. Soc. 2018, 144, 344–364. [Google Scholar] [CrossRef]
- Daeseong, K.; Hyung-sup, J.; Jeong-cheol, K. Comparison of Snow Cover Fraction Functions to Estimate Snow Depth of South Korea from MODIS Imagery. Korean J. Remote Sens. 2017, 33, 401–410. [Google Scholar]
- Cescatti, A.; Marcolla, B.; Vannan, S.K.S.; Pan, J.Y.; Román, M.O.; Yang, X.; Ciais, P.; Cook, R.B.; Law, B.E.; Matteucci, G.; et al. Intercomparison of MODIS albedo retrievals and in situ measurements across the global FLUXNET network. Remote Sens. Environ. 2012, 121, 323–334. [Google Scholar] [CrossRef] [Green Version]
- Campagnolo, M.L.; Sun, Q.; Liu, Y.; Schaaf, C.; Wang, Z.; Román, M.O. Estimating the effective spatial resolution of the operational BRDF, albedo, and nadir reflectance products from MODIS and VIIRS. Remote Sens. Environ. 2016, 175, 52–64. [Google Scholar] [CrossRef]
- Hovi, A.; Lindberg, E.; Lang, M.; Arumäe, T.; Peuhkurinen, J.; Sirparanta, S.; Pyankov, S.; Rautiainen, M. Seasonal dynamics of albedo across European boreal forests: Analysis of MODIS albedo and structural metrics from airborne LiDAR. Remote Sens. Environ. 2019, 224, 365–381. [Google Scholar] [CrossRef]
- Yamazaki, T. A One-dimensional Land Surface Model Adaptable to Intensely Cold Regions and its Applications in Eastern Siberia. J. Meteorol. Soc. Jpn. Ser. II 2001, 79, 1107–1118. [Google Scholar] [CrossRef]
- Jordan, R. A One-Dimensional Temperature Model for a Snow Cover: Technical Documentation for SNTHERM89; Cold Regions Research and Engineering Laboratory: Hanover, NH, USA; Engineer Research and Development Center: Vicksburg, MS, USA, 1991; Available online: https://erdc-library.erdc.dren.mil/xmlui/handle/11681/11677 (accessed on 11 December 2018).
- Rautiainen, M.; Nilson, T.; Lükk, T. Seasonal reflectance trends of hemiboreal birch forests. Remote. Sens. Environ. 2009, 113, 805–815. [Google Scholar] [CrossRef]
- Kuusk, A.; Lang, M.; Kuusk, J.; Lükk, T.; Nilson, T.; Mõttus, M.; Rautiainen, M.; Eenmäe, A. Database of Optical and Structural Data for the Validation of Radiative Transfer Models; Technical Report Version 04.2015; Tartu Observatory: Tõravere, Estonia, 2015; p. 60. Available online: http://www.aai.ee/bgf/jarvselja_db/jarvselja_db.pdf (accessed on 2 December 2018).
- Borden, J.H.; Campbell, S.A. Bark reflectance spectra of conifers and angiosperms: Implications for host discrimination by coniferophagous bark and timber beetles. Can. Èntomol. 2005, 137, 719–722. [Google Scholar]
- Warren, S.G. Optical properties of snow. Rev. Geophys. 1982, 20, 67–89. [Google Scholar] [CrossRef]
- Hovi, A.; Raitio, P.; Rautiainen, M. A spectral analysis of 25 boreal tree species. Silva Fenn. 2017, 51. [Google Scholar] [CrossRef] [Green Version]
- Hollinger, D.Y.; Ollinger, S.V.; Richardson, A.D.; Meyers, T.P.; Dail, D.B.; Martín, M.E.; Scott, N.A.; Arkebauer, T.J.; Baldocchi, D.D.; Clark, K.L.; et al. Albedo estimates for land surface models and support for a new paradigm based on foliage nitrogen concentration. Glob. Chang. Boil. 2010, 16, 696–710. [Google Scholar] [CrossRef] [Green Version]




| Model | R2 | |||||
|---|---|---|---|---|---|---|
| SW | NIR | VIS | ||||
| BS | WS | BS | WS | BS | WS | |
| Nominal resolution | ||||||
| ef + SC | 0.756 | 0.747 | 0.593 | 0.543 | 0.805 | 0.804 |
| ef + SC + T | 0.791 | 0.780 | 0.642 | 0.598 | 0.832 | 0.830 |
| ef +SC +T + V | 0.845 | 0.833 | 0.707 | 0.668 | 0.880 | 0.876 |
| ef +SC +T + B | 0.845 | 0.833 | 0.707 | 0.668 | 0.880 | 0.876 |
| Effective resolution | ||||||
| ef + SC | 0.761 | 0.752 | 0.601 | 0.553 | 0.808 | 0.808 |
| ef + SC + T | 0.796 | 0.786 | 0.650 | 0.608 | 0.836 | 0.834 |
| ef +SC +T + V | 0.851 | 0.839 | 0.715 | 0.679 | 0.884 | 0.881 |
| ef +SC +T + B | 0.851 | 0.839 | 0.715 | 0.679 | 0.885 | 0.881 |
| CRO | PAS | O-v | O-pv | O-sv | O-nv | PB-f | PB-nf | U&T | FW | |
|---|---|---|---|---|---|---|---|---|---|---|
| Shortwave (SW) | ||||||||||
| 0.570 | 0.562 | 0.692 | 0.643 | 0.591 | 0.594 | 0.755 | 0.679 | 0.483 | 0.562 | |
| 0.126 | 0.142 | 0.178 | 0.142 | 0.144 | 0.149 | 0.198 | 0.148 | 0.112 | 0.059 | |
| −0.045 | −0.040 | −0.027 | −0.037 | −0.030 | −0.012 | −0.054 | −0.041 | −0.033 | −0.054 | |
| 0.002 | 7.5 × 10−4 | −0.003 | −0.002 | −0.003 | −0.003 | −0.004 | −6.4 × 10−11 | 9.8 × 10−4 | 0.001 | |
| Near-infrared (NIR) | ||||||||||
| 0.492 | 0.457 | 0.525 | 0.503 | 0.470 | 0.414 | 0.574 | 0.523 | 0.430 | 0.440 | |
| 0.183 | 0.241 | 0.229 | 0.186 | 0.177 | 0.180 | 0.240 | 0.224 | 0.151 | 0.102 | |
| −0.036 | −0.027 | −0.021 | −0.029 | −0.022 | −0.011 | −0.044 | −0.033 | −0.029 | −0.048 | |
| 0.006 | 0.001 | 5.4 × 10−4 | 0.001 | −1.8 × 10−6 | −0.001 | 0.001 | 7.3 × 10−4 | 0.003 | 6.9 × 10−4 | |
| Visible (VIS) | ||||||||||
| 0.666 | 0.688 | 0.855 | 0.780 | 0.714 | 0.753 | 0.939 | 0.835 | 0.564 | 0.687 | |
| 0.058 | 0.028 | 0.104 | 0.080 | 0.093 | 0.134 | 0.114 | 0.056 | 0.066 | 0.018 | |
| −0.057 | −0.051 | −0.032 | −0.049 | −0.042 | −0.012 | −0.067 | −0.049 | −0.039 | −0.063 | |
| −4.6 × 10−4 | 9.4 × 10−4 | −0.005 | −0.003 | −0.004 | −0.007 | −0.006 | −0.001 | −0.001 | 1.4 × 10−4 | |
| Shortwave (SW) | ||||||||
| 0.610 | Spruce | 0.340 | 1.2 × 10−3 | −0.025 | 0.068 | −2.5 × 10−4 | −0.023 | |
| −0.020 | Pine | 0.262 | 2.5 × 10−3 | −0.022 | 0.061 | −4.4 × 10−4 | −0.025 | |
| 0.151 | DBF | 0.212 | 3.0 × 10−3 | −0.007 | 0.041 | 6.6 × 10−4 | −0.004 | |
| 1.0 × 10−3 | ||||||||
| Near-infrared (NIR) | ||||||||
| 0.447 | Spruce | 0.214 | 1.7 × 10−3 | −0.023 | 0.097 | −1.1 × 10−4 | −0.021 | |
| −0.014 | Pine | 0.146 | 2.1 × 10−3 | −0.021 | 0.082 | −2.6 × 10−4 | −0.019 | |
| 0.242 | DBF | 0.132 | 2.7 × 10−3 | −0.004 | 0.073 | −2.2 × 10−4 | −0.002 | |
| 1.8 × 10−3 | ||||||||
| Visible (VIS) | ||||||||
| 0.784 | Spruce | 0.470 | 2.5 × 10−3 | −0.028 | 0.024 | −7.6 × 10−5 | −0.026 | |
| −0.027 | Pine | 0.391 | 3.2 × 10−3 | −0.025 | 0.021 | −1.3 × 10−4 | −0.024 | |
| 0.042 | DBF | 0.309 | 3.5 × 10−3 | −0.008 | 0.004 | 1.1 × 10−3 | −0.007 | |
| 7.0 × 10−4 | ||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bright, R.M.; Astrup, R. Combining MODIS and National Land Resource Products to Model Land Cover-Dependent Surface Albedo for Norway. Remote Sens. 2019, 11, 871. https://doi.org/10.3390/rs11070871
Bright RM, Astrup R. Combining MODIS and National Land Resource Products to Model Land Cover-Dependent Surface Albedo for Norway. Remote Sensing. 2019; 11(7):871. https://doi.org/10.3390/rs11070871
Chicago/Turabian StyleBright, Ryan M., and Rasmus Astrup. 2019. "Combining MODIS and National Land Resource Products to Model Land Cover-Dependent Surface Albedo for Norway" Remote Sensing 11, no. 7: 871. https://doi.org/10.3390/rs11070871
APA StyleBright, R. M., & Astrup, R. (2019). Combining MODIS and National Land Resource Products to Model Land Cover-Dependent Surface Albedo for Norway. Remote Sensing, 11(7), 871. https://doi.org/10.3390/rs11070871





