A New Integrated Vegetation Index for the Estimation of Winter Wheat Leaf Chlorophyll Content
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Site and Experimental Design
2.2. Field Measurements
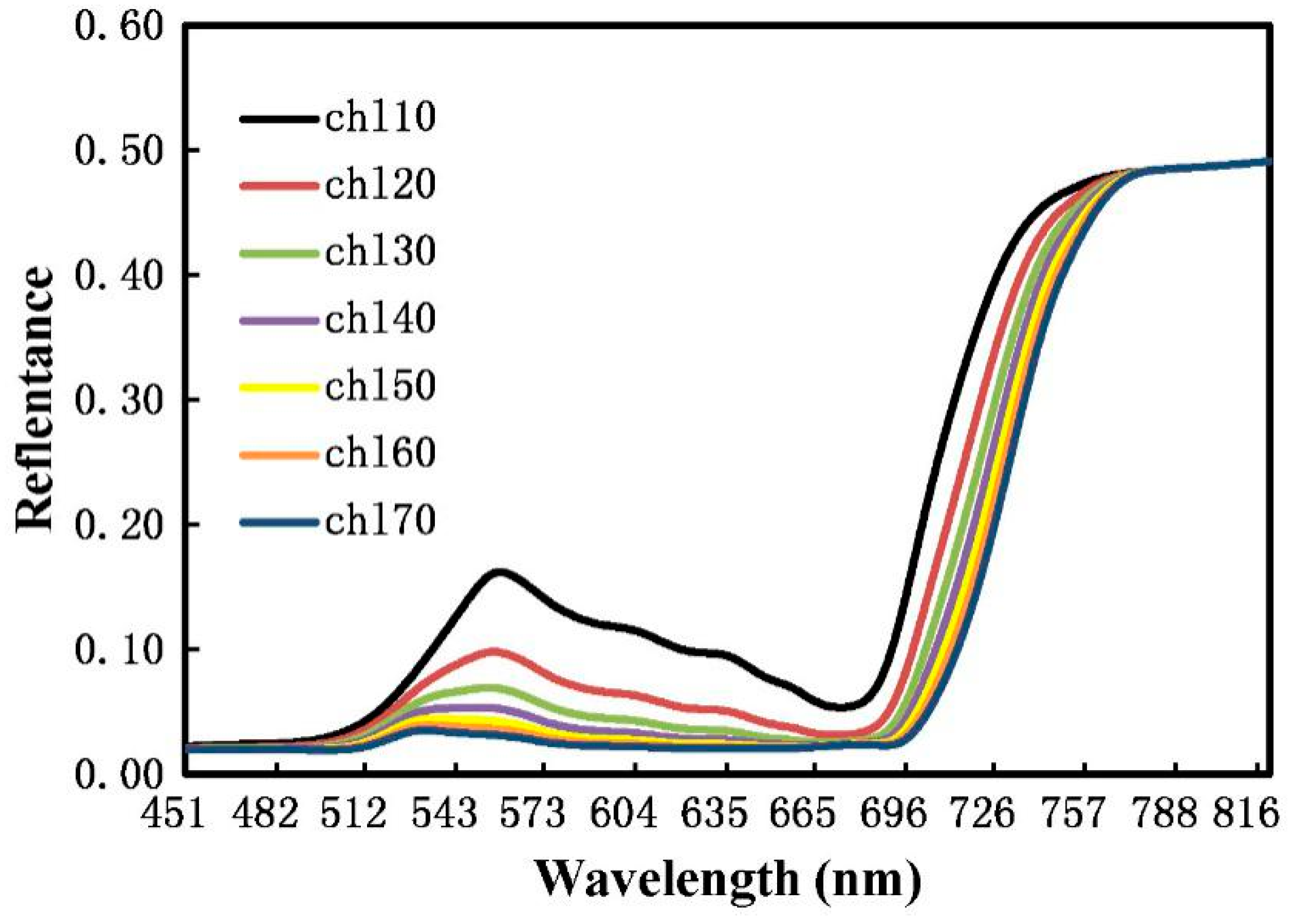
2.2.1. Measurement of the Reflectance Spectrum from the Winter Wheat Canopy
2.2.2. Measurement of Plant Parameters
2.3. Spectral Indices
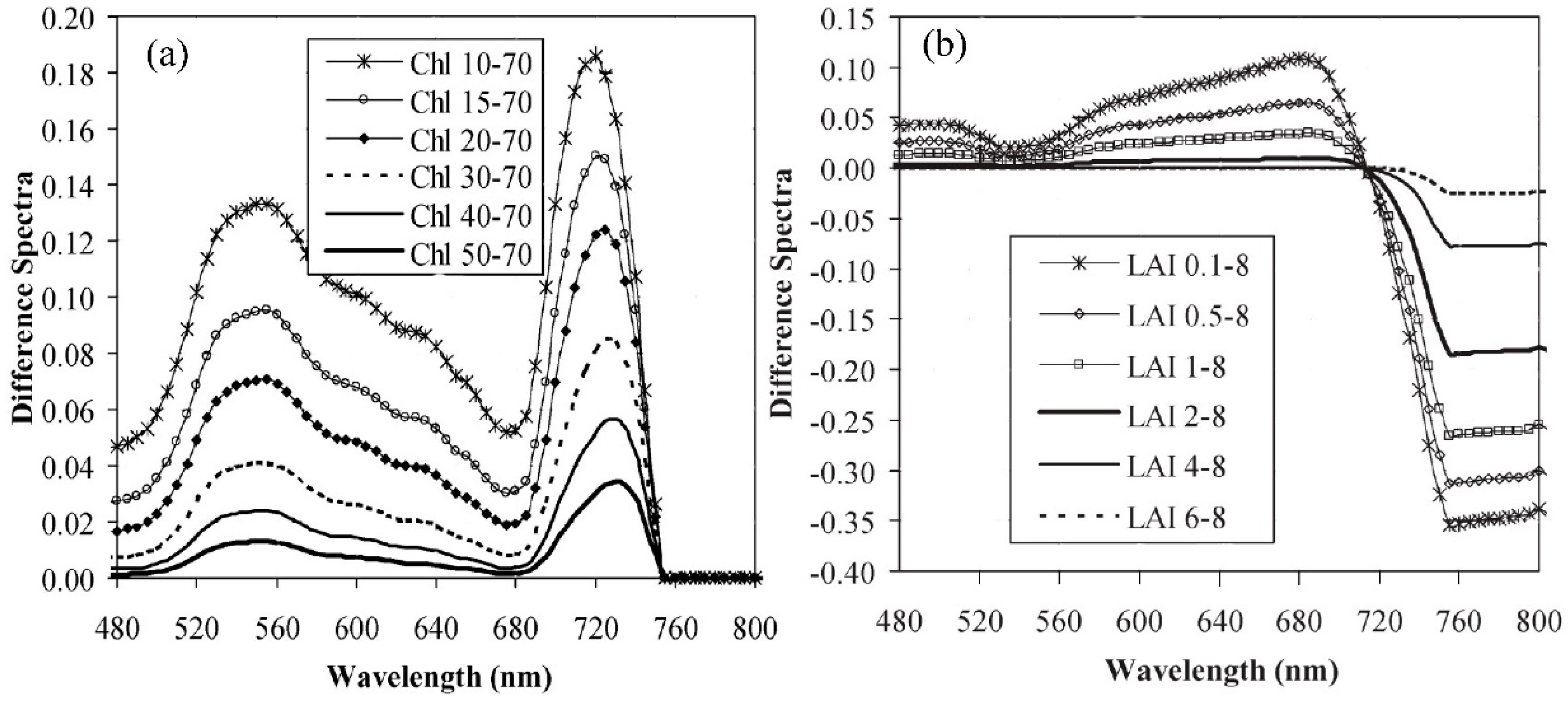
2.3.1. New Spectral Index
2.3.2. Spectral Indices in this Study
2.4. Analysis Method and Software
3. Results
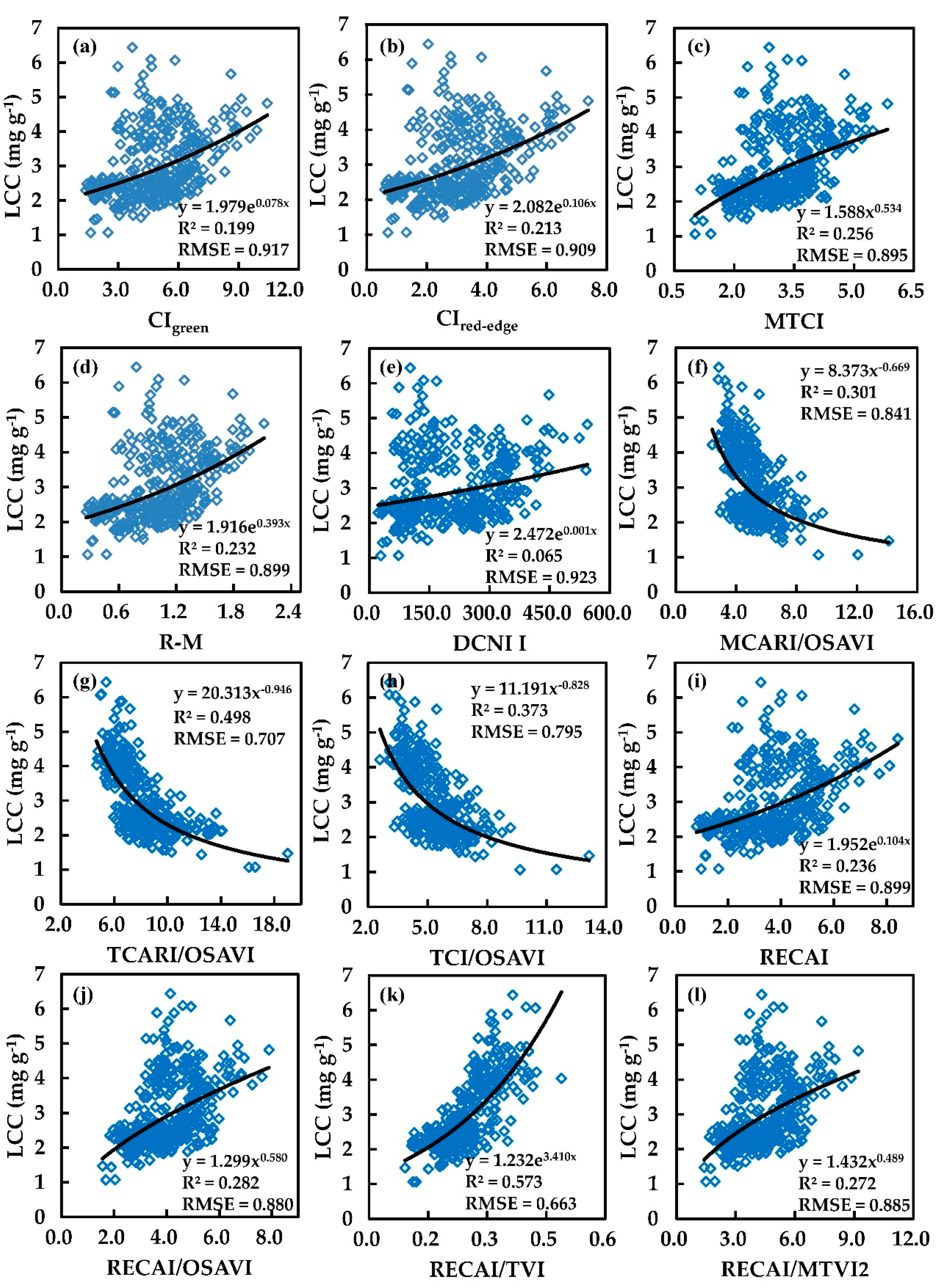
3.1. Prediction LCC by VIs
3.2. Comparing the LCC Estimation Performances of the Indices
3.3. Effect of LAI on the Assessment of LCC
4. Discussion
4.1. Building a New Vegetation Index for Retrieving Winter Wheat Leaf Chlorophyll Content
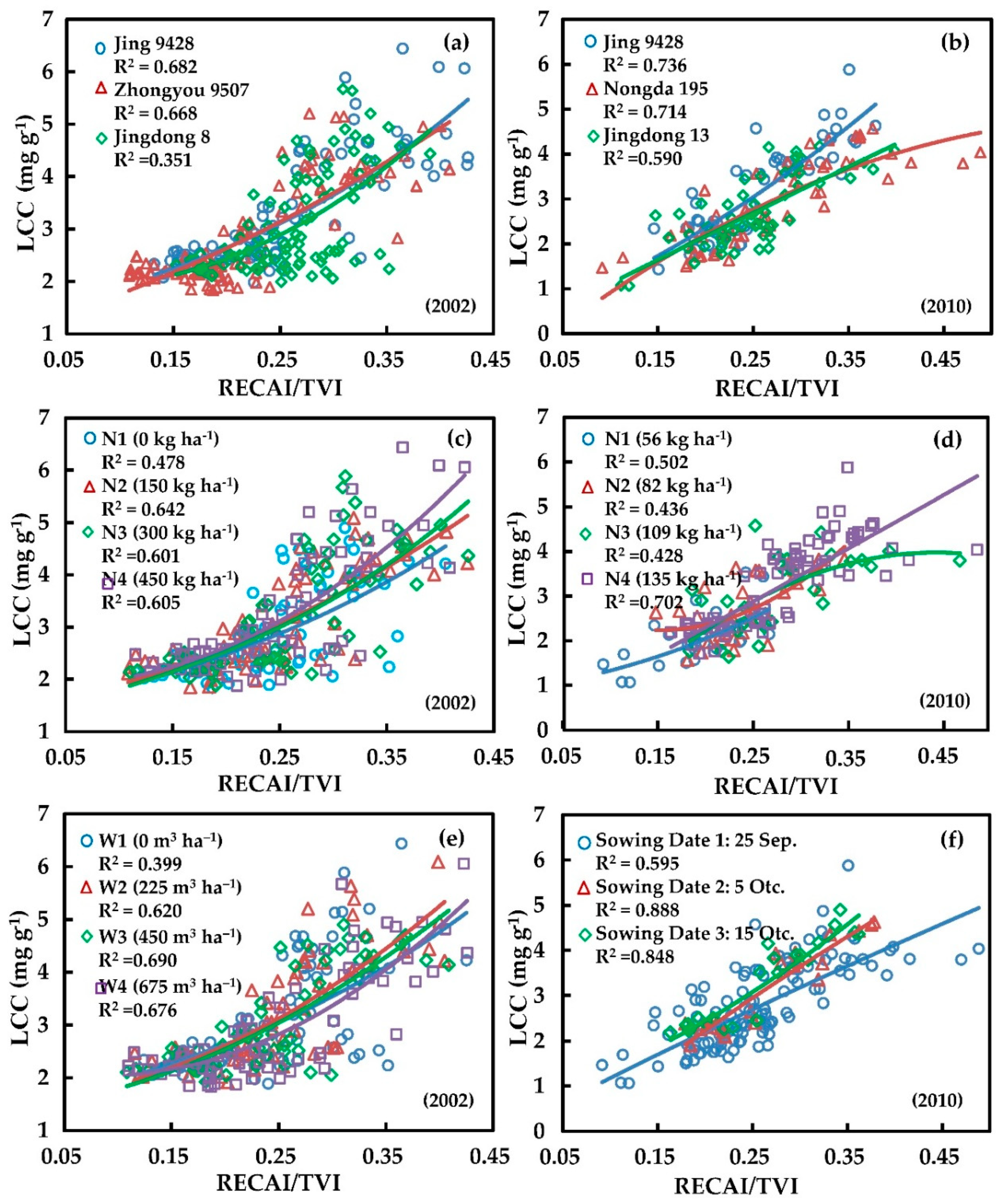
4.2. Effect of Field Management Measures on the RECAI/TVI Index
4.3. Comparison of the Performances of Different VIs
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Carter, G.A. Ratios of leaf reflectances in narrow wavebands as indicators of plant stress. Int. J. Remote Sens. 1994, 15, 697–704. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote estimation of chlorophyll content in higher plant leaves. Int. J. Remote Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- Osborne, B.A.; Raven, J.A. Light absorption by plants and its implications for photosynthesis. Biol. Rev. 1986, 61, 1–60. [Google Scholar] [CrossRef]
- Curran, P.J.; Dungan, J.L.; Gholz, H.L. Exploring the relationship between reflectance red edge and chlorophyll content in slash pine. Tree Physiol. 1990, 7, 33–48. [Google Scholar] [CrossRef] [PubMed]
- Sage, R.F.; Robert, W.P.; Seemann, J.R. The Nitrogen Use Efficiency of C3 and C4 Plants. Plant Physiol. 1987, 85, 355–359. [Google Scholar] [CrossRef]
- Miao, Y.; Mulla, D.J.; Randall, G.W.; Vetsch, J.A.; Vintila, R. Combining chlorophyll meter readings and high spatial resolution remote sensing images for in-season site-specific nitrogen management of corn. Precis. Agric. 2008, 10, 45–62. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Kooistra, L. Using Hyperspectral Remote Sensing Data for Retrieving Canopy Chlorophyll and Nitrogen Content. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 574–583. [Google Scholar] [CrossRef]
- Schlemmer, M.; Gitelson, A.; Schepers, J.; Ferguson, R.; Peng, Y.; Shanahan, J.; Rundquist, D. Remote estimation of nitrogen and chlorophyll contents in maize at leaf and canopy levels. Int. J. Appl. Earth Obs. Geoinf. 2013, 25, 47–54. [Google Scholar] [CrossRef]
- Baret, F.; Houles, V.; Guerif, M. Quantification of plant stress using remote sensing observations and crop models: The case of nitrogen management. J. Exp. Bot. 2007, 58, 869–880. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Peng, Y.; Arkebauer, T.J.; Schepers, J. Relationships between gross primary production, green LAI, and canopy chlorophyll content in maize: Implications for remote sensing of primary production. Remote Sens. Environ. 2014, 144, 65–72. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Ustin, S.L.; Gitelson, A.A.; Jacquemoud, S.; Schaepman, M.; Asner, G.P.; Gamon, J.A.; Zarco-Tejada, P. Retrieval of foliar information about plant pigment systems from high resolution spectroscopy. Remote Sens. Environ. 2009, 113, S67–S77. [Google Scholar] [CrossRef]
- Li, F.; Miao, Y.X.; Feng, G.H.; Yuan, F.; Yue, S.; Gao, X.; Liu, Y.; Liu, B.; Ustin, S.L.; Chen, X. Improving estimation of summer maize nitrogen status with red edge-based spectral vegetation indices. Field Crops Res. 2014, 157, 111–123. [Google Scholar] [CrossRef]
- Yao, F.Q.; Cai, H.J.; Li, Y.L.; Luo, W.B. Monitoring Winter Wheat SPAD Based on Red Edge Parameter Derived from Hyperspectral Reflectance. China Rural Water Hydropower 2015, 3, 84–87. [Google Scholar]
- Liu, W.Y.; Pan, J. A hyperspectral assessment model for leaf chlorophyll content of Pinus massoniana based on neural network. Chin. J. Appl. Ecol. 2017, 28, 1128–1136. [Google Scholar]
- Zillmann, E.; Schönert, M.; Lilienthal, H.; Siegmann, B.; Jarmer, T.; Rosso, P.; Weichelt, H. Crop Ground Cover Fraction and Canopy Chlorophyll Content Mapping using RapidEye imagery. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 149–155. [Google Scholar] [CrossRef]
- Kim, M.; Daughtry, C.; Chappelle, E.; McMurtrey, J., III; Walthall, C. The use of high spectral resolution bands for estimating absorbed photosynthetically active radiation (Apar). In Proceedings of the 6th Symposium on Physical Measurements and Signatures in Remote Sensing, Val D’Isere, France, 17–21 January 1994; pp. 299–306. [Google Scholar]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; Colstoun, E.B.D.; Mcmurtrey, J.E.I. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Haboudane, D.; Millera, J.R.; Tremblay, N.; Zarco-Tejadad, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Keydan, G.P.; Merzlyak, M.N. Three-band model for noninvasive estimation of chlorophyll, carotenoids, and anthocyanin contents in higher plant leaves. Geophys. Res. Lett. 2016, 33, L11402. [Google Scholar] [CrossRef]
- Ciganda, V.; Gitelson, A.; Schepers, J. Non-destructive determination of maize leaf and canopy chlorophyll content. J. Plant Physiol. 2009, 166, 157–167. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Maire, L.G.; François, C.; Dufrêne, E. Towards universal broad leaf chlorophyll indices using PROSPECT simulated database and hyperspectral reflectance measurements. Remote Sens. Environ. 2004, 89, 1–28. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Feng, H.; Xu, X.; Yang, G. Newly Combined Spectral Indices to Improve Estimation of Total Leaf Chlorophyll Content in Cotton. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4589–4600. [Google Scholar] [CrossRef]
- Lamb, D.W.; Steyn-Ross, M.; Schaare, P.; Hanna, M.M.; Silvester, W.; Steyn-Ross, A. Estimating leaf nitrogen concentration in ryegrass (Lolium spp.) pasture using the chlorophyll red-edge: Theoretical modelling and experimental observations. Int. J. Remote Sens. 2002, 23, 3619–3648. [Google Scholar] [CrossRef]
- Liu, J.; Pattey, E.; Jégo, G. Assessment of vegetation indices for regional crop green LAI estimation from Landsat images over multiple growing seasons. Remote Sens. Environ. 2012, 123, 347–358. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Zhang, L.; Deng, M.; Qin, Z.; Zhao, S.; Lin, H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Kooistra, L.; Clevers, J.G.P.W. Estimating potato leaf chlorophyll content using ratio vegetation indices. Remote Sens. Lett. 2016, 7, 611–620. [Google Scholar] [CrossRef]
- Clevers, J.; Kooistra, L.; Marnix, V.D.B. Using Sentinel-2 Data for Retrieving LAI and Leaf and Canopy Chlorophyll Content of a Potato Crop. Remote Sens. 2017, 9, 405. [Google Scholar] [CrossRef]
- Cui, S.; Zhou, K. A comparison of the predictive potential of various vegetation indices for leaf chlorophyll content. Earth Sci. Inf. 2017, 10, 169–181. [Google Scholar] [CrossRef]
- Haboudane, D.; Tremblay, N.; Miller, J.R.; Vigneault, P. Remote Estimation of Crop Chlorophyll Content Using Spectral Indices Derived From Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 423–437. [Google Scholar] [CrossRef]
- Porra, R.J. The chequered history of the development and use of simultaneous equations for the accurate determination of chlorophylls a and b. Photosynth. Res. 2002, 73, 149–156. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Liu, L.; Huang, W.; Zhao, C.; Lu, Y. Estimation of Nitrogen Status in Middle and Bottom Layers of Winter Wheat Canopy by Using Ground-Measured Canopy Reflectance. Commun. Soil Sci. Plant Anal. 2005, 36, 2289–2302. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, W.; Kong, W.; Ye, H.; Dong, Y.; Casa, R. Assessment of leaf carotenoids content with a new carotenoid index: Development and validation on experimental and model data. Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 24–35. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2000, 76, 156–172. [Google Scholar] [CrossRef]
- Haboudane, D. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Gates, D.M.; Keegan, H.J.; Schleter, J.C.; Weidner, V.R. Spectral Properties of Plants. Appl. Opt. 1965, 4, 11–20. [Google Scholar] [CrossRef]
- Horler, D.N.H.; Dockray, M.; Barber, J. The red edge of plant leaf reflectance. Int. J. Remote Sens. 1983, 4, 273–288. [Google Scholar] [CrossRef]
- Datt, B.A. New Reflectance Index for Remote Sensing of Chlorophyll Content in Higher Plants: Tests using Eucalyptus Leaves. J. Plant Physiol. 1999, 154, 30–36. [Google Scholar] [CrossRef]
- Blackburn, G.A. Hyperspectral remote sensing of plant pigments. J. Exp. Bot. 2007, 58, 855–867. [Google Scholar] [CrossRef] [PubMed]
- Hatfield, J.L.; Gitelson, A.A.; Schepers, J.S.; Walthall, C.L. Application of Spectral Remote Sensing for Agronomic Decisions. Agron. J. 2008, 100, S117–S131. [Google Scholar] [CrossRef]
- Richter, K.; Atzberger, C.; Hank, T.B.; Mauser, W. Derivation of biophysical variables from Earth observation data: Validation and statistical measures. J. Appl. Remote Sens. 2012, 6, 063557. [Google Scholar] [CrossRef]
- Croft, H.; Chen, J.; Zhang, Y. The applicability of empirical vegetation indices for determining leaf chlorophyll content over different leaf and canopy structures. Ecol. Complex. 2014, 17, 119–130. [Google Scholar] [CrossRef]
- Brogea, N.; Mortensen, J. Deriving green crop area index and canopy chlorophyll density of winter wheat from spectral reflectance data. Remote Sens. Environ. 2002, 81, 45–57. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Berjón, A.; López-Lozano, R.; Miller, J.R.; Martín, P.; Cachorro, V.; González, M.R.; de Frutos, A. Assessing vineyard condition with hyperspectral indices: leaf and canopy reflectance simulation in a row-structured discontinuous canopy. Remote Sens. Environ. 2005, 99, 271–287. [Google Scholar] [CrossRef]

| Water | W1 (0 m3 ha−1) | W2 (225 m3 ha−1) | W3 (450 m3 ha−1) | W4 (675 m3 ha−1) | Variety | |
|---|---|---|---|---|---|---|
| N fertilizer | ||||||
| N1 (0 kg ha−1) | 12 | 13 | 36 | 37 | Zhongyou 9507 | |
| 11 | 14 | 35 | 38 | Jing 9428 | ||
| 10 | 15 | 34 | 39 | Jingdong 8 | ||
| N2 (150 kg ha−1) | 9 | 16 | 33 | 40 | Zhongyou 9507 | |
| 8 | 17 | 32 | 41 | Jing 9428 | ||
| 7 | 18 | 31 | 42 | Jingdong 8 | ||
| N3 (300 kg ha−1) | 6 | 19 | 30 | 43 | Zhongyou 9507 | |
| 5 | 20 | 29 | 44 | Jing 9428 | ||
| 4 | 21 | 28 | 45 | Jingdong 8 | ||
| N4 (450 kg ha−1) | 3 | 22 | 27 | 46 | Zhongyou 9507 | |
| 2 | 23 | 26 | 47 | Jing 9428 | ||
| 11 | 24 | 25 | 48 | Jingdong 8 | ||
| Sowing Date | Variety | |||||||
|---|---|---|---|---|---|---|---|---|
| 25 September | 5 October | 15 October | ||||||
| N fertilizer | 56 kg ha−1 | 2 | 1 1 | / 2 | / | / | / | Nongda 195 |
| 10 | 9 | / | / | / | / | Jing 9428 | ||
| 18 | 17 | / | / | / | / | Jingdong 13 | ||
| 82 kg ha−1 | 4 | 3 | / | / | / | / | Nongda 195 | |
| 12 | 11 | / | / | / | / | Jing 9428 | ||
| 20 | 19 | / | / | / | / | Jingdong 13 | ||
| 109 kg ha−1 | 6 | 5 | 26 | 25 | 32 | 31 | Nongda 195 | |
| 14 | 13 | 28 | 27 | 34 | 33 | Jing 9428 | ||
| 22 | 21 | 30 | 29 | 36 | 35 | Jingdong 13 | ||
| 135 kg ha−1 | 8 | 7 | / | / | / | / | Nongda 195 | |
| 16 | 15 | / | / | / | / | Jing 9428 | ||
| 24 | 23 | / | / | / | / | Jingdong 13 | ||
| Datasets | Parameter | Mean | Min | Max | SD | CV (%) | n |
|---|---|---|---|---|---|---|---|
| 2002 | LCC | 3.102 | 1.832 | 6.439 | 1.014 | 32.688 | 288 |
| LAI | 2.311 | 0.434 | 4.859 | 1.017 | 43.995 | 288 | |
| 2010 | LCC | 2.913 | 1.066 | 5.879 | 0.925 | 31.741 | 168 |
| LAI | 2.069 | 0.394 | 5.374 | 0.869 | 42.030 | 168 |
| Index | Formula | Reference |
|---|---|---|
| Green chlorophyll index (CIgreen) | R783/R550 − 1 | [11,20] |
| Red-edge chlorophyll index (CIred-edge) | R783/R705 − 1 | [11,20] |
| Moderate-resolution imaging spectrometer terrestrial chlorophyll index (MTCI) | (R750 − R710)/(R710 − R680) | [23] |
| Red-edge model index (R-M) | (R750/R720) − 1 | [11] |
| Double-peak canopy nitrogen index I (DCNI I) | [(R750 − R670+0.09)(R750 − R700)]/(R700 − R670) | [25] |
| The modified chlorophyll absorption ratio index/optimized soil-adjusted vegetation index (MCARI/OSAVI) | [(R700 − R670) − 0.2(R700 − R550)](R700/R670)/[1.16(R800-R670)/(R800+R670+0.16)] | [32] |
| The transformed chlorophyll absorption in the reflectance index/optimized soil-adjusted vegetation index (TCARI/OSAVI) | 3[(R700 − R670) − 0.2(R700 − R550)(R700/R670)]/[1.16(R800 − R670)/(R800+R670+0.16)] | [19] |
| The triangular chlorophyll index/optimized soil-adjusted vegetation index (TCI/OSAVI) | /[1.16(R800 − R670)/(R800+R670+0.16)] | [32] |
| The red-edge-chlorophyll absorption index (RECAI) | (R800 − R720)/R550*(R700/R550) | This study |
| The red-edge-chlorophyll absorption index/ optimized soil-adjusted vegetation index (RECAI/OSAVI) | RECAI/OSAVI | This study |
| The red-edge-chlorophyll absorption index/ the triangular vegetation index (RECAI/TVI) | 100RECAI/TVI | This study |
| The red-edge-chlorophyll absorption index/ the modified triangular vegetation index (RECAI/MTVI2) | RECAI/MTVI2 | This study |
| 0 < LAI < 1 (n1 = 52) | 1 ≤ LAI < 2 (n = 143) | 2 ≤ LAI < 3 (n = 154) | 3 ≤ LAI < 4 (n = 94) | LAI ≥ 4 (n = 13) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LCC | LAI | LCC | LAI | LCC | LAI | LCC | LAI | LCC | LAI | |
| CIgreen | 0.665 ** | 0.422 ** | 0.468 ** | 0.469 ** | 0.426 ** | 0.366 ** | 0.692 ** | 0.014 | 0.613 * | 0.116 |
| CIred-edge | 0.661 ** | 0.422 ** | 0.465 ** | 0.481 ** | 0.464 ** | 0.346 ** | 0.725 ** | −0.004 | 0.581 * | 0.182 |
| MTCI | 0.526 ** | 0.233 | 0.432 ** | 0.453 ** | 0.454 ** | 0.293 ** | 0.758 ** | −0.111 | 0.673 * | −0.043 |
| R-M | 0.664 ** | 0.426 ** | 0.486 ** | 0.497 ** | 0.485 ** | 0.347 ** | 0.746 ** | −0.024 | 0.630 * | 0.085 |
| DCNI I | 0.102 | 0.333 * | 0.022 | 0.508 ** | 0.177 * | 0.388 ** | 0.533 ** | 0.078 | 0.359 | 0.049 |
| MCARI/OSAVI | −0.570 ** | 0.185 | −0.526 ** | −0.150 | −0.524 ** | 0.146 | −0.519 ** | 0.364 ** | −0.523 | 0.249 |
| TCARI/OSAVI | −0.668 ** | 0.054 | −0.652 ** | −0.246 ** | −0.669 ** | 0.040 | −0.676 ** | 0.264 * | −0.568 * | 0.017 |
| TCI/OSAVI | −0.608 ** | 0.155 | −0.588 ** | -0.148 | −0.585 ** | 0.133 | −0.568 ** | 0.338 ** | −0.551 | 0.186 |
| RECAI | 0.688 ** | 0.398 ** | 0.542 ** | 0.427 ** | 0.454 ** | 0.357 ** | 0.698 ** | −0.009 | 0.730 ** | −0.103 |
| RECAI/OSAVI | 0.621 ** | 0.255 | 0.545 ** | 0.341 ** | 0.450 ** | 0.335 ** | 0.693 ** | −0.041 | 0.750 ** | −0.207 |
| RECAI/TVI | 0.777 ** | 0.029 | 0.819 ** | 0.109 | 0.708 ** | 0.053 | 0.722 ** | −0.167 | 0.730 ** | −0.106 |
| RECAI/MTVI2 | 0.615 ** | 0.238 | 0.535 ** | 0.353 ** | 0.445 ** | 0.342 ** | 0.694 ** | −0.035 | 0.742 ** | −0.177 |
| LCC | LAI | |||||
|---|---|---|---|---|---|---|
| TVI | −0.193 ** | 0.167 * | −0.037 | 0.800 ** | 0.735 ** | 0.779 ** |
| OSAVI | 0.308 ** | 0.220 ** | 0.326 ** | 0.799 ** | 0.643 ** | 0.764 ** |
| MTVI2 | 0.307 ** | 0.370 ** | 0.269 ** | 0.761 ** | 0.720 ** | 0.690 ** |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, B.; Zhao, Q.; Huang, W.; Song, X.; Ye, H.; Zhou, X. A New Integrated Vegetation Index for the Estimation of Winter Wheat Leaf Chlorophyll Content. Remote Sens. 2019, 11, 974. https://doi.org/10.3390/rs11080974
Cui B, Zhao Q, Huang W, Song X, Ye H, Zhou X. A New Integrated Vegetation Index for the Estimation of Winter Wheat Leaf Chlorophyll Content. Remote Sensing. 2019; 11(8):974. https://doi.org/10.3390/rs11080974
Chicago/Turabian StyleCui, Bei, Qianjun Zhao, Wenjiang Huang, Xiaoyu Song, Huichun Ye, and Xianfeng Zhou. 2019. "A New Integrated Vegetation Index for the Estimation of Winter Wheat Leaf Chlorophyll Content" Remote Sensing 11, no. 8: 974. https://doi.org/10.3390/rs11080974
APA StyleCui, B., Zhao, Q., Huang, W., Song, X., Ye, H., & Zhou, X. (2019). A New Integrated Vegetation Index for the Estimation of Winter Wheat Leaf Chlorophyll Content. Remote Sensing, 11(8), 974. https://doi.org/10.3390/rs11080974






