Airborne LIDAR-Derived Aboveground Biomass Estimates Using a Hierarchical Bayesian Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Random Sampling
2.3. DBH and AGB Models
2.4. Bayesian Method
2.5. Model Evaluation
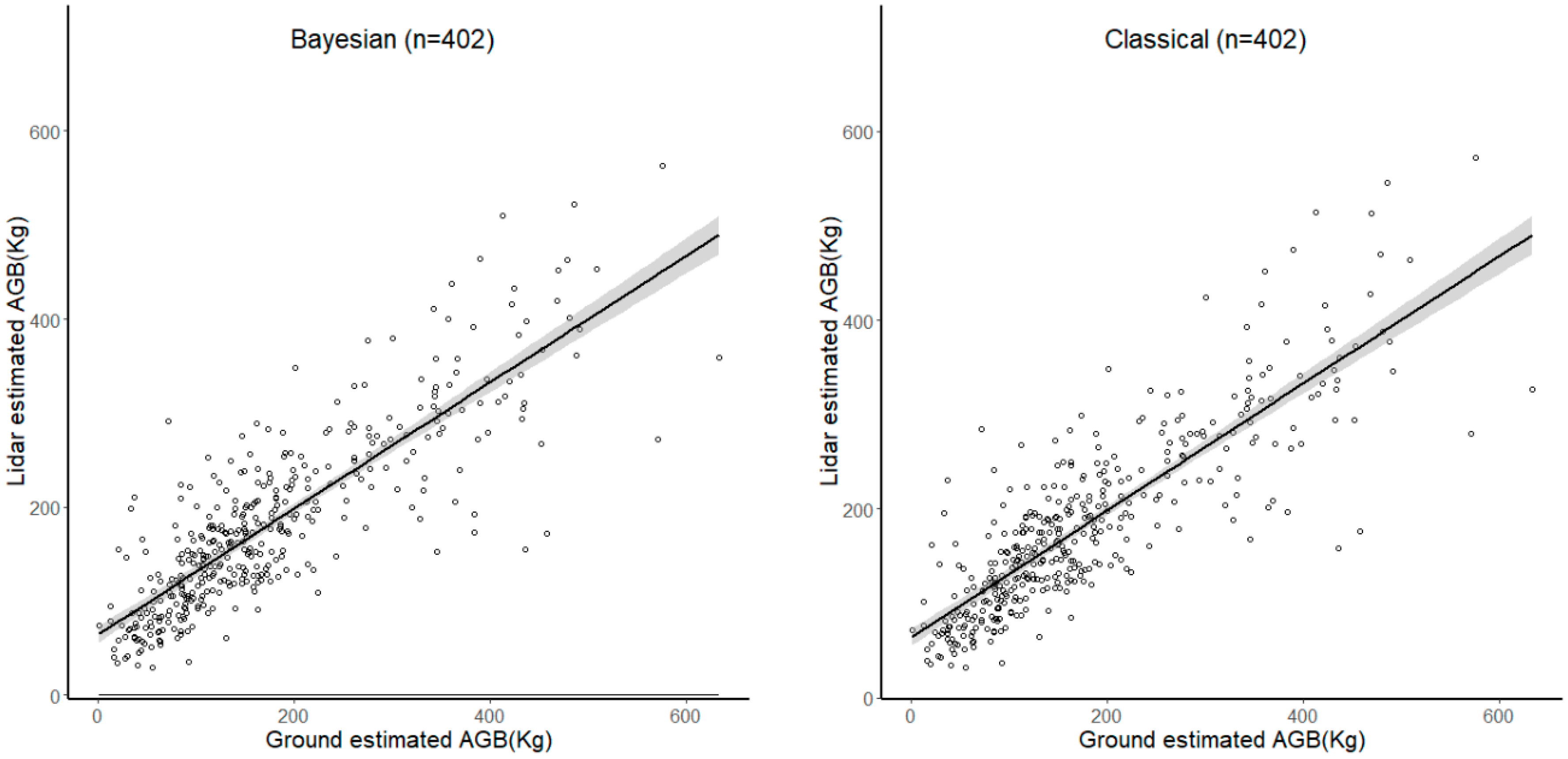
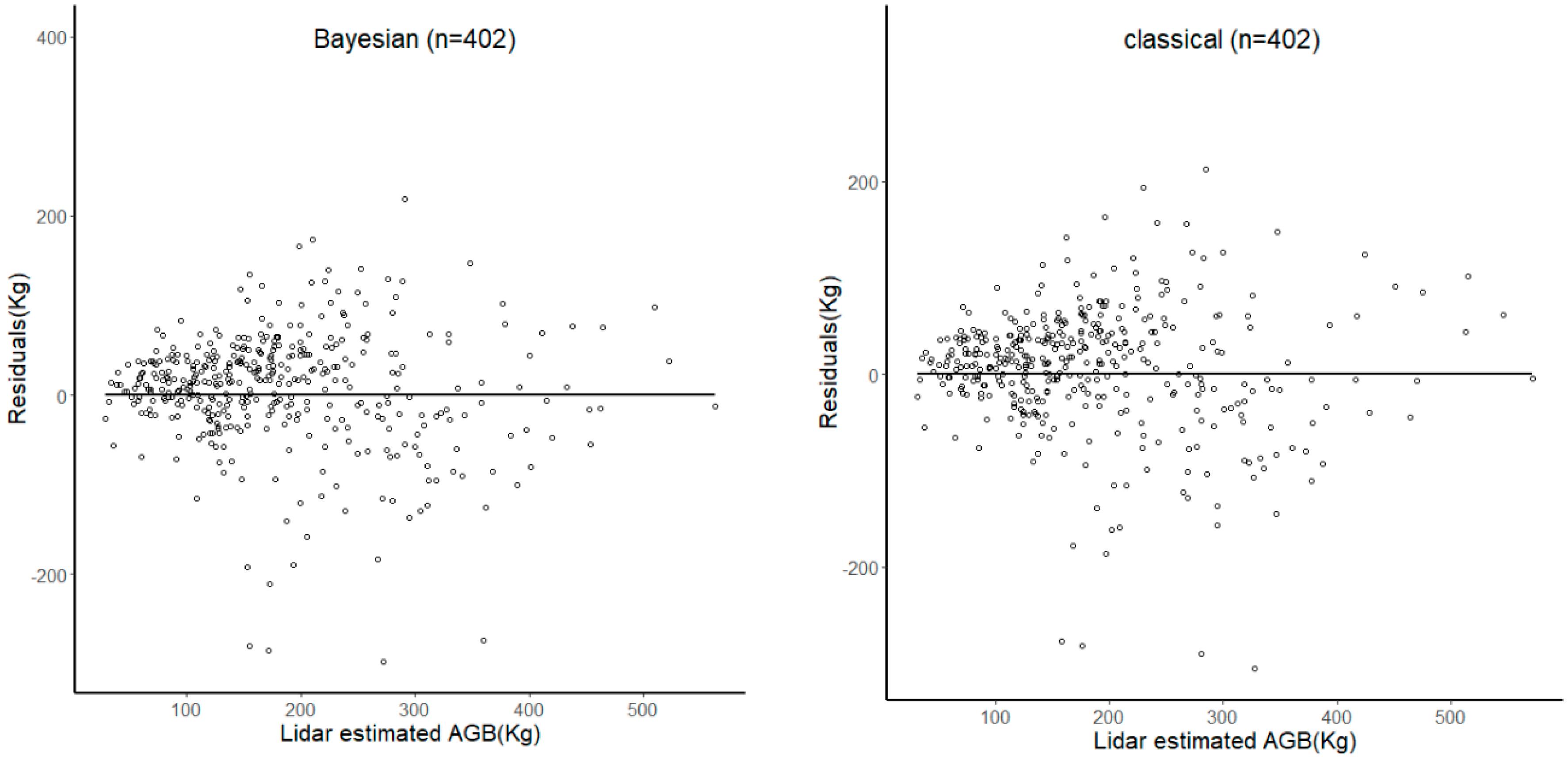
3. Results
3.1. Model Selection
3.2. Comparing the Hierarchical Bayesian and NLME Methods
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhu, J.; Hu, H.; Tao, S.; Chi, X.; Li, P.; Jiang, L.; Ji, C.; Zhu, J.; Tang, Z.; Pan, Y.; et al. Carbon stocks and changes of dead organic matter in China’s forests. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef]
- He, Q.; Chen, E.; An, R.; Li, Y. Above-ground biomass and biomass components estimation using Lidar data in a coniferous forest. Forests 2013, 4, 984–1002. [Google Scholar] [CrossRef]
- Fu, L.; Liu, Q.; Sun, H.; Wang, Q.; Li, Z.; Chen, E.; Pang, Y.; Song, X.; Wang, G. Development of a system of compatible individual tree diameter and aboveground biomass prediction models using error-in-variable regression and airborne Lidar data. Remote Sens. 2018, 10, 325. [Google Scholar] [CrossRef]
- Fu, L.; Lei, Y.; Wang, G.; Bi, H.; Tang, S.; Song, X. Comparison of seemingly unrelated regressions with error-in-variable models for developing a system of nonlinear additive biomass equations. Trees 2016, 30, 839–857. [Google Scholar] [CrossRef]
- Nelson, R.; Krabill, W.; Tonelli, J. Estimating forest biomass and volume using airborne laser data. Remote Sens. Environ. 1988, 24, 247–267. [Google Scholar] [CrossRef]
- Neumann, M.; Saatchi, S.S.; Ulander, L.M.H.; Fransson, J.E.S. Assessing performance of l- and p-band polarimetric interferometric SAR data in estimating boreal forest above-ground biomass. IEEE Trans. Geosci. Remote Sens. 2012, 50, 714–726. [Google Scholar] [CrossRef]
- Tian, X.; Su, Z.; Chen, E.; Li, Z.; van der Tol, C.; Guo, J.; He, Q. Estimation of forest above-ground biomass using multi-parameter remote sensing data over a cold and arid area. Int. J. Appl. Earth Obs. 2012, 14, 160–168. [Google Scholar] [CrossRef]
- Zheng, C.; Mason, E.G.; Jia, L.; Wei, S.; Sun, C.; Duan, J. A single-tree additive biomass model of Quercus variabilis Blume forests in north China. Trees 2015, 29, 705–716. [Google Scholar] [CrossRef]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and stem volume equations for tree species in Europe. Silva Fenn. Monogr. 2005, 4, 1–63. [Google Scholar]
- Zianis, D.; Mencuccini, M. On simplifying allometric analyses of forest biomass. For. Ecol. Manag. 2004, 187, 311–332. [Google Scholar] [CrossRef]
- Holmgren, J.; Nilsson, M.; Olsson, H. Estimation of tree height and stem volume on plots using airborne laser scanning. For. Sci. 2003, 49, 419–428. [Google Scholar]
- Næsset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ. 1997, 61, 246–253. [Google Scholar] [CrossRef]
- Hansen, E.; Ene, L.; Mauya, E.; Patocka, Z.; Mikita, T.; Gobakken, T.; Næsset, E. Comparing empirical and semi-empirical approaches to forest biomass modelling in different biomes using airborne laser scanner data. Forests 2017, 8, 170. [Google Scholar] [CrossRef]
- Zapata-Cuartas, M.; Sierra, C.A.; Alleman, L. Probability distribution of allometric coefficients and Bayesian estimation of aboveground tree biomass. For. Ecol. Manag. 2012, 277, 173–179. [Google Scholar] [CrossRef]
- Zell, J.; Bösch, B.; Kändler, G. Estimating above-ground biomass of trees: Comparing Bayesian calibration with regression technique. Eur. J. For. Res. 2014, 133, 649–660. [Google Scholar] [CrossRef]
- Zhang, X.; Duan, A.; Zhang, J.; Xiang, C. Estimating tree height-diameter models with the Bayesian method. Sci. World J. 2014, 2014, 683–691. [Google Scholar] [CrossRef] [PubMed]
- Zianis, D.; Spyroglou, G.; Tiakas, E.; Radoglou, K. Bayesian and classical models to predict above ground tree biomass allometry. For. Sci. 2016, 62, 247–259. [Google Scholar]
- Farid, A.; Goodrich, D.; Sorooshian, S. Using airborne Lidar to discern Age classes of cottonwood trees in a riparian Area. West. J. Appl. For. 2006, 21, 149–158. [Google Scholar]
- Hauglin, M.; Gobakken, T.; Astrup, R.; Ene, L.; Næsset, E. Estimating single-tree crown biomass of Norway spruce by airborne laser scanning: A comparison of methods with and without the use of terrestrial laser scanning to obtain the ground reference data. Forests 2014, 5, 384–403. [Google Scholar] [CrossRef]
- Kuyah, S.; Sileshi, G.; Rosenstock, T. Allometric models based on Bayesian frameworks give better estimates of aboveground biomass in the Miombo woodlands. Forests 2016, 7, 13. [Google Scholar] [CrossRef]
- Picard, N.; Henry, M.; Mortier, F.; Trotta, C.; Saint-Andre, L. Using Bayesian model averaging to predict tree aboveground biomass in tropical moist forests. For. Sci. 2011, 58, 15–23. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian model averaging: A tutorial. Stat. Sci. 1999, 14, 382–417. [Google Scholar]
- Olubusoye, O.; Okonkwo, O. Choice of priors and variable selection in Bayesian regression. J. Asian Sci. Res. 2018, 2, 354–377. [Google Scholar]
- Tenneson, K. Development of a regional Lidar-derived forest inventory model with Bayesian model averaging for use in ponderosa pine and mixed conifer forests in Arizona and new Mexico, USA. Remote Sens. 2018, 10, 442. [Google Scholar] [CrossRef]
- Wang, J.; Che, K.; Fu, H.; Chang, X.; Song, C.; He, H. Study on biomass of water conservation forest on north Slope of Qilian mountains. J. Fujian Coll. For. 1998, 18, 319–323. (In Chinese) [Google Scholar]
- Bi, H.; Fox, J.; Li, Y.; Lei, Y.; Pang, Y. Evaluation of nonlinear equations for predicting diameter from tree height. Can. J. For. Res. 2012, 42, 789–806. [Google Scholar] [CrossRef]
- Yang, R.C.; Kozak, A.; Smith, J.H.G. The potential of Weibull-type functions as a flexible growth curve. Can. J. For. Res. 1978, 8, 424–431. [Google Scholar] [CrossRef]
- Ruark, G.A.; Martin, G.L.; Bockheim, J.G. Comparison of constant and variable allometric ratios for estimating Populus tremuloides biomass. For. Sci. 1987, 33, 294–300. [Google Scholar]
- Zhang, X.; Duan, A.; Zhang, J. Tree biomass estimation of Chinese fir (Cunninghamia lanceolata) based on Bayesian method. PLoS ONE 2013, 8, e79868. [Google Scholar] [CrossRef]
- Ellison, A.M. Bayesian inference in ecology. Ecol. Lett. 2004, 7, 509–520. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J.; Duan, A. A hierarchical Bayesian model to predict self-thinning line for Chinese Fir in southern China. PLoS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhang, J.; Duan, A. Tree-height growth model for Chinese fir plantation based on Bayesian method. Sci. Silvae Sin. 2014, 50, 69–75. (In Chinese) [Google Scholar]
- Heidelberger, P.; Welch, P.D. Simulation run length control in the presence of an initial transient. Opns. Res. 1983, 31, 1109–1144. [Google Scholar] [CrossRef]
- Heidelberger, P.; Welch, P.D. A spectral method for confidence interval generation and run length control in simulations. Commun. ACM 1981, 24, 233–245. [Google Scholar] [CrossRef]
- Kipiński, L.; König, R.; Sielużycki, C.; Kordecki, W. Application of modern tests for stationarity to single-trial meg: Data transferring powerful statistical tools from econometrics to neuroscience. Biol. Cybern 2011, 105, 183–195. [Google Scholar] [CrossRef] [PubMed]
- SAS Institute, Inc. SAS/STAT 9.3 User’s Guide; SAS Institute, Inc.: Cary, NC, USA, 2011; 3316p. [Google Scholar]
- Huang, X.; Chen, D.; Sun, X.; Zhang, S. Estimation on above-ground tree biomass based on probability distribution of allometric parameters. Sci. Silvae Sin. 2014, 50, 34–41. (In Chinese) [Google Scholar]
- Yao, D. Individual Tree Growth Model for Mongolia Oak Forest with Bayesian Statistical Inference. Master’s Thesis, Chinese Academy of Forestry, Beijing, China, 2015. (In Chinese). [Google Scholar]
- Sileshi, G.W. A critical review of forest biomass estimation models, common mistakes and corrective measures. For. Ecol. Manag. 2014, 329, 237–254. [Google Scholar] [CrossRef]

| Sample Size | Factor | Maximum | Minimum | Mean | SD |
|---|---|---|---|---|---|
| 10% (39) | DBH | 36.40 | 2.50 | 21.26 | 7.84 |
| LH | 9.79 | 1.96 | 6.81 | 2.17 | |
| AGB | 395.83 | 1.45 | 153.08 | 102.39 | |
| CPA | 11.06 | 2.94 | 7.42 | 2.20 | |
| 25% (99) | DBH | 40.50 | 8.20 | 23.38 | 7.77 |
| LH | 10.10 | 2.21 | 6.80 | 1.88 | |
| AGB | 508.02 | 15.68 | 178.08 | 119.52 | |
| CPA | 12.80 | 3.56 | 7.32 | 1.97 | |
| 50% (199) | DBH | 54.50 | 2.50 | 22.73 | 7.41 |
| LH | 11.29 | 1.96 | 6.96 | 1.85 | |
| AGB | 959.49 | 1.45 | 169.51 | 118.90 | |
| CPA | 13.50 | 2.94 | 7.48 | 2.03 | |
| 75% (303) | DBH | 54.50 | 2.50 | 23.09 | 7.78 |
| LH | 11.30 | 1.96 | 6.92 | 1.89 | |
| AGB | 959.49 | 1.45 | 176.03 | 125.55 | |
| CPA | 13.50 | 2.94 | 7.41 | 2.06 | |
| 100% (402) | DBH | 81.10 | 2.50 | 23.40 | 8.30 |
| LH | 11.20 | 1.90 | 6.90 | 1.90 | |
| AGB | 1142.50 | 1.45 | 181.30 | 134.10 | |
| CPA | 13.50 | 2.90 | 7.43 | 2.06 |
| Model | DIC | Stationarity Test |
|---|---|---|
| I.1 | 2557.572 | passed |
| I.2 | 2556.442 | passed |
| I.3 | 2541.001 | passed |
| I.4 | 2545.794 | passed |
| I.5 | - | failed |
| I.6 | 2580.574 | passed |
| I.7 | 2547.292 | passed |
| n | 39 | 99 | 199 | 303 | 402 |
|---|---|---|---|---|---|
| Bayesian | |||||
| β1 | 49.34 (6.428) | 99.62 (7.66) | 99.58 (6.7) | 99.44 (6.68) | 111.3 (24.46) |
| β2 | 8.326 (1.326) | 11.92 (1.408) | 13.2 (1.223) | 11.96 (1.213) | 13.6 (2.79) |
| β3 | −0.036 (0.045) | 0.108 (0.04) | 0.148 (0.025) | 0.107 (0.03) | 0.114 (0.024) |
| β4 | 0.297 (0.055) | 0.068 (0.037) | 0.043 (0.021) | 0.072 (0.026) | 0.066 (0.022) |
| NLME | |||||
| β1 | 49.48 (9.75) | 99.57 (64.35) | 99.37 (50.25) | 99.2 (47.63) | 99.36 (42.52) |
| β2 | 8.246 (1.792) | 11.75 (7.07) | 13.04 (5.968) | 11.83 (5.282) | 12.29 (4.76) |
| β3 | −0.036 (0.07) | 0.108 (0.043) | 0.146 (0.03) | 0.109 (0.033) | 0.118 (0.026) |
| β4 | 0.292 (0.092) | 0.067 (0.042) | 0.044 (0.026) | 0.068 (0.03) | 0.065 (0.025) |
| Model No. | DIC | Stationarity Test |
|---|---|---|
| II.1 | 4763.795 | passed |
| II.2 | - | failed |
| II.3 | 4754.906 | passed |
| II.4 | 4777.023 | passed |
| II.5 | - | failed |
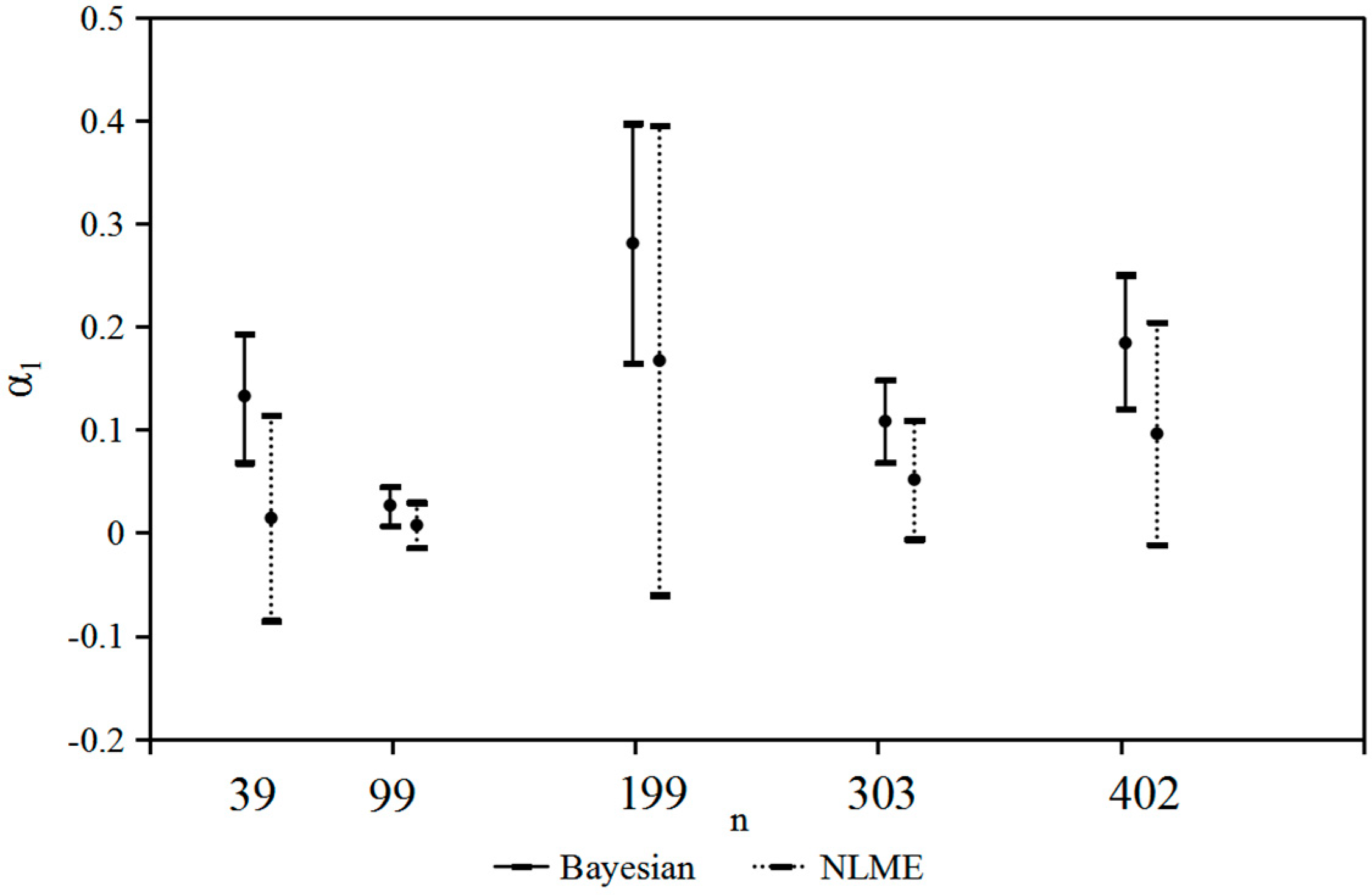
| n | 39 | 99 | 199 | 303 | 402 |
|---|---|---|---|---|---|
| Bayesian | |||||
| α1 | 0.133 (0.0320) | 0.027 (0.0097) | 0.281 (0.0604) | 0.281 (0.0604) | 0.184 (0.0339) |
| α2 | 2.334 (0.3959) | 3.385 (0.2338) | 1.370 (0.1881) | 1.37 (0.1881) | 2.383 (0.1428) |
| α3 | −0.246 (0.5815) | −1.332 (0.3225) | 0.990 (0.2447) | 0.990 (0.2447) | −0.346 (0.1825) |
| NLME | |||||
| α1 | 0.014 (0.0461) | 0.007 (0.0101) | 0.167 (0.1068) | 0.052 (0.0371) | 0.096 (0.0506) |
| α2 | 3.522 (1.7199) | 4.463 (0.8609) | 1.670 (0.4611) | 2.973 (0.3612) | 2.781 (0.3620) |
| α3 | −0.967 (1.254) | −2.019 (0.726) | 0.765 (0.4559) | −0.617 (0.3463) | −0.652 (0.3438) |
| Sample Size | Method | R2 | MAD |
|---|---|---|---|
| 10% (39) | Bayesian | 0.8611 | 31.0571 |
| classical | 0.7741 | 34.2188 | |
| 25% (99) | Bayesian | 0.7704 | 43.2709 |
| classical | 0.7529 | 43.1827 | |
| 50% (199) | Bayesian | 0.7529 | 40.5010 |
| classical | 0.7503 | 40.2283 | |
| 75% (303) | Bayesian | 0.7080 | 44.8375 |
| classical | 0.7046 | 44.6531 | |
| 100% (402) | Bayesian | 0.5867 | 48.3125 |
| classical | 0.5719 | 49.3627 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Liu, Q.; Fu, L.; Wang, G.; Zhang, X. Airborne LIDAR-Derived Aboveground Biomass Estimates Using a Hierarchical Bayesian Approach. Remote Sens. 2019, 11, 1050. https://doi.org/10.3390/rs11091050
Wang M, Liu Q, Fu L, Wang G, Zhang X. Airborne LIDAR-Derived Aboveground Biomass Estimates Using a Hierarchical Bayesian Approach. Remote Sensing. 2019; 11(9):1050. https://doi.org/10.3390/rs11091050
Chicago/Turabian StyleWang, Mengxi, Qingwang Liu, Liyong Fu, Guangxing Wang, and Xiongqing Zhang. 2019. "Airborne LIDAR-Derived Aboveground Biomass Estimates Using a Hierarchical Bayesian Approach" Remote Sensing 11, no. 9: 1050. https://doi.org/10.3390/rs11091050
APA StyleWang, M., Liu, Q., Fu, L., Wang, G., & Zhang, X. (2019). Airborne LIDAR-Derived Aboveground Biomass Estimates Using a Hierarchical Bayesian Approach. Remote Sensing, 11(9), 1050. https://doi.org/10.3390/rs11091050







