An Iterative ICA-Based Reconstruction Method to Produce Consistent Time-Variable Total Water Storage Fields Using GRACE and Swarm Satellite Data
Abstract
1. Introduction
2. Data
2.1. GRACE L2 Fields
2.2. Swarm L2 Gravity Field Models
2.3. Treatment of the Degree One and Two Coefficients
2.4. Data Post-Processing
2.5. Glacial Isostatic Adjustment (GIA) Corrections
2.6. Conversion to the TWSC Fields and Reducing the Leakage
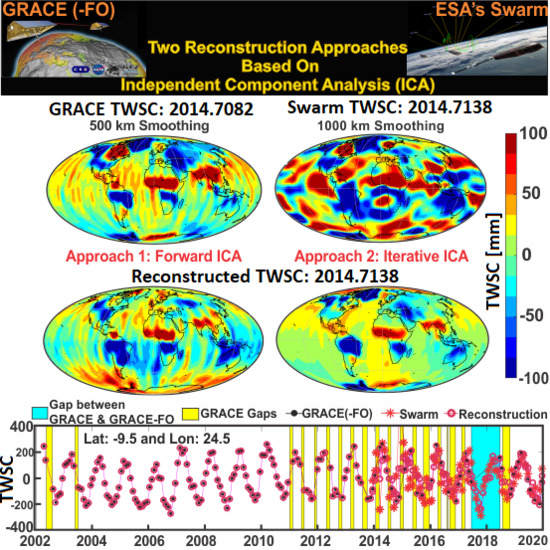
3. Method
3.1. Joint Diagonalization (JD)
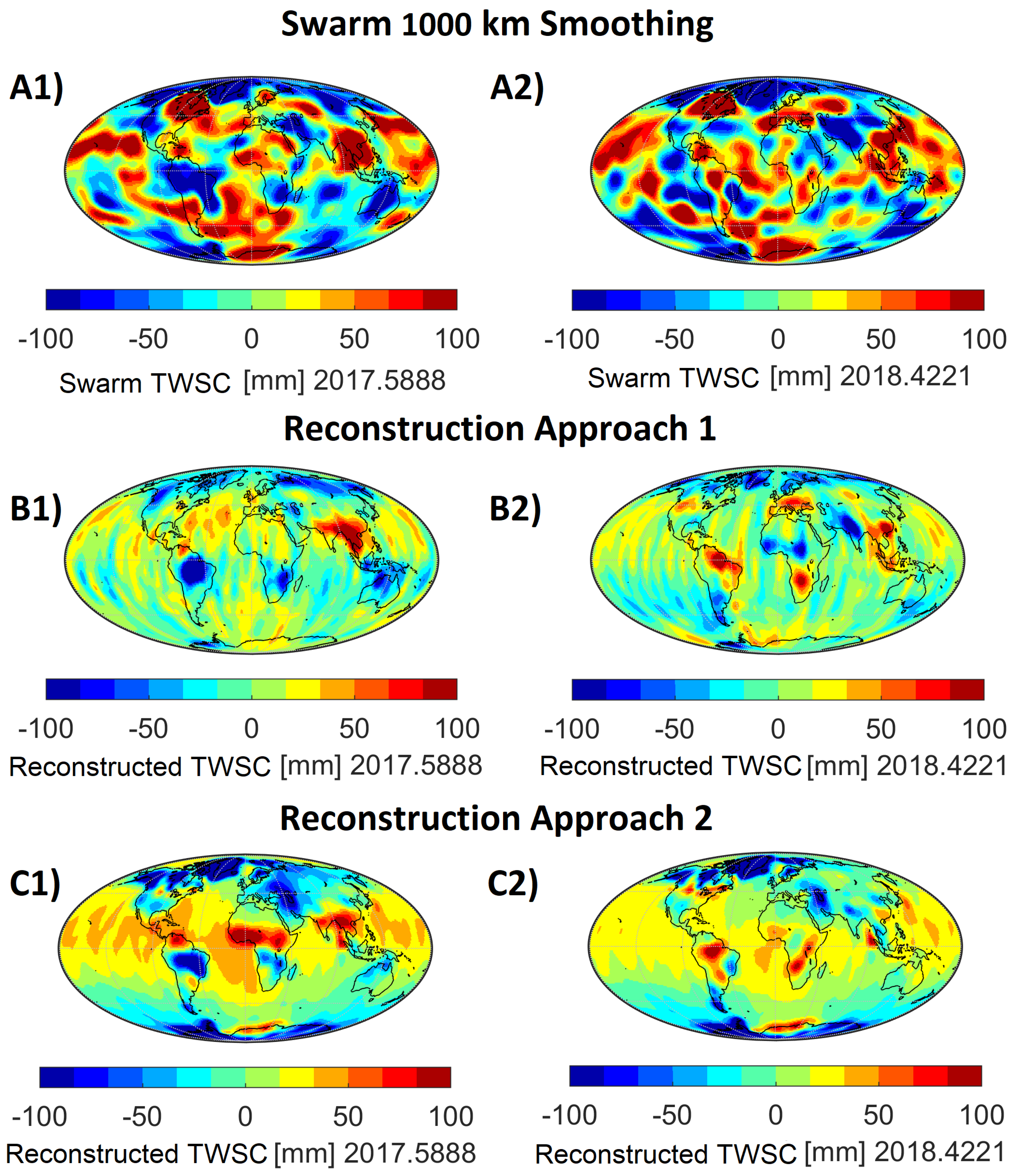
3.2. Data Reconstruction—Approach 1
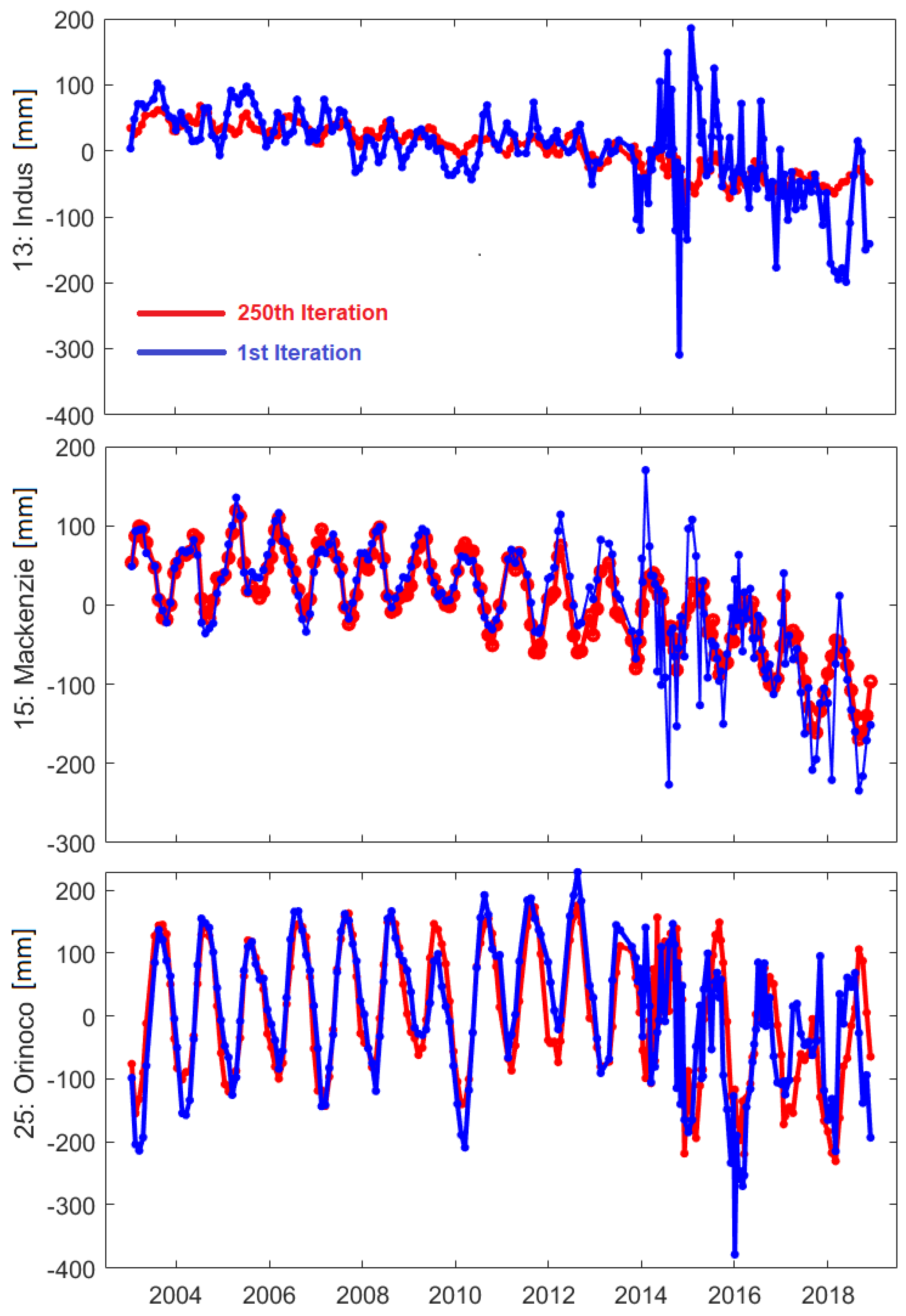
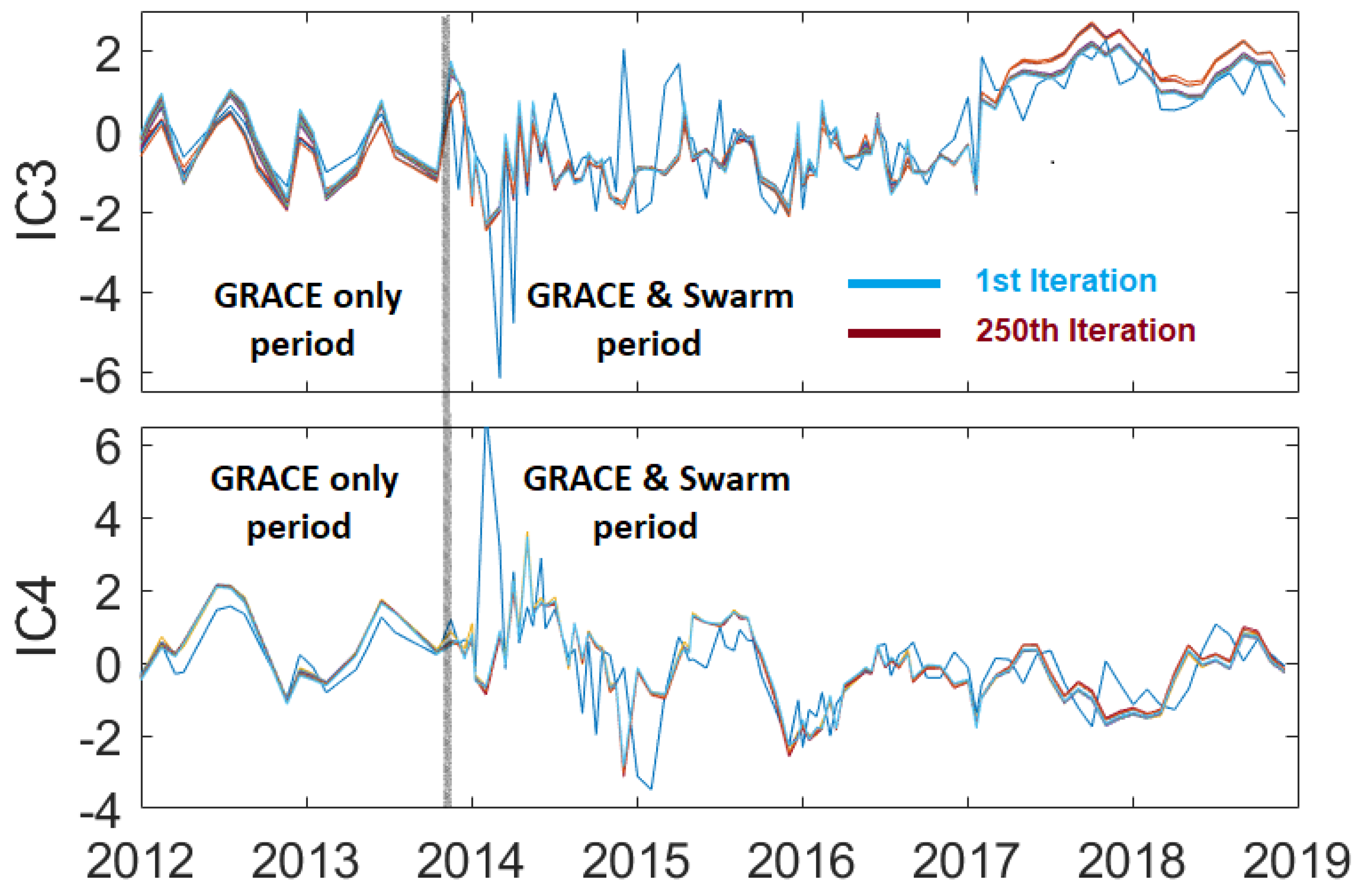
3.3. Iterative Reconstruction—Approach 2
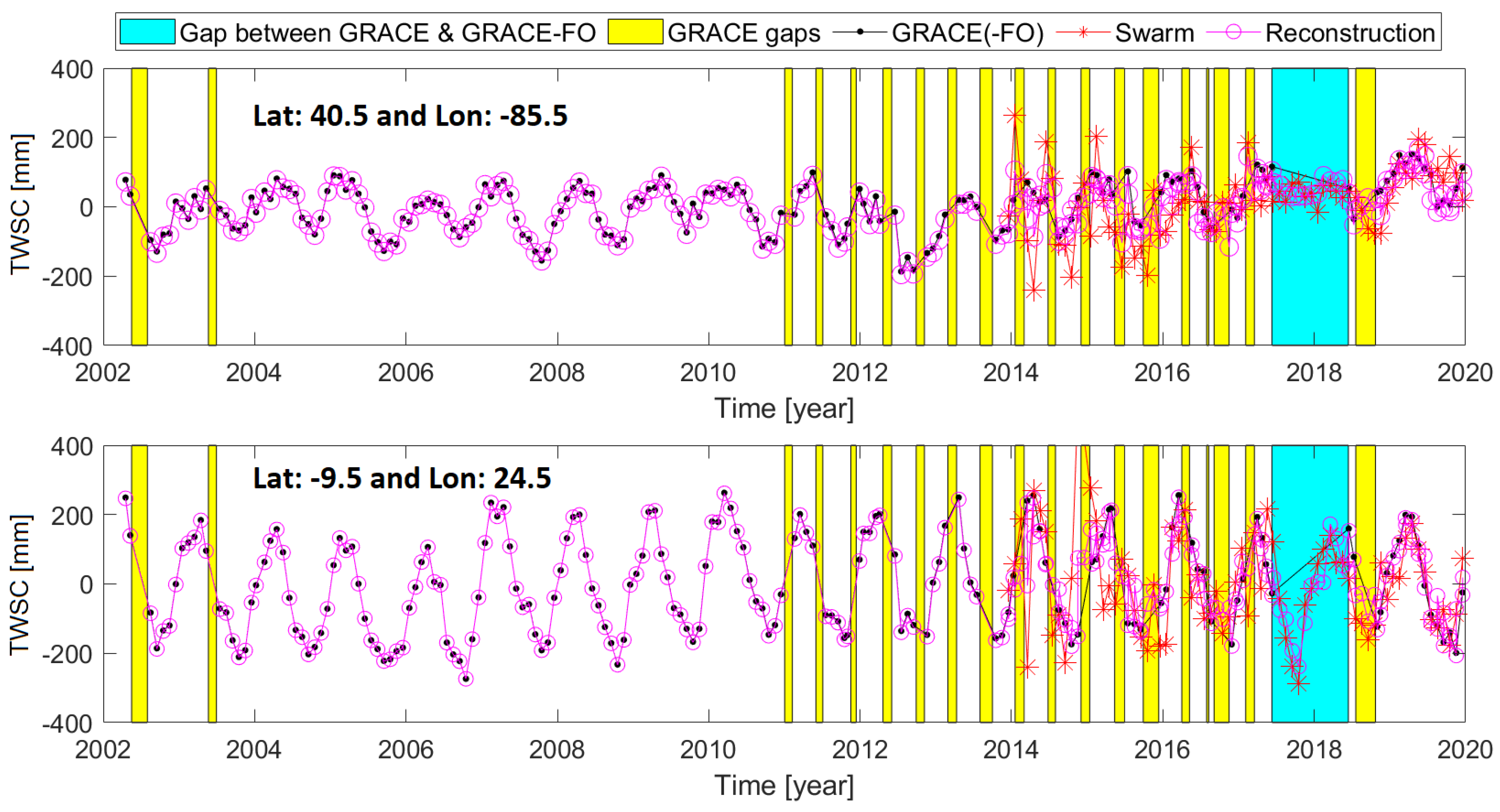
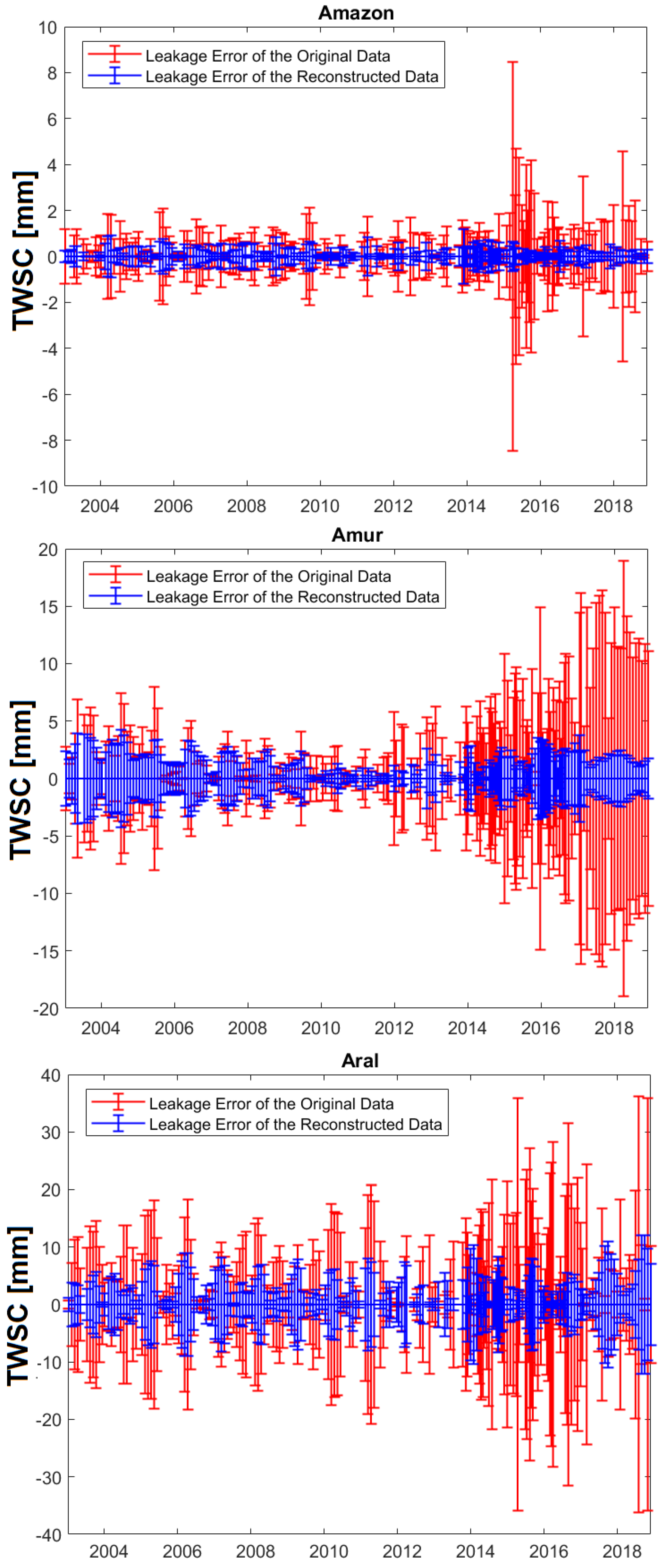
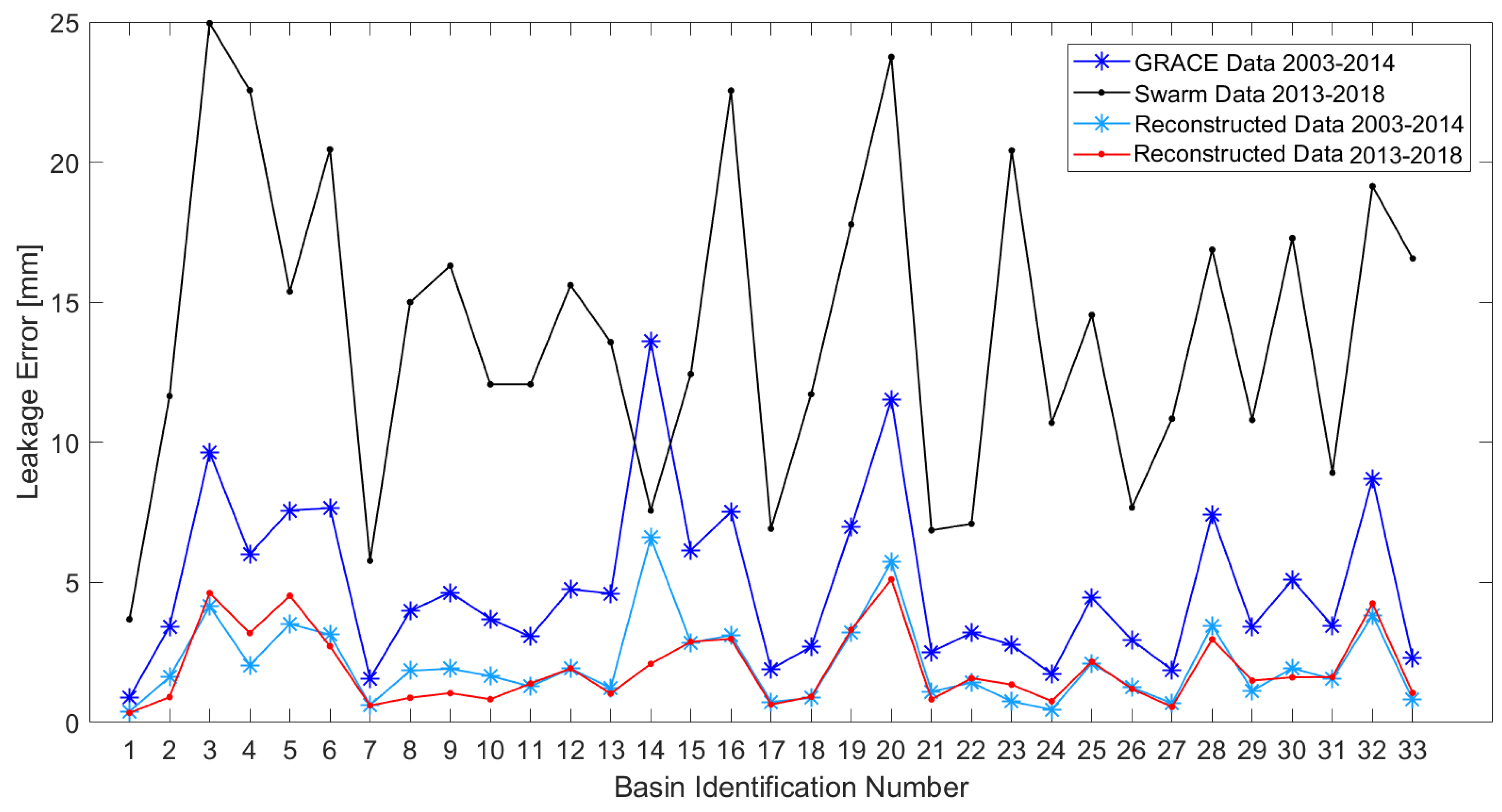
3.4. Estimation of Reconstructions Errors
4. Results
4.1. Evaluating the Reconstruction Results of Approach 1 and 2
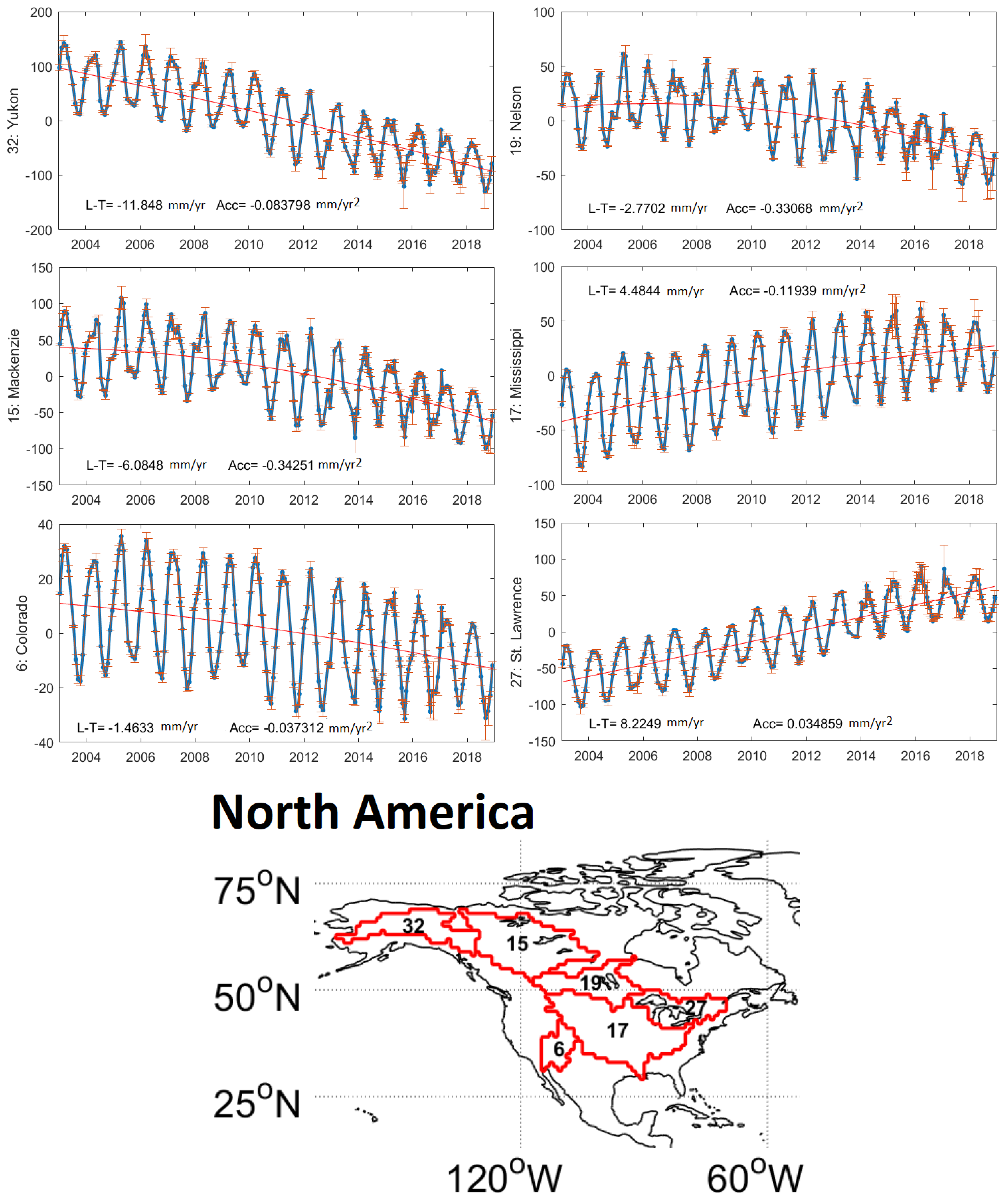
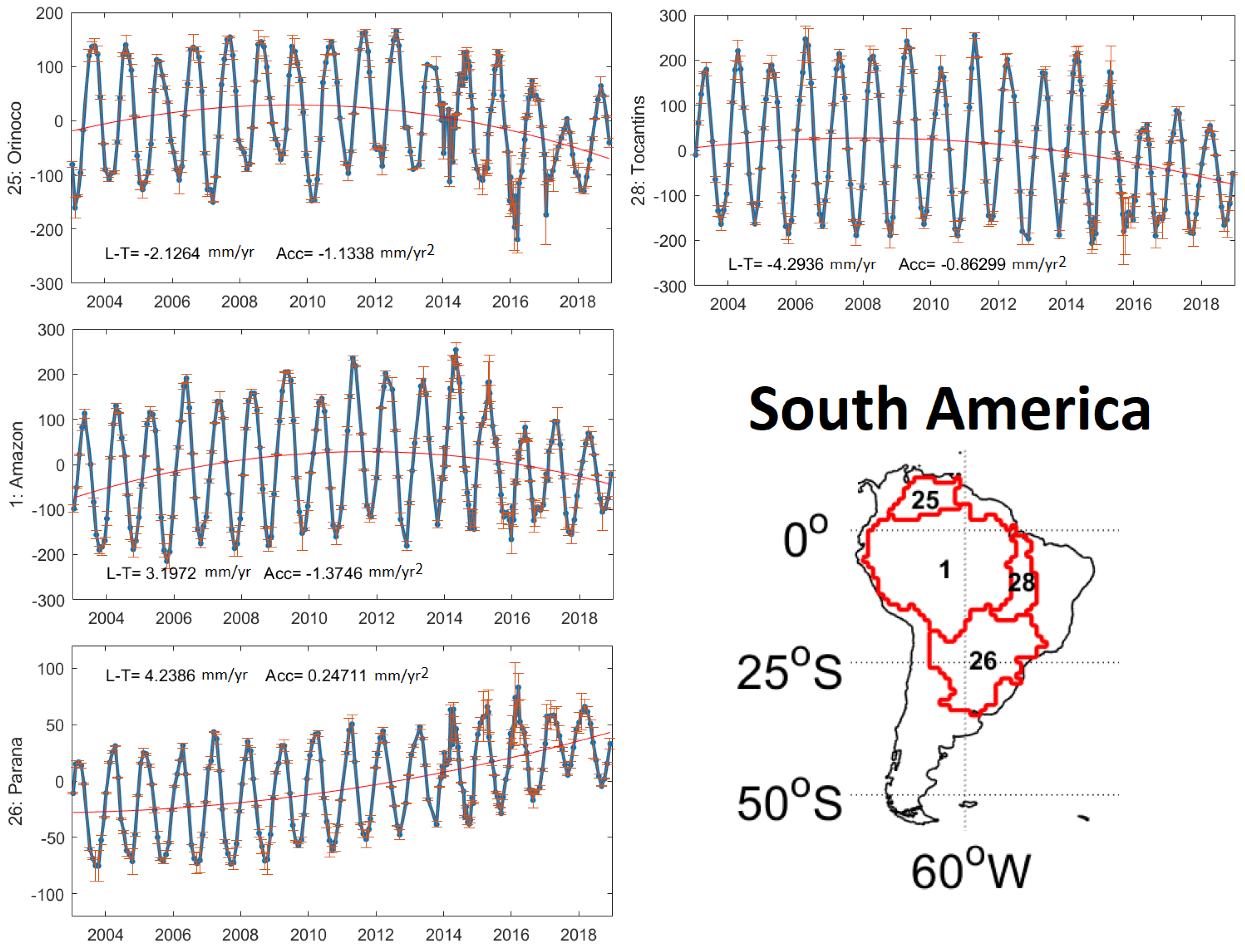
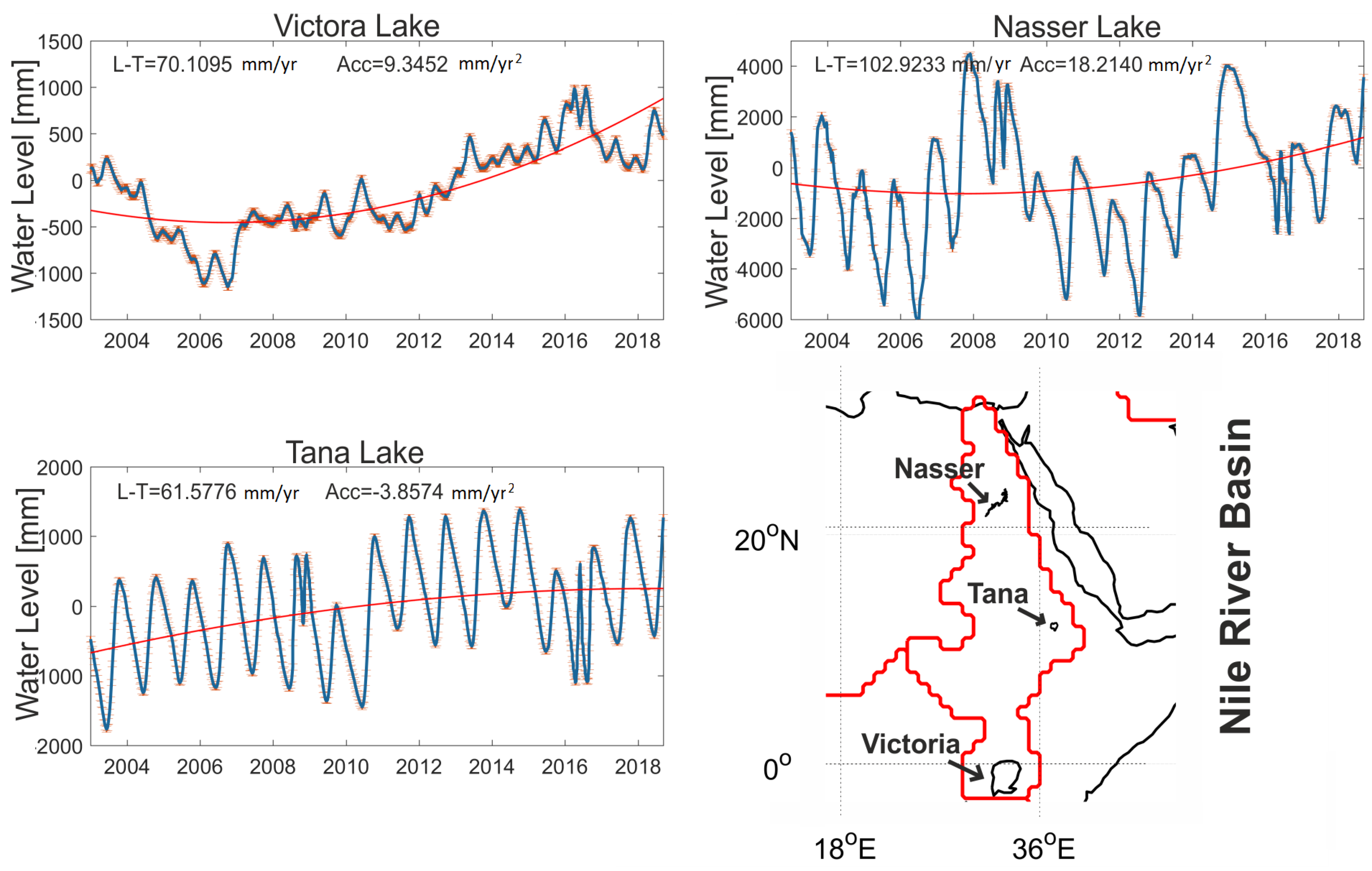
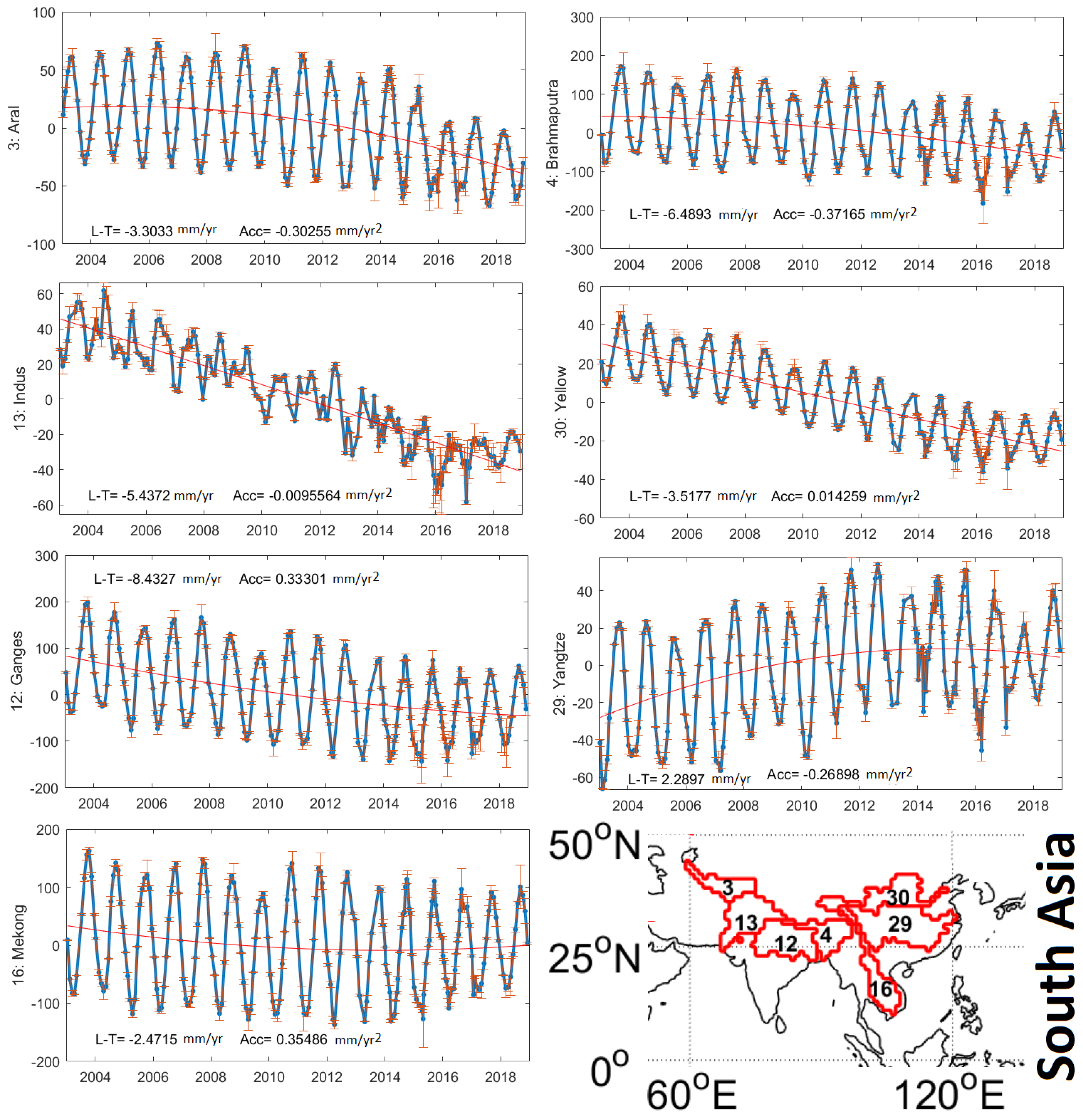
4.2. Mass Changes over 2003–2018 within the World’s 33 Largest River Basins
5. Summary and Conclusions
- positive linear temporary trends in the St. Lawrence and Mississippi River Basins, caused by changes in surface water compartment and confirmed by altimetry measurements as an independent comparison;
- negative linear temporary trends in TWSC of the Yukon, Nelson, Mackenzie, and Colorado River Basin, which can be associated to both irrigation and global warming;
- a considerable decrease in the magnitude of the seasonal cycle within the four investigated basins in South America (Amazon, Orinoco, Tocantins, and Parana) that is attributed to the drought events of 2016–2018;
- a mixed positive and negative temporary trends in the basins within Africa, where that of Nile was dominated by the surface water in lakes such as Victoria, but that of Niger was associated to groundwater; and those of Congo, Okavango, Orange, and Zambezi were influenced by an increase in the rainfall;
- the impact of anthropogenic impacts on Euphrates, Ganges, Indus, and Brahmaputra, Murray (negative trend) as well as Amur (positive trend).
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Impact of Iterations in Approach 2 on Independent Components
Appendix B. Noise and Leakage Estimation of the Reconstructed TWSC Fields

References
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Elsaka, B.; Forootan, E.; Alothman, A. Improving the recovery of monthly regional water storage using one year simulated observations of two pairs of GRACE-type satellite gravimetry constellation. J. Appl. Geophys. 2014, 109, 195–209. [Google Scholar] [CrossRef]
- Flechtner, F. GFZ Level-2 Processing Standards Document for Level-2 Product Release 0004. 2007. Available online: http://icgem.gfz-potsdam.de/L2-GFZ_ProcStds_0005_v1.1-1.pdf (accessed on 20 May 2020).
- Shum, C.K.; Guo, J.Y.; Hossain, F.; Duan, J.; Alsdorf, D.E.; Duan, X.J.; Kuo, C.Y.; Lee, H.; Schmidt, M.; Wang, L. Inter-annual water storage changes in Asia from GRACE data. In Climate Change and Food Security in South Asia; Springer: Amsterdam, The Netherlands, 2010; pp. 69–83. [Google Scholar] [CrossRef]
- Forootan, E.; Rietbroek, R.; Kusche, J.; Sharifi, M.A.; Awange, J.L.; Schmidt, M.; Omondi, P.; Famiglietti, J.S. Separation of large scale water storage patterns over Iran using GRACE, altimetry and hydrological data. Remote. Sens. Environ. 2014, 140, 580–595. [Google Scholar] [CrossRef]
- Forootan, E.; Safari, A.; Mostafaie, A.; Schumacher, M.; Delavar, M.; Awange, J.L. Large-scale total water storage and water flux changes over the arid and semiarid parts of the Middle East from GRACE and reanalysis products. Surv. Geophys. 2017, 38, 591–615. [Google Scholar] [CrossRef]
- Awange, J.L.; Forootan, E.; Kuhn, M.; Kusche, J.; Heck, B. Water storage changes and climate variability within the Nile Basin between 2002 and 2011. Adv. Water Resour. 2014, 73, 1–15. [Google Scholar] [CrossRef]
- Ahmed, M.; Sultan, M.; Wahr, J.; Yan, E. The use of GRACE data to monitor natural and anthropogenic induced variations in water availability across Africa. Earth Sci. Rev. 2014, 136, 289–300. [Google Scholar] [CrossRef]
- Forootan, E.; Awange, J.L.; Kusche, J.; Heck, B.; Eicker, A. Independent patterns of water mass anomalies over Australia from satellite data and models. Remote. Sens. Environ. 2012, 124, 427–443. [Google Scholar] [CrossRef]
- Andrew, R.L.; Guan, H.; Batelaan, O. Large-scale vegetation responses to terrestrial moisture storage changes. Hydrol. Earth Syst. Sci. 2017, 21, 4469–4478. [Google Scholar] [CrossRef]
- Tangdamrongsub, N.; Han, S.C.; Tian, S.; Müller Schmied, H.; Sutanudjaja, E.H.; Ran, J.; Feng, W. Evaluation of groundwater storage variations estimated from GRACE data assimilation and state-of-the-art land surface models in Australia and the North China Plain. Remote. Sens. 2018, 10, 483. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Rodell, M.; Chen, J.; Wilson, C.R. Analysis of terrestrial water storage changes from GRACE and GLDAS. Water Resour. Res. 2008, 44, W02433. [Google Scholar] [CrossRef]
- Forootan, E.; Kusche, J. Separation of global time-variable gravity signals into maximally independent components. J. Geod. 2012, 86, 477–497. [Google Scholar] [CrossRef]
- Kusche, J.; Eicker, A.; Forootan, E.; Springer, A.; Longuevergne, L. Mapping probabilities of extreme continental water storage changes from space gravimetry. Geophys. Res. Lett. 2016, 43, 8026–8034. [Google Scholar] [CrossRef]
- Long, D.; Pan, Y.; Zhou, J.; Chen, Y.; Hou, X.; Hong, Y.; Scanlon, B.R.; Longuevergne, L. Global analysis of spatiotemporal variability in merged total water storage changes using multiple GRACE products and global hydrological models. Remote. Sens. Environ. 2017, 192, 198–216. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Sun, A.Y.; Schmied, H.M.; Van Beek, L.P.; Wiese, D.N.; Wada, Y.; Long, D.; Reedy, R.C.; et al. Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data. Proc. Natl. Acad. Sci. USA 2018, 115, E1080–E1089. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef]
- Flechtner, F.; Neumayer, K.H.; Dahle, C.; Dobslaw, H.; Fagiolini, E.; Raimondo, J.C.; Güntner, A. What can be expected from the GRACE-FO laser ranging interferometer for Earth science applications? Surv. Geophys. 2016, 33, 453–470. [Google Scholar] [CrossRef]
- Rietbroek, R.; Fritsche, M.; Dahle, C.; Brunnabend, S.E.; Behnisch, M.; Kusche, J.; Flechtner, F.; Schröter, J.; Dietrich, R. Can GPS-derived surface loading bridge a GRACE mission gap? Surv. Geophys. 2014, 35, 1267–1283. [Google Scholar] [CrossRef]
- Cecilia Peralta, F.; James H., M.; Wallace, J.M. Proxy representation of Arctic ocean bottom pressure variability: Bridging gaps in GRACE observations. Geophys. Res. Lett. 2016, 43, 9183–9199. [Google Scholar] [CrossRef]
- Lück, C.; Kusche, J.; Rietbroek, R.; Löcher, A. Time-variable gravity fields and ocean mass change from 37 months of kinematic Swarm orbits. Solid Earth 2018, 9, 323–339. [Google Scholar] [CrossRef]
- Cheng, M.K.; Shum, C.K.; Tapley, B.D. Determination of long-term changes in the Earth’s gravity field from satellite laser ranging observations. J. Geophys. Res. Solid Earth 1997, 102, 22377–22390. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D. Seasonal variations in low degree zonal harmonics of the Earth’s gravity field from satellite laser ranging observations. J. Geophys. Res. Solid Earth 1999, 104, 2667–2681. [Google Scholar] [CrossRef]
- Cox, C.M.; Chao, B.F. Detection of a large-scale mass redistribution in the terrestrial system since 1998. Science 2002, 297, 831–833. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.; Tapley, B.D. Variations in the Earth’s oblateness during the past 28 years. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Sośnica, K.; Jäggi, A.; Meyer, U.; Thaller, D.; Beutler, G.; Arnold, D.; Dach, R. Time variable Earth’s gravity field from SLR satellites. J. Geod. 2015, 89, 945–960. [Google Scholar] [CrossRef]
- Talpe, M.J.; Nerem, R.S.; Forootan, E.; Schmidt, M.; Lemoine, F.G.; Enderlin, E.M.; Landerer, F.W. Ice mass change in Greenland and Antarctica between 1993 and 2013 from satellite gravity measurements. J. Geod. 2017, 91, 1283–1298. [Google Scholar] [CrossRef]
- Haberkorn, C.; Bloßfeld, M.; Bouman, J.; Fuchs, M.; Schmidt, M. Towards a consistent estimation of the earth’s gravity field by combining normal equation matrices from GRACE and SLR. In IAG 150 Years; Springer: Berlin, Germany, 2015; pp. 375–381. [Google Scholar] [CrossRef]
- Friis Christensen, E.; Lühr, H.; Knudsen, D.; Haagmans, R. Swarm–an Earth observation mission investigating geospace. Adv. Space Res. 2008, 41, 210–216. [Google Scholar] [CrossRef]
- Jäggi, A.; Dahle, C.; Arnold, D.; Bock, H.; Meyer, U.; Beutler, G.; Van den IJssel, J. Swarm kinematic orbits and gravity fields from 18 months of GPS data. Adv. Space Res. 2016, 57, 218–233. [Google Scholar] [CrossRef]
- Bezděk, A.; Sebera, J.; Teixeira da Encarnação, J.; Klokočník, J. Time-variable gravity fields derived from GPS tracking of Swarm. Geophys. J. Int. 2016, 205, 1665–1669. [Google Scholar] [CrossRef]
- Meyer, U.; Sosnica, K.; Arnold, D.; Dahle, C.; Thaller, D.; Dach, R.; Jäggi, A. SLR, GRACE and SWARM gravity field determination and combination. Remote. Sens. 2019, 11, 956. [Google Scholar] [CrossRef]
- Dahle, C.; Flechtner, F.; Murböck, M.; Michalak, G.; Neumayer, K.; Abrykosov, O.; Reinhold, A.; König, R. GRACE 327-743 (Gravity Recovery and Climate Experiment): GFZ Level-2 Processing Standards Document for Level-2 Product Release 06 (Rev. 1.0, October 26, 2018); Scientific Technical Report STR—Data; 18/04; GFZ German Research Centre for Geosciences: Potsdam, Germany, 2018; p. 20. [Google Scholar] [CrossRef]
- Jekeli, C. Alternative Methods to Smooth the Earth’s Gravity Field; Reports of the Department of Geodetic Science; 327; The Ohio State University: Columbus, OH, USA, 1981. [Google Scholar]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Kusche, J. Approximate decorrelation and non-isotropic smoothing of time-variable GRACE-type gravity field models. J. Geod. 2007, 81, 733–749. [Google Scholar] [CrossRef]
- Kusche, J.; Schmidt, R.; Petrovic, S.; Rietbroek, R. Decorrelated GRACE time-variable gravity solutions by GFZ, and their validation using a hydrological model. J. Geod. 2009, 83, 903–913. [Google Scholar] [CrossRef]
- Khaki, M.; Forootan, E.; Kuhn, M.; Awange, J.L.; Longuevergne, L.; Wada, Y. Efficient basin scale filtering of GRACE satellite products. Remote. Sens. Environ. 2018, 204, 76–93. [Google Scholar] [CrossRef]
- Da Encarnação, J.T.; Arnold, D.; Bezděk, A.; Dahle, C.; Doornbos, E.; Van den IJssel, J.; Jäggi, A.; Mayer-Gürr, T.; Sebera, J.; Visser, P.; et al. Gravity field models derived from Swarm GPS data. Earth Planets Space 2016, 68, 127. [Google Scholar] [CrossRef]
- Longuevergne, L.; Wilson, C.; Scanlon, B.; Cretaux, J. GRACE water storage estimates for the Middle East and other regions with significant reservoir and lake storage. Hydrol. Earth Syst. Sci. Discuss. 2013, 17, 4817–4830. [Google Scholar] [CrossRef]
- Li, F.; Kusche, J.; Rietbroek, R.; Wang, Z.; Forootan, E.; Schulze, K.; Lück, C. Comparison of data-driven techniques to reconstruct (1992–2002) and predict (2017–2018) GRACE-like gridded total water storage changes using climate inputs. Water Resour. Res. 2020, 56, e2019WR026551. [Google Scholar] [CrossRef]
- Preisendorfer, R.W.; Mobley, C.D.; Barnett, T.P. The principal discriminant method of prediction: Theory and evaluation. J. Geophys. Res. Atmos. 1988, 931, 10815–10830. [Google Scholar] [CrossRef]
- Forootan, E.; Kusche, J. Separation of deterministic signals using Independent Component Analysis (ICA). Stud. Geophys. Geod. 2013, 57, 17–26. [Google Scholar] [CrossRef]
- Forootan, E.; Kusche, J.; Talpe, M.; Shum, C.K.; Schmidt, M. Developing a Complex Independent Component Analysis (CICA) technique to extract non-stationary patterns from geophysical time series. Surv. Geophys. 2018, 39, 435–465. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G.; Maisongrande, P.; Bonnet, M.P. Denoising satellite gravity signals by independent component analysis. IEEE Geosci. Remote. Sens. Lett. 2011, 7, 421–425. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G.; Leblanc, M.; Tweed, S.O.; Bonnet, M.P.; Maisongrande, P. An independent component analysis filtering approach for estimating continental hydrology in the GRACE gravity data. Remote. Sens. Environ. 2011, 115, 187–204. [Google Scholar] [CrossRef]
- Forootan, E. Statistical Signal Decomposition Ttechniques for Analyzing Time-Variable Satellite Gravimetry Data. Ph.D. Thesis, University of Bonn, Bonn, Germany, 2014. [Google Scholar]
- Church, J.A.; White, N.J.; Coleman, R.; Lambeck, K.; Mitrovica, J.X. Estimates of the regional distribution of sea level rise over the 1950–2000 period. J. Clim. 2004, 17, 2609–2625. [Google Scholar] [CrossRef]
- Güntner, A.; Stuck, J.; Werth, S.; Döll, P.; Verzano, K.; Merz, B. A global analysis of temporal and spatial variations in continental water storage. Water Resour. Res. 2007, 43, W05416. [Google Scholar] [CrossRef]
- Mehrnegar, N.; Jones, O.; Singer, M.B.; Schumacher, M.; Bates, P.; Forootan, E. Comparing global hydrological models and combining them with GRACE by dynamic model data averaging (DMDA). Adv. Water Resour. 2020, 138, 103528. [Google Scholar] [CrossRef]
- Chambers, D.P.; Willis, J.K. A global evaluation of ocean bottom pressure from GRACE, OMCT, and steric-corrected altimetry. J. Atmos. Ocean. Technol. 2010, 27, 1395–1402. [Google Scholar] [CrossRef]
- Macrander, A.; Boening, C.; Boebel, O.; Schroeter, J. Validation of GRACE Gravity Fields by In-Situ Data of Ocean Bottom Pressure. In System Earth via Geodetic-Geophysical Space Techniques. Advanced Technologies in Earth Sciences (2190-1643); Flechtner, F., Ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Chen, Q.; Poropat, L.; Zhang, L.; Dobslaw, H.; Weigelt, M.; Van Dam, T. Validation of the EGSIEM GRACE gravity fields using GNSS coordinate timeseries and in-situ ocean bottom pressure records. Remote Sens. 2018, 10, 1976. [Google Scholar] [CrossRef]
- Moore, P.; Williams, S.D.P. Integration of altimetric lake levels and GRACE gravimetry over Africa: Inferences for terrestrial water storage change 2003–2011. Water Resour. Res. 2014, 50, 9696–9720. [Google Scholar] [CrossRef]
- Awange, J.L.; Forootan, E.; Fleming, K.; Odhiambo, G. Dominant patterns of water storage changes in the Nile Basin during 2003–2013. Remote. Sens. Terr. Water Cycle 2014, 206, 367. [Google Scholar] [CrossRef]
- Eicker, A.; Forootan, E.; Springer, A.; Longuevergne, L.; Kusche, J. Does GRACE see the terrestrial water cycle “intensifying”? J. Geophys. Res. Atmos. 2016, 121, 733–745. [Google Scholar] [CrossRef]
- Bettadpur, S. Gravity Recovery and Climate Experiment Level-2 Gravity Field Product User Handbook. Center for Space Research at The University of Texas at Austin, 2018. Available online: https://podaac-tools.jpl.nasa.gov/drive/files/allData/grace/docs/L2-UserHandbook_v4.0.pdf (accessed on 20 May 2020).
- Visser, P.; Doornbos, E.; Van den IJssel, J.; Da Encarnação, J.T. Thermospheric density and wind retrieval from Swarm observations. Earth Planets Space 2013, 65, 12. [Google Scholar] [CrossRef]
- Olsen, N.; Friis-Christensen, E.; Floberghagen, R.; Alken, P.; Beggan, C.D.; Chulliat, A.; Doornbos, E.; Da Encarnação, J.T.; Hamilton, B.; Hulot, G.; et al. The Swarm satellite constellation application and research facility (SCARF) and Swarm data products. Earth Planets Space 2013, 65, 1189–1200. [Google Scholar] [CrossRef]
- Zehentner, N.; Mayer-Gürr, T. Precise orbit determination based on raw GPS measurements. J. Geod. 2016, 90, 275–286. [Google Scholar] [CrossRef]
- Guo, J.; Shang, K.; Jekeli, C.; Shum, C. On the energy integral formulation of gravitational potential differences from satellite-to-satellite tracking. Celest. Mech. Dyn. Astron. 2015, 121, 415–429. [Google Scholar] [CrossRef]
- Bezděk, A.; Sebera, J.; Klokočník, J.; Kosteleckỳ, J. Gravity field models from kinematic orbits of CHAMP, GRACE and GOCE satellites. Adv. Space Res. 2014, 53, 412–429. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. Solid Earth 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Wahr, J.; Zhong, S. Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: An application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 108, 30205–30229. [Google Scholar] [CrossRef]
- Anyah, R.; Forootan, E.; Awange, J.; Khaki, M. Influence of global climate indices and teleconnections on regional total water storage: Exploring GRACE-TWS data over sub-Saharan Africa. Sci. Total. Environ. 2018, 635, 1405–1416. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Rotation of principal components: Choice of normalization constraints. J. Appl. Stat. 1995, 22, 29–35. [Google Scholar] [CrossRef]
- Comon, P. Independent component analysis, A new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Cardoso, J.F. High-order contrasts for independent component analysis. Neural Comput. 1999, 11, 157–192. [Google Scholar] [CrossRef] [PubMed]
- Hyvärinen, A. Survey on independent component analysis. Neural Comput. Surv. 1999, 2, 94–128. [Google Scholar]
- Cardoso, J.F.; Souloumiac, A. Jacobi angles for simultaneous diagonalization. SIAM. J. Math. Anal. Appl. 1995, 17, 161–164. [Google Scholar] [CrossRef]
- Ilin, A.; Kaplan, A. Bayesian PCA for reconstruction of historical sea surface temperatures. In Proceedings of the 2009 International Joint Conference on Neural Networks, Atlanta, GA, USA, 30 October 2009; pp. 1322–1327. [Google Scholar] [CrossRef]
- Westra, S.; Brown, C.; Lall, U.; Koch, I.; Sharma, A. Interpreting variability in global SST data using independent component analysis and principal component analysis. Int. J. Climatol. 2010, 30, 333–346. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J. Sea-level rise from the late 19th to the early 21st century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- Huang, W.; Wang, R.; Zhou, Y.; Chen, Y.; Yang, R. Improved principal component analysis for 3D seismic data simultaneous reconstruction and denoising. In SEG Technical Program Expanded Abstracts 2016; Society of Exploration Geophysicists (SEG): Tulsa, OK, USA, 2016; pp. 4102–4106. [Google Scholar] [CrossRef]
- Boyd, J.D.; Kennelly, E.P.; Pistek, P. Estimation of EOF expansion coefficients from incomplete data. Deep. Sea Res. Part Oceanogr. Res. Pap. 1994, 41, 1479–1488. [Google Scholar] [CrossRef]
- Humphrey, V.; Gudmundsson, L.; Seneviratne, S.I. Assessing global water storage variability from GRACE: Trends, seasonal cycle, subseasonal anomalies and extremes. Surv. Geophys. 2016, 37, 357–395. [Google Scholar] [CrossRef]
- Llovel, W.; Becker, M.; Cazenave, A.; Jevrejeva, S.; Alkama, R.; Decharme, B.; Douville, H.; Ablain, M.; Beckley, B. Terrestrial waters and sea level variations on interannual time scale. Glob. Planet. Chang. 2011, 75, 76–82. [Google Scholar] [CrossRef]
- Forootan, E.; Didova, O.; Schumacher, M.; Kusche, J.; Elsaka, B. Comparisons of atmospheric mass variations derived from ECMWF reanalysis and operational fields, over 2003–2011. J. Geod. 2014, 88, 503–514. [Google Scholar] [CrossRef]
- Gao, F.; Feng, G.; Han, M.; Dash, P.; Jenkins, J.; Liu, C. Assessment of Surface Water Resources in the Big Sunflower River Watershed Using Coupled SWAT–MODFLOW Model. Water 2019, 11, 528. [Google Scholar] [CrossRef]
- Cohen, S. Impacts of global warming in an Arctic watershed. Can. Water Resour. J. 1992, 17, 55–62. [Google Scholar] [CrossRef]
- Yang, D.; Shi, X.; Marsh, P. Variability and extreme of Mackenzie River daily discharge during 1973–2011. Quat. Int. 2015, 380, 159–168. [Google Scholar] [CrossRef]
- Suzuki, K.; Matsuo, K.; Yamazaki, D.; Ichii, K.; Iijima, Y.; Papa, F.; Yanagi, Y.; Hiyama, T. Hydrological variability and changes in the Arctic circumpolar tundra and the three largest pan-Arctic river basins from 2002 to 2016. Remote. Sens. 2018, 10, 402. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Reedy, R.C.; Poor, D.R.; Save, H.; Long, D.; Chen, J.; Wolock, D.M.; Conway, B.D.; Winester, D. Hydrologic implications of GRACE satellite data in the Colorado River Basin. Adv. Earth Space Sci. 2015, 51, 9891–9903. [Google Scholar] [CrossRef]
- Erfanian, A.; Wang, G.; Fomenko, L. Unprecedented drought over tropical South America in 2016: Significantly under-predicted by tropical SST. Sci. Rep. 2017, 7, 5811. [Google Scholar] [CrossRef]
- Forootan, E.; Khaki, M.; Schumacher, M.; Wulfmeyer, V.; Mehrnegar, N.; Dijk, A.I.J.M.V.; Brocca, L.; Farzaneh, S.; Akinluyi, F.; Ramillien, G.; et al. Understanding the global hydrological droughts of 2003–2016 and their relationships with teleconnections. Sci. Total. Environ. 2019, 650, 2587–2604. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Mattar, C.; Barichivich, J.; Santamaría-Artigas, A.; Takahashi, K.; Malhi, Y.; Sobrino, J.A.; Van Der Schrier, G. Record-breaking warming and extreme drought in the Amazon rainforest during the course of El Niño 2015–2016. Sci. Rep. 2016, 6, 33130. [Google Scholar] [CrossRef]
- Chen, Y. Overview of the 2016 Fire Season Severity Prediction. Available online: http://www.ess.uci.edu/~amazonfirerisk/ForecastWeb/SAMFSS2016.html (accessed on 23 March 2020).
- Lee, E.; Livino, A.; Han, S.C.; Zhang, K.; Briscoe, J.; Kelman, J.; Moorcroft, P. Land cover change explains the increasing discharge of the Paraná River. Reg. Environ. Chang. 2018, 18, 1871–1881. [Google Scholar] [CrossRef]
- Fleischmann, A.; Fan, F.; Collischonn, B.; Collischonn, W.; Pontes, P.; Ruhoff, A. Precipitation as a proxy for climate variables: Application for hydrological modelling. Hydrol. Sci. J. 2019, 64, 361–379. [Google Scholar] [CrossRef]
- Mahé, G.; Lienou, G.; Descroix, L.; Bamba, F.; Paturel, J.E.; Laraque, A.; Meddi, M.; Habaieb, H.; Adeaga, O.; Dieulin, C.; et al. The rivers of Africa: Witness of climate change and human impact on the environment. Hydrol. Process. 2013, 27, 2105–2114. [Google Scholar] [CrossRef]
- Roudier, P.; Ducharne, A.; Feyen, L. Climate change impacts on runoff in West Africa: A review. Hydrol. Earth Syst. Sci. 2014, 18, 2789–2801. [Google Scholar] [CrossRef]
- Grijsen, J.; Tarhule, A.; Brown, C.; Ghile, Y.; Taner, Ü.; Talbi-Jordan, A.; Doffou, H.; Guero, A.; Dessouassi, R.; Kone, S.; et al. climate Risk Assessment for Water Resources Development in the Niger River Basin Part II: Runoff Elasticity and Probabilistic Analysis. In Climate Variability-Regional and Thematic Patterns; IntechOpen: London, UK, 2013; pp. 37–56. [Google Scholar] [CrossRef]
- Favreau, G.; Cappelaere, B.; Massuel, S.; Leblanc, M.; Boucher, M.; Boulain, N.; Leduc, C. Land clearing, climate variability, and water resources increase in semiarid southwest Niger: A review. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Ibrahim, M.; Favreau, G.; Scanlon, B.R.; Seidel, J.L.; Le Coz, M.; Demarty, J.; Cappelaere, B. Long-term increase in diffuse groundwater recharge following expansion of rainfed cultivation in the Sahel, West Africa. Hydrogeol. J. 2014, 22, 1293–1305. [Google Scholar] [CrossRef]
- Werth, S.; White, D.; Bliss, D.W. GRACE detected rise of groundwater in the Sahelian Niger River basin. J. Geophys. Res. Solid Earth 2017, 122. [Google Scholar] [CrossRef]
- McCarthy, T.S.; Bloem, A.; Larkin, P.A. Observations on the hydrology and geohydrology of the Okavango Delta. South Afr. J. Geol. Afr. Tydskr. Vir Geol. 1998, 101, 101–117. [Google Scholar]
- Kruger, A.C.; Nxumalo, M.P. Historical rainfall trends in South Africa: 1921–2015. Water SA 2017, 43, 285–297. [Google Scholar] [CrossRef]
- García-García, D.; Ummenhofer, C.C. Multidecadal variability of the continental precipitation annual amplitude driven by AMO and ENSO. Geophys. Res. Lett. 2015, 42, 526–535. [Google Scholar] [CrossRef]
- Voss, K.A.; Famiglietti, J.S.; Lo, M.; De Linage, C.; Rodell, M.; Swenson, S.C. Groundwater depletion in the Middle East from GRACE with implications for transboundary water management in the Tigris-Euphrates-Western Iran region. Water Resour. Res. 2013, 49, 904–914. [Google Scholar] [CrossRef]
- Sokolova, G.V.; Korolev, S.P. Impact of Deforestation on Streamflow in the Amur River Basin. Geosciences 2019, 9, 262. [Google Scholar] [CrossRef]
- Makarieva, O.; Nesterova, N.; Post, D.A.; Sherstyukov, A.; Lebedeva, L. Warming temperatures are impacting the hydrometeorological regime of Russian rivers in the zone of continuous permafrost. Cryosphere 2019, 13, 1635–1659. [Google Scholar] [CrossRef]
- Grigoriev, V.Y.; Frolova, N.L. Terrestrial water storage change of European Russia and its impact on water balance. Geogr. Environ. Sustain. 2018, 11, 38–50. [Google Scholar] [CrossRef]
- Khandu, K.; Forootan, E.; Schumacher, M.; Awange, J.L.; Müller-Schmied, H. Exploring the influence of precipitation extremes and human water use on total water storage (TWS) changes in the Ganges-Brahmaputra-Meghna River Basin. Water Resour. Res. 2016, 52, 2240–2258. [Google Scholar] [CrossRef]
- Zhu, Y.; Lin, Z.; Wang, J.; Zhao, Y.; He, F. Impacts of climate changes on water resources in Yellow River Basin, China. Procedia Eng. 2016, 154, 687–695. [Google Scholar] [CrossRef]
- Awange, J.L.; Kuhn, M.; Anyah, R.O.; Forootan, E. Changes and variability of precipitation and temperature in the Ganges–Brahmaputra–Meghna River Basin based on global high-resolution reanalyses. Int. J. Climatol. 2017, 37, 2141–2159. [Google Scholar] [CrossRef]
- Micklin, P. Irrigation in the Aral Sea Basin. In The Aral Sea; Springer: Berlin, Germany, 2014; Volume 10178, pp. 207–232. [Google Scholar] [CrossRef]
- Li, D.; Long, D.; Zhao, J.; Lu, H.; Hong, Y. Observed changes in flow regimes in the Mekong River basin. J. Hydrol. 2017, 551, 217–232. [Google Scholar] [CrossRef]
- Shibuo, Y.; Jarsjö, J.; Destouni, G. Hydrological responses to climate change and irrigation in the Aral Sea drainage basin. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Sun, Z.; Zhu, X.; Pan, Y.; Zhang, J. Assessing terrestrial water storage and flood potential using GRACE data in the Yangtze River Basin, China. Remote. Sens. 2017, 9, 1011. [Google Scholar] [CrossRef]
- Lakshmi, V.; Fayne, J.; Bolten, J. A comparative study of available water in the major river basins of the world. J. Hydrol. 2018, 567, 510–532. [Google Scholar] [CrossRef]
- Chen, Z.; Grasby, S.E.; Osadetz, K.G. Predicting average annual groundwater levels from climatic variables: An empirical model. J. Hydrol. 2002, 260, 102–117. [Google Scholar] [CrossRef]
- Awange, J.; Gebremichael, M.; Forootan, E.; Wakbulcho, G.; Anyah, R.; Ferreira, V.; Alemayehu, T. Characterization of Ethiopian mega hydrogeological regimes using GRACE, TRMM and GLDAS datasets. Adv. Water Resour. 2014, 74, 64–78. [Google Scholar] [CrossRef]
- Soni, A.; Syed, T.H. Diagnosing land water storage variations in major Indian river basins using GRACE observations. Glob. Planet. Chang. 2015, 133, 263–271. [Google Scholar] [CrossRef]
- Forootan, E.; Awange, J.L.; Schumacher, M.; Anyah, R.O.; Van Dijk, A.I.J.M.; Kusche, J. Quantifying the impacts of ENSO and IOD on rain gauge and remotely sensed precipitation products over Australia. Remote. Sens. Environ. 2016, 172, 50–66. [Google Scholar] [CrossRef]
- Schumacher, M.; Forootan, E.; Van Dijk, A.; Schmied, H.M.; Crosbie, R.; Kusche, J.; Döll, P. Improving drought simulations within the Murray-Darling Basin by combined calibration/assimilation of GRACE data into the WaterGAP Global Hydrology Model. Remote. Sens. Environ. 2018, 204, 212–228. [Google Scholar] [CrossRef]







| 2014.7082 | Ocean (mm) | Land (mm) | 2015.3192 | Ocean (mm) | Land (mm) |
|---|---|---|---|---|---|
| Approach 2 | 25.30 | 29.16 | Approach 2 | 32.50 | 38.66 |
| Approach 1 | 67.36 | 56.20 | Approach 1 | 48.75 | 58.88 |
| ID | Basin Name | Linear Trend [mm/yr] | Acceleration ID [mm/] | Basin Name | Linear Trend | Acceleration [mm/yr] | [mm/] |
|---|---|---|---|---|---|---|---|
| North America | South America | ||||||
| 32 | Yukon | −11.84 ± 0.16 | −0.08 ± 0.04 | 25 | Orinoco | −2.12 ± 0.18 | −1.13 ± 0.04 |
| 19 | Nelson | −2.77 ± 0.10 | −0.33 ± 0.02 | 28 | Tocantins | −4.29 ± 0.21 | −0.86 ± 0.05 |
| 15 | Mackenzie | −6.08 ± 0.13 | −0.34 ± 0.03 | 1 | Amazon | 3.19 ± 0.19 | −1.37 ± 0.04 |
| 17 | Mississippi | 4.48 ± 0.11 | −0.11 ± 0.02 | 26 | Parana | 4.23 ± 0.13 | 0.24 ± 0.03 |
| 6 | Colorado | −1.46 ± 0.09 | −0.03 ± 0.02 | ||||
| 27 | St. Lawrence | 8.22 ± 0.14 | 0.03 ± 0.02 | ||||
| Europe-West Asia-East Asia | South Asia | ||||||
| 8 | Danube | −0.30 ± 0.10 | −0.09 ± 0.02 | 3 | Aral | −0.30 ± 0.11 | −0.30 ± 0.02 |
| 5 | Caspian-Volga | −3.09 ± 0.12 | 0.054 ± 0.03 | 4 | Brahmaputra | −6.49 ± 0.16 | −0.37 ± 0.04 |
| 9 | Dnieper | −4.53 ± 0.12 | −0.15 ± 0.03 | 13 | Indus | −5.44 ± 0.09 | −0.01 ± 0.009 |
| 10 | Euphrates | −9.85 ± 0.14 | 0.04 ± 0.03 | 30 | Yellow | −3.51 ± 0.09 | 0.01 ± 0.009 |
| 22 | Ob | 1.60 ± 0.13 | −0.16 ± 0.03 | 12 | Ganges | −8.43 ± 0.17 | 0.33 ± 0.04 |
| 14 | Lena | −1.14 ± 0.10 | −0.37 ± 0.02 | 29 | Yangtze | 2.28 ± 0.10 | −0.26 ± 0.02 |
| 31 | Yenisei | 1.14 ± 0.10 | −0.27 ± 0.02 | 16 | Mekong | −2.47 ± 0.16 | 0.35 ± 0.03 |
| 2 | Amur | 1.87 ± 0.07 | −0.18 ± 0.01 | ||||
| Africa | Australia | ||||||
| 20 | Niger | 5.40 ± 0.13 | 0.30 ± 0.03 | 11 | Lake Eyre | −0.45 ± 0.11 | −0.21 ± 0.02 |
| 33 | Zambezi | 4.50 ± 0.17 | −0.36 ± 0.04 | 18 | Murray | 0.67 ± 0.09 | −0.26 ± 0.02 |
| 21 | Nile | 4.01 ± 0.11 | 0.27 ± 0.02 | ||||
| 7 | Congo | 3.97 ± 0.11 | 0.41 ± 0.02 | ||||
| 23 | Okavango | 7.67 ± 0.13 | −0.36 ± 0.03 | ||||
| 24 | Orange | 2.42 ± 0.08 | −0.16 ± 0.02 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forootan, E.; Schumacher, M.; Mehrnegar, N.; Bezděk, A.; Talpe, M.J.; Farzaneh, S.; Zhang, C.; Zhang, Y.; Shum, C.K. An Iterative ICA-Based Reconstruction Method to Produce Consistent Time-Variable Total Water Storage Fields Using GRACE and Swarm Satellite Data. Remote Sens. 2020, 12, 1639. https://doi.org/10.3390/rs12101639
Forootan E, Schumacher M, Mehrnegar N, Bezděk A, Talpe MJ, Farzaneh S, Zhang C, Zhang Y, Shum CK. An Iterative ICA-Based Reconstruction Method to Produce Consistent Time-Variable Total Water Storage Fields Using GRACE and Swarm Satellite Data. Remote Sensing. 2020; 12(10):1639. https://doi.org/10.3390/rs12101639
Chicago/Turabian StyleForootan, Ehsan, Maike Schumacher, Nooshin Mehrnegar, Aleš Bezděk, Matthieu J. Talpe, Saeed Farzaneh, Chaoyang Zhang, Yu Zhang, and C. K. Shum. 2020. "An Iterative ICA-Based Reconstruction Method to Produce Consistent Time-Variable Total Water Storage Fields Using GRACE and Swarm Satellite Data" Remote Sensing 12, no. 10: 1639. https://doi.org/10.3390/rs12101639
APA StyleForootan, E., Schumacher, M., Mehrnegar, N., Bezděk, A., Talpe, M. J., Farzaneh, S., Zhang, C., Zhang, Y., & Shum, C. K. (2020). An Iterative ICA-Based Reconstruction Method to Produce Consistent Time-Variable Total Water Storage Fields Using GRACE and Swarm Satellite Data. Remote Sensing, 12(10), 1639. https://doi.org/10.3390/rs12101639