Evaluation of Six High-Spatial Resolution Clear-Sky Surface Upward Longwave Radiation Estimation Methods with MODIS
Abstract
:1. Introduction
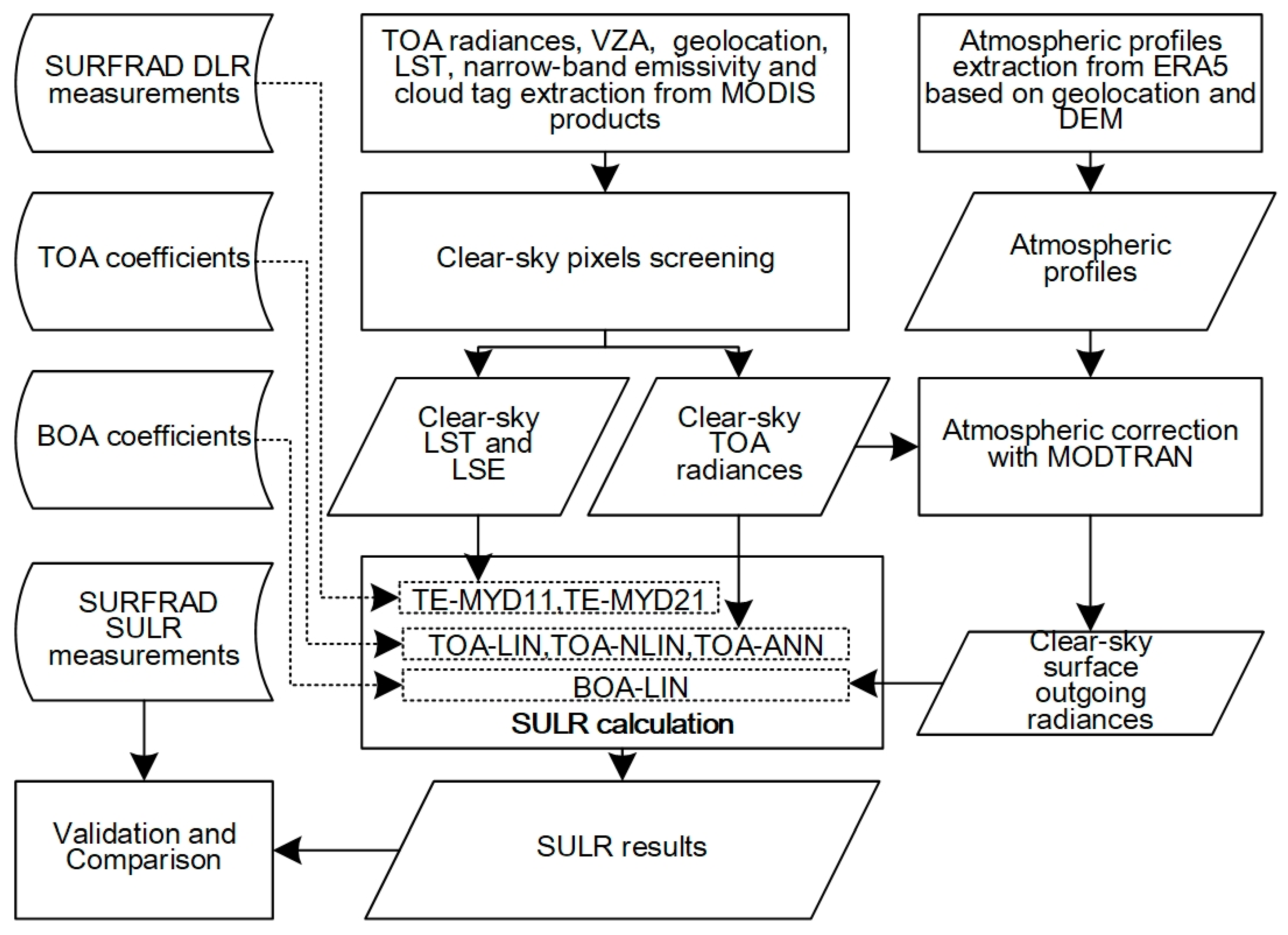
2. Data and Processing
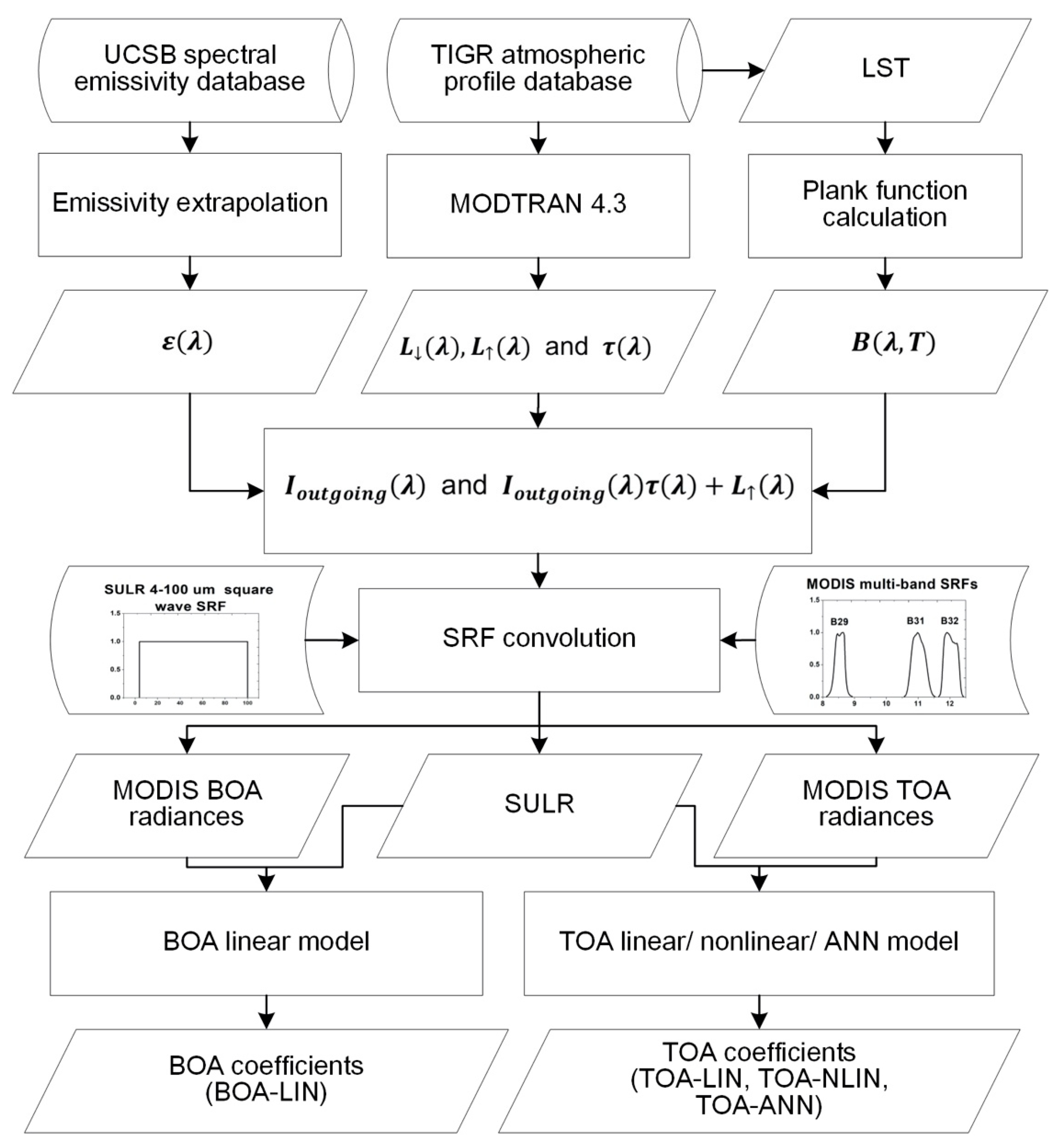
2.1. The Simulation Dataset for Hybrid Method
2.2. The Evaluation Datasets with MODIS, ERA5 and In Situ Measurements
2.2.1. MODIS Datasets
2.2.2. ERA5 Global Reanalysis Product
2.2.3. Ground Measurements
3. Method
3.1. Temperature-Emissivity Method
3.2. Hybrid Method
3.2.1. TOA-LIN
3.2.2. TOA-NLIN
3.2.3. TOA-ANN
3.2.4. BOA-LIN
4. Results and Discussion
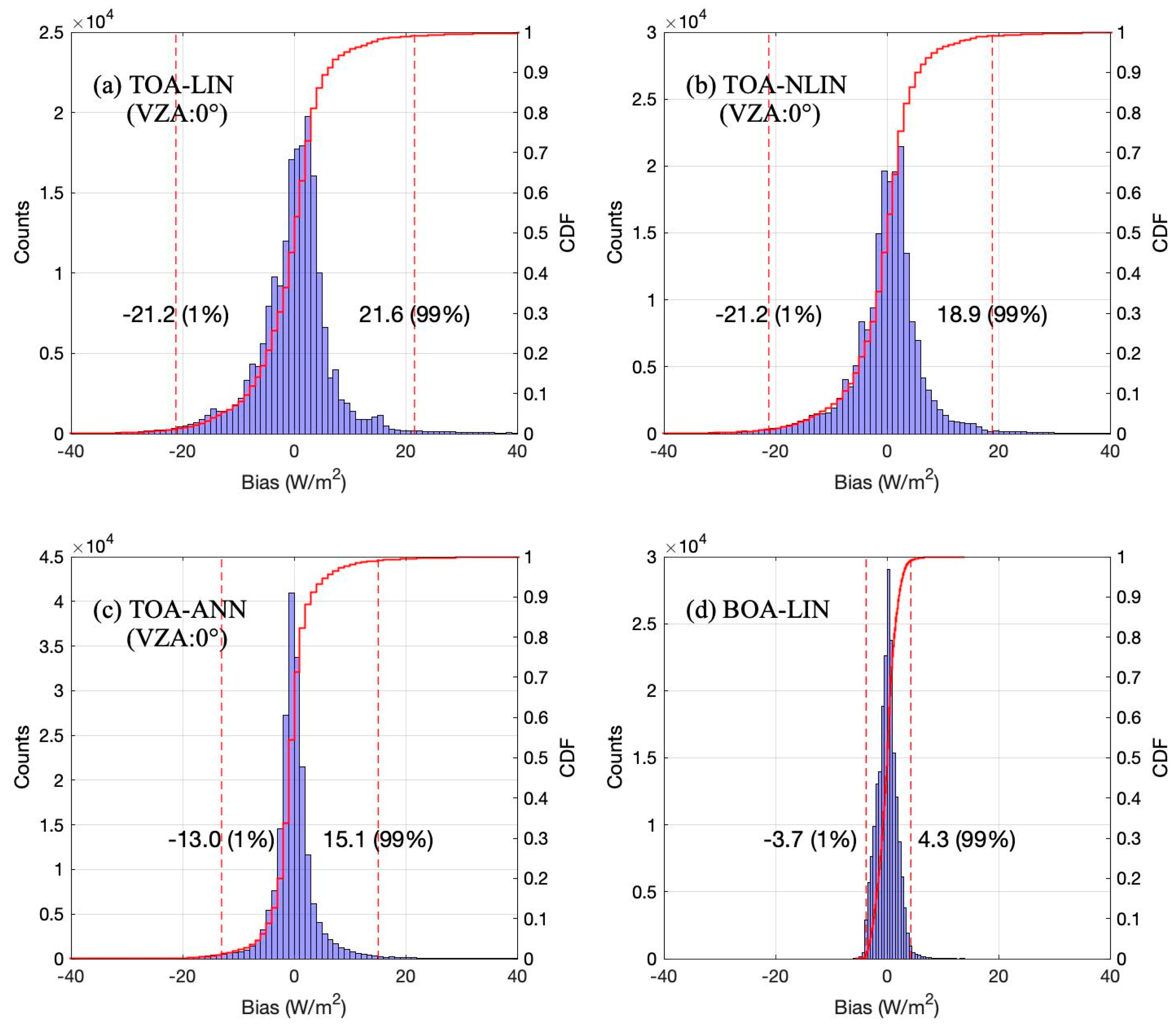
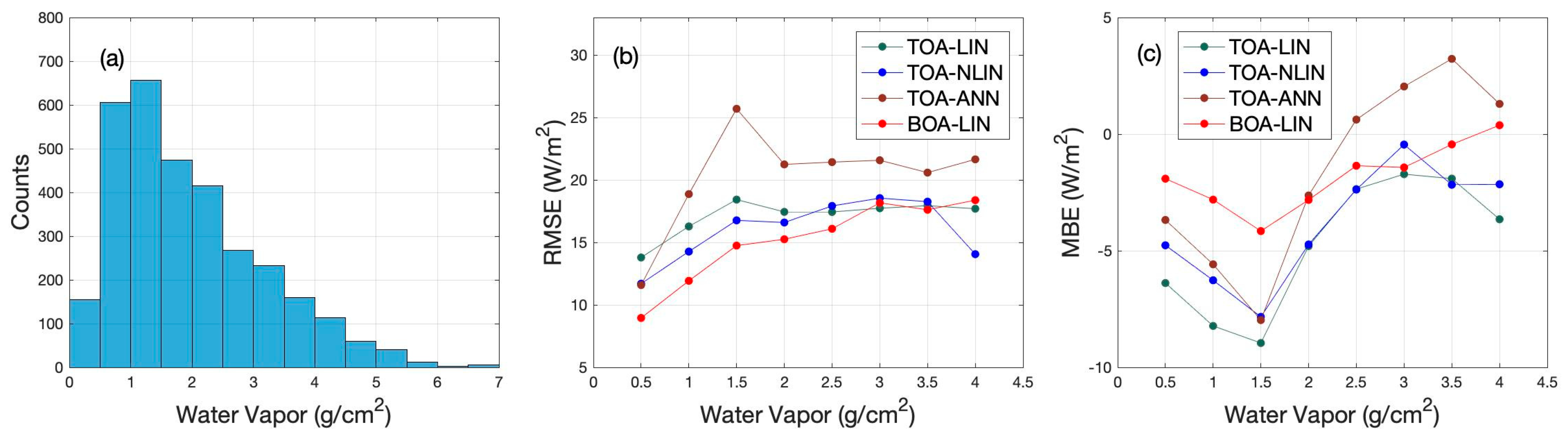
4.1. Results and Analysis Based on Simulated Datasets
4.2. Results and Analysis Based on In Situ Measurements
4.2.1. Six Methods Comparison for All Clear-Sky Data
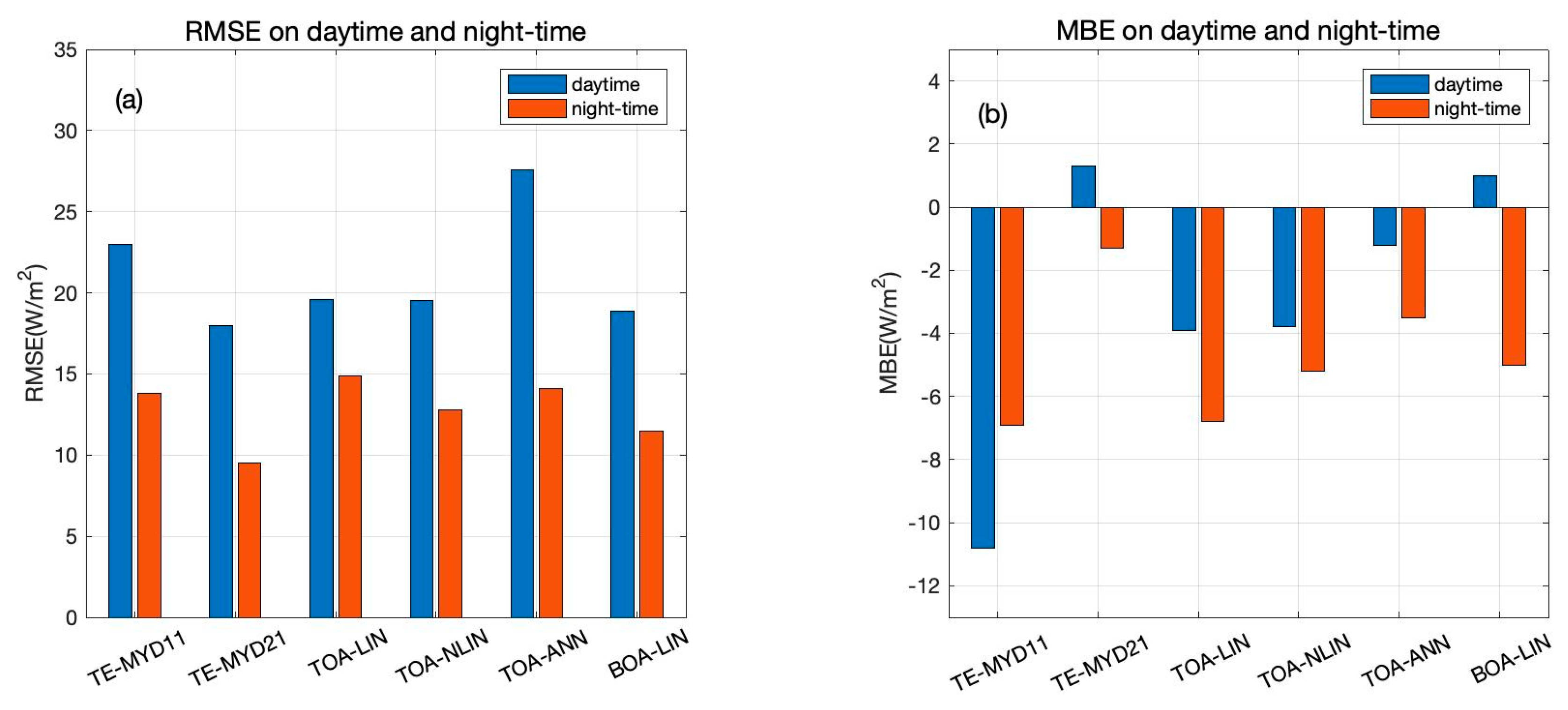
4.2.2. Six Methods Comparison for Daytime and Night-Time Data
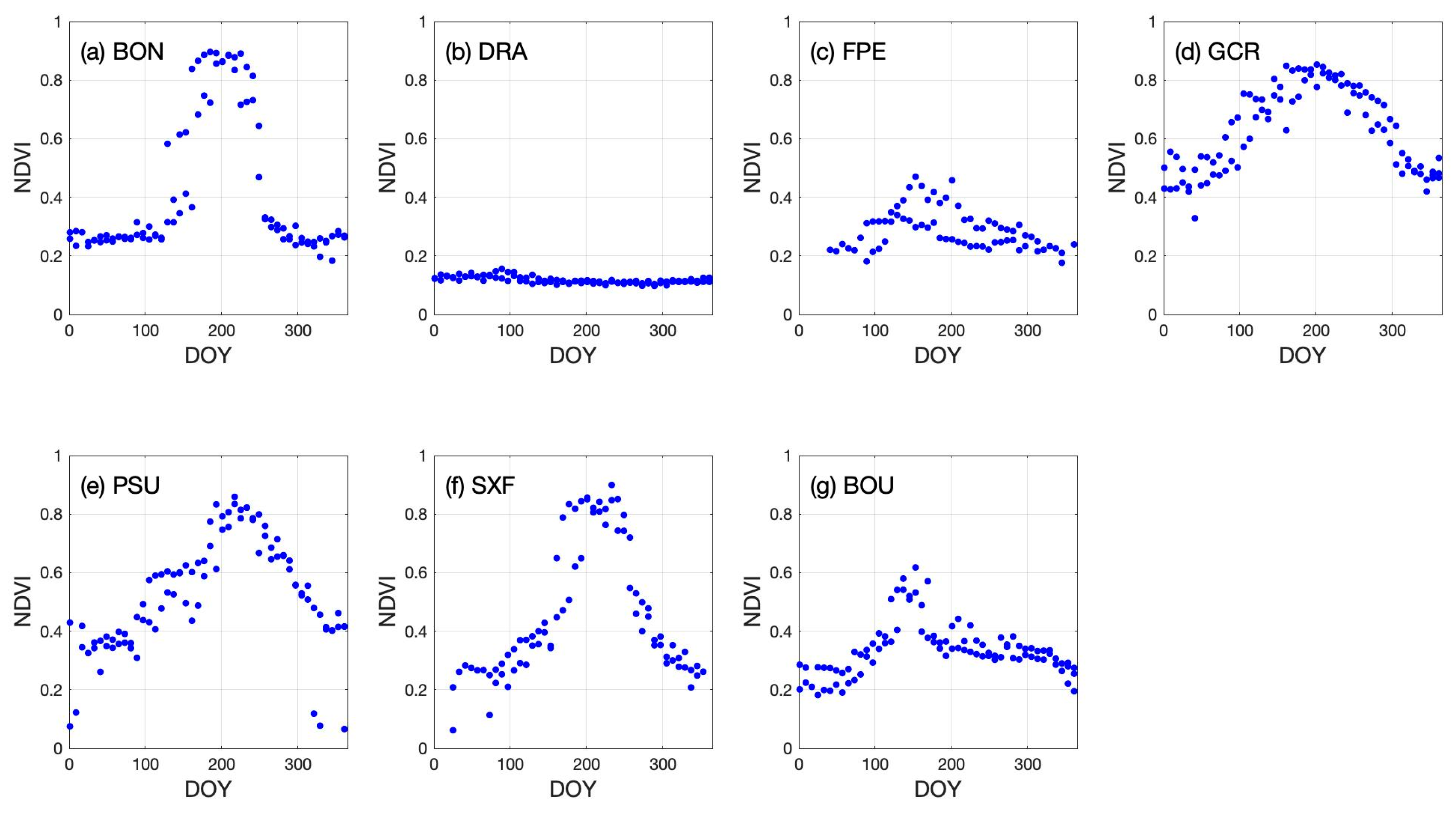
4.2.3. Six Methods Comparison for Each Site
4.2.4. The Intercomparison of Two Temperature-Emissivity Methods
4.2.5. The Intercomparison of Four Hybrid Methods
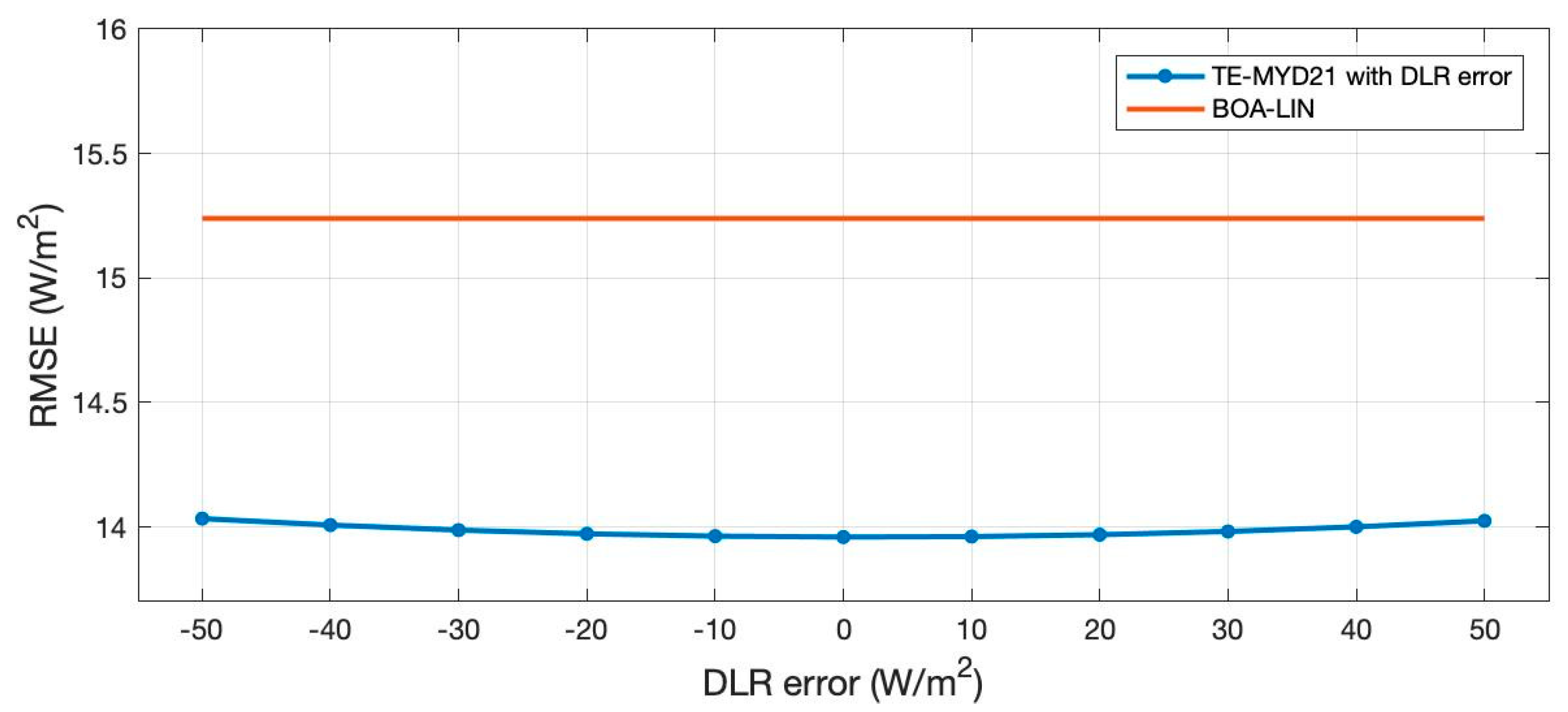
4.2.6. The Comparison of TE-MYD21 and BOA-LIN
5. Conclusions
- (1)
- For the theoretical analysis of TOA hybrid methods (TOA-LIN, TOA-NLIN, TOA-ANN), the fitting RMSE decreases with increasing model nonlinearity. The fitting RMSE of BOA-LIN (1.75 W/m2) is much less than the RMSE of the TOA hybrid methods assuming an accurate atmospheric correction has been achieved. The performance of BOA-LIN decays with the increase of atmospheric profile wv error. The BOA hybrid method has great potential in application if accurate atmospheric profiles can be obtained as input.
- (2)
- The TE-MYD21 performs the best among all the six methods with RMSE of 14.0 W/m2 and MBE of −0.2 W/m2, and the BOA-LIN performs best among the four hybrid methods with RMSE of 15.2 W/m2 and MBE of −2.3 W/m2 based on the two-year satellite products. The performance of six methods in descending order is TE-MYD21, BOA-LIN, TOA-NLIN, TOA-LIN, TE-MYD11, and TOA-ANN. TE-MYD21 has a much better accuracy than the TE-MYD11 over barren surfaces (NDVI < 0.3) and a similar accuracy over non-barren surfaces (NDVI ≥ 0.3). The BOA-LIN is more accurate than other TOA hybrid methods due to the inclusion of atmospheric correction.
Author Contributions
Funding
Conflicts of Interest
References
- Gupta, S.K.; Ritchey, N.A.; Wilber, A.C.; Whitlock, C.H.; Gibson, G.G.; Stackhouse, P.W., Jr. A climatology of surface radiation budget derived from satellite data. J. Clim. 1999, 12, 2691–2710. [Google Scholar] [CrossRef]
- Liang, S.; Wang, K.; Zhang, X.; Wild, M. Review on Estimation of Land Surface Radiation and Energy Budgets From Ground Measurement, Remote Sensing and Model Simulations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 225–240. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S. Global Estimates for High-Spatial-Resolution Clear-Sky Land Surface Upwelling Longwave Radiation From MODIS Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4115–4129. [Google Scholar] [CrossRef]
- Wang, W.; Liang, S. Estimation of high-spatial resolution clear-sky longwave downward and net radiation over land surfaces from MODIS data. Remote Sens. Environ. 2009, 113, 745–754. [Google Scholar] [CrossRef]
- Yang, J.; Gong, P.; Fu, R.; Zhang, M.; Chen, J.; Liang, S.; Xu, B.; Shi, J.; Dickinson, R. The role of satellite remote sensing in climate change studies. Nat. Clim. Chang. 2013, 3, 875–883. [Google Scholar] [CrossRef]
- Weng, Q. Thermal infrared remote sensing for urban climate and environmental studies: Methods, applications, and trends. ISPRS J. Photogramm. Remote Sens. 2009, 64, 335–344. [Google Scholar] [CrossRef]
- Wielicki, B.A.; Barkstrom, B.R.; Baum, B.A.; Charlock, T.P.; Green, R.N.; Kratz, D.P.; Lee, R.B.; Minnis, P.; Smith, G.L.; Wong, T. Clouds and the Earth’s Radiant Energy System (CERES): Algorithm overview. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1127–1141. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.; Huang, J.; Minnis, P.; Wang, T.; Bi, J. Comparison of CERES surface radiation fluxes with surface observations over Loess Plateau. Remote Sens. Environ. 2011, 115, 1489–1500. [Google Scholar] [CrossRef] [Green Version]
- Liang, S.; Wang, D.; He, T.; Yu, Y. Remote sensing of earth’s energy budget: Synthesis and review. Int. J. Digit. Earth 2019, 12, 737–780. [Google Scholar] [CrossRef] [Green Version]
- Wielicki, B.A.; Barkstrom, B.R.; Harrison, E.F.; Lee, R.B.; Louis Smith, G.; Cooper, J.E. Clouds and the Earth’s Radiant Energy System (CERES): An Earth Observing System Experiment. Bull. Am. Meteorol. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef] [Green Version]
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L. Estimation of the net radiation using MODIS (Moderate Resolution Imaging Spectroradiometer) data for clear sky days. Remote Sens. Environ. 2005, 97, 52–67. [Google Scholar] [CrossRef]
- Tang, B.; Li, Z.-L. Estimation of instantaneous net surface longwave radiation from MODIS cloud-free data. Remote Sens. Environ. 2008, 112, 3482–3492. [Google Scholar] [CrossRef]
- Wang, W.; Liang, S.; Augustine, J.A. Estimating High Spatial Resolution Clear-Sky Land Surface Upwelling Longwave Radiation From MODIS Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1559–1570. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Snyder, W.C.; Wan, Z.; Zhang, Y.; Feng, Y.-Z. Classification-based emissivity for land surface temperature measurement from space. Int. J. Remote Sens. 1998, 19, 2753–2774. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, X.; Liang, S.; Yang, H.; Zhou, G. Estimation of clear-sky land surface longwave radiation from MODIS data products by merging multiple models. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Wang, T.; Yan, G.; Chen, L. Consistent retrieval methods to estimate land surface shortwave and longwave radiative flux components under clear-sky conditions. Remote Sens. Environ. 2012, 124, 61–71. [Google Scholar] [CrossRef]
- Wang, C.; Tang, B.H.; Huo, X.; Li, Z.L. New method to estimate surface upwelling long-wave radiation from MODIS cloud-free data. Opt. Express 2017, 25, A574–A588. [Google Scholar] [CrossRef]
- Jiao, Z.; Yan, G.; Zhao, J.; Wang, T.; Chen, L. Estimation of surface upward longwave radiation from MODIS and VIIRS clear-sky data in the Tibetan Plateau. Remote Sens. Environ. 2015, 162, 221–237. [Google Scholar] [CrossRef]
- Cao, B.; Liu, Q.; Du, Y.; Roujean, J.-L.; Gastellu-Etchegorry, J.-P.; Trigo, I.F.; Zhan, W.; Yu, Y.; Cheng, J.; Jacob, F. A review of earth surface thermal radiation directionality observing and modeling: Historical development, current status and perspectives. Remote Sens. Environ. 2019, 232, 111304. [Google Scholar] [CrossRef]
- Hu, T.; Cao, B.; Du, Y.; Li, H.; Wang, C.; Bian, Z.; Sun, D.; Liu, Q. Estimation of surface upward longwave radiation using a direct physical algorithm. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4412–4426. [Google Scholar] [CrossRef]
- Chedin, A.; Scott, N.; Wahiche, C.; Moulinier, P. The improved initialization inversion method: A high resolution physical method for temperature retrievals from satellites of the TIROS-N series. J. Clim. Appl. Meteorol. 1985, 24, 128–143. [Google Scholar] [CrossRef] [Green Version]
- Chevallier, F.; Chéruy, F.; Scott, N.A.; Chédin, A. A Neural Network Approach for a Fast and Accurate Computation of a Longwave Radiative Budget. J. Appl. Meteorol. 1998, 37, 1385–1397. [Google Scholar] [CrossRef]
- Ren, H.; Du, C.; Liu, R.; Qin, Q.; Yan, G.; Li, Z.L.; Meng, J. Atmospheric water vapor retrieval from Landsat 8 thermal infrared images. J. Geophys. Res. Atmos. 2015, 120, 1723–1738. [Google Scholar] [CrossRef]
- Ye, X.; Ren, H.; Liu, R.; Qin, Q.; Liu, Y.; Dong, J. Land surface temperature estimate from chinese gaofen-5 satellite data using split-window algorithm. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5877–5888. [Google Scholar] [CrossRef]
- Li, Z.-L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.-H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens. 2013, 34, 3084–3127. [Google Scholar] [CrossRef]
- Wang, K.; Wan, Z.; Wang, P.; Sparrow, M.; Liu, J.; Zhou, X.; Haginoya, S. Estimation of surface long wave radiation and broadband emissivity using Moderate Resolution Imaging Spectroradiometer (MODIS) land surface temperature/emissivity products. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.; Acharya, P.; Hoke, M.; Chetwynd, J.; Bernstein, L.; Shettle, E.; Matthew, M.; Adler-Golden, S. MODTRAN4 version 3 revision 1 user’s manual. Air Force Res. Lab. Space Veh. Dir. Air Force Mater. Command AFB MA 2003, 1731, 3010. [Google Scholar]
- Rodriguez, E.; Morris, C.S.; Belz, J.E. A global assessment of the SRTM performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Liu, Q.; Du, Y.; Jiang, J.; Wang, H. Evaluation of the NCEP and MODIS Atmospheric Products for Single Channel Land Surface Temperature Retrieval With Ground Measurements: A Case Study of HJ-1B IRS Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1399–1408. [Google Scholar] [CrossRef]
- Meng, X.; Cheng, J. Evaluating Eight Global Reanalysis Products for Atmospheric Correction of Thermal Infrared Sensor—Application to Landsat 8 TIRS10 Data. Remote Sens. 2018, 10, 474. [Google Scholar] [CrossRef] [Green Version]
- Augustine, J.A.; Hodges, G.B.; Cornwall, C.R.; Michalsky, J.J.; Medina, C.I. An Update on SURFRAD—The GCOS Surface Radiation Budget Network for the Continental United States. J. Atmos. Ocean. Technol. 2005, 22, 1460–1472. [Google Scholar] [CrossRef]
- Philipona, R.; Fröhlich, C.; Dehne, K.; DeLuisi, J.; Augustine, J.; Dutton, E.; Nelson, D.; Forgan, B.; Novotny, P.; Hickey, J. The Baseline Surface Radiation Network pyrgeometer round-robin calibration experiment. J. Atmos. Ocean. Technol. 1998, 15, 687–696. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z.L. Validation of the land-surface temperature products retrieved from Terra Moderate Resolution Imaging Spectroradiometer data. Remote Sens. Environ. 2002, 83, 163–180. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z.L. Quality assessment and validation of the MODIS global land surface temperature. Int. J. Remote Sens. 2010, 25, 261–274. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z.-L. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 980–996. [Google Scholar]
- Li, Z.-L.; Becker, F. Feasibility of land surface temperature and emissivity determination from AVHRR data. Remote Sens. Environ. 1993, 43, 67–85. [Google Scholar] [CrossRef]
- Tonooka, H. Accurate atmospheric correction of ASTER thermal infrared imagery using the WVS method. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2778–2792. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hughes, C.G.; Hook, S.J. Quantifying uncertainties in land surface temperature and emissivity retrievals from ASTER and MODIS thermal infrared data. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Hulley, G.; Veraverbeke, S.; Hook, S. Thermal-based techniques for land cover change detection using a new dynamic MODIS multispectral emissivity product (MOD21). Remote Sens. Environ. 2014, 140, 755–765. [Google Scholar] [CrossRef]
- Lee, H.-T.; Ellingson, R.G. Development of a Nonlinear Statistical Method for Estimating the Downward Longwave Radiation at the Surface from Satellite Observations. J. Atmos. Ocean. Technol. 2002, 19, 1500–1515. [Google Scholar] [CrossRef] [Green Version]
- Mao, K.; Tang, H.; Wang, X.; Zhou, Q.; Wang, D. Near-surface air temperature estimation from ASTER data based on neural network algorithm. Int. J. Remote Sens. 2008, 29, 6021–6028. [Google Scholar] [CrossRef]
- Ahmad, S.; Kalra, A.; Stephen, H. Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010, 33, 69–80. [Google Scholar] [CrossRef]
- Walthall, C.; Dulaney, W.; Anderson, M.; Norman, J.; Fang, H.; Liang, S. A comparison of empirical and neural network approaches for estimating corn and soybean leaf area index from Landsat ETM+ imagery. Remote Sens. Environ. 2004, 92, 465–474. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S.; Wang, W.; Guo, Y. An efficient hybrid method for estimating clear-sky surface downward longwave radiation from MODIS data. J. Geophys. Res. Atmos. 2017, 122, 2616–2630. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Sobrino, J.A. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2010, 22, 3719–3746. [Google Scholar] [CrossRef]
- Hu, T.; Du, Y.; Cao, B.; Li, H.; Bian, Z.; Sun, D.; Liu, Q. Estimation of Upward Longwave Radiation From Vegetated Surfaces Considering Thermal Directionality. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6644–6658. [Google Scholar] [CrossRef]
- Li, H.; Li, R.; Yang, Y.; Cao, B.; Bian, Z.; Hu, T.; Du, Y.; Sun, L.; Liu, Q. Temperature-based and Radiance-based Validation of the Collection 6 MYD11 and MYD21 Land Surface Temperature Products Over Barren Surfaces in Northwestern China. IEEE Trans. Geosci. Remote Sens. (in press).
- Li, H.; Sun, D.L.; Yu, Y.Y.; Wang, H.Y.; Liu, Y.L.; Liu, Q.H.; Du, Y.M.; Wang, H.S.; Cao, B.A. Evaluation of the VIIRS and MODIS LST products in an arid area of Northwest China. Remote Sens. Environ. 2014, 142, 111–121. [Google Scholar] [CrossRef] [Green Version]


| MODIS Products | Spatial Resolution (km) | Temporal Resolution | Products Description (Used Layers) | Model to Drive |
|---|---|---|---|---|
| MYD021KM | 1 | Daily | TOA radiance acquired by Aqua (Bands 29, 31 and 32 only) | Four hybrid methods |
| MYD03 | 1 | Daily | Locations and ancillary information corresponding to the swath data of Aqua (Latitude, Longitude and VZA) | All SULR methods |
| MYD35_L2 | 1 | Daily | Cloud mask and spectral test results corresponding to the swath data of Aqua (Cloud mask) | All SULR methods |
| MYD11B1 | 5.6 | Daily | LST&LSE generated with the day/night algorithm (LSEs for bands 29, 31 and 32) | TE-MYD11 |
| MYD11_L2 | 1 | Daily | LST&LSE generated with the generalized split-window algorithm (LSTs for bands 29, 31 and 32) | TE-MYD11 |
| MYD21_L2 | 1 | Daily | LST&LSE generated with the TES algorithm (LST, LSE) | TE-MYD21 |
| MOD13A2& MYD13A2 | 1 | 8-day with MOD&MYD combined | Vegetation Index values (NDVI) | - |
| Station Name | Latitude, Longitude | Land Cover | Elevation (m) | Station ID |
|---|---|---|---|---|
| Bondville | 40.05192°N, 88.37309°W | Cropland | 230 | BON |
| Desert Rock | 36.62373°N, 116.01947°W | Open Shrubland | 1007 | DRA |
| Fort Peck | 48.30783°N, 105.10170°W | Grassland | 634 | FPE |
| Goodwin Creek | 34.2547°N, 89.8729°W | Cropland/natural vegetation mosaic | 98 | GCR |
| Penn. State Univ. | 40.72012°N, 77.93085°W | Cropland/natural vegetation mosaic | 376 | PSU |
| Sioux Falls | 43.73403°N, 96.62328°W | Grassland | 473 | SXF |
| Boulder | 40.12498°N, 105.23680°W | Grassland | 1689 | BOU |
| 85.549 | −1.846 | 132.003 | −95.882 | |
| 85.951 | −1.924 | 133.113 | −97.023 | |
| 87.201 | −2.158 | 136.524 | −100.536 | |
| 89.437 | −2.543 | 142.488 | −106.704 | |
| 92.931 | −3.059 | 151.479 | −116.076 | |
| 98.178 | −3.607 | 164.247 | −129.571 | |
| 106.052 | −3.810 | 181.853 | −148.694 |
| 36.424 | −18.351 | 0.462 | 0.853 | 2.121 | 37.823 | |
| 34.546 | −16.185 | 0.462 | 0.435 | 14.874 | 31.081 | |
| 33.621 | −15.965 | 0.464 | 0.451 | 3.695 | 30.254 | |
| 31.868 | −15.502 | 0.469 | 0.480 | 1.621 | 28.609 | |
| 33.587 | −14.051 | 0.459 | 0.510 | 0.860 | 25.582 | |
| 32.267 | −11.813 | 0.458 | 0.572 | 0.516 | 19.891 | |
| 30.139 | −7.192 | 0.452 | 0.677 | 0.320 | 8.273 |
| Network Structure | Input | Output | Number of Epochs | |
|---|---|---|---|---|
| (3-7-1) | Radiances of MODIS B29, 31, and 32 from the simulation dataset | Corresponding SULR from the simulation dataset | 500 | |
| 50.528 | 7.754 | 7.532 | 29.540 |
| TOA-LIN | TOA-NLIN | TOA-ANN | BOA-LIN (No wv Error) | BOA-LIN_5% (5% wv Error) | BOA-LIN_10% (10% wv Error) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE &MBE | Bias Range | R2 | RMSE &MBE | Bias Range | R2 | RMSE &MBE | Bias Range | R2 | RMSE &MBE | Bias Range | R2 | RMSE &MBE | Bias Range | R2 | RMSE &MBE | Bias Range | |
| 0° | 0.995 | 7.37, 0.00 | −21.2, 21.6 | 0.996 | 6.91, 0.00 | −21.2, 18.9 | 0.998 | 4.46, 0.00 | −13.0, 15.1 | 0.9997 | 1.75, 0.00 | −3.7, 4.3 | 0.999 | 2.89, 0.01 | −8.3, 10.1 | 0.998 | 4.99, 0.14 | −14.3, 19.9 |
| 10° | 0.995 | 7.43, 0.00 | −21.4, 21.9 | 0.996 | 6.25, 0.00 | −23.3, 14.3 | 0.998 | 4.44, 0.00 | −13.4, 13.9 | 0.999 | 2.93, 0.01 | −8.4, 10.3 | 0.998 | 5.09, 0.15 | −14.6, 20.3 | |||
| 20° | 0.995 | 7.63, 0.00 | −21.9, 22.5 | 0.996 | 6.37, 0.00 | −23.8, 14.5 | 0.998 | 4.55, 0.00 | −13.6, 15.0 | 0.999 | 3.06, 0.01 | −8.8, 10.9 | 0.997 | 5.39, 0.17 | −15.4, 21.9 | |||
| 30° | 0.994 | 7.99, 0.00 | −22.9, 23.8 | 0.996 | 6.59, 0.00 | −24.8, 15.0 | 0.998 | 4.76, 0.02 | −14.1, 15.7 | 0.999 | 3.31, 0.02 | −9.5, 12.0 | 0.997 | 6.01, 0.21 | −17.0, 24.5 | |||
| 40° | 0.993 | 8.58, 0.00 | −24.1, 26.0 | 0.996 | 6.96, 0.00 | −26.2, 16.0 | 0.998 | 5.06, 0.01 | −14.4, 17.0 | 0.999 | 3.79, 0.30 | −11.0, 14.3 | 0.995 | 7.17, 0.30 | −19.6, 29.8 | |||
| 50° | 0.992 | 9.54, 0.00 | −26.7, 29.8 | 0.995 | 7.60, 0.00 | −28.3, 17.9 | 0.997 | 5.46, 0.03 | −15.8, 18.4 | 0.998 | 4.81, 0.09 | −13.7, 18.8 | 0.992 | 9.63, 0.51 | −24.6, 40.8 | |||
| 60° | 0.989 | 11.2, 0.00 | −30.4, 37.1 | 0.993 | 8.82, 0.00 | −31.8, 22.2 | 0.996 | 6.38, −0.01 | −17.6, 21.9 | 0.995 | 7.63, 0.25 | −20.4, 29.8 | 0.977 | 16.72, 1.13 | −36.2, 67.5 | |||
| Mean | 0.993 | 8.53, 0.00 | −24.1, 26.1 | 0.995 | 7.07,0.00 | −25.6,17.0 | 0.998 | 5.02, 0.01 | −14.6, 16.7 | 0.9997 | 1.75, 0.00 | −3.7, 4.3 | 0.998 | 4.06, 0.01 | −11.4, 15.2 | 0.993 | 7.86, 0.37 | −20.2, 32.1 |
| Site Name | # of obs | TE-MYD11 | TE-MYD21 | TOA-LIN | TOA-NLIN | TOA-ANN | BOA-LIN | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE &MBE | RMSE &MBE | RMSE &MBE | RMSE &MBE | RMSE &MBE | RMSE &MBE | ||||||||
| BON | 336 | 13.9 | −0.1 | 17.1 | 7.1 | 15.7 | 3.3 | 14.9 | 3.0 | 16.4 | 6.7 | 18.4 | 5.0 |
| DRA | 855 | 28.8 | −25.3 | 15.9 | −8.8 | 25.5 | −22.4 | 22.7 | −18.7 | 33.1 | −24.2 | 17.5 | −11.3 |
| FPE | 538 | 9.9 | −3.5 | 9.2 | 1.2 | 9.3 | −0.7 | 10.0 | 0.4 | 11.7 | 4.2 | 10.3 | −0.7 |
| GCR | 393 | 16.8 | −6.0 | 14.1 | 2.1 | 14.2 | −0.7 | 14.5 | −1.8 | 14.8 | 3.6 | 14.7 | −0.5 |
| PSU | 184 | 9.0 | 0.8 | 11.7 | 7.3 | 10.3 | 2.8 | 9.7 | 2.6 | 13.5 | 8.8 | 12.5 | 4.8 |
| SXF | 426 | 11.9 | −1.0 | 13.6 | 3.9 | 12.8 | 1.4 | 13.0 | 1.2 | 15.0 | 5.5 | 14.2 | 2.0 |
| BOU | 465 | 12.8 | −2.9 | 13.1 | 0.2 | 13.8 | −0.2 | 14.1 | −0.3 | 16.5 | 6.1 | 15.4 | −1.2 |
| Weighted mean | 18.5 | −8.6 | 14.0 | −0.2 | 17.2 | −5.5 | 16.1 | −4.6 | 21.2 | −2.5 | 15.2 | −2.3 | |
| Site Name | # of obs | Percentage | Mean NDVI | TE-MYD11 | TE-MYD21 | |||
|---|---|---|---|---|---|---|---|---|
| RMSE | MBE | RMSE | MBE | |||||
| Barren Surfaces (NDVI < 0.3) | BON | 144 | 42.9% | 0.25 | 14.7 | 2.6 | 19.8 | 8.8 |
| DRA | 855 | 100% | 0.12 | 28.8 | −25.3 | 16.0 | −8.8 | |
| FPE | 352 | 65.4% | 0.18 | 9.5 | −3.6 | 8.8 | 0.1 | |
| GCR | 0 | 0% | - | - | - | - | - | |
| PSU | 0 | 0% | - | - | - | - | - | |
| SXF | 124 | 29.1% | 0.16 | 8.2 | −4.0 | 7.6 | −2.2 | |
| BOU | 94 | 20.2% | 0.25 | 9.2 | −4.0 | 8.3 | −0.8 | |
| Weighted mean | - | - | 0.15 | 22.4 | −14.9 | 14.2 | −4.2 | |
| Non-Barren Surfaces (NDVI ≥ 0.3) | BON | 192 | 57.1% | 0.65 | 13.5 | −2.1 | 14.8 | 5.9 |
| DRA | 0 | 0% | - | - | - | - | - | |
| FPE | 186 | 34.6% | 0.37 | 10.7 | −3.4 | 10.0 | 3.2 | |
| GCR | 393 | 100% | 0.64 | 16.8 | −6.0 | 14.1 | 2.1 | |
| PSU | 184 | 100% | 0.61 | 9.0 | 0.8 | 11.7 | 7.3 | |
| SXF | 302 | 70.9% | 0.61 | 13.1 | 0.3 | 15.4 | 6.4 | |
| BOU | 371 | 79.8% | 0.39 | 13.6 | −2.6 | 14.1 | 0.5 | |
| Weighted mean | - | - | 0.35 | 13.6 | −2.5 | 13.8 | 3.7 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, B.; Cao, B.; Li, H.; Bian, Z.; Hu, T.; Du, Y.; Yang, Y.; Xiao, Q.; Liu, Q. Evaluation of Six High-Spatial Resolution Clear-Sky Surface Upward Longwave Radiation Estimation Methods with MODIS. Remote Sens. 2020, 12, 1834. https://doi.org/10.3390/rs12111834
Qin B, Cao B, Li H, Bian Z, Hu T, Du Y, Yang Y, Xiao Q, Liu Q. Evaluation of Six High-Spatial Resolution Clear-Sky Surface Upward Longwave Radiation Estimation Methods with MODIS. Remote Sensing. 2020; 12(11):1834. https://doi.org/10.3390/rs12111834
Chicago/Turabian StyleQin, Boxiong, Biao Cao, Hua Li, Zunjian Bian, Tian Hu, Yongming Du, Yingpin Yang, Qing Xiao, and Qinhuo Liu. 2020. "Evaluation of Six High-Spatial Resolution Clear-Sky Surface Upward Longwave Radiation Estimation Methods with MODIS" Remote Sensing 12, no. 11: 1834. https://doi.org/10.3390/rs12111834
APA StyleQin, B., Cao, B., Li, H., Bian, Z., Hu, T., Du, Y., Yang, Y., Xiao, Q., & Liu, Q. (2020). Evaluation of Six High-Spatial Resolution Clear-Sky Surface Upward Longwave Radiation Estimation Methods with MODIS. Remote Sensing, 12(11), 1834. https://doi.org/10.3390/rs12111834







