Surface Mass Variations from GPS and GRACE/GFO: A Case Study in Southwest China
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. GPS Vertical Displacement Data
2.3. GRACE/GFO-Inferred Surface Mass Variations
2.4. GRACE Mascon Solutions
3. Surface Mass Variations Inverted by GPS Vertical Displacements
3.1. Post-Processing of GPS Vertical Displacements
3.2. Inversion Model for Surface Mass Variations
4. Results and Discussions
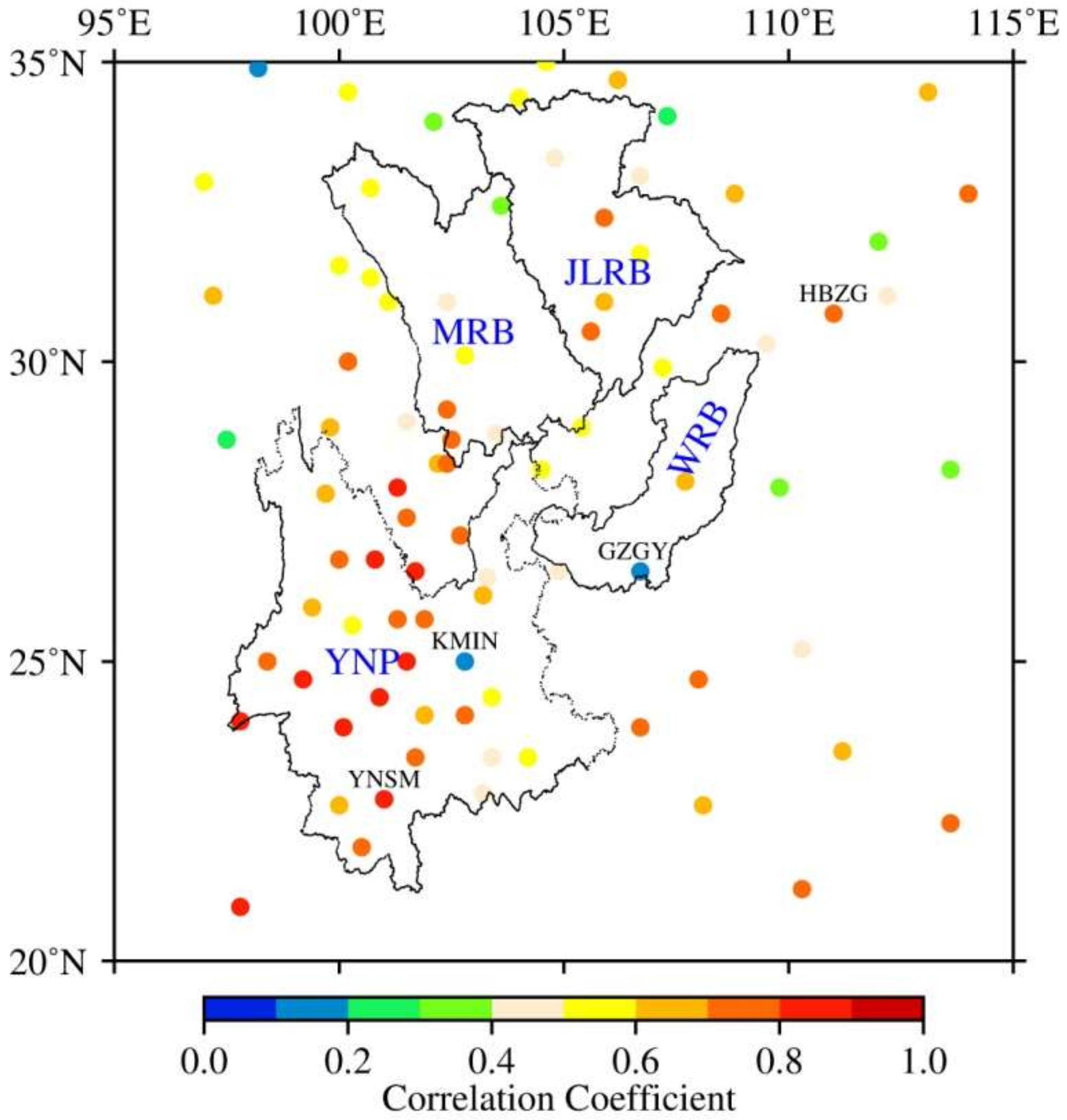
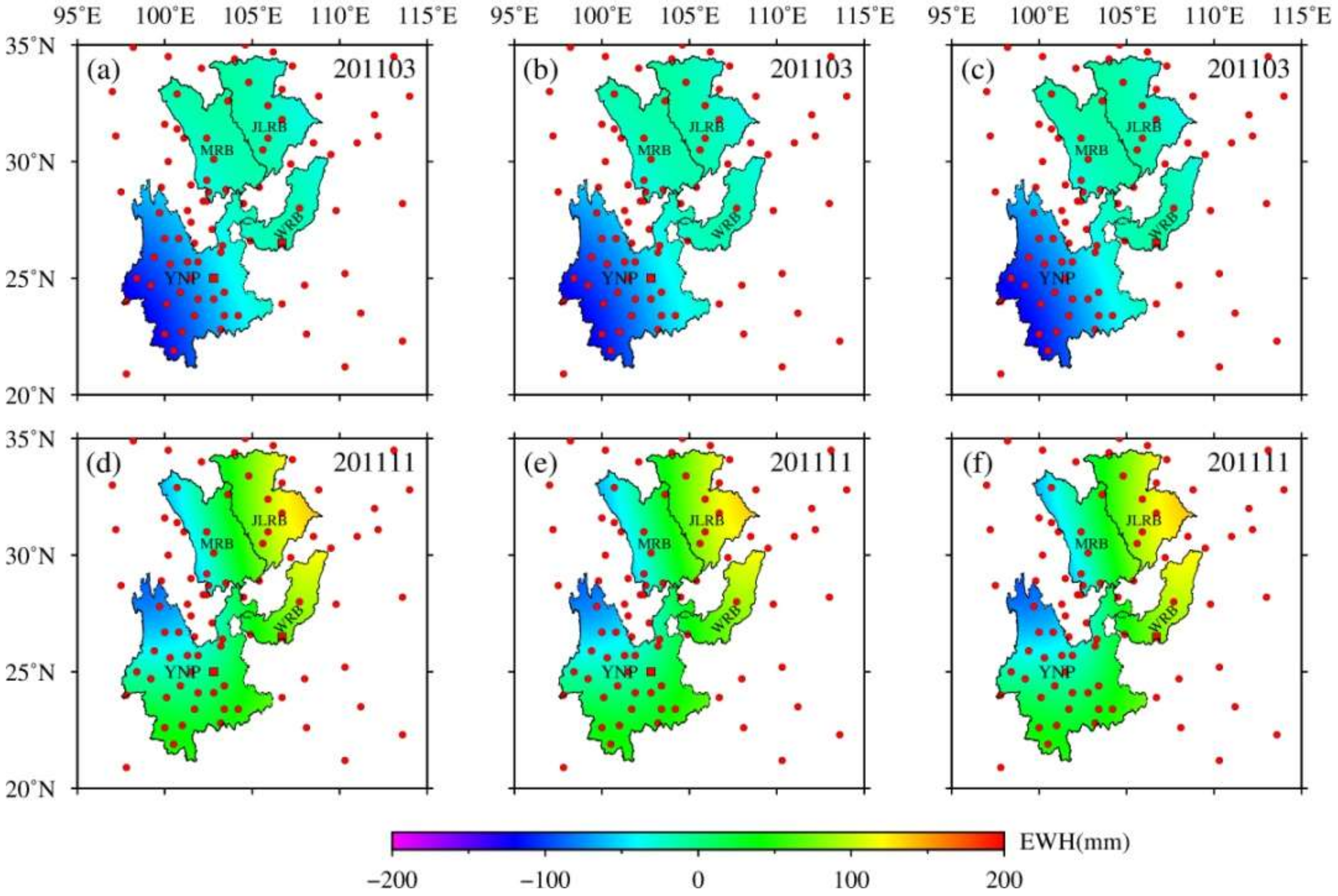
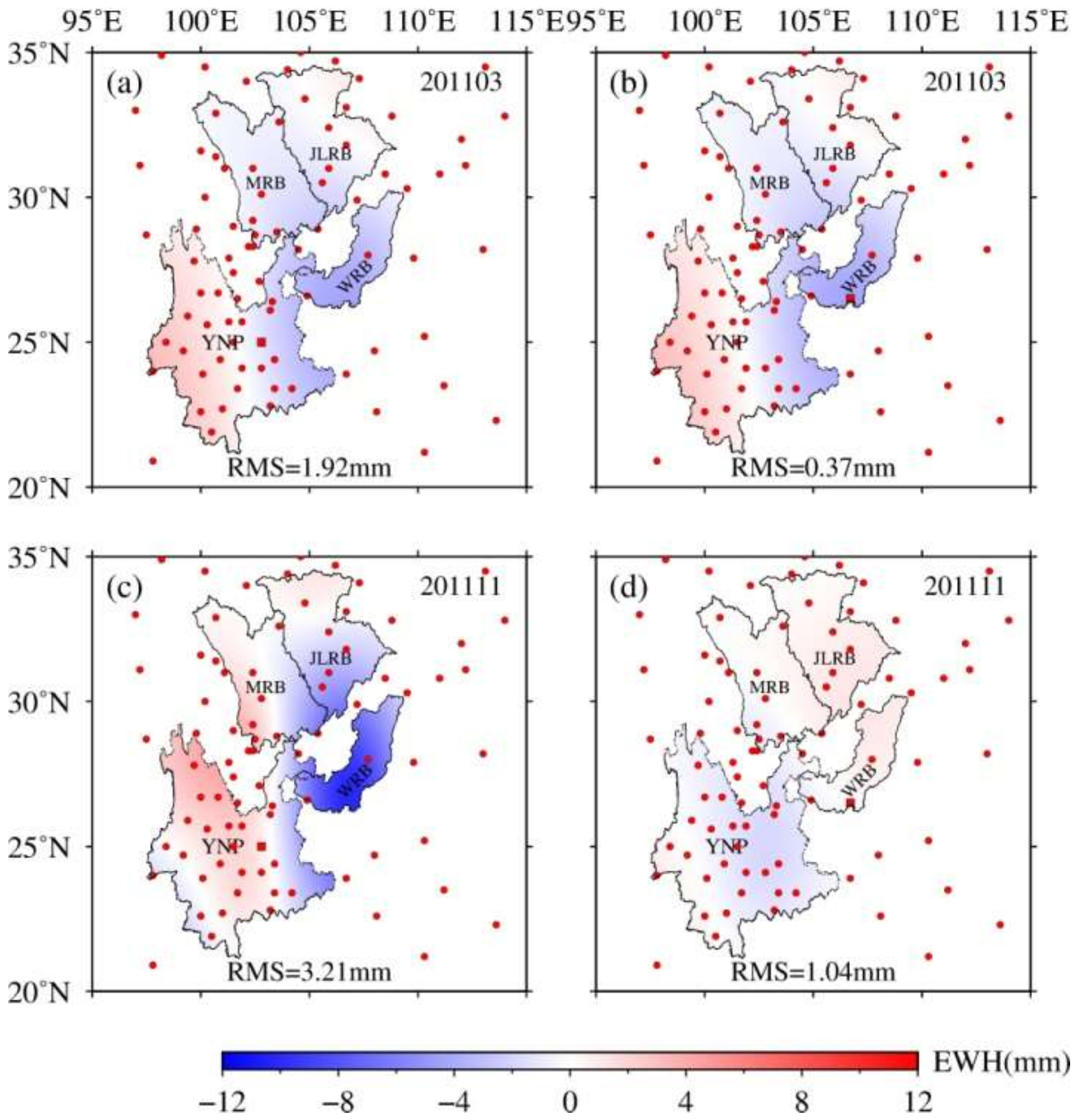
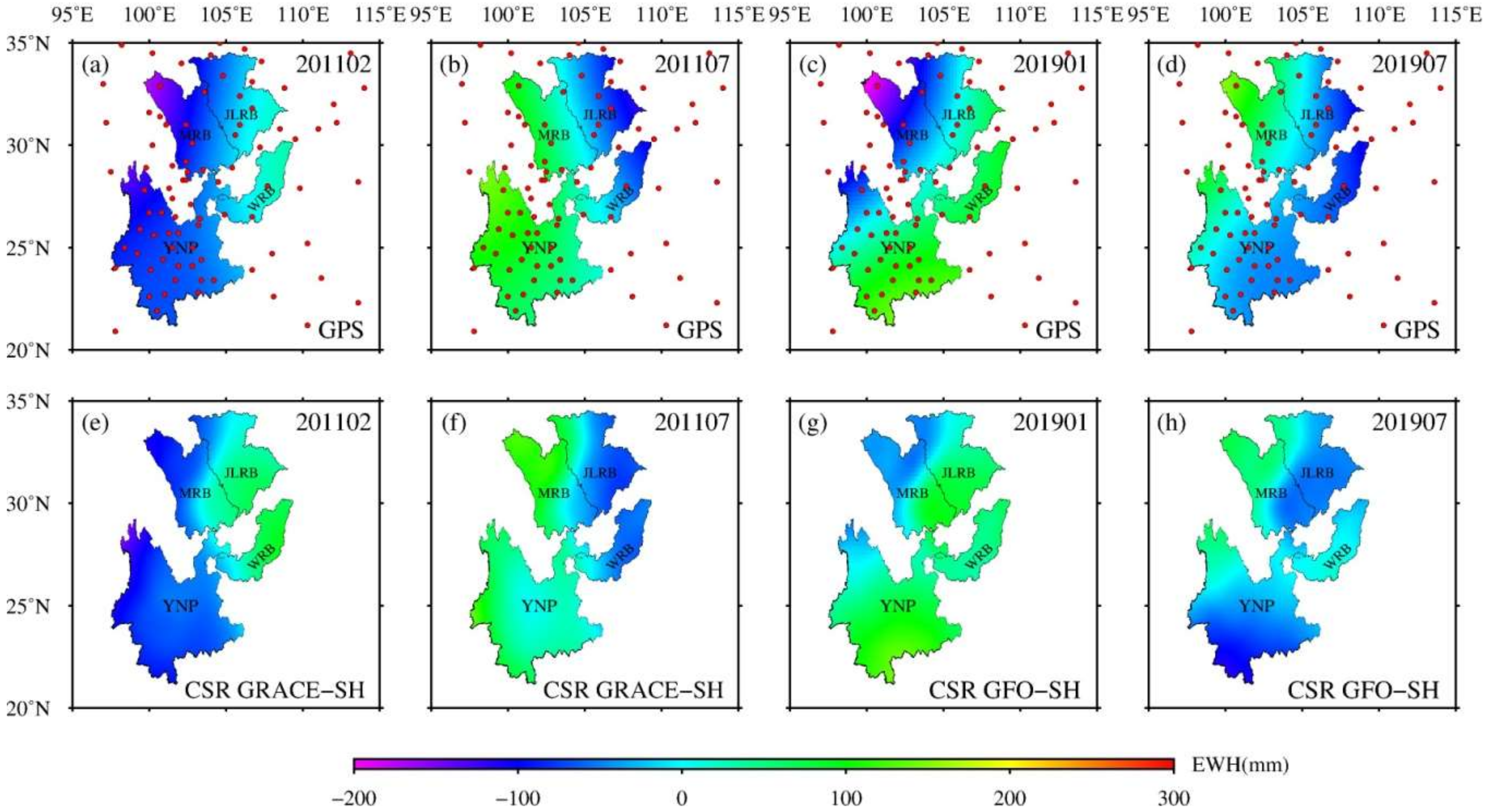
4.1. Spatial Distributions of Surface Mass Variations Derived from GPS and GRACE/GFO
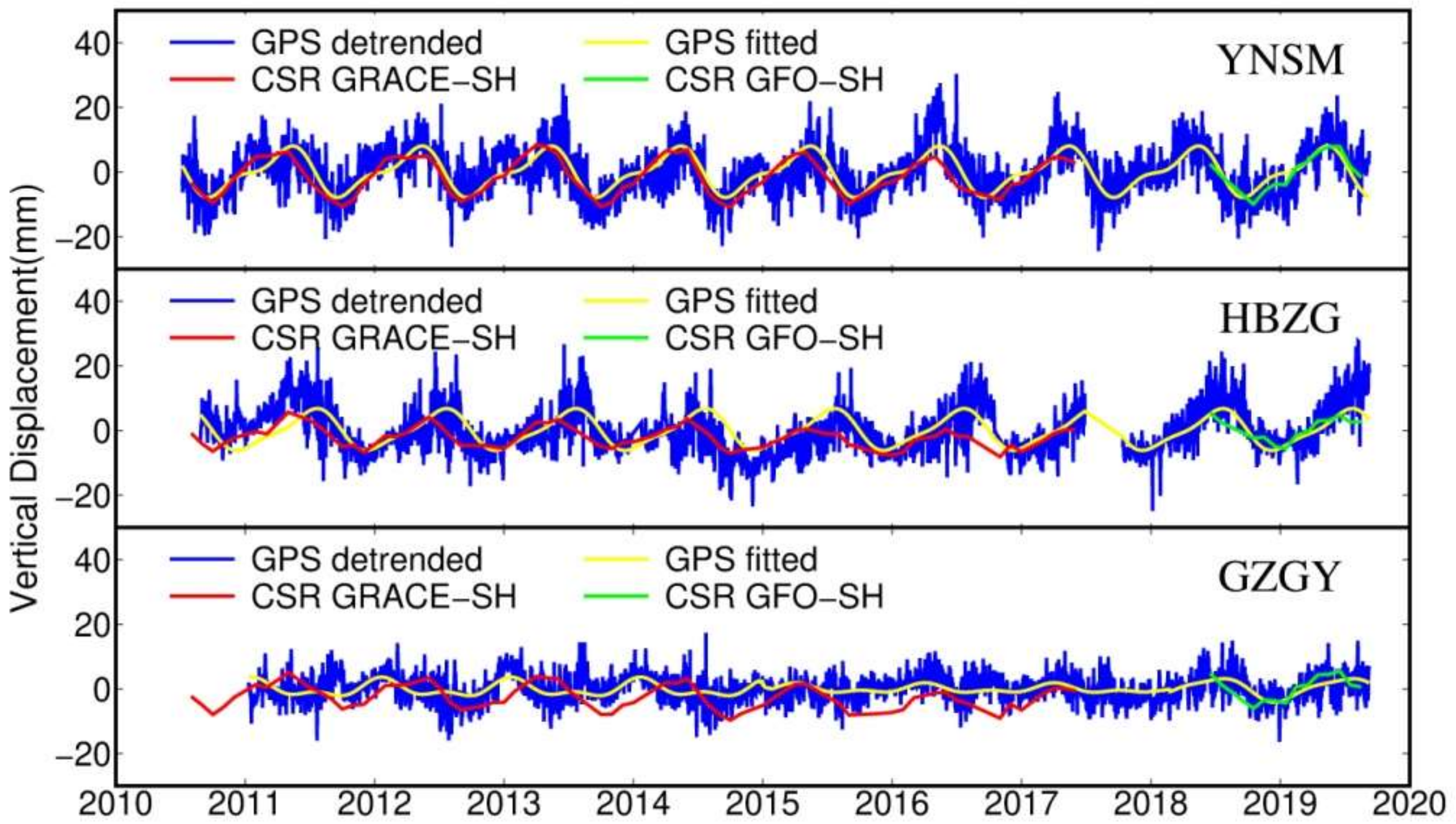
4.2. Seasonal Surface Mass Variations Revealed by GPS and GRACE/GFO
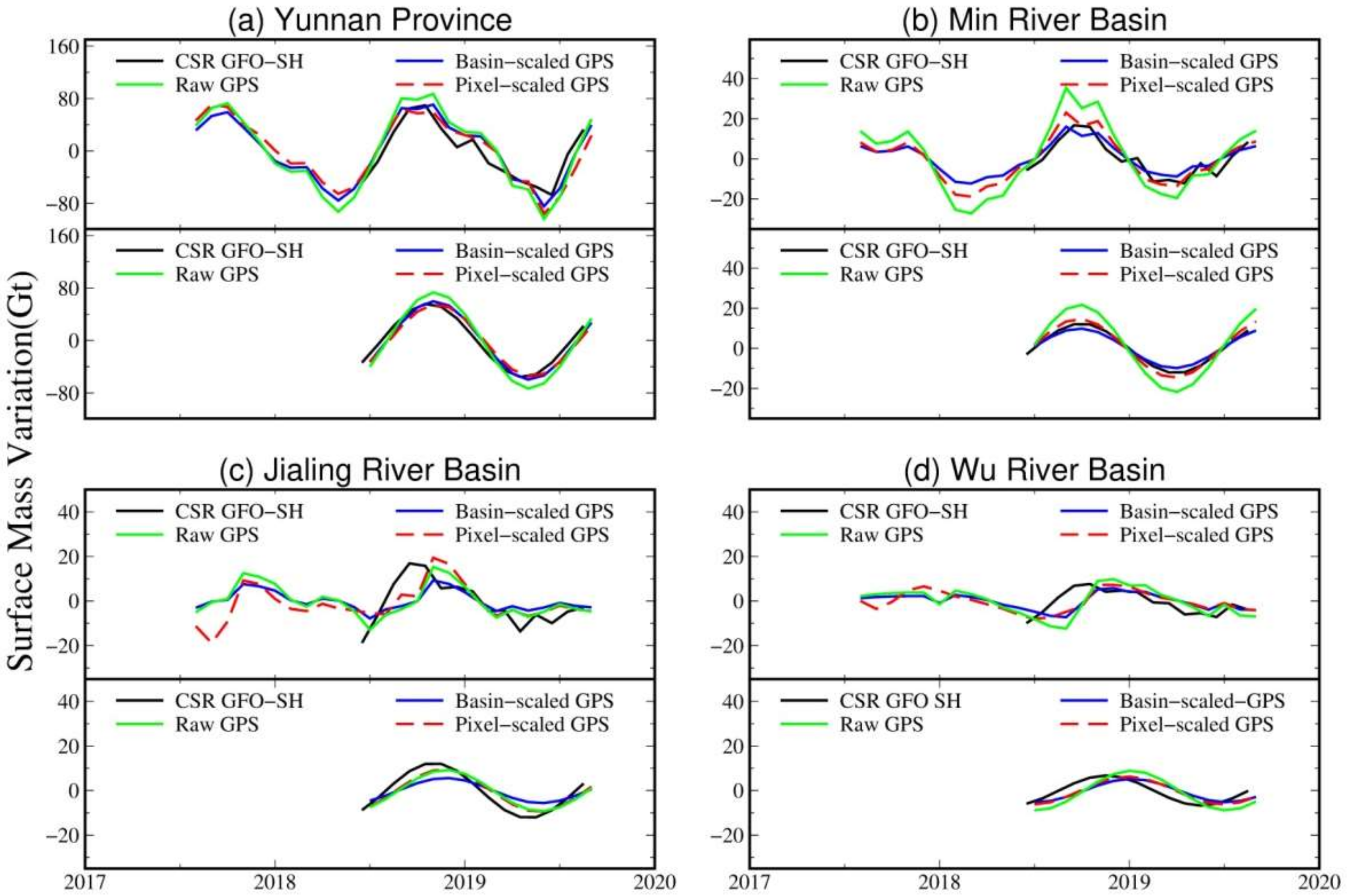
4.3. GPS-Derived Surface Mass Variations to Bridge GRACE/GFO Mission Gap
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wahr, J.; Swenson, S.; Velicogna, I. Accuracy of GRACE mass estimates. Geophys. Res. Lett. 2006, 33, 178–196. [Google Scholar] [CrossRef] [Green Version]
- Chen, J. Satellite gravimetry and mass transport in the earth system. Geod. Geodyn. 2019, 10, 402–415. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.; Landerer, F.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Wouters, B.; Schrama, E. Improved accuracy of GRACE gravity solutions through empirical orthogonal function filtering of spherical harmonics. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Wilson, C.R.; Li, J.; Zhang, Z. Reducing leakage error in GRACE-observed long-term ice mass change: A case study in West Antarctica. J. Geod. 2015, 89, 925–940. [Google Scholar] [CrossRef]
- Sośnica, K.; Jaggi, A.; Meyer, U.; Thaller, D.; Beutler, G.; Arnold, D.; Dach, R. Time variable Earth’s gravity field from SLR satellites. J. Geod. 2015, 89, 945–960. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.; Ries, J. The unexpected signal in GRACE estimates in C20. J. Geod. 2017, 91, 897–914. [Google Scholar] [CrossRef]
- Blewitt, G.; Lavallée, D.; Clarke, P.J.; Nurutdinov, K. A New Global Mode of Earth Deformation: Seasonal Cycle Detected. Science 2001, 294, 2342–2345. [Google Scholar] [CrossRef] [Green Version]
- Blewitt, G.; Clarke, P. Inversion of Earth’s changing shape to weigh sea level in static equilibrium with surface mass redistribution. J. Geophys. Res. Solid Earth 2003, 108, 2311. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Heflin, M.B.; Ivins, E.R.; Argus, D.F.; Webb, F.H. Large-scale global surface mass variations inferred from GPS measurements of load-induced deformation. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef] [Green Version]
- Kusche, J.; Schrama, E. Surface mass redistribution inversion from global GPS deformation and Gravity Recovery and Climate Experiment (GRACE) gravity data. J. Geophys. Res. Space Phys. 2005, 110, 09409. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Jin, S.; Lu, X. Global Surface Mass Variations from Continuous GPS Observations and Satellite Altimetry Data. Remote Sens. 2017, 9, 1000. [Google Scholar] [CrossRef] [Green Version]
- Rietbroek, R.; Fritsche, M.; Dahle, C.; Brunnabend, S.-E.; Behnisch, M.; Kusche, J.; Flechtner, F.; Schröter, J.; Dietrich, R. Can GPS-Derived Surface Loading Bridge a GRACE Mission Gap? Surv. Geophys. 2014, 35, 1267–1283. [Google Scholar] [CrossRef] [Green Version]
- Argus, D.F.; Fu, Y.; Landerer, F. Seasonal variation in total water storage in California inferred from GPS observations of vertical land motion. Geophys. Res. Lett. 2014, 41, 1971–1980. [Google Scholar] [CrossRef]
- Fu, Y.; Argus, D.F.; Landerer, F. GPS as an independent measurement to estimate terrestrial water storage variations in Washington and Oregon. J. Geophys. Res. Solid Earth 2015, 120, 552–566. [Google Scholar] [CrossRef]
- Davis, J.L.; Elosegui, P.; Mitrovica, J.X.; Tamisiea, M.E. Climate-driven deformation of the solid Earth from GRACE and GPS. Geophys. Res. Lett. 2004, 31, 24605. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Freymueller, J. Seasonal and long-term vertical deformation in the Nepal Himalaya constrained by GPS and GRACE measurements. J. Geophys. Res. Space Phys. 2012, 117, 03407. [Google Scholar] [CrossRef]
- Nahmani, S.; Bock, O.; Bouin, M.-N.; Santamaria, A.; Boy, J.-P.; Collilieux, X.; Métivier, L.; Panet, I.; Genthon, P.; De Linage, C.; et al. Hydrological deformation induced by the West African Monsoon: Comparison of GPS, GRACE and loading models. J. Geophys. Res. Space Phys. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Bevis, M.; Wahr, J.; Khan, S.A.; Madsen, F.B.; Brown, A.; Willis, M.; Kendrick, E.; Knudsen, P.; Box, J.; Van Dam, T.; et al. Bedrock displacements in Greenland manifest ice mass variations, climate cycles and climate change. Proc. Natl. Acad. Sci. USA 2012, 109, 11944–11948. [Google Scholar] [CrossRef] [Green Version]
- Godah, W.; Szelachowska, M.; Ray, J.D.; Krynski, J. Comparison of vertical deformations of the Earth’s surface obtained using GRACE-based GGMs and GNSS data—A case study of South-Eastern Poland. Acta Geodyn. Geomater. 2020, 17, 169–176. [Google Scholar] [CrossRef]
- Hao, M.; Freymueller, J.; Wang, Q.; Cui, D.; Qin, S. Vertical crustal movement around the southeastern Tibetan Plateau constrained by GPS and GRACE data. Earth Planet. Sci. Lett. 2016, 437, 1–8. [Google Scholar] [CrossRef]
- Zhan, W.; Li, F.; Hao, W.; Yan, J. Regional characteristics and influencing factors of seasonal vertical crustal motions in Yunnan, China. Geophys. J. Int. 2017, 210, 1295–1304. [Google Scholar] [CrossRef]
- Liu, R.; Zou, R.; Li, J.; Zhang, C.; Bin, Z.; Zhang, Y. Vertical Displacements Driven by Groundwater Storage Changes in the North China Plain Detected by GPS Observations. Remote Sens. 2018, 10, 259. [Google Scholar] [CrossRef] [Green Version]
- Wahr, J.; Khan, S.A.; Van Dam, T.; Liu, L.; Van Angelen, J.H.; Broeke, M.R.V.D.; Meertens, C. The use of GPS horizontals for loading studies, with applications to northern California and southeast Greenland. J. Geophys. Res. Solid Earth 2013, 118, 1795–1806. [Google Scholar] [CrossRef] [Green Version]
- King, M.; Moore, P.; Clarke, P.J.; Lavallee, D. Choice of optimal averaging radii for temporal GRACE gravity solutions, a comparison with GPS and satellite altimetry. Geophys. J. Int. 2006, 166, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Van Dam, T.; Wahr, J.; Lavallee, D. A comparison of annual vertical crustal displacements from GPS and Gravity Recovery and Climate Experiment (GRACE) over Europe. J. Geophys. Res. Space Phys. 2007, 112, 03404. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.; Zhang, T. Terrestrial Water Storage Anomalies Associated with Drought in Southwestern USA from GPS Observations. Surv. Geophys. 2016, 37, 1139–1156. [Google Scholar] [CrossRef]
- Enzminger, T.L.; Small, E.E.; Borsa, A.A. Accuracy of Snow Water Equivalent Estimated from GPS Vertical Displacements: A Synthetic Loading Case Study for Western U.S. Mountains. Water Resour. Res. 2018, 54, 581–599. [Google Scholar] [CrossRef]
- Zhang, B.; Yao, Y.; Fok, H.S.; Hu, Y.; Chen, Q. Potential Seasonal Terrestrial Water Storage Monitoring from GPS Vertical Displacements: A Case Study in the Lower Three-Rivers Headwater Region, China. Sensors 2016, 16, 1526. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Ndehedehe, C.E.; Montecino, H.; Gourley, J.J.; Yuan, P.; Abdalla, A.; Mohammed, A.S. Prospects for Imaging Terrestrial Water Storage in South America Using Daily GPS Observations. Remote Sens. 2019, 11, 679. [Google Scholar] [CrossRef] [Green Version]
- Fok, H.S.; Liu, Y. An Improved GPS-Inferred Seasonal Terrestrial Water Storage Using Terrain-Corrected Vertical Crustal Displacements Constrained by GRACE. Remote Sens. 2019, 11, 1433. [Google Scholar] [CrossRef] [Green Version]
- Landerer, F.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Zhao, B.; Huang, Y.; Zhang, C.; Wang, W.; Tan, K.; Du, R. Crustal deformation on the Chinese mainland during 1998–2014 based on GPS data. Geod. Geodyn. 2015, 6, 7–15. [Google Scholar] [CrossRef] [Green Version]
- Schmid, R.; Dach, R.; Collilieux, X.; Jäggi, A.; Schmitz, M.; Dilssner, F. Absolute IGS antenna phase center model igs08.atx: Status and potential improvements. J. Geod. 2015, 90, 343–364. [Google Scholar] [CrossRef] [Green Version]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H.; Böhm, J. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, 07304. [Google Scholar] [CrossRef] [Green Version]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Landerer, F. Monthly Estimates of Degree-1 (Geocenter) Gravity Coefficients, Generated from GRACE (04-2002-06/2017) and GRACE-FO (06/2018 onward) RL06 Solutions; GRACE Technical Note 13, the GRACE Project; NASA Jet Propulsion Laboratory: Pasadena, CA, USA, 2019. [Google Scholar]
- Loomis, B.D.; Rachlin, K.E.; Wiese, D.N.; Landerer, F.W.; Luthcke, S.B. Replacing GRACE/GRACE-FO With Satellite Laser Ranging: Impacts on Antarctic Ice Sheet Mass Change. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Grand, S. GRACE detects coseismic and postseismic deformation from the Sumatra-Andaman e earthquake. Geophys. Res. Lett. 2007, 34, L13302. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Houser, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.R.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Li, J.; Zhang, Z.; Ni, S. Long-term groundwater variations in Northwest India from satellite gravity measurements. Glob. Planet. Change 2014, 116, 130–138. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Wilson, C.R.; Tapley, B.; Scanlon, B.; Guntner, A. Long-term groundwater storage change in Victoria, Australia from satellite gravity and in situ observations. Glob. Planet. Change 2016, 139, 56–65. [Google Scholar] [CrossRef] [Green Version]
- Wiese, D.N.; Landerer, F.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Save, H. “CSR GRACE RL06 Mascon Solutions”, Texas Data Repository Dataverse, V1. 2019. Available online: https://doi.org/10.18738/T8/UN91VR (accessed on 25 May 2020).
- Chen, J.; Wilson, C.R.; Tapley, B.D.; Save, H.; Cretaux, J.-F. Long-term and seasonal Caspian Sea level change from satellite gravity and altimeter measurements. J. Geophys. Res. Solid Earth 2017, 122, 2274–2290. [Google Scholar] [CrossRef]
- Ray, J.; Altamimi, Z.; Collilieux, X.; Van Dam, T. Anomalous harmonics in the spectra of GPS position estimates. GPS Solut. 2007, 12, 55–64. [Google Scholar] [CrossRef]
- Glaser, S.; Fritsche, M.; Sośnica, K.; Rodriguez-Solano, C.J.; Wang, K.; Dach, R.; Hugentobler, U.; Rothacher, M.; Dietrich, R. A consistent combination of GNSS and SLR with minimum constraints. J. Geod. 2015, 89, 1165–1180. [Google Scholar] [CrossRef]
- Nikolaidis, R. Observation of Geodetic and Seismic Deformation with the Global Positioning System. Ph.D. Thesis, University of California San Deigo, San Deigo, CA, USA, 2002. [Google Scholar]
- Oliveira, P.; Gomes, L. Interpolation of signals with missing data using Principal Component Analysis. Multidimens. Syst. Signal Process. 2009, 21, 25–43. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by surface loads. Rev. Geophys. 1972, 10, 761. [Google Scholar] [CrossRef]
- Rajner, M.; Liwosz, T. Studies of crustal deformation due to hydrological loading on GPS height estimates. Geod. Cartogr. 2011, 60, 135–144. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Xiang, L.; Jia, L.; Jiang, L.; Wang, Z.; Hu, B.; Gao, P. Load Love numbers and Green’s functions for elastic Earth models PREM, iasp91, ak135, and modified models with refined crustal structure from Crust 2.0. Comp. Geosci. 2012, 49, 190–199. [Google Scholar] [CrossRef]
- Van Dam, E.; Omidi, G. Graphs whose normalized Laplacian has three eigenvalues. Linear Algebra Appl. 2011, 435, 2560–2569. [Google Scholar] [CrossRef]
- Golub, G.H.; Wahba, H.G. Generalized Cross-Validation as a Method for Choosing a Good Ridge Parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Liao, H.; Ng, M.K. Blind Deconvolution Using Generalized Cross-Validation Approach to Regularization Parameter Estimation. IEEE Trans. Image Process. 2011, 20, 670–680. [Google Scholar] [CrossRef]



| Study Region | Area (km2) | Number of Stations | Station Density 1 |
|---|---|---|---|
| Yunnan Province | 428,154.75 | 26 | 60.73 |
| Min River Basin | 190,205.44 | 8 | 42.06 |
| Jialing River Basin | 187,125.19 | 5 | 26.72 |
| Wu River Basin | 97,797.94 | 2 | 20.45 |
| Study Region | Data Type | Annual (Semi-Annual) Amplitude 1 (Gt) | Annual (Semi-Annual) Phase 1 (Year) | RMS (Gt) |
|---|---|---|---|---|
| YNP | GPS | 52.00 ± 3.24 (20.00 ± 3.24) | 0.09 ± 0.06 (−0.35 ± 0.16) | / |
| CSR-SH | 55.71 ± 2.16 (11.28 ± 2.16) | 0.06 ± 0.04 (0.00 ± 0.19) | 24.61 | |
| CSR-M | 53.66 ± 2.13 (10.15 ± 2.13) | 0.31 ± 0.04 (0.49 ± 0.21) | 26.11 | |
| MRB | GPS | 10.11 ± 1.42 (1.46 ± 1.41) | 0.01 ± 0.14 (−0.24 ± 0.97) | / |
| CSR-SH | 8.75 ± 0.82 (2.49 ± 0.82) | 0.48 ± 0.09 (−0.33 ± 0.33) | 8.74 | |
| CSR-M | 8.88 ± 0.48 (2.73 ± 0.48) | 0.48 ± 0.05 (−0.43 ± 0.18) | 7.48 | |
| JLRB | GPS | 10.45 ± 0.97 (3.14 ± 0.98) | 0.71 ± 0.09 (0.67 ± 0.31) | / |
| CSR-SH | 9.78 ± 0.92 (3.41 ± 0.92) | 0.45 ± 0.10 (0.17 ± 0.27) | 7.82 | |
| CSR-M | 11.46 ± 0.59 (3.46 ± 0.58) | 0.37 ± 0.05 (0.30 ± 0.17) | 6.33 | |
| WRB | GPS | 3.60 ± 0.60 (1.38 ± 0.60) | 0.94 ± 0.17 (0.51 ± 0.43) | / |
| CSR-SH | 5.63 ± 0.43 (0.45 ± 0.43) | 0.43 ± 0.08 (−0.02 ± 0.97) | 4.42 | |
| CSR-M | 6.04 ± 0.37 (0.97 ± 0.37) | 0.57 ± 0.06 (0.70 ± 0.38) | 3.96 |
| Study Region | Data Type | Annual Amplitude 1 (Gt) | Annual Phase 1 (Year) | RMS (Gt) |
|---|---|---|---|---|
| YNP | CSR GFO-SH | 59.19 ± 8.50 | 0.74 ± 0.12 | 8.12 |
| Raw GPS | 72.69 ± 6.66 | 0.17 ± 0.09 | 16.71 | |
| Basin-scaled GPS | 59.84 ± 7.16 | 0.77 ± 0.11 | 13.61 | |
| Pixel-scaled GPS | 56.00 ± 7.43 | 0.74 ± 0.12 | 18.04 | |
| MRB | CSR GFO-SH | 12.53 ± 1.93 | 0.12 ± 0.13 | 2.95 |
| Raw GPS | 22.42 ± 1.91 | 0.58 ± 0.09 | 5.50 | |
| Basin-scaled GPS | 10.03 ± 0.87 | 0.15 ± 0.09 | 2.49 | |
| Pixel-scaled GPS | 14.71 ± 1.33 | 0.31 ± 0.09 | 3.46 | |
| JLRB | CSR GFO-SH | 12.96 ± 2.63 | 0.58 ± 0.18 | 4.05 |
| Raw GPS | 7.54 ± 1.07 | 0.13 ± 0.13 | 3.05 | |
| Basin-scaled GPS | 4.65 ± 0.88 | 0.06 ± 0.17 | 1.85 | |
| Pixel-scaled GPS | 8.30 ± 1.99 | 0.06 ± 0.22 | 2.91 | |
| WRB | CSR GFO-SH | 7.05 ± 1.16 | 0.33 ± 0.15 | 1.88 |
| Raw GPS | 5.99 ± 1.31 | 0.57 ± 0.22 | 2.58 | |
| Basin-scaled GPS | 3.56 ± 0.74 | 0.56 ± 0.21 | 1.51 | |
| Pixel-scaled GPS | 5.62 ± 0.72 | 0.71 ± 0.12 | 1.87 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, B.; Li, X.; Chen, J.; Li, Q.; Liu, T. Surface Mass Variations from GPS and GRACE/GFO: A Case Study in Southwest China. Remote Sens. 2020, 12, 1835. https://doi.org/10.3390/rs12111835
Zhong B, Li X, Chen J, Li Q, Liu T. Surface Mass Variations from GPS and GRACE/GFO: A Case Study in Southwest China. Remote Sensing. 2020; 12(11):1835. https://doi.org/10.3390/rs12111835
Chicago/Turabian StyleZhong, Bo, Xianpao Li, Jianli Chen, Qiong Li, and Tao Liu. 2020. "Surface Mass Variations from GPS and GRACE/GFO: A Case Study in Southwest China" Remote Sensing 12, no. 11: 1835. https://doi.org/10.3390/rs12111835
APA StyleZhong, B., Li, X., Chen, J., Li, Q., & Liu, T. (2020). Surface Mass Variations from GPS and GRACE/GFO: A Case Study in Southwest China. Remote Sensing, 12(11), 1835. https://doi.org/10.3390/rs12111835






