Novel Air Temperature Measurement Using Midwave Hyperspectral Fourier Transform Infrared Imaging in the Carbon Dioxide Absorption Band
Abstract
1. Introduction
2. Materials for FTIR Analysis
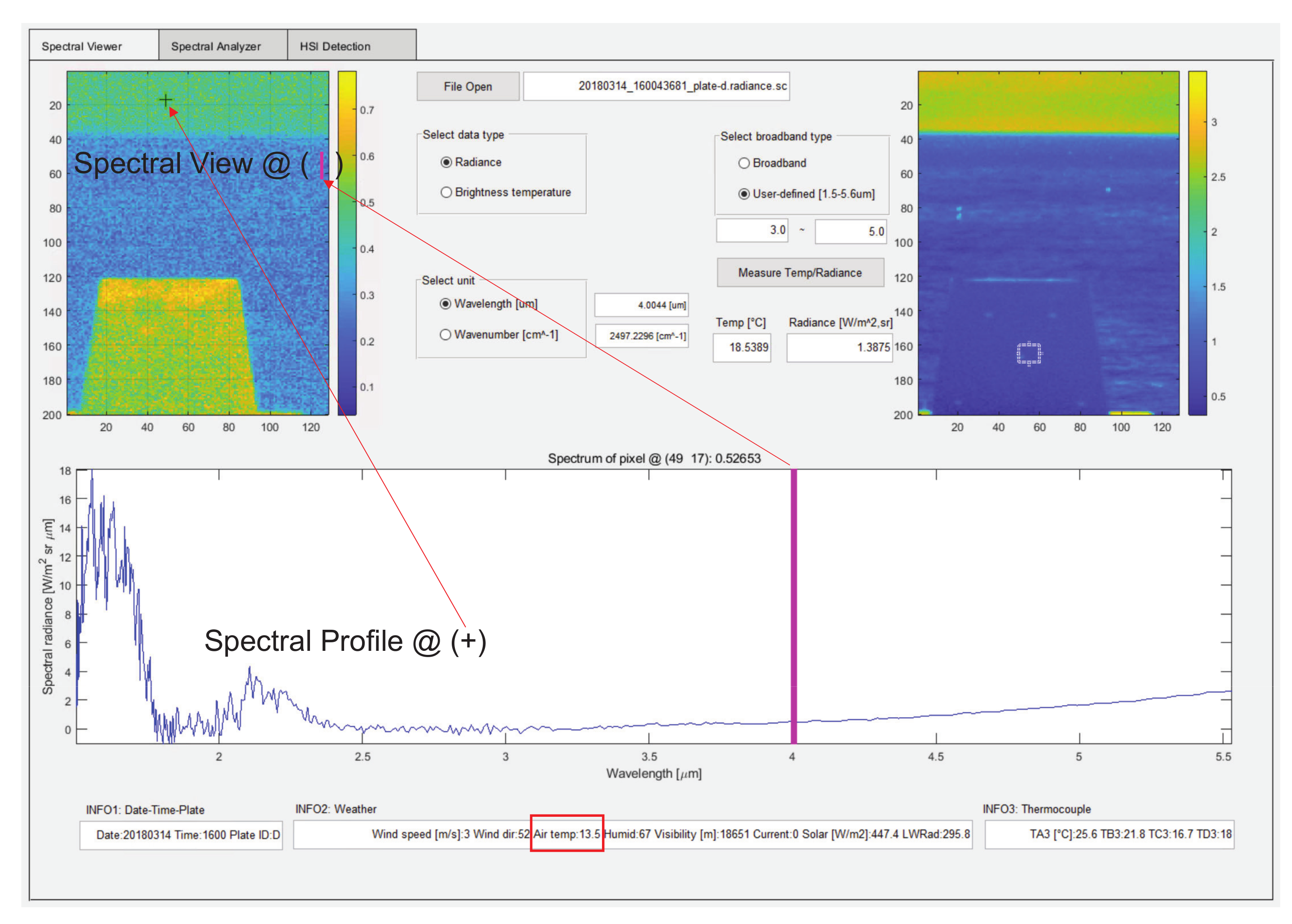
2.1. Outdoor Hyperspectral Data Acquisition System
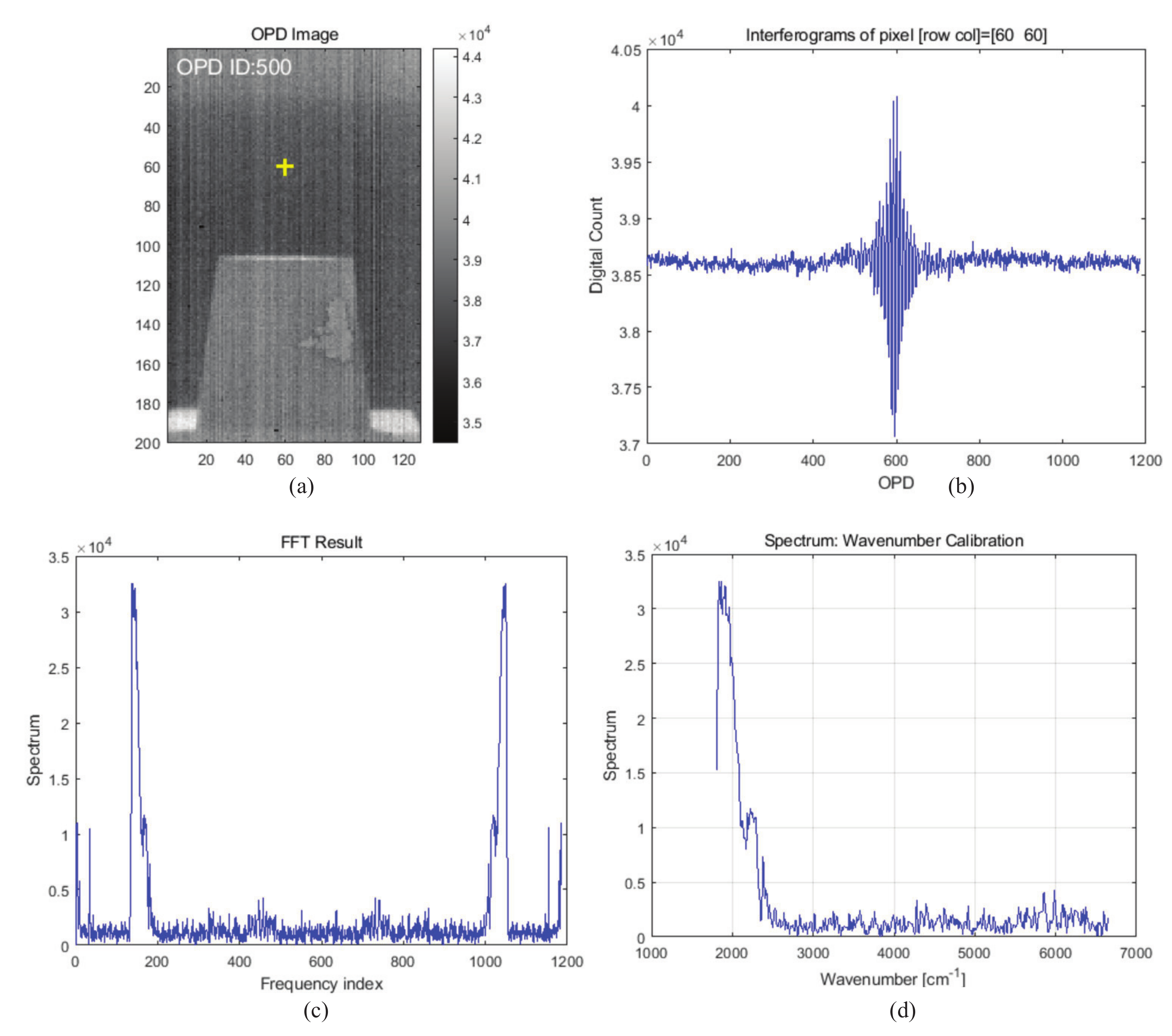
2.2. FTIR Data Acquisition Interface
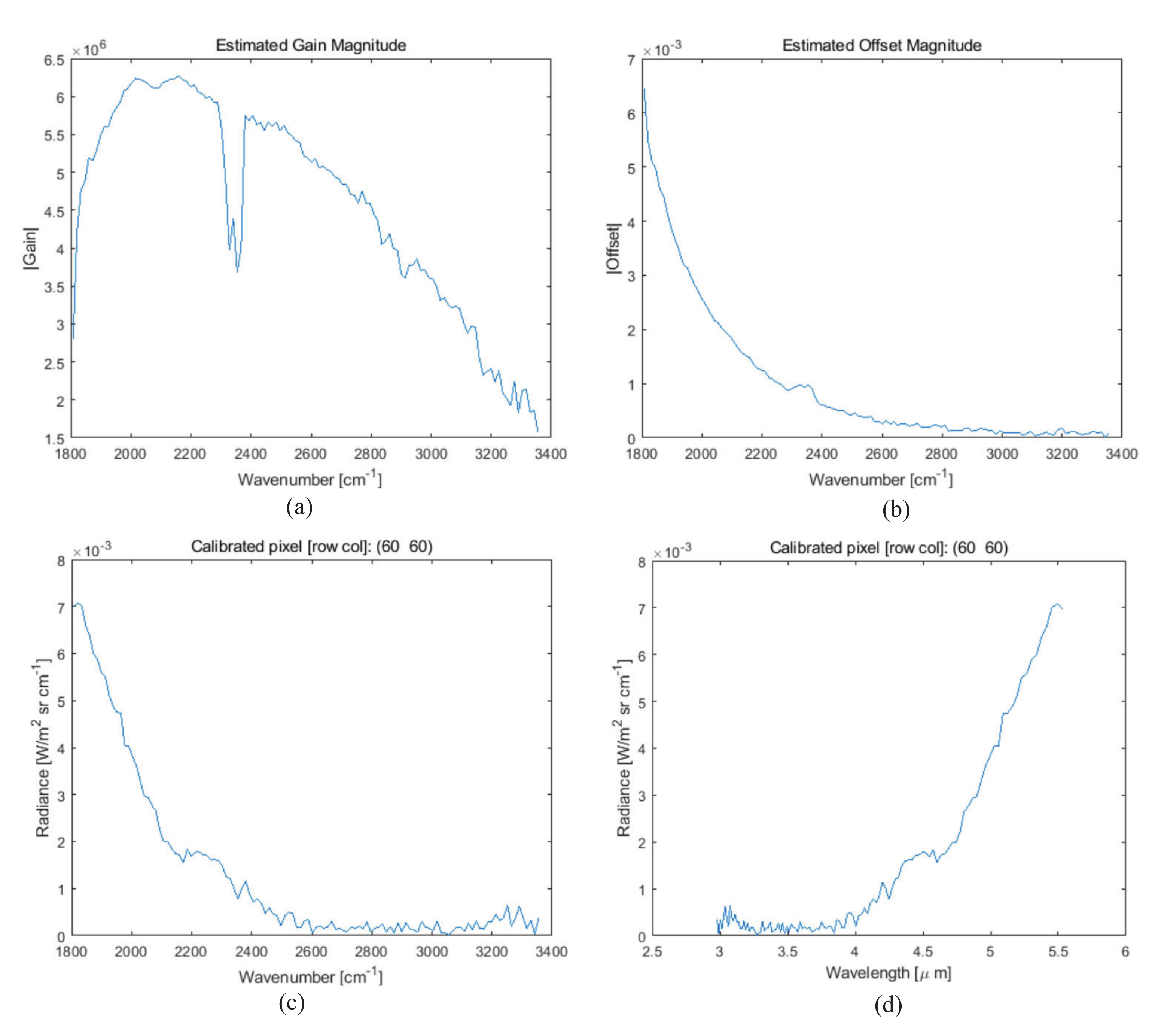
2.3. Radiometric Calibration of FTIR Imaging
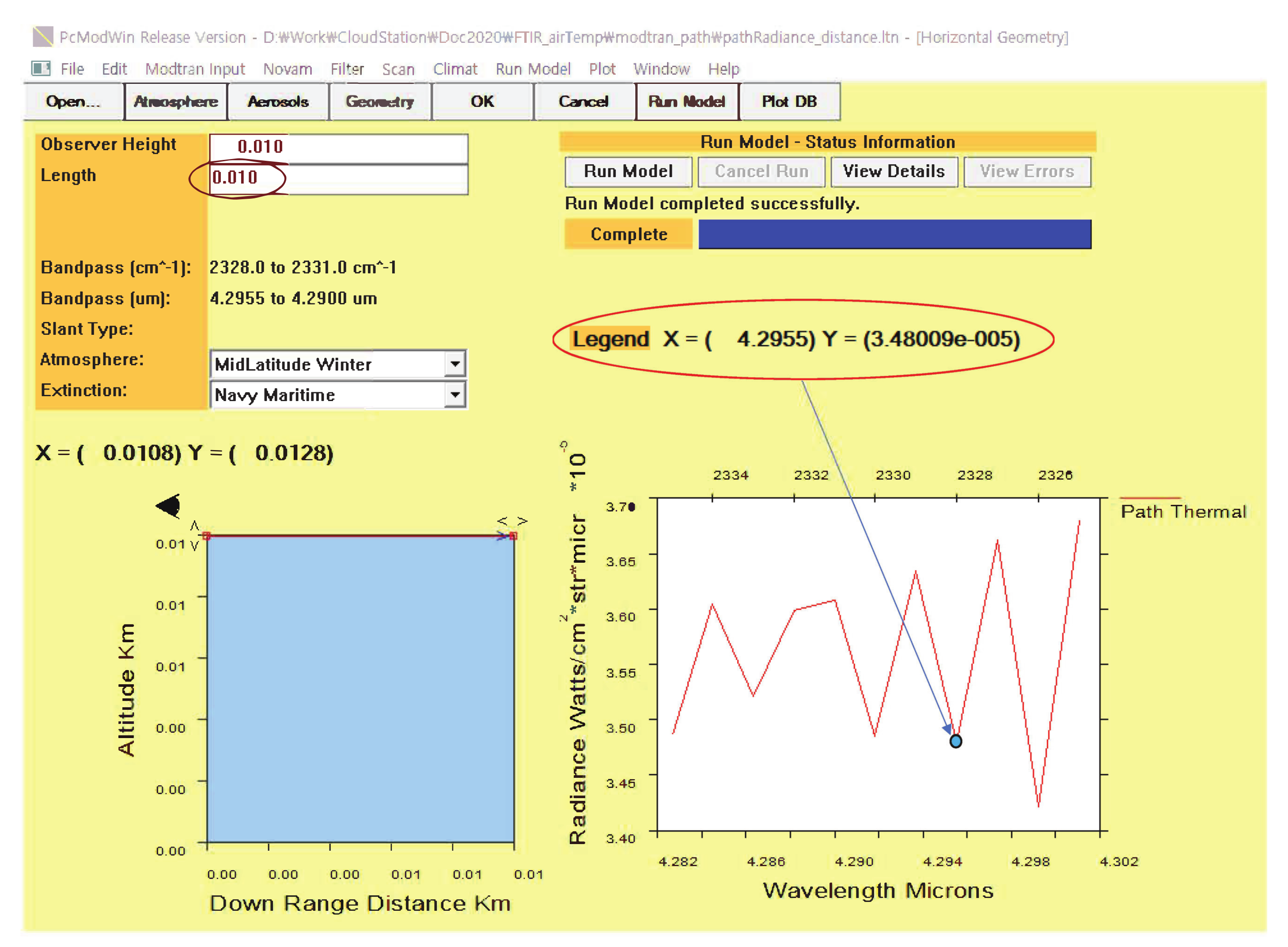
2.4. MODTRAN Simulator
3. Proposed Visual Air Temperature Measurement Method
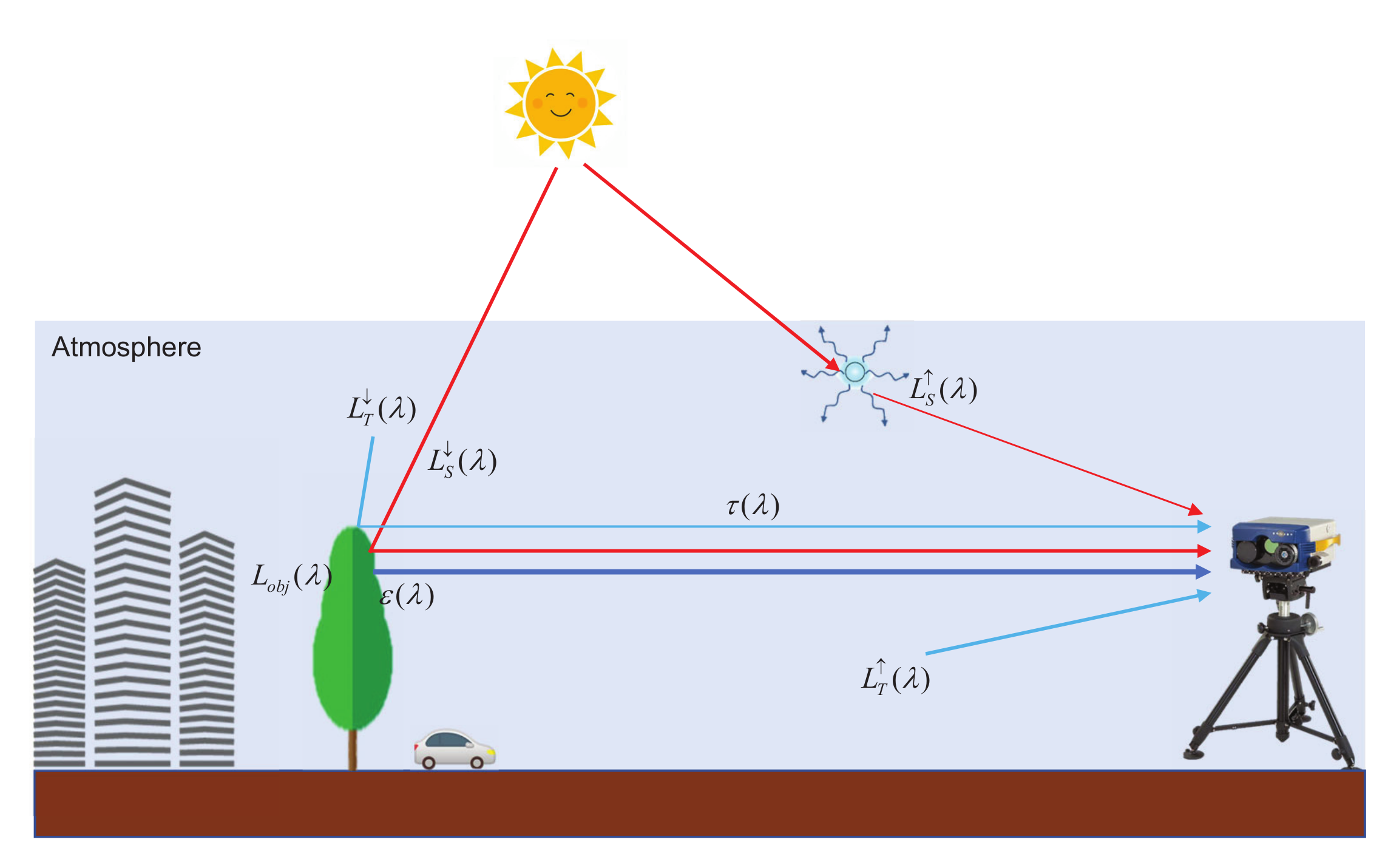
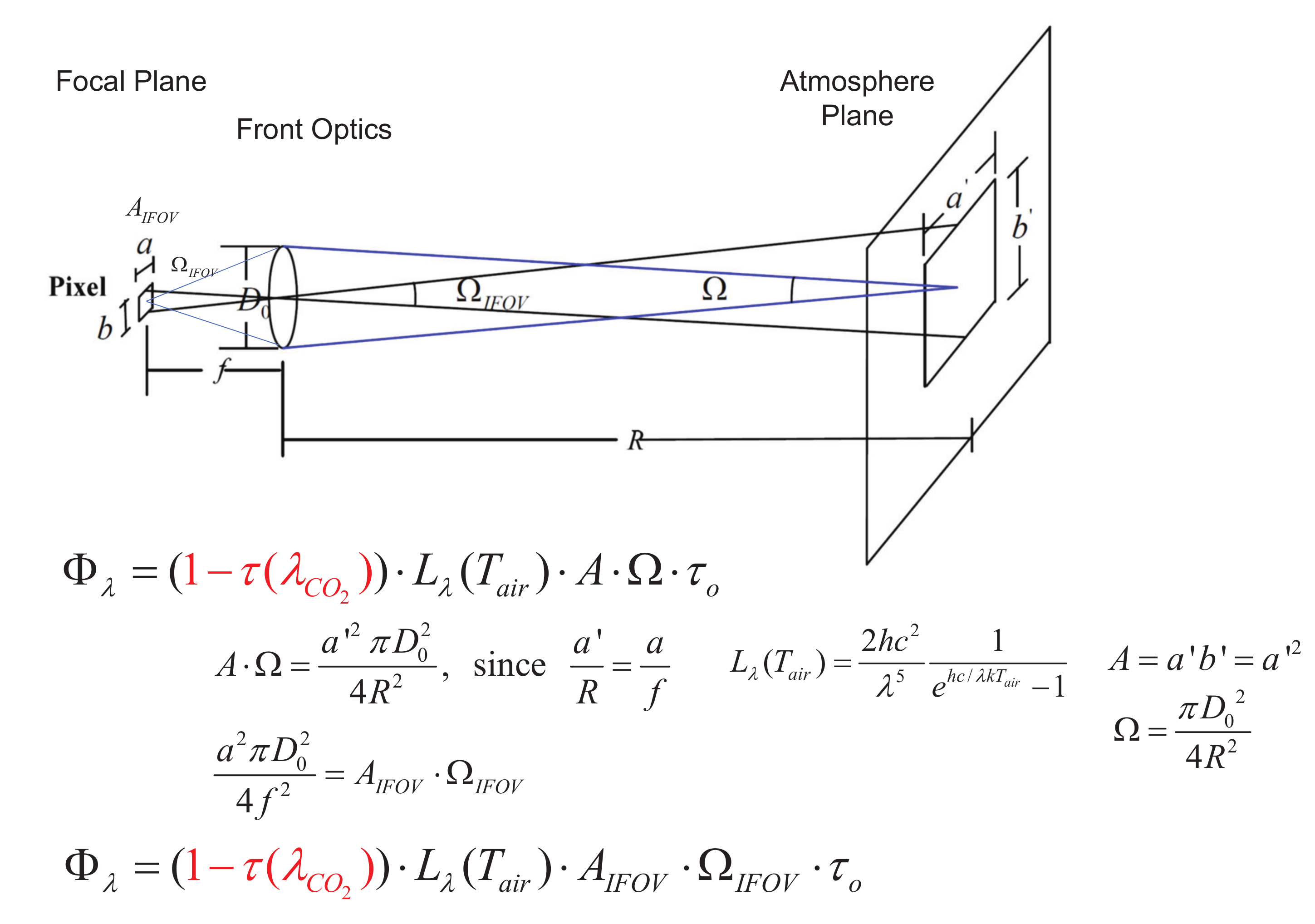
3.1. Derivation of Radiative Ttransfer Equation
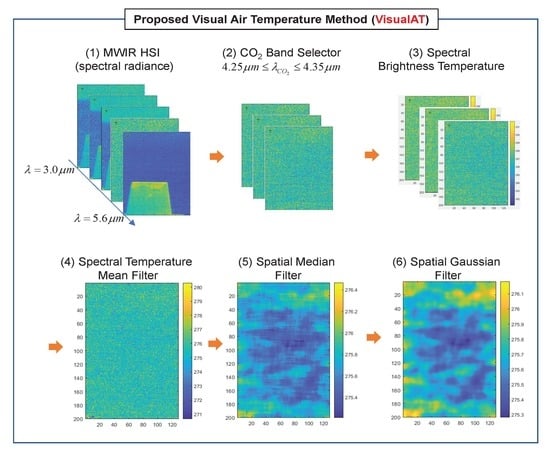
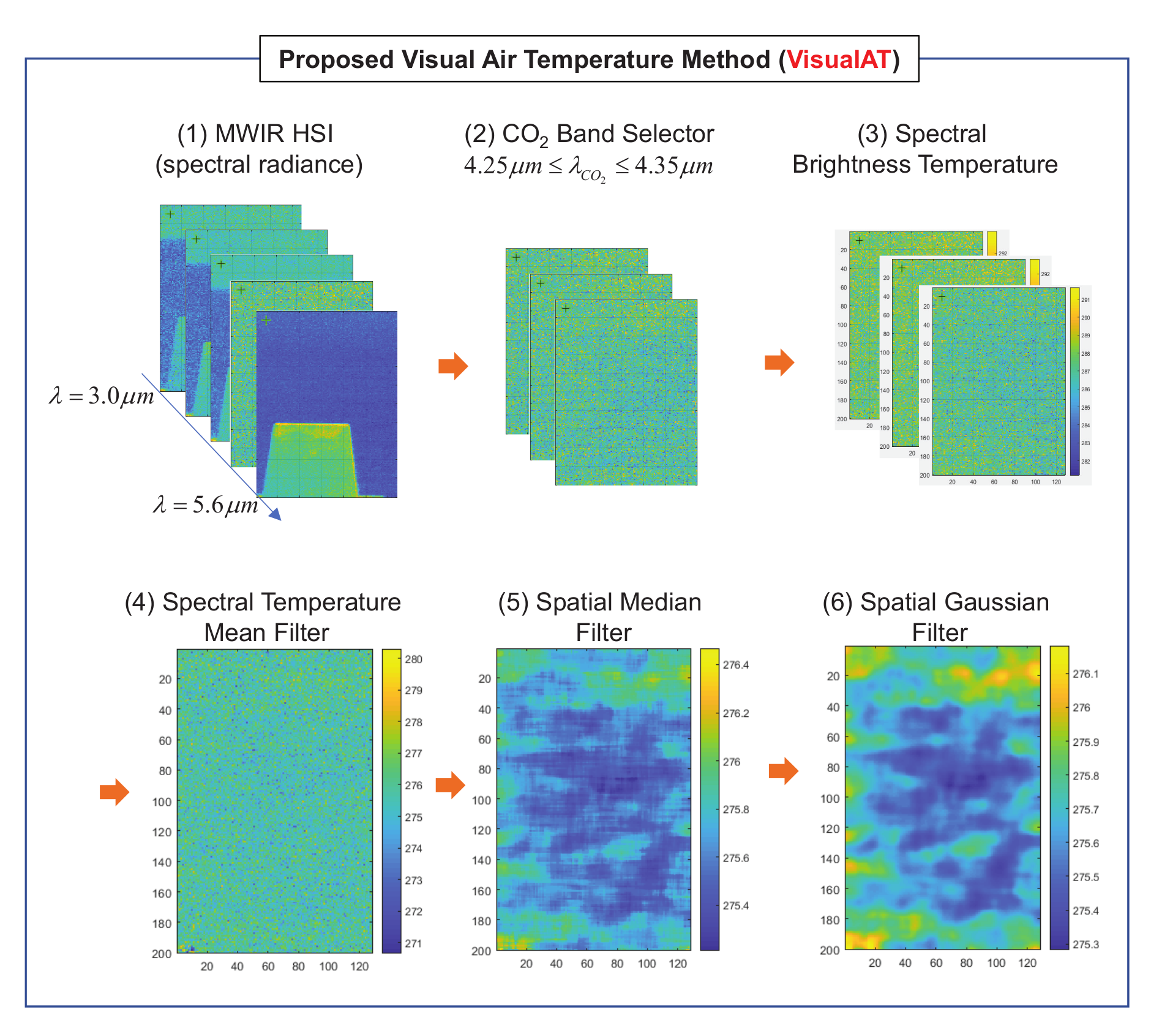
3.2. VisualAT: Proposed Visual Air Temperature Measurement
- (1)
- Given is an MWIR hyperspectral image cube (374 bands, spatial resolution: ).
- (2)
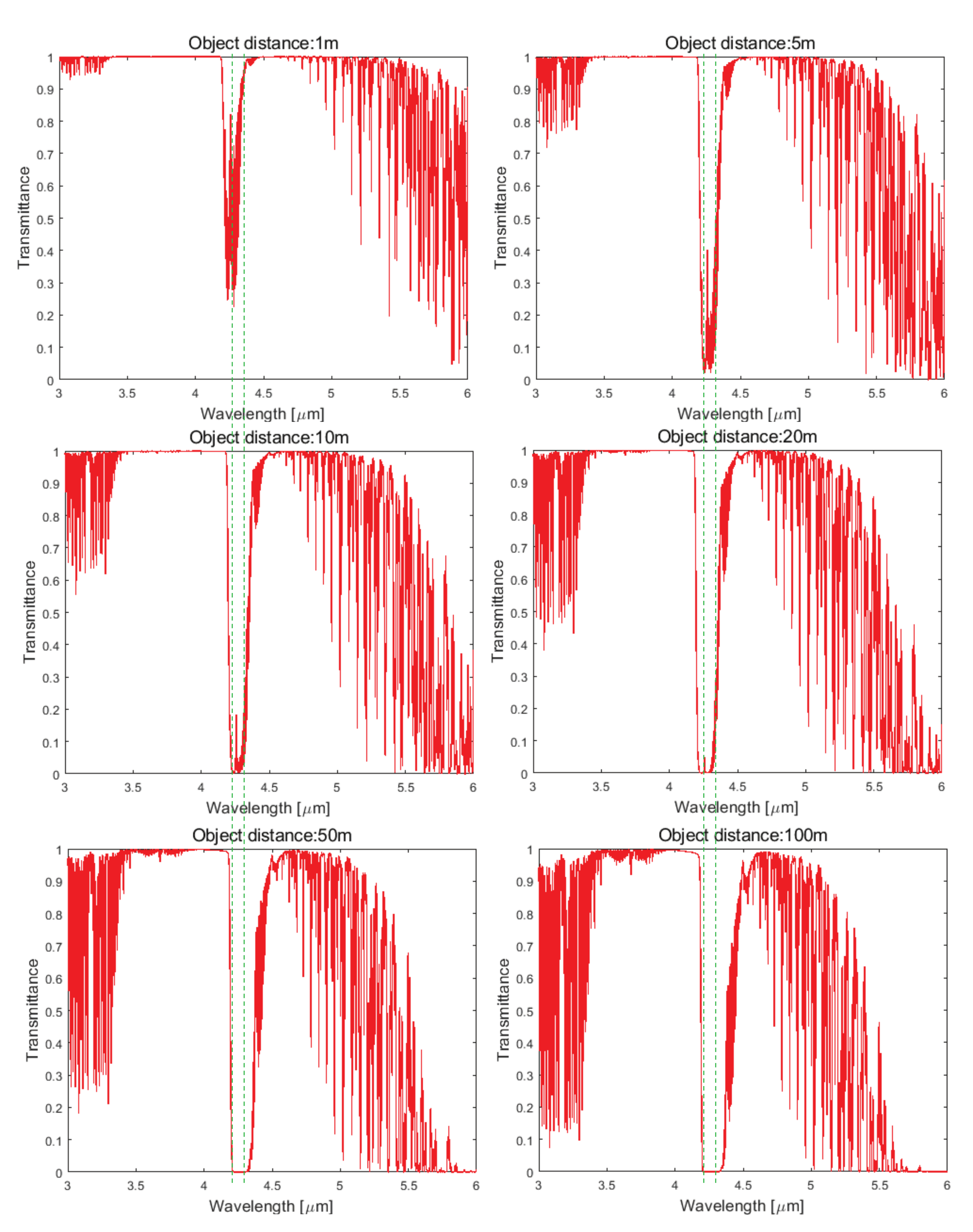
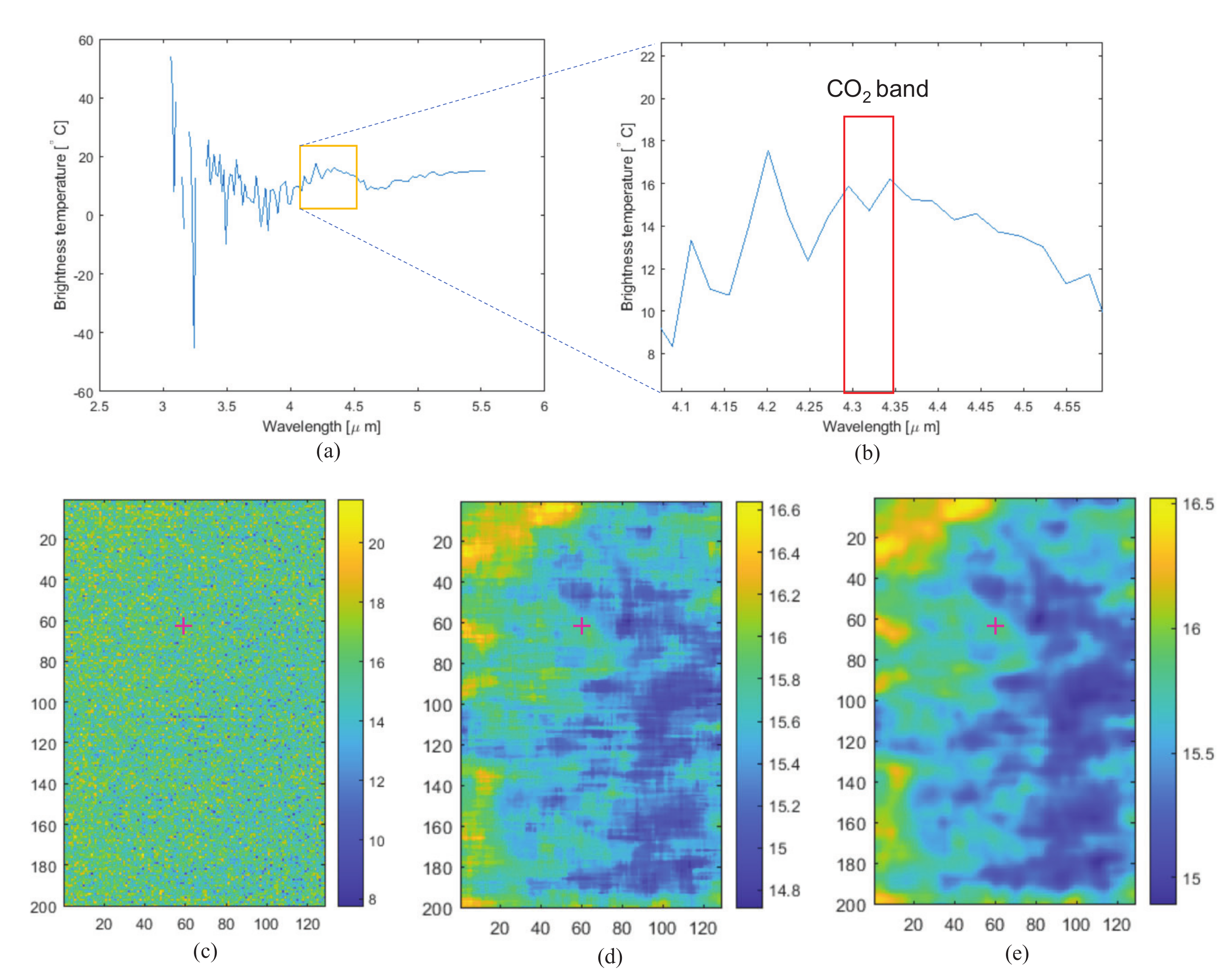
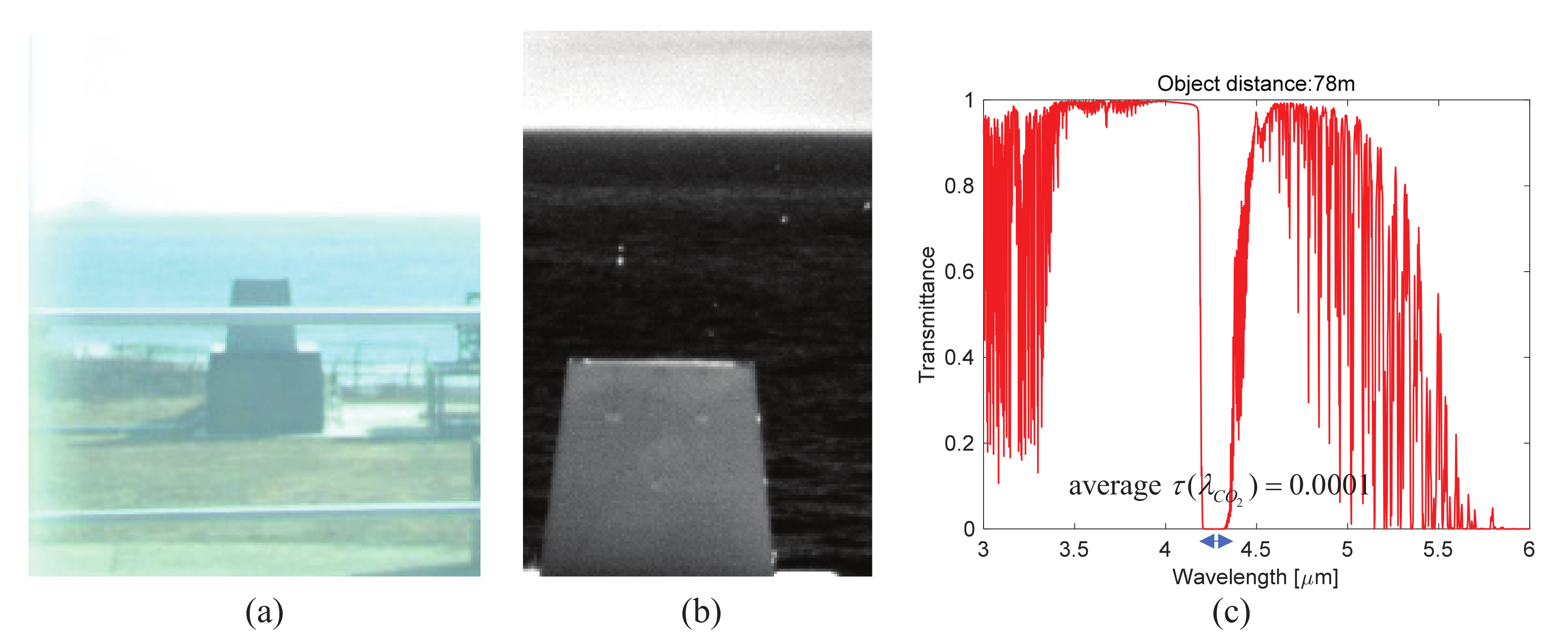
- CO band images (4.29, 4.31, 4.34 m) are selected. The band region between 4.25–4.35 m is selected based on the MODTRAN-based transmissivity analysis () and visual inspection. A wavelength can be in the CO absorption band if there is no object signature and it looks like a noisy image.
- (3)
- The selected spectral radiance images are converted to spectral brightness images using Equation (8).
- (3)
- The second row of Figure 9 represents the image processing for visual air temperature image generation, explained in the following steps.
- (4)
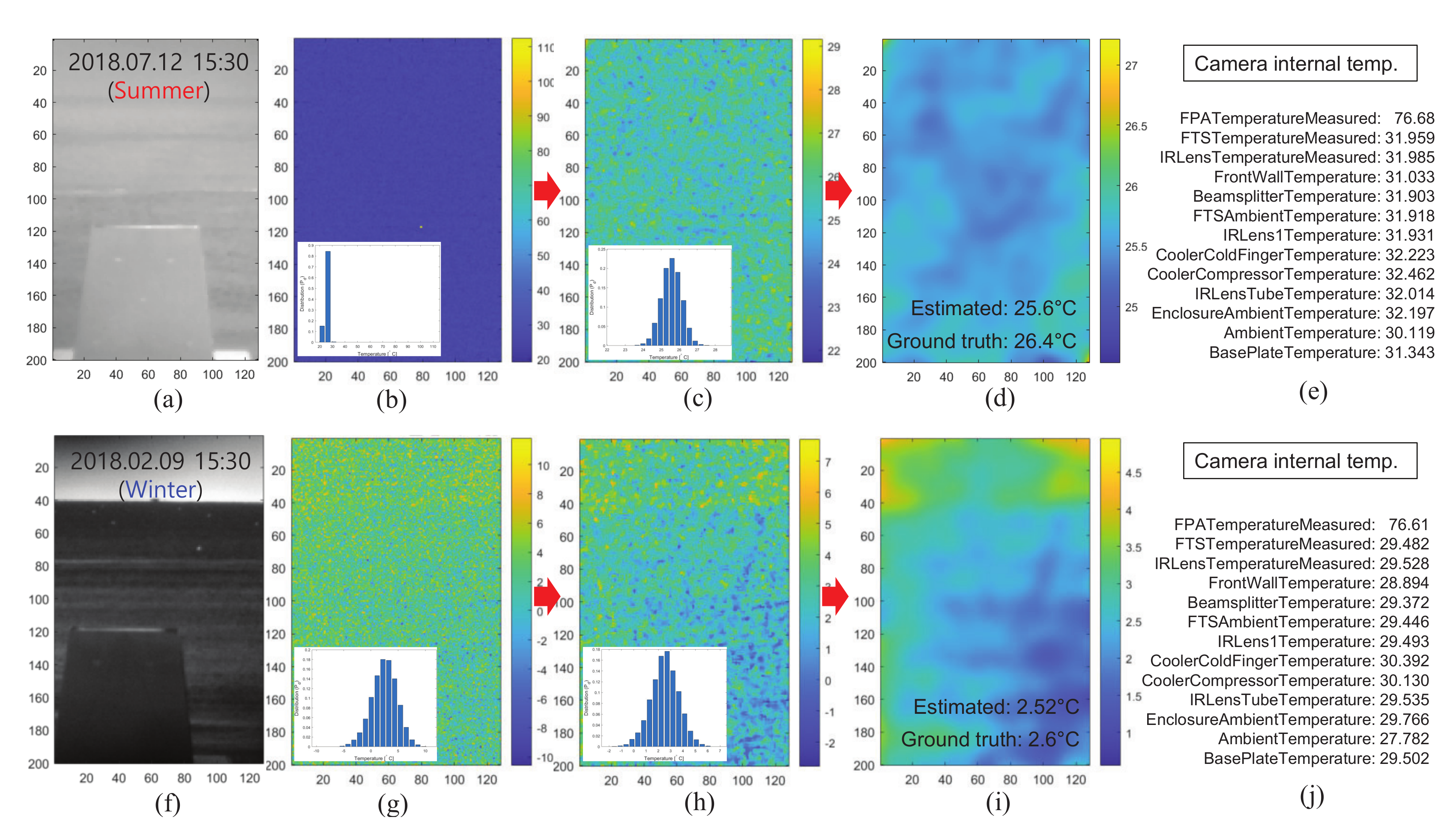
- A raw temperature image is extracted via pixel-wise temperature mean filter along the spectral axis. It still shows a noise-like image consisting of salt-and-pepper noise and thermal noise. This can be removed by consecutive spatial 2D median filtering and Gaussian filtering [34]. The Gaussian filtering is adopted to reduce spatial thermal noise. The empirically tuned kernel size of the median filter is , and sigma of the Gaussian filter is set to 2.
3.3. Analysis of Air Temperature Measurement
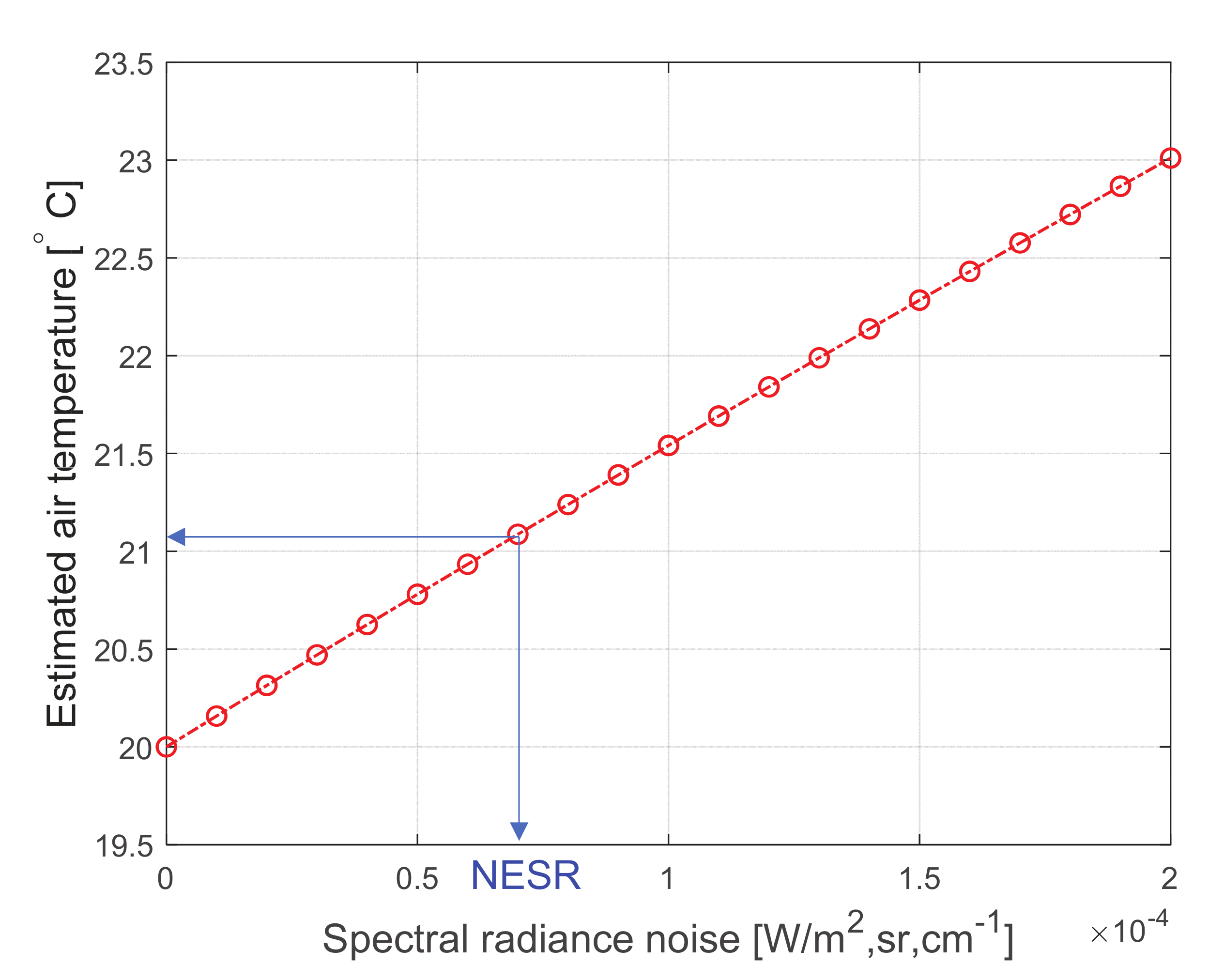
3.4. Signal Analysis of Air Temperature Monitoring
3.5. Performance Metric
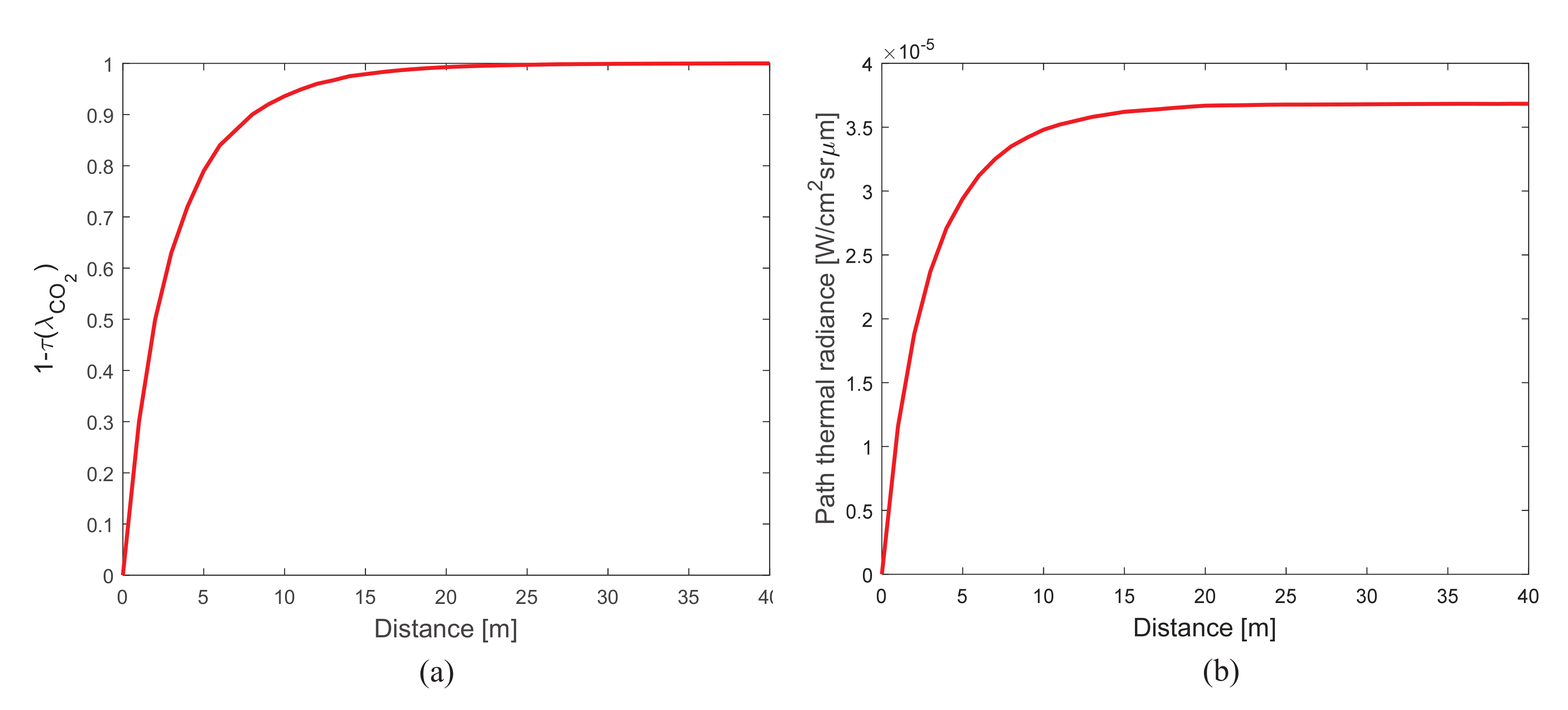
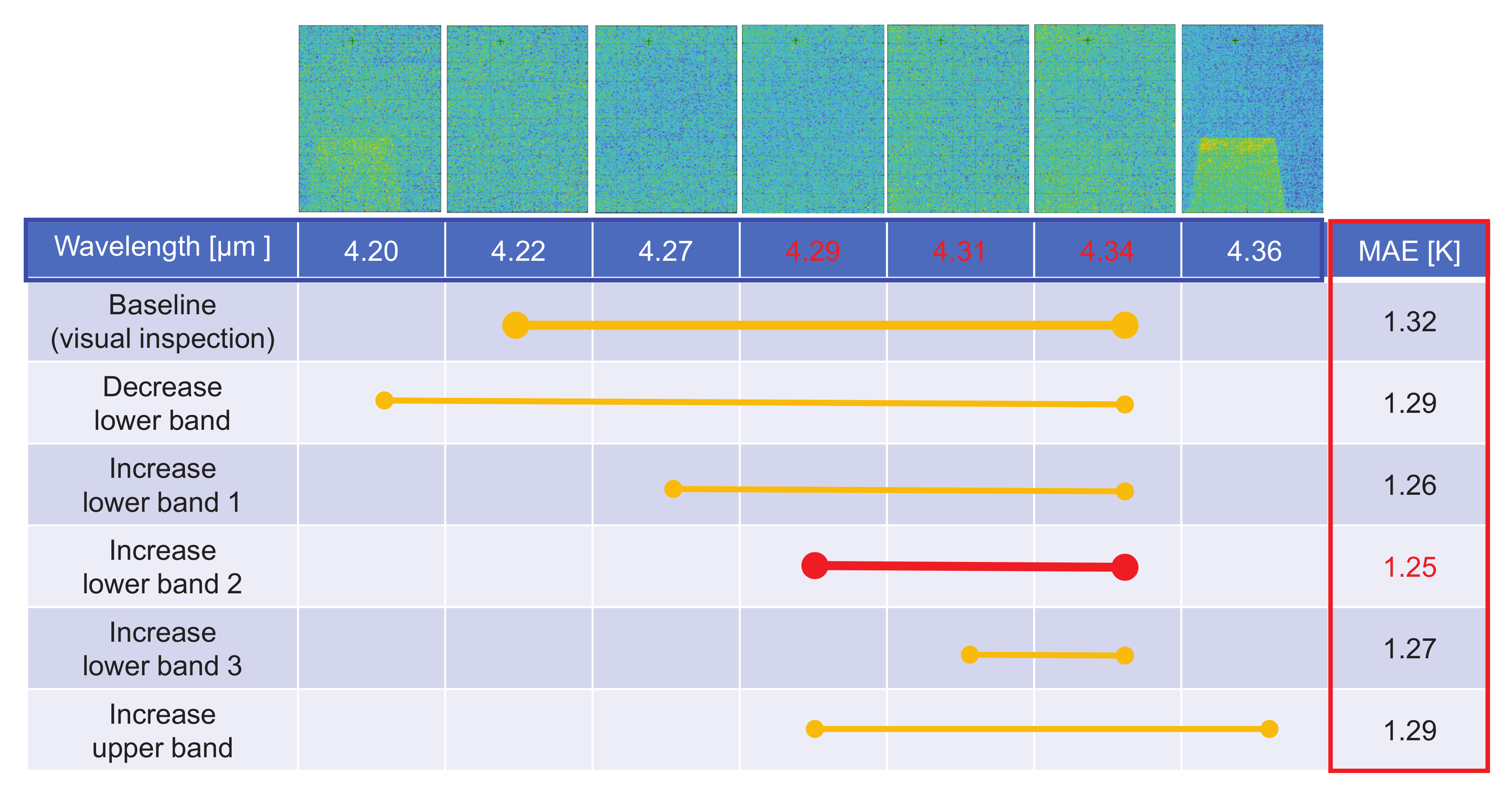
3.6. Parameter Analysis
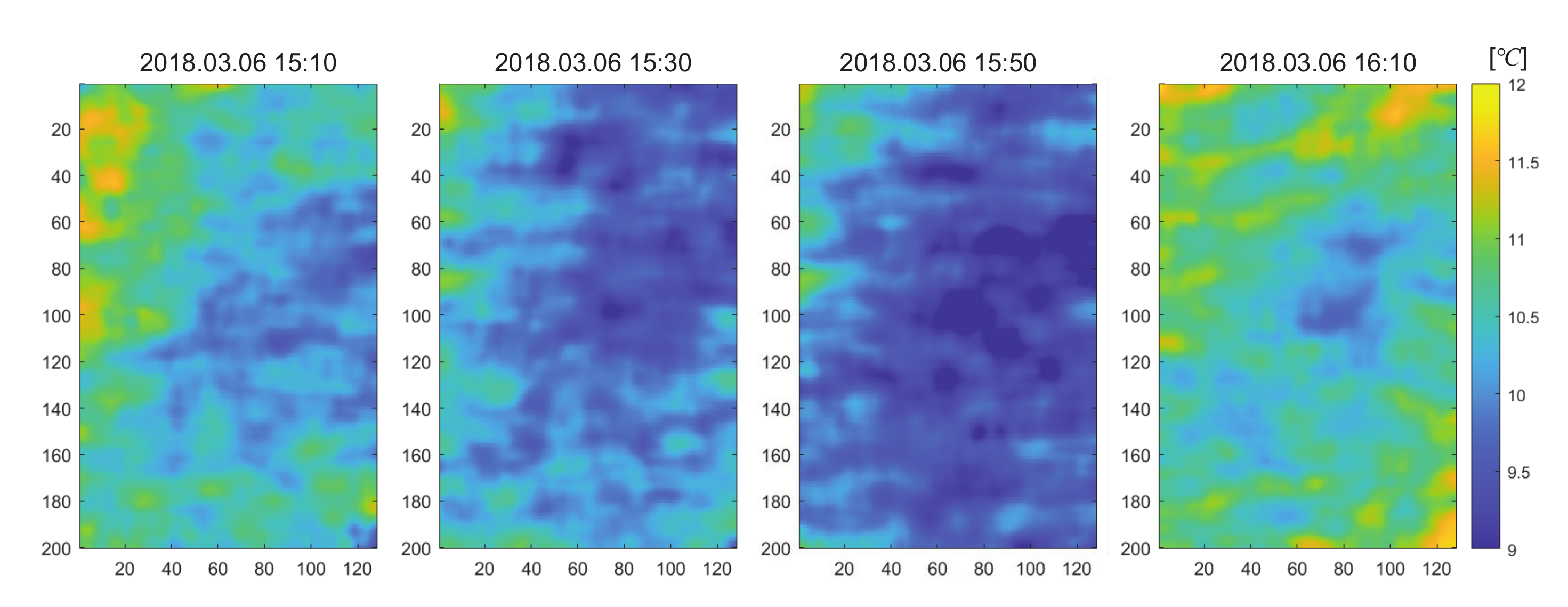
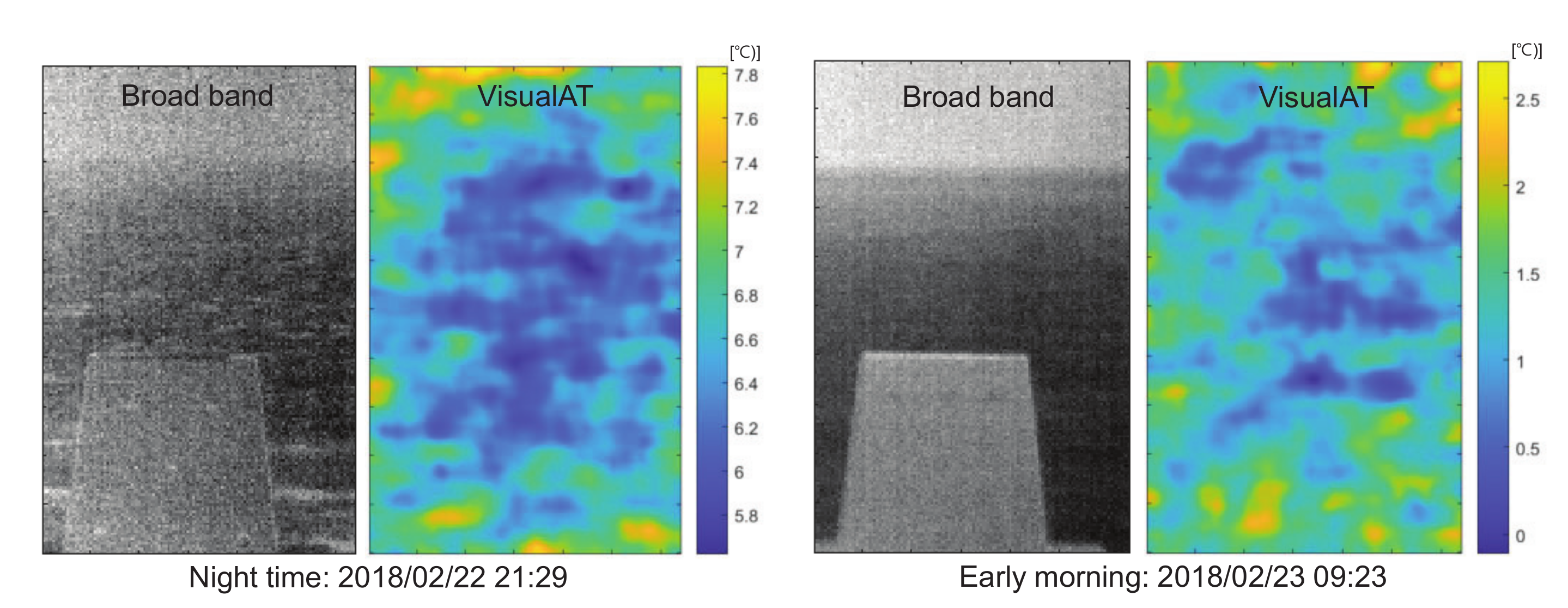
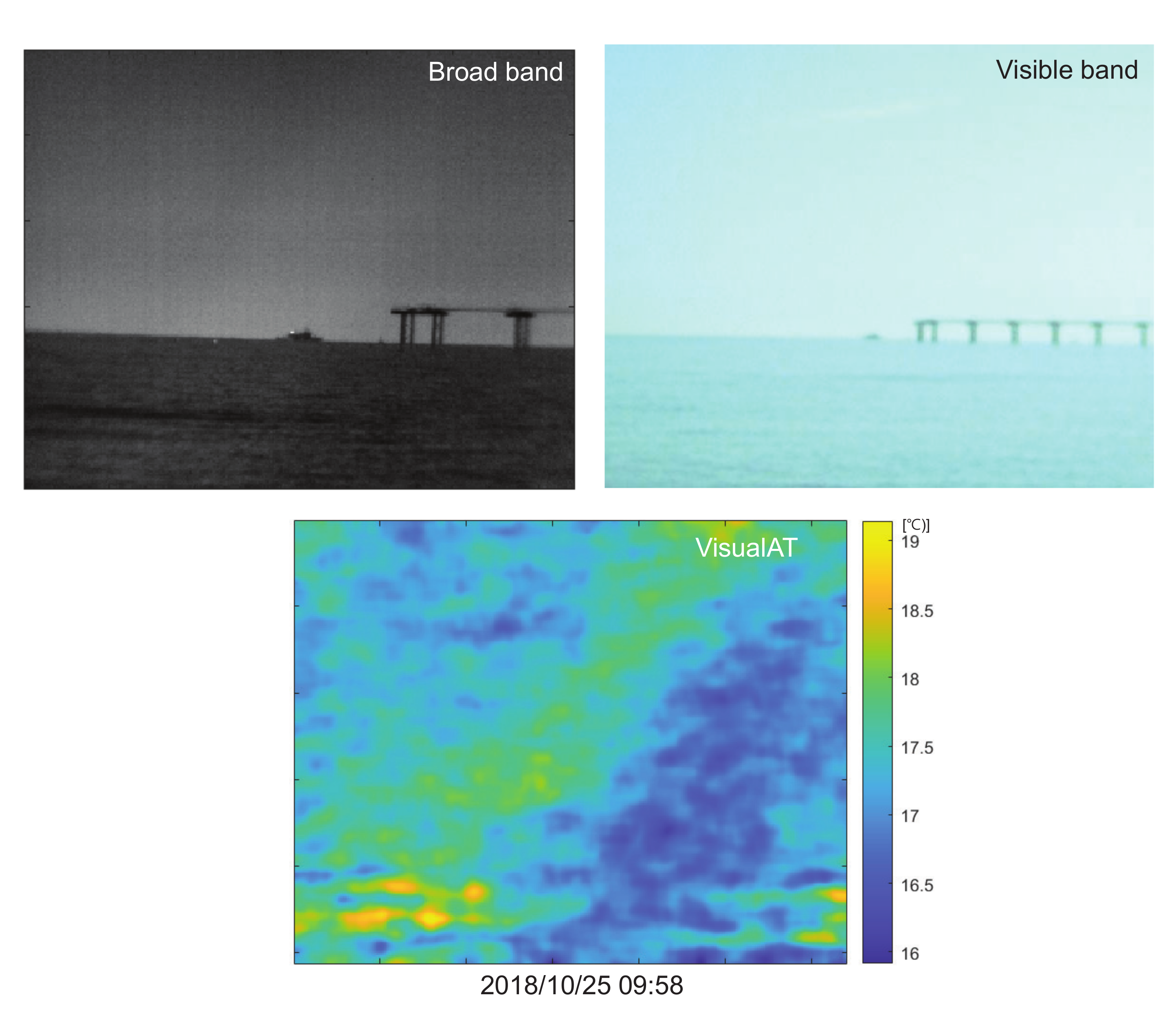
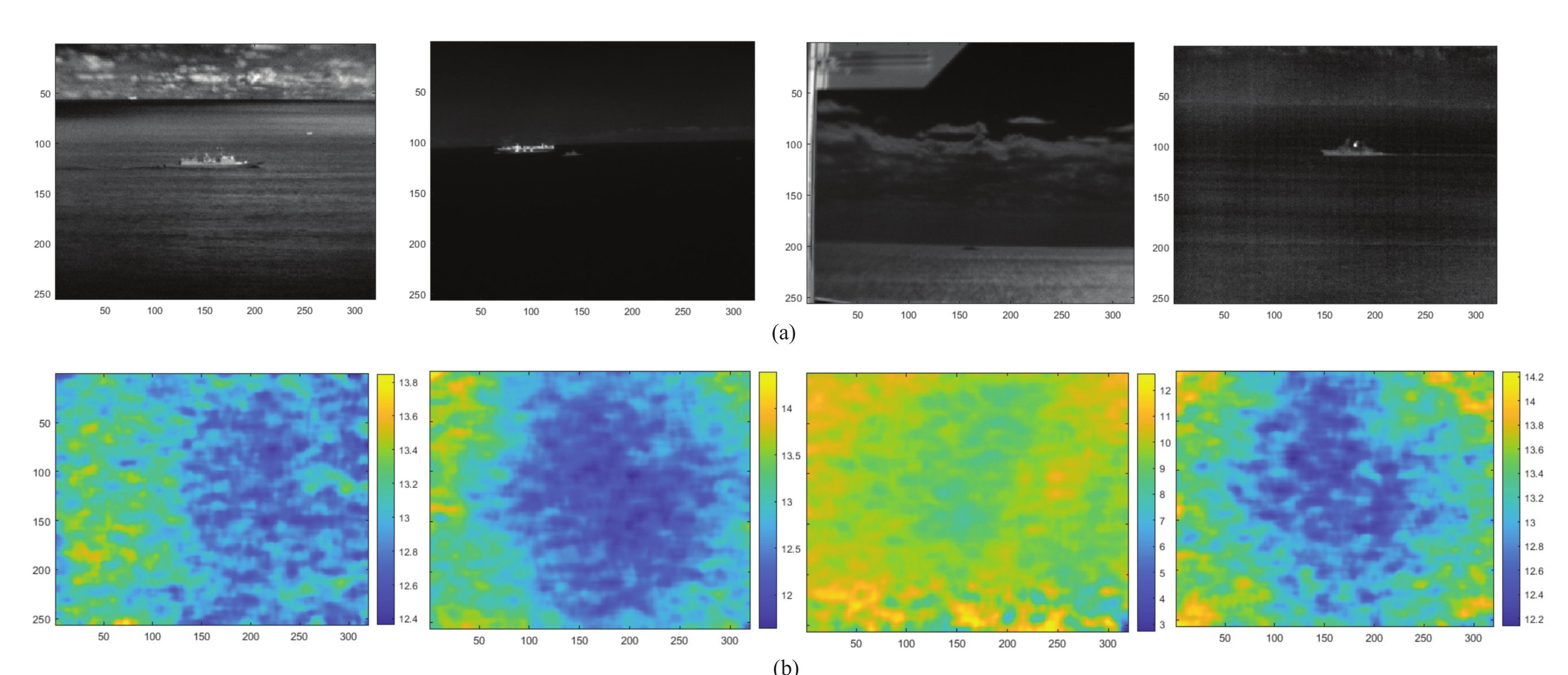
4. Experiment Results
5. Discussions and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, L.; Li, Z.L.P. The effects of air temperature on office workers’ well-being, workload and productivity-evaluated with subjective ratings. Appl. Ergon. 2010, 42, 29–36. [Google Scholar]
- Lowen, A.C.; Steel, S.M.J.; Palese, P. Influenza virus transmission is dependent on relative humidity and temperature. PLoS Pathog. 2007, 3, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Hatfield, J.L.; Prueger, J.H. Temperature extremes: Effect on plant growth and development. Weather Clim. Extrem. 2015, 10, 4–10. [Google Scholar] [CrossRef]
- Robeson, S.M. Relationships between mean and standard deviation of air temperature: Implications for global warming. Clim. Res. 2002, 22, 205–213. [Google Scholar] [CrossRef]
- Lin, S.; Moore, N.J.; Messina, J.P.; DeVisser, M.H.; Wu, J. Evaluation of estimating daily maximum and minimum air temperature with MODIS data in east Africa. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 128–140. [Google Scholar] [CrossRef]
- Mukherjee, R.; Basu, J.; Mandal, P.; Guha, P.K. A review of micromachined thermal accelerometers. J. Micromech. Microeng. 2017, 27, 123002. [Google Scholar] [CrossRef]
- Pollock, D.D. Thermocouples: Theory and Properties; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Pivovarník, M.; Khalsa, S.J.S.; Jiménez-Muñoz, J.C.; Zemek, F. Improved Temperature and Emissivity Separation Algorithm for Multispectral and Hyperspectral Sensors. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1944–1953. [Google Scholar] [CrossRef]
- Li, Z.L.; Becker, F.; Stoll, M.P.; Wan, Z. Evaluation of Six Methods for Extracting Relative Emissivity Spectra from Thermal Infrared Images. Remote Sens. Environ. 1999, 69, 197–514. [Google Scholar] [CrossRef]
- Khopkar, P.; Agnihotri, S. Modelling Temperature-Vegetation Index (TVX) space and Quality of Life (QoL) for enhanced change detection analysis: A Case Study of Ahmedabad City. In Proceedings of the 38th Asian Conference on Remote Sensing (ACRS), New Delhi, India, 23–27 October 2017. [Google Scholar]
- Parviz, L.; Kholghi, M.; Valizadeh, K.H. Estimation of Air Temperature Using Temperature-Vegetation Index (TVX) Method. J. Water Soil Sci. 2011, 15, 21–34. [Google Scholar]
- Hou, P.; Chen, Y.; Jiang, W.Q.G.C.W.; Li, J. Near-surface air temperature retrieval from satellite images and influence by wetlands in urban region. Appl. Climatol. 2013, 111, 109–118. [Google Scholar] [CrossRef]
- Sun, Y.J.; Wang, J.F.; Zhang, R.H.; Gillies, R.R.; Xue, Y.; Bo, Y.C. Air temperature retrieval from remote sensing data based on thermodynamics. Theor. Appl. Climatol. 2005, 80, 37–48. [Google Scholar] [CrossRef]
- Shi, Y.; Jiang, Z.; Dong, L.; Shen, S. Statistical estimation of high-resolution surface air temperature from MODIS over the Yangtze River Delta. China. J. Meteorol. Res. 2017, 31, 448–454. [Google Scholar] [CrossRef]
- Shen, H.; Jiang, Y.; Li, T.; Cheng, Q.; Zeng, C.; Zhang, L. Deep learning-based air temperature mapping by fusing remote sensing, station, simulation and socioeconomic data. Remote Sens. Environ. 2020, 240, 111692. [Google Scholar] [CrossRef]
- Liu, S.; Su, H.; Zhang, R.; Tian, J.; Wang, W. Estimating the Surface Air Temperature by Remote Sensing in Northwest China Using an Improved Advection-Energy Balance for Air Temperature Model. Adv. Meteorol. 2015, 2016, 4294219. [Google Scholar] [CrossRef]
- Lu, N.; Liang, S.; Huang, G.; Qin, J.; Yao, L.; Wang, D.; Yang, K. Hierarchical Bayesian space-time estimation of monthly maximum and minimum surface air temperature. Remote Sens. Environ. 2018, 211, 48–58. [Google Scholar] [CrossRef]
- Hooker, J.; Duveiller, G.; Cescatti, A. Data Descriptor: A global dataset of air temperature derived from satellite remote sensing and weather stations. Sci. Data 2018, 5, 180246. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; OuYang, X.; Li, Z.L.; Zhang, R. A New Method for Temperature/Emissivity Separation from Hyperspectral Thermal Infrared Data. In Proceedings of the 2008 IEEE International Geoscience and Remote Sensing Symposium IGARSS 2008), Boston, MA, USA, 8–11 July 2008; pp. III-286–III-289. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, Q.; Li, H.; Zhong, B. Temperature and emissivity separation algorithm for TASI airborne thermal hyperspectral data. In Proceedings of the 2011 International Conference on Electronics, Communications and Control (ICECC), Ningbo, China, 9–11 September 2011; pp. 1075–1078. [Google Scholar] [CrossRef]
- Tan, K.; Liao, Z.; Du, P.; Wu, L. Land surface temperature retrieval from Landsat 8 data and validation with geosensor network. Front. Earth Sci. 2017, 11, 20–34. [Google Scholar] [CrossRef]
- Harig, R. Passive remote sensing of pollutant clouds by Fourier-transform infrared spectrometry: Signal-to-noise ratio as a function of spectral resolution. Appl. Opt. 2004, 43, 4603–4610. [Google Scholar] [CrossRef] [PubMed]
- Gagnon, M.A.; Gagnon, J.P.; Tremblay, P.; Savary, S.; Farley, V.; Éric, G.; Lagueux, P.; Chamberland, M. Standoff midwave infrared hyperspectral imaging of ship plumes. Proc. SPIE 2016, 9988, 998806. [Google Scholar] [CrossRef]
- Kim, S.; Kim, J.; Lee, J.; Ahn, J. Midwave FTIR-Based Remote Surface Temperature Estimation Using a Deep Convolutional Neural Network in a Dynamic Weather Environment. Micromachines 2018, 9, 495. [Google Scholar] [CrossRef]
- Schlerf, M.; Rock, G.; Lagueux, P.; Ronellenfitsch, F.; Gerhards, M.; Hoffmann, L.; Udelhoven, T. A Hyperspectral Thermal Infrared Imaging Instrument for Natural Resources Applications. Remote Sens. 2012, 4, 3995–4009. [Google Scholar] [CrossRef]
- Trishchenko, A.P. Solar Irradiance and Effective Brightness Temperature for SWIR Channels of AVHRR/NOAA and GOES Imagers. J. Atmos. Ocean. Technol. 2006, 23, 198–210. [Google Scholar] [CrossRef]
- Romaniello, V.; Spinetti, C.; Silvestri, M.; Buongiorno, M.F. A Sensitivity Study of the 4.8 um Carbon Dioxide Absorption Band in the MWIR Spectral Range. Remote Sens. 2020, 12, 172. [Google Scholar] [CrossRef]
- Griffin, M.K.; Hua, K.; Burke, H.; Kerekes, J.P. Understanding radiative transfer in the midwave infrared: A precursor to full-spectrum atmospheric compensation. Proc. SPIE 2004, 5425, 348–356. [Google Scholar] [CrossRef]
- Andrews, D. An Introduction to Atmospheric Physics; Cambridge Press: Cambridge, UK, 2000. [Google Scholar]
- Hohn, D.H. Atmospheric Vision 0.35 um < x < 14 um. Appl. Opt. 1975, 14, 404–412. [Google Scholar]
- Sobrino, J.; Li, Z.L.; Stoll, P.; Becker, F. Multi-channel and multi-angle algorithms for estimating sea and land surface temperature with ATSR data. Int. J. Remote Sens. 2004, 17, 2089–2114. [Google Scholar] [CrossRef]
- Driggers, R.G.; Friedman, M.H.; Nichols, J. Introduction to Infrared and Electro-Optical Systems; ARTECH HOUSE: Washington, DC, USA, 2012. [Google Scholar]
- Eismann, M.T. Hyperspectral Remote Sensing; SPIE Press: Bellingham, WA, USA, 2012. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 4th ed.; Pearson: London, UK, 2012. [Google Scholar]
- Iersel, M.V.; Mack, A.; Degache, M.A.C.; Eijk, A.M.J.V. Ship plume modelling in EOSTAR. Proc. SPIE 2014, 9242, 92421S. [Google Scholar]
- Papoulis, A.; Pillai, U. Probability, Random Variables and Stochastic Processes, 4th ed.; McGraw-Hill Europe: New York, NY, USA, 2002. [Google Scholar]
- Wei, P.S.; Hsieh, Y.C.; Chiu, H.H.; Yen, D.L.; Lee, C.; Tsai, Y.C.; Ting, T.C. Absorption coefficient of carbon dioxide across atmospheric troposphere layer. Heliyon 2018, 4, 1–20. [Google Scholar] [CrossRef]








© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S. Novel Air Temperature Measurement Using Midwave Hyperspectral Fourier Transform Infrared Imaging in the Carbon Dioxide Absorption Band. Remote Sens. 2020, 12, 1860. https://doi.org/10.3390/rs12111860
Kim S. Novel Air Temperature Measurement Using Midwave Hyperspectral Fourier Transform Infrared Imaging in the Carbon Dioxide Absorption Band. Remote Sensing. 2020; 12(11):1860. https://doi.org/10.3390/rs12111860
Chicago/Turabian StyleKim, Sungho. 2020. "Novel Air Temperature Measurement Using Midwave Hyperspectral Fourier Transform Infrared Imaging in the Carbon Dioxide Absorption Band" Remote Sensing 12, no. 11: 1860. https://doi.org/10.3390/rs12111860
APA StyleKim, S. (2020). Novel Air Temperature Measurement Using Midwave Hyperspectral Fourier Transform Infrared Imaging in the Carbon Dioxide Absorption Band. Remote Sensing, 12(11), 1860. https://doi.org/10.3390/rs12111860