Comparison of Multi-Temporal PlanetScope Data with Landsat 8 and Sentinel-2 Data for Estimating Airborne LiDAR Derived Canopy Height in Temperate Forests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Airborne LiDAR Data
2.3. PlanetScope, Landsat 8, and Sentinel-2 Data
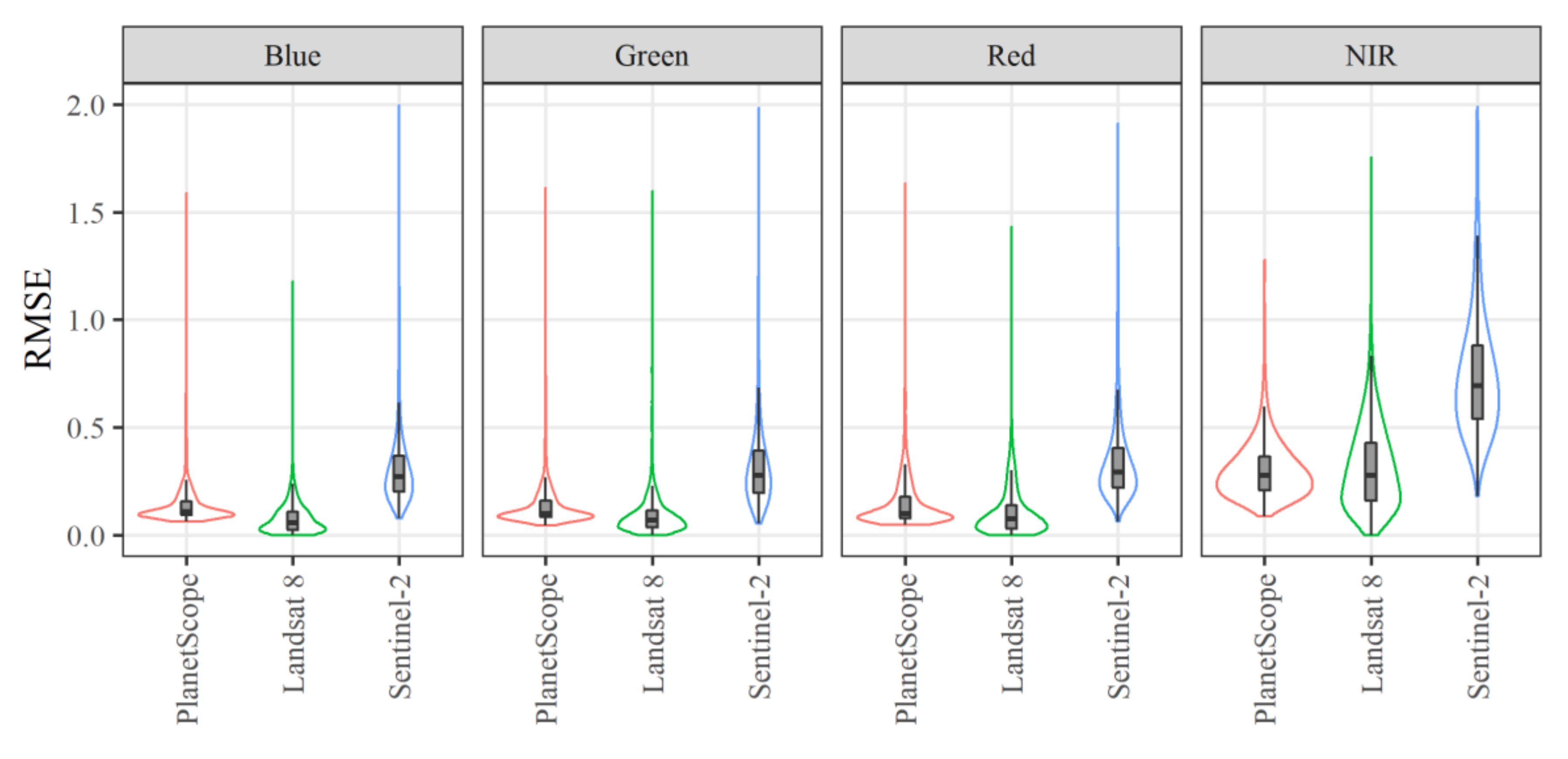
2.4. Predictor Variables from PlanetScope, Landsat 8, and Sentinel-2 Data
2.5. Random Forest Model Building
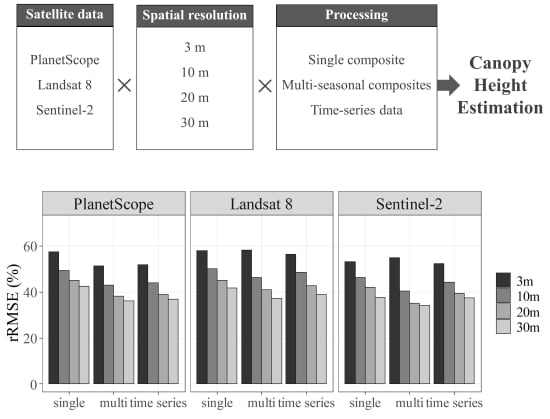
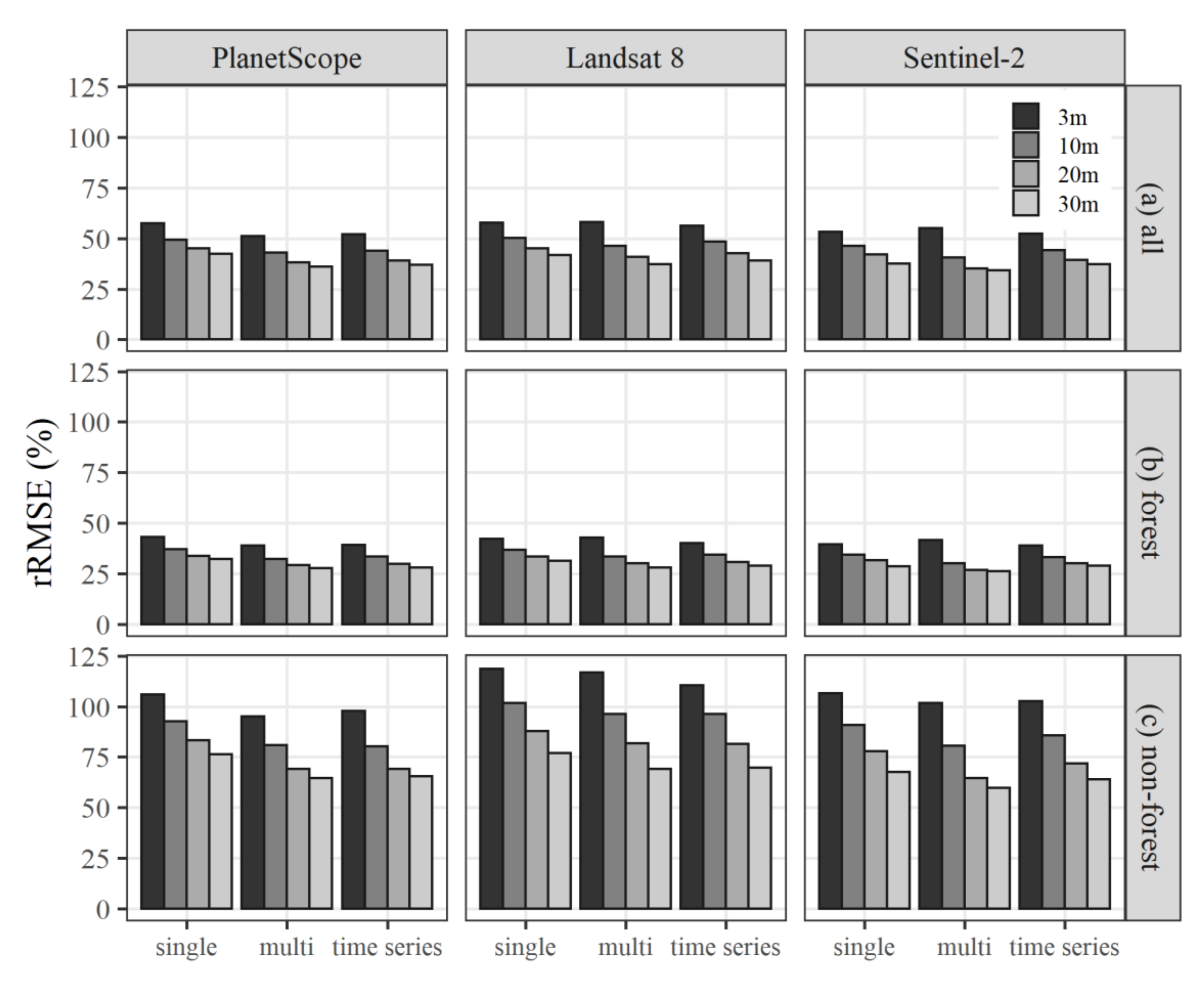
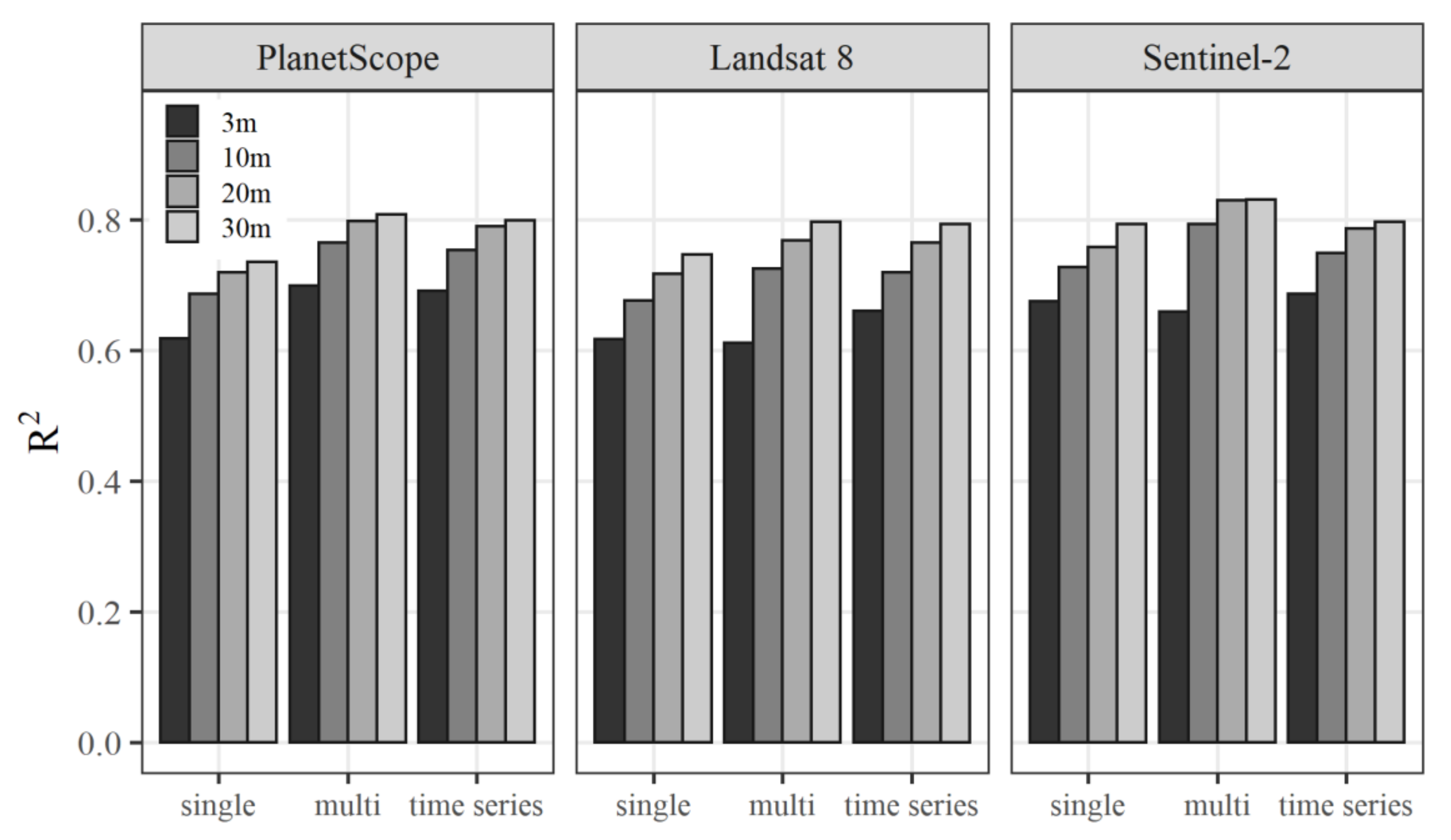
3. Results
3.1. Accuracy Assessment of RF Models
3.2. MCH Mapping
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Skovsgaard, J.P.; Vanclay, J.K. Forest site productivity: A review of the evolution of dendrometric concepts for even-aged stands. For. Int. J. For. Res. 2008, 81, 13–31. [Google Scholar] [CrossRef] [Green Version]
- Skidmore, A.K.; Pettorelli, N.; Coops, N.C.; Geller, G.N.; Hansen, M.; Lucas, R.; Mücher, C.A.; O’Connor, B.; Paganini, M.; Pereira, H.M.; et al. Environmental science: Agree on biodiversity metrics to track from space. Nature 2015, 523, 403–405. [Google Scholar] [CrossRef] [Green Version]
- Asner, G.P.; Mascaro, J. Mapping tropical forest carbon: Calibrating plot estimates to a simple LiDAR metric. Remote Sens. Environ. 2014, 140, 614–624. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef] [Green Version]
- Wilkes, P.; Jones, S.; Suarez, L.; Mellor, A.; Woodgate, W.; Soto-Berelov, M.; Haywood, A.; Skidmore, A. Mapping Forest Canopy Height Across Large Areas by Upscaling ALS Estimates with Freely Available Satellite Data. Remote Sens. 2015, 7, 12563–12587. [Google Scholar] [CrossRef] [Green Version]
- Ota, T.; Ahmed, O.S.; Franklin, S.; Wulder, M.; Kajisa, T.; Mizoue, N.; Yoshida, S.; Takao, G.; Hirata, Y.; Furuya, N.; et al. Estimation of Airborne Lidar-Derived Tropical Forest Canopy Height Using Landsat Time Series in Cambodia. Remote Sens. 2014, 6, 10750–10772. [Google Scholar] [CrossRef] [Green Version]
- Staben, G.; Lucieer, A.; Scarth, P. Modelling LiDAR derived tree canopy height from Landsat TM, ETM+ and OLI satellite imagery—A machine learning approach. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 666–681. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Tsakiri, M.; Patias, P. Evaluation of single-date and multi-seasonal spatial and spectral information of Sentinel-2 imagery to assess growing stock volume of a Mediterranean forest. Int. J. Appl. Earth Obs. Geoinf. 2019, 77, 1–14. [Google Scholar] [CrossRef]
- Astola, H.; Häme, T.; Sirro, L.; Molinier, M.; Kilpi, J. Comparison of Sentinel-2 and Landsat 8 imagery for forest variable prediction in boreal region. Remote Sens. Environ. 2019, 223, 257–273. [Google Scholar] [CrossRef]
- Lang, N.; Schindler, K.; Wegner, J.D. Country-wide high-resolution vegetation height mapping with Sentinel-2. Remote Sens. Environ. 2019, 233, 111347. [Google Scholar] [CrossRef] [Green Version]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Zald, H.S.J. Large-area mapping of Canadian boreal forest cover, height, biomass and other structural attributes using Landsat composites and lidar plots. Remote Sens. Environ. 2018, 209, 90–106. [Google Scholar] [CrossRef]
- Hirata, Y.; Furuya, N.; Saito, H.; Pak, C.; Leng, C.; Sokh, H.; Ma, V.; Kajisa, T.; Ota, T.; Mizoue, N. Object-Based Mapping of Aboveground Biomass in Tropical Forests Using LiDAR and Very-High-Spatial-Resolution Satellite Data. Remote Sens. 2018, 10, 438. [Google Scholar] [CrossRef] [Green Version]
- Finer, M.; Novoa, S.; Weisse, J.; Petersen, R.; Souto, T.; Stearns, F.; Martinez, R.G. Combating deforestation: From satellite to intervention. Science 2018, 360, 1303–1305. [Google Scholar] [CrossRef]
- Fagua, J.C.; Jantz, P.; Rodriguez-Buritica, S.; Duncanson, L.; Goetz, S.J. Integrating LiDAR, Multispectral and SAR Data to Estimate and Map Canopy Height in Tropical Forests. Remote Sens. 2019, 11, 2697. [Google Scholar] [CrossRef] [Green Version]
- Mura, M.; Bottalico, F.; Giannetti, F.; Bertani, R.; Giannini, R.; Mancini, M.; Orlandini, S.; Travaglini, D.; Chirici, G. Exploiting the capabilities of the Sentinel-2 multi spectral instrument for predicting growing stock volume in forest ecosystems. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 126–134. [Google Scholar] [CrossRef]
- Bolton, D.K.; White, J.C.; Wulder, M.A.; Coops, N.C.; Hermosilla, T.; Yuan, X. Updating stand-level forest inventories using airborne laser scanning and Landsat time series data. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 174–183. [Google Scholar] [CrossRef]
- Bolton, D.K.; Gray, J.M.; Melaas, E.K.; Moon, M.; Eklundh, L.; Friedl, M.A. Continental-scale land surface phenology from harmonized Landsat 8 and Sentinel-2 imagery. Remote Sens. Environ. 2020, 240, 111685. [Google Scholar] [CrossRef]
- Poghosyan, A.; Golkar, A. CubeSat evolution: Analyzing CubeSat capabilities for conducting science missions. Prog. Aerosp. Sci. 2017, 88, 59–83. [Google Scholar] [CrossRef]
- Planet Team. Planet Imagery Product Specifications; Planet: San Francisco, CA, USA, 2020. [Google Scholar]
- Riihimäki, H.; Luoto, M.; Heiskanen, J. Estimating fractional cover of tundra vegetation at multiple scales using unmanned aerial systems and optical satellite data. Remote Sens. Environ. 2019, 224, 119–132. [Google Scholar] [CrossRef]
- Csillik, O.; Kumar, P.; Mascaro, J.; O’Shea, T.; Asner, G.P. Monitoring tropical forest carbon stocks and emissions using Planet satellite data. Sci. Rep. 2019, 9, 17831. [Google Scholar] [CrossRef] [Green Version]
- Baloloy, A.B.; Blanco, A.C.; Candido, C.G.; Argamosa, R.J.L.; Dumalag, J.B.L.C.; Dimapilis, L.L.C.; Paringit, E.C. Estimation of mangrove forest aboveground biomass using multispectral bands, vegetation indices and biophysical variables derived from optical satellite imageries: RapidEye, Planetscope and Sentinel-2. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, IV-3, 29–36. [Google Scholar] [CrossRef] [Green Version]
- Mulatu, K.A.; Decuyper, M.; Brede, B.; Kooistra, L.; Reiche, J.; Mora, B.; Herold, M. Linking Terrestrial LiDAR Scanner and Conventional Forest Structure Measurements with Multi-Modal Satellite Data. Forests 2019, 10, 291. [Google Scholar] [CrossRef] [Green Version]
- Csillik, O.; Kumar, P.; Asner, G.P. Challenges in Estimating Tropical Forest Canopy Height from Planet Dove Imagery. Remote Sens. 2020, 12, 1160. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Auty, D. lidR: Airborne LiDAR Data Manipulation and Visualization for Forestry Applications. 2020. Available online: https://cran.r-project.org/web/packages/lidR/index.html (accessed on 6 April 2020).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Roy, S. Porder: Simple CLI for Planet Orders V2 API. 2020. Available online: https://zenodo.org/record/3875911 (accessed on 6 April 2020).
- Planet Team. Planet Application Program Interface: In Space for Life on Earth; Planet: San Francisco, CA, USA, 2018. [Google Scholar]
- Zhu, X.; Helmer, E.H. An automatic method for screening clouds and cloud shadows in optical satellite image time series in cloudy regions. Remote Sens. Environ. 2018, 214, 135–153. [Google Scholar] [CrossRef]
- Leach, N.; Coops, N.C.; Obrknezev, N. Normalization method for multi-sensor high spatial and temporal resolution satellite imagery with radiometric inconsistencies. Comput. Electron. Agric. 2019, 164, 104893. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M. Daily Retrieval of NDVI and LAI at 3 m Resolution via the Fusion of CubeSat, Landsat, and MODIS Data. Remote Sens. 2018, 10, 890. [Google Scholar] [CrossRef] [Green Version]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4–7, 8, and Sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Ranghetti, L.; Boschetti, M.; Nutini, F.; Busetto, L. “sen2r”: An R toolbox for automatically downloading and preprocessing Sentinel-2 satellite data. Comput. Geosci. 2020, 139, 104473. [Google Scholar] [CrossRef]
- Main-Knorn, M.; Pflug, B.; Louis, J.; Debaecker, V.; Müller-Wilm, U.; Gascon, F. Sen2Cor for Sentinel-2. In Proceedings of the Image and Signal Processing for Remote Sensing XXIII, Warsaw, Poland, 11–13 September 2017; Bruzzone, L., Bovolo, F., Benediktsson, J.A., Eds.; SPIE: Warsaw, Poland, 2017; 10427, p. 1042704. [Google Scholar]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Derwin, J.M.; Thomas, V.A.; Wynne, R.H.; Coulston, J.W.; Liknes, G.C.; Bender, S.; Blinn, C.E.; Brooks, E.B.; Ruefenacht, B.; Benton, R.; et al. Estimating tree canopy cover using harmonic regression coefficients derived from multitemporal Landsat data. Int. J. Appl. Earth Obs. Geoinf. 2020, 86, 101985. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [Green Version]
- Chavent, M.; Kuentz-Simonet, V.; Liquet, B.; Saracco, J. ClustOfVar: An R package for the clustering of variables. J. Stat. Softw. 2012, 50, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Wood, E.M.; Pidgeon, A.M.; Radeloff, V.C.; Keuler, N.S. Image texture as a remotely sensed measure of vegetation structure. Remote Sens. Environ. 2012, 121, 516–526. [Google Scholar] [CrossRef]
- Sánchez-Ruiz, S.; Moreno-Martínez, Á.; Izquierdo-Verdiguier, E.; Chiesi, M.; Maselli, F.; Gilabert, M.A. Growing stock volume from multi-temporal landsat imagery through google earth engine. Int. J. Appl. Earth Obs. Geoinf. 2019, 83, 101913. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Gitas, I.; Tsakiri-Strati, M. Estimating Mediterranean forest parameters using multi seasonal Landsat 8 OLI imagery and an ensemble learning method. Remote Sens. Environ. 2017, 199, 154–166. [Google Scholar] [CrossRef]
- Murakami, T. Seasonal variation in classification accuracy of forest-cover types examined by a single band or band combinations. J. For. Res. 2004, 9, 211–215. [Google Scholar] [CrossRef]
- Wilson, B.T.; Knight, J.F.; McRoberts, R.E. Harmonic regression of Landsat time series for modeling attributes from national forest inventory data. ISPRS J. Photogramm. Remote Sens. 2018, 137, 29–46. [Google Scholar] [CrossRef]
- Cheng, K.; Wang, J. Forest Type Classification Based on Integrated Spectral-Spatial-Temporal Features and Random Forest Algorithm—A Case Study in the Qinling Mountains. Forests 2019, 10, 559. [Google Scholar] [CrossRef]
- Adams, B.; Iverson, L.; Matthews, S.; Peters, M.; Prasad, A.; Hix, D. Mapping Forest Composition with Landsat Time Series: An Evaluation of Seasonal Composites and Harmonic Regression. Remote Sens. 2020, 12, 610. [Google Scholar] [CrossRef] [Green Version]
- Mauya, E.W.; Koskinen, J.; Tegel, K.; Hämäläinen, J.; Kauranne, T.; Käyhkö, N. Modelling and Predicting the Growing Stock Volume in Small-Scale Plantation Forests of Tanzania Using Multi-Sensor Image Synergy. Forests 2019, 10, 279. [Google Scholar] [CrossRef] [Green Version]
- Mascaro, J.; Detto, M.; Asner, G.P.; Muller-Landau, H.C. Evaluating uncertainty in mapping forest carbon with airborne LiDAR. Remote Sens. Environ. 2011, 115, 3770–3774. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Goetz, S.J.; Turubanova, S.; Tyukavina, A.; Krylov, A.; Kommareddy, A.; Egorov, A. Mapping tree height distributions in Sub-Saharan Africa using Landsat 7 and 8 data. Remote Sens. Environ. 2016, 185, 221–232. [Google Scholar] [CrossRef] [Green Version]





| Images | Days | Average Valid Pixels | |
|---|---|---|---|
| PlanetScope | 148 | 35 | 22.3 |
| Landsat 8 | 15 | 15 | 8.3 |
| Sentinel-2 | 58 | 33 | 20.7 |
| Processing | Variables | PlanetScope | Landsat 8 | Sentinel-2 |
|---|---|---|---|---|
| Single | Spectral bands | 4 | 6 | 9 |
| Spectral indices | 2 | 4 | 4 | |
| GLCM | 7 | 7 | 7 | |
| Multi | Four composites × spectral bands | 16 | 24 | 36 |
| Four composites × spectral indices | 8 | 16 | 16 | |
| Four composites × GLCM | 28 | 28 | 28 | |
| Time series | Harmonic model spectral bands coefficients | 20 | 18 | 45 |
| Harmonic model spectral indices coefficients | 10 | 12 | 20 | |
| Harmonic model RMSE | 6 | 10 | 13 | |
| Average of spectral bands and indices | 6 | 10 | 13 |
| rRMSE (%) | R2 | ||||||
|---|---|---|---|---|---|---|---|
| Type | Combination | Median | Min | Max | Median | Min | Max |
| (1) Spatial resolution | 3 to 10 m | −8.0 | −14.5 | −7.0 | 0.06 | 0.05 | 0.13 |
| 10 to 20 m | −5.0 | −5.8 | −4.3 | 0.04 | 0.03 | 0.05 | |
| 20 to 30 m | −2.7 | −4.4 | −1.0 | 0.02 | 0.00 | 0.04 | |
| (2) Processing | Single to multi | −5.1 | −6.8 | 1.8 | 0.06 | −0.02 | 0.08 |
| Multi to time series | 1.4 | −2.7 | 4.3 | −0.01 | −0.04 | 0.05 | |
| Single to time series | −2.4 | −6.1 | −0.3 | 0.04 | 0.00 | 0.07 | |
| (3) Satellite data | PlanetScope to Landsat 8 | 2.4 | −0.7 | 6.9 | −0.02 | −0.09 | 0.01 |
| Landsat 8 to Sentinel-2 | −4.0 | −5.8 | −1.7 | 0.04 | 0.00 | 0.07 | |
| PlanetScope to Sentinel-2 | −2.2 | −4.8 | 3.7 | 0.03 | −0.04 | 0.06 | |
| PlanetScope | Landsat 8 | Sentinel-2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Resolution | Rank | Single | Multi | Time Series | Single | Multi | Time Series | Single | Multi | Time Series |
| (a) 3 m | 1 | EVI | spring-b4 | NDVI-mean | b5 | summer-b5 | NBR-mean | EVI | winter-b3 | b2-mean |
| 2 | b2 | winter-NDVI | b1-mean | b6 | winter-b3 | b2-mean | b8 | spring-b7 | NBR-mean | |
| 3 | NDVI | summer-b4 | b3-RMSE | EVI | spring-NBR | EVI-mean | NDVI | winter-b7 | NDVI-mean | |
| 4 | glcm-variance | winter-b4 | NDVI-a0 | b3 | summer-b4 | b4-mean | b7 | summer-b4 | b11-mean | |
| 5 | b4 | summer-NDVI | EVI-mean | NDVI | spring-glcm-homo | NBR-a1 | NBR | winter-glcm-homo | b3-mean | |
| (b) 10 m | 1 | EVI | winter-NDVI | b1-mean | b5 | autumn-EVI | NBR-mean | b2 | spring-b8 | NBR-mean |
| 2 | NDVI | summer-NDVI | NDVI-mean | b7 | winter-NDVI | b6-mean | NBR | winter-EVI | b2-mean | |
| 3 | b4 | summer-EVI | b3-RMSE | NDVI | winter-NBR | EVI-mean | EVI | spring-NDVI | b7-RMSE | |
| 4 | b2 | winter-EVI | NDVI-a0 | b6 | summer-EVI | b4-mean | b7 | winter-NDVI | NDVI-b1 | |
| 5 | glcm-mean | spring-b4 | EVI-mean | b3 | spring-EVI | b4-a0 | b5 | autumn-EVI | b3-mean | |
| (c) 20 m | 1 | EVI | winter-NDVI | b1-mean | EVI | spring-EVI | NBR-mean | NBR | winter-EVI | NBR-mean |
| 2 | b4 | summer-NDVI | NDVI-mean | b5 | autumn-EVI | NDMI-RMSE | EVI | winter-NDVI | b7-RMSE | |
| 3 | NDVI | winter-EVI | b3-RMSE | b7 | winter-NDVI | NDMI-mean | b3 | spring-b8 | b2-mean | |
| 4 | b2 | summer-EVI | EVI-mean | NBR | winter-EVI | EVI-mean | b7 | autumn-b11 | b4-mean | |
| 5 | glcm-mean | spring-b4 | b3-b1 | b6 | winter-NBR | NDVI-RMSE | b5 | spring-NDVI | b7-mean | |
| (d) 30 m | 1 | EVI | winter-EVI | b1-mean | b6 | winter-NDVI | NBR-mean | EVI | spring-b7 | NBR-mean |
| 2 | b4 | winter-NDVI | NDVI-a1 | b5 | spring-EVI | NDVI-mean | b11 | winter-NBR | b2-mean | |
| 3 | b2 | summer-NDVI | b3-RMSE | b7 | winter-NBR | EVI-mean | b8 | winter-EVI | b6-mean | |
| 4 | NDVI | summer-EVI | EVI-a0 | glcm-mean | summer-EVI | NDMI-mean | b12 | autumn-EVI | NDMI-a1 | |
| 5 | glcm-mean | spring-b4 | NDVI-RMSE | glcm-contrast | autumn-EVI | NDVI-RMSE | b6 | winter-b3 | b6-RMSE | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shimizu, K.; Ota, T.; Mizoue, N.; Saito, H. Comparison of Multi-Temporal PlanetScope Data with Landsat 8 and Sentinel-2 Data for Estimating Airborne LiDAR Derived Canopy Height in Temperate Forests. Remote Sens. 2020, 12, 1876. https://doi.org/10.3390/rs12111876
Shimizu K, Ota T, Mizoue N, Saito H. Comparison of Multi-Temporal PlanetScope Data with Landsat 8 and Sentinel-2 Data for Estimating Airborne LiDAR Derived Canopy Height in Temperate Forests. Remote Sensing. 2020; 12(11):1876. https://doi.org/10.3390/rs12111876
Chicago/Turabian StyleShimizu, Katsuto, Tetsuji Ota, Nobuya Mizoue, and Hideki Saito. 2020. "Comparison of Multi-Temporal PlanetScope Data with Landsat 8 and Sentinel-2 Data for Estimating Airborne LiDAR Derived Canopy Height in Temperate Forests" Remote Sensing 12, no. 11: 1876. https://doi.org/10.3390/rs12111876
APA StyleShimizu, K., Ota, T., Mizoue, N., & Saito, H. (2020). Comparison of Multi-Temporal PlanetScope Data with Landsat 8 and Sentinel-2 Data for Estimating Airborne LiDAR Derived Canopy Height in Temperate Forests. Remote Sensing, 12(11), 1876. https://doi.org/10.3390/rs12111876