Post-Earthquake Night-Time Light Piecewise (PNLP) Pattern Based on NPP/VIIRS Night-Time Light Data: A Case Study of the 2015 Nepal Earthquake
Abstract
1. Introduction
2. Materials
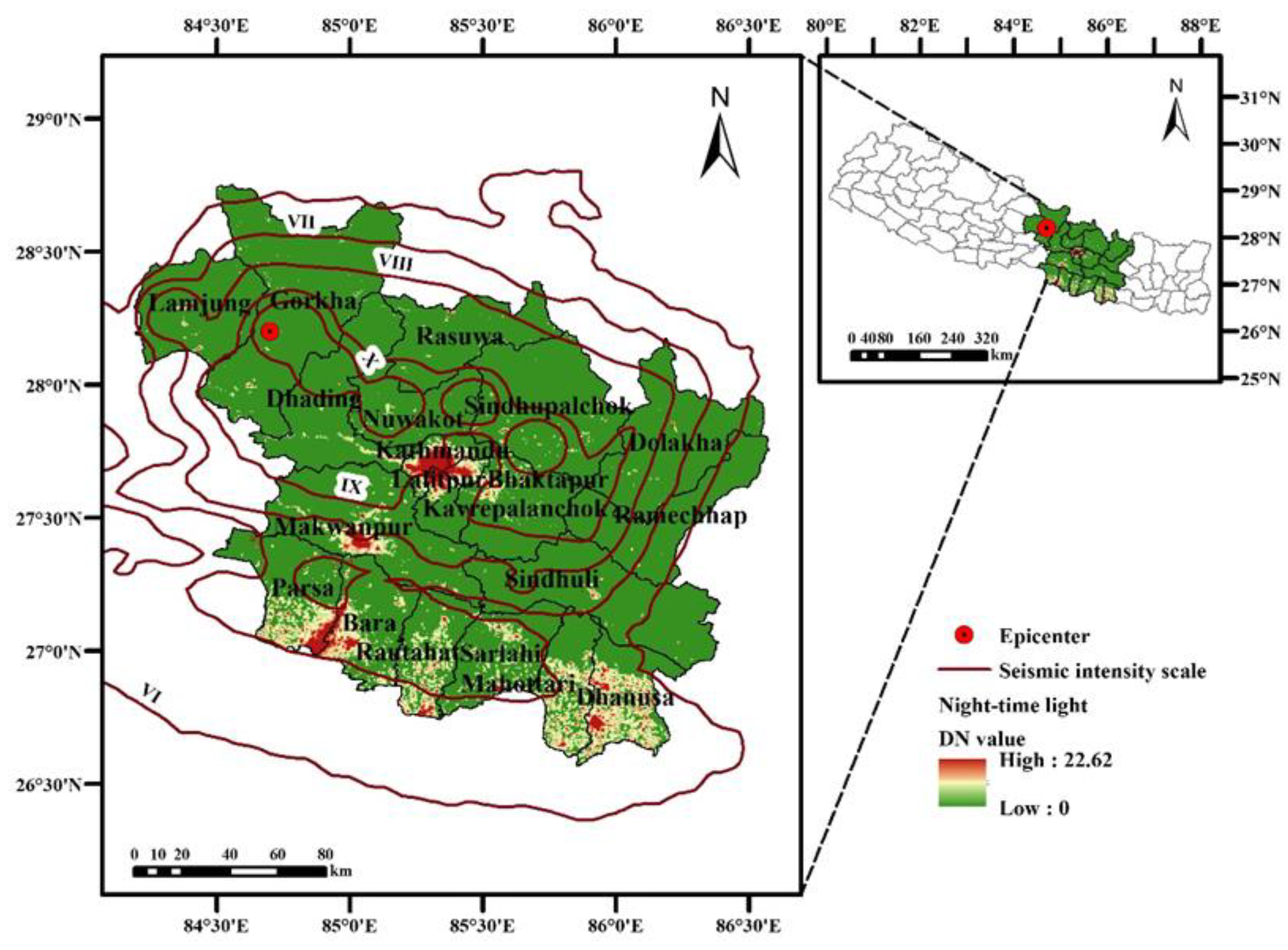
2.1. Study Area
2.2. Data Collection
2.2.1. NPP/VIIRS Monthly Composite Data
2.2.2. Auxiliary Data
3. Methods
3.1. Data Pre-Processing
- The study area is clipped based on GADM data.
- For images starting in January 2017, we subtract 0.15 nW cm−2 sr−1 [47].
- The normalized GHSL data are divided into several categories at 0.2 intervals.
- Samples of different population densities are generated based on random sampling and the mean value of DN is counted under different population densities.
- The monthly background noise threshold is chosen according to mean value of DN. NPP/VIIRS data below threshold are replaced by zero in order to remove the background noise.
- In order to eliminate the outliers, the maximum value of Kathmandu is taken as the maximum value of the study area and a value greater than the DN value in the study area is replaced by zero.
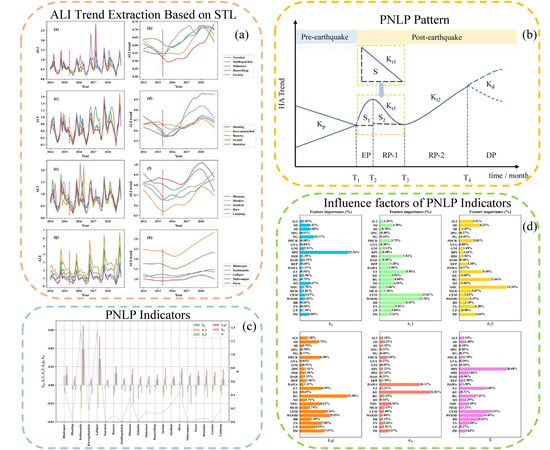
3.2. PNLP Conceptual Pattern
3.3. Calculation of PNLP Pattern
3.3.1. HA Intensity Indicator
3.3.2. ALI Trend Extraction Based on STL Algorithm
3.3.3. Solution of PNLP Parameters
3.4. Ineffective Factors of PNLP Indicators Based on Ramdom Forest Regression (RFR)
- For each decision tree, the prediction error (err1) of out-of-bag (OOB) is recorded.
- Randomly transform each predictor to form new OOB, then prediction error (err2) of new OOB is recorded.
- For a predictor variable, its importance is calculated as the mean of the difference between the transformed prediction error and the original. The formula is as follows:
3.5. ALI Sequence Test Based on Mann-Kendall Mutation Test
4. Results
4.1. The Level of Background Noise
4.2. Trend Analysis of STL Algorithm
4.3. PNLP Pattern Analysis
4.3.1. PNLP Pattern Analysis in Different Areas.
4.3.2. Influencing Factors of PNLP Pattern
5. Discussion
5.1. Analysis of Noise Level
5.2. Applicability Analysis of STL Algorithm
5.2.1. Mutation Test
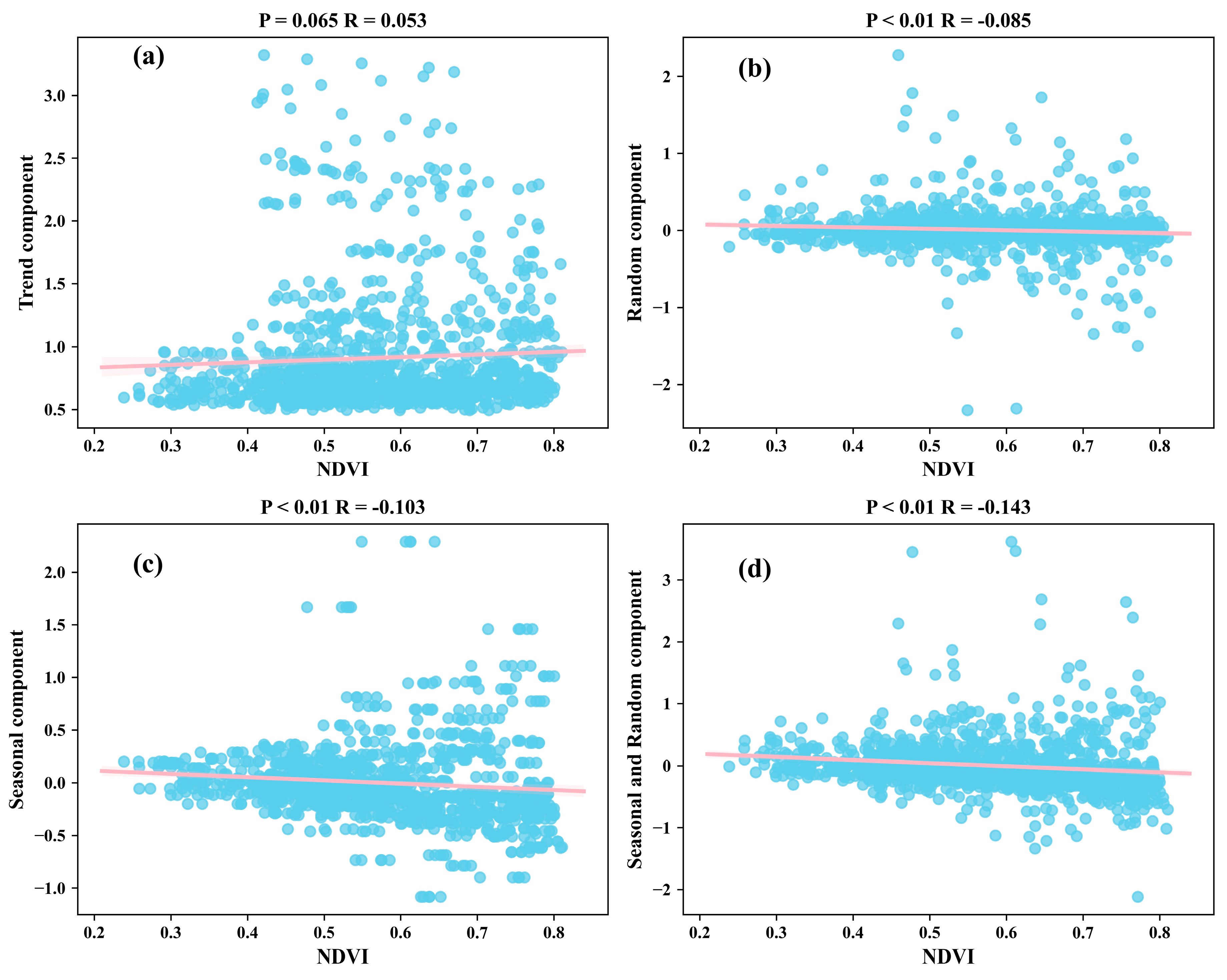
5.2.2. Seasonal Impact Analysis
5.2.3. Trend Analysis
5.3. Diversity of PNLP Conceptual Pattern
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Abbreviation | Full Name |
|---|---|
| ALI | Average light index |
| SD | The total of structural damage |
| HI | The total of human injured |
| SPG | Squared poverty gap, 2011 |
| PG | Poverty gap, 2011 |
| PHCR | Poverty head count ratio, 2011 |
| GVA | Gross value added at basic price (in millions), 2013 |
| GNI | GNI per capita based on purchasing power parity (PPP), 2013 |
| HPI | Human poverty index, 2013 |
| HDI | Human development index, 2013 |
| DAH | Percentage distribution of agricultural holdings |
| DFP | Percentage distribution of farm population as of total population |
| DAHA | Percentage distribution of agricultural holding area |
| ET | Electricity (Percentage of households with selected energy source for lighting by district, 2011) |
| KE | Kerosene (Percentage of households with selected energy source for lighting by district, 2011) |
| BG | Bio-gas (Percentage of households with selected energy source for lighting by district, 2011) |
| SO | Solar (Percentage of households with selected energy source for lighting by district, 2011) |
| NHU | Number of housing units |
| MUD | Mud (Percentage of households by type of house walls and district) |
| CEM | Cement (Percentage of households by type of house walls and district) |
| WOOD | Wood (Percentage of households by type of house walls and district) |
| BB | Bamboo (Percentage of households by type of house walls and district) |
| TN | Transportation network |
| CP | Percentage change in population |
| PD | Population density |
References
- De Boer, J.Z.; Sanders, D.T. Earthquakes in Human History: The Far-Reaching Effects of Seismic Disruptions; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Zhang, J.; Hull, V.; Huang, J.; Yang, W.; Zhou, S.; Xu, W.; Huang, Y.; Ouyang, Z.; Zhang, H.; Liu, J. Natural recovery and restoration in giant panda habitat after the Wenchuan earthquake. For. Ecol. Manag. 2014, 319, 1–9. [Google Scholar] [CrossRef]
- Khazai, B.; Anhorn, J.; Girard, T.; Brink, S.; Daniell, J.; Bessel, T.; Mühr, B.; Flörchinger, V.; Kunz-Plapp, T. Shelter Response and Vulnerability of Displaced Populations in the April 25, 2015 Nepal Earthquake. In Center for Disaster Management and Risk Reduction Technology of the Karlsruhe Institute of Technology, and the South Asia Institute; Heidelberg University: Heidelberg, Germany, 2015; Volume 5, p. 2015. [Google Scholar]
- Ehring, T.; Razik, S.; Emmelkamp, P.M. Prevalence and predictors of posttraumatic stress disorder, anxiety, depression, and burnout in Pakistani earthquake recovery workers. Psychiatry Res. 2011, 185, 161–166. [Google Scholar] [CrossRef] [PubMed]
- Okamura, M.; Bhandary, N.P.; Mori, S.; Marasini, N.; Hazarika, H. Report on a reconnaissance survey of damage in Kathmandu caused by the 2015 Gorkha Nepal earthquake. Soils Found. 2015, 55, 1015–1029. [Google Scholar] [CrossRef]
- Dizhur, D.; Dhakal, R.P.; Bothara, J.; Ingham, J.M. Building typologies and failure modes observed in the 2015 Gorkha (Nepal) earthquake. Bull. New Zealand Soc. Earthq. Eng. 2016, 49, 211–232. [Google Scholar] [CrossRef]
- Wei, C.; Liu, Y.; Wang, S.; Zhang, L.-F.; Huang, X.-X. Investigation and assessment of damage in earthquake Wenchuan Sichuan quake based on remote sensing. J. Remote Sens. 2008, 12, 673–682. [Google Scholar]
- Fan, J.-R.; Zhang, J.-Q.; Tian, B.-W.; Yan, D.; Tao, H.-P. Investigation to the damaged farmland as a result of disasters induced by Wenchuan earthquake based on remote sensing: A case study of Tangjiashan area, Beichuan County, Sichuan Province. J. Remote Sens. 2008, 12, 918–925. [Google Scholar]
- Zhao, W.; Li, A.; Nan, X.; Zhang, Z.; Lei, G. Postearthquake landslides mapping from Landsat-8 data for the 2015 Nepal earthquake using a pixel-based change detection method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1758–1768. [Google Scholar] [CrossRef]
- Zhuo, L.; Ichinose, T.; Zheng, J.; Chen, J.; Shi, P.; Li, X. Modelling the population density of China at the pixel level based on DMSP/OLS non-radiance-calibrated night-time light images. Int. J. Remote Sens. 2009, 30, 1003–1018. [Google Scholar] [CrossRef]
- Chen, X.; Nordhaus, W. A test of the new VIIRS lights data set: Population and economic output in Africa. Remote Sens. 2015, 7, 4937–4947. [Google Scholar] [CrossRef]
- Wang, X.; Rafa, M.; Moyer, J.D.; Li, J.; Scheer, J.; Sutton, P. Estimation and mapping of sub-national GDP in Uganda Using NPP-VIIRS imagery. Remote Sens. 2019, 11, 163. [Google Scholar] [CrossRef]
- Chand, T.K.; Badarinath, K.; Elvidge, C.; Tuttle, B. Spatial characterization of electrical power consumption patterns over India using temporal DMSP-OLS night-time satellite data. Int. J. Remote Sens. 2009, 30, 647–661. [Google Scholar] [CrossRef]
- He, C.; Ma, Q.; Li, T.; Yang, Y.; Liu, Z. Spatiotemporal dynamics of electric power consumption in Chinese Mainland from 1995 to 2008 modeled using DMSP/OLS stable nighttime lights data. J. Geogr. Sci. 2012, 22, 125–136. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.E.; Kihn, E.A.; Kroehl, H.W.; Davis, E.R.; Davis, C.W. Relation between satellite observed visible-near infrared emissions, population, economic activity and electric power consumption. Int. J. Remote Sens. 1997, 18, 1373–1379. [Google Scholar] [CrossRef]
- Henderson, M.; Yeh, E.T.; Gong, P.; Elvidge, C.; Baugh, K. Validation of urban boundaries derived from global night-time satellite imagery. Int. J. Remote Sens. 2003, 24, 595–609. [Google Scholar] [CrossRef]
- Ma, T.; Zhou, Y.; Zhou, C.; Haynie, S.; Pei, T.; Xu, T. Night-time light derived estimation of spatio-temporal characteristics of urbanization dynamics using DMSP/OLS satellite data. Remote Sens. Environ. 2015, 158, 453–464. [Google Scholar] [CrossRef]
- Li, K.; Chen, Y. A Genetic Algorithm-based urban cluster automatic threshold method by combining VIIRS DNB, NDVI, and NDBI to monitor urbanization. Remote Sens. 2018, 10, 277. [Google Scholar] [CrossRef]
- Li, X.; Li, D. Can night-time light images play a role in evaluating the Syrian Crisis? Int. J. Remote Sens. 2014, 35, 6648–6661. [Google Scholar] [CrossRef]
- Li, X.; Zhang, R.; Huang, C.; Li, D. Detecting 2014 Northern Iraq Insurgency using night-time light imagery. Int. J. Remote Sens. 2015, 36, 3446–3458. [Google Scholar] [CrossRef]
- Elvidge, C.; Baugh, K.; Hobson, V.; Kihn, E.; Kroehl, H. Detection of fires and power outages using DMSP-OLS data. Remote Sens. Chang. Detect. Environ. Monit. Methods Appl. 1998, 123–135. [Google Scholar]
- Levin, N.; Kyba, C.C.; Zhang, Q.; de Miguel, A.S.; Román, M.O.; Li, X.; Portnov, B.A.; Molthan, A.L.; Jechow, A.; Miller, S.D. Remote sensing of night lights: A review and an outlook for the future. Remote Sens. Environ. 2020, 237, 111443. [Google Scholar] [CrossRef]
- De La Cruz, A.; Laneve, G.; Cerra, D.; Mielewczyk, M.; Garcia, M.; Santilli, G.; Cadau, E.; Joyanes, G. On the Application of Nighttime Sensors for Rapid Detection of Areas Impacted by Disasters. In Geomatics Solutions for Disaster Management; Springer Science and Business Media LLC: Berlin, Germany, 2007; pp. 17–36. [Google Scholar]
- Wang, Z.; Román, M.; Sun, Q.; Molthan, A.; Schultz, L.; Kalb, V. Monitoring disaster-related power outages using NASA black marble nighttime light product. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2018, 1853–1856. [Google Scholar] [CrossRef]
- Zhao, X.; Yu, B.; Liu, Y.; Yao, S.; Lian, T.; Chen, L.; Yang, C.; Chen, Z.; Wu, J. NPP-VIIRS DNB daily data in natural disaster assessment: Evidence from selected case studies. Remote Sens. 2018, 10, 1526. [Google Scholar] [CrossRef]
- Chen, T.-H.K.; Prishchepov, A.V.; Fensholt, R.; Sabel, C.E. Detecting and monitoring long-term landslides in urbanized areas with nighttime light data and multi-seasonal Landsat imagery across Taiwan from 1998 to 2017. Remote Sens. Environ. 2019, 225, 317–327. [Google Scholar] [CrossRef]
- Hashitera, S.; Kohiyama, M.; Maki, N.; Fujita, H. Use of DMSP-OLS images for early identification of impacted areas due to the 1999 Marmara earthquake disaster. In Proceedings of the 20th Asian Conference on Remote Sensing, Hong Kong, China, 22–25 November 1999; pp. 1291–1296. [Google Scholar]
- Kohiyama, M.; Hayashi, H.; Maki, N.; Higashida, M.; Kroehl, H.; Elvidge, C.; Hobson, V. Early damaged area estimation system using DMSP-OLS night-time imagery. Int. J. Remote Sens. 2004, 25, 2015–2036. [Google Scholar] [CrossRef]
- Takashima, M.; Hayashi, H.; Kimura, H.; Kohiyama, M. Earthquake damaged area estimation using DMSP/OLS night-time imagery-application for Hanshin-Awaji Earthquake. In Proceedings of the IGARSS 2000. IEEE 2000 International Geoscience and Remote Sensing Symposium. Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment. Proceedings (Cat. No. 00CH37120), Honolulu, HI, USA, 24–28 July 2000; Volume 331, pp. 336–338. [Google Scholar]
- Fan, X.; Nie, G.; Deng, Y.; An, J.; Zhou, J.; Li, H. Rapid detection of earthquake damage areas using VIIRS nearly constant contrast night-time light data. Int. J. Remote Sens. 2019, 40, 2386–2409. [Google Scholar] [CrossRef]
- Fan, X.; Nie, G.; Deng, Y.; An, J.; Zhou, J.; Xia, C.; Pang, X. Estimating earthquake-damage areas using Landsat-8 OLI surface reflectance data. Int. J. Disaster Risk Reduct. 2019, 33, 275–283. [Google Scholar] [CrossRef]
- Cao, C.; Shao, X.; Uprety, S. Detecting Light Outages After Severe Storms Using the S-NPP/VIIRS Day/Night Band Radiances. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1582–1586. [Google Scholar] [CrossRef]
- Roman, M.O.; Stokes, E.C.; Shrestha, R.; Wang, Z.; Schultz, L.; Carlo, E.A.S.; Sun, Q.; Bell, J.; Molthan, A.; Kalb, V.; et al. Satellite-based assessment of electricity restoration efforts in Puerto Rico after Hurricane Maria. PLoS ONE 2019, 14, e0218883. [Google Scholar] [CrossRef]
- Li, X.; Zhan, C.; Tao, J.; Li, L. Long-term monitoring of the impacts of disaster on human activity using dmsp/ols nighttime light data: A case study of the 2008 Wenchuan, china earthquake. Remote Sens. 2018, 10, 588. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z.; Chen, X.; Meng, Q. Assessment of the impact of the 2010 Haiti earthquake on human activity based on DMSP/OLS time series nighttime light data. J. Appl. Remote Sens. 2019, 13. [Google Scholar] [CrossRef]
- Levin, N. The impact of seasonal changes on observed nighttime brightness from 2014 to 2015 monthly VIIRS DNB composites. Remote Sens. Environ. 2017, 193, 150–164. [Google Scholar] [CrossRef]
- Li, X.; Ma, R.; Zhang, Q.; Li, D.; Liu, S.; He, T.; Zhao, L. Anisotropic characteristic of artificial light at night – Systematic investigation with VIIRS DNB multi-temporal observations. Remote Sens. Environ. 2019, 233. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Earthquake, N.N. Post Disaster Needs Assessment. In Sector Reports; National Planning Commission: Kathmandu, Nepal, 2015. [Google Scholar]
- Goda, K.; Kiyota, T.; Pokhrel, R.M.; Chiaro, G.; Katagiri, T.; Sharma, K.; Wilkinson, S. The 2015 Gorkha Nepal earthquake: Insights from earthquake damage survey. Front. Built Environ. 2015, 1, 8. [Google Scholar] [CrossRef]
- Lawrence, W. A technique for using composite DMSP/OLS’city lights’ satellite data to accurately map urban areas. Remote Sens. Environ. 1997, 61, 361–370. [Google Scholar]
- Elvidge, C.D.; Keith, D.M.; Tuttle, B.T.; Baugh, K.E. Spectral identification of lighting type and character. Sensors 2010, 10, 3961–3988. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Zhizhin, M.; Hsu, F.-C.; Baugh, K.E. VIIRS nightfire: Satellite pyrometry at night. Remote Sens. 2013, 5, 4423–4449. [Google Scholar] [CrossRef]
- Shi, K.; Yu, B.; Huang, Y.; Hu, Y.; Yin, B.; Chen, Z.; Chen, L.; Wu, J. Evaluating the ability of NPP-VIIRS nighttime light data to estimate the gross domestic product and the electric power consumption of China at multiple scales: A comparison with DMSP-OLS data. Remote Sens. 2014, 6, 1705–1724. [Google Scholar] [CrossRef]
- Li, X.; Xu, H.; Chen, X.; Li, C. Potential of NPP-VIIRS nighttime light imagery for modeling the regional economy of China. Remote Sens. 2013, 5, 3057–3081. [Google Scholar] [CrossRef]
- Uprety, S.; Cao, C.; Gu, Y.; Shao, X. Improving the low light radiance calibration of S-NPP VIIRS Day/Night Band in the NOAA operations. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 4726–4729. [Google Scholar]
- Coesfeld, J.; Kuester, T.; Kuechly, H.U.; Kyba, C.C.M. Reducing Variability and Removing Natural Light from Nighttime Satellite Imagery: A Case Study Using the VIIRS DNB. Sensors (Basel) 2020, 20, 3287. [Google Scholar] [CrossRef]
- Miles, S.B.; Chang, S.E. Urban Disaster Recovery: A Framework and Simulation Model; Multidisciplinary Center for Earthquake Engineering Research: Buffalo, NY, USA, 2003. [Google Scholar]
- Haas, J.E.; Kates, R.W.; Bowden, M.J. Reconstruction following disaster. In Reconstruction Following Disaster; US The Massachusetts Institute of Technology: Cambridge, MA, USA, 1977. [Google Scholar]
- Comerio, M.C. Disaster Hits Home: New Policy for Urban. Housing Recovery; University of California Press: Oakland, CA, USA, 1998. [Google Scholar]
- Rubin, C.B. The community recovery process in the United States after a major natural disaster. Int. J. Mass Emergencies Disasters 1985, 3, 9–28. [Google Scholar]
- Wang, W.; Cheng, H.; Zhang, L. Poverty assessment using DMSP/OLS night-time light satellite imagery at a provincial scale in China. Adv. Space Res. 2012, 49, 1253–1264. [Google Scholar] [CrossRef]
- Lu, H.; Raupach, M.R.; McVicar, T.R.; Barrett, D.J. Decomposition of vegetation cover into woody and herbaceous components using AVHRR NDVI time series. Remote Sens. Environ. 2003, 86, 1–18. [Google Scholar] [CrossRef]
- Jacquin, A.; Sheeren, D.; Lacombe, J.-P. Vegetation cover degradation assessment in Madagascar savanna based on trend analysis of MODIS NDVI time series. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S3–S10. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Levin, N.; Jendryke, M. Tracing cultural festival patterns using time-series of VIIRS monthly products. Remote Sens. Lett. 2019, 10, 1172–1181. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Jiang, S.; Li, J.; Duan, P.; Wei, Y. An image layer difference index method to extract light area from NPP/VIIRS nighttime light monthly data. Int. J. Remote Sens. 2019, 40, 4839–4855. [Google Scholar] [CrossRef]
- Paul, B.K.; Acharya, B.; Ghimire, K. Effectiveness of earthquakes relief efforts in Nepal: Opinions of the survivors. Nat. Hazards 2016, 85, 1169–1188. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- Xiong, X.; Wilson, T.; Angal, A.; Sun, J.; Neeck, S.P.; Kimura, T.; Martimort, P. Using the moon and stars for VIIRS day/night band on-orbit calibration. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XXIII, Bellingham, WA, USA, 10 October 2019. [Google Scholar]
- Hogg, S.J. Reconstruction following seismic disaster in Venzone, Friuli. Disasters 1980, 4, 173–185. [Google Scholar] [CrossRef] [PubMed]
- Berke, P.R.; Kartez, J.; Wenger, D. Recovery after disaster: Achieving sustainable development, mitigation and equity. Disasters 1993, 17, 93–109. [Google Scholar] [CrossRef] [PubMed]
- Finucane, M.L.; Acosta, J.; Wicker, A.; Whipkey, K. Short-Term Solutions to a Long-Term Challenge: Rethinking Disaster Recovery Planning to Reduce Vulnerabilities and Inequities. Int. J. Environ. Res. Public Health 2020, 17, 482. [Google Scholar] [CrossRef] [PubMed]











| Parameter | Descriptions |
|---|---|
| Kp | Reflects the changing levels of human activity intensity before the earthquake |
| Kr1 | Reflects the changing levels of human activity intensity in RP-1 |
| Kr2 | Reflects the changing levels of human activity intensity in RP-2 |
| Kd | Reflects the changing levels of human activity intensity in DP |
| Krp | Reflects the changing levels of HA intensity relative to the pre-earthquake level |
| S | Reflects the amount of HA loss during the EP and RP-1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, S.; Chen, Y.; Liang, L.; Gong, A. Post-Earthquake Night-Time Light Piecewise (PNLP) Pattern Based on NPP/VIIRS Night-Time Light Data: A Case Study of the 2015 Nepal Earthquake. Remote Sens. 2020, 12, 2009. https://doi.org/10.3390/rs12122009
Gao S, Chen Y, Liang L, Gong A. Post-Earthquake Night-Time Light Piecewise (PNLP) Pattern Based on NPP/VIIRS Night-Time Light Data: A Case Study of the 2015 Nepal Earthquake. Remote Sensing. 2020; 12(12):2009. https://doi.org/10.3390/rs12122009
Chicago/Turabian StyleGao, Shengjun, Yunhao Chen, Long Liang, and Adu Gong. 2020. "Post-Earthquake Night-Time Light Piecewise (PNLP) Pattern Based on NPP/VIIRS Night-Time Light Data: A Case Study of the 2015 Nepal Earthquake" Remote Sensing 12, no. 12: 2009. https://doi.org/10.3390/rs12122009
APA StyleGao, S., Chen, Y., Liang, L., & Gong, A. (2020). Post-Earthquake Night-Time Light Piecewise (PNLP) Pattern Based on NPP/VIIRS Night-Time Light Data: A Case Study of the 2015 Nepal Earthquake. Remote Sensing, 12(12), 2009. https://doi.org/10.3390/rs12122009