1. Introduction
Airborne laser scanning (ALS) is a globally established technology for building enhanced forest inventories (EFIs) and supplementing effective forest management [
1,
2]. ALS point clouds are most often derived using near-infrared (NIR; most commonly 1064 nm) tuned lasers. Apart from high reflectivity from vegetated surfaces, NIR lasers offer benefits including eye safety and low atmospheric interference [
3]. As a result, NIR-tuned ALS systems have become common place, improving the cost-effectiveness of characterizing vegetation structure and generating best available geo-spatial terrain information.
Since the adoption of ALS technologies in forestry, point cloud-derived height data have been used to characterize forest structure. The intensity of return pulses also provides additional and often complementary information about surface materials [
4]. In a review on the role of radiometric ALS correction and calibration, Kashani et al. [
5] highlighted the interdisciplinary value of intensity data for classifying natural and urban cover surfaces [
6]. Intensity data have been shown to improve the separation of typical landcover surfaces such as concrete and vegetation [
7], though careful attention to intensity correction and calibration methods is a prerequisite [
8]. The lack of a calibrated intensity response makes the development of models that utilize intensity limited, as they are unable to be reliably transferred between ALS acquisitions and across different sensors and locations.
The desire to amalgamate structural descriptions from ALS and spectral characterizations from multi-spectral imagery has been met with the development and testing of multi-spectral ALS (M-ALS) [
9,
10,
11,
12], and the experimental use of hyperspectral ALS systems [
13,
14,
15,
16,
17]. These systems use multiple laser scanners at varying wavelengths, designed to be sensitive to both the structural assemblage, and spectral response of vegetation from the top of the canopy through to the ground.
A potential benefit of M-ALS intensity data when compared to that from single-wavelength ALS (S-ALS) is that intensity from multiple wavelengths may improve the capacity for applications such as health and species-based forest inventory information. The potential to leverage multiple wavelengths to produce multi-spectral intensity information, as well as to mimic passive optical data by calculating vegetation indices, could be an important step towards improving estimates of vegetation composition and vigor [
18]. Passive optical data continue to be indispensable for forest management [
19,
20,
21,
22], facilitating the computation of spectral indices such as the Normalized Difference Vegetation Index (NDVI), and providing a means to derive information on land cover, species, and health. These data are, however, limited to capturing information on the top of the canopy, and are unable to detail potentially important information about internal canopy structure and understorey composition [
23,
24,
25], both areas where M-ALS data may prove useful and provide otherwise unattainable data products.
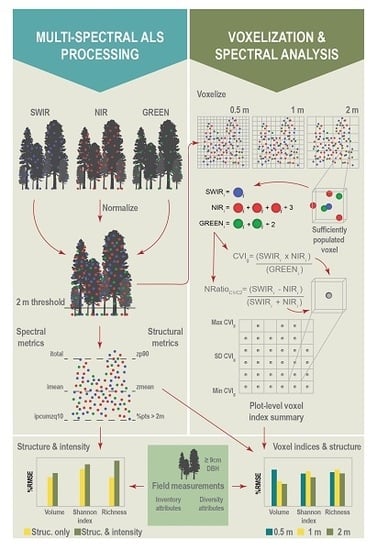
With computation of spectral indices in mind, a critical consideration of M-ALS data is that sensors are made up of laser scanners with diverging beams. Each point within a multi-spectral point cloud, therefore, contains intensity data from a single wavelength only. This contrasts to other three-dimensional remote sensing technologies such as digital aerial photogrammetry (DAP), where all points are attributed with all spectral information derived from overlapping imagery [
23,
24]. In order to compute vegetation indices using M-ALS point clouds, voxelization approaches can be applied, where all points within a voxel of predetermined size are used to calculate vegetation indices. Okhrimenko et al. [
9] found that voxelization of M-ALS wavelengths facilitated the computation of vertical spectral vegetation index profiles using Optech Titan data for stand-level analyses. The aggregation of points to voxels leads to loss in three-dimensional detail, however, also allows for the calculation of spectral indices using M-ALS data. Apart from voxel-based indices, calculations can also be conducted within delineated features such as individual tree extents [
26], and at the plot level [
10].
Examples of the application of M-ALS data in the literature are growing, with many studies utilizing the Optech Titan M-ALS sensor for land cover and forest inventory analyses [
6,
10,
11,
12,
26,
27,
28]. The addition of the 532 nm wavelength is largely driven by the desire to improve sampling of terrain, vegetation, and riparian environments. Canopy attenuation has been more of a challenge with the 532 nm wavelength than the 1064 and 1550 nm wavelengths, likely due to leaf absorption, limiting point densities and vertical distributions within point clouds [
3]. The addition of the 1550 nm wavelength has increased water absorption properties and remains eye safe when emitting higher energy pulses.
Land-cover classification studies such as Wang et al. [
4] investigated the potential to combine different ALS wavelength data from separate acquisitions, indicating that multiple wavelengths improved the ability to discriminate low vegetation compared to a single wavelength. Hopkinson et al. [
3] likewise tested differences between data acquired using a M-ALS sensor and three S-ALS sensors for forest classification. Incorporation of spectral and structural laser return data were found to improve foliage profiling and land surface classifications. Vertical distribution of points, number of ground returns, and characterization of canopy foliage differed among S- and M-ALS datasets, while acquisition configurations such as flight altitude influenced intensity-based characterizations of the canopy [
3,
29].
Individual tree-based classification studies such as Axelsson et al. [
11] have also highlighted the value of M-ALS data. Intensity distributions and features from the upper and outer parts of tree canopies combined with structural characterizations were found to improve classification accuracies. Yu et al. [
30] compared S- and M-ALS data to discriminate between three tree species, with findings indicating that models incorporating metrics derived from M-ALS data were most accurate, but were not markedly higher than S-ALS alternatives. Budei et al. [
26] corroborated these findings, where the effectiveness of S- and M-ALS for classifying individual trees into forest type, genus, and species was compared. Additional intensity data, and derived vegetation indices such as the NDVI, were found to be influential in improving classification accuracies, especially when species diversity was high (seven classes or more). Application of M-ALS data to predict individual tree attributes such as volume [
12] indicated that M-ALS data performed better than S-ALS data, but were not as effective as the combination of optical imagery and S-ALS. The prediction accuracy of above-ground carbon storage using M-ALS was found to be 11% higher than S-ALS in urban trees, and that the combination of spectral and structural data were influential in improving tree detection and delineation outputs [
27].
Given the success of land-cover and individual tree-based classifications, there is an opportunity to further assess the potential of these data for area-based approaches (ABA; [
31]). The ABA combines geo-located field samples and ALS metrics to create predictive models of inventory attributes. Following model creation, these models can be applied over the entire coverage of ALS acquisitions, providing managers with wall-to-wall coverage of inventory predictions with known errors [
1]. Boreal tree species composition predictions using M-ALS data were found to be comparable to those from conventional ALS and optical data combined [
28], indicating that intensity values from M-ALS improve tree species discrimination. Comparison of ALS and DAP metrics for ABA inventory modelling indicated that the use of DAP spectral metrics provided no benefit [
24]. Further investigations into the benefit of additional wavelengths for structural and spectral characterizations of inventory attributes is warranted, especially given the success of the ABA using traditional S-ALS systems.
In this study, we assess the potential of M-ALS structural metrics for modelling conventional forest inventory attributes, as well as determine the added benefit of intensity information for estimating a number of plot-level forest stand attributes, including species richness, a variable commonly estimated poorly from S-ALS. To do so, we develop predictive models under two scenarios. First, structural and intensity metrics from each M-ALS wavelength, and all wavelengths combined, were generated and used as predictor variables within random forest (RF) models. Second, the point clouds were voxelized, and a variety of spectral indices calculated, for each voxel. Computed indices were summarized to the plot level and used as RF predictors. By comparing the two approaches, we investigate the potential benefit of M-ALS vegetation indices for improving forest attribute model predictions using an ABA, as well as better understand the potential value of voxel-based vegetation indices derived from M-ALS intensity data.
4. Discussion
This study utilized structural and spectral data from M-ALS point clouds to assess their potential for modelling forest inventory and diversity attributes. Results indicated that although Titan Optech M-ALS sensors provide additional intensity information for SWIR and green spectral channels, that structural metrics were predominantly found to be the best-performing predictors for plot-level estimates of forest inventory and diversity attributes. These results were further supported by variable importance rankings, where structural metrics largely exceeded intensity metrics and voxelized indices at all resolutions. Upper height percentiles (zp95), point densities within vertical strata (prop_d_05, prop_d_15), and point cloud skewness (zskew) were found to be important for most models, highlighting that the distribution of points, particularly those characterizing stand height and density of the canopy structure at low (0.5 m) and intermediate (15 m) heights were more effective than intensity metrics for explaining variance. Modelling results were predominantly most accurate when using structural metrics from wavelengths individually, or all wavelengths combined. The inclusion of intensity metrics was, however, found to be important and resulted in small accuracy improvements in some models, particularly those for diversity indices, indicating that there is still potential to leverage these data for improving non-traditional forest attribute models using M-ALS. Modelling gains when including the cumulative intensity of points at height percentiles (ipzcum30, ipzcum90) indicate that these metrics may have value for isolating differences between internal canopy structure. Future work into the potential of these metrics to detail information about understory canopy could be valuable.
Addition of NIRstruc metrics to voxel-based models reduced %RMSE for all models, with HL, V, and D realizing the largest improvements. Results confirming that structural predictors were the most appropriate for modelling V, BA, and HL confirm those of numerous past studies, though few have tested and compared differences between traditional NIR sensors and additional SWIR and GREEN channels. Negligible differences between NIR, SWIR, GREEN and all channels combined indicate that structural metrics from any of these channels were appropriate for modelling HL, BA, and V. Given the more widespread availability and research surrounding the use of traditional NIR sensors, their continued use is supported by results herein.
A potential cause of diminished importance for intensity metrics within models could be due to heterogeneity in species composition. Intensity metrics may be more capable of improving attribute predictions within plots with lower species diversity as intensity variables may provide information related to species fractions. As diversity increases, however, intensity differences driven by species may become mixed, leading to their reduced importance within models. Studies such as Gallus et al. [
49] indicated that the inclusion of forest type information such as conifer and broadleaf proportions was beneficial to improving model accuracies. The inclusion of such data alongside intensity metrics could be a method for improving their predictive potential, especially in diverse and complex forest types.
Reductions in %RMSE, though to a lesser degree for H, D, and R models, as well as intensity metrics being important variables from conditional random forest, indicate that intensity data from M-ALS channels may play an important role in future endeavors to model forest diversity. Findings from Dalponte et al. [
10] indicated that intensity metrics were found to be important for modelling diversity indices, including H. Findings herein that the ratio between NIR and GREEN as well as CVI
SWIR metrics were important for modelling D, and to a lesser degree H, show similarities between these studies. Higher %RMSE overall when using voxelized indices alone align with comments from Kukkonen et al. [
12], who suggested that spectral ratios from M-ALS wavelengths should not be considered equivalent to the same indices derived from optical imagery. Voxelization to compute spectral indices using mean intensity values from M-ALS is likely not directly comparable to optical imagery products due to spectral averaging.
Marginal improvements and similarities amongst model accuracies using M-ALS intensity data for ABA are similar to results from Tompalski et al. [
24], who found that spectral information from DAP point clouds also did not significantly increase model accuracy. In contrast to M-ALS, DAP spectral indices can be calculated at the point level due to each point being attributed all wavelength attributes. The need to voxelize or spatially amalgamate M-ALS data to compute comparable indices reduces the three-dimensional detail of point clouds, potentially limiting the utility of these metrics for ABA. Findings from other studies have indicated that best modelling results were achieved by structural metrics from ALS and spectral metrics from ortho imagery [
12]. Methods to facilitate the computation of M-ALS spectral indices without having to voxelize may improve the capabilities of these data for modelling purposes and facilitate calculation of additional spectrally derived metrics.
The lack of realized improvement from plot-level summaries of voxel spectral indices could be due to the observed relationship in sufficiently populated voxel counts (
Figure 4). Mean counts of sufficiently populated voxels were highest for the 2 m resolution, followed by the 1 m and 0.5 m resolutions respectively (
Figure 4). As resolution decreases, the total number of potentially available voxels within a plot increases; however, the chances of having a point from all three wavelengths decreases due to constriction of three-dimensional space. Unsurprisingly, the 0.5 m resolution was found to have the fewest sufficiently populated voxels, while the 2 m resolution was found to have more sufficiently populated voxels than 1 m. The difference between voxel resolution and number of sufficiently populated voxels is interesting when compared with the importance of spectral indices within diversity index models. The 1 and 2 m resolutions were found to have higher importance measures for some spectral indices, while spectral indices were not found to be important for the 0.5 m models. This indicates that voxel resolution, and the continued investigation of the potential to utilize intensity metrics from M-ALS in a three-dimensional context could improve modelling outcomes.
A limitation for increasing the number of sufficiently populated voxels relates to the point density of each M-ALS point cloud, the divergence of each M-ALS laser, and utilizing Optech Titan data without scanline banding effects (
Table 2). The reduction in point cloud density (
Table 2) following the removal of inward scanlines resulted in substantial losses to point density for each M-ALS channel. The green point cloud had much fewer points than the NIR and SWIR point clouds, which was found to be the largest limiting factor for sufficiently populated voxel counts. This is especially evident in the 2 m resolution distributions in
Figure 4, where sufficiently populated voxel and green band voxel counts mimic a similar trend. Hopkinson et al. [
3] noted that leaf absorption is a likely cause of reduction in the penetration of points from the green wavelength, potentially leading to the reduced number of points found in our results. Flying lower could improve the intensity based predictive results, as this would diminish the influence of attenuation on the green channel and thus normalize the return sampling densities across the three channels. Similar point densities and counts within voxels for SWIR and NIR wavelengths are likely related to their higher energy pulses.
Given that few ABA studies exist where M-ALS structure and intensity metrics are utilized, a thorough comparison to results found using individual-tree detection (ITD) approaches is not yet possible. Preliminary comparisons do, however, indicate that M-ALS intensity metrics may be better served for tree-level classification and attribute prediction applications. High modelling accuracies for species delineation in a variety of forest settings have indicated that both structure and intensity metrics improve model performance [
11,
26,
30]. The ability for these metrics to differentiate between forest attributes and types could, therefore, be scale dependent. ABA, where metrics are summarized at the plot level, could lead to a reduced signal to those found in individually delineated tree crowns, reducing their effectiveness. Further comparisons between ABA and ITD results are needed to confirm these assumptions and to better understand the role that these M-ALS data have in forest inventory practices.