Ionospheric Responses to the June 2015 Geomagnetic Storm from Ground and LEO GNSS Observations
Abstract
1. Introduction
2. Data and Methods
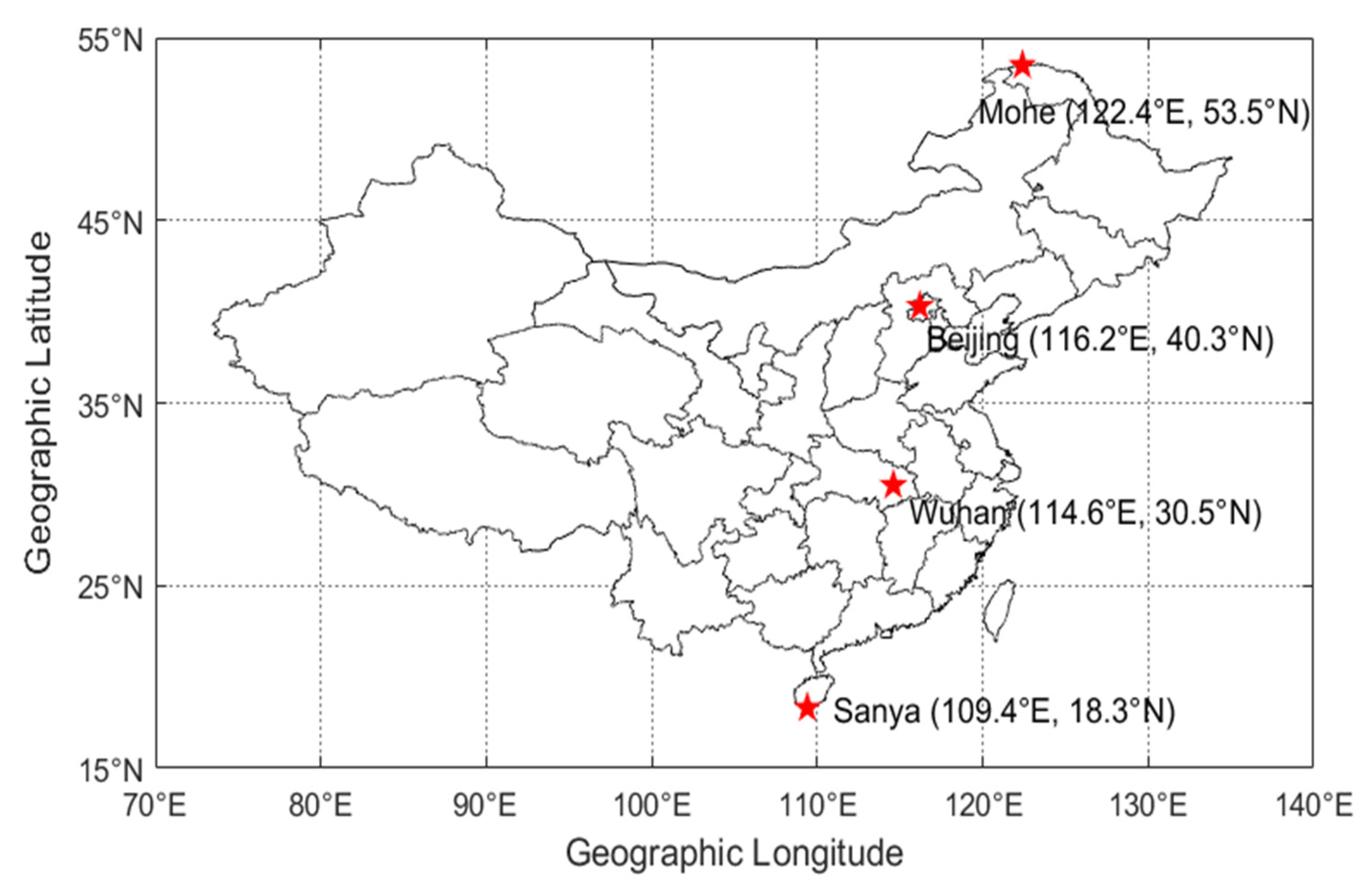
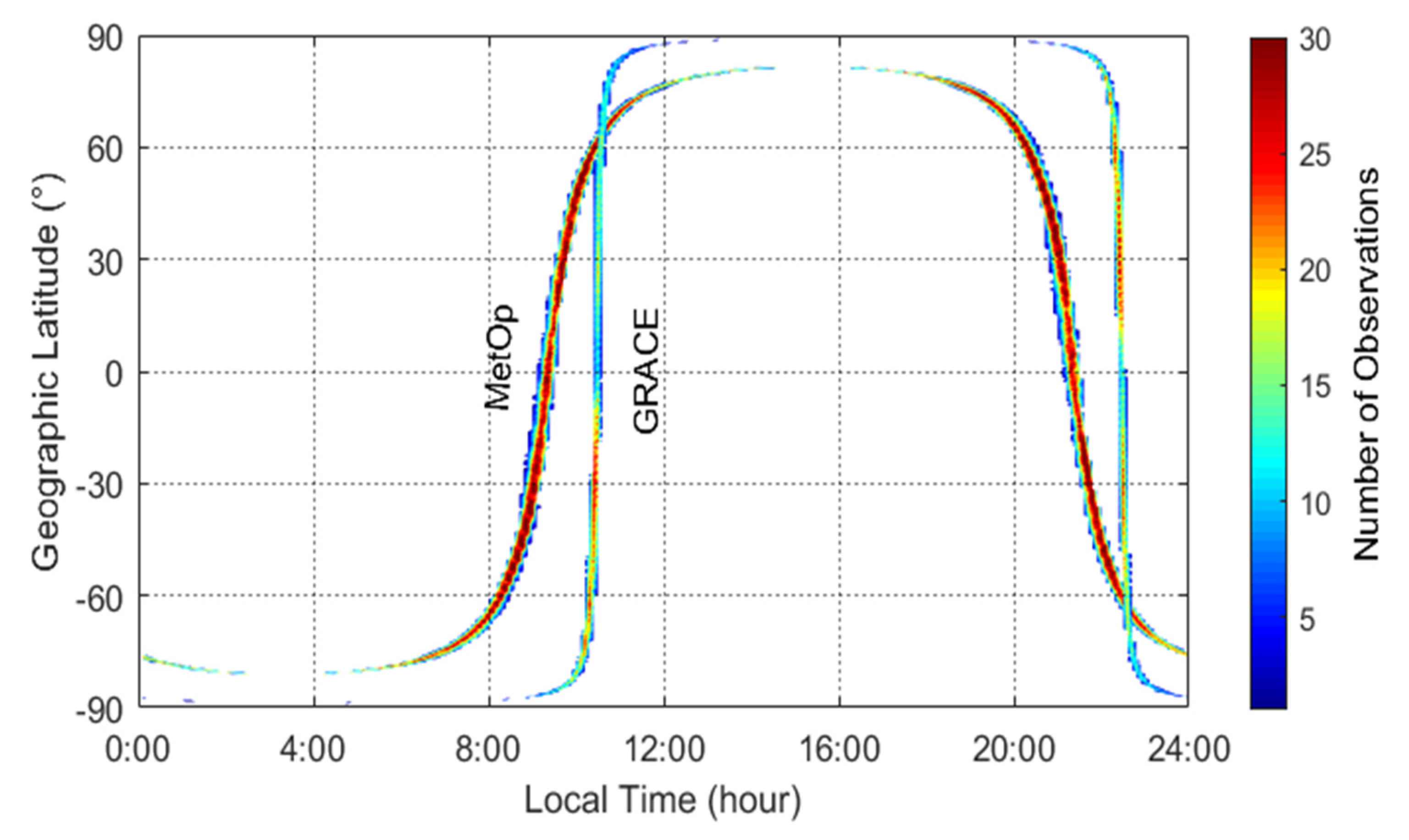
2.1. Observational Data
2.2. Multi-Layer Mapping Function
3. Results and Analysis
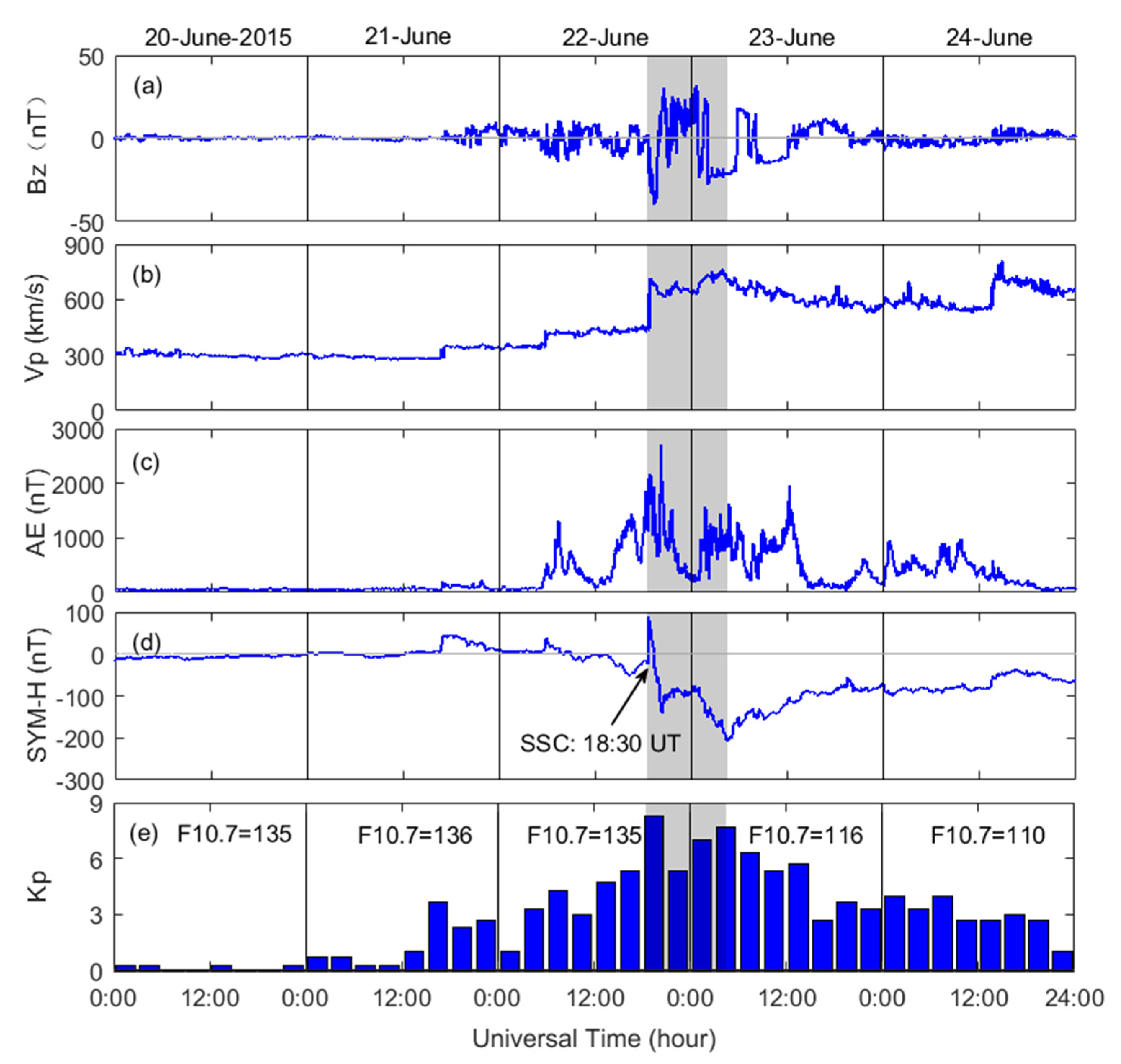
3.1. Interplanetary and Geomagnetic Indexes
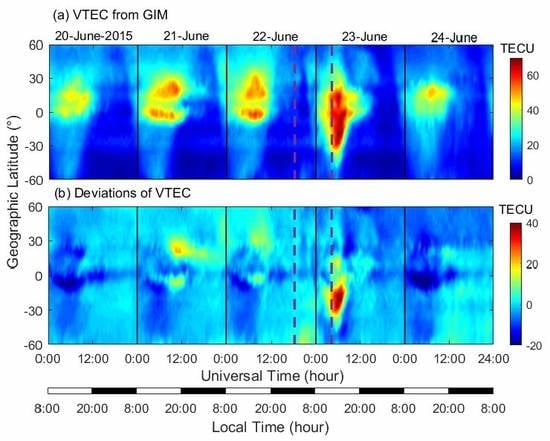
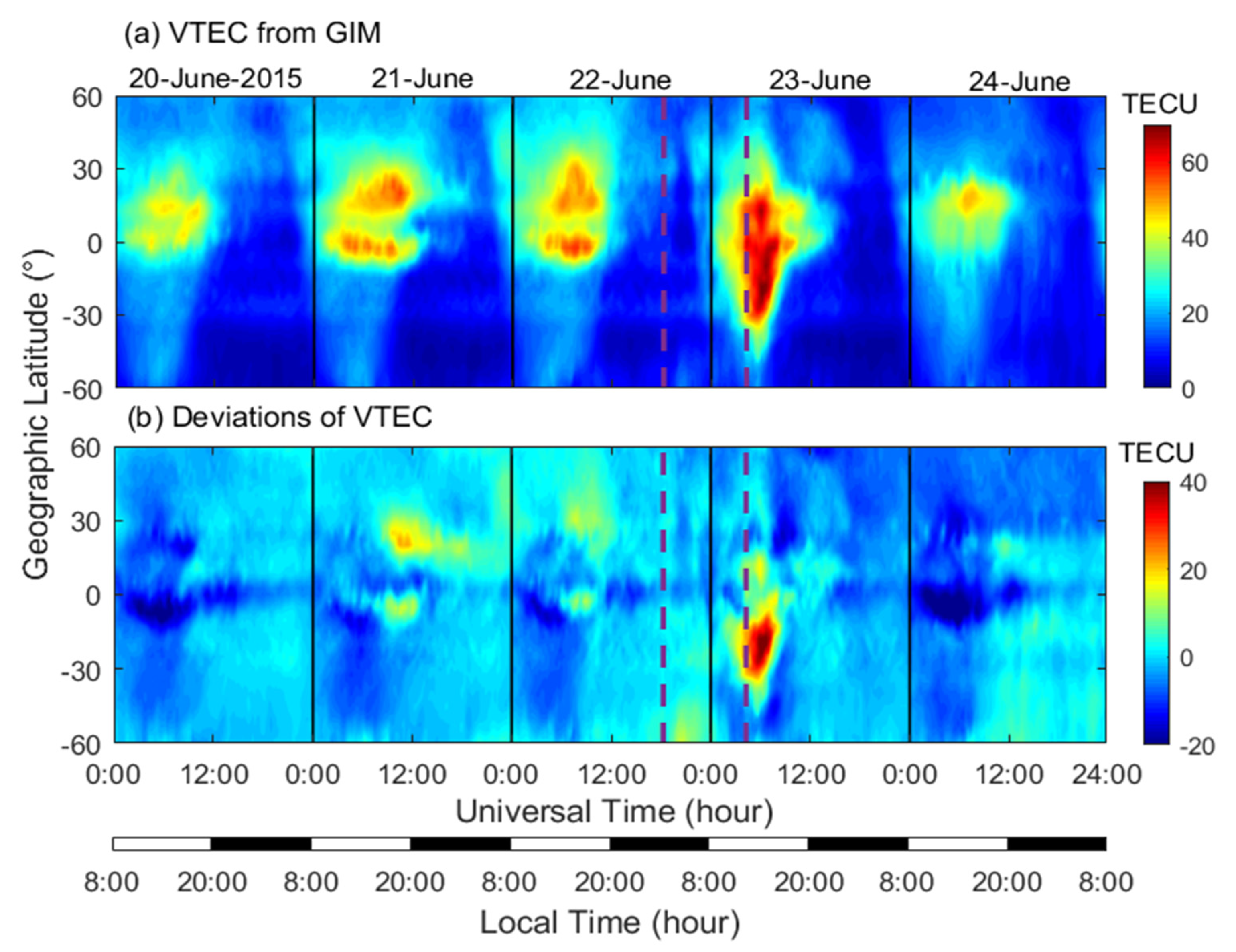
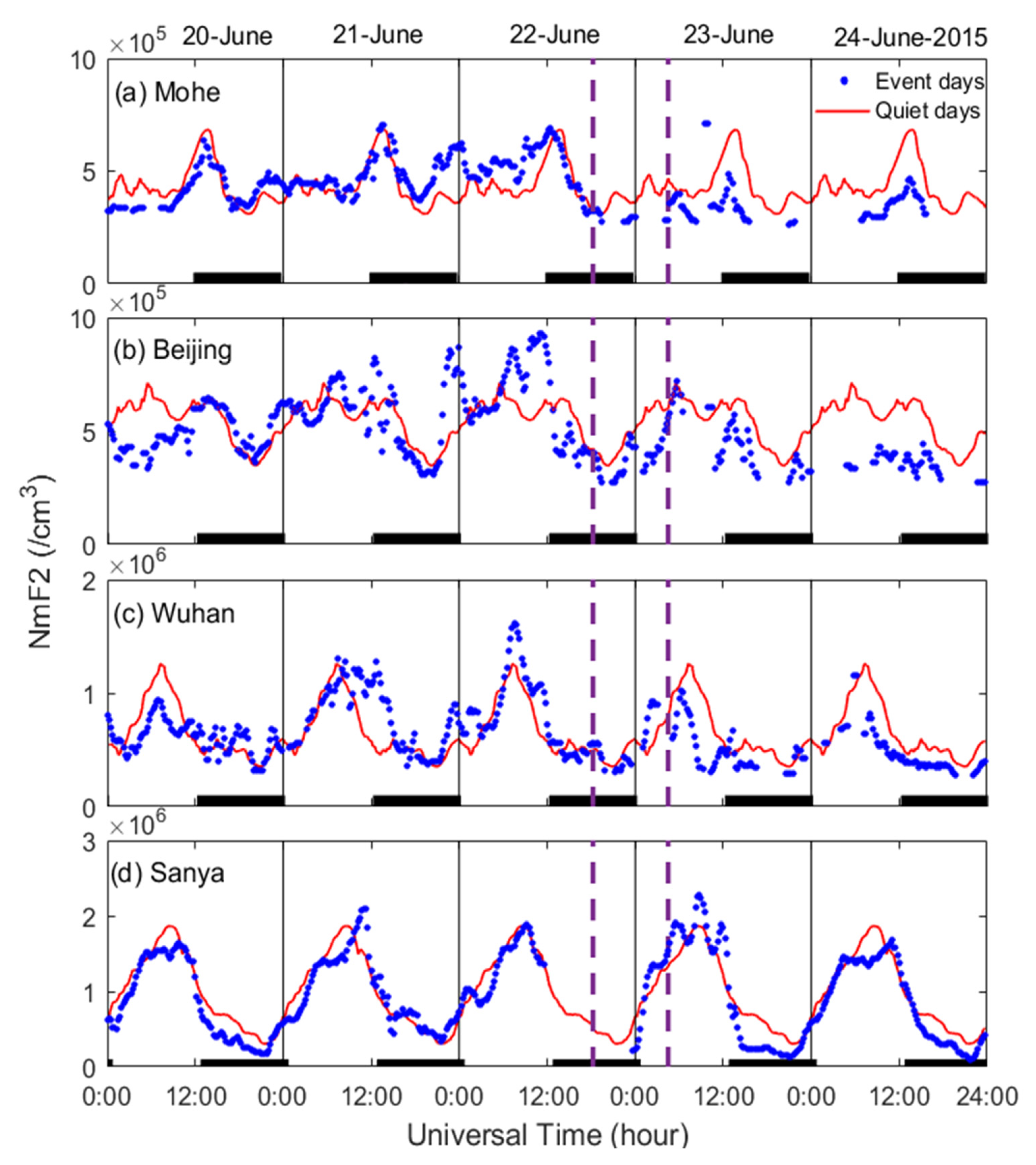
3.2. Ionospheric Responses From Ground Observations
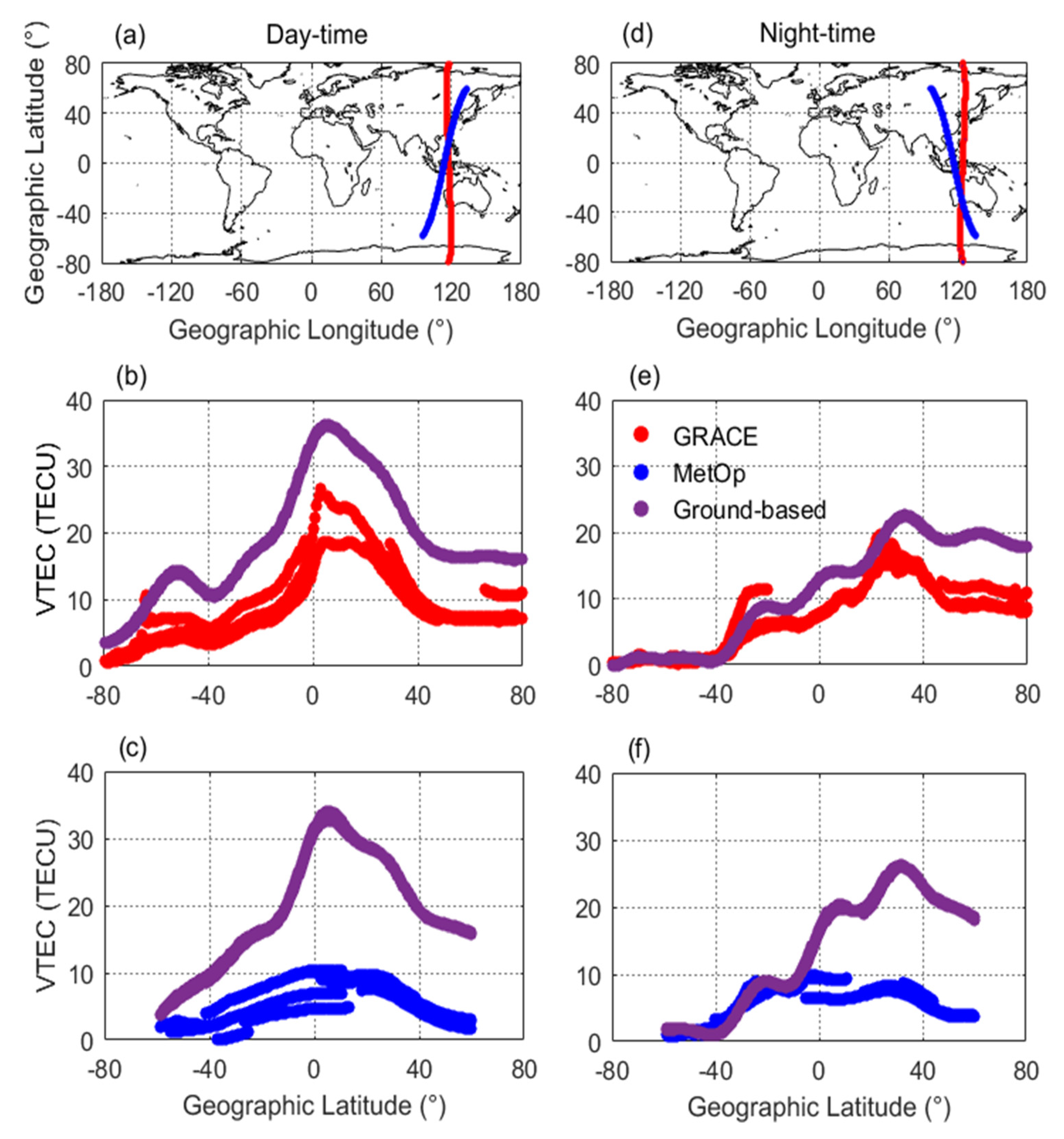
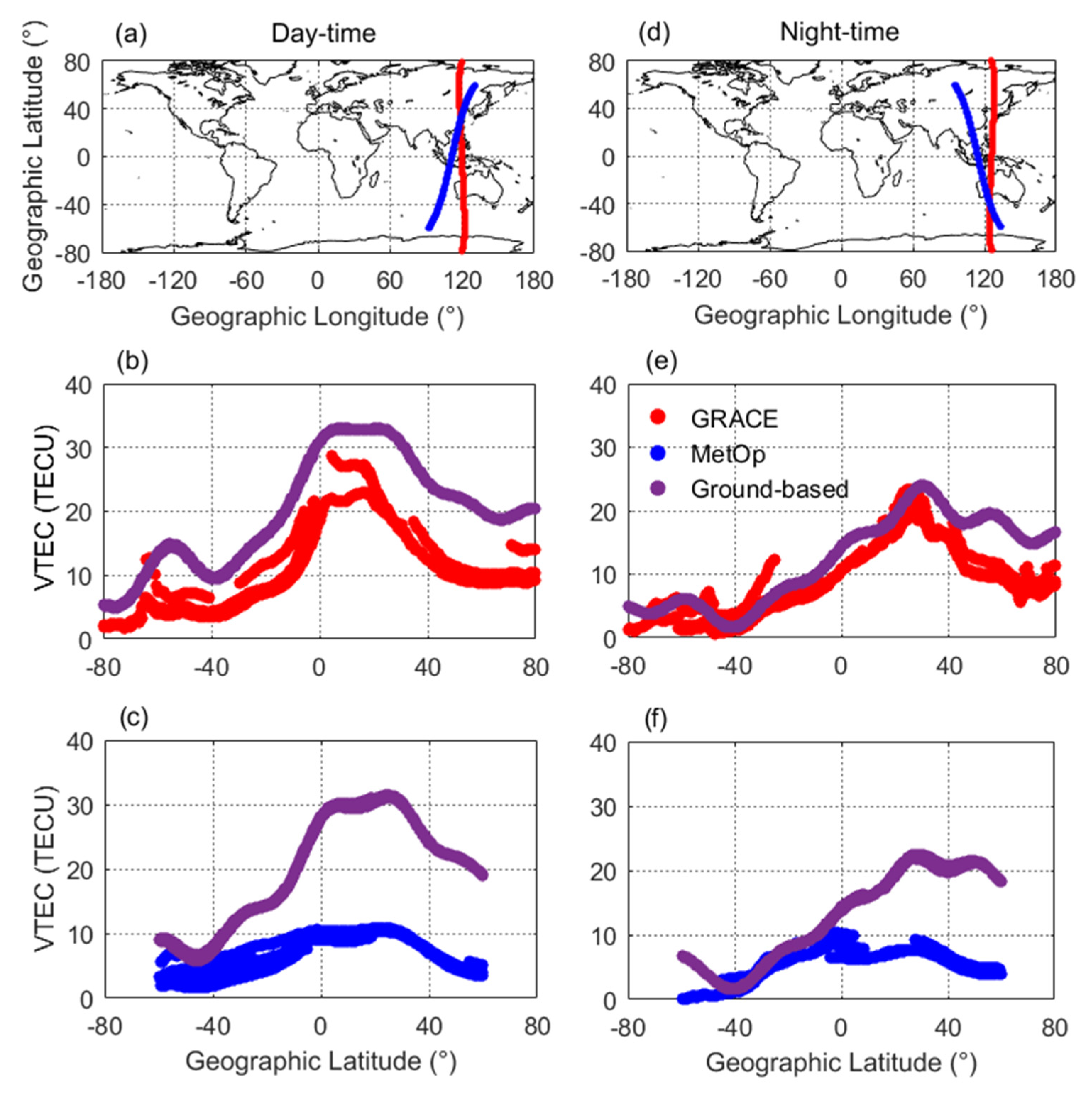
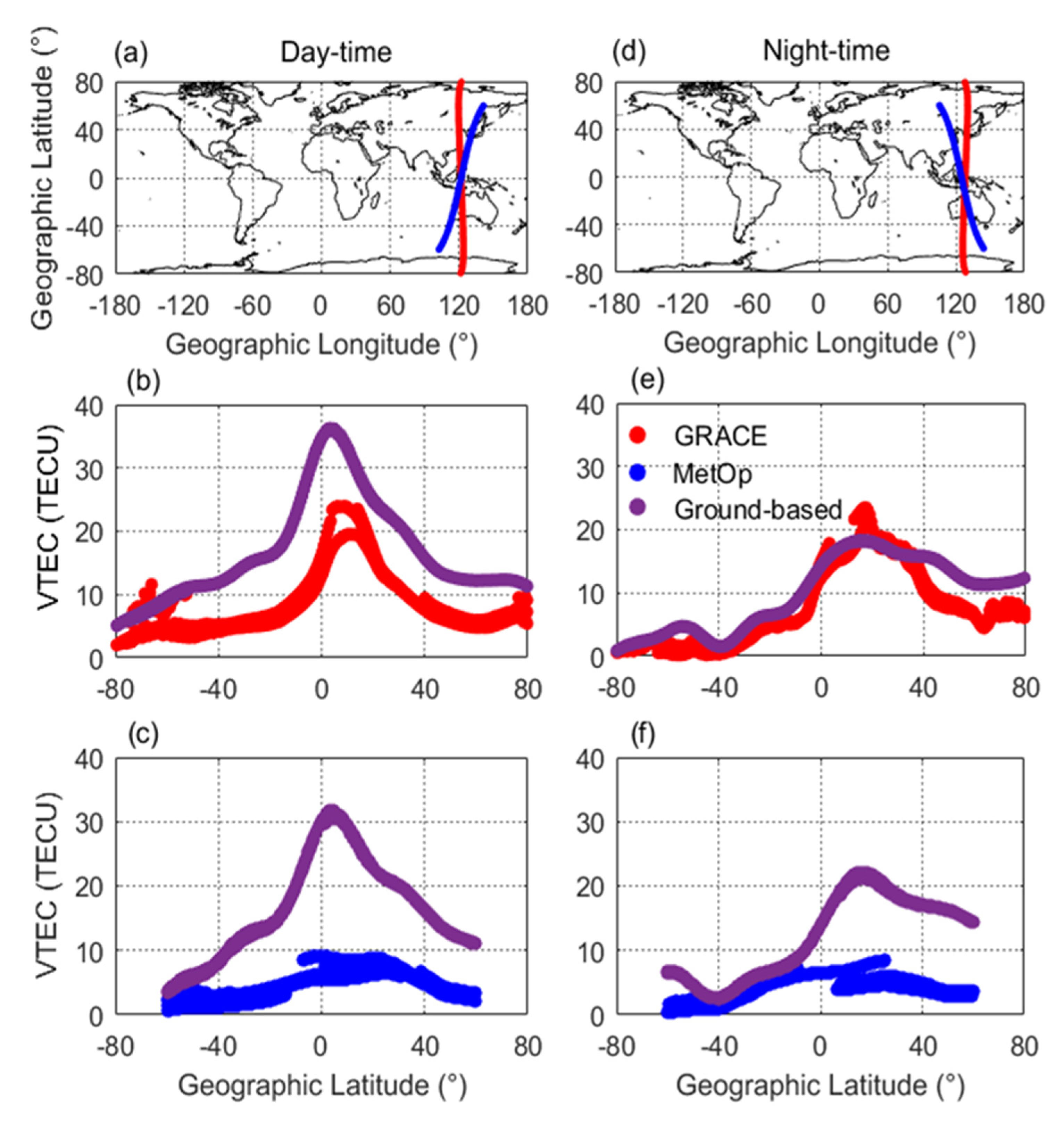
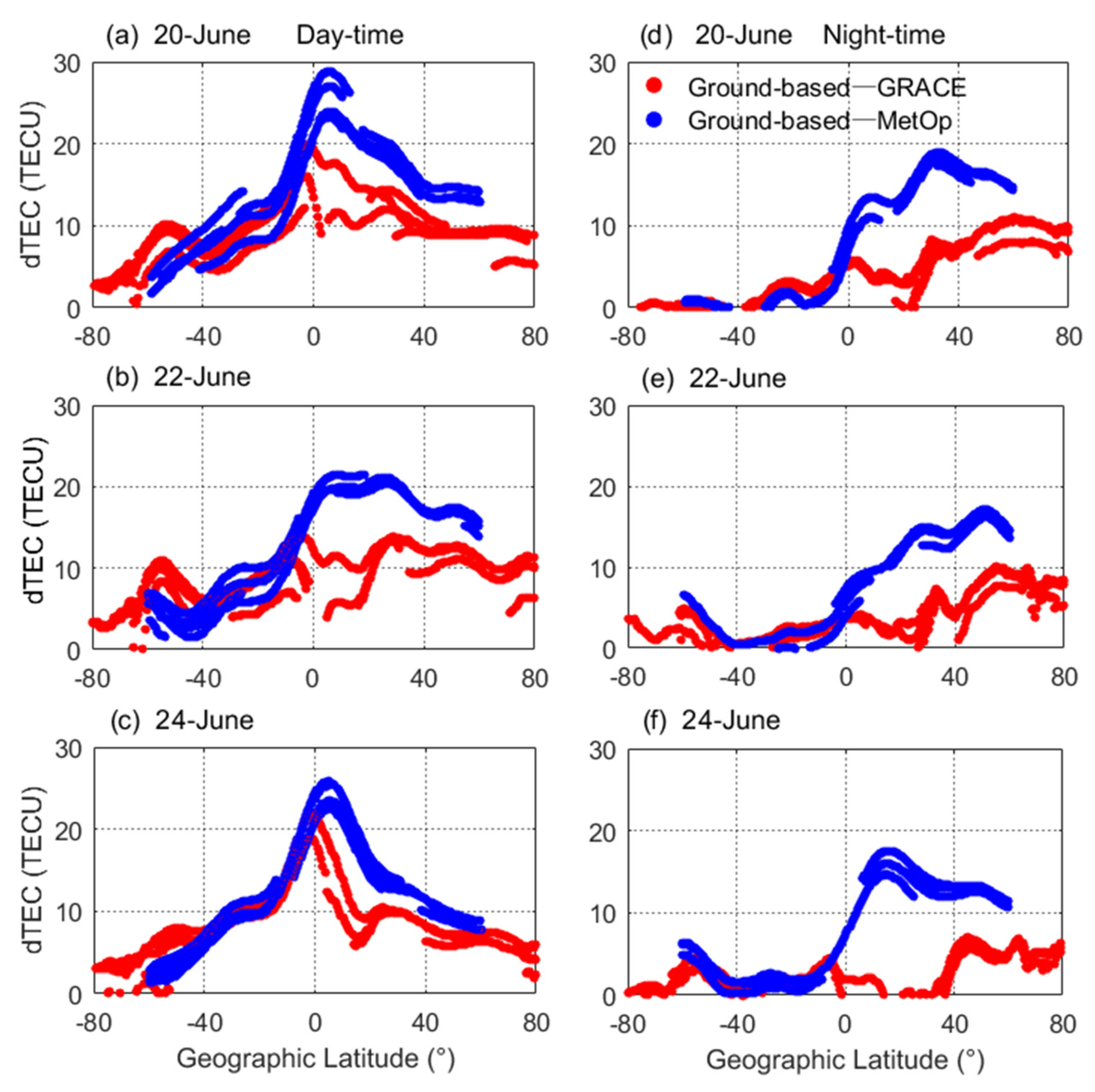
3.3. Ionospheric Responses From Ground- and Satellite-Based Observations
4. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Richardson, I.G.; Cane, H.V. Solar wind drivers of geomagnetic storms during more than four solar cycles. J. Space Weather Space Clim. 2012, 2, A01. [Google Scholar] [CrossRef]
- Volland, H. Handbook of Atmospheric Electrodynamics; CRC Press: Boca Rotan, FL, USA, 1995. [Google Scholar]
- Martyn, D.F. The Morphology of the Ionospheric Variations Associated with Magnetic Disturbance. I. Variations at Moderately Low Latitudes. Proc. R. Soc. Lond. 1953, 218, 1–18. [Google Scholar]
- Seaton, M.J. A possible explanation of the drop in f-region critical densities accompanying major ionospheric storms. J. Atmos. Terr. Phys. 1956, 8, 122–124. [Google Scholar] [CrossRef]
- Duncan, R.A. F-region seasonal and magnetic-storm behaviour. J. Atmos. Terr. Phys. 1969, 31, 59–70. [Google Scholar] [CrossRef]
- Afraimovich, E.L.; Palamartchouk, K.S.; Perevalova, N.P. GPS radio interferometry of travelling ionospheric disturbances. J. Atmos. Sol. Terr. Phys. 1998, 60, 1205–1223. [Google Scholar] [CrossRef]
- Fuller-Rowell, T.J.; Codrescu, M.V.; Rishbeth, H.; Moffett, R.J.; Quegan, S. On the seasonal response of the thermosphere and ionosphere to geomagnetic storms. J. Geophys. Res. 1996, 101, 2343–2353. [Google Scholar] [CrossRef]
- Rishbeth, H. F-region storms and thermospheric circulation. J. Atmos. Terr. Phys. 1975, 37, 1055–1064. [Google Scholar] [CrossRef]
- Chakrabarty, D.; Sekar, R.; Narayanan, R.; Devasia, C.V.; Pathan, B.M. Evidence for the interplanetary electric field effect on the OI 630.0 nm airglow over low latitude. J. Geophys. Res. Atmos. 2005, 110, A11301. [Google Scholar] [CrossRef]
- Blanc, M.; Richmond, A.D. The ionospheric disturbance dynamo. J. Geophys. Res. Space Phys. 1980, 85, 1669–1686. [Google Scholar] [CrossRef]
- Tsurutani, B.; Mannucci, A.J.; Iijima, B.; Abdu, M.A.; Sobral, J.H.; Gonzalez, W.D.; Guarnieri, F.L.; Tsuda, T.; Saito, A.; Yumoto, K.; et al. Global dayside ionospheric uplift and enhancement associated with interplanetary electric fields. J. Geophys. Res. 2004, 109, A08302. [Google Scholar] [CrossRef]
- Zhao, B.Q.; Wan, W.X.; Liu, L.B. Responses of equatorial anomaly to the October-November 2003 superstorms. Ann. Geophys. 2005, 23, 693–706. [Google Scholar] [CrossRef]
- Lei, J.H.; Zhu, Q.Y.; Wang, W.B.; Burns, A.G.; Zhao, B.Q.; Luan, X.L.; Zhong, J.H.; Dou, X.K. Response of the topside and bottomside ionosphere at low and middle latitudes to the October 2003 superstorms. J. Geophys. Res. Space Phys. 2015, 120, 6974–6986. [Google Scholar] [CrossRef]
- Li, G.Z.; Ning, B.Q.; Zhao, B.Q.; Liu, L.B.; Wan, W.X.; Ding, F.; Xu, J.S.; Liu, J.Y.; Yumoto, K. Characterizing the 10 November 2004 storm-time middle-latitude plasma bubble event in Southeast Asia using multi-instrument observations. J. Geophys. Res. Space Phys. 2009, 114, A07304. [Google Scholar] [CrossRef]
- Sun, W.J.; Ning, B.Q.; Zhao, B.Q.; Li, G.Z.; Hu, L.H.; Chang, S.M. Analysis of ionospheric features in middle and low latitude region of China during the geomagnetic storm in March 2015. Chin. J. Geophys. 2017, 60, 1–10. [Google Scholar]
- Chen, Y.D.; Liu, L.B.; Le, H.J.; Wan, W.X. Geomagnetic activity effect on the global ionosphere during the 2007–2009 deep solar minimum. J. Geophys. Res. Space Phys. 2014, 119, 3747–3754. [Google Scholar] [CrossRef]
- Kuai, J.W.; Liu, L.B.; Liu, J.; Sripathi, S.; Zhao, B.Q.; Chen, Y.D.; Le, H.J.; Hu, L.H. Effects of disturbed electric fields in the low-latitude and equatorial ionosphere during the 2015 St. Patrick’s Day storm. J. Geophys. Res. Space Phys. 2016, 121, 9111–9126. [Google Scholar] [CrossRef]
- Jin, S.G.; Su, K. PPP models and performances from single- to quad-frequency BDS observations. Satell. Navig. 2020, 1, 16. [Google Scholar] [CrossRef]
- Jin, S.G.; Jin, R.; Kutoglu, H. Positive and negative ionospheric responses to the March 2015 geomagnetic storm from BDS observations. J. Geod. 2017, 91, 613–626. [Google Scholar] [CrossRef]
- Jin, S.C.; Luo, O.F.; Park, P. GPS observations of the ionospheric F2-layer behavior during the 20th November 2003 geomagnetic storm over South Korea. J. Geod. 2008, 82, 883–892. [Google Scholar] [CrossRef]
- Feltens, J.; Schaer, S. IGS Products for the Ionosphere. In Proceedings of the IGS Position Paper, IGS Analysis Centers Workshop ESOC, Darmstadt, Germany, 9–11 February 1998. [Google Scholar]
- Feltens, J. The International GPS Service (IGS) ionosphere working group. Adv. Space Res. 2003, 31, 635–644. [Google Scholar] [CrossRef]
- Chen, P.; Yao, Y.B. Research on global plasmaspheric electron content by using LEO occultation and GPS data. Adv. Space Res. 2015, 55, 2248–2255. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Yue, X.A.; Schreiner, W.S.; Hunt, D.C.; Rocken, C.; Kuo, Y.H. Quantitative evaluation of the low Earth orbit satellite based slant total electron content determination. Space Weather 2011, 9, S09001. [Google Scholar] [CrossRef]
- Hoque, M.M.; Jakowski, N. Mitigation of Ionospheric Mapping Function Error. In Proceedings of the ION GNSS+ 2013, Nashville, Tennessee, 16–20 September 2013; pp. 1848–1855. [Google Scholar]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Aragón-Àngel, À.; García-Rigo, A.; Salazar, D.; Escudero, M. The ionosphere: Effects, GPS modeling and the benefits for space geodetic techniques. J. Geod. 2011, 85, 887–907. [Google Scholar] [CrossRef]
- Foelsche, U.; Kirchengast, G. A simple “geometric” mapping function for the hydrostatic delay at radio frequencies and assessment of its performance. Geophys. Res. Lett. 2002, 29, 111-1–111-4. [Google Scholar] [CrossRef]
- Huang, Z.; Yuan, H. Analysis and improvement of ionospheric thin shell model used in SBAS for China region. Adv. Space Res. 2013, 51, 2035–2042. [Google Scholar] [CrossRef]
- Zhong, J.H.; Lei, J.H.; Dou, X.K.; Yue, X.N. Assessment of vertical TEC mapping functions for space-based GNSS observations. GPS Solut. 2016, 20, 353–362. [Google Scholar] [CrossRef]
- Garriott, O.K.; Rishbeth, H. Introduction to Ionospheric Physics; Academic: New York, NY, USA, 1969. [Google Scholar]
- Jakowski, N.; Hoque, M.M. A new electron density model of the plasmasphere for operational applications and services. J. Space Weather Space Clim. 2018, 8, A16. [Google Scholar] [CrossRef]
- Hoque, M.; Jakowski, N. A new global model for the ionospheric F2 peak height for radio wave propagation. Ann. Geophys. 2012, 30, 797–809. [Google Scholar] [CrossRef]
- Jakowski, N.; Hoque, M.M.; Mayer, C. A new global TEC model for estimating transionospheric radio wave propagation errors. J. Geod. 2011, 85, 965–974. [Google Scholar] [CrossRef]
- Hoque, M.M.; Jakowski, N.; Berdermann, J. A new approach for mitigating ionospheric mapping function errors. In Proceedings of the ION GNSS+ 2014, Tampa, Florida, 8–12 September 2014; pp. 1183–1189. [Google Scholar]
- Gonzalez, W.D. A study on the peak Dst and peak negative Bz relationship during intense geomagnetic storms. Geophys. Res. Lett. 2005, 32, L18103. [Google Scholar] [CrossRef]
- Cowley, S.W.H.; Lockwood, M. Excitation and decay of solar wind-driven flows in the magnetosphere-ionosphere system. Ann. Geophys. 1992, 10, 103–115. [Google Scholar]
- Astafyeva, E.; Zakharenkova, I.; Huba, J.D.; Doornbos, E.; van den IJssel, J. Global Ionospheric and Thermospheric Effects of the June 2015 Geomagnetic Disturbances: Multi-Instrumental Observations and Modeling. J. Geophys. Res. Space Phys. 2017, 122, 11716–11742. [Google Scholar] [CrossRef] [PubMed]
- Astafyeva, E.; Zakharenkova, I.; Hozumi, K.; Alken, P.; Coïsson, P.; Hairston, M.R.; Coley, W.R. Study of the Equatorial and Low-Latitude Electrodynamic and Ionospheric Disturbances During the 22–23 June 2015 Geomagnetic Storm Using Ground-Based and Spaceborne Techniques. J. Geophys. Res. Space Phys. 2018, 123, 2424–2440. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, L.J.; Wang, J.L.; Zhang, C.X. Studying Ionosphere Responses to a Geomagnetic Storm in June 2015 with Multi-Constellation Observations. Remote Sens. 2018, 10, 666. [Google Scholar] [CrossRef]
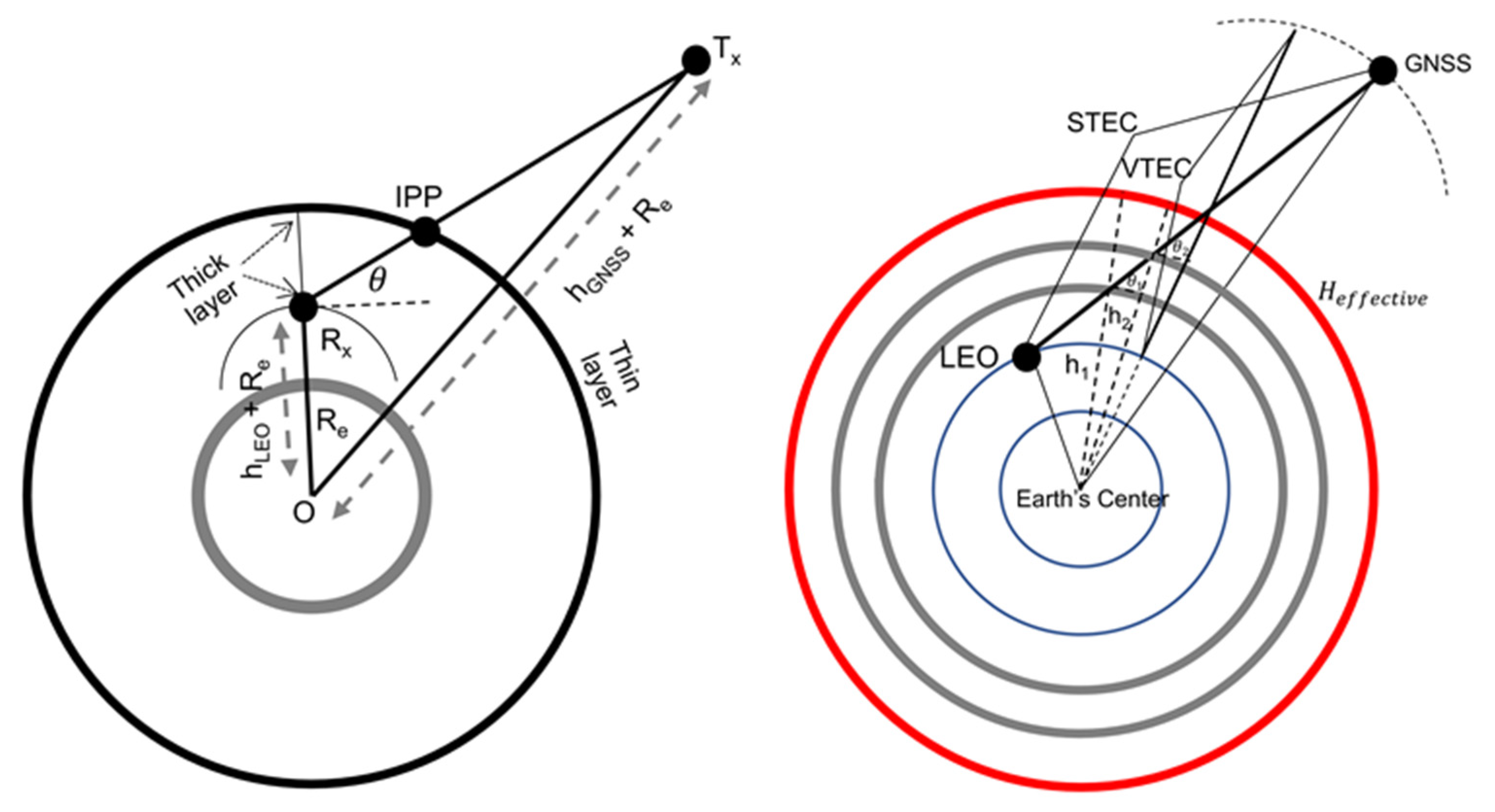

| Items | Properties |
|---|---|
| Observational data | Level 1 podTec (.nc) |
| Lower boundary of observation | Orbital altitudes of GRACE and MetOp satellites (~400 km and ~820 km, respectively) |
| Upper boundary of observation | Orbital altitude of GPS satellites (~20,200 km) |
| Cut-off elevation angle | 40° |
| Sampling rate | 10 s |
| Boundary between ionosphere and plasmasphere | 2000 km |
| Thin shell interval in ionosphere | 50 km |
| Thin shell interval in plasmasphere | 200 km |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.; Jin, S.; Yuan, L. Ionospheric Responses to the June 2015 Geomagnetic Storm from Ground and LEO GNSS Observations. Remote Sens. 2020, 12, 2200. https://doi.org/10.3390/rs12142200
Gao C, Jin S, Yuan L. Ionospheric Responses to the June 2015 Geomagnetic Storm from Ground and LEO GNSS Observations. Remote Sensing. 2020; 12(14):2200. https://doi.org/10.3390/rs12142200
Chicago/Turabian StyleGao, Chao, Shuanggen Jin, and Liangliang Yuan. 2020. "Ionospheric Responses to the June 2015 Geomagnetic Storm from Ground and LEO GNSS Observations" Remote Sensing 12, no. 14: 2200. https://doi.org/10.3390/rs12142200
APA StyleGao, C., Jin, S., & Yuan, L. (2020). Ionospheric Responses to the June 2015 Geomagnetic Storm from Ground and LEO GNSS Observations. Remote Sensing, 12(14), 2200. https://doi.org/10.3390/rs12142200