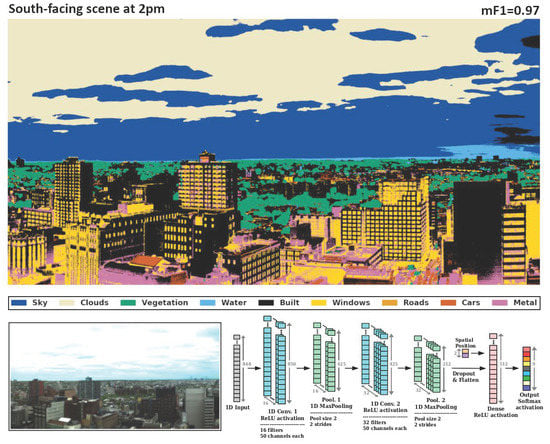
Pixel-Wise Classification of High-Resolution Ground-Based Urban Hyperspectral Images with Convolutional Neural Networks
Abstract
:1. Introduction
- identifying the wavelength scale of spectral features in urban scenes;
- testing the extent to which the addition of spatial information contributes to CNN model performance when segmenting these scenes;
- comparing the performance of CNN models trained and tested on each scene separately as well as a single CNN model trained on all scenes at once;
- assessing the transferability of the CNN models by training on one scene and testing on another;
- evaluating the performance of CNN models as the spectral resolution is reduced;
- evaluating the performance of a CNN model as the number of training instances is reduced.
2. Materials and Methods
2.1. Hyperspectral Imaging Data from the Urban Observatory
2.2. Model Architecture
2.3. Model Training and Assessment
3. Results
3.1. Identifying the Scale of Spectral Features in Urban Scenes
3.2. Comparing the Lowest and Highest Performing Models
3.3. Evaluating the Effect of Spatial Information
3.4. Single Model Trained on All Scenes
3.5. Transferability of the Model
3.6. Reduced Spectral Resolution
3.7. Reduced Number of Training Instances
4. Discussion
4.1. Identifying the Scale of Spectral Features in Urban Scenes
4.2. Evaluating the Effect of Spatial Information
4.3. Transferability of the Model
4.4. Reduced Spectral Resolution
4.5. Reduced Number of Training Instances
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
Appendix A. Confusion Matrices




Appendix B. Exploring Other Classification Methods
Appendix B.1. Gradient Boosted Decision Trees
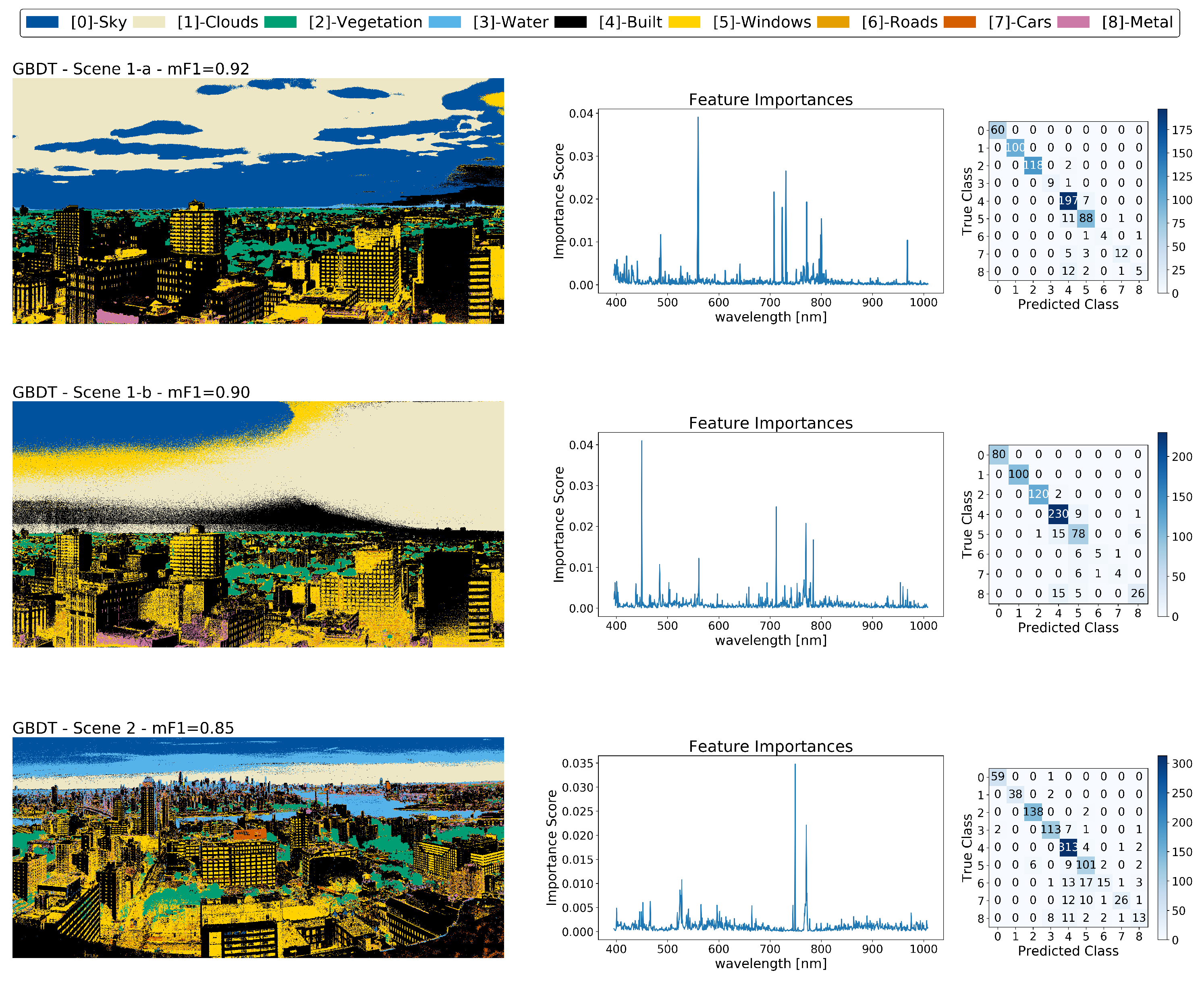
Appendix B.2. Principal Component Analysis and Support Vector Machines

References
- United Nations. 2018 Revision of World Urbanization Prospects; United Nations: New York, NY, USA, 2018. [Google Scholar]
- Theobald, D.M. Development and applications of a comprehensive land use classification and map for the US. PLoS ONE 2014, 9, e94628. [Google Scholar] [CrossRef] [Green Version]
- Schneider, A.; Friedl, M.A.; Potere, D. A new map of global urban extent from MODIS data. Environ. Res. Lett. 2009, 4, 44003–44011. [Google Scholar] [CrossRef] [Green Version]
- Baklanov, A.; Molina, L.T.; Gauss, M. Megacities, air quality and climate. Atmos. Environ. 2016, 126, 235–249. [Google Scholar] [CrossRef]
- Mills, G. Cities as agents of global change. Int. J. Climatol. J. R. Meteorol. Soc. 2007, 27, 1849–1857. [Google Scholar] [CrossRef]
- Abrantes, P.; Fontes, I.; Gomes, E.; Rocha, J. Compliance of land cover changes with municipal land use planning: Evidence from the Lisbon metropolitan region (1990–2007). Land Use Policy 2016, 51, 120–134. [Google Scholar] [CrossRef]
- Vargo, J.; Habeeb, D.; Stone Jr, B. The importance of land cover change across urban–rural typologies for climate modeling. J. Environ. Manag. 2013, 114, 243–252. [Google Scholar] [CrossRef]
- Chu, A.; Lin, Y.C.; Chiueh, P.T. Incorporating the effect of urbanization in measuring climate adaptive capacity. Land Use Policy 2017, 68, 28–38. [Google Scholar] [CrossRef]
- Tavares, P.A.; Beltrão, N.; Guimarães, U.S.; Teodoro, A.; Gonçalves, P. Urban Ecosystem Services Quantification through Remote Sensing Approach: A Systematic Review. Environments 2019, 6, 51. [Google Scholar] [CrossRef] [Green Version]
- Kettig, R.L.; Landgrebe, D. Classification of multispectral image data by extraction and classification of homogeneous objects. IEEE Trans. Geosci. Electron. 1976, 14, 19–26. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Troy, A. An object-oriented approach for analysing and characterizing urban landscape at the parcel level. Int. J. Remote Sens. 2008, 29, 3119–3135. [Google Scholar] [CrossRef]
- Albert, A.; Kaur, J.; Gonzalez, M.C. Using convolutional networks and satellite imagery to identify patterns in urban environments at a large scale. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1357–1366. [Google Scholar]
- Smith, R.B. Introduction to Remote Sensing of Environment (RSE); Microimages Inc.: Lincoln, NE, USA, 2012. [Google Scholar]
- Geladi, P.; Grahn, H.; Burger, J. Multivariate images, hyperspectral imaging: Background and equipment. In Techniques and Applications of Hyperspectral Image Analysis; Willey: Hoboken, NJ, USA, 2007; pp. 1–15. [Google Scholar]
- Herold, M.; Roberts, D.A.; Gardner, M.E.; Dennison, P.E. Spectrometry for urban area remote sensing—Development and analysis of a spectral library from 350 to 2400 nm. Remote Sens. Environ. 2004, 91, 304–319. [Google Scholar] [CrossRef]
- Marion, R.; Michel, R.; Faye, C. Measuring trace gases in plumes from hyperspectral remotely sensed data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 854–864. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral image classification using deep pixel-pair features. IEEE Trans. Geosci. Remote Sens. 2016, 55, 844–853. [Google Scholar] [CrossRef]
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in hyperspectral image and signal processing: A comprehensive overview of the state of the art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef] [Green Version]
- Imani, M.; Ghassemian, H. An overview on spectral and spatial information fusion for hyperspectral image classification: Current trends and challenges. Inf. Fusion 2020, 59, 59–83. [Google Scholar] [CrossRef]
- Fauvel, M.; Tarabalka, Y.; Benediktsson, J.A.; Chanussot, J.; Tilton, J.C. Advances in spectral-spatial classification of hyperspectral images. Proc. IEEE 2012, 101, 652–675. [Google Scholar] [CrossRef] [Green Version]
- Yue, J.; Zhao, W.; Mao, S.; Liu, H. Spectral–spatial classification of hyperspectral images using deep convolutional neural networks. Remote Sens. Lett. 2015, 6, 468–477. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, G.; Sun, Q.; Siegel, M. Hyperspectral classification via deep networks and superpixel segmentation. Int. J. Remote Sens. 2015, 36, 3459–3482. [Google Scholar] [CrossRef]
- Song, W.; Li, S.; Fang, L.; Lu, T. Hyperspectral image classification with deep feature fusion network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3173–3184. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Semisupervised hyperspectral image segmentation using multinomial logistic regression with active learning. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4085–4098. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral–spatial hyperspectral image segmentation using subspace multinomial logistic regression and Markov random fields. IEEE Trans. Geosci. Remote Sens. 2011, 50, 809–823. [Google Scholar] [CrossRef]
- Pal, M.; Mather, P.M. An assessment of the effectiveness of decision tree methods for land cover classification. Remote Sens. Environ. 2003, 86, 554–565. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Tatnall, A.R. Introduction neural networks in remote sensing. Int. J. Remote Sens. 1997, 18, 699–709. [Google Scholar] [CrossRef]
- Foody, G.; Arora, M. An evaluation of some factors affecting the accuracy of classification by an artificial neural network. Int. J. Remote Sens. 1997, 18, 799–810. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhang, L. An adaptive artificial immune network for supervised classification of multi-/hyperspectral remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2011, 50, 894–909. [Google Scholar] [CrossRef]
- Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Kruger, N.; Janssen, P.; Kalkan, S.; Lappe, M.; Leonardis, A.; Piater, J.; Rodriguez-Sanchez, A.J.; Wiskott, L. Deep hierarchies in the primate visual cortex: What can we learn for computer vision? IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 1847–1871. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral–spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Ghamisi, P.; Chen, Y.; Zhu, X.X. A self-improving convolution neural network for the classification of hyperspectral data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1537–1541. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Long, Y.; Gong, Y.; Xiao, Z.; Liu, Q. Accurate object localization in remote sensing images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2486–2498. [Google Scholar] [CrossRef]
- Dobler, G.; Ghandehari, M.; Koonin, S.E.; Nazari, R.; Patrinos, A.; Sharma, M.S.; Tafvizi, A.; Vo, H.T.; Wurtele, J.S. Dynamics of the urban lightscape. Inf. Syst. 2015, 54, 115–126. [Google Scholar] [CrossRef] [Green Version]
- Bianco, F.B.; Koonin, S.E.; Mydlarz, C.; Sharma, M.S. Hypertemporal imaging of NYC grid dynamics: Short paper. In Proceedings of the 3rd ACM International Conference on Systems for Energy-Efficient Built Environments, Palo Alto, CA, USA, 16–17 November 2016; pp. 61–64. [Google Scholar]
- Dobler, G.; Bianco, F.B.; Sharma, M.S.; Karpf, A.; Baur, J.; Ghandehari, M.; Wurtele, J.S.; Koonin, S.E. The Urban Observatory: A Multi-Modal Imaging Platform for the Study of Dynamics in Complex Urban Systems. arXiv 2019, arXiv:1909.05940. [Google Scholar]
- Dobler, G.; Ghandehari, M.; Koonin, S.E.; Sharma, M.S. A hyperspectral survey of New York City lighting technology. Sensors 2016, 16, 2047. [Google Scholar] [CrossRef] [Green Version]
- Baur, J.; Dobler, G.; Bianco, F.; Sharma, M.; Karpf, A. Persistent Hyperspectral Observations of the Urban Lightscape. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–29 November 2018; pp. 983–987. [Google Scholar]
- Ghandehari, M.; Aghamohamadnia, M.; Dobler, G.; Karpf, A.; Buckland, K.; Qian, J.; Koonin, S. Mapping refrigerant gases in the new york city skyline. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef]
- Lee, M.A.; Prasad, S.; Bruce, L.M.; West, T.R.; Reynolds, D.; Irby, T.; Kalluri, H. Sensitivity of hyperspectral classification algorithms to training sample size. In Proceedings of the 2009 IEEE First Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Grenoble, France, 26–28 August 2009; pp. 1–4. [Google Scholar]
- Ul Haq, Q.S.; Tao, L.; Sun, F.; Yang, S. A fast and robust sparse approach for hyperspectral data classification using a few labeled samples. IEEE Trans. Geosci. Remote Sens. 2011, 50, 2287–2302. [Google Scholar] [CrossRef]
- Li, F.; Xu, L.; Siva, P.; Wong, A.; Clausi, D.A. Hyperspectral image classification with limited labeled training samples using enhanced ensemble learning and conditional random fields. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2427–2438. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Lake Tahoe, NV, USA, 2012; pp. 1097–1105. [Google Scholar]
- Cao, F.; Yang, Z.; Ren, J.; Jiang, M.; Ling, W.K. Does normalization methods play a role for hyperspectral image classification? arXiv 2017, arXiv:1710.02939. [Google Scholar]
- Goutte, C.; Gaussier, E. A probabilistic interpretation of precision, recall and F-score, with implication for evaluation. In European Conference on Information Retrieval; Springer: Berlin/Heidelberg, Germany, 2005; pp. 345–359. [Google Scholar]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ghamisi, P.; Maggiori, E.; Li, S.; Souza, R.; Tarablaka, Y.; Moser, G.; De Giorgi, A.; Fang, L.; Chen, Y.; Chi, M.; et al. New frontiers in spectral-spatial hyperspectral image classification: The latest advances based on mathematical morphology, Markov random fields, segmentation, sparse representation, and deep learning. IEEE Geosci. Remote Sens. Mag. 2018, 6, 10–43. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent advances on spectral–spatial hyperspectral image classification: An overview and new guidelines. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1579–1597. [Google Scholar] [CrossRef]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Yang, Y.; Li, C.; Zhang, X.; Zhao, J.; Yao, D. Convolutional neural network for spectral–spatial classification of hyperspectral images. Neural Comput. Appl. 2019, 31, 8997–9012. [Google Scholar] [CrossRef]
- Wei, L.; Huang, C.; Wang, Z.; Wang, Z.; Zhou, X.; Cao, L. Monitoring of Urban Black-Odor Water Based on Nemerow Index and Gradient Boosting Decision Tree Regression Using UAV-Borne Hyperspectral Imagery. Remote Sens. 2019, 11, 2402. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, A.; El-Ghazawi, T.; El-Askary, H.; Le-Moigne, J. Efficient hierarchical-PCA dimension reduction for hyperspectral imagery. In Proceedings of the 2007 IEEE International Symposium on Signal Processing and Information Technology, Giza, Egypt, 15–18 December 2007; pp. 353–356. [Google Scholar]
- Kang, X.; Xiang, X.; Li, S.; Benediktsson, J.A. PCA-based edge-preserving features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7140–7151. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Raczko, E.; Zagajewski, B. Comparison of support vector machine, random forest and neural network classifiers for tree species classification on airborne hyperspectral APEX images. Eur. J. Remote Sens. 2017, 50, 144–154. [Google Scholar] [CrossRef] [Green Version]















| Performance Metrics: Models with Different Filter Sizes and Numbers Trained and Tested on Each Image Separately | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | |||||||
| Image | Class | Support | Precision | Recall | Score | Precision | Recall | Score |
| Scene 1-a | Sky | 60 | 0.98 | 1.00 | 0.99 | 1.00 | 0.98 | 0.99 |
| Clouds | 100 | 1.00 | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 | |
| Vegetation | 120 | 1.00 | 0.98 | 0.99 | 1.00 | 1.00 | 1.00 | |
| Water | 10 | 1.00 | 0.90 | 0.95 | 1.00 | 1.00 | 1.00 | |
| Built | 204 | 0.82 | 0.97 | 0.89 | 0.98 | 0.96 | 0.97 | |
| Windows | 100 | 0.90 | 0.91 | 0.91 | 0.95 | 0.97 | 0.96 | |
| Roads | 6 | 0.00 | 0.00 | 0.00 | 1.00 | 0.67 | 0.80 | |
| Cars | 20 | 0.88 | 0.35 | 0.50 | 0.94 | 0.80 | 0.86 | |
| Metal | 20 | 0.50 | 0.05 | 0.09 | 0.61 | 0.85 | 0.71 | |
| Total/Weighted Mean | 640 | 0.90 | 0.91 | 0.89 | 0.97 | 0.97 | 0.97 | |
| Scene 1-b | Sky | 80 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Clouds | 100 | 0.98 | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 | |
| Vegetation | 122 | 1.00 | 0.98 | 0.99 | 1.00 | 0.98 | 0.99 | |
| Built | 240 | 0.86 | 0.88 | 0.87 | 0.90 | 0.94 | 0.92 | |
| Windows | 100 | 0.64 | 0.76 | 0.69 | 0.93 | 0.76 | 0.84 | |
| Roads | 12 | 0.73 | 0.92 | 0.81 | 0.67 | 1.00 | 0.80 | |
| Cars | 11 | 0.83 | 0.45 | 0.59 | 1.00 | 0.64 | 0.78 | |
| Metal | 46 | 0.64 | 0.35 | 0.45 | 0.62 | 0.72 | 0.67 | |
| Total/Weighted Mean | 711 | 0.87 | 0.87 | 0.86 | 0.92 | 0.92 | 0.92 | |
| Scene 2 | Sky | 60 | 0.94 | 1.00 | 0.97 | 1.00 | 1.00 | 1.00 |
| Clouds | 40 | 0.98 | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 | |
| Vegetation | 140 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 1.00 | |
| Water | 124 | 0.92 | 0.92 | 0.92 | 0.98 | 0.99 | 0.98 | |
| Built | 320 | 0.89 | 0.88 | 0.88 | 0.91 | 0.98 | 0.94 | |
| Windows | 120 | 0.56 | 0.82 | 0.66 | 0.78 | 0.84 | 0.81 | |
| Roads | 50 | 0.53 | 0.62 | 0.57 | 0.73 | 0.64 | 0.68 | |
| Cars | 50 | 0.96 | 0.44 | 0.60 | 0.82 | 0.62 | 0.70 | |
| Metal | 37 | 0.00 | 0.00 | 0.00 | 0.79 | 0.30 | 0.43 | |
| Total/Weighted Mean | 941 | 0.82 | 0.83 | 0.82 | 0.90 | 0.91 | 0.90 | |
| Performance Metrics: Models with and Without Spatial Information Trained and Tested on Each Image Separately | ||||||||
|---|---|---|---|---|---|---|---|---|
| Spatial | No Spatial | |||||||
| Image | Class | Support | Precision | Recall | F 1 Score | Precision | Recall | F 1 Score |
| Scene 1-a | Sky | 60 | 1.00 | 0.98 | 0.99 | 1.00 | 0.98 | 0.99 |
| Clouds | 100 | 0.99 | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 | |
| Vegetation | 120 | 1.00 | 1.00 | 1.00 | 1.00 | 0.98 | 0.99 | |
| Water | 10 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Built | 204 | 0.98 | 0.96 | 0.97 | 0.89 | 0.97 | 0.93 | |
| Windows | 100 | 0.95 | 0.97 | 0.96 | 0.93 | 0.94 | 0.94 | |
| Roads | 6 | 1.00 | 0.67 | 0.80 | 1.00 | 0.50 | 0.67 | |
| Cars | 20 | 0.94 | 0.80 | 0.86 | 0.86 | 0.60 | 0.71 | |
| Metal | 20 | 0.61 | 0.85 | 0.71 | 0.75 | 0.45 | 0.56 | |
| Total/Weighted Mean | 640 | 0.97 | 0.97 | 0.97 | 0.94 | 0.94 | 0.94 | |
| Scene 1-b | Sky | 80 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Clouds | 100 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Vegetation | 122 | 1.00 | 0.98 | 0.99 | 1.00 | 0.98 | 0.99 | |
| Built | 240 | 0.90 | 0.94 | 0.92 | 0.84 | 0.95 | 0.89 | |
| Windows | 100 | 0.93 | 0.76 | 0.84 | 0.92 | 0.66 | 0.77 | |
| Roads | 12 | 0.67 | 1.00 | 0.80 | 0.71 | 1.00 | 0.83 | |
| Cars | 11 | 1.00 | 0.64 | 0.78 | 0.78 | 0.64 | 0.70 | |
| Metal | 46 | 0.62 | 0.72 | 0.67 | 0.63 | 0.59 | 0.61 | |
| Total/Weighted Mean | 711 | 0.92 | 0.92 | 0.92 | 0.90 | 0.90 | 0.89 | |
| Scene 2 | Sky | 60 | 1.00 | 1.00 | 1.00 | 0.92 | 1.00 | 0.96 |
| Clouds | 40 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Vegetation | 140 | 0.99 | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 | |
| Water | 124 | 0.98 | 0.99 | 0.98 | 0.98 | 0.89 | 0.93 | |
| Built | 320 | 0.91 | 0.98 | 0.94 | 0.88 | 0.96 | 0.92 | |
| Windows | 120 | 0.78 | 0.84 | 0.81 | 0.68 | 0.87 | 0.76 | |
| Roads | 50 | 0.73 | 0.64 | 0.68 | 0.88 | 0.44 | 0.59 | |
| Cars | 50 | 0.82 | 0.62 | 0.70 | 0.96 | 0.48 | 0.64 | |
| Metal | 37 | 0.79 | 0.30 | 0.43 | 0.48 | 0.38 | 0.42 | |
| Total/Weighted Mean | 941 | 0.90 | 0.91 | 0.90 | 0.88 | 0.87 | 0.87 | |
| Performance Metrics: Trained and Tested on Each Image Separately vs. Trained on All Images Simultaneously and Tested on Each Image Separately | ||||||||
|---|---|---|---|---|---|---|---|---|
| Self-Trained and Tested | Trained on All | |||||||
| Image | Class | Support | Precision | Recall | F 1 Score | Precision | Recall | F 1 Score |
| Scene 1-a | Sky | 60 | 1.00 | 0.98 | 0.99 | 1.00 | 0.98 | 0.99 |
| Clouds | 100 | 0.99 | 1.00 | 1.00 | 0.97 | 1.00 | 0.99 | |
| Vegetation | 120 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Water | 10 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Built | 204 | 0.98 | 0.96 | 0.97 | 0.95 | 0.95 | 0.95 | |
| Windows | 100 | 0.95 | 0.97 | 0.96 | 0.91 | 0.96 | 0.93 | |
| Roads | 6 | 1.00 | 0.67 | 0.80 | 0.75 | 1.00 | 0.86 | |
| Cars | 20 | 0.94 | 0.80 | 0.86 | 0.92 | 0.55 | 0.69 | |
| Metal | 20 | 0.61 | 0.85 | 0.71 | 0.79 | 0.75 | 0.77 | |
| Total/Weighted Mean | 640 | 0.97 | 0.97 | 0.97 | 0.95 | 0.95 | 0.95 | |
| Scene 1-b | Sky | 80 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Clouds | 100 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Vegetation | 122 | 1.00 | 0.98 | 0.99 | 1.00 | 0.98 | 0.99 | |
| Built | 240 | 0.90 | 0.94 | 0.92 | 0.88 | 0.90 | 0.89 | |
| Windows | 100 | 0.93 | 0.76 | 0.84 | 0.80 | 0.85 | 0.83 | |
| Roads | 12 | 0.67 | 1.00 | 0.80 | 0.71 | 1.00 | 0.83 | |
| Cars | 11 | 1.00 | 0.64 | 0.78 | 1.00 | 0.55 | 0.71 | |
| Metal | 46 | 0.62 | 0.72 | 0.67 | 0.69 | 0.52 | 0.59 | |
| Total/Weighted Mean | 711 | 0.92 | 0.92 | 0.92 | 0.90 | 0.90 | 0.90 | |
| Scene 2 | Sky | 60 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Clouds | 40 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Vegetation | 140 | 0.99 | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 | |
| Water | 124 | 0.98 | 0.99 | 0.98 | 0.98 | 0.99 | 0.99 | |
| Built | 320 | 0.91 | 0.98 | 0.94 | 0.94 | 0.95 | 0.95 | |
| Windows | 120 | 0.78 | 0.84 | 0.81 | 0.76 | 0.76 | 0.76 | |
| Roads | 50 | 0.73 | 0.64 | 0.68 | 0.46 | 0.74 | 0.57 | |
| Cars | 50 | 0.82 | 0.62 | 0.70 | 0.94 | 0.58 | 0.72 | |
| Metal | 37 | 0.79 | 0.30 | 0.43 | 0.74 | 0.38 | 0.50 | |
| Total/Weighted Mean | 941 | 0.90 | 0.91 | 0.90 | 0.90 | 0.89 | 0.89 | |
| Performance Metrics: Transferring Models with Different Filter Sizes and Numbers Trained on Scene 1-a Tested on Scene 1-b and Scene 2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | |||||||
| Image | Class | Support | Precision | Recall | F 1 Score | Precision | Recall | F 1 Score |
| Scene 1-a | Sky | 60 | 0.97 | 1.00 | 0.98 | 1.00 | 0.98 | 0.99 |
| Clouds | 100 | 1.00 | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 | |
| Vegetation | 120 | 1.00 | 0.98 | 0.99 | 1.00 | 0.98 | 0.99 | |
| Water | 10 | 1.00 | 0.70 | 0.82 | 1.00 | 1.00 | 1.00 | |
| Built | 204 | 0.80 | 0.96 | 0.88 | 0.89 | 0.97 | 0.93 | |
| Windows | 100 | 0.86 | 0.93 | 0.89 | 0.93 | 0.94 | 0.94 | |
| Roads | 6 | 0.00 | 0.00 | 0.00 | 1.00 | 0.50 | 0.67 | |
| Cars | 20 | 0.00 | 0.00 | 0.00 | 0.86 | 0.60 | 0.71 | |
| Metal | 20 | 1.00 | 0.05 | 0.10 | 0.75 | 0.45 | 0.56 | |
| Total/Weighted Mean | 640 | 0.87 | 0.90 | 0.87 | 0.94 | 0.94 | 0.94 | |
| Scene 1-b | Sky | 400 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Clouds | 500 | 1.00 | 0.01 | 0.01 | 1.00 | 0.01 | 0.03 | |
| Vegetation | 610 | 0.97 | 0.93 | 0.95 | 0.97 | 0.94 | 0.95 | |
| Built | 1200 | 0.67 | 0.95 | 0.78 | 0.72 | 0.97 | 0.83 | |
| Windows | 500 | 0.53 | 0.47 | 0.50 | 0.65 | 0.46 | 0.54 | |
| Roads | 60 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Cars | 55 | 1.00 | 0.02 | 0.04 | 0.09 | 0.51 | 0.16 | |
| Metal | 230 | 0.78 | 0.12 | 0.21 | 0.85 | 0.22 | 0.35 | |
| Total/Weighted Mean | 3555 | 0.67 | 0.55 | 0.51 | 0.70 | 0.58 | 0.55 | |
| Scene 2 | Sky | 300 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Clouds | 200 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Vegetation | 700 | 0.61 | 1.00 | 0.76 | 0.98 | 1.00 | 0.99 | |
| Water | 620 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Built | 1600 | 0.32 | 0.51 | 0.39 | 0.43 | 0.49 | 0.46 | |
| Windows | 600 | 0.25 | 0.41 | 0.31 | 0.28 | 0.42 | 0.34 | |
| Roads | 250 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Cars | 250 | 1.00 | 0.00 | 0.01 | 0.04 | 0.16 | 0.06 | |
| Metal | 185 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Total/Weighted Mean | 4705 | 0.28 | 0.37 | 0.28 | 0.33 | 0.38 | 0.35 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qamar, F.; Dobler, G. Pixel-Wise Classification of High-Resolution Ground-Based Urban Hyperspectral Images with Convolutional Neural Networks. Remote Sens. 2020, 12, 2540. https://doi.org/10.3390/rs12162540
Qamar F, Dobler G. Pixel-Wise Classification of High-Resolution Ground-Based Urban Hyperspectral Images with Convolutional Neural Networks. Remote Sensing. 2020; 12(16):2540. https://doi.org/10.3390/rs12162540
Chicago/Turabian StyleQamar, Farid, and Gregory Dobler. 2020. "Pixel-Wise Classification of High-Resolution Ground-Based Urban Hyperspectral Images with Convolutional Neural Networks" Remote Sensing 12, no. 16: 2540. https://doi.org/10.3390/rs12162540
APA StyleQamar, F., & Dobler, G. (2020). Pixel-Wise Classification of High-Resolution Ground-Based Urban Hyperspectral Images with Convolutional Neural Networks. Remote Sensing, 12(16), 2540. https://doi.org/10.3390/rs12162540