Information Content of Ice Cloud Properties from Multi-Spectral, -Angle and -Polarization Observations
Abstract
:1. Introduction
2. Method
2.1. Information Content Analysis Theory
2.2. The Measurement Vectors and Forward Model
2.3. The State Vectors and Ice Cloud Model
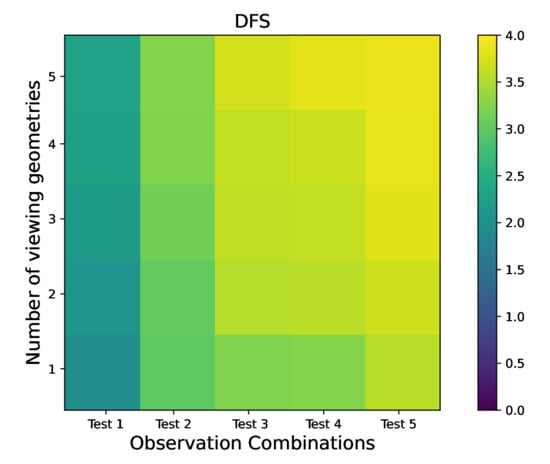
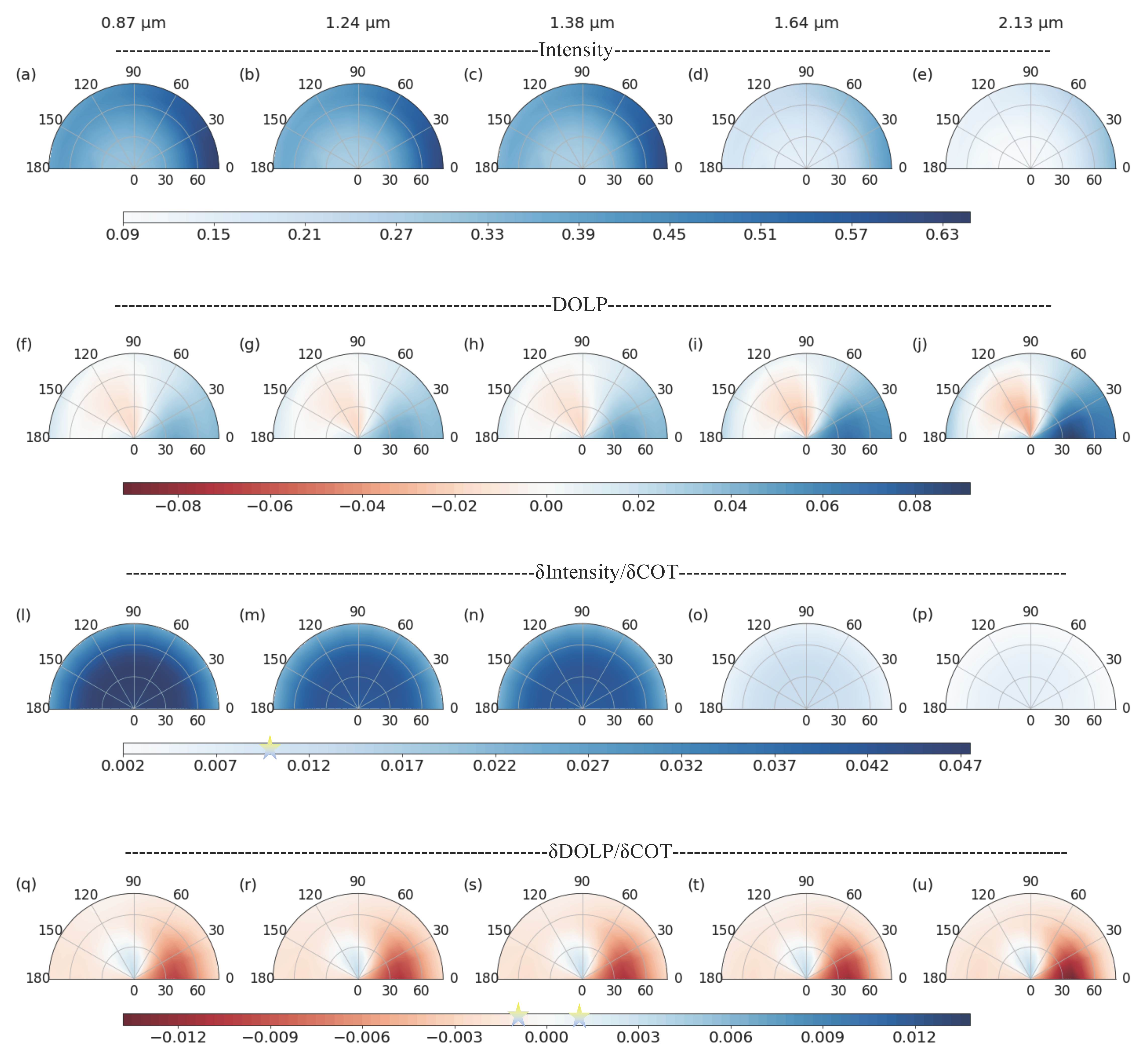
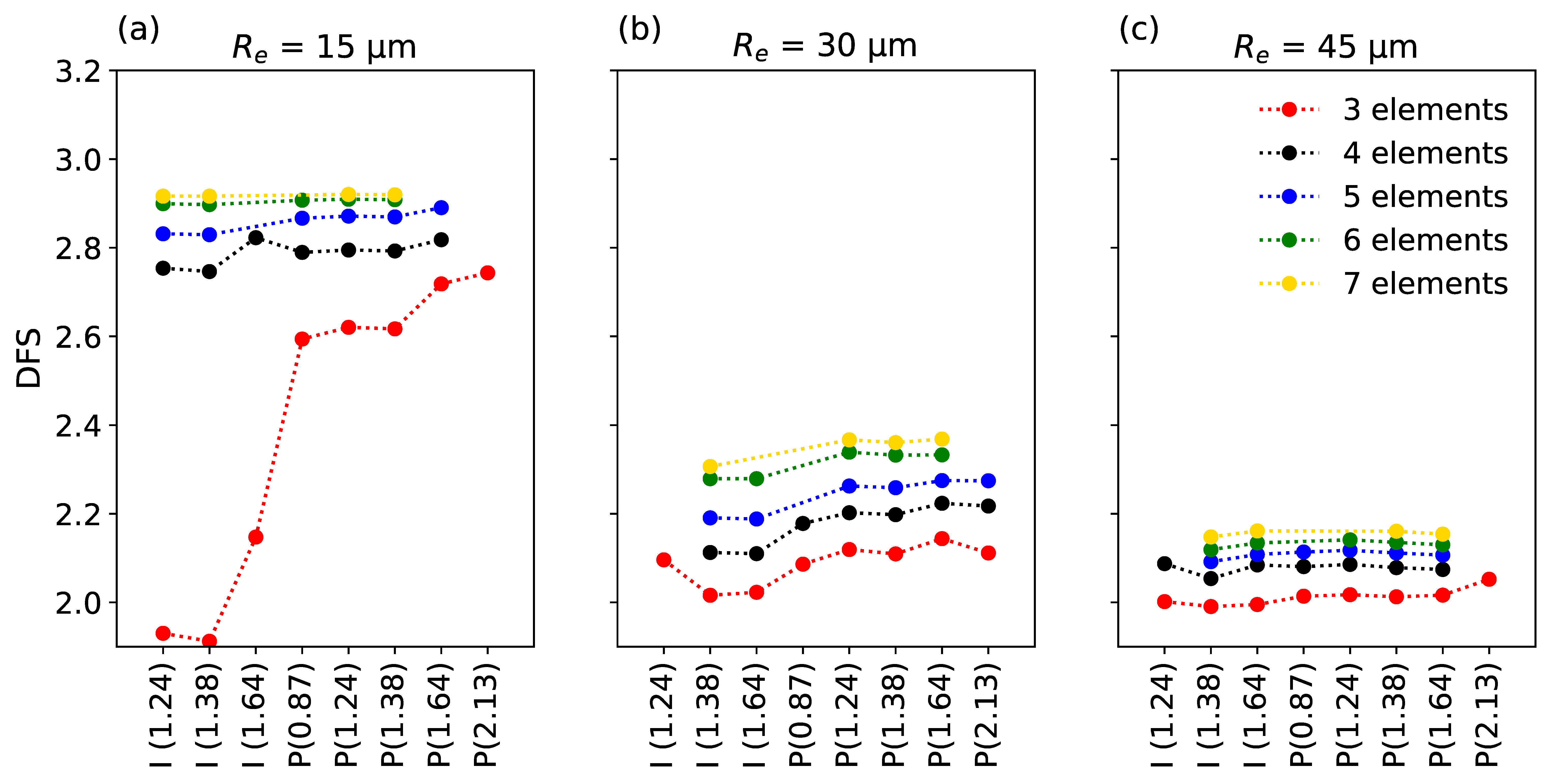
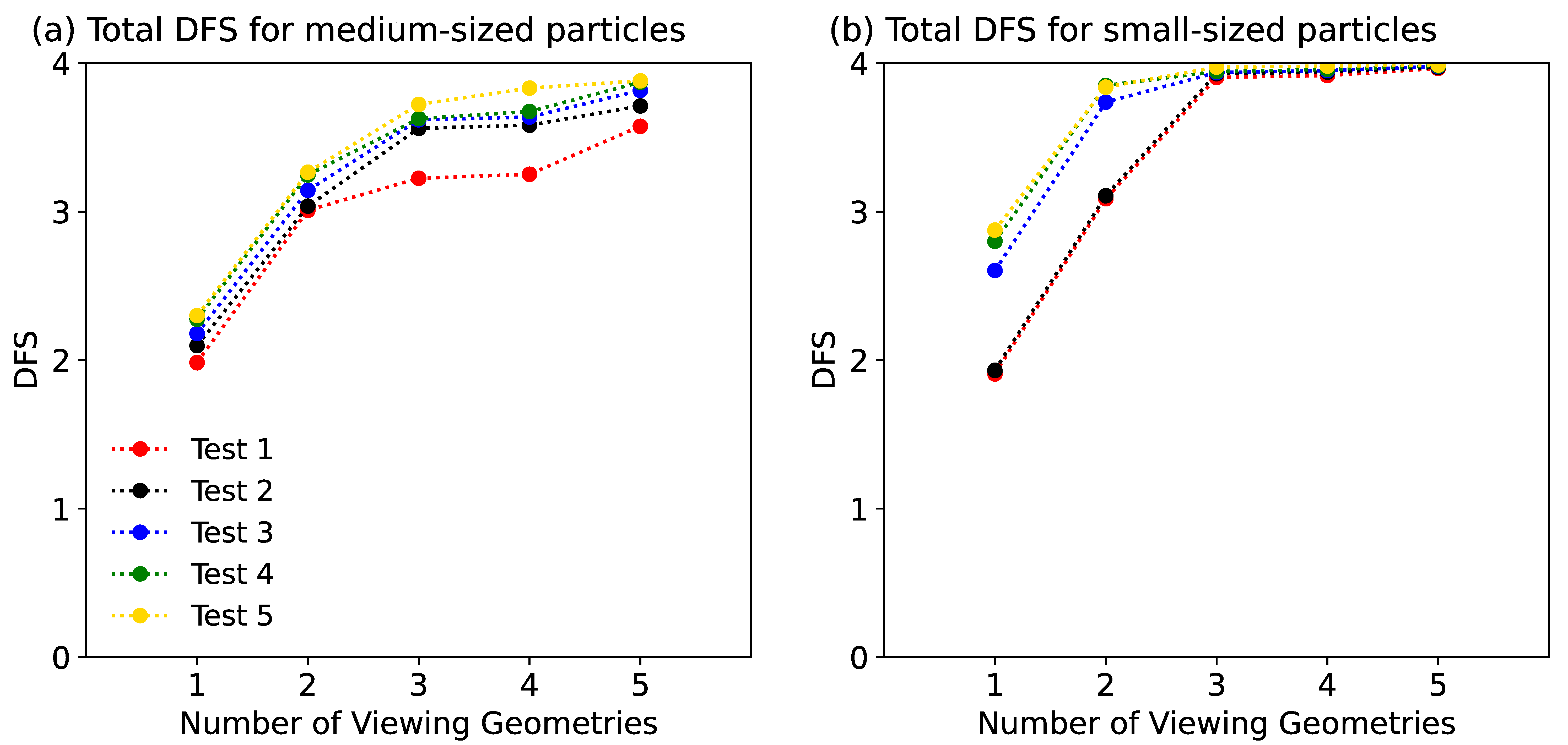
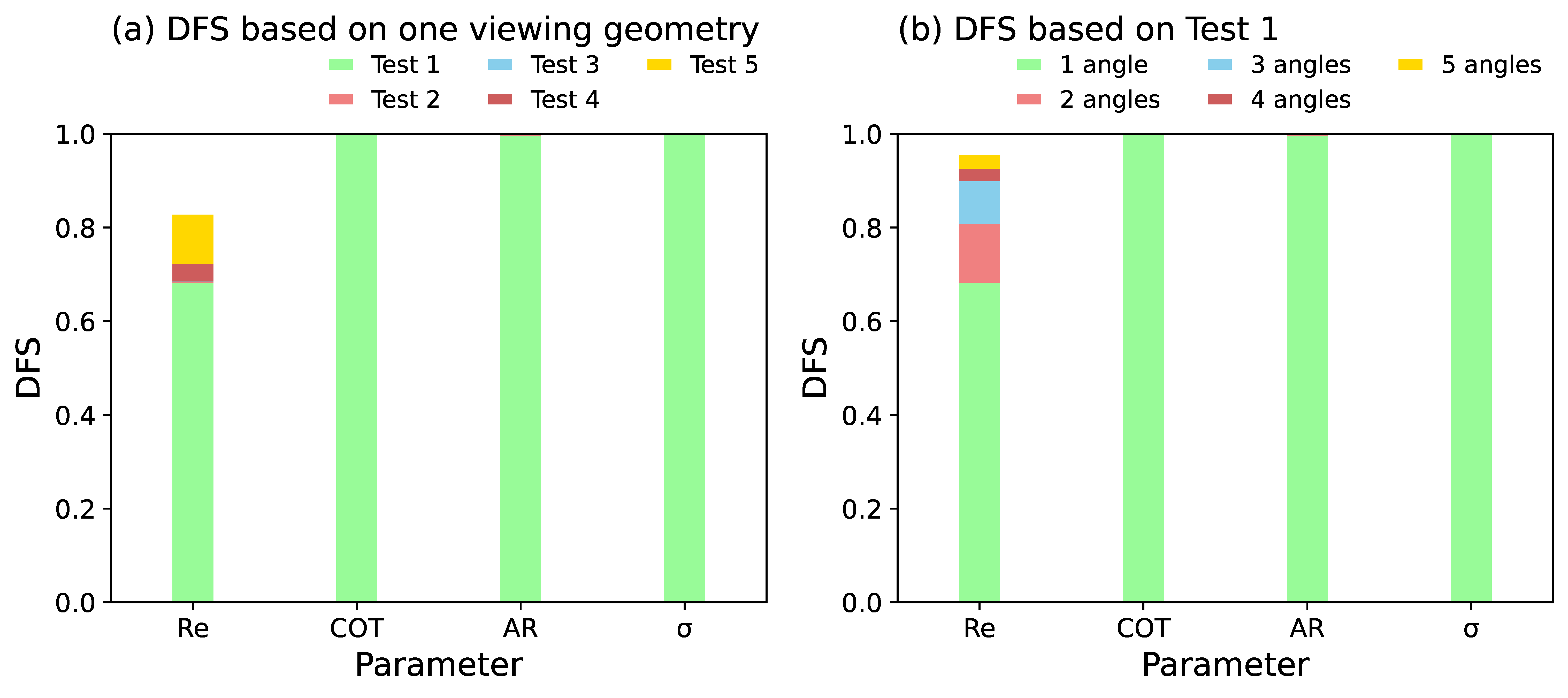
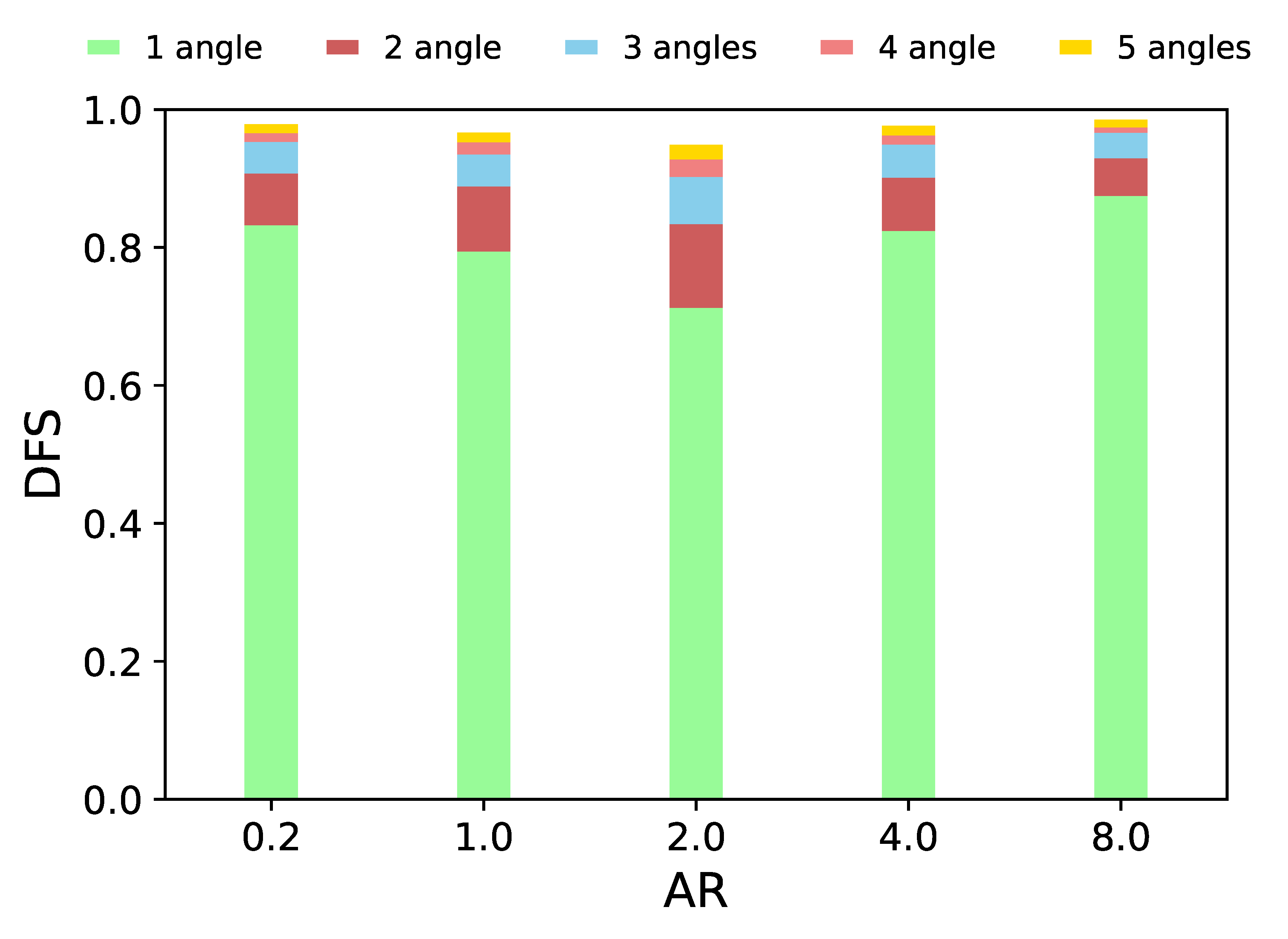
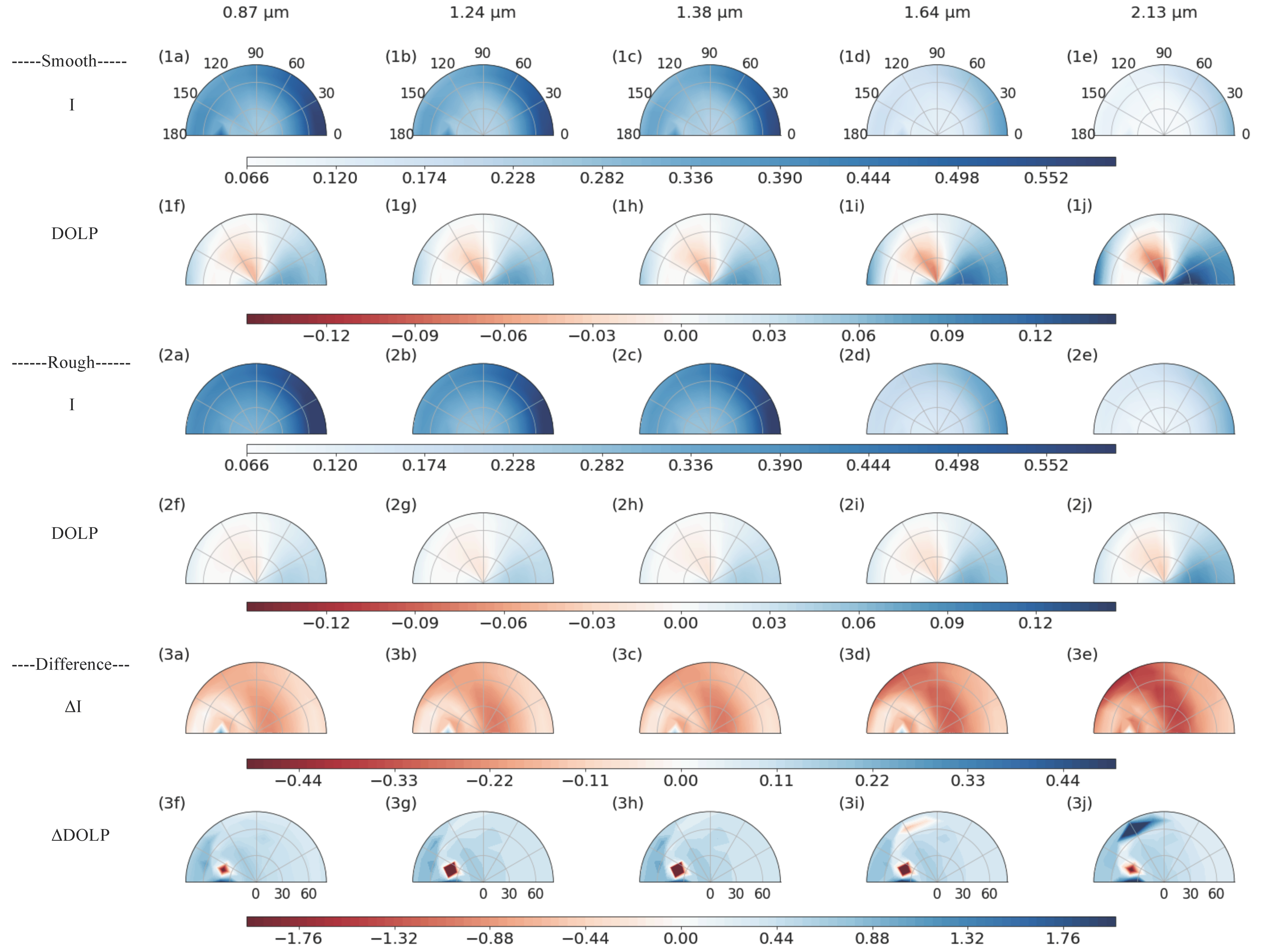
3. Results
4. Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nazaryan, H.; McCormick, M.P.; Menzel, W.P. Global characterization of cirrus clouds using CALIPSO data. J. Geophys. Res. 2008, 113, D16211. [Google Scholar] [CrossRef]
- Baker, M.B.; Peter, T. Small-scale cloud processes and climate. Nature 2008, 451, 299–300. [Google Scholar] [CrossRef] [PubMed]
- Liou, K.N.; Yang, P. Light Scattering by Ice Crystals: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Chepfer, H.; Brogniez, G.; Fouquart, Y. Cirrus clouds’ microphysical properties deduced from POLDER observations. J. Quant. Spectrosc. Radiat. Transf. 1998, 60, 375–390. [Google Scholar] [CrossRef]
- Saito, M.; Iwabuchi, H.; Yang, P.; Tang, G.; King, M.D.; Sekiguchi, M. Ice particle morphology and microphysical properties of cirrus clouds inferred from combined CALIOP-IIR measurements. J. Geophys. Res. Atmos. 2017, 122, 4440–4462. [Google Scholar] [CrossRef]
- Lai, R.; Teng, S.; Yi, B.; Letu, H.; Min, M.; Tang, S.; Liu, C. Comparison of clouds properties from Hamawari-8 and FengYun-4A geostationary satellite radiometers with MODIS cloud retrievals. Remote Sens. 2019, 11, 1703. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Su, H.; Jiang, J.H.; Xu, F.; Yung, Y.L. Impact of cloud ice particle size uncertainty in a climate model and implications for future satellite missions. J. Geophys. Res. 2020, 125, D032119. [Google Scholar]
- Kidd, C.; Levizzani, V.; Bauer, P. A review of satellite meteorology and climatology at the start of the twenty-first century. Prog. Phys. Geogr. 2009, 33, 474–489. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, C.; Wang, Y.; Yang, Y. Evaluation of cloud microphysical properties derived from MODIS and Himawari-8 using in situ aircraft measurements over the Southern Ocean. Earth Space Sci. 2020, 7, e2020EA001137. [Google Scholar] [CrossRef] [Green Version]
- King, M.D.; Platnick, S.; Menzel, W.P.; Ackerman, S.A.; Hubanks, P.A. Spatial and temporal distribution of clouds observed by MODIS onboard the Terra and Aqua satellites. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3826–3852. [Google Scholar] [CrossRef]
- King, M.D.; Menzel, W.P.; Kaufman, Y.J.; Tanre, D.; Gao, B.-C.; Platnick, S.; Ackerman, S.; Remer, L.; Pincus, R.; Hubanks, P. Cloud and aerosol properties, precipitable water, and profiles of temperature and water vapor from MODIS. IEEE Trans. Geosci. Remote Sens. 2003, 41, 442–458. [Google Scholar] [CrossRef] [Green Version]
- Hsu, N.C.; Lee, J.; Sayer, A.M.; Carletta, N.; Chen, S.H.; Tucker, C.J.; Holben, B.N.; Tsay, S.C. Retrieving near-global aerosol loading over land and ocean from AVHRR. J. Geophys. Res. Atmos. 2017, 122, 9968–9989. [Google Scholar] [CrossRef] [Green Version]
- Parol, F.; Buriez, J.C.; Brogniez, G.; Fouquart, Y. Information content of AVHRR Channels 4 and 5 with respect to the effective radius of Cirrus Cloud particles. J. Appl. Meteorol. 1991, 30, 973–984. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Z.; Wei, C.; Lu, F.; Guo, Q. Introducing the new generation of Chinese geostationary weather satellites-FengYun 4 (FY-4). Bull. Am. Meteorol. Soc. 2017, 98, 1637–1658. [Google Scholar] [CrossRef]
- Da, C. Preliminary assessment of the Advanced Himawari Imager (AHI) measurement onboard Himawari-8 geostationary satellite. Remote Sens. Lett. 2015, 6, 637–646. [Google Scholar] [CrossRef]
- Nakajima, T.; King, M.D. Determination of the optical thickness and effective particle radius of clouds from reflected solar radiation measurements. Part I: Theory. J. Atmos. Sci. 1990, 47, 1878–1893. [Google Scholar] [CrossRef] [Green Version]
- Platnick, S.; Meyer, K.; King, M.D.; Wind, G.; Amarasinghe, N.; Marchant, B.; Arnold, G.T.; Zhang, Z.; Hubanks, P.A.; Holz, R.E.; et al. The MODIS cloud optical and microphysical products: Collection 6 updates and examples from Terra and Aqua. IEEE Trans. Geosci. Remote Sens. 2017, 55, 502–525. [Google Scholar] [CrossRef] [Green Version]
- Marshak, A.; Platnick, S.; Várnai, T.; Wen, G.; Cahalan, R.F. Impact of three-dimensional radiative effects on satellite retrievals of cloud droplet sizes. J. Geophys. Res. 2006, 111, D09027. [Google Scholar] [CrossRef]
- Fu, D.; Girolamo, L.D.; Liang, L.; Zhao, G. Regional biases in Moderate Resolution Imaging Spectroradiometer (MODIS) marine liquid water cloud drop effective radius deduced through fusion with Multi-angle Imaging SpectroRadiometer (MISR). J. Geophys. Res. 2019, 124, 13182–13196. [Google Scholar]
- Ohring, G.; Wielicki, B.A.; Spencer, R.W.; Emery, B.; Datla, R.V. Satellite instrument calibration for measuring global climate change: Report of a workshop. Bull. Am. Meteorol. Soc. 2005, 86, 1303–1313. [Google Scholar] [CrossRef]
- Diner, D.J.; Bruegge, C.J.; Martonchik, J.V.; Ackerman, T.P.; Davies, R.; Gerstl, S.A.W.; Gordon, H.R.; Sellers, P.J.; Clark, J.; Daniels, J.A.; et al. MISR: A Multi-angle Imaging SpectroRadiometer for geophysical and climatological research from EOS. IEEE Trans. Geosci. Remote Sens. 1989, 27, 200–214. [Google Scholar] [CrossRef]
- Liang, L.; Girolamo, L.D. A global analysis on the view-angle dependence of plane-parallel oceanic liquid water cloud optical thickness using data synergy from MISR and MODIS. J. Geophys. Res. 2013, 118, 2389–2403. [Google Scholar] [CrossRef]
- Lee, B.; Girolamo, L.D.; Zhao, G.; Zhan, Y. Three-dimensional cloud volume reconstruction from the multi-angle Imaging SpectroRadiometer. Remote Sens. 2018, 10, 1858. [Google Scholar] [CrossRef] [Green Version]
- Bréon, F.M. Parasol Level-1 Product Data Format and User Manual; CNES: Paris, France, 2005; Available online: http://www.icare.univ-lille1.fr/parasol/?rubrique=overview_product (accessed on 5 August 2020).
- Deschamps, P.Y.; Bréon, F.; Leroy, M.; Bricaud, A.; Buriez, J.C.; Seze, G. The POLDER mission: Instrument characteristics and scientific objectives. IEEE Trans. Geosci. Remote Sens. 1994, 32, 598–615. [Google Scholar] [CrossRef]
- Parol, F.; Buriez, J.C.; Vanbauce, C.; Riedi, J.; Labonnote, L.C.; Doutriaux-Boucher, M.; Vesperini, M.; Seze, G.; Couvert, P.; Viollier, M.; et al. Review of capabilities of multi-angle and polarization cloud measurements from POLDER. Adv. Space Res. 2004, 33, 1080–1088. [Google Scholar] [CrossRef]
- Zheng, F.; Hou, W.; Li, Z. Optimal estimation retrieval for directional polarimetric camera onboard Chinese Gaofen-5 satellite: An analysis on multi-angle dependence and a posteriori error. Acta Phys. Sin. 2019, 68, 040701. [Google Scholar]
- Chen, F.; Huang, C.; Hong, J.; Luo, D.; Sun, L.; Sun, X.; Wei, W. In Flight Radiation evaluation and validation of Directional Polarimetric Camera. Aerosp. Shanghai 2019, 36, 126–136. [Google Scholar]
- Manolis, I.; Caron, J.; Grabarnik, S.; Bézy, J.L.; Betto, M.; Barrè, H.; Mason, G.; Meynart, R. The MetOp second generation 3MI mission. In Proceedings of the International Conference on Space Optics, Ajaccio, Corsica, France, 9–12 October 2012. Available online: https://doi.org/10.1117/12.2309178 (accessed on 5 August 2020).
- Girolamo, L.D.; Wilson, M.J. A first look at band-differenced angular signatures for cloud detection from MISR. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1730–1734. [Google Scholar] [CrossRef]
- Buriez, J.C.; Vanbauce, C.; Parol, F.; Goloub, P.; Herman, M.; Bonnel, B.; Fouquart, Y.; Couvert, P.; Seze, G. Cloud detection and derivation of cloud properties from POLDER. Int. J. Remote Sens. 1997, 18, 2785–2813. [Google Scholar] [CrossRef]
- Yi, B.; Huang, X.; Yang, P.; Baum, B.A.; Kattawar, G.W. Considering polarization in MODIS-based cloud property retrievals by using a vector radiative transfer code. J. Quant. Spectrosc. Radiat. Transf. 2014, 146, 540–548. [Google Scholar] [CrossRef]
- Goloub, P.; Deuze, J.L.; Herman, M.; Fouquart, Y. Analysis of the POLDER polarization measurements performed over cloud covers. IEEE Trans. Geosci. Remote Sens. 1994, 32, 78–88. [Google Scholar] [CrossRef]
- van Diedenhoven, B.; Cairns, B.; Geogdzhayev, I.V.; Fridlind, A.M.; Ackerman, A.S.; Yang, P.; Baum, B.A. Remote sensing of ice crystal asymmetry parameter using multi-directional polarization measurements-Part 1: Methodology and evaluation with simulated measurements. Atmos. Meas. Tech. 2012, 5, 2361–2374. [Google Scholar] [CrossRef] [Green Version]
- Cole, B.H.; Yang, P.; Baum, B.A.; Riedi, J.; Labonnote, L.C.; Thieuleux, F.; Platnick, S. Comparison of PARASOL observations with polarized reflectances simulated using different ice habit mixtures. J. Appl. Meteorol. Climatol. 2013, 52, 186–196. [Google Scholar] [CrossRef]
- Chepfer, H.; Goloub, P.; Riedi, J.; De Haan, J.F.; Hovenier, J.W.; Flamant, P.H. Ice crystal shapes in cirrus clouds derived from POLDER-1/ADEOS-1. J. Geophys. Res. 2001, 106, 7955–7966. [Google Scholar] [CrossRef] [Green Version]
- Cole, B.H.; Yang, P.; Baum, B.A.; Riedi, J.; Labonnote, L.C. Ice particle habit and surface roughness derived from PARASOL polarization measurements. Atmos. Chem. Phys. 2013, 14, 3739–3750. [Google Scholar] [CrossRef] [Green Version]
- Hioki, S.; Yang, P.; Baum, B.A.; Platnick, S.; Meyer, K.; King, M.D.; Riedi, J. Degree of ice particle surface roughness inferred from polarimetric observations. Atmos. Chem. Phys. 2015, 16, 7545–7558. [Google Scholar] [CrossRef] [Green Version]
- Shang, H.; Chen, L.; Bréon, F.M.; Letu, H.; Li, S.; Wang, Z.; Su, L. Impact of cloud horizontal inhomogeneity and directional sampling on the retrieval of cloud droplet size by the POLDER instrument. Atmos. Meas. Tech. 2015, 8, 4931–4945. [Google Scholar] [CrossRef] [Green Version]
- Shang, H.; Letu, H.; Bréon, F.M.; Riedi, J.; Ma, R.; Wang, Z.; Nakajima, T.Y.; Wang, Z.; Chen, L. An Improved Algorithm of Cloud Droplet Size Distribution from POLDER Polarized Measurements. Remote Sens. Environ. 2019, 228, 61–74. [Google Scholar] [CrossRef]
- Masuda, K.; Ishimoto, H.; Takashima, T. Retrieval of cirrus optical thickness and ice-shape information using total and polarized reflectance from satellite measurements. J. Quant. Spectrosc. Radiat. Transf. 2002, 1, 39–51. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.; Liu, Y.; Xu, X.; Cai, Z.; Yang, D.; Yan, C.-X.; Feng, L. Angular dependence of aerosol information content in CAPI/TanSat observation over land: Effect of polarization and synergy with A-train satellites. Remote Sens. Environ. 2017, 196, 163–177. [Google Scholar] [CrossRef]
- Chen, X.; Yang, D.; Cai, Z.; Liu, Y.; Spurr, R. Aerosol retrieval sensitivity and error analysis for the cloud and aerosol polarimetric imager on board TanSat: The effect of multi-angle measurement. Remote Sens. 2017, 9, 183. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Yang, P.; Kattawar, G.W.; Liou, K.N. Effect of mineral dust aerosol aspect ratio on polarized reflectance. J. Quant. Spectrosc. Radiat. Transf. 2015, 151, 97–109. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: Singapore, 2000. [Google Scholar]
- Wang, C.; Platnick, S.; Zhang, Z.; Meyer, K.; Yang, P. Retrieval of ice cloud properties using an optimal estimation algorithm and MODIS infrared observations: 1. Forward model, error analysis, and information content. J. Geophys. Res. Atmos. 2016, 121, 5809–5826. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.; Blarel, L.; Podvin, T.; Goloub, P.; Chen, L. Calibration of the degree of linear polarization measurement of polarized radiometer using solar light. Opt. Soc. Am. 2010, 49, 1249–1256. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Wang, J. Retrieval of aerosol microphysical properties from AERONET photopolarimetric measurements: Q. Information content analysis. J. Geophys. Res. Atmos. 2015, 120, 7059–7078. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Loeb, N.G.; Yang, P. On the retrieval of ice cloud particle shapes from POLDER measurements. J. Quant. Spectrosc. Radiat. Transf. 2006, 101, 435–447. [Google Scholar] [CrossRef]
- De Haan, J.F.; Bosma, P.B.; Hovenier, J.W. The adding method for multiple scattering calculations of polarized light. Astron. Phys. 1987, 183, 371–391. [Google Scholar]
- Tomasi, C.; Vitale, V.; Petkov, B.; Lupi, A.; Cacciari, A. Improved algorithm for calculations of Rayleigh scattering optical depth in standard atmosphere. Appl. Opt. 2005, 44, 3320–3341. [Google Scholar] [CrossRef]
- Duan, M.; Min, Q.; Lu, D. A polarized radiative transfer model based on successive order of Scattering. Adv. Atmos. Sci. 2010, 27, 891–900. [Google Scholar] [CrossRef]
- Wang, C.; Platnick, S.; Zhang, Z.; Meyer, K.; Wind, G.; Yang, P. Retrieval of ice cloud properties using an optimal estimation algorithm and MODIS infrared observations: 2. Retrieval evaluation. J. Geophys. Res. Atmos. 2016, 121, 5827–5845. [Google Scholar] [CrossRef]
- Liu, C.; Panetta, R.L.; Yang, P. The effects of surface roughness on the scattering properties with sizes from the Rayleigh to the geometric-optics regimes. J. Quant. Spectrosc. Radiat. Transf. 2013, 129, 169–185. [Google Scholar] [CrossRef]
- Yang, P.; Bi, L.; Baum, B.A.; Liou, K.N.; Kattawar, G.W.; Mishchenko, M.I.; Cole, B.H. Spectrally consistent scattering, absorption, and polarization properties of atmospheric ice crystals at wavelengths from 0.2 to 100 μm. J. Atmos. Sci. 2013, 70, 330–347. [Google Scholar] [CrossRef]
- Liu, C.; Panetta, R.L.; Yang, P.; Macke, A.; Baran, A.J. Modeling the scattering properties of mineral aerosols using concave fractal polyhedral. Appl. Opt. 2013, 52, 640–652. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Liou, K.N. Single-scattering properties of complex ice crystals in terrestrial atmosphere. Contrib. Atmos. Phys. 1998, 71, 223–248. [Google Scholar]
- Baum, B.A.; Yang, P.; Heymsfield, A.J.; Bansemer, A.; Cole, B.H.; Merrelli, A.; Schmitt, C.; Wang, C. Ice cloud single-scattering property models with the full phase matrix at wave lengths from 0.2 to 100 μm. J. Quant. Spectrosc. Radiat. Transf. 2014, 146, 123–139. [Google Scholar] [CrossRef]
- Lawless, R.; Xie, Y.; Yang, P.; Kattawar, G.W.; Laszlo, I. Polarization and effective Mueller matrix for multiple scattering of light by nonspherical ice crystals. Opt. Express 2006, 14, 6381–6393. [Google Scholar] [CrossRef]



| Cloud Property Parameter | Variations |
|---|---|
| Ice particle habit | Solid hexagonal column |
| AR | 0.2, 1.0, 2.0, 4.0, 8.0 |
| σ * | 0, 0.1, 0.2, 0.3, 0.4, 0.5 |
| Re | 1–90 µm |
| COT | >5 |
| Test | Observation Combination |
|---|---|
| 1 | I0.87, I2.13 |
| 2 | I0.87, I2.13, I1.24 |
| 3 | I0.87, I2.13, I1.24, DOLP0.87 |
| 4 | I0.87, I2.13, I1.24, DOLP0.87, DOLP2.13 |
| 5 | I0.87, I2.13, I1.24, DOLP0.87, DOLP2.13, I1.64 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Teng, S.; Di, D.; Hu, X.; Letu, H.; Min, M.; Liu, C. Information Content of Ice Cloud Properties from Multi-Spectral, -Angle and -Polarization Observations. Remote Sens. 2020, 12, 2548. https://doi.org/10.3390/rs12162548
Zhang M, Teng S, Di D, Hu X, Letu H, Min M, Liu C. Information Content of Ice Cloud Properties from Multi-Spectral, -Angle and -Polarization Observations. Remote Sensing. 2020; 12(16):2548. https://doi.org/10.3390/rs12162548
Chicago/Turabian StyleZhang, Manting, Shiwen Teng, Di Di, Xiuqing Hu, Husi Letu, Min Min, and Chao Liu. 2020. "Information Content of Ice Cloud Properties from Multi-Spectral, -Angle and -Polarization Observations" Remote Sensing 12, no. 16: 2548. https://doi.org/10.3390/rs12162548