Performance Evaluation of Spaceborne Integrated Path Differential Absorption Lidar for Carbon Dioxide Detection at 1572 nm
Abstract
:1. Introduction
2. Method
2.1. IPDA Lidar Principle
2.2. XCO2 Retrieval Algorithm
2.3. Random and System Error Analysis
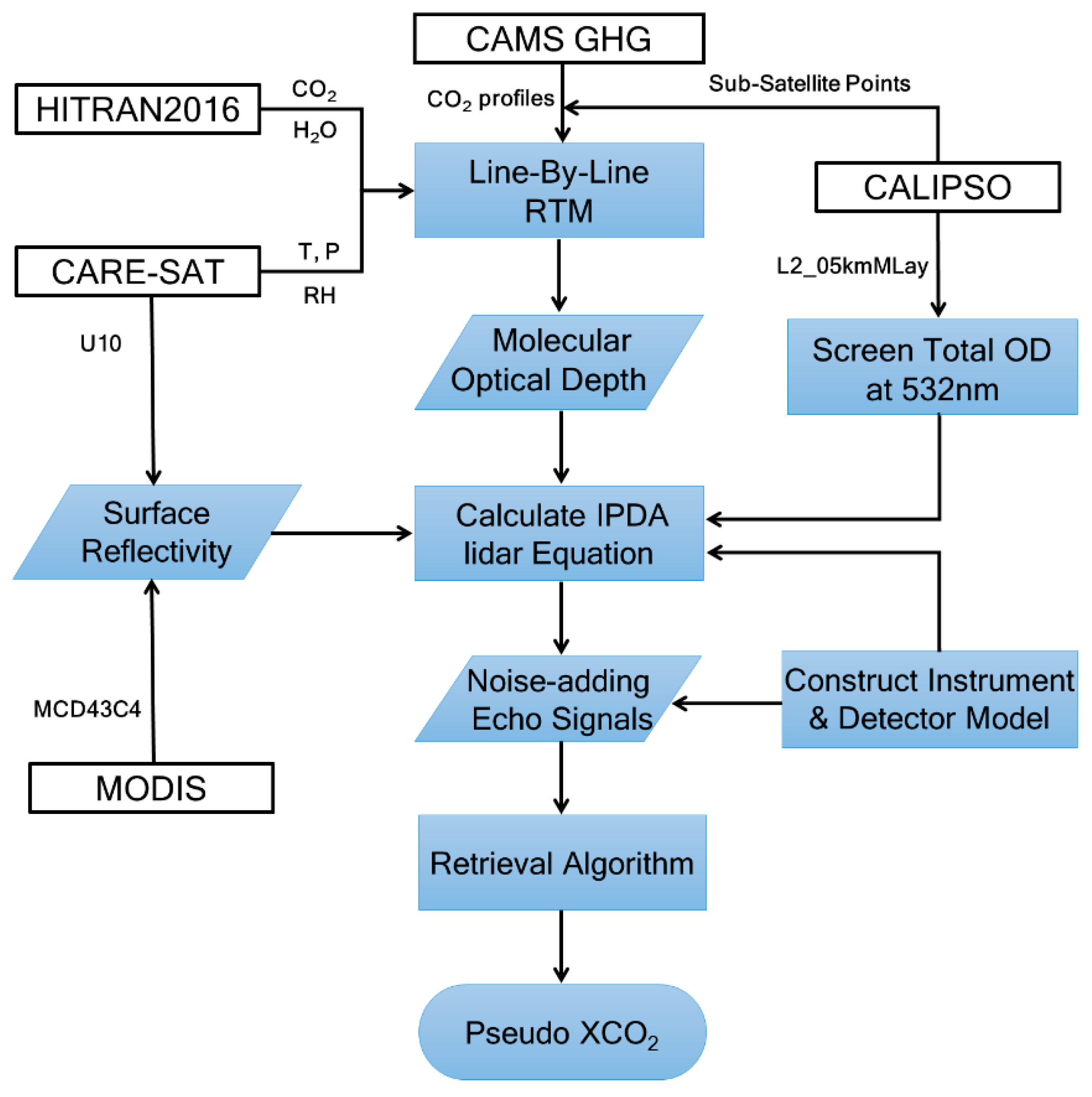
3. Dataset Screening
4. Results
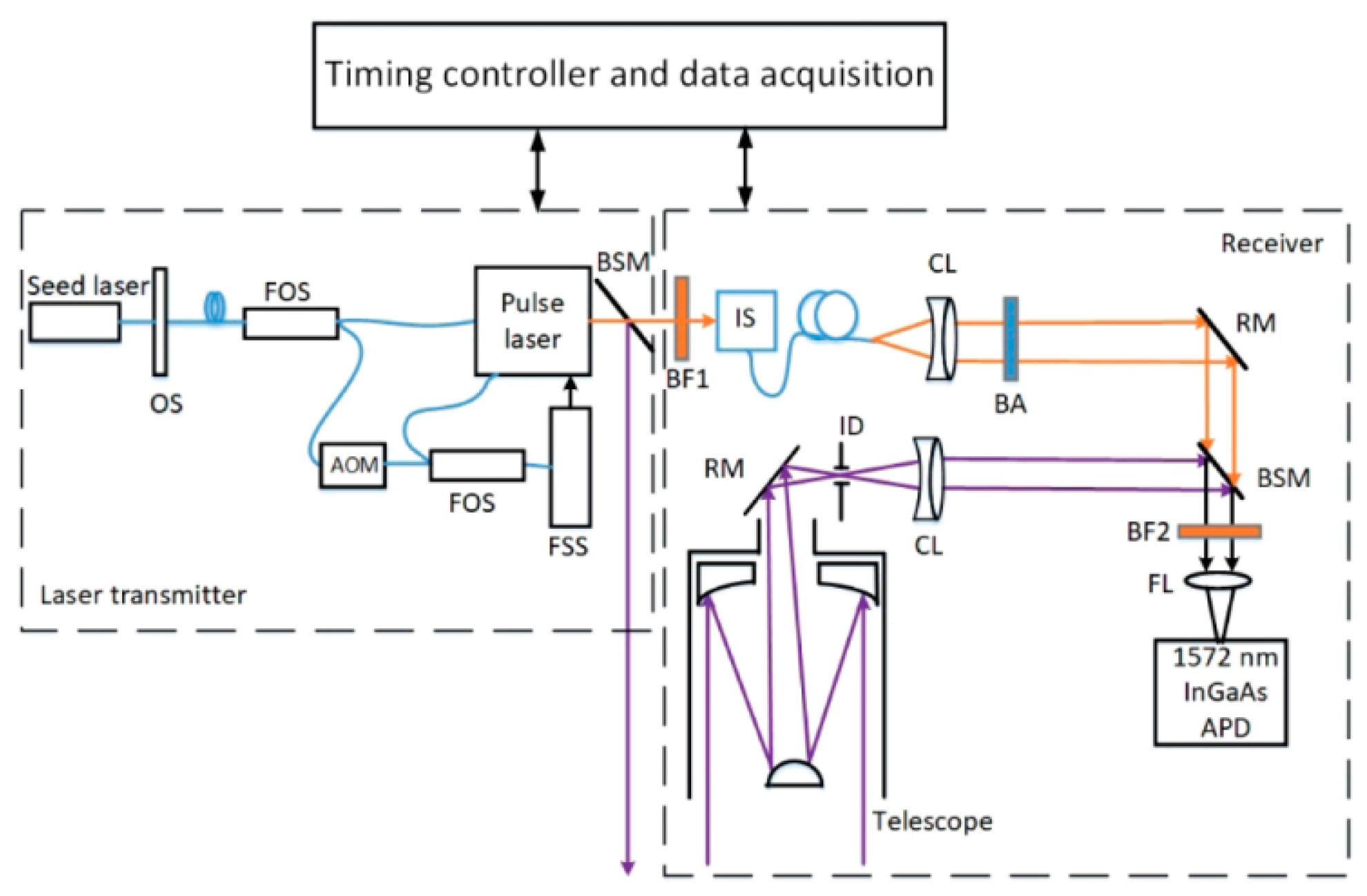
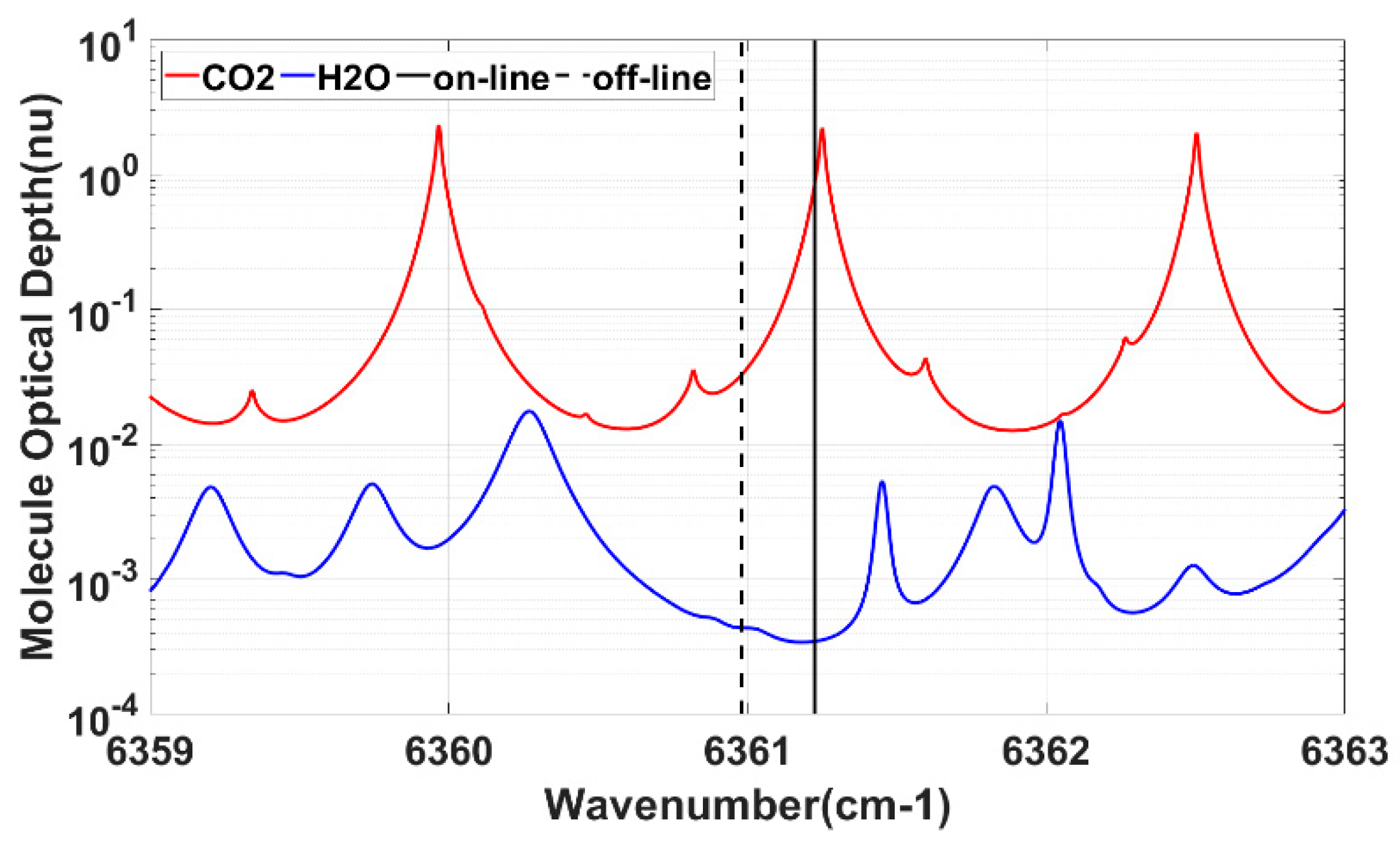
4.1. Simulation of AC-IPDA Lidar
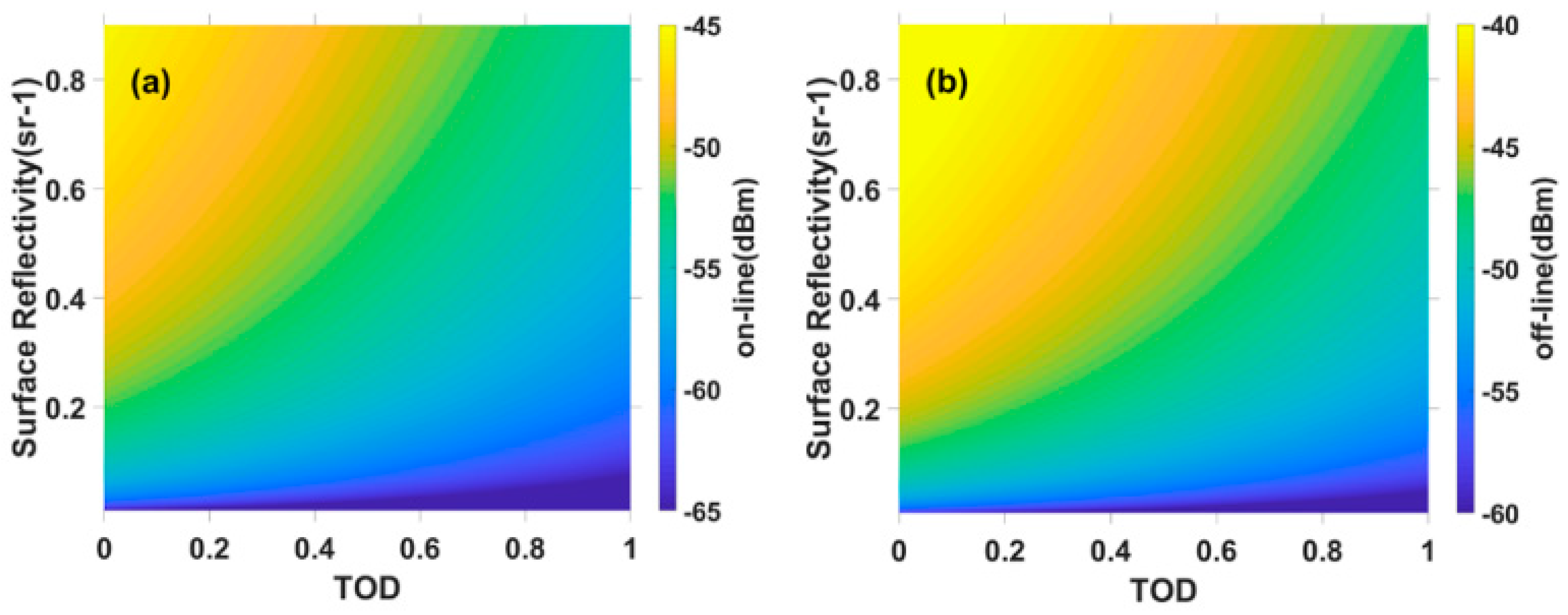
4.2. Error Analysis Results
4.3. Pseudo XCO2 of AC-IPDA Lidar
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- IPCC. Climate Change 2013—The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2014; p. 1535. [Google Scholar]
- Friedlingstein, P.; Cox, P.; Betts, R.; Bopp, L.; von Bloh, W.; Brovkin, V.; Cadule, P.; Doney, S.; Eby, M.; Fung, I.; et al. Climate–Carbon Cycle Feedback Analysis: Results from the C4MIP Model Intercomparison. J. Clim. 2006, 19, 3337–3353. [Google Scholar] [CrossRef]
- Crisp, D.; Team, O.C.O. Measuring Atmospheric Carbon Dioxide from Space with the Orbiting Carbon Observatory-2 (OCO-2). In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 9–13 August 2015. [Google Scholar]
- Wunch, D.; Toon, G.C.; Blavier, J.F.L.; Washenfelder, R.A.; Notholt, J.; Connor, B.J.; Griffith, D.W.T.; Sherlock, V.; Wennberg, P.O. The Total Carbon Column Observing Network. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 2087–2112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuze, A.; Suto, H.; Shiomi, K.; Kawakami, S.; Tanaka, M.; Ueda, Y.; Deguchi, A.; Yoshida, J.; Yamamoto, Y.; Kataoka, F.; et al. Update on GOSAT TANSO-FTS performance, operations, and data products after more than 6 years in space. Atmos. Meas. Tech. 2016, 9, 2445–2461. [Google Scholar] [CrossRef] [Green Version]
- O’Dell, C.W.; Connor, B.; Boesch, H.; O’Brien, D.; Frankenberg, C.; Castano, R.; Christi, M.; Eldering, D.; Fisher, B.; Gunson, M.; et al. The ACOS CO2 retrieval algorithm—Part 1: Description and validation against synthetic observations. Atmos. Meas. Tech. 2012, 5, 99–121. [Google Scholar] [CrossRef] [Green Version]
- Gurney, K.R.; Law, R.M.; Denning, A.S.; Rayner, P.J.; Baker, D.; Bousquet, P.; Bruhwiler, L.; Chen, Y.-H.; Ciais, P.; Fan, S.; et al. Towards robust regional estimates of CO2 sources and sinks using atmospheric transport models. Nature 2002, 415, 626–630. [Google Scholar] [CrossRef] [Green Version]
- Bruhwiler, L.M.P.; Michalak, A.M.; Tans, P.P. Spatial and temporal resolution of carbon flux estimates for 1983–2002. Biogeosciences 2011, 8, 1309–1331. [Google Scholar] [CrossRef]
- Houweling, S.; Hartmann, W.; Aben, I.; Schrijver, H.; Skidmore, J.; Roelofs, G.J.; Breon, F.M. Evidence of systematic errors in SCIAMACHY-observed CO2 due to aerosols. Atmos. Chem. Phys. 2005, 5, 3003–3013. [Google Scholar] [CrossRef] [Green Version]
- Buchwitz, M.; de Beek, R.; Burrows, J.P.; Bovensmann, H.; Warneke, T.; Notholt, J.; Meirink, J.F.; Goede, A.P.H.; Bergamaschi, P.; Korner, S.; et al. Atmospheric methane and carbon dioxide from SCIAMACHY satellite data: Initial comparison with chemistry and transport models. Atmos. Chem. Phys. 2005, 5, 941–962. [Google Scholar] [CrossRef] [Green Version]
- Han, G.; Gong, W.; Lin, H.; Ma, X.; Xiang, Z.C. Study on Influences of Atmospheric Factors on Vertical CO2 Profile Retrieving From Ground-Based DIAL at 1.6 mu m. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3221–3234. [Google Scholar] [CrossRef]
- Caron, J.; Durand, Y.; Bezy, J.-L.; Meynart, R. Performance Modeling for A-SCOPE: A Space-Borne Lidar Measuring Atmospheric CO2; SPIE Remote Sensing: Edinburgh, UK, 2009; Volume 7479. [Google Scholar]
- Ehret, G.; Bousquet, P.; Pierangelo, C.; Alpers, M.; Millet, B.; Abshire, J.B.; Bovensmann, H.; Burrows, J.P.; Chevallier, F.; Ciais, P.; et al. MERLIN: A French-German Space Lidar Mission Dedicated to Atmospheric Methane. Remote Sens. 2017, 9, 1052. [Google Scholar] [CrossRef] [Green Version]
- NTRS-NASA Technical Reports Server. NASA/TP–2018-219034. 2018. Available online: https://ntrs.nasa.gov/ciations/20190000855 (accessed on 10 August 2020).
- Abshire, J.B.; Ramanathan, A.K.; Riris, H.; Allan, G.R.; Sun, X.; Hasselbrack, W.E.; Mao, J.; Wu, S.; Chen, J.; Numata, K.; et al. Airborne measurements of CO2 column concentrations made with a pulsed IPDA lidar using a multiple-wavelength-locked laser and HgCdTe APD detector. Atmos. Meas. Tech. 2018, 11, 2001–2025. [Google Scholar] [CrossRef] [Green Version]
- Abshire, J.B.; Riris, H.; Allan, G.R.; Weaver, C.J.; Mao, J.; Sun, X.; Hasselbrack, W.E.; Kawa, S.R.; Biraud, S.C. Pulsed airborne lidar measurements of atmospheric CO2 column absorption. Tellus Ser. B Chem. Phys. Meteorol. 2010, 62, 770–783. [Google Scholar] [CrossRef]
- Lin, B.; Nehrir, A.R.; Harrison, F.W.; Browell, E.V.; Ismail, S.; Obland, M.D.; Campbell, J.; Dobler, J.; Meadows, B.; Fan, T.-F.; et al. Atmospheric CO2 column measurements in cloudy conditions using intensity-modulated continuous-wave lidar at 1.57 micron. Opt. Express 2015, 23, A582–A593. [Google Scholar] [CrossRef]
- Refaat, T.F.; Singh, U.N.; Yu, J.; Petros, M.; Remus, R.; Ismail, S. Double-pulse 2-μm integrated path differential absorption lidar airborne validation for atmospheric carbon dioxide measurement. Appl. Opt. 2016, 55, 4232–4246. [Google Scholar] [CrossRef]
- Liu, D.; Zheng, Z.; Chen, W.; Wang, Z.; Li, W.; Ke, J.; Zhang, Y.; Chen, S.; Cheng, C.; Wang, S. Performance estimation of space-borne high-spectral-resolution lidar for cloud and aerosol optical properties at 532 nm. Opt. Express 2019, 27, A481–A494. [Google Scholar] [CrossRef] [PubMed]
- Ehret, G.; Kiemle, C.; Wirth, M.; Amediek, A.; Fix, A.; Houweling, S. Space-borne remote sensing of CO2, CH4, and N2O by integrated path differential absorption lidar: A sensitivity analysis. Appl. Phys. B Lasers Opt. 2008, 90, 593–608. [Google Scholar] [CrossRef] [Green Version]
- Kawa, S.R.; Mao, J.; Abshire, J.B.; Collatz, G.J.; Sun, X.; Weaver, C.J. Simulation studies for a space-based CO2 lidar mission. Tellus Ser. B Chem. Phys. Meteorol. 2010, 62, 759–769. [Google Scholar] [CrossRef]
- Singh, U.N.; Refaat, T.F.; Ismail, S.; Davis, K.J.; Kawa, S.R.; Menzies, R.T.; Petros, M. Feasibility study of a space-based high pulse energy 2 μm CO2 IPDA lidar. Appl. Opt. 2017, 56, 6531–6547. [Google Scholar] [CrossRef]
- Han, G.; Ma, X.; Liang, A.; Zhang, T.; Zhao, Y.; Zhang, M.; Gong, W. Performance Evaluation for China’s Planned CO2-IPDA. Remote Sens. 2017, 9, 768. [Google Scholar] [CrossRef] [Green Version]
- Han, G.; Xu, H.; Gong, W.; Liu, J.; Du, J.; Ma, X.; Liang, A. Feasibility Study on Measuring Atmospheric CO2 in Urban Areas Using Spaceborne CO2-IPDA LIDAR. Remote Sens. 2018, 10, 985. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Liu, J.; Chen, X.; Zhu, X.; Bi, D.; Chen, W. Sensitivity analysis and correction algorithms for atmospheric CO2 measurements with 1.57-mu m airborne double-pulse IPDA LIDAR. Opt. Express 2019, 27, 32679–32699. [Google Scholar] [CrossRef] [PubMed]
- Kiemle, C.; Kawa, S.R.; Quatrevalet, M.; Browell, E.V. Performance simulations for a spaceborne methane lidar mission. J. Geophys. Res. Atmos. 2014, 119, 4365–4379. [Google Scholar] [CrossRef] [Green Version]
- Amediek, A.; Fix, A.; Ehert, G. Airborne measurements of ground reflectance at 1.6μm. In Proceedings of the SPIE Remote Sensing, Cardiff, Wales, 15–18 October 2008; Volume 7111, pp. 1–15. [Google Scholar]
- Winker, D.M.; Vaughan, M.A.; Omar, A.; Hu, Y.; Powell, K.A.; Liu, Z.; Hunt, W.H.; Young, S.A. Overview of the CALIPSO Mission and CALIOP Data Processing Algorithms. J. Atmos. Ocean. Technol. 2009, 26, 2310–2323. [Google Scholar] [CrossRef]
- Lancaster, R.S.; Spinhirne, J.D.; Palm, S.P. Laser pulse reflectance of the ocean surface from the GLAS satellite lidar. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hill, C.; Kochanov, R.V.; Tan, Y.; Bernath, P.F.; Birk, M.; Boudon, V.; Canpargue, A.; Chance, K.V.; et al. The HITRAN2016 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 3–69. [Google Scholar] [CrossRef]
- Ramanathan, A.K.; Mao, J.; Abshire, J.B.; Allan, G.R. Remote sensing measurements of the CO2 mixing ratio in the planetary boundary layer using cloud slicing with airborne lidar. Geophys. Res. Lett. 2015, 42, 2055–2062. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, X.; Bi, D.; Liu, J.; Chen, W.; Benítez, P.; Matoba, O. Inversion algorithm validation of 1.57-μm double-pulse IPDA lidar for atmospheric CO2 measurement. In Proceedings of the SPIE Optical Design and Testing IX, Hangzhou, China, 21–22 October 2019; Volume 11185. [Google Scholar] [CrossRef]
- Mao, J.P.; Ramanathan, A.; Abshire, J.B.; Kawa, S.R.; Riris, H.; Allan, G.R.; Rodriguez, M.; Hasselbrack, W.E.; Sun, X.; Numata, K.; et al. Measurement of atmospheric CO2 column concentrations to cloud tops with a pulsed multi-wavelength airborne lidar. Atmos. Meas. Tech. 2018, 11, 127–140. [Google Scholar] [CrossRef] [Green Version]
- Du, J.; Zhu, Y.; Li, S.; Zhang, J.; Sun, Y.; Zang, H.; Liu, D.; Ma, X.; Bi, D.; Liu, J.; et al. Double-pulse 1.57 mu m integrated path differential absorption lidar ground validation for atmospheric carbon dioxide measurement. Appl. Opt. 2017, 56, 7053–7058. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, J.; Chen, X.; Zhu, X.; Zhang, J.; Li, S.; Sun, Y.; Hou, X.; Bi, D.; Bu, L.; et al. Airborne Validation Experiment of 1.57-μm Double-Pulse IPDA LIDAR for Atmospheric Carbon Dioxide Measurement. Remote Sens. 2020, 12, 1999. [Google Scholar] [CrossRef]
- Anqi, W.; Zhixin, M.; Yanying, F. Widely tunable laser frequency offset locking to the atomic resonance line with frequency modulation spectroscopy. Chin. Opt. Lett. 2018, 16, 050201. [Google Scholar] [CrossRef]
- Du, J.; Sun, Y.; Chen, D.; Mu, Y.; Huang, M.; Yang, Z.; Liu, J.; Bi, D.; Hou, X.; Chen, W. Frequency-stabilized laser system at 1572 nm for space-borne CO2 detection LIDAR. Chin. Opt. Lett. 2017, 15, 031401. [Google Scholar]

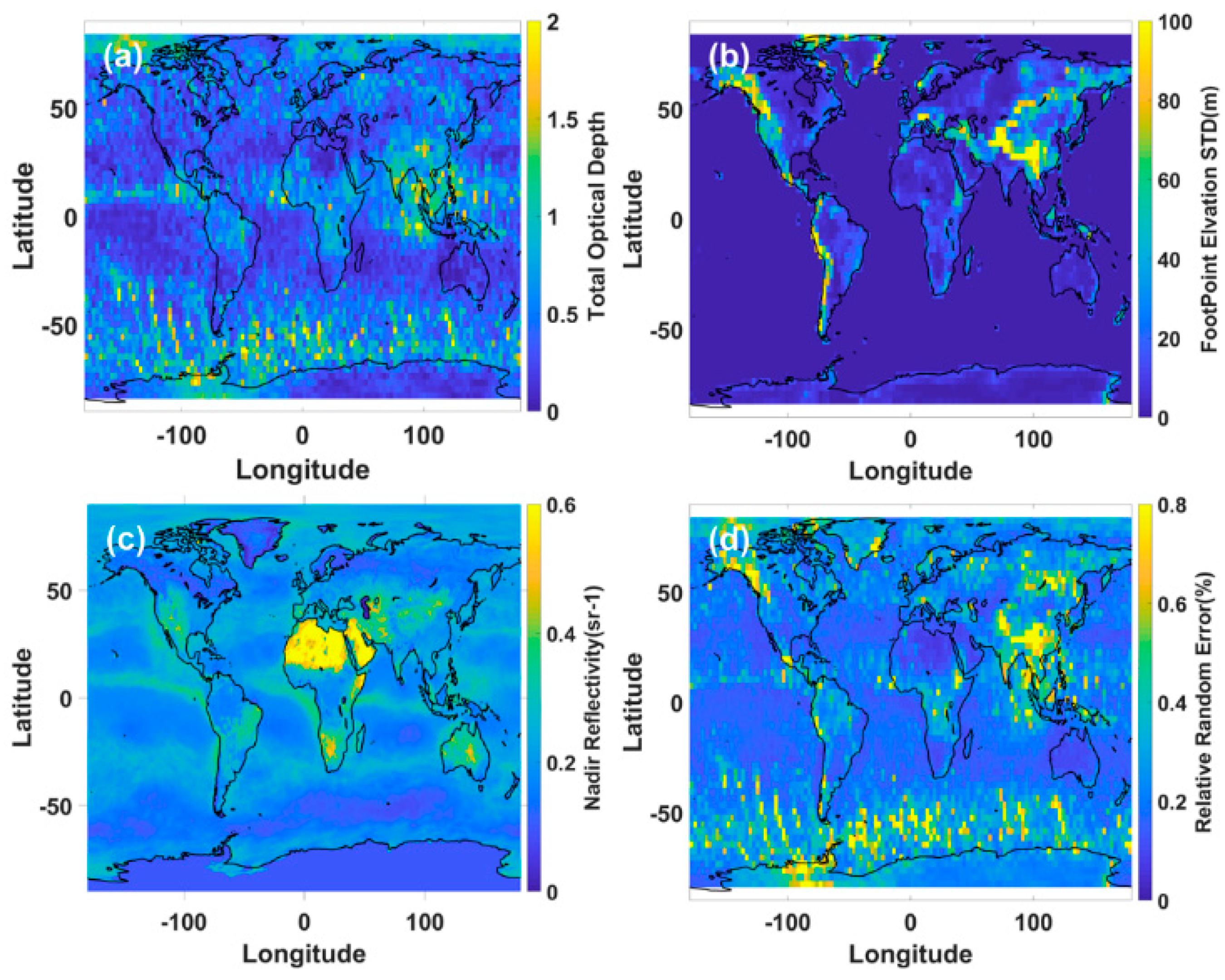

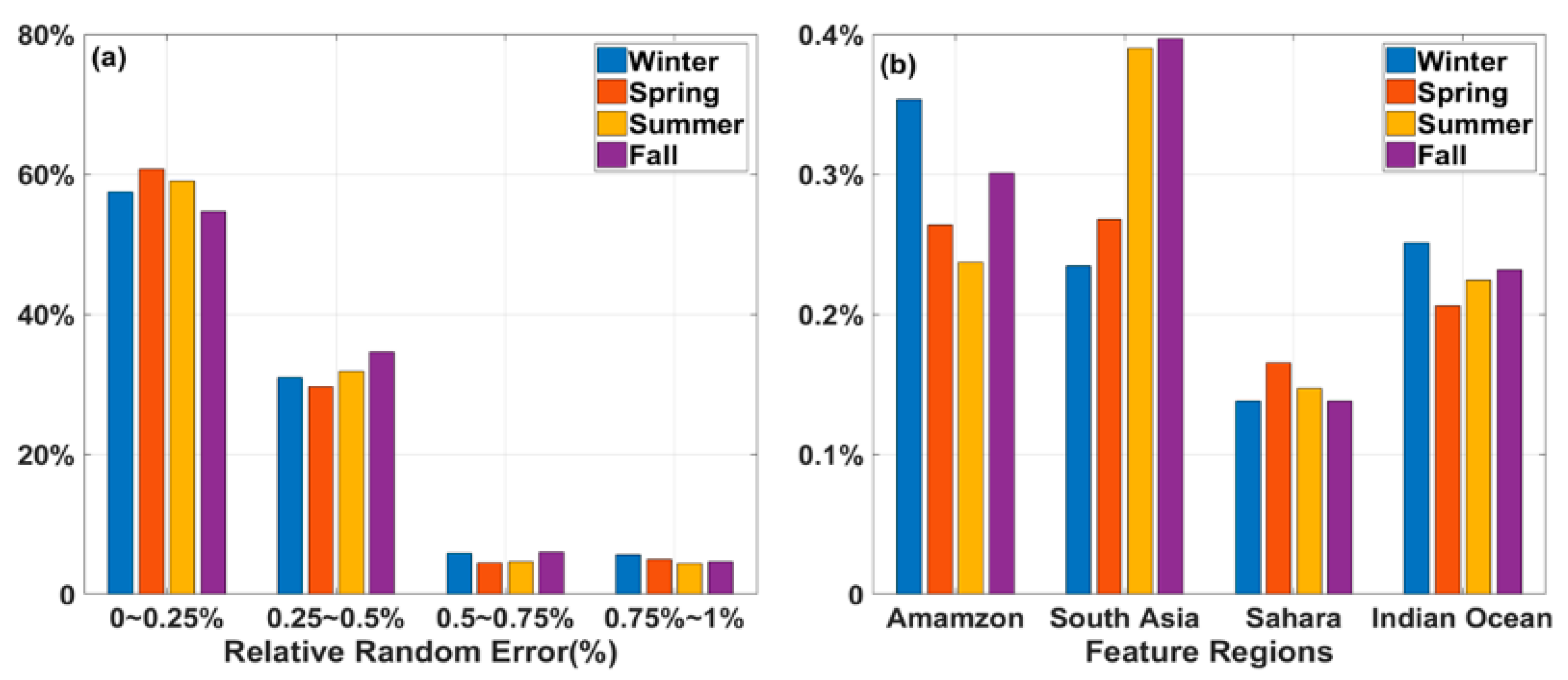
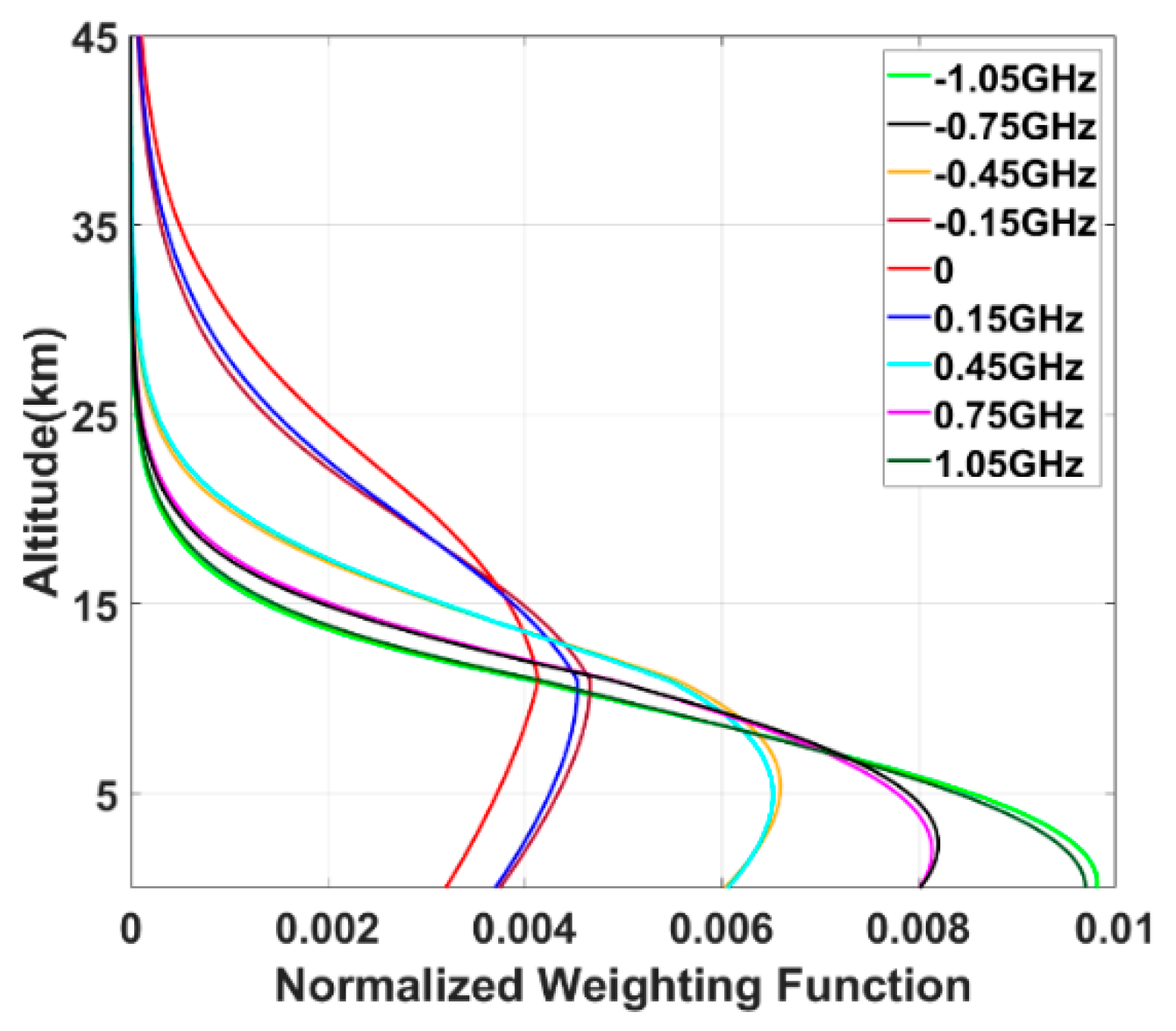

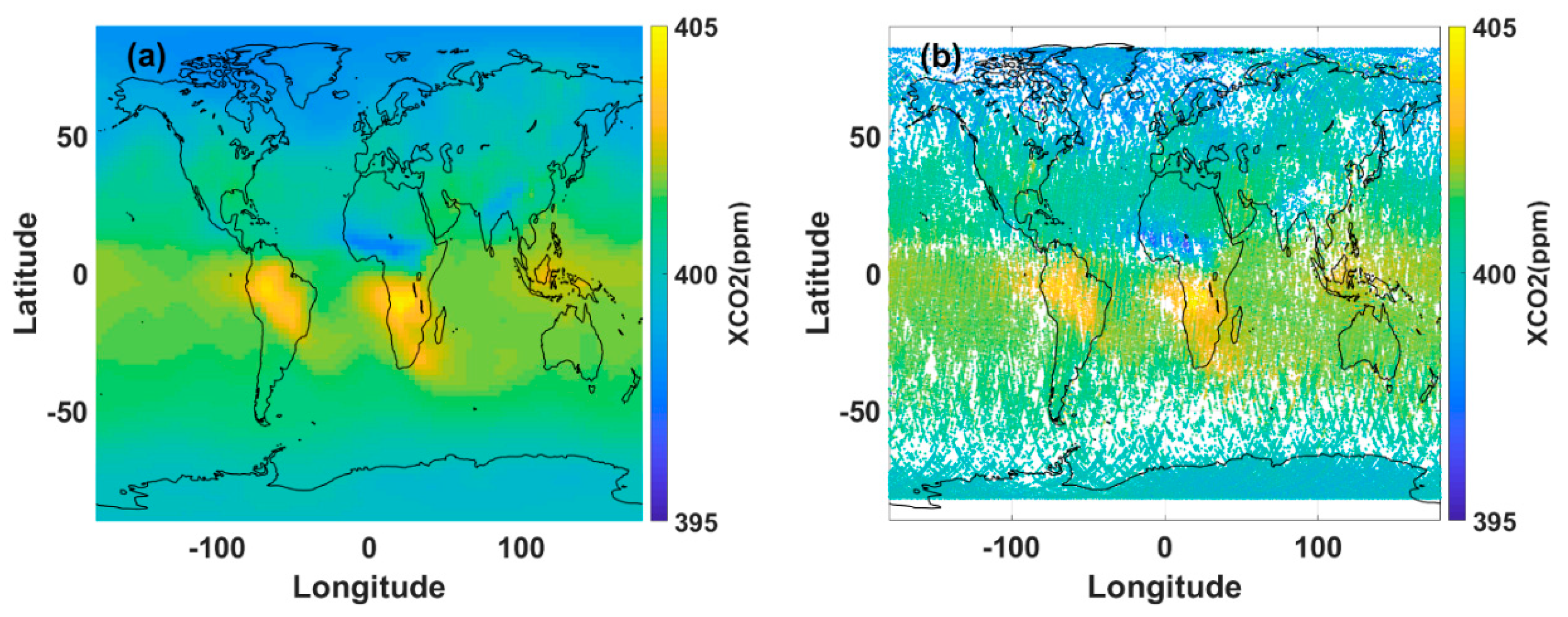

| Category | Parameter | Value | Unit |
| Satellite Platform | Orbit altitude | 705 | km |
| Viewing mode | Nadir | - | |
| Spatial resolution | Land:50/Sea:100 | km | |
| Transmitter System | On-line | 1572.024 | nm |
| Off-line | 1572.085 | nm | |
| Linewidth | 50 | MHz | |
| Pulse energy | 75 | mJ | |
| Pulse width | 15 | ns | |
| Repetition rate | 20 | Hz | |
| Receiver System | Detector type | InGaAs APD | - |
| Telescope diameter | 1 | m | |
| Field of view | 0.2 | mrad | |
| Optical efficiency | 0.6455 | - | |
| Digitization rate | 50 | MHz | |
| Optical filter bandwidth | 0.45 | nm | |
| Responsively | 0.94 | A/W | |
| Bandwidth | 1 | MHz | |
| Feedback resistance | 1 | MΩ | |
| Excess noise factor | 3.2(@M=10) | - | |
| Noise equivalent power | 64 | fw/√Hz |
| Latitude | Sea | Land | ||||
|---|---|---|---|---|---|---|
| RREs (%) | RREs_STD 1 | Number | RREs (%) | RREs_STD | Number | |
| 70°N–85°N | 0.239 | 0.094 | 289 | 0.230 | 0.100 | 311 |
| 50°N–70°N | 0.163 | 0.062 | 183 | 0.260 | 0.181 | 657 |
| 30°N–50°N | 0.137 | 0.036 | 371 | 0.256 | 0.39 | 469 |
| 0–30°N | 0.181 | 0.101 | 725 | 0.256 | 0.218 | 475 |
| 0–30°S | 0.146 | 0.064 | 825 | 0.171 | 0.098 | 375 |
| 30°S–50°S | 0.239 | 0.348 | 647 | 0.203 | 0.109 | 73 |
| 50°S–70°S | 0.348 | 0.391 | 703 | 0.295 | 0.358 | 137 |
| 70°S–85°S | 0.184 | 0.086 | 68 | 0.253 | 0.175 | 412 |
| Category | Parameters | Uncertainty | RSE | Errors (ppm) |
|---|---|---|---|---|
| Atmosphere | Temperature | 1 K | 0.033% | 0.132 |
| Pressure | 1 hPa | 0.071% | 0.284 | |
| Humidity | 10% | 0.037% | 0.148 | |
| Laser Transmitter | Laser Energy Fluctuation | 0.05% | 0.037% | 0.148 |
| Frequency Drift | 0.6 MHz | 0.038% | 0.152 | |
| Spectral Purity | 99.9% (0.45 nm IF) | 0.079% | 0.316 | |
| Laser Linewidth | 50 MHz | 0.07% | 0.28 | |
| Satellite Platform | Doppler Effect across track | 140 μrad | 0.038% | 0.152 |
| Doppler Effect along track | 1 mrad | 0.0005% | 0.002 | |
| Non-overlap Footprints | 25 μrad | 0.006% | 0.024 | |
| Laser Path | 2 m | 0.01% | 0.04 | |
| Total | 0.589 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Ke, J.; Chen, S.; Zheng, Z.; Cheng, C.; Tong, B.; Liu, J.; Liu, D.; Chen, W. Performance Evaluation of Spaceborne Integrated Path Differential Absorption Lidar for Carbon Dioxide Detection at 1572 nm. Remote Sens. 2020, 12, 2570. https://doi.org/10.3390/rs12162570
Wang S, Ke J, Chen S, Zheng Z, Cheng C, Tong B, Liu J, Liu D, Chen W. Performance Evaluation of Spaceborne Integrated Path Differential Absorption Lidar for Carbon Dioxide Detection at 1572 nm. Remote Sensing. 2020; 12(16):2570. https://doi.org/10.3390/rs12162570
Chicago/Turabian StyleWang, Shuaibo, Ju Ke, Sijie Chen, Zhuofan Zheng, Chonghui Cheng, Bowen Tong, Jiqiao Liu, Dong Liu, and Weibiao Chen. 2020. "Performance Evaluation of Spaceborne Integrated Path Differential Absorption Lidar for Carbon Dioxide Detection at 1572 nm" Remote Sensing 12, no. 16: 2570. https://doi.org/10.3390/rs12162570
APA StyleWang, S., Ke, J., Chen, S., Zheng, Z., Cheng, C., Tong, B., Liu, J., Liu, D., & Chen, W. (2020). Performance Evaluation of Spaceborne Integrated Path Differential Absorption Lidar for Carbon Dioxide Detection at 1572 nm. Remote Sensing, 12(16), 2570. https://doi.org/10.3390/rs12162570







