Combining Interior Orientation Variables to Predict the Accuracy of Rpas–Sfm 3D Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
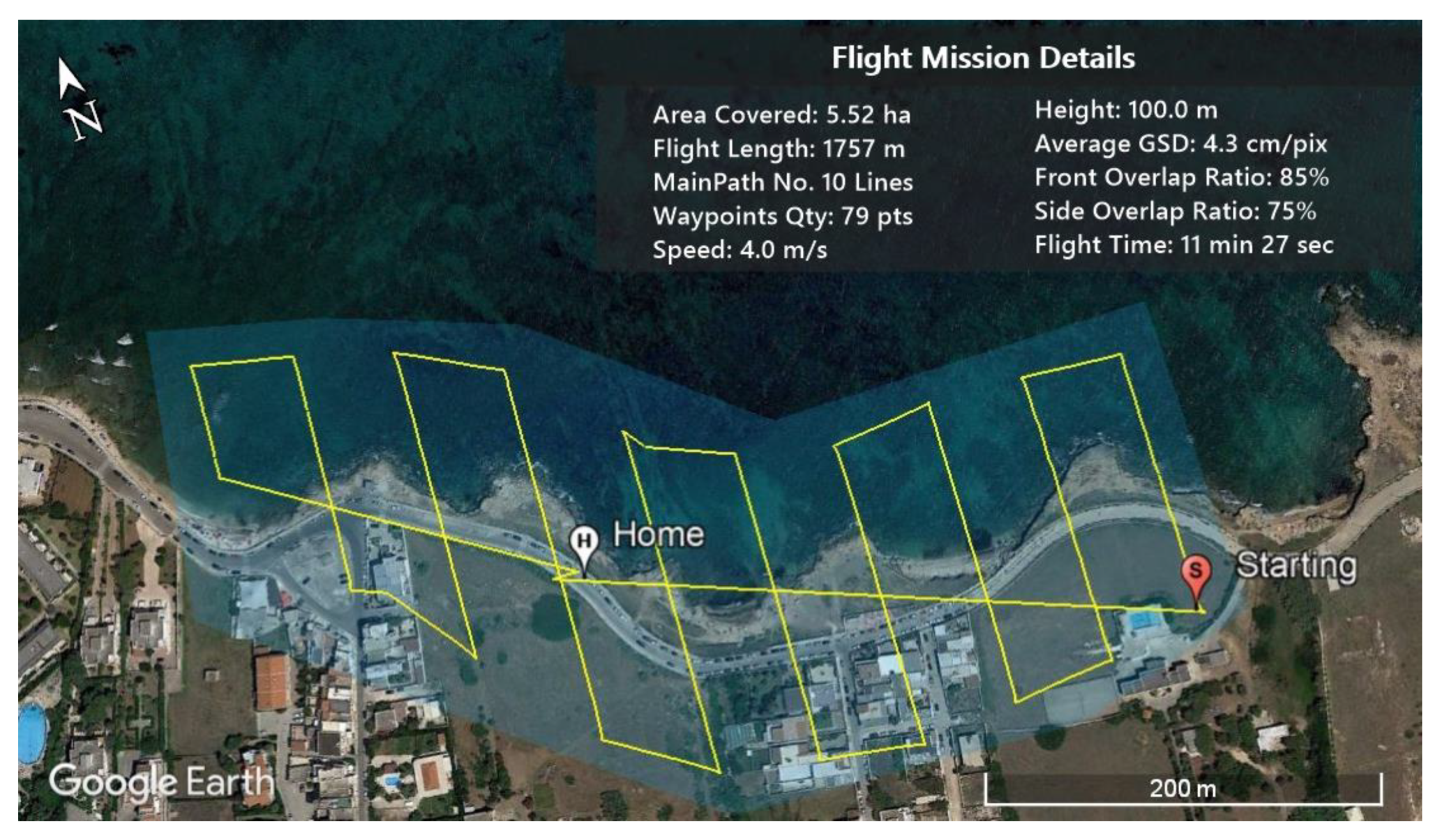
2.2. Field Data Campaigns and Operative Workflow
2.3. Photogrammetric Products Generation
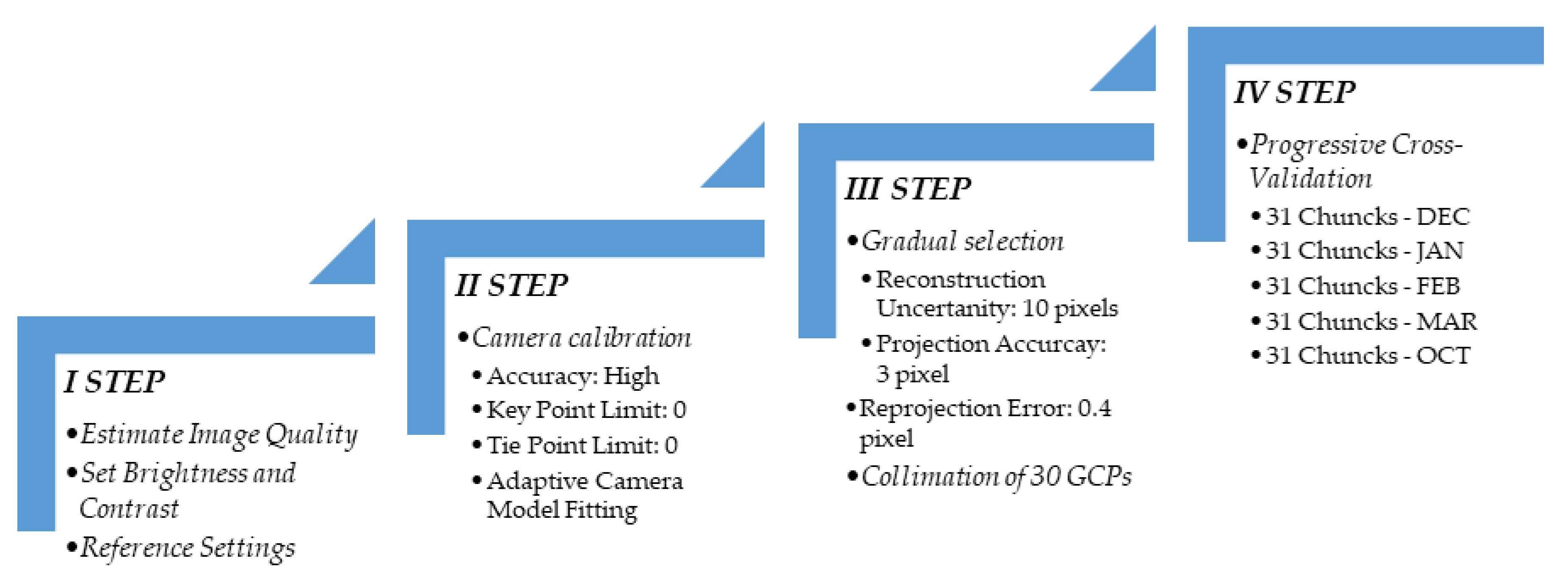
2.3.1. First Step: Setting-Up Workspace and Dataset
2.3.2. Second Step: Image Block Orientation
2.3.3. Third Step: Filtering and Georeferencing
2.3.4. Fourth Step: Progressive Cross-Validation
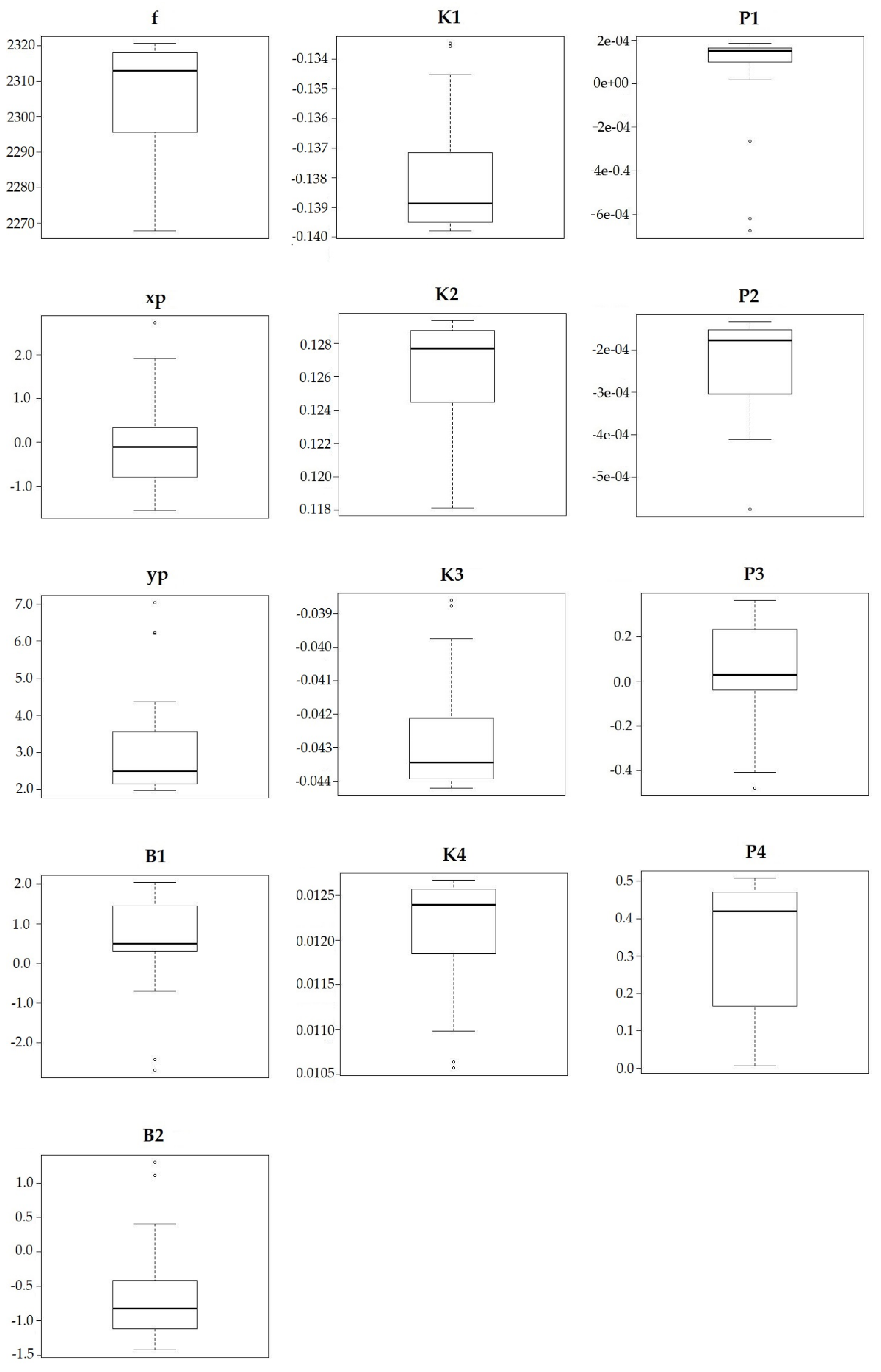
2.4. Analyses of I.O. Parameters Estimates
2.5. Accuracy Assessment
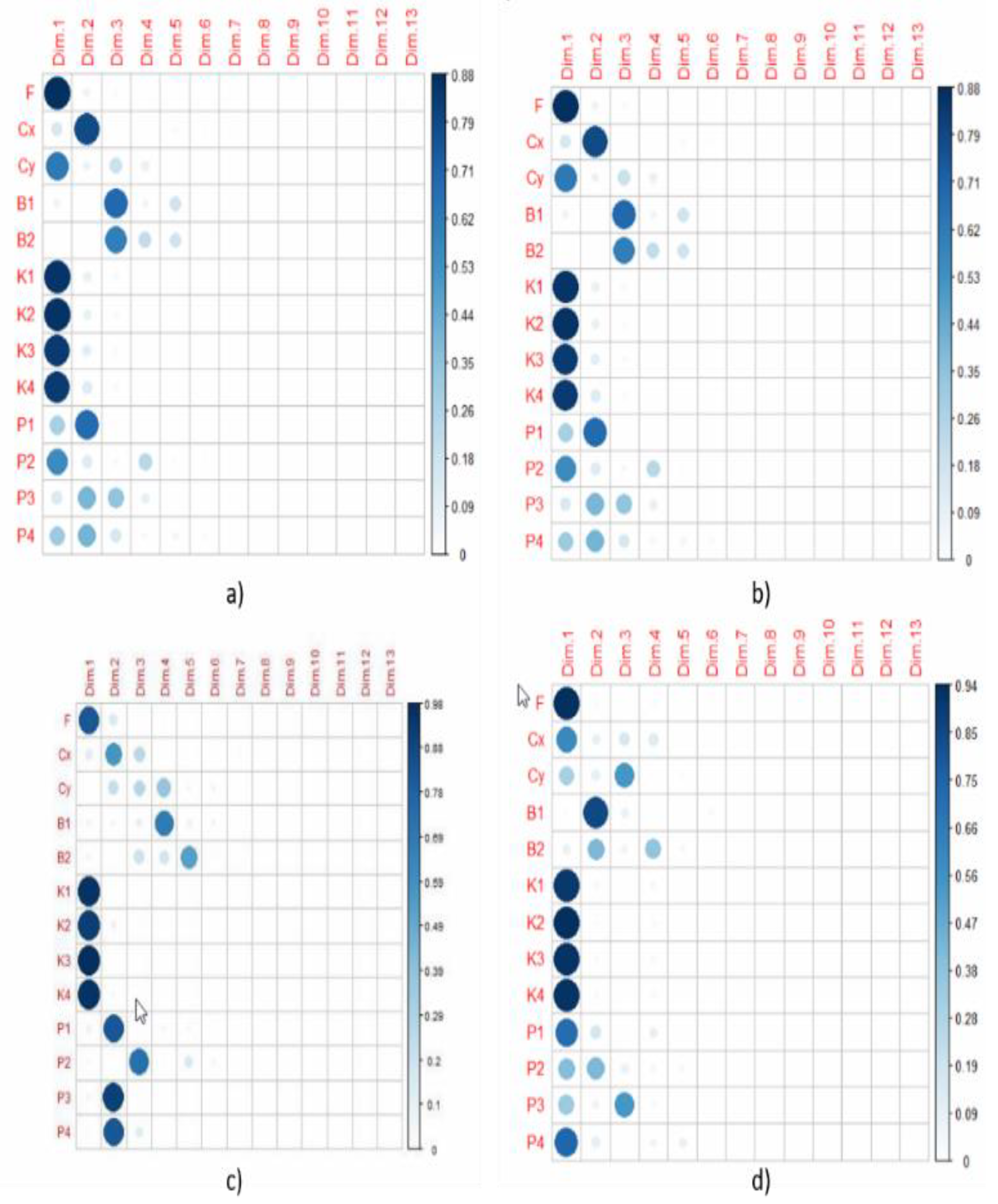
2.6. PCA and Synthetic Index Generation
2.7. Predicting Accuracy of Measurements: Model Definition
3. Results
3.1. Accuracy of Photogrammetric Measurements
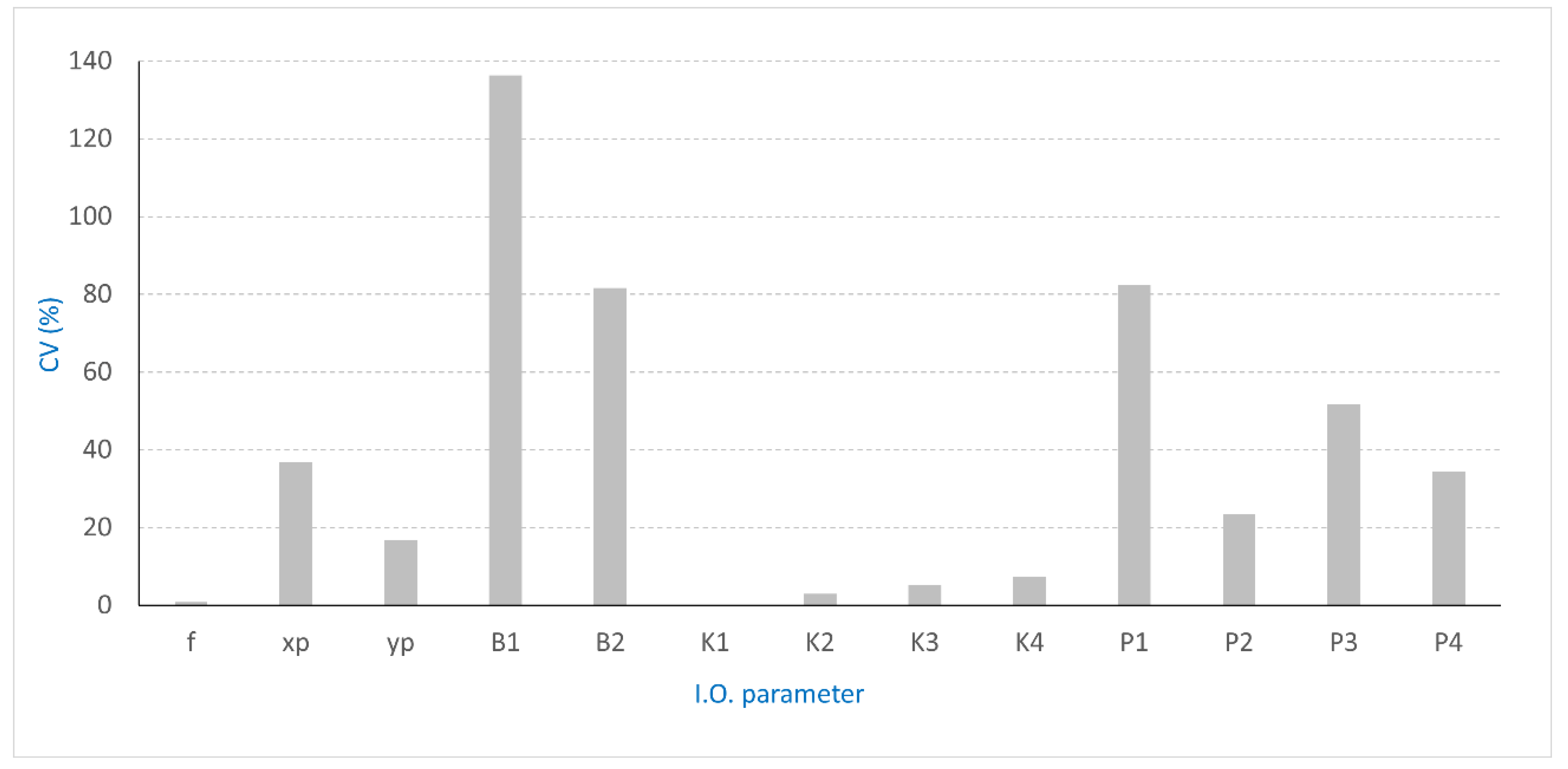
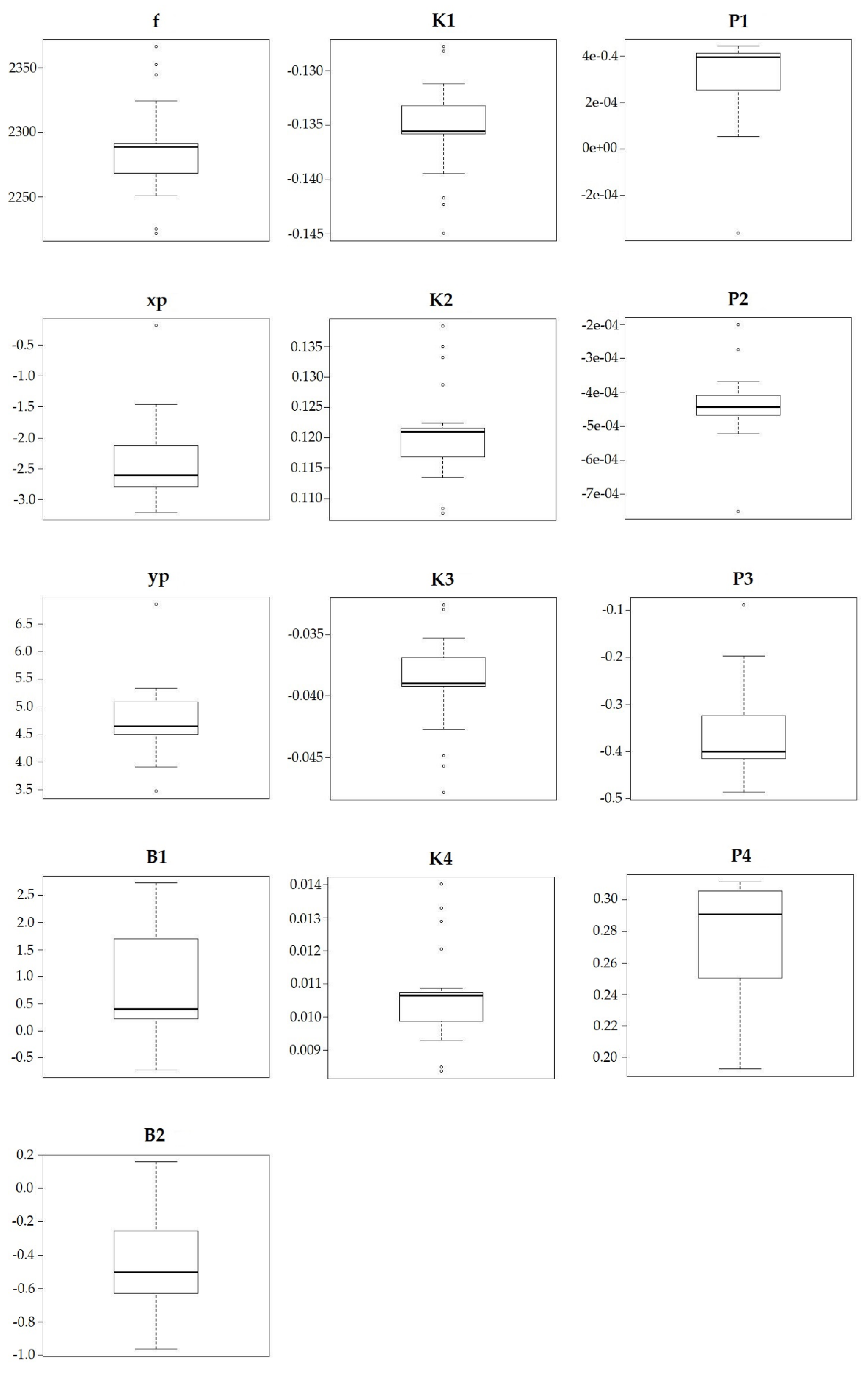
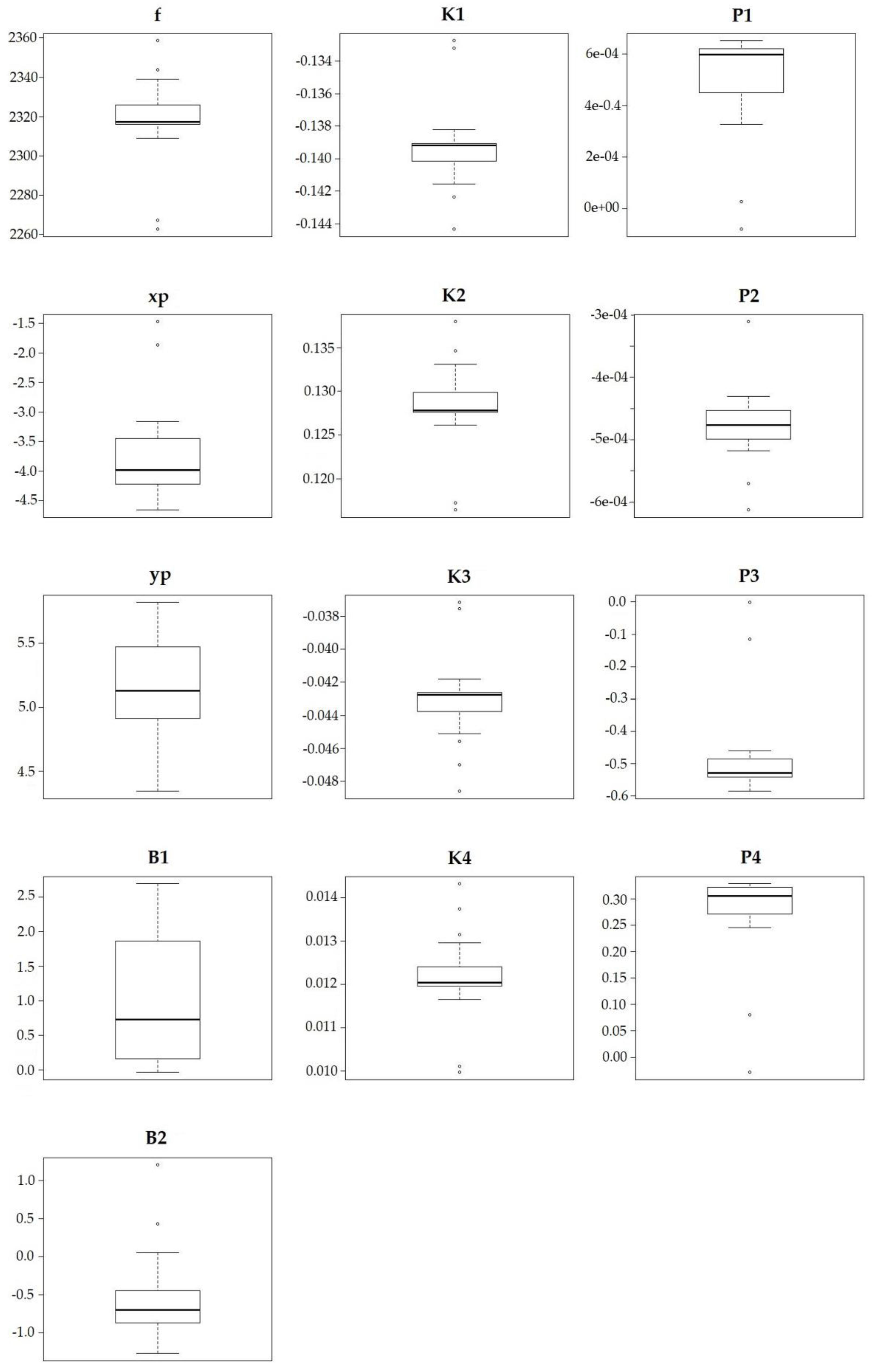
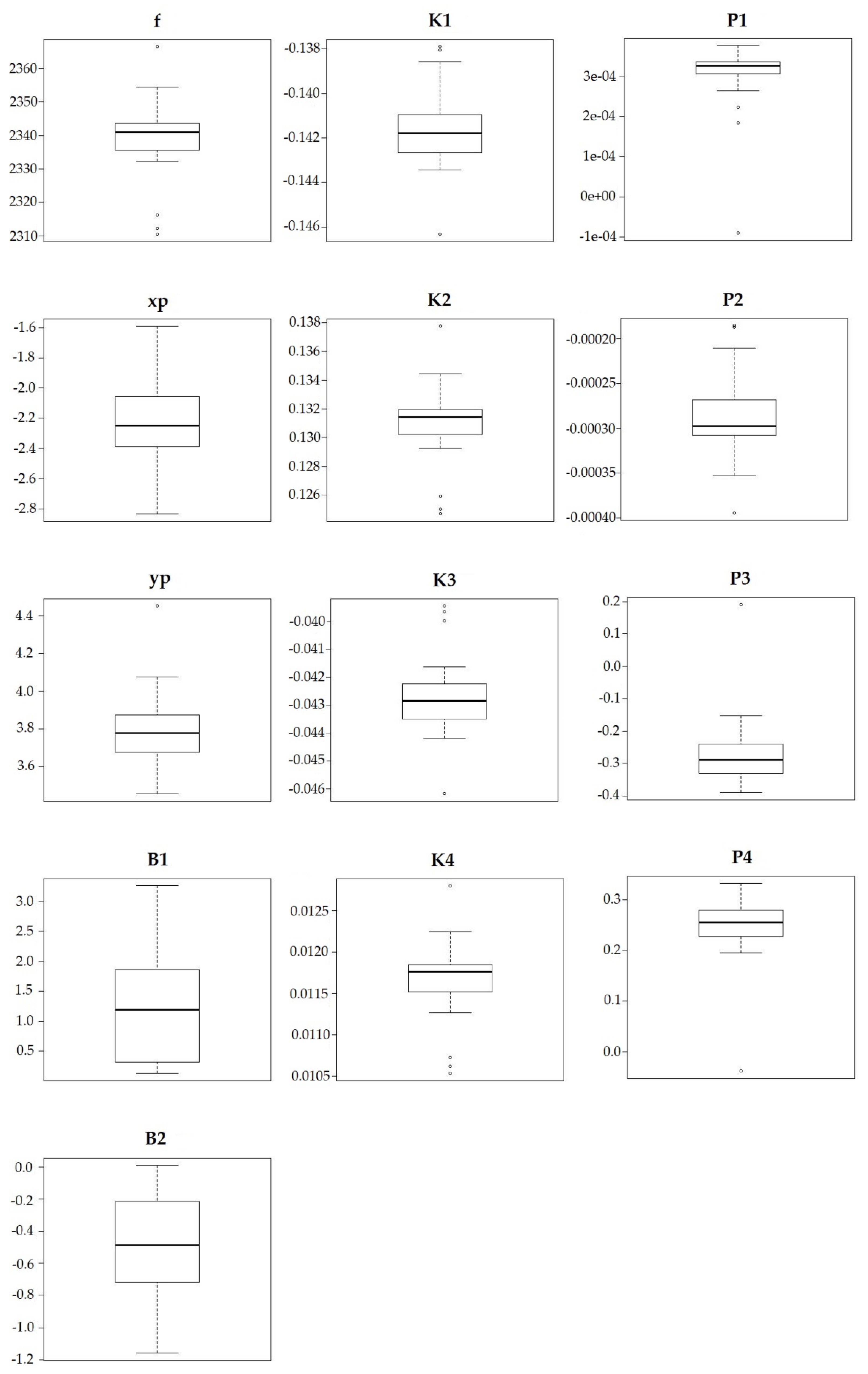
3.2. Testing Relationship between Errors and I.O Parameters
3.3. Calibrating Predictive Models
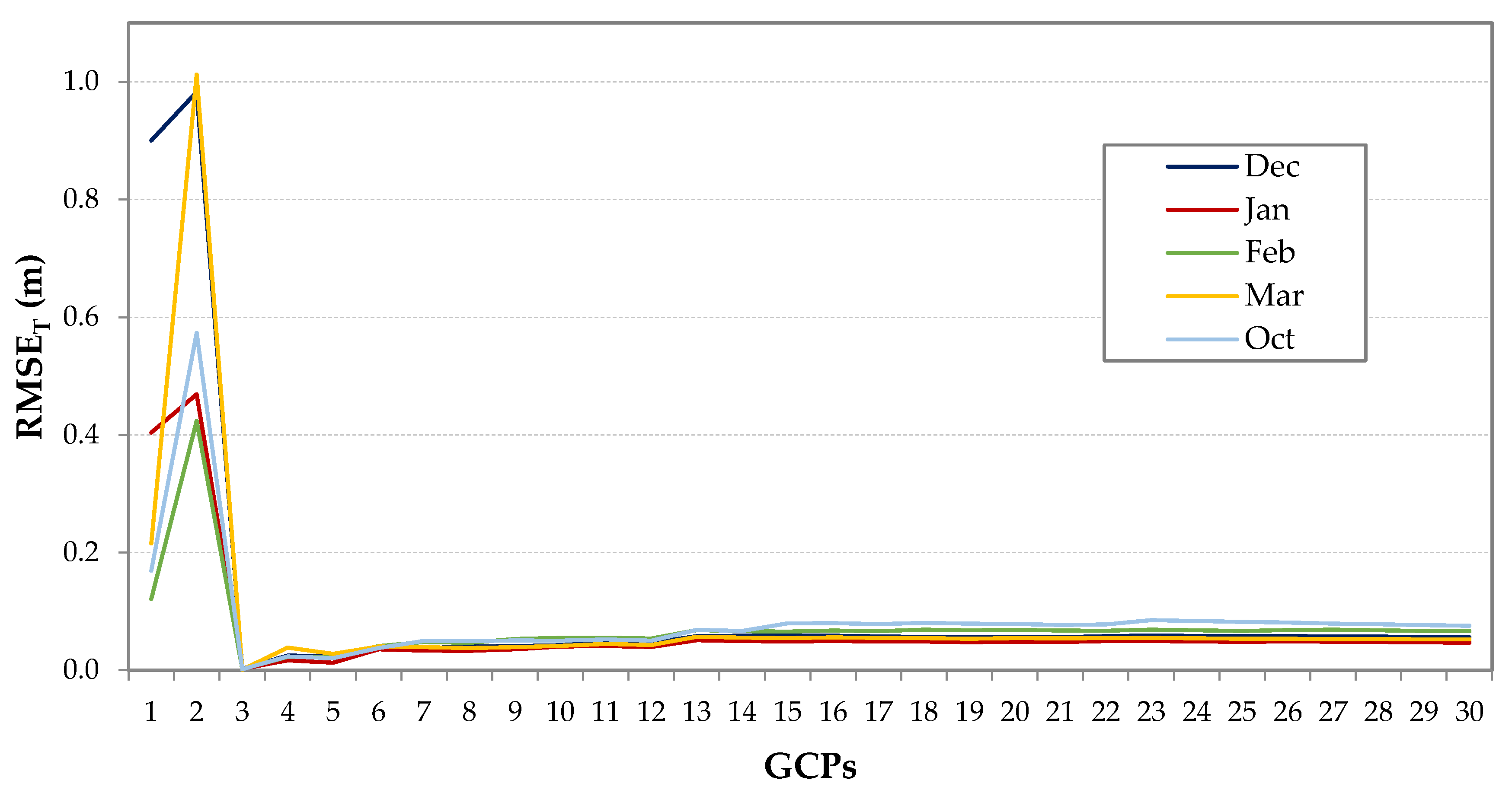
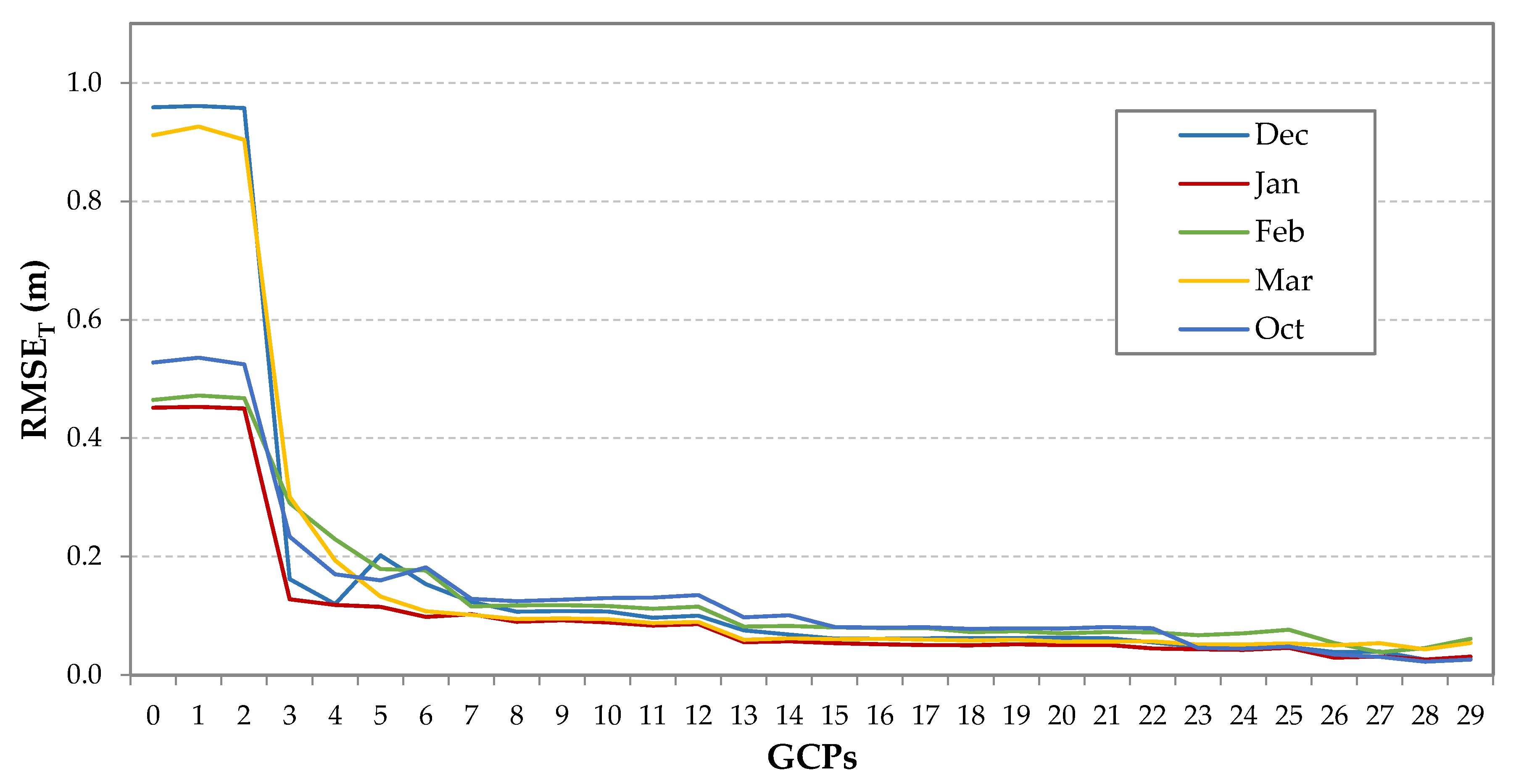
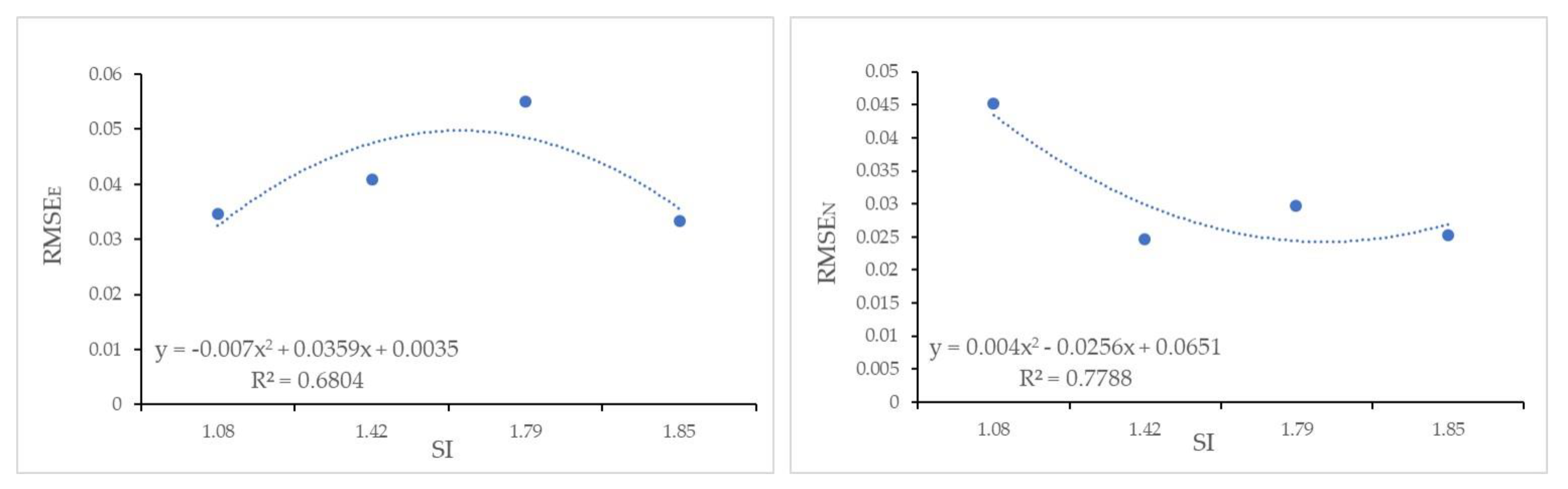
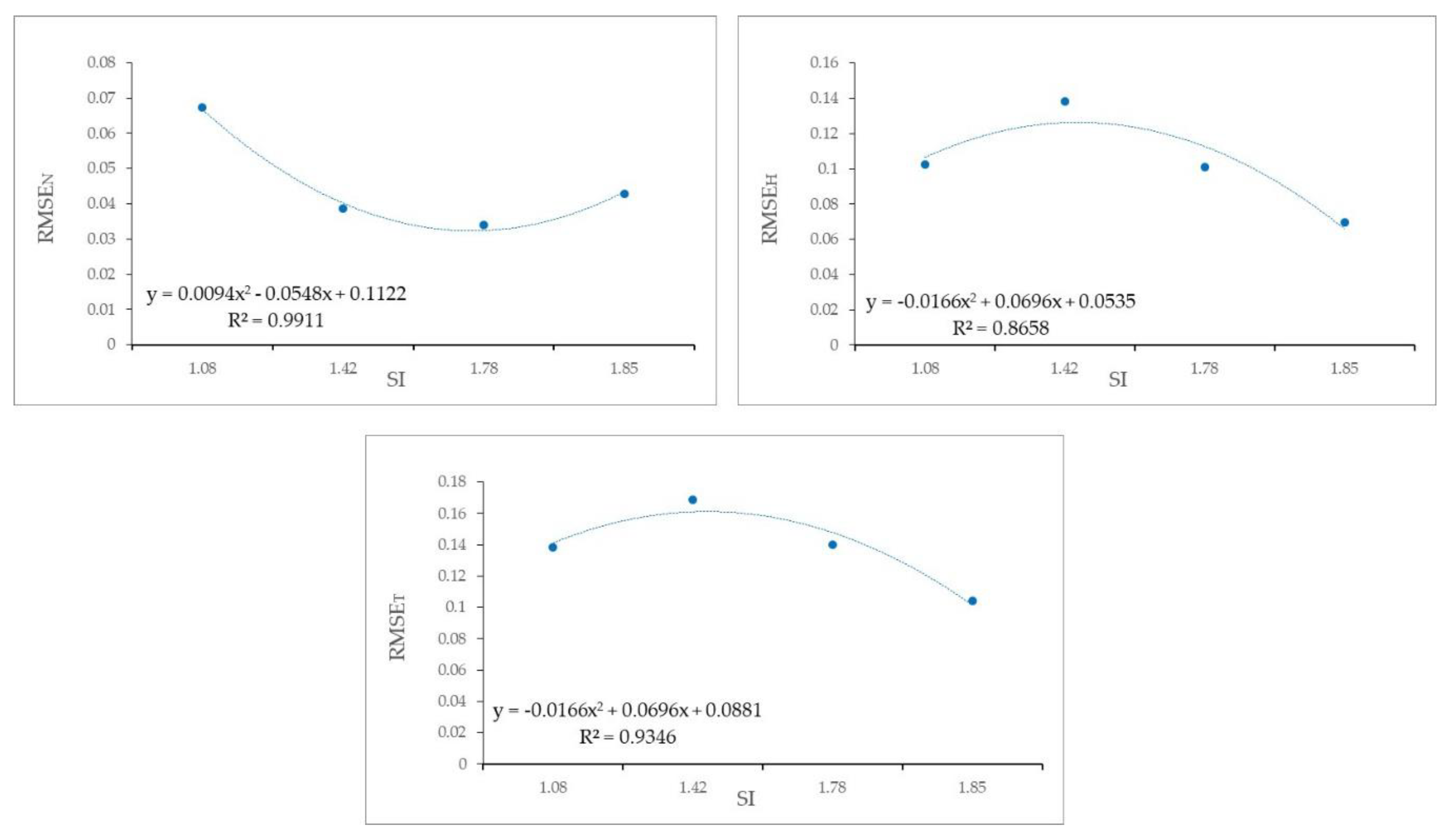
3.4. Validating Predictive Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gold, D.P.; Parizek, R.R.; Alexander, S.A. Analysis and application of ERTS-1 data for regional geological mapping. In Proceedings of the First Symposium of Significant Results obtained from the Earth Resources Technology Satellite-1, NASA, New Carrollton, MD, USA, 5–9 March 1973; Volume 1, pp. 231–246. [Google Scholar]
- Hooke, J.M.; Horton, B.P.; Moore, J.; Taylor, M.P. Upper river Severn (Caersws) channel study. In Report to the Countryside Council for Wales; University of Portsmouth: Portsmouth, UK, 1994. [Google Scholar]
- Evans, I.S. World-wide variations in the direction and concentration of cirque and glacier aspects. Geogr. Ann. Ser. A Phys. Geogr. 1977, 59, 151–175. [Google Scholar] [CrossRef]
- Drăguț, L.; Eisank, C. Object representations at multiple scales from digital elevation models. Geomorphology 2011, 129, 183–189. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Capolupo, A.; Pindozzi, S.; Okello, C.; Boccia, L. Indirect field technology for detecting areas object of illegal spills harmful to human health: Application of drones, photogrammetry and hydrological models. Geospat. Heal. 2014, 8, 699. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Medjkane, M.; Maquaire, O.; Costa, S.; Roulland, T.; Letortu, P.; Fauchard, C.; Antoine, R.; Davidson, R. High-resolution monitoring of complex coastal morphology changes: Cross-efficiency of SfM and TLS-based survey (Vaches-Noires cliffs, Normandy, France). Landslides 2018, 15, 1097–1108. [Google Scholar] [CrossRef]
- Rieke-Zapp, D.H.; Wegmann, H.; Santel, F.; Nearing, M.A. Digital photogrammetry for measuring soil surface roughness. In Proceedings of the American Society of Photogrammetry & Remote Sensing 2001 Conference–Gateway to the New Millennium’, St Louis, MO, USA, 23–27 April 2001; American Society of Photogrammetry & Remote Sensing: Bethesda, MD, USA, 2001. [Google Scholar]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomatics 2013, 6, 1–15. [Google Scholar] [CrossRef]
- Salamí, E.; Barrado, C.; Pastor, E. UAV Flight Experiments Applied to the Remote Sensing of Vegetated Areas. Remote Sens. 2014, 6, 11051–11081. [Google Scholar] [CrossRef] [Green Version]
- Capolupo, A.; Pindozzi, S.; Okello, C.; Fiorentino, N.; Boccia, L. Photogrammetry for environmental monitoring: The use of drones and hydrological models for detection of soil contaminated by copper. Sci. Total. Environ. 2015, 514, 298–306. [Google Scholar] [CrossRef]
- Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.M.; Madrigal, V.P.; Mallinis, G.; Ben Dor, E.; Helman, D.; Estes, L.; Ciraolo, G.; et al. On the Use of Unmanned Aerial Systems for Environmental Monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef] [Green Version]
- Capolupo, A.; Nasta, P.; Palladino, M.; Cervelli, E.; Boccia, L.; Romano, N. Assessing the ability of hybrid poplar for in-situ phytoextraction of cadmium by using UAV-photogrammetry and 3D flow simulator. Int. J. Remote. Sens. 2018, 39, 5175–5194. [Google Scholar] [CrossRef]
- Palladino, M.; Nasta, P.; Capolupo, A.; Romano, N. Monitoring and modelling the role of phytoremediation to mitigate non-point source cadmium pollution and groundwater contamination at field scale. Ital. J. Agron. 2018, 13, 59–68. [Google Scholar]
- Capolupo, A.; Kooistra, L.; Boccia, L. A novel approach for detecting agricultural terraced landscapes from historical and contemporaneous photogrammetric aerial photos. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 800–810. [Google Scholar] [CrossRef]
- Cramer, M.; Przybilla, H.-J.; Zurhorst, A. UAV cameras: Overview and geometric calibration benchmark. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 85–92. [Google Scholar] [CrossRef] [Green Version]
- Kraft, T.; Geßner, M.; Meißner, H.; Przybilla, H.J.; Gerke, M. Introduction of a photogrammetric camera system for rpas with highly accurate gnss/imu information for standardized workflows. In Proceedings of the EuroCOW 2016, the European Calibration and Orientation Workshop (Volume XL-3/W4), Lausanne, Switzerland, 10–12 February 2016; pp. 71–75. [Google Scholar]
- Caroti, G.; Piemonte, A.; Nespoli, R. UAV-Borne photogrammetry: A low cost 3D surveying methodology for cartographic update. In Proceedings of the MATEC Web of Conferences, Seoul, South Korea, 22–25 August 2017; EDP Sciences: Les Ulis, France, 2017; Volume 120, p. 9005. [Google Scholar]
- Saponaro, M.; Capolupo, A.; Tarantino, E.; Fratino, U. Comparative Analysis of Different UAV-Based Photogrammetric Processes to Improve Product Accuracies; Lecture Notes in Computer Science; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2019; pp. 225–238. [Google Scholar]
- Mesas-Carrascosa, F.-J.; Torres-Sánchez, J.; Rumbao, I.C.; García-Ferrer, A.; Peña-Barragan, J.M.; Borra-Serrano, I.; López-Granados, F. Assessing Optimal Flight Parameters for Generating Accurate Multispectral Orthomosaicks by UAV to Support Site-Specific Crop Management. Remote Sens. 2015, 7, 12793–12814. [Google Scholar] [CrossRef] [Green Version]
- Saponaro, M.; Tarantino, E.; Reina, A.; Furfaro, G.; Fratino, U. Assessing the Impact of the Number of GCPS on the Accuracy of Photogrammetric Mapping from UAV Imagery. Baltic Surv. 2019, 10, 43–51. [Google Scholar]
- Padró, J.-C.; Muñoz, F.-J.; Planas, J.; Pons, X. Comparison of four UAV georeferencing methods for environmental monitoring purposes focusing on the combined use with airborne and satellite remote sensing platforms. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 130–140. [Google Scholar] [CrossRef]
- Rangel, J.M.G.; Gonçalves, G.; Pérez, J.A. The impact of number and spatial distribution of GCPs on the positional accuracy of geospatial products derived from low-cost UASs. Int. J. Remote Sens. 2018, 39, 7154–7171. [Google Scholar] [CrossRef]
- Lumban-Gaol, Y.A.; Murtiyoso, A.; Nugroho, B.H. Investigations on The Bundle Adjustment Results From Sfm-Based Software For Mapping Purposes. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 623–628. [Google Scholar] [CrossRef] [Green Version]
- Benassi, F.; Dall’Asta, E.; Diotri, F.; Forlani, G.; Di Cella, U.M.; Roncella, R.; Santise, M. Testing Accuracy and Repeatability of UAV Blocks Oriented with GNSS-Supported Aerial Triangulation. Remote Sens. 2017, 9, 172. [Google Scholar] [CrossRef] [Green Version]
- Salvi, J.; Armangué, X.; Batlle, J. A comparative review of camera calibrating methods with accuracy evaluation. Pattern Recognit. 2002, 35, 1617–1635. [Google Scholar] [CrossRef] [Green Version]
- Remondino, F.; Fraser, C. Digital camera calibration methods: Considerations and comparisons. Int. Arch. Photogramm. Remote Sens. 2006, 36, 266–272. [Google Scholar]
- Warner, W.S.; Carson, W.W. Improving Interior Orientation For Asmall Standard Camera. Photogramm. Rec. 2006, 13, 909–916. [Google Scholar] [CrossRef]
- Perez, M.; Agüera, F.; Carvajal, F. Digital camera calibration using images taken from an unmanned aerial vehicle. ISPRS Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2012, 1, 167–171. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Pix4D—Drone Mapping Software. Swiss Federal Institute of Technology Lausanne, Route Cantonale, Switzerland. Available online: https://pix4d.com/ (accessed on 14 November 2014).
- Pierrot, D.M.; Clery, I. Apero, An open source bundle adjustment software for automatic calibration and orientation of set of images. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XXXVIII–5/W16, Proceedings of ISPRS Workshop, Trento, Italy, 2–4 March 2011. [Google Scholar]
- González-Aguilera, D.; López-Fernández, L.; Rodríguez-Gonzálvez, P.; Hernández-López, D.; Guerrero, D.; Remondino, F.; Menna, F.; Nocerino, E.; Toschi, I.; Ballabeni, A.; et al. GRAPHOS—Open-source software for photogrammetric applications. Photogramm. Rec. 2018, 33, 11–29. [Google Scholar] [CrossRef] [Green Version]
- VisualSFM. Available online: http://www.cs.washington.edu/homes/ccwu/vsfm/ (accessed on 18 May 2013).
- Rupnik, E.; Daakir, M.; Deseilligny, M.P. MicMac—A free, open-source solution for photogrammetry. Open Geospat. Data Softw. Stand. 2017, 2, 1–9. [Google Scholar] [CrossRef]
- Ballarin, M. Fotogrammetria Aerea Low Cost in Archeologia. Ph.D. Thesis, Politecnico di Milano, Milano, Italy, December 2014. [Google Scholar]
- Oniga, V.-E.; Pfeifer, N.; Loghin, A.-M. 3D Calibration Test-Field for Digital Cameras Mounted on Unmanned Aerial Systems (UAS). Remote. Sens. 2018, 10, 2017. [Google Scholar] [CrossRef] [Green Version]
- De Lucia, A. La Comunità neolitica di Cala Colombo presso Torre a mare, Bari contributo del Gruppo interdisciplinare di storia delle civiltà antiche dell’Università degli studi di Bari; Società di storia patria per la Puglia: Bari BA, Italy, 1977. [Google Scholar]
- Geniola, A. La Comunità Neolitica di cala Colombo Presso Torre a Mare (Bari). Archeologia e Cultura. Rivista di Antropologia; Istituto Italiano di Antropologia: Roma, Italy, 1974; Volume 59, pp. 189–275. [Google Scholar]
- ENAC. Regolamento Mezzi Aerei a Pilotaggio Remoto, 3rd ed.; ENAC, Ed.; Italian Civil Aviation Authority (ENAC): Rome, Italy, 2019.
- Stöcker, C.; Bennett, R.; Nex, F.; Gerke, M.; Zevenbergen, J. Review of the Current State of UAV Regulations. Remote. Sens. 2017, 9, 459. [Google Scholar] [CrossRef] [Green Version]
- DJI. Dà-Jiāng Innovations. 2020. Available online: https=//www.dji.com (accessed on 11 December 2019).
- Dandois, J.P.; Olano, M.; Ellis, E.C. Optimal Altitude, Overlap, and Weather Conditions for Computer Vision UAV Estimates of Forest Structure. Remote. Sens. 2015, 7, 13895–13920. [Google Scholar] [CrossRef] [Green Version]
- Gagliolo, S.; Fagandini, R.; Passoni, D.; Federici, B.; Ferrando, I.; Pagliari, D.; Pinto, L.; Sguerso, D. Parameter optimization for creating reliable photogrammetric models in emergency scenarios. Appl. Geomat. 2018, 10, 501–514. [Google Scholar] [CrossRef]
- Beretta, F.; Shibata, H.; Cordova, R.; Peroni, R.L.; Azambuja, J.; Costa, J.F.C.L. Topographic modelling using UAVs compared with traditional survey methods in mining. REM Int. Eng. J. 2018, 71, 463–470. [Google Scholar] [CrossRef]
- Barazzetti, L.; Scaioni, M.; Remondino, F. Orientation and 3D modelling from markerless terrestrial images: Combining accuracy with automation. Photogramm. Rec. 2010, 25, 356–381. [Google Scholar] [CrossRef]
- Yao, H.; Qin, R.; Chen, X. Unmanned Aerial Vehicle for Remote Sensing Applications—A Review. Remote Sens. 2019, 11, 1443. [Google Scholar] [CrossRef] [Green Version]
- Saponaro, M.; Tarantino, E.; Fratino, U. Generation of 3D surface models from UAV imagery varying flight patterns and processing parameters. CENTRAL Eur. Symp. Thermophys. 2019 (CEST) 2019, 2116, 280009. [Google Scholar] [CrossRef]
- Mayer, C.; Pereira, L.M.G.; Kersten, T.P. A Comprehensive Workflow to Process UAV Images for the Efficient Production of Accurate Geo-information. In Proceedings of the IX National Conference on Cartography and Geodesy, Amadora, Portugal, 25–26 October 2018. [Google Scholar]
- Agisoft, L.L.C. Agisoft Photoscan User Manual, Professional ed.; Agisoft LLC: St Petersburg, Russia, 2014. [Google Scholar]
- James, M.R.; Robson, S.; D’Oleire-Oltmanns, S.; Niethammer, U. Optimising UAV topographic surveys processed with structure-from-motion: Ground control quality, quantity and bundle adjustment. Geomorphology 2017, 280, 51–66. [Google Scholar] [CrossRef] [Green Version]
- Daakir, M.; Pierrot-Deseilligny, M.; Bosser, P.; Pichard, F.; Thom, C.; Rabot, Y. Study of lever-arm effect using embedded photogrammetry and on-board gps receiver on uav for metrological mapping purpose and proposal of a free ground measurements calibration procedure. In ISPRS Annals of Photogrammetry, Remote Sensing & Spatial Information Sciences; International Society for Photogrammetry and Remote Sensing: Lausanne, Switzerland, 2016. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Lowe, G. SIFT-The Scale Invariant Feature Transform. Int. J. 2004, 2, 91–110. [Google Scholar]
- Gruen, A.; Beyer, H.A. System calibration through self-calibration. In Calibration and Orientation of Cameras in Computer Vision; Springer: Berlin/Heidelberg, Germany, 2001; pp. 163–193. [Google Scholar]
- Triggs, B.; Mclauchlan, P.F.; Hartley, R.; FitzGibbon, A.W. Bundle Adjustment—A Modern Synthesis. In Lecture Notes in Computer Science; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2000; Volume 1883, pp. 298–372. [Google Scholar]
- Saponaro, M.; Tarantino, E.; Fratino, U. Geometric Accuracy Evaluation of Geospatial Data Using Low-Cost Sensors on Small UAVs. In Proceedings of the Lecture Notes in Computer Science; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2018; pp. 364–374. [Google Scholar]
- Villanueva, J.K.S.; Blanco, A.C. Optimization of ground control point (gcp) configuration for unmanned aerial vehicle (uav) survey using structure from motion (SFM). ISPRS Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2019, 167–174. [Google Scholar] [CrossRef] [Green Version]
- Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. Assessment of photogrammetric mapping accuracy based on variation ground control points number using unmanned aerial vehicle. Measurement 2017, 98, 221–227. [Google Scholar] [CrossRef]
- Smith, D.; Heidemann, H.K. New standard for new era: Overview of the 2015 ASPRS positional accuracy standards for digital geospatial data. Photogramm. Eng. Remote Sens. 2015, 81, 173–176. [Google Scholar]
- Fraser, C.S. Automatic Camera Calibration in Close Range Photogrammetry. Photogramm. Eng. Remote Sens. 2013, 79, 381–388. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, D.; Burningham, H. Comparison of pre- and self-calibrated camera calibration models for UAS-derived nadir imagery for a SfM application. Prog. Phys. Geogr. Earth Environ. 2018, 43, 215–235. [Google Scholar] [CrossRef] [Green Version]
- Duane, C.B. Close-range camera calibration. Photogramm. Eng. 1971, 37, 855–866. [Google Scholar]
- Fryer, J.G.; Brown, D.C. Lens distortion for close-range photogrammetry. Photogrammetric Engineering and Remote Sensing; Geodetic Services, Inc.: Melbourne, FL, USA, 1986; Volume 52, pp. 51–58. [Google Scholar]
- Chandler, J.H.; Fryer, J.G.; Jack, A. Metric capabilities of low-cost digital cameras for close range surface measurement. Photogramm. Rec. 2005, 20, 12–26. [Google Scholar] [CrossRef]
- Fryer, J.G. Camera calibration. In Close Range Photogrammetry and Machine Vision; Atkinson, K.B., Ed.; Wittles Publishing: Caithness, Scotland, 1996; pp. 156–179. [Google Scholar]
- Chambers, J. Software for Data Analysis; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. In Wiley Interdisciplinary Reviews: Computational Statistics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; Volume 2, pp. 433–459. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Abdi, H. Singular value decomposition (SVD) and generalized singular value decomposition. In Encyclopedia of Measurement and Statistics; Salkind, N., Ed.; Sage: Thousand Oaks, CA, USA, 2007; pp. 907–912. [Google Scholar]
- Kaiser, H.F. The Application of Electronic Computers to Factor Analysis. Educ. Psychol. Meas. 1960, 20, 141–151. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K.; Kumar, L.; Ferwerda, J. Estimating tropical pasture quality at canopy level using band depth analysis with continuum removal in the visible domain. Int. J. Remote. Sens. 2005, 26, 1093–1108. [Google Scholar] [CrossRef]




| Acquisition Date | #N Images | GSD (M/Pix) |
|---|---|---|
| December 12, 2018 | 77 | 0.041 |
| January 8, 2019 | 77 | 0.047 |
| February 19, 2019 | 77 | 0.048 |
| March 16, 2019 | 77 | 0.041 |
| October 16, 2019 | 77 | 0.042 |
| Agisoft PhotoScan Parameter | Value |
|---|---|
| Coordinate system | RDN2008/UTM Zone 33N (NE) (EPSG: 6708) |
| Initial principal point position (Xp, Yp) | (0, 0) |
| Camera positioning accuracy | 3 m |
| Camera accuracy, attitude | 10 deg |
| 3D marker accuracy (object space) | 0.02 m |
| Marker accuracy (image space) | 0.5 pixel |
| GPS/INS offset vector value |
| #GCP | Label | #GCP | Label |
|---|---|---|---|
| 29 GCPs | 3R0024 | 14 GCPS | 3R0019 |
| 28 GCPs | 3R0026 | 13 GCPS | 3R0031 |
| 27 GCPs | 3R0030 | 12 GCPS | 3R0017 |
| 26 GCPs | 3R0018 | 11 GCPS | 3R0027 |
| 25 GCPs | 3R0004 | 10 GCPS | 3R0025 |
| 24 GCPs | 3R0013 | 9 GCPS | 3R0022 |
| 23 GCPs | 3R0010 | 8 GCPS | 3R0014 |
| 22 GCPs | 3R0005 | 7 GCPS | 3R0007 |
| 21 GCPs | 3R0020 | 6 GCPS | 3R0023 |
| 20 GCPs | 3R0021 | 5 GCPS | 3R0015 |
| 19 GCPs | 3R0029 | 4 GCPS | 3R0003 |
| 18 GCPs | 3R0011 | 3 GCPS | 3R0012 |
| 17 GCPs | 3R0001 | 2 GCPS | 3R0016 |
| 16 GCPs | 3R0008 | 1 GCP | 3R0028 |
| 15 GCPs | 3R0002 | 0 GCP | 3R0009 |
| Survey | Stat. | f (pix) | xp (pix) | yp (pix) | B1 | B2 | K1 | K2 | K3 | K4 | P1 | P2 | P3 | P4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dec. | Max | 2366.210 | −0.190 | 6.850 | 2.720 | 0.160 | −0.1300 | 0.1400 | −0.0300 | 0.0140 | 0.0004 | −0.0002 | −0.0900 | 0.3100 |
| Min | 2221.830 | −3.200 | 3.480 | −0.730 | −0.960 | −0.1400 | 0.1100 | −0.0500 | 0.0084 | −0.0004 | −0.0008 | −0.4900 | 0.1900 | |
| Mean | 2285.310 | −2.310 | 4.880 | 0.800 | −0.440 | −0.1400 | 0.1200 | −0.0400 | 0.0106 | 0.0003 | −0.0005 | −0.3700 | 0.2700 | |
| SD | 31.570 | 0.820 | 0.770 | 0.990 | 0.310 | 0.0000 | 0.0100 | 0.0030 | 0.0012 | 0.0002 | 0.0001 | 0.0800 | 0.0400 | |
| Jan. | Max | 2358.480 | −1.470 | 5.820 | 2.690 | 1.210 | −0.1300 | 0.1400 | −0.0372 | 0.0143 | 0.0007 | −0.0003 | −0.0018 | 0.3300 |
| Min | 2262.760 | −4.660 | 4.350 | −0.030 | −1.270 | −0.1400 | 0.1200 | −0.0486 | 0.0100 | −0.0001 | −0.0006 | −0.5856 | −0.0300 | |
| Mean | 2319.960 | −3.680 | 5.180 | 0.930 | −0.540 | −0.1400 | 0.1300 | −0.0433 | 0.0122 | 0.0005 | −0.0005 | −0.4703 | 0.2700 | |
| SD | 18.790 | 0.930 | 0.340 | 0.850 | 0.530 | 0.0000 | 0.0000 | 0.0023 | 0.0009 | 0.0002 | 0.0001 | 0.1548 | 0.0900 | |
| Feb. | Max | 2366.490 | −1.590 | 4.450 | 3.250 | 0.010 | −0.1400 | 0.1400 | −0.0400 | 0.0100 | 0.0004 | −0.0002 | 0.1900 | 0.3300 |
| Min | 2310.470 | −2.830 | 3.460 | 0.130 | −1.160 | −0.1500 | 0.1200 | −0.0500 | 0.0100 | −0.0001 | −0.0004 | −0.3900 | −0.0400 | |
| Mean | 2339.330 | −2.190 | 3.780 | 1.150 | −0.480 | −0.1400 | 0.1300 | −0.0400 | 0.0100 | 0.0003 | −0.0003 | −0.2500 | 0.2300 | |
| SD | 11.711 | 0.300 | 0.200 | 0.870 | 0.280 | 0.0000 | 0.0030 | 0.0010 | 0.0005 | 0.0001 | 0.0001 | 0.1550 | 0.0940 | |
| Mar. | Max | 2320.640 | 2.730 | 7.040 | 2.040 | 1.300 | −0.1300 | 0.1300 | −0.0400 | 0.0100 | 0.0002 | −0.0001 | 0.3600 | 0.5100 |
| Min | 2267.750 | −1.550 | 1.960 | −2.690 | −1.420 | −0.1400 | 0.1200 | −0.0400 | 0.0100 | −0.0007 | −0.0006 | −0.4800 | 0.0100 | |
| Mean | 2305.520 | −0.070 | 3.290 | 0.450 | −0.590 | −0.1400 | 0.1300 | −0.0400 | 0.0100 | 0.0000 | −0.0002 | 0.0300 | 0.3300 | |
| SD | 16.800 | 1.070 | 1.660 | 1.380 | 0.790 | 0.0000 | 0.0000 | 0.0016 | 0.0006 | 0.0003 | 0.0001 | 0.2300 | 0.1700 | |
| Oct. | Max | 2363.460 | −0.490 | 4.760 | 1.680 | 0.180 | −0.1400 | 0.1400 | −0.0400 | 0.0150 | 0.0003 | −0.0003 | −0.1860 | 0.2910 |
| Min | 2275.080 | −2.450 | 2.940 | −1.220 | −2.040 | −0.1600 | 0.1200 | −0.0500 | 0.0110 | −0.0003 | −0.0007 | −0.4720 | 0.1190 | |
| Mean | 2338.246 | −1.650 | 3.790 | 0.220 | −0.990 | −0.1400 | 0.1340 | −0.0470 | 0.0140 | 0.0002 | −0.0004 | −0.3010 | 0.2260 | |
| SD | 26.293 | 0.530 | 0.520 | 0.750 | 0.570 | 0.0000 | 0.0060 | 0.0030 | 0.0010 | 0.0002 | 0.0001 | 0.0830 | 0.0630 |
| f (pix) | xp (pix) | yp (pix) | B1 | B2 | K1 | K2 | K3 | K4 | P1 | P2 | P3 | P4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f (pix) | 1.00 | −0.15 | −0.56 | 0.10 | 0.03 | −1.00 | 1.00 | −1.00 | 0.99 | 0.27 | 0.51 | 0.37 | 0.44 |
| xp (pix) | −0.15 | 1.00 | 0.51 | −0.26 | −0.04 | 0.12 | −0.12 | 0.08 | −0.07 | −0.96 | −0.58 | 0.43 | −0.73 |
| yp (pix) | −0.56 | 0.51 | 1.00 | −0.49 | 0.29 | 0.54 | −0.55 | 0.53 | −0.53 | −0.69 | −0.91 | −0.48 | −0.43 |
| B1 | 0.10 | −0.26 | −0.49 | 1.00 | −0.59 | −0.06 | 0.12 | −0.08 | 0.10 | 0.35 | 0.20 | 0.44 | −0.17 |
| B2 | 0.03 | −0.04 | 0.29 | −0.59 | 1.00 | −0.04 | 0.02 | −0.04 | 0.03 | −0.12 | −0.02 | −0.37 | 0.12 |
| K1 | −1.00 | 0.12 | 0.54 | −0.06 | −0.04 | 1.00 | −1.00 | 1.00 | −1.00 | −0.23 | −0.51 | −0.38 | −0.42 |
| K2 | 1.00 | −0.12 | −0.55 | 0.12 | 0.02 | −1.00 | 1.00 | −1.00 | 1.00 | 0.24 | 0.50 | 0.40 | 0.41 |
| K3 | −1.00 | 0.08 | 0.53 | −0.08 | −0.04 | 1.00 | −1.00 | 1.00 | −1.00 | −0.20 | −0.49 | −0.42 | −0.38 |
| K4 | 0.99 | −0.07 | −0.53 | 0.10 | 0.03 | −1.00 | 1.00 | −1.00 | 1.00 | 0.19 | 0.48 | 0.43 | 0.37 |
| P1 | 0.27 | −0.96 | −0.69 | 0.35 | −0.12 | −0.23 | 0.24 | −0.20 | 0.19 | 1.00 | 0.68 | −0.26 | 0.78 |
| P2 | 0.51 | −0.58 | −0.91 | 0.20 | −0.02 | −0.51 | 0.50 | −0.49 | 0.48 | 0.68 | 1.00 | 0.31 | 0.49 |
| P3 | 0.37 | 0.43 | −0.48 | 0.44 | −0.37 | −0.38 | 0.40 | −0.42 | 0.43 | −0.26 | 0.31 | 1.00 | −0.46 |
| P4 | 0.44 | −0.73 | −0.43 | −0.17 | 0.12 | −0.42 | 0.41 | −0.38 | 0.37 | 0.78 | 0.49 | −0.46 | 1.00 |
| f (pix) | xp (pix) | yp (pix) | B1 | B2 | K1 | K2 | K3 | K4 | P1 | P2 | P3 | P4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f (pix) | 1 | 0.51 | −0.30 | −0.27 | 0.59 | −1.00 | 1.00 | −0.99 | 0.98 | −0.52 | −0.17 | 0.55 | −0.52 |
| xp (pix) | 0.51 | 1 | −0.46 | −0.02 | 0.72 | −0.52 | 0.57 | −0.63 | 0.65 | −0.98 | −0.36 | 0.95 | −0.92 |
| yp (pix) | −0.30 | −0.46 | 1 | 0.43 | −0.25 | 0.32 | −0.30 | 0.32 | −0.32 | 0.35 | −0.37 | −0.55 | 0.44 |
| B1 | −0.27 | −0.02 | 0.43 | 1 | −0.39 | 0.27 | −0.25 | 0.29 | −0.29 | 0.08 | 0.04 | −0.24 | 0.18 |
| B2 | 0.59 | 0.72 | −0.25 | −0.39 | 1 | −0.60 | 0.64 | −0.70 | 0.72 | −0.81 | −0.21 | 0.83 | −0.87 |
| K1 | −1.00 | −0.52 | 0.32 | 0.27 | −0.60 | 1 | −1.00 | 0.99 | −0.98 | 0.54 | 0.15 | −0.57 | 0.54 |
| K2 | 1.00 | 0.57 | −0.30 | −0.25 | 0.64 | −1.00 | 1 | −0.99 | 0.99 | −0.58 | −0.19 | 0.60 | −0.58 |
| K3 | −0.99 | −0.63 | 0.32 | 0.29 | −0.70 | 0.99 | −0.99 | 1 | −1.00 | 0.65 | 0.23 | −0.67 | 0.65 |
| K4 | 0.98 | 0.65 | −0.32 | −0.29 | 0.72 | −0.98 | 0.99 | −1.00 | 1 | −0.67 | −0.25 | 0.69 | −0.67 |
| P1 | −0.52 | −0.98 | 0.35 | 0.08 | −0.81 | 0.54 | −0.58 | 0.65 | −0.67 | 1 | 0.43 | −0.95 | 0.95 |
| P2 | −0.17 | −0.36 | −0.37 | 0.04 | −0.21 | 0.15 | −0.19 | 0.23 | −0.25 | 0.43 | 1 | −0.24 | 0.22 |
| P3 | 0.55 | 0.95 | −0.55 | −0.24 | 0.83 | −0.57 | 0.60 | −0.67 | 0.69 | −0.95 | −0.24 | 1 | −0.98 |
| P4 | −0.52 | −0.92 | 0.44 | 0.18 | −0.87 | 0.54 | −0.58 | 0.65 | −0.67 | 0.95 | 0.22 | −0.98 | 1 |
| f (pix) | xp (pix) | yp (pix) | B1 | B2 | K1 | K2 | K3 | K4 | P1 | P2 | P3 | P4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f (pix) | 1 | 0.008 | 0.18 | 0.16 | −0.16 | −0.88 | 0.99 | −0.93 | 0.97 | 0.14 | −0.15 | −0.12 | 0.19 |
| xp (pix) | 0.01 | 1 | −0.51 | 0.18 | −0.34 | −0.35 | 0.12 | −0.27 | 0.20 | −0.77 | 0.26 | 0.74 | −0.56 |
| yp (pix) | 0.18 | −0.51 | 1 | 0.48 | 0.08 | −0.09 | 0.18 | −0.14 | 0.18 | 0.18 | −0.40 | −0.33 | 0.19 |
| B1 | 0.16 | 0.18 | 0.48 | 1 | −0.32 | −0.14 | 0.20 | −0.16 | 0.19 | −0.04 | 0.16 | −0.17 | 0.22 |
| B2 | −0.16 | −0.34 | 0.08 | −0.32 | 1 | 0.15 | −0.18 | 0.18 | −0.20 | 0.05 | −0.01 | −0.01 | −0.03 |
| K1 | −0.88 | −0.35 | −0.09 | −0.14 | 0.15 | 1 | −0.93 | 0.99 | −0.95 | 0.27 | 0.09 | −0.27 | 0.17 |
| K2 | 0.99 | 0.12 | 0.18 | 0.20 | −0.18 | −0.93 | 1 | −0.97 | 0.99 | 0.01 | −0.14 | −0.01 | 0.08 |
| K3 | −0.93 | −0.27 | −0.14 | −0.16 | 0.18 | 0.99 | −0.97 | 1 | −0.99 | 0.19 | 0.14 | −0.18 | 0.10 |
| K4 | 0.97 | 0.20 | 0.18 | 0.19 | −0.20 | −0.95 | 0.99 | −0.99 | 1 | −0.09 | −0.16 | 0.08 | −0.01 |
| P1 | 0.14 | −0.77 | 0.18 | −0.04 | 0.05 | 0.27 | 0.01 | 0.19 | −0.09 | 1 | 0.11 | −0.94 | 0.90 |
| P2 | −0.15 | 0.26 | −0.40 | 0.16 | −0.01 | 0.09 | −0.14 | 0.14 | −0.16 | 0.11 | 1 | −0.27 | 0.43 |
| P3 | −0.12 | 0.74 | −0.33 | −0.17 | −0.01 | −0.27 | −0.01 | −0.18 | 0.08 | −0.94 | −0.27 | 1 | −0.97 |
| P4 | 0.19 | −0.56 | 0.19 | 0.22 | −0.03 | 0.17 | 0.08 | 0.10 | −0.01 | 0.90 | 0.43 | −0.97 | 1 |
| f (pix) | xp (pix) | yp (pix) | B1 | B2 | K1 | K2 | K3 | K4 | P1 | P2 | P3 | P4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f (pix) | 1.00 | 0.04 | −0.70 | 0.13 | −0.40 | −0.95 | 1.00 | −0.94 | 0.96 | 0.53 | 0.77 | 0.66 | 0.78 |
| xp (pix) | 0.04 | 1.00 | 0.49 | −0.94 | 0.76 | −0.31 | 0.10 | −0.32 | 0.28 | −0.73 | −0.30 | −0.38 | 0.06 |
| yp (pix) | −0.70 | 0.49 | 1.00 | −0.66 | 0.85 | 0.46 | −0.64 | 0.43 | −0.47 | −0.94 | −0.93 | −0.93 | −0.81 |
| B1 | 0.13 | −0.94 | −0.66 | 1.00 | −0.90 | 0.16 | 0.06 | 0.18 | −0.13 | 0.85 | 0.50 | 0.58 | 0.12 |
| B2 | −0.40 | 0.76 | 0.85 | −0.90 | 1.00 | 0.14 | −0.34 | 0.10 | −0.14 | −0.91 | −0.70 | −0.78 | −0.45 |
| K1 | −0.95 | −0.31 | 0.46 | 0.16 | 0.14 | 1.00 | −0.97 | 1.00 | −0.99 | −0.25 | −0.60 | −0.45 | −0.69 |
| K2 | 1.00 | 0.10 | −0.64 | 0.06 | −0.34 | −0.97 | 1.00 | −0.97 | 0.98 | 0.46 | 0.73 | 0.61 | 0.75 |
| K3 | −0.94 | −0.32 | 0.43 | 0.18 | 0.10 | 1.00 | −0.97 | 1.00 | −1.00 | −0.22 | −0.57 | −0.42 | −0.65 |
| K4 | 0.96 | 0.28 | −0.47 | −0.13 | −0.14 | −0.99 | 0.98 | −1.00 | 1.00 | 0.27 | 0.60 | 0.46 | 0.67 |
| P1 | 0.53 | −0.73 | −0.94 | 0.85 | −0.91 | −0.25 | 0.46 | −0.22 | 0.27 | 1.00 | 0.85 | 0.84 | 0.61 |
| P2 | 0.77 | −0.30 | −0.93 | 0.50 | −0.70 | −0.60 | 0.73 | −0.57 | 0.60 | 0.85 | 1.00 | 0.85 | 0.81 |
| P3 | 0.66 | −0.38 | −0.93 | 0.58 | −0.78 | −0.45 | 0.61 | −0.42 | 0.46 | 0.84 | 0.85 | 1.00 | 0.78 |
| P4 | 0.78 | 0.06 | −0.81 | 0.12 | −0.45 | −0.69 | 0.75 | −0.65 | 0.67 | 0.61 | 0.81 | 0.78 | 1.00 |
| f (pix) | xp (pix) | yp (pix) | B1 | B2 | K1 | K2 | K3 | K4 | P1 | P2 | P3 | P4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f (pix) | 1.00 | −0.63 | −0.50 | −0.26 | −0.26 | −1.00 | 1.00 | −1.00 | 1.00 | 0.70 | 0.51 | −0.54 | 0.83 |
| xp (pix) | −0.63 | 1.00 | 0.28 | −0.28 | 0.30 | 0.58 | −0.63 | 0.60 | −0.62 | −0.91 | −0.66 | 0.73 | −0.65 |
| yp (pix) | −0.50 | 0.28 | 1.00 | 0.01 | 0.13 | 0.46 | −0.49 | 0.47 | −0.48 | −0.63 | −0.77 | −0.28 | −0.43 |
| B1 | −0.26 | −0.28 | 0.01 | 1.00 | −0.64 | 0.31 | −0.26 | 0.28 | −0.27 | 0.27 | 0.42 | 0.12 | −0.41 |
| B2 | −0.26 | 0.30 | 0.13 | −0.64 | 1.00 | 0.23 | −0.27 | 0.25 | −0.26 | −0.35 | −0.38 | 0.10 | 0.04 |
| K1 | −1.00 | 0.58 | 0.46 | 0.31 | 0.23 | 1.00 | −1.00 | 1.00 | −1.00 | −0.65 | −0.46 | 0.53 | −0.81 |
| K2 | 1.00 | −0.63 | −0.49 | −0.26 | −0.27 | −1.00 | 1.00 | −1.00 | 1.00 | 0.70 | 0.50 | −0.54 | 0.82 |
| K3 | −1.00 | 0.60 | 0.47 | 0.28 | 0.25 | 1.00 | −1.00 | 1.00 | −1.00 | −0.67 | −0.48 | 0.54 | −0.82 |
| K4 | 1.00 | −0.62 | −0.48 | −0.27 | −0.26 | −1.00 | 1.00 | −1.00 | 1.00 | 0.69 | 0.49 | −0.55 | 0.82 |
| P1 | 0.70 | −0.91 | −0.63 | 0.27 | −0.35 | −0.65 | 0.70 | −0.67 | 0.69 | 1.00 | 0.83 | −0.47 | 0.71 |
| P2 | 0.51 | −0.66 | −0.77 | 0.42 | −0.38 | −0.46 | 0.50 | −0.48 | 0.49 | 0.83 | 1.00 | −0.04 | 0.32 |
| P3 | −0.54 | 0.73 | −0.28 | 0.12 | 0.10 | 0.53 | −0.54 | 0.54 | −0.55 | −0.47 | −0.04 | 1.00 | −0.65 |
| P4 | 0.83 | −0.65 | −0.43 | −0.41 | 0.04 | −0.81 | 0.82 | −0.82 | 0.82 | 0.71 | 0.32 | −0.65 | 1.00 |
| Survey | Statistics | GCPs | CPs | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSEE (m) | RMSEN (m) | RMSEH (m) | RMSET (m) | RMSEI (pix) | RMSEE (m) | RMSEN (m) | RMSEH (m) | RMSET (m) | RMSEI (pix) | ||
| Dec. | Max | 0.20 | 0.09 | 0.96 | 0.98 | 0.27 | 0.21 | 0.09 | 0.93 | 0.96 | 0.27 |
| Min | 0.00 | 0.00 | 0.00 | 0.00 | 0.18 | 0.01 | 0.02 | 0.00 | 0.03 | 0.19 | |
| Mean | 0.04 | 0.02 | 0.09 | 0.11 | 0.25 | 0.07 | 0.04 | 0.14 | 0.17 | 0.25 | |
| SD | 0.04 | 0.02 | 0.23 | 0.23 | 0.03 | 0.05 | 0.02 | 0.27 | 0.27 | 0.03 | |
| Jan. | Max | 0.11 | 0.090 | 0.45 | 0.47 | 0.27 | 0.130 | 0.109 | 0.421 | 0.453 | 0.311 |
| Min | 0.002 | 0.0012 | 0.00018 | 0.0023 | 0.20 | 0.011 | 0.020 | 0.010 | 0.026 | 0.220 | |
| Mean | 0.035 | 0.025 | 0.044 | 0.068 | 0.24 | 0.052 | 0.043 | 0.070 | 0.104 | 0.237 | |
| SD | 0.019 | 0.016 | 0.10 | 0.10 | 0.016 | 0.035 | 0.026 | 0.119 | 0.121 | 0.019 | |
| Feb. | Max | 0.20 | 0.22 | 0.31 | 0.42 | 0.31 | 0.21 | 0.21 | 0.37 | 0.47 | 0.22 |
| Min | 0.0017 | 0.0011 | 0.0006 | 0.0022 | 0.21 | 0.02 | 0.03 | 0.02 | 0.04 | 0.17 | |
| Mean | 0.033 | 0.045 | 0.044 | 0.072 | 0.23 | 0.06 | 0.07 | 0.10 | 0.14 | 0.21 | |
| SD | 0.033 | 0.035 | 0.051 | 0.069 | 0.023 | 0.054 | 0.051 | 0.103 | 0.124 | 0.010 | |
| Mar. | Max | 0.461 | 0.259 | 0.863 | 1.012 | 0.273 | 0.451 | 0.221 | 0.778 | 0.926 | 0.360 |
| Min | 0.0005 | 0.001 | 0.000 | 0.001 | 0.110 | 0.028 | 0.027 | 0.018 | 0.044 | 0.243 | |
| Mean | 0.057 | 0.030 | 0.048 | 0.085 | 0.236 | 0.094 | 0.056 | 0.117 | 0.166 | 0.266 | |
| SD | 0.083 | 0.044 | 0.154 | 0.178 | 0.032 | 0.122 | 0.057 | 0.225 | 0.259 | 0.023 | |
| Oct. | Max | 0.306 | 0.129 | 0.467 | 0.573 | 0.234 | 0.304 | 0.114 | 0.426 | 0.536 | 0.278 |
| Min | 0.001 | 0.001 | 0.001 | 0.002 | 0.182 | 0.005 | 0.002 | 0.020 | 0.023 | 0.221 | |
| Mean | 0.055 | 0.030 | 0.055 | 0.085 | 0.222 | 0.089 | 0.034 | 0.101 | 0.140 | 0.235 | |
| SD | 0.051 | 0.024 | 0.080 | 0.097 | 0.015 | 0.081 | 0.030 | 0.113 | 0.141 | 0.011 | |
| Survey | Error Components | GCPs | CPs | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSEE | RMSEN | RMSEH | RMSET | RMSEI | RMSEE | RMSEN | RMSEH | RMSET | RMSEI | ||
| Dec. | RMSEE | 1 | 0.813 | 0.894 | 0.906 | −0.033 | 1 | 0.929 | 0.918 | 0.932 | 0.530 |
| RMSEN | 0.813 | 1 | 0.884 | 0.894 | 0.072 | 0.929 | 1 | 0.952 | 0.957 | 0.292 | |
| RMSEH | 0.894 | 0.884 | 1 | 0.999 | −0.283 | 0.918 | 0.952 | 1 | 0.999 | 0.227 | |
| RMSET | 0.906 | 0.894 | 0.999 | 1 | −0.258 | 0.932 | 0.957 | 0.999 | 1 | 0.254 | |
| RMSEI | −0.033 | 0.072 | −0.283 | −0.258 | 1 | 0.530 | 0.292 | 0.227 | 0.254 | 1 | |
| Jan. | RMSEE | 1 | 0.88 | 0.82 | 0.85 | −0.06 | 1 | 0.95 | 0.80 | 0.87 | −0.13 |
| RMSEN | 0.88 | 1 | 0.96 | 0.97 | −0.27 | 0.95 | 1 | 0.89 | 0.95 | −0.02 | |
| RMSEH | 0.82 | 0.96 | 1 | 1.00 | −0.33 | 0.80 | 0.89 | 1 | 0.99 | 0.03 | |
| RMSET | 0.85 | 0.97 | 1.00 | 1 | −0.33 | 0.87 | 0.95 | 0.99 | 1 | −0.002 | |
| RMSEI | −0.06 | −0.27 | −0.33 | −0.33 | 1 | −0.13 | −0.02 | 0.03 | −0.002 | 1 | |
| Feb. | RMSEE | 1 | 0.96 | 0.96 | 0.98 | −0.08 | 1 | 0.97 | 0.91 | 0.95 | 0.31 |
| RMSEN | 0.96 | 1 | 0.99 | 1.00 | 0.07 | 0.97 | 1 | 0.94 | 0.98 | 0.27 | |
| RMSEH | 0.96 | 0.99 | 1 | 1.00 | 0.12 | 0.91 | 0.94 | 1 | 0.99 | 0.27 | |
| RMSET | 0.98 | 1.00 | 1.00 | 1 | 0.07 | 0.95 | 0.98 | 0.99 | 1 | 0.28 | |
| RMSEI | −0.08 | 0.07 | 0.12 | 0.07 | 1 | 0.31 | 0.27 | 0.27 | 0.28 | 1 | |
| Mar. | RMSEE | 1.00 | 0.94 | 0.94 | 0.98 | −0.64 | 1.00 | 0.97 | 0.99 | 0.99 | −0.34 |
| RMSEN | 0.94 | 1.00 | 1.00 | 0.99 | −0.44 | 0.97 | 1.00 | 1.00 | 0.99 | −0.26 | |
| RMSEH | 0.94 | 1.00 | 1.00 | 0.99 | −0.45 | 0.99 | 1.00 | 1.00 | 1.00 | −0.27 | |
| RMSET | 0.98 | 0.99 | 0.99 | 1.00 | −0.53 | 0.99 | 0.99 | 1.00 | 1.00 | −0.29 | |
| RMSEI | −0.64 | −0.44 | −0.45 | −0.53 | 1.00 | −0.34 | −0.26 | −0.27 | −0.29 | 1.00 | |
| Oct. | RMSEE | 1.00 | 0.89 | 0.99 | 0.99 | −0.07 | 1.00 | 0.98 | 0.96 | 0.99 | −0.16 |
| RMSEN | 0.89 | 1.00 | 0.87 | 0.90 | −0.08 | 0.98 | 1.00 | 0.97 | 0.99 | −0.19 | |
| RMSEH | 0.99 | 0.87 | 1.00 | 1.00 | −0.20 | 0.96 | 0.97 | 1.00 | 0.99 | −0.14 | |
| RMSET | 0.99 | 0.90 | 1.00 | 1.00 | −0.16 | 0.99 | 0.99 | 0.99 | 1.00 | −0.15 | |
| RMSEI | −0.07 | −0.08 | −0.20 | −0.16 | 1.00 | −0.16 | −0.19 | −0.14 | −0.15 | 1.00 | |
| Variable | December | January | February | October |
|---|---|---|---|---|
| SI | 1.42 | 1.85 | 1.08 | 1.79 |
| GCPs | CPs | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSEE | RMSEN | RMSEH | RMSET | RMSEI | RMSEE | RMSEN | RMSEH | RMSET | RMSEI | |
| Pearson’s R | 0.5 | −0.8 | −0.10 | −0.12 | −0.11 | 0.28 | −0.80 | −0.50 | −0.49 | 0.67 |
| RMSEE (M)– GCPS | RMSEN (M)– GCPS | RMSEN (M)– CPS | RMSEH (M)– CPS | RMSET (PIX)– CPS | |
|---|---|---|---|---|---|
| a | −0.0070 | 0.0040 | 0.0094 | −0.0166 | −0.0166 |
| b | 0.0359 | −0.0256 | −0.0548 | 0.0696 | 0.0696 |
| c | 0.0035 | 0.0651 | 0.1122 | 0.0535 | 0.0881 |
| Errors | March Dataset Difference (m) |
|---|---|
| RMSEE (GCPs) | 0.0024 |
| RMSEN (GCPs) | 0.0047 |
| RMSEN (CPs) | 0.0110 |
| RMSEH (CPs) | 0.0039 |
| RMSEI (CPs) | 0.0014 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capolupo, A.; Saponaro, M.; Borgogno Mondino, E.; Tarantino, E. Combining Interior Orientation Variables to Predict the Accuracy of Rpas–Sfm 3D Models. Remote Sens. 2020, 12, 2674. https://doi.org/10.3390/rs12172674
Capolupo A, Saponaro M, Borgogno Mondino E, Tarantino E. Combining Interior Orientation Variables to Predict the Accuracy of Rpas–Sfm 3D Models. Remote Sensing. 2020; 12(17):2674. https://doi.org/10.3390/rs12172674
Chicago/Turabian StyleCapolupo, Alessandra, Mirko Saponaro, Enrico Borgogno Mondino, and Eufemia Tarantino. 2020. "Combining Interior Orientation Variables to Predict the Accuracy of Rpas–Sfm 3D Models" Remote Sensing 12, no. 17: 2674. https://doi.org/10.3390/rs12172674
APA StyleCapolupo, A., Saponaro, M., Borgogno Mondino, E., & Tarantino, E. (2020). Combining Interior Orientation Variables to Predict the Accuracy of Rpas–Sfm 3D Models. Remote Sensing, 12(17), 2674. https://doi.org/10.3390/rs12172674









