An Improved Frequency-Domain Image Formation Algorithm for Mini-UAV-Based Forward-Looking Spotlight BiSAR Systems
Abstract
:1. Introduction
2. Mini-UAV-Based BFSAR Echo Model
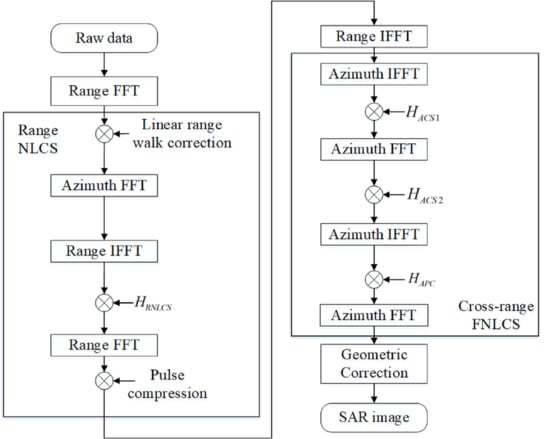
3. NLCS Algorithm
3.1. Range Processing Using NLCS
3.2. Cross-Range Processing Using FNLCS
4. Simulations
5. Processing Results of Real Data
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Cross-Range Operators
References
- Cumming, I.G.; Wong, F.H. The Digital Processing of Seasat Synthetic Aperture Radar Data; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Quegan, S. Spotlight synthetic aperture radar: Signal processing algorithms. J. Atmos. Sol.-Terr. Phys. 1997, 59, 597–598. [Google Scholar] [CrossRef]
- Qiu, X.; Hu, D.; Ding, C. Some Reflections on Bistatic SAR of Forward-Looking Configuration. IEEE Geosci. Remote Sens. Lett. 2008, 5, 735–739. [Google Scholar] [CrossRef]
- Neo, Y.L.; Wong, F.; Cumming, I.G. A Two-Dimensional Spectrum for Bistatic SAR Processing Using Series Reversion. IEEE Geosci. Remote Sens. Lett. 2007, 4, 93–96. [Google Scholar] [CrossRef]
- Yin, W.; Ding, Z.; Lu, X.; Zhu, Y. Beam scan mode analysis and design for geosynchronous SAR. Sci. China Inf. Sci. 2017, 60, 060306. [Google Scholar] [CrossRef]
- Walterscheid, I.; Ender, J.; Brenner, A.; Loffeld, O. Bistatic SAR Processing and Experiments. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2710–2717. [Google Scholar] [CrossRef]
- Zheng, W.; Hu, J.; Zhang, W.; Yang, C.; Li, Z.; Zhu, J. Potential of geosynchronous SAR interferometric measurements in estimating three-dimensional surface displacements. Sci. China 2017, 60, 060304. [Google Scholar] [CrossRef]
- Long, T.; Liang, Z.; Liu, Q. Advanced technology of high-resolution radar: Target detection, tracking, imaging, and recognition. Sci. China Inf. Sci. 2019, 62, 40301. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.; Zhang, H.; Long, T.; Liu, Q.; Zheng, L. A radar waveform bandwidth selection strategy for wideband tracking. Science China Inf. Sci. 2019, 62, 40306. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Cheng, L.; Wang, Z.; Sun, C. Position tracking and attitude control for quadrotors via active disturbance rejection control method. Sci. China Inf. Sci. 2018, 62. [Google Scholar] [CrossRef]
- Heidarpour Shahrezaei, I.; Kazerooni, M.; Fallah, M. A complex target terrain SAR raw data generation and evaluation based on inversed equalized hybrid-domain algorithm processing. Waves Random Complex Media 2017, 27, 47–66. [Google Scholar] [CrossRef]
- Zhang, Y.; Mao, D.; Zhang, Q.; Zhang, Y.; Huang, Y.; Yang, J. Airborne Forward-Looking Radar Super-Resolution Imaging Using Iterative Adaptive Approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2044–2054. [Google Scholar] [CrossRef]
- Liang, Y.; Li, G.; Wen, J.; Zhang, G.; Dang, Y.; Xing, M. A Fast Time-Domain SAR Imaging and Corresponding Autofocus Method Based on Hybrid Coordinate System. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8627–8640. [Google Scholar] [CrossRef]
- Rodriguez-Cassola, M.; Prats, P.; Krieger, G.; Moreira, A. Efficient Time-Domain Image Formation with Precise Topography Accommodation for General Bistatic SAR Configurations. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2949–2966. [Google Scholar] [CrossRef] [Green Version]
- Ran, L.; Liu, Z.; Li, T.; Xie, R.; Zhang, L. An Adaptive Fast Factorized Back-Projection Algorithm With Integrated Target Detection Technique for High-Resolution and High-Squint Spotlight SAR Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 171–183. [Google Scholar] [CrossRef]
- Zhong, H.; Zhang, Y.; Chang, Y.; Liu, E.; Tang, X.; Zhang, J. Focus High-Resolution Highly Squint SAR Data Using Azimuth-Variant Residual RCMC and Extended Nonlinear Chirp Scaling Based on a New Circle Model. IEEE Geosci. Remote Sens. Lett. 2018, 15, 547–551. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Xu, F.; Yang, J. A New Nonlinear Chirp Scaling Algorithm for High-Squint High-Resolution SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2225–2229. [Google Scholar] [CrossRef]
- Liao, Y.; Liu, Q.H. Modified Chirp Scaling Algorithm for Circular Trace Scanning Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7081–7091. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.W.; Yang, J. Wide Nonlinear Chirp Scaling Algorithm for Spaceborne Stripmap Range Sweep SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6922–6936. [Google Scholar] [CrossRef]
- Amein, A.S.; Soraghan, J. Azimuth fractional transformation of the fractional chirp scaling algorithm (FrCSA). IEEE Trans. Geosci. Remote Sens. 2006, 44, 2871–2879. [Google Scholar] [CrossRef]
- Huang, L.; Qiu, X.; Hu, D.; Ding, C. Focusing of Medium-Earth-Orbit SAR With Advanced Nonlinear Chirp Scaling Algorithm. IEEE Trans. Geosci. Remote Sens. 2011, 49, 500–508. [Google Scholar] [CrossRef]
- Ding, Z.; Xiao, F.; Xie, Y.; Yu, W.; Yang, Z.; Chen, L.; Long, T. A Modified Fixed-Point Chirp Scaling Algorithm Based on Updating Phase Factors Regionally for Spaceborne SAR Real-Time Imaging. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7436–7451. [Google Scholar] [CrossRef]
- Li, Z.; Yi, L.; Xing, M.; Huai, Y.; Zheng, B. Focusing of Highly Squinted SAR Data With Frequency Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2016, 13, 23–27. [Google Scholar] [CrossRef]
- An, D.; Huang, X.; Tian, J.; Zhou, Z. Extended Nonlinear Chirp Scaling Algorithm for High-Resolution Highly Squint SAR Data Focusing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3595–3609. [Google Scholar] [CrossRef]
- Yi, T.; He, Z.; He, F.; Dong, Z.; Wu, M. Generalized Nonlinear Chirp Scaling Algorithm for High-Resolution Highly Squint SAR Imaging. Sensors 2017, 17, 2568. [Google Scholar] [CrossRef] [Green Version]
- Yue, Y.; Si, C.; Zhang, S.; Zhao, H. A Chirp Scaling Algorithm for Forward-Looking Linear-Array SAR with Constant Acceleration. IEEE Geosci. Remote Sens. Lett. 2017, 15, 88–91. [Google Scholar]
- Wu, J.; Sun, Z.; Li, Z.; Huang, Y.; Yang, J.; Liu, Z. Focusing Translational Variant Bistatic Forward-Looking SAR Using Keystone Transform and Extended Nonlinear Chirp Scaling. Remote Sens. 2016, 8, 840. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Huang, P.; Lin, C. Focus improvement of highly squint bistatic synthetic aperture radar based on non-linear chirp scaling. Iet Radar Sonar Navig. 2017, 11, 171–176. [Google Scholar] [CrossRef]
- Liang, M.; Su, W.; Gu, H. Focusing High-Resolution High Forward-Looking Bistatic SAR With Nonequal Platform Velocities Based on Keystone Transform and Modified Nonlinear Chirp Scaling Algorithm. IEEE Sens. J. 2019, 19, 901–908. [Google Scholar] [CrossRef]
- Li, Z.; Wu, J.; Li, W.; Huang, Y.; Yang, J. One-Stationary Bistatic Side-Looking SAR Imaging Algorithm Based on Extended Keystone Transforms and Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2013, 10, 211–215. [Google Scholar]
- Qiu, X.; Hu, D.; Ding, C. An Improved NLCS Algorithm With Capability Analysis for One-Stationary BiSAR. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3179–3186. [Google Scholar] [CrossRef]
- Hua, Z.; Liu, X. An Extended Nonlinear Chirp-Scaling Algorithm for Focusing Large-Baseline Azimuth-Invariant Bistatic SAR Data. IEEE Geosci. Remote Sens. Lett. 2009, 6, 548–552. [Google Scholar]
- Shi, X.; Xue, Y.; Qi, C.; Bian, M. Focusing forward-looking bistatic SAR data with chirp scaling. Electron. Lett. 2014, 50, 206–207. [Google Scholar]
- Zeng, T.; Wang, R.; Li, F.; Long, T. A Modified Nonlinear Chirp Scaling Algorithm for Spaceborne/Stationary Bistatic SAR Based on Series Reversion. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3108–3118. [Google Scholar] [CrossRef]
- Wei, W.; Liao, G.; Dong, L.; Xu, Q. Focus Improvement of Squint Bistatic SAR Data Using Azimuth Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2013, 11, 229–233. [Google Scholar]
- Li, F.; Li, S.; Zhao, Y. Focusing Azimuth-Invariant Bistatic SAR Data With Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2008, 5, 484–486. [Google Scholar]
- Wang, R.; Loffeld, O.; Nies, H.; Knedlik, S.; Ender, J. Chirp-Scaling Algorithm for Bistatic SAR Data in the Constant-Offset Configuration. IEEE Trans. Geosci. Remote Sens. 2009, 47, 952–964. [Google Scholar] [CrossRef]
- Li, D.; Liao, G.; Wang, W.; Xu, Q. Extended Azimuth Nonlinear Chirp Scaling Algorithm for Bistatic SAR Processing in High-Resolution Highly Squinted Mode. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1134–1138. [Google Scholar] [CrossRef]
- Wong, F.H.; Cumming, I.G.; Neo, Y.L. Focusing Bistatic SAR Data Using the Nonlinear Chirp Scaling Algorithm. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2493–2505. [Google Scholar] [CrossRef] [Green Version]
- Hua, Z.; Song, Z.; Jian, H.; Sun, M. Focusing Nonparallel-Track Bistatic SAR Data Using Extended Nonlinear Chirp Scaling Algorithm Based on a Quadratic Ellipse Model. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2390–2394. [Google Scholar]
- Li, Z.; Xing, M.; Liang, Y.; Gao, Y.; Chen, J.; Huai, Y.; Zeng, L.; Sun, G.C.; Bao, Z. A Frequency-Domain Imaging Algorithm for Highly Squinted SAR Mounted on Maneuvering Platforms With Nonlinear Trajectory. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4023–4038. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, S.; Zhao, H.; Chen, Y. A New Chirp Scaling Algorithm for Highly Squinted Missile-Borne SAR Based on FrFT. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3977–3987. [Google Scholar] [CrossRef]
- Sun, G.; Xing, M.; Xia, X.; Yang, J.; Wu, Y.; Bao, Z. A Unified Focusing Algorithm for Several Modes of SAR Based on FrFT. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3139–3155. [Google Scholar] [CrossRef]
- Huang, P.; Xia, X.; Gao, Y.; Liu, X.; Liao, G.; Jiang, X. Ground Moving Target Refocusing in SAR Imagery Based on RFRT-FrFT. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5476–5492. [Google Scholar] [CrossRef]
- Li, X.; Bi, G.; Ju, Y. Quantitative SNR Analysis for ISAR Imaging using LPFT. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1241–1248. [Google Scholar] [CrossRef]
- Djurovic, I. Robust adaptive local polynomial Fourier transform. IEEE Signal Process. Lett. 2004, 11, 201–204. [Google Scholar] [CrossRef]
- Zhang, S.; Xing, M.; Xia, X.; Li, J.; Guo, R.; Bao, Z. A Robust Imaging Algorithm for Squint Mode Multi-Channel High-Resolution and Wide-Swath SAR With Hybrid Baseline and Fluctuant Terrain. IEEE J. Sel. Top. Signal Process. 2015, 9, 1583–1598. [Google Scholar] [CrossRef]
- Davidson, G.; Cumming, I. Signal properties of spaceborne squint-mode SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 611–617. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Ding, Z.; Tian, W.; Zeng, T.; Yin, W. A 2-D Nonlinear Chirp Scaling Algorithm for High Squint GEO SAR Imaging Based on Optimal Azimuth Polynomial Compensation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5724–5735. [Google Scholar] [CrossRef]















| Parameter | Values |
|---|---|
| Radar wavelength | m |
| Sampling frequency | 120 MHz |
| Range bandwidth | 50 MHz |
| Signal pulse width | 3 s |
| Chirp rate | MHz/s |
| Pulse repeat frequency | 1200 Hz |
| Synthetic aperture time | s |
| Receiver slant range | 3024 m |
| Receiver squint angle | |
| Receiver incident angle | |
| Receiver velocity | m/s |
| Receiver acceleration | m/s2 |
| Receiver jerk | m/s3 |
| Transmitter slant range | 1905 m |
| Transmitter squint angle | 47 |
| Transmitter incident angle | 64 |
| Transmitter velocity | m/s |
| Transmitter acceleration | m/s2 |
| Transmitter jerk | m/s3 |
| Target 1 | Target 5 | Target 21 | Target 25 | ||
|---|---|---|---|---|---|
| Traditional NLCS algorithm [41] | |||||
| Resolution (m) | Range | 3.75 | 3.75 | 3.70 | 3.77 |
| Cross-range | 1.46 | 1.48 | 1.51 | 1.54 | |
| PSLR (dB) | Range | −10.86 | −11.1 | −10.12 | −10.89 |
| Cross-range | −9.73 | −9.82 | −10.73 | −7.22 | |
| ISLR (dB) | Range | −10.12 | −10.82 | −9.63 | −9.32 |
| Cross-range | −9.32 | −8.88 | 9.96 | −6.52 | |
| Proposed algorithm | |||||
| Resolution (m) | Range | 3.75 | 3.73 | 3.70 | 3.72 |
| Cross-range | 1.42 | 1.46 | 1.44 | 1.44 | |
| PSLR (dB) | Range | −13.31 | −13.01 | −12.84 | −12.54 |
| Cross-range | −12.7 | −12.62 | −13 | −12.64 | |
| ISLR (dB) | Range | −11.33 | −11.02 | −11.42 | −11.56 |
| Cross-range | −10.87 | −10.37 | −11.24 | −11.42 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, T.; Wang, Z.; Liu, F.; Wang, C. An Improved Frequency-Domain Image Formation Algorithm for Mini-UAV-Based Forward-Looking Spotlight BiSAR Systems. Remote Sens. 2020, 12, 2680. https://doi.org/10.3390/rs12172680
Zeng T, Wang Z, Liu F, Wang C. An Improved Frequency-Domain Image Formation Algorithm for Mini-UAV-Based Forward-Looking Spotlight BiSAR Systems. Remote Sensing. 2020; 12(17):2680. https://doi.org/10.3390/rs12172680
Chicago/Turabian StyleZeng, Tao, Zhanze Wang, Feifeng Liu, and Chenghao Wang. 2020. "An Improved Frequency-Domain Image Formation Algorithm for Mini-UAV-Based Forward-Looking Spotlight BiSAR Systems" Remote Sensing 12, no. 17: 2680. https://doi.org/10.3390/rs12172680
APA StyleZeng, T., Wang, Z., Liu, F., & Wang, C. (2020). An Improved Frequency-Domain Image Formation Algorithm for Mini-UAV-Based Forward-Looking Spotlight BiSAR Systems. Remote Sensing, 12(17), 2680. https://doi.org/10.3390/rs12172680