Estimation of Equivalent Number of Looks in Time-Series Pol(In)SAR Data

Abstract

As an essential parameter in synthetic aperture radar (SAR) images, the equivalent number of looks (ENL) not only indicates the speckle noise level in multi-look SAR data but also can be used for evaluating the region homogeneity level. Currently, time-series polarimetric (interferometric) SAR (TSPol(In)SAR) data are increasingly abundant, but traditional equivalent number of looks (ENL) estimators only use polarimetric information from a mono-temporal observation and do not consider the temporal characteristics or interferometric coherence of ground targets. Therefore, this paper puts forward four novel ENL estimators to overcome the restrictions of inadequate observation information. Firstly, based on the traditional trace moment estimator for polarimetric SAR data (TM-PolSAR), we extend it to both PolInSAR and TSPolInSAR data and then propose both TM-PolInSAR and TM-TSPolInSAR estimators, respectively. Secondly, for both TSPolSAR and single-reference TSPolInSAR data, we estimate the ENL by stacking the trace moments (STM) of multitemporal coherency matrices, called STM-TSPolSAR and STM-TSPolInSAR estimators, respectively. Therefore, these proposed ENL estimators can effectively deal with most of the requirements of TSPol(In)SAR data types in practical applications, mainly including statistical distribution modeling and region homogeneity evaluation. The simulation and real experiments detailedly compare the proposed four ENL estimators to the classical TM-PolSAR estimator and quantitatively analyze the estimation performance. The proposed estimators have obtained the ENL with less bias and standard deviation than the traditional estimator, especially in case of small spatial samples coherency matrices. Additionally, these STM-TSPolSAR, STM-TSPolInSAR, and TM-TSPolInSAR estimators have provided more effective statistical characteristics with the increase of the time-series size. It has been demonstrated that the proposed STM-TSPolSAR estimator considers the time-varying polarimetric characteristics of the crop and detects many edges that the traditional estimator cannot discover, which means a superior capability of region homogeneity evaluation.

1. Introduction

As an essential parameter in synthetic aperture radar (SAR) images, the equivalent number of looks (ENL) indicates the speckle noise level, and smaller ENL value means a higher level of speckle noise [1]. During the SAR data generation and postprocessing procedure, multi-looking processing is usually performed for suppressing the inherent speckle noise in coherent radar imaging systems. Specifically, one observation is divided into several “looks” and then it averages them. However, there exists a spatial correlation between adjacent pixels in the image, and the actual total effect is always smaller than the nominal number of looks. Therefore, the equivalent number of looks (ENL) is proposed to describe the degree of averaging in the postprocessing procedure accurately. It is necessary for many statistical-theory-based applications to accurately estimate the ENL value because it is an important input parameter in the statistical distribution modeling of multi-look SAR data, including sigma filter [2,3,4], change detection [5,6], and target classification [7,8,9,10,11]. For example, based on the Wishart distribution [7,10] or more complex data models [8,9,11], Bayesian classifiers need an estimated ENL as the input parameter to distinguish different ground objects, and so does the change detection [5,6] based on likelihood ratio test to evaluate the equality of two temporal coherency matrices. Additionally, the ENL indicator can be used for effectively evaluating the region homogeneity level and determining whether it is in a homogeneous or textured area, including a region-evaluation-based filter [12,13,14], edge detection [15,16], and superpixel generation [17,18]. For instance, Lang et al. [13] derive a polarimetric homogeneity measurement by combining the ENL and a line-and-edge detector to adaptively select local homogeneous pixels for PolSAR data filtering. Xiang et al. [17,18] integrate the aforementioned homogeneity measurement into the superpixel generation method for significantly improving the performance of discriminating homogeneous and heterogeneous areas.

For single polarimetric SAR data, a homogeneous area is usually selected manually from the original images before the ENL estimation, where the assumptions of fully developed speckle noise and ignorable texture assure that the observed images follow complex circular Gaussian distribution [1]. The ENL estimation is based on the SAR intensity statistics and computed by the coefficient of variance (CoV) estimator [19] and fractional moment (FM)-based estimator [8]. Cui et al. [20] and Ren et al. [21] analyzed the statistic characteristics of the logarithmically transformed speckle noise, and automatically estimate the ENL in the original SAR. However, both estimators introduce the estimation bias easily due to the strong compression effect of the logarithmic operation [1].

For full polarimetric SAR (PolSAR), the common processing strategy is based on these estimators mentioned above to estimate the ENLs from each polarization channel and then average them [8]. To make full use of the inter-channel correlation information, Anfinsen et al. [22] were founded on complex Wishart distribution, utilized the full sample polarimetric coherency matrix and put forward a trace moment (TM)-based estimator and a maximum likelihood (ML) estimator based on the log-determinant moment. Doulgeris et al. [23] were based on the first-order log-cumulant (FOL) expression of K-Wishart distribution to estimate ENL. However, the texture-corrected estimator is applied to K-Wishart distributed PolSAR data, and it needs much time cost and maybe has incorrect estimation results because of shape parameters pre-estimation. Tao et al. [24] proposed a texture-invariant ENL estimator applied to any product model, called the development of trace moments (DTM), which is an extension of the TM-based estimator based on complex Wishart distribution. Then, Tao et al. [25] presented some novel ENL estimators via the log-cumulants of the sub-matrices of the multi-look polarimetric coherency matrix, which are suitable for any texture model. Bouhlel et al. [26] were based on fractional moments of the determinant of the multi-look polarimetric covariance (FMDC) matrix to estimate the ENL, which is also independent of the texture distribution.

The aforementioned ENL estimators are limited to the use of mono-temporal multipolarization information, and do not consider the temporal characteristics or interferometric coherence as the available observation data. With the increasing number of available SAR satellites, such as TerraSAR-X (TSX), TanDEM-X (TDX), RADARSAT-2, COSMO-SkyMed, Sentinel-1A/1B and GF-3, more and more applications using time-series polarimetric (interferometric) SAR (PolInSAR) (TSPol(In)SAR) for observing the temporal characteristics of ground objects has drawn a wide attention in last decades, including forest parameter investigation [27,28], refined crop monitoring [29,30], vessel monitoring [31,32], and surface displacement inversion [33,34,35]. Meanwhile, abundant TSPol(In)SAR data can provide a higher possibility for the performance improvement of the ENL estimation.

Therefore, this paper introduces the temporal characteristics or interferometric coherence, and proposes four novel ENL estimators for overcoming the restrictions of inadequate observation information. Firstly, we extend TM estimator to PolInSAR and TSPolInSAR data, called both TM-PolInSAR and TM-TSPolInSAR methods, respectively; Secondly, we estimate the ENL by stacking trace moments (STM) of multitemporal coherency matrices in both TSPolSAR and single reference TSPolInSAR data, called STM-TSPolSAR and STM-TSPolInSAR methods, respectively. The proposed four ENL estimators have better estimation performance in both statistical characteristics and homogeneity evaluation aspects than traditional TM estimator of PolSAR data, called TM-PolSAR method. Additionally, the estimation performance is less affected by the number of sample coherency matrix.

This paper is organized as follows. Section 2 introduces multi-dimension SAR statistics and ENL estimation. Section 3 illustrates several classical TSPol(In)SAR data generation and proposes corresponding novel ENL estimators. The simulation in Section 4 and both real experiments in Section 5 and Section 6 demonstrate the superior performance of these proposed ENL estimators than the traditional TM-PolSAR estimator. Finally, we draw a conclusion in Section 6.

2. Multi-dimension SAR Statistics and ENL Estimation

2.1. PolSAR Coherency Matrix Generation

For PolSAR, a SAR sensor can obtain the Sinclair matrix S describing the full polarimetric information of a single target. In the linear horizontal and vertical polarization base, the scattering matrix S is expressed as follows [1]:

$$S=\left[\begin{array}{cc}{S}_{HH}& S_{HV}\\ S_{VH}& S_{VV}\end{array}\right]$$

(1)

In case of the reciprocal condition, $S_{HV}=S_{VH}$. A complex Pauli basis vector can represent the matrix S [1]

$$k_{Pol}={\left[\begin{array}{ccc}{S}_{HH+VV}& S_{HH-VV}& 2S_{HV}\end{array}\right]}^T/\sqrt{2}$$

(2)

where ${}^T$ denotes the matrix transpose. And the total power (TP) of $k_{Pol}$ or S is obtained as

$$TP=\left(S_{HH+VV}^2+S_{HH-VV}^2+4S_{HV}^2\right)/2$$

(3)

Usually, the polarimetric information of a distributed target is expressed by the coherency matrix as follows [1]:

$$T_{Pol}=\langle k_{Pol}{k}_{Pol}^H\rangle$$

(4)

where ${}^H$ denotes the complex conjugated transpose and $\langle ·\rangle$ means the statistical average. It is worth noting that $T_{Pol}$ is a positive semidefinite Hermitian matrix.

2.2. Multi-dimension SAR Coherency Matrix Statistics

A complex scattering vector for a multi-dimension SAR sensor can be obtained from the temporal dimension and the polarization channel [1]

$$k={\left[\begin{array}{cccc}{S}_1& S_2& \cdots & S_q\end{array}\right]}^T$$

(5)

where q denotes the dimension of the vector $k$. Usually, one resolution cell contains many elementary scatterers, and hence k follows a multivariate complex Gaussian distribution with mean zero and covariance matrix $\Sigma$, i.e., $k\in \mathrm{N}\left(0,\Sigma \right)$. The corresponding distribution function is expressed as [1]

$$\mathrm{P}\left(k\right)=\frac{1}{{\pi }^3\left|\Sigma \right|}\exp \left(-k^H{\Sigma }^{-1}k\right)$$

(6)

where $\Sigma =\mathrm{E}\left(k{k}^H\right)$, $|·|$ denotes the matrix determinant, and ${\Sigma }^{-1}$ is the inverse of $\Sigma$.

Usually, it needs to perform the multi-looking processing for reducing the speckle noise in the coherency matrix. After averaging several independent single-look samples, the resulting n-look coherency matrix is expressed as [36]

$$T=\frac{1}{n}{\displaystyle \sum _{i=1}^n{k}_i^H{k}_i}$$

(7)

Let $A=nT$, and the matrix $A$ can be modeled following a complex Wishart distribution, i.e., $A\in \mathrm{W}\left(q,n,\Sigma \right)$, and the distribution function is expressed as [36]

$${\mathrm{P}}^{\left(q,n,\Sigma \right)}\left(A\right)=\frac{{\left|A\right|}^{n-q}\exp \left[-\mathrm{Tr}\left({\Sigma }^{-1}A\right)\right]}{{\pi }^{q(q-1)/2}{\left|\Sigma \right|}^n{\displaystyle {\prod }_{j=1}^q\Gamma \left(n-j+1\right)}}$$

(8)

where $\mathrm{Tr}(·)$ is the trace of the matrix, $\Pi$ denotes the product operation, and $\Gamma (·)$ is the gamma function.

2.3. TM Estimator of ENL

Compared to both CoV and FM estimators using single polarimetric intensity statistics, the TM estimator [22] proposed by Anfinsen et al. firstly makes full use of the full sample polarimetric coherency matrix, which is founded on complex Wishart distribution. Besides, other ML [22], FOL [23], and MFDC [26] estimators also use full polarimetric information but are only applied to multi-look PolSAR data. On the contrary, the TM and corresponding extension estimators have unique advantages in single-look data processing, which means the class of methods helps to maintain the original image resolution. The following is to introduce the TM estimator of PolSAR data in this paper, called the TM-PolSAR estimator.

In case of PolSAR data, it is assumed for a 3-dimension polarimetric coherency matrix $T_{Pol}$ that the corresponding random matrix $A_{Pol}$ follows complex Wishart distribution with L degrees of freedom and scale matrix ${\Sigma }_{Pol}=\mathrm{E}\left(T_{Pol}\right)$, i.e., $A_{Pol}\in \mathrm{W}\left(3,L,{\Sigma }_{Pol}\right)$. The following trace moment of $A_{Pol}$ is derived in [37]:

$$\langle \mathrm{Tr}\left(A_{Pol}{A}_{Pol}\right)\rangle =L^2\mathrm{Tr}\left({\Sigma }_{Pol}{\Sigma }_{Pol}\right)+L\mathrm{Tr}{\left({\Sigma }_{Pol}\right)}^2$$

(9)

In terms of $T_{Pol}=A_{Pol}/L$, a much simpler equation can be obtained as follows

$$L\langle \mathrm{Tr}\left(T_{Pol}{T}_{Pol}\right)\rangle =L\mathrm{Tr}\left({\Sigma }_{Pol}{\Sigma }_{Pol}\right)+\mathrm{Tr}{\left({\Sigma }_{Pol}\right)}^2$$

(10)

Therefore, the aforementioned expression directly leads to the TM-PolSAR estimator of ENL [22]

$$L=\frac{\mathrm{Tr}{\left({\Sigma }_{Pol}\right)}^2}{\langle \mathrm{Tr}\left(T_{Pol}{T}_{Pol}\right)\rangle -\mathrm{Tr}\left({\Sigma }_{Pol}{\Sigma }_{Pol}\right)}$$

(11)

3. Novel ENL Estimators for TSPol(In)SAR Data

In this section, we introduce the generation and statistics of four common TSPol(In)SAR data, including PolInSAR, TSPolSAR, single reference TSPolInSAR, and standard TSPolInSAR data. And then based on classical TM-PolSAR estimator, four corresponding ENL estimators are proposed, including TM-PolInSAR, STM-TSPolSAR, STM-PolInSASR, and TM-TSPolInSAR. Compared to the traditional TM-PolSAR estimator, these proposed ENL estimators can be flexibly applied to multiple types of TSPol(In)SAR SAR data in the practical applications.

3.1. PolInSAR Data Statistics and TM-PolInSAR Estimator

For PolInSAR, a PolSAR sensor operated in an interferometric mode obtains both master and slave complex Pauli basis vectors $k_{Pol}^1$ and $k_{Pol}^2$, and it can construct a six-dimension polarimetric interferometric scattering vector $k_{PolIn}$ [1]

$$k_{PolIn}=\left[\begin{array}{c}{k}_{Pol}^1\\ k_{Pol}^2\end{array}\right]$$

(12)

The $6\times 6$ positive semidefinite Hermitian PolInSAR coherency matrix is expressed as [1]

$$T_{PolIn}=\langle k_{PolIn}{k}_{PolIn}^H\rangle =\left[\begin{array}{cc}\langle T_{11}\rangle & \langle {\Omega }_{12}\rangle \\ \langle {\Omega }_{12}^H\rangle & \langle T_{22}\rangle \end{array}\right]$$

(13)

where $T_{11}$ and $T_{22}$ are master and slave polarimetric coherency matrices, respectively, and ${\Omega }_{12}$ is the interferometric coherency matrix that contains polarimetric and interferometric information of different temporal channels.

Let $A_{PolIn}=L{T}_{PolIn}$, and the matrix $A$ can be modeled following a complex Wishart distribution, i.e., $A_{PolIn}\in \mathrm{W}\left(6,L,{\Sigma }_{PolIn}\right)$ according to the multi-dimension SAR coherency matrix statistics mentioned in Section 2.2. Analogously, based on the complex Wishart distribution, the trace moment of $A_{PolIn}$ is also indicated as:

$$\langle \mathrm{Tr}\left(A_{PolIn}{A}_{PolIn}\right)\rangle =L^2\mathrm{Tr}\left({\Sigma }_{PolIn}{\Sigma }_{PolIn}\right)+L\mathrm{Tr}{\left({\Sigma }_{PolIn}\right)}^2$$

(14)

Therefore, this paper proposes to apply the TM estimator to PolInSAR data for estimating the imagery ENL, and the corresponding TM-PolInSAR estimator can be expressed as

$$L=\frac{\mathrm{Tr}{\left({\Sigma }_{PolIn}\right)}^2}{\langle \mathrm{Tr}\left(T_{PolIn}{T}_{PolIn}\right)\rangle -\mathrm{Tr}\left({\Sigma }_{PolIn}{\Sigma }_{PolIn}\right)}$$

(15)

As mentioned above, the proposed TM-PolInSAR estimator utilizes both polarimetric information and interferometric coherence and has a more significant potential of estimating ENL with both high accuracy and robustness. It has been demonstrated that the TM-PolInSAR estimator can better improve the well-known Lee method in central pixel value estimation [14] than the CoV-based estimator. For further investigation, this paper will make a quantitative analysis of traditional TM-PolSAR and proposed TM-PolInSAR estimators in the following experimental sections.

3.2. Standard TSPolInSAR Data Statistics and TM-TSPolInSAR Estimator

Assuming that a PolSAR sensor acquires N observation covering the same area, N complex Pauli basis vector set $\left\{k_{Pol}^i,i=1,2,\dots ,N\right\}$ can be obtained, and the constructed time-series polarimetric interferometric vector $k_{TSPolIn}$ [38]

$$k_{TSPolIn}=\left[\begin{array}{c}{k}_{Pol}^1\\ k_{Pol}^2\\ ⋮\\ k_{Pol}^N\end{array}\right]$$

(16)

The $3N\times 3N$ semidefinite Hermitian TSPolInSAR coherency matrix is expressed as [38]

$$T_{TSPolIn}=\langle k_{TSPolIn}{k}_{TSPolIn}^H\rangle =\left[\begin{array}{cccc}{T}_{11}& {\Omega }_{12}& \cdots & {\Omega }_{1N}\\ {\Omega }_{12}^H& T_{22}& \cdots & {\Omega }_{2N}\\ ⋮& ⋮& \ddots & ⋮\\ {\Omega }_{1N}^H& {\Omega }_{2N}^H& \cdots & T_{NN}\end{array}\right]$$

(17)

where $T_{ii}$ is polarimetric coherency matrix corresponding to ith observation, and ${\Omega }_{ij}$ is interferometric coherency matrix between both ith and jth observations.

As the multi-dimension SAR coherency matrix statistics is mentioned in Section 2.2, the matrix $A_{TSPolIn}$ also follows a complex Wishart distribution, i.e., $A_{TSPolIn}\in \mathrm{W}\left(3N,L,{\Sigma }_{TSPolIn}\right)$.

Similarly, the trace moment of $A_{TSPolIn}$ is obtained as follows:

$$\langle \mathrm{Tr}\left(A_{TSPolIn}{A}_{TSPolIn}\right)\rangle =L^2\mathrm{Tr}\left({\Sigma }_{TSPolIn}{\Sigma }_{TSPolIn}\right)+L\mathrm{Tr}{\left({\Sigma }_{TSPolIn}\right)}^2$$

(18)

This paper proposes to apply the TM estimator to the TSPolInSAR data for estimating the imagery ENL, called the TM-TSPolInSAR estimator.

$$L=\frac{\mathrm{Tr}{\left({\Sigma }_{TSPolIn}\right)}^2}{\langle \mathrm{Tr}\left(T_{TSPolIn}{T}_{TSPolIn}\right)\rangle -\mathrm{Tr}\left({\Sigma }_{TSPolIn}{\Sigma }_{TSPolIn}\right)}$$

(19)

The matrix $T_{TSPolIn}$ describes a ground target using the full polarimetric and interferometric responses among all the acquisitions. Therefore, the proposed TM-TSPolInSAR estimator has utilized the most comprehensive feature information, and the estimation capability will be improved significantly.

3.3. TSPolSAR Data Statistics and STM-TSPolSAR Estimator

In the multitemporal polarimetric SAR application, TSPolSAR data with N observations acquires all polarimetric responses of a target in time. Specifically, in the crop refine monitoring [30], TSPolSAR data usually consist of N polarimetric coherency matrices set $\left\{T_{Pol}^i|i=1,2,\dots ,N\right\}$.

Referring to Section 2.2, the matrix $A_{Pol}^i$ of ith observation has a complex Wishart distribution, i.e., $A_{Pol}^i\in \mathrm{W}\left(3,L,{\Sigma }_{Pol}^i\right)$ with ${\Sigma }_{Pol}^i=E\left(A_{Pol}^i\right)/L$, and the corresponding trace moment is obtained as follows:

$$\langle \mathrm{Tr}\left(A_{Pol}^i{A}_{Pol}^i\right)\rangle =L^2\mathrm{Tr}\left({\Sigma }_{Pol}^i{\Sigma }_{Pol}^i\right)+L\mathrm{Tr}{\left({\Sigma }_{Pol}^i\right)}^2$$

(20)

To make full use of all sample polarimetric coherency matrix in time, this paper proposes to the STM-TSPolSAR ENL estimator by stacking all trace moments. The stacking trace moment is expressed as

$${\displaystyle \sum _{i=1}^N\langle \mathrm{Tr}\left(A_{Pol}^i{A}_{Pol}^i\right)\rangle }=L^2{\displaystyle \sum _{i=1}^N\mathrm{Tr}\left({\Sigma }_{Pol}^i{\Sigma }_{Pol}^i\right)}+L{\displaystyle \sum _{i=1}^N\mathrm{Tr}{\left({\Sigma }_{Pol}^i\right)}^2}$$

(21)

Therefore, according to $A_{Pol}^i=L{T}_{Pol}^i$, the aforementioned expression can be simplified, and then the proposed STM-TSPolSAR estimator can be derived as follows

$$L=\frac{{\displaystyle \sum _{i=1}^N\mathrm{Tr}{\left({\Sigma }_{Pol}\right)}^2}}{{\displaystyle \sum _{i=1}^N\langle \mathrm{Tr}\left(T_{Pol}{T}_{Pol}\right)\rangle }-{\displaystyle \sum _{i=1}^N\mathrm{Tr}\left({\Sigma }_{Pol}{\Sigma }_{Pol}\right)}}$$

(22)

The proposed STM-TSPolSAR estimator considers multitemporal polarimetric responses, and it has been demonstrated in the following experimental sections that it has a better estimation performance than the TM-PolSAR estimator, especially in case of the observed target with time-varying polarimetric characteristics.

3.4. Single Reference TSPolInSAR Statistics and STM-TSPolInSAR Estimator

As mentioned in Section 3.2, standard TSPolInSAR data with N acquisitions consists of $N\left(N-1\right)/2$ PolInSAR data with different baselines. However, it is necessary for parameter inversion in the practical applications to select several effective PolInSAR data, whose range is between $N-1$ and $N\left(N-1\right)/2$, according to both spatial or temporal baselines. Usually, one of the most straightforward strategies is to use single reference TSPolInSAR data for estimating the deformation velocity in the PSI technology [34,35], which contains N-1 PolInSAR data

Therefore, to simplify the subsequent analysis, the STM-TSPolInSAR estimator proposed in this section mainly focuses on the single reference TSPolInSAR data framework. Specifically, one image needs to be selected as the master one, and then the PolInSAR data set $\left\{T_{PolIn}^i|i=1,2,\dots ,N-1\right\}$ is constructed by N-1 PolInSAR coherency matrices.

In ith PolInSAR data, the matrix $A_{PolIn}^i$ of the matrix $T_{PolIn}^i$ also can be modeled following a complex Wishart distribution mentioned in Section 3.1, i.e., $A_{PolIn}^i\in \mathrm{W}\left(6,L,{\Sigma }_{PolIn}^i\right)$ with ${\Sigma }_{PolIn}^i=E\left(A_{PolIn}^i\right)/L$. The trace moment of the matrix $A_{PolIn}^i$ is expressed as

$$\langle \mathrm{Tr}\left(A_{PolIn}^i{A}_{PolIn}^i\right)\rangle =L^2\mathrm{Tr}\left({\Sigma }_{PolIn}^i{\Sigma }_{PolIn}^i\right)+L\mathrm{Tr}{\left({\Sigma }_{PolIn}^i\right)}^2$$

(23)

Similar to the STM-TSPolSAR estimator, this paper proposes to make full use of all selected PolInSAR coherency matrices and puts forward the STM-TSPolInSAR estimator by stacking all trace moments of $\left\{A_{PolIn}\right\}$. As a result, the stacking trace moment is obtained and expressed as follows

$${\displaystyle \sum _{i=1}^N\langle \mathrm{Tr}\left(A_{PolIn}^i{A}_{PolIn}^i\right)\rangle }=L^2{\displaystyle \sum _{i=1}^N\mathrm{Tr}\left({\Sigma }_{PolIn}^i{\Sigma }_{PolIn}^i\right)}+L{\displaystyle \sum _{i=1}^N\mathrm{Tr}{\left({\Sigma }_{PolIn}^i\right)}^2}$$

(24)

Therefore, in term of $A_{PolIn}^i=L{T}_{PolIn}^i$, the above equation can be derived into the proposed STM-TSPolInSAR estimator

$$L=\frac{{\displaystyle \sum _{i=1}^N\mathrm{Tr}{\left({\Sigma }_{PolIn}\right)}^2}}{{\displaystyle \sum _{i=1}^N\langle \mathrm{Tr}\left(T_{PolIn}{T}_{PolIn}\right)\rangle }-{\displaystyle \sum _{i=1}^N\mathrm{Tr}\left({\Sigma }_{PolIn}{\Sigma }_{PolIn}\right)}}$$

(25)

Obviously, the proposed STM-TSPolInSAR estimator is based on the single reference TSPolInSAR data framework and obtains the staking trace moment of N-1 PolInSAR data for estimating the ENL. It is worth noting that this proposed estimator also can be applied to the TSPolInSAR data application with the small baseline set, not necessarily the single-reference one.

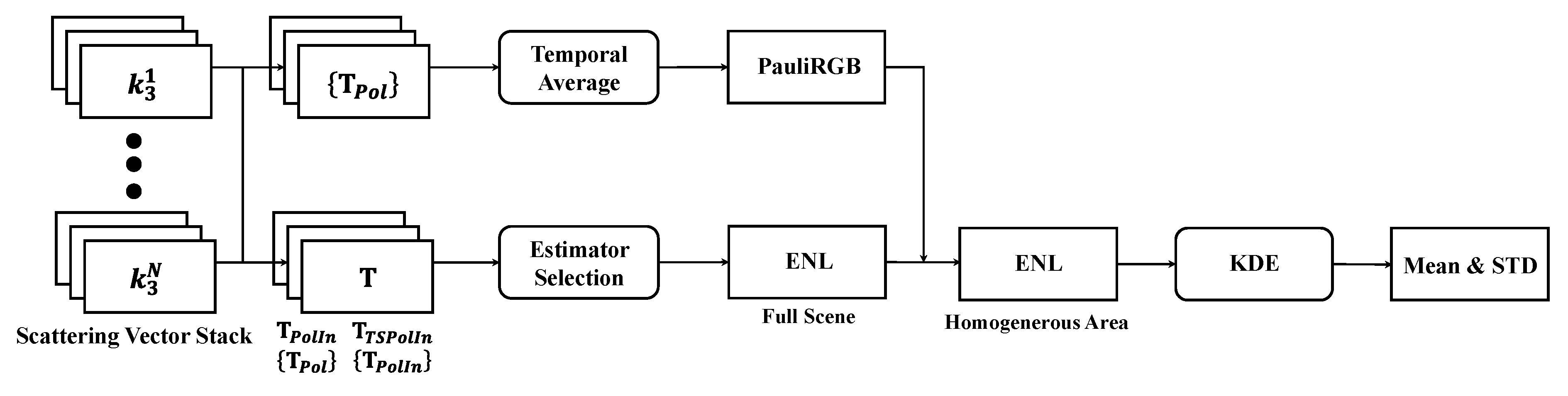
3.5. ENL Estimation Procedure Based on The Selected Estimator

According to different application requirements, the appropriate TSPol(In)SAR data is selected, and the corresponding ENL estimator is used for computing the ENL from a manually selected homogeneous area. As shown in Figure 1, the detailed estimation steps are as follows:

(1)

Based on the acquired scattering vector stack with N SAR observation, construct the TSPolSAR data and the corresponding TSPol(In)SAR data according to the practical application.

(2)

Perform a temporal average of time-series polarimetric coherency matrices, and create the Pauli basis RGB (PauliRGB) image.

(3)

Select an appropriate estimator according to the TSPol(In)SAR data type and estimate the ENL of the full scene with a sliding window.

(4)

With the help of both PauliRGB and estimated ENL images, select a homogeneous area manually for the following ENL statistics.

(5)

Perform a kernel density estimator (KDE) implemented with the normal kernel function to estimate the mean and standard deviation (STD) for avoiding the unpredictable sharp and possible multimodality of the distribution.

4. Results and Analyses of Simulated TSPol(In)SAR data

Based on the simulated TSPolInSAR data, this section uses both bias and STD indicators for analyzing the statistical performance difference quantitatively between the traditional TM-PolSAR estimator and the proposed four ENL estimators under different spatial window sizes and different time-series sizes.

4.1. Simulated TSPolInSAR Data Generation and Parameter Settings

These estimators are tested on the simulated 10-look TSPolInSAR data with six acquisitions, which are constructed by an extended Bragg scatterer and time-series interferometric matrix. The corresponding polarimetric coherency matrix is given by [39]

$${\widehat{T}}_{Pol}=\left[\begin{array}{ccc}{c}_1& c_2\mathrm{sinc}\left(2\beta \right)& 0\\ c_2^{*}\mathrm{sinc}\left(2\beta \right)& c_3\left(1+\mathrm{sinc}\left(4\beta \right)\right)& 0\\ 0& 0& c_3\left(1-\mathrm{sinc}\left(4\beta \right)\right)\end{array}\right]$$

(26)

where ${}^{*}$ denotes the conjugated operation, $c_1=1$, $c_2=0.2+0.2i$, $c_3=0.5$, and $\beta =0.03\pi$ in the simulation. In the time-series interferometric matrix $\widehat{\mathsf{\Upsilon }}$, the element $\widehat{\mathsf{\Upsilon }}\left(i,j\right)$ in the ith row and jth col is equal to the complex coherence between the ith and jth observations, and the corresponding decorrelation can be modeled as an exponential function with the observation interval $\Delta$ = 30 and the temporal threshold $t$ = 180

$$\widehat{\mathsf{\Upsilon }}\left(i,j\right)=\exp \left(-\left(\Delta \left|i-j\right|\right)/t\right)$$

(27)

Therefore, the modeled TSPolInSAR data ${\widehat{T}}_{TSPolIn}$ can be obtained by the Kronecker product between polarimetric coherency matrix ${\widehat{T}}_{Pol}$ and time-series interferometric matrix $\widehat{\mathsf{\Upsilon }}$ [40]

$${\widehat{T}}_{TSPolIn}={\widehat{T}}_{Pol}\otimes \widehat{\mathsf{\Upsilon }}$$

(28)

where $\otimes$ donates the Kronecker product.

Finally, the simulated TSPolInSAR data ${\widehat{T}}_{TSPolIn}$ can be obtained by the Monte Carlo method [1]

$$T_{TSPolIn}={\widehat{T}}_{TSPolIn}^{1/2}\left(\frac{1}{L}{\displaystyle \sum _{i=1}^L{u}_i{u}_i^H}\right){\widehat{T}}_{TSPolIn}^{1/2}$$

(29)

where $u_i$ are independent Gaussian vector of zero mean and unit covariance matrix. L = 10 is the number of looks and set throughout the simulation.

It is worth noting in the following simulated experiments that the traditional TM-PolSAR, the TM-PolInSAR, and the STM-TSPolInSAR estimators are applied to the first acquired PolSAR data, the PolInSAR data between first and second observations, and single reference TSPolInSAR data with first observation as the master image, respectively.

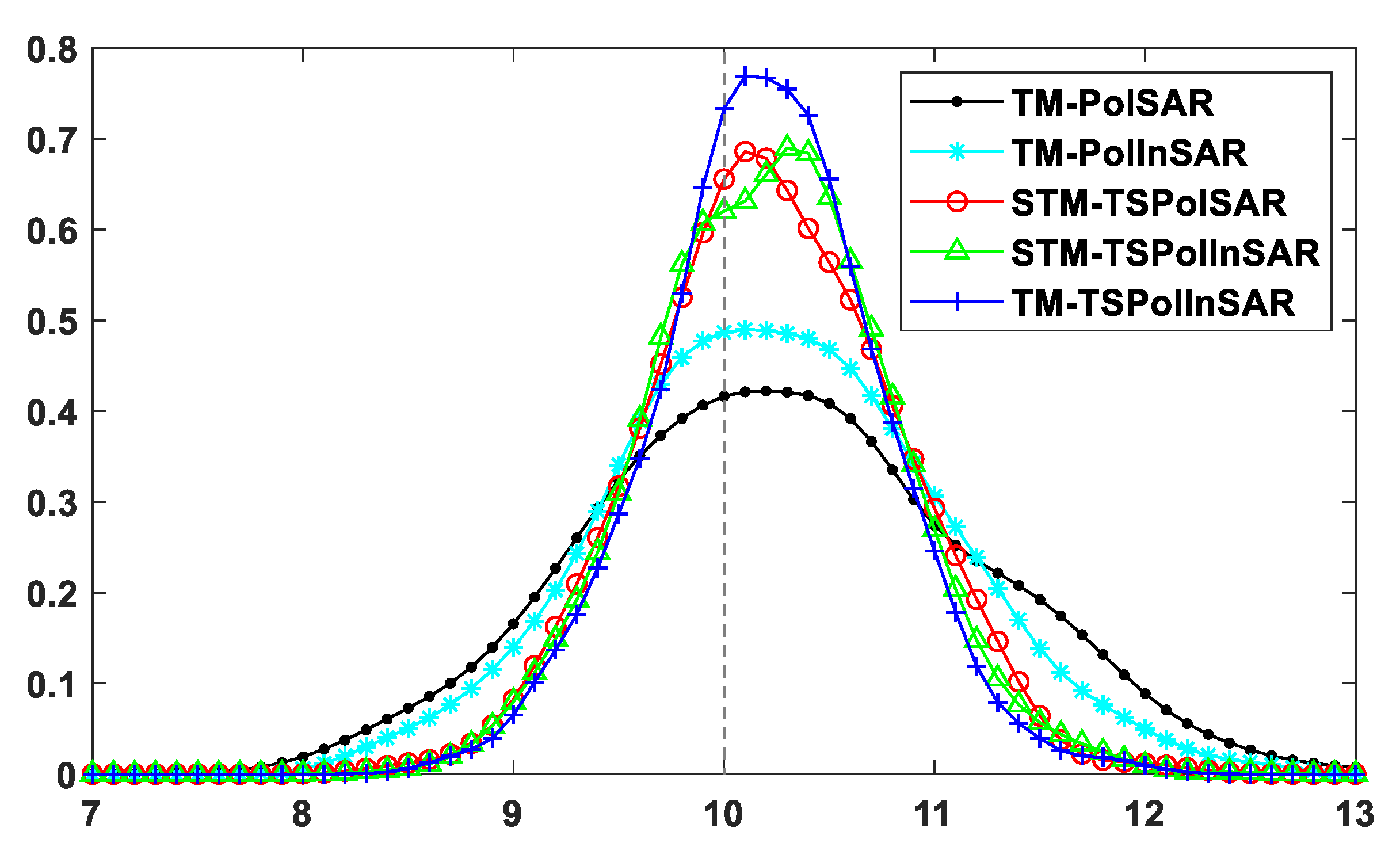
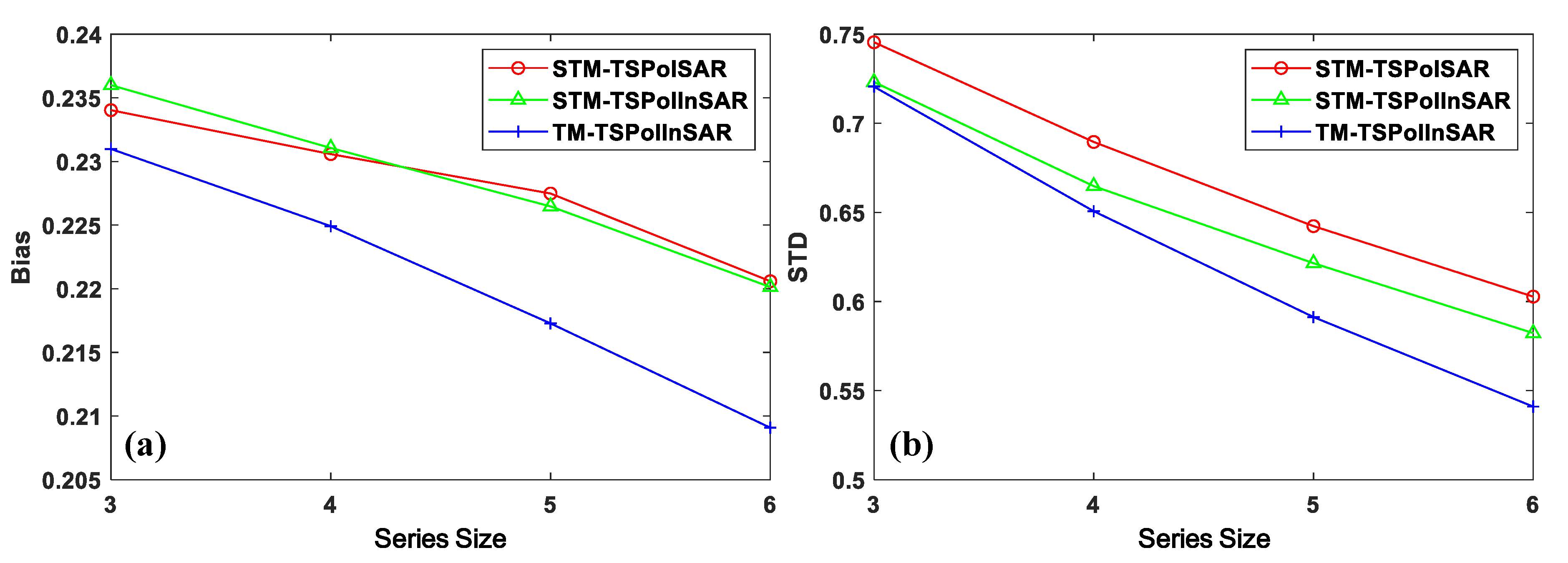
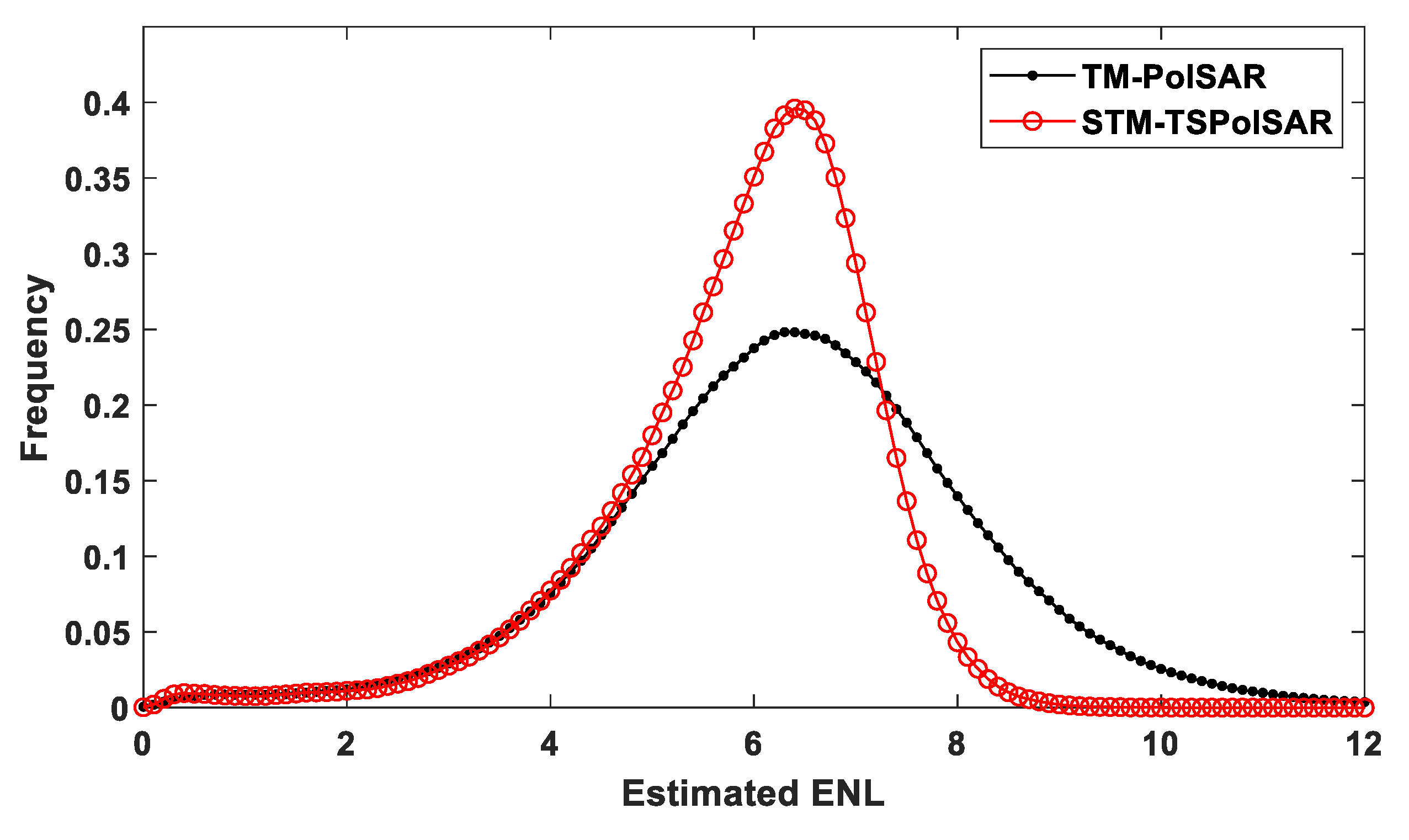
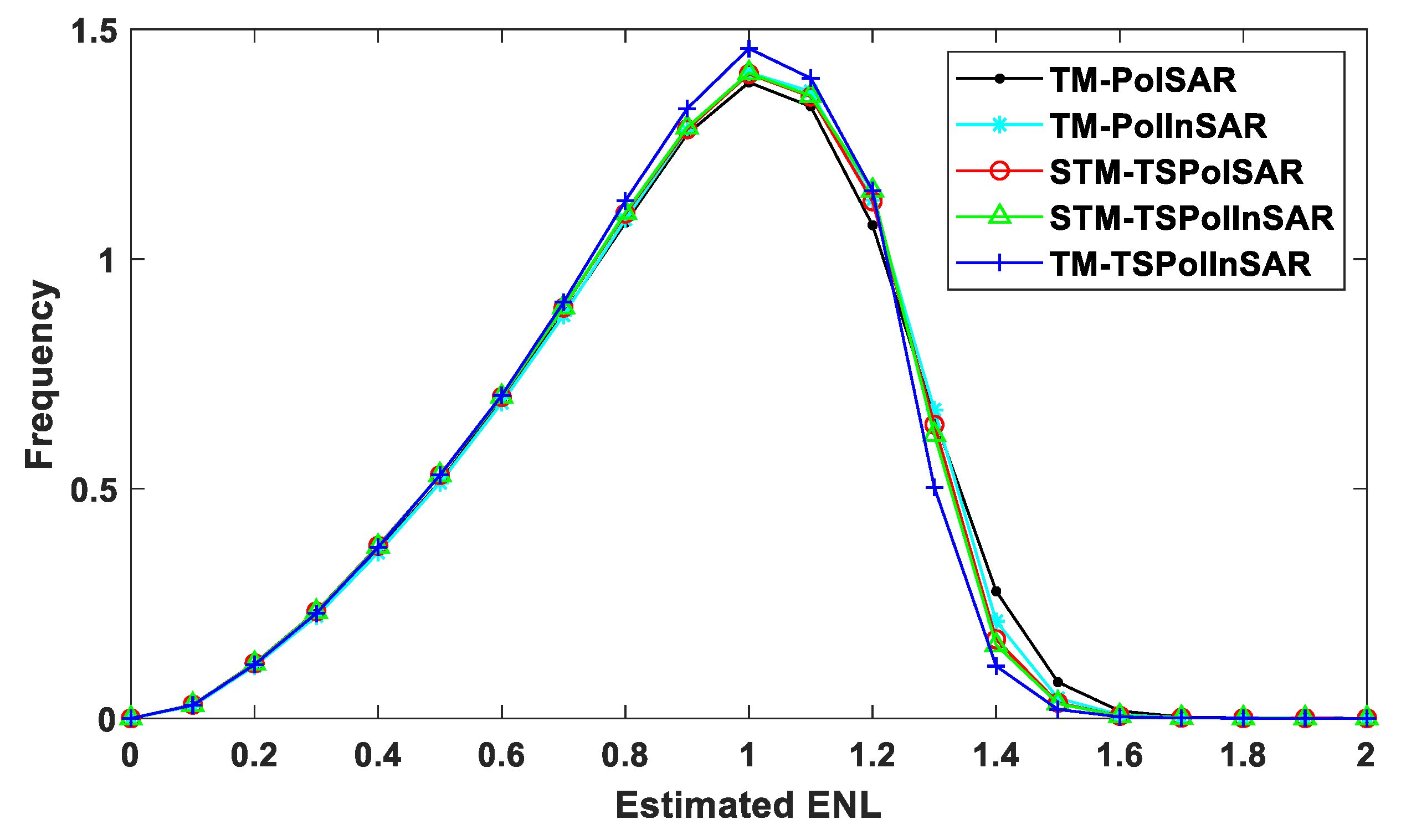
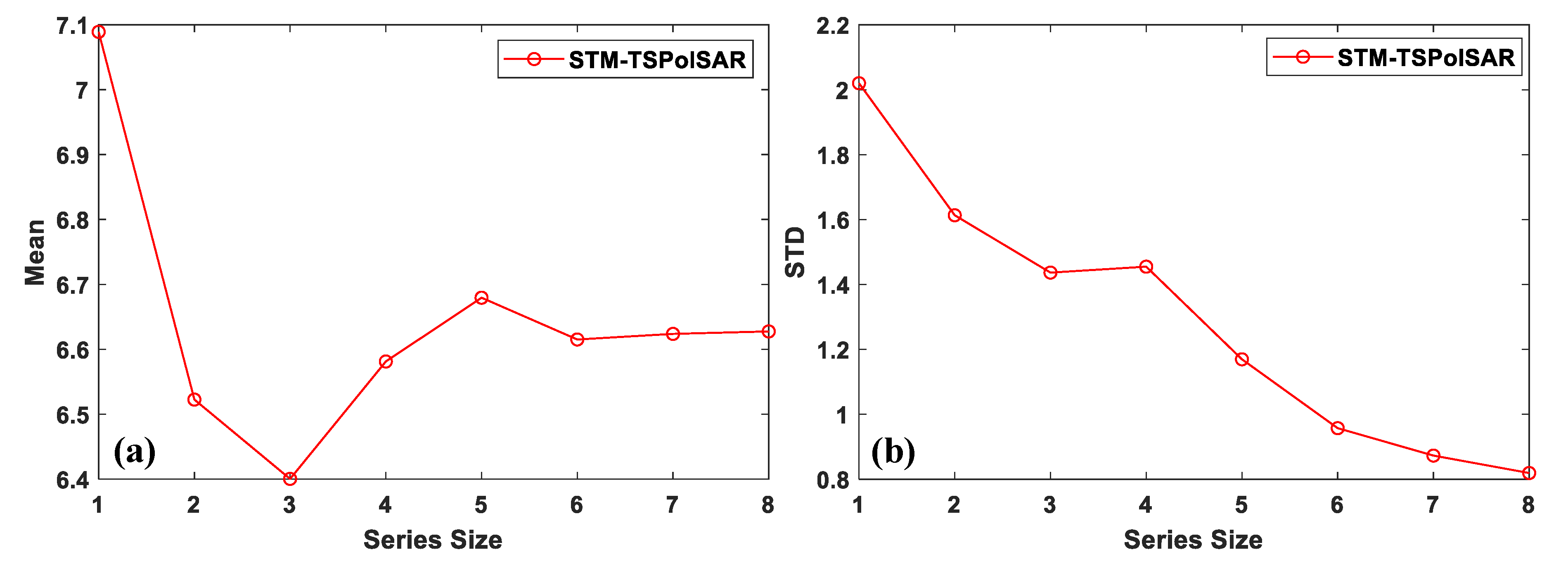
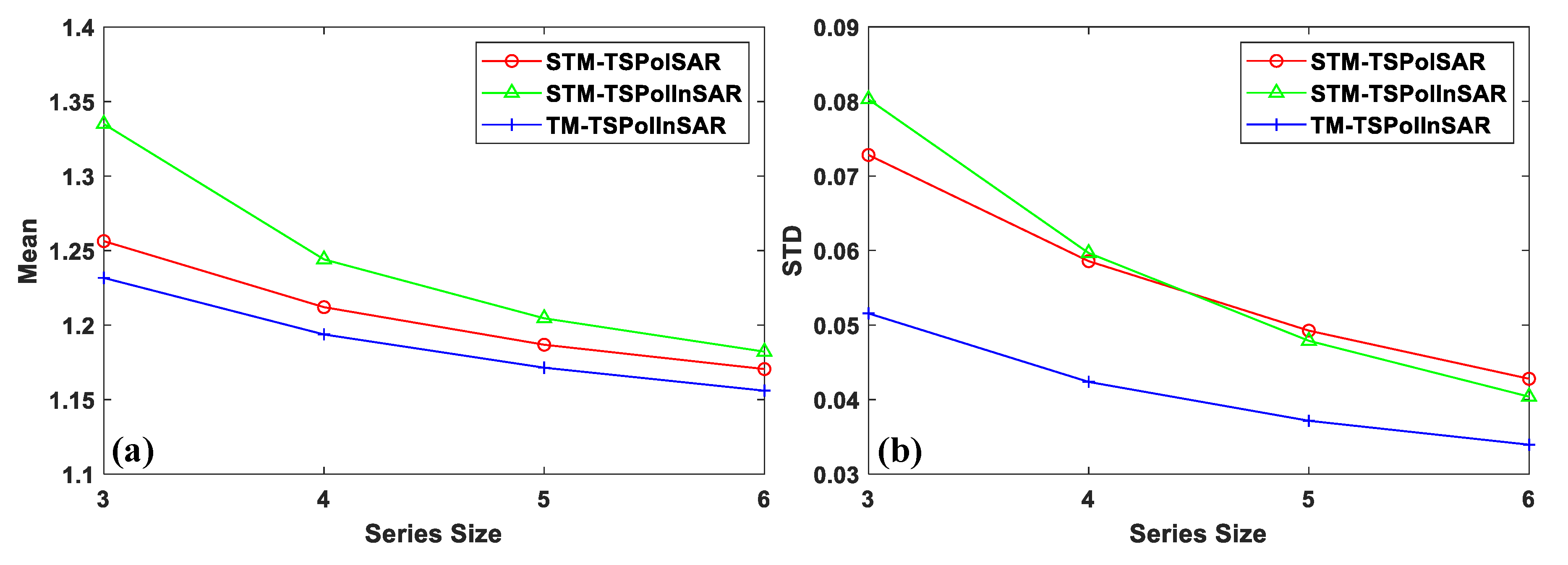
4.2. Results and Analyses of Different ENL Estimators

To evaluate the estimation performance of these estimators, we apply these estimators to the simulated 10-look TSPolInSAR data with 64 sample size and 1000 independent simulations. Figure 2 shows the distribution of different ENL estimators. The estimated means of TM-PolSAR, TM-PolInSAR, STM-TSPolSAR, STM-TSPolInSAR, and TM-TSPolInSAR estimators are 10.287, 10.247, 10.221, 10.220, and 10.209, respectively. The estimated means of all ENL estimators are greater than the true 10, which is called the positively biased effect with finite samples estimates, and the traditional TM-PolSAR estimated result is more serious. As shown in Figure 2, the estimated results of four proposed ENL estimators have more concentrated around the true 10 than the traditional TM-PolSAR estimator. The estimated STDs of TM-PolSAR, TM-PolInSAR, STM-TSPolSAR, STM-TSPolInSAR, and TM-TSPolInSAR estimators are 0.945, 0.796, 0.603, 0.582, and 0.541, respectively.

For further analyzing the estimation performance under different sample sizes, the following experiments are performed over multiple sample size set {8, 16, 32, 64, 128, 256, 512} to calculate both bias and STD statistics. With the increase of sample sizes, the estimated biases and STDs of all estimators decreases. In case of all sample sizes, the numerical ranking of the estimated biases shown in Figure 3 is TM-PolSAR > TM-PolInSAR > STM-TSPolSAR $\ge$ STM-TSPolInSAR > TM-TSPolInSAR, whose situation is the same as that of STDs. It has been demonstrated that the number of sample coherency matrix has less effect on the proposed four estimators than the traditional TM-PolSAR estimator, which means higher estimation accuracy and robustness. It is worth noticing that the proposed four ENL estimators also have more superior potential of detail preservation, which will be further discussed in Section 5 and Section 6.

It is the most suitable choice for PolInSAR data to select the proposed TM-PolInSAR estimator among these ENL estimators. However, it is necessary to quantitatively analyze the effect of the series size on the estimation performance of the other three estimators, including STM-TSPolSAR, STM-PolInSAR, and TM-TSPolInSAR. We perform the following experiments with multiple series size set {3, 4, 5, 6} and fixed sample size 64 to calculate both bias and STD statistics. As we expect in Figure 4, the estimated biases and STDs of all estimators reduce down with the increase of the series size, because the observation information is continuously enhanced to a certain extent from both temporal characteristics or interferometric coherence aspects. On the whole, according to the estimated bias indicator, the numerical ranking is STM-TSPolSAR $\approx$ STM-TSPolInSAR > TM-TSPolInSAR; based on the estimated STDs, the numerical ranking is STM-TSPolSAR > STM-TSPolInSAR > TM-TSPolInSAR.

Therefore, the simulated experiment has demonstrated that the proposed TM-PolInSAR estimator is more suitable to PolInSAR data than the traditional TM-PolSAR estimator; both STM-PolSAR and STM-PolInSAR estimators show the similar estimation performance on the mean aspect, but the STM-PolInSAR estimator has a lower estimated variance than the STM-PolSAR estimator; the proposed TM-TSPolInSAR estimator achieves the best effect among all estimators.

5. Experimental Results of Two Real TSPol(In)SAR Datasets

The ENL can describe the speckle noise level in the SAR data model and evaluate the region homogeneity level in both edge detection and superpixel generation. In order to verify the effectiveness of four proposed ENL estimators in the aforementioned aspects, we select a C-band RADARSAT-2 TSPolSAR data with long-term observation and a P-band E-SAR TSPolInSAR data with short-term observation for detailed comparison and quantitative analysis in Section 6, mainly including statistical characteristics and homogeneity evaluation performance. The following is to introduce both TSPol(In)SAR datasets and the experimental results of different ENL estimators.

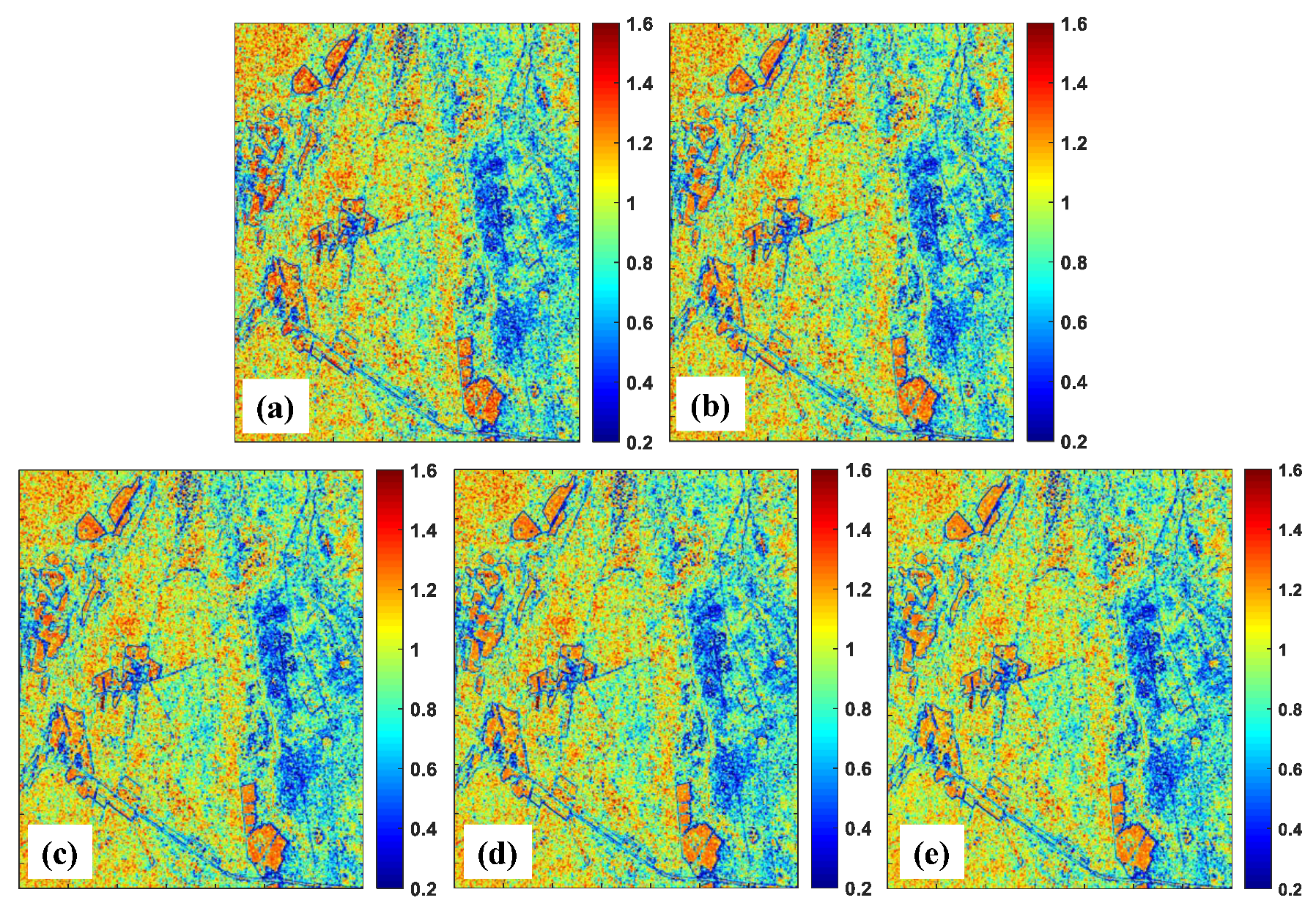
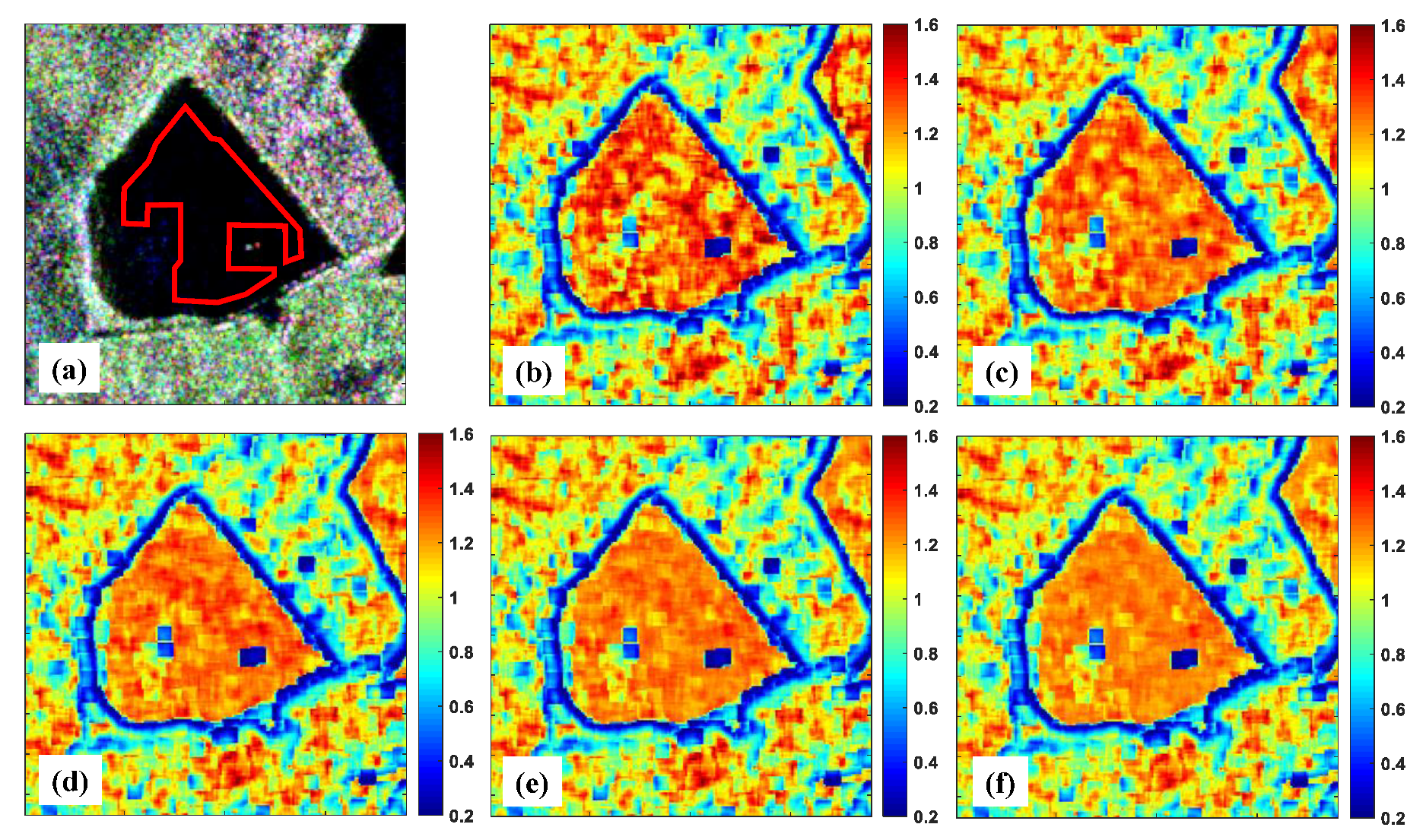
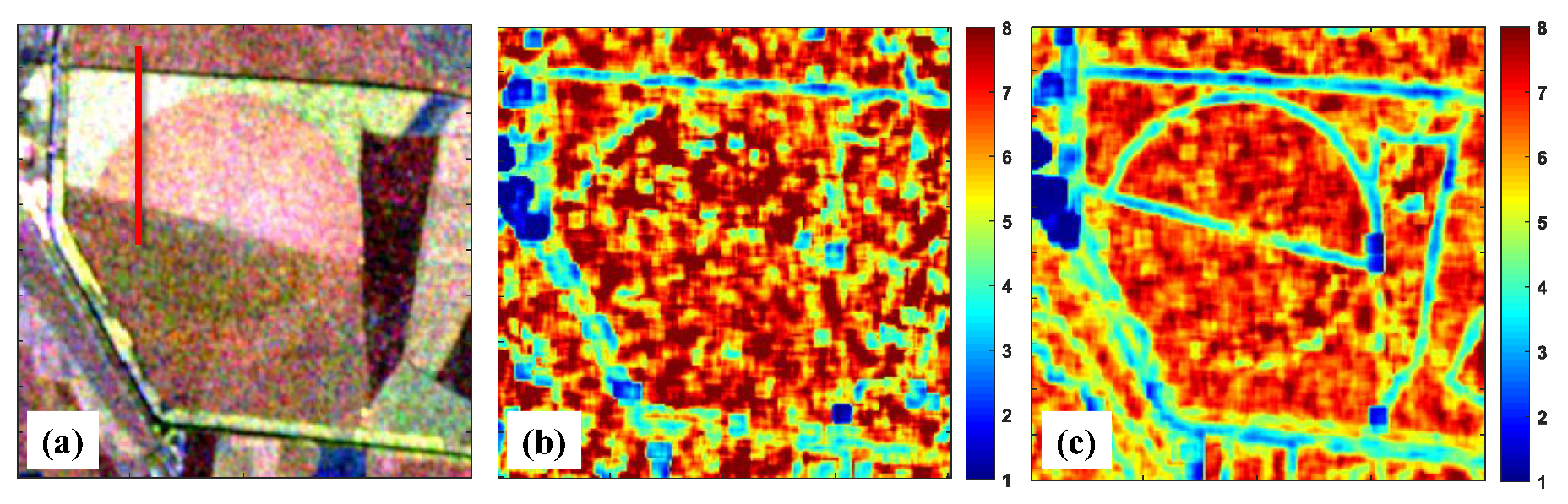
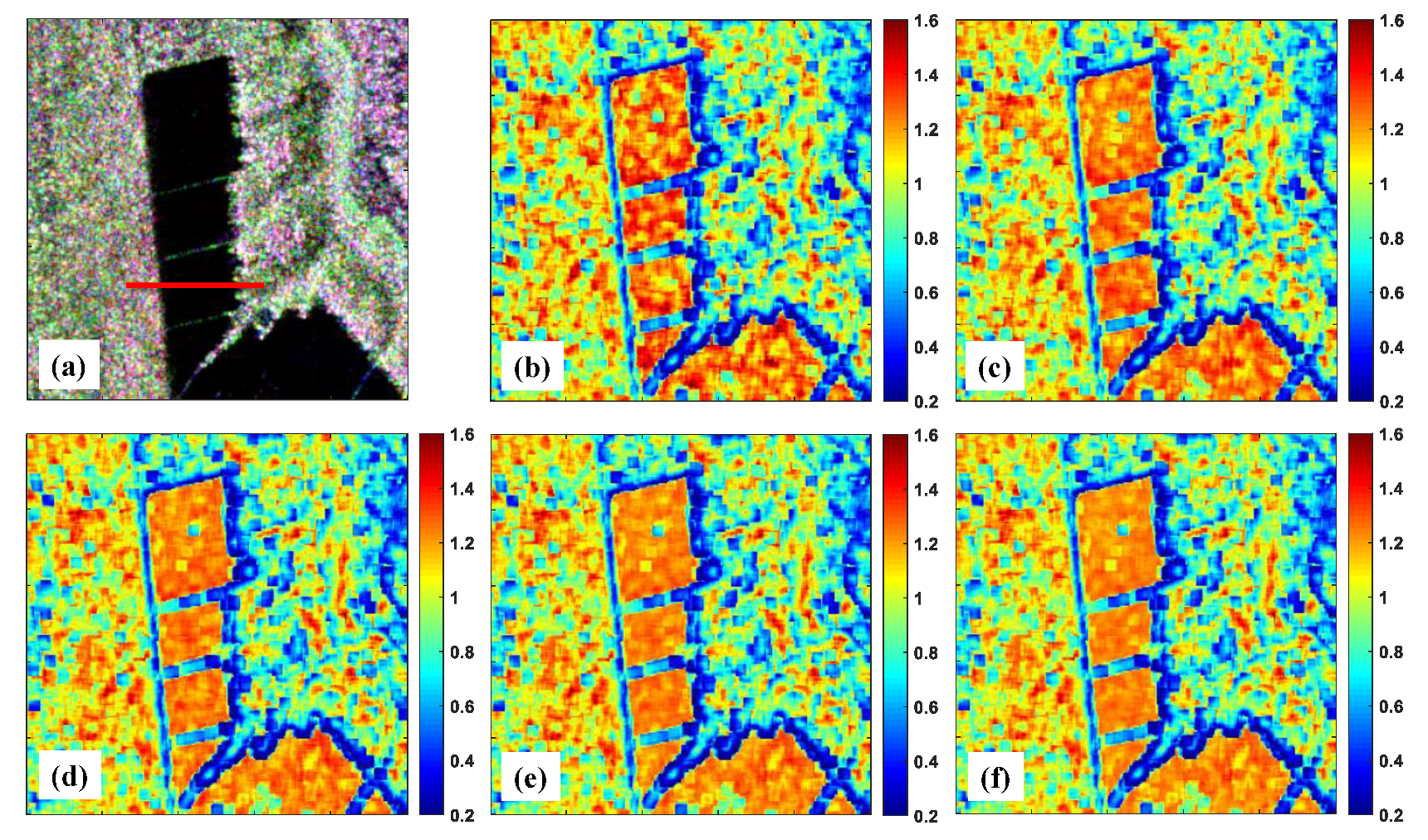
5.1. Experimental Results Based on C-band RADARSAT-2 TSPolSAR Data

Eight C-band RADARSAT-2 Fine Quad-Pol SAR images with beam mode FQ14 are selected from AgriSAR 2009 campaign, which covers the Barrax test area, La Mancha plateau, Spain. The purpose of the AgriSAR 2009 campaign is to understand and demonstrate the superior potential of employing time-series PolSAR data in refined crop classification and phenological monitoring. The selected images are acquired in the ascending passes and with the beam FQ14 using the same incidence angle, from 9 April, 2009 to 24 September, 2009, with an acquisition interval 24 days. The original provided TSPolSAR data consists of eight polarimetric coherency matrices, and hence in this section we mainly compare and analyze the estimation performance of traditional TM-PolSAR and proposed STM-TSPolSAR estimators. Figure 5 shows the PauliRGB image, which is obtained by the temporal average of RADARSAT-2 time-series polarimetric coherency matrices. The landscape in the averaged PauliRGB image mainly contains many kinds of the crop with time-varying polarimetric characteristics, mainly including alfalfa, barley, wheat, and corn.

To evaluate the overall estimation capability of both TM-PolSAR and STM-TSPolSAR estimators, we perform both estimators with a sliding window of size 7 × 7 to estimate the full scene ENL, as shown in Figure 6. Taking the averaged PauliRGB image as the reference, most of the edges of the STM-TSPolSAR estimated result correspond to the farmland boundary obviously. However, the TM-PolSAR estimator overestimates the overall scene and cannot identify many boundaries. Because the proposed STM-TSPolSAR estimator utilizes multitemporal sample coherency matrix and takes the time-varying polarimetric characteristics of crop into consideration. It can be seen in Figure 7 that the proposed STM-TSPolSAR estimator makes the ENL more concentrated and more effectively reduces the positively biased effect due to finite samples estimates.

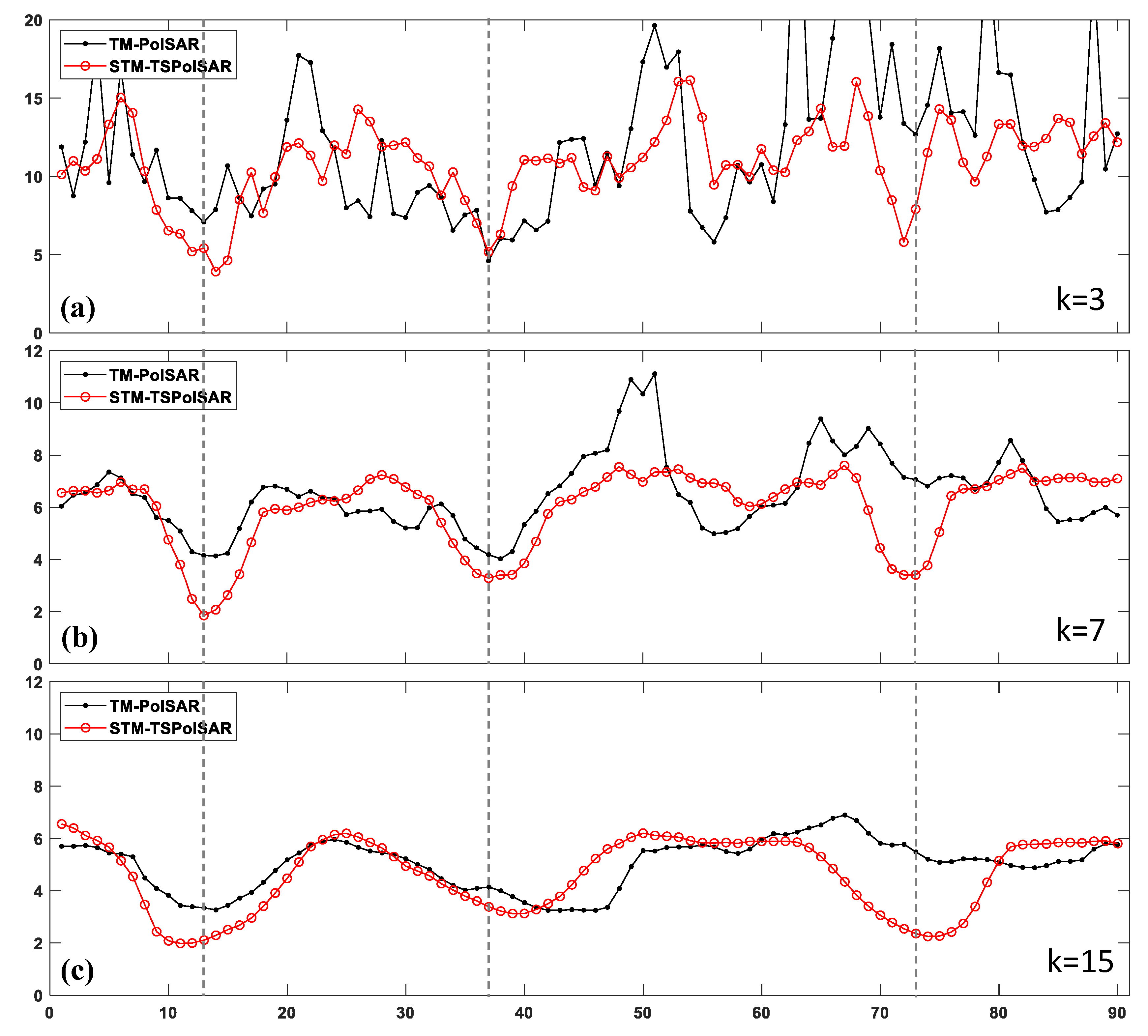
5.2. Experimental Results Based on P-band E-SAR TSPolInSAR Data

The P-band E-SAR full polarimetric SAR images acquired in BioSAR 2008 project cover the forest area, which is located in the Kcycklan catchment, Sweden. In the BioSAR 2008 project, the primary purpose is to support the development of forest biomass estimation algorithms under long-wavelength SAR signal and the earth observation task simulation of future BIOMASS satellite. Six full polarimetric SAR images are acquired from the same ascending orbit on 14 October 2008, with an acquisition every around 17 min. After 2:1 multi-looking operation in both azimuth and range directions, we select a 1700 × 1400 area for further investigation shown in Figure 8. The original provided SLC data can construct the TSPolInSAR data, and the following is to compare the overall estimation performance of the traditional TM-PolSAR and proposed four estimators. As shown in Figure 8, the selected test area mainly consists of coniferous forests, broadleaved forests, grassland, roads, and some houses. It is worth noting that the short-term observation interval and long-wavelength SAR observation mean that the polarimetric stationarity of the ground objects can be maintained.

To see the overall effect of the estimation, these estimated ENL images of different ENL estimators with a sliding window size 7 × 7 are shown in Figure 9. On the whole, this estimator achieves a similar effect, but there exist some difference in Figure 9 which requires further detailed analysis. From the estimated ENL distribution in Figure 10, the traditional TM-PolSAR estimator still has a positively biased effect, but these proposed estimators are less affected. Especially, the estimated results with the proposed TM-TSPolInSAR estimator are the most concentrated, because the proposed method is based on the standard TSPolInSAR data and maximizes the use of all observed information from the ground object.

6. Discussion and Analysis Based on Two Real TSPol(In)SAR Datasets

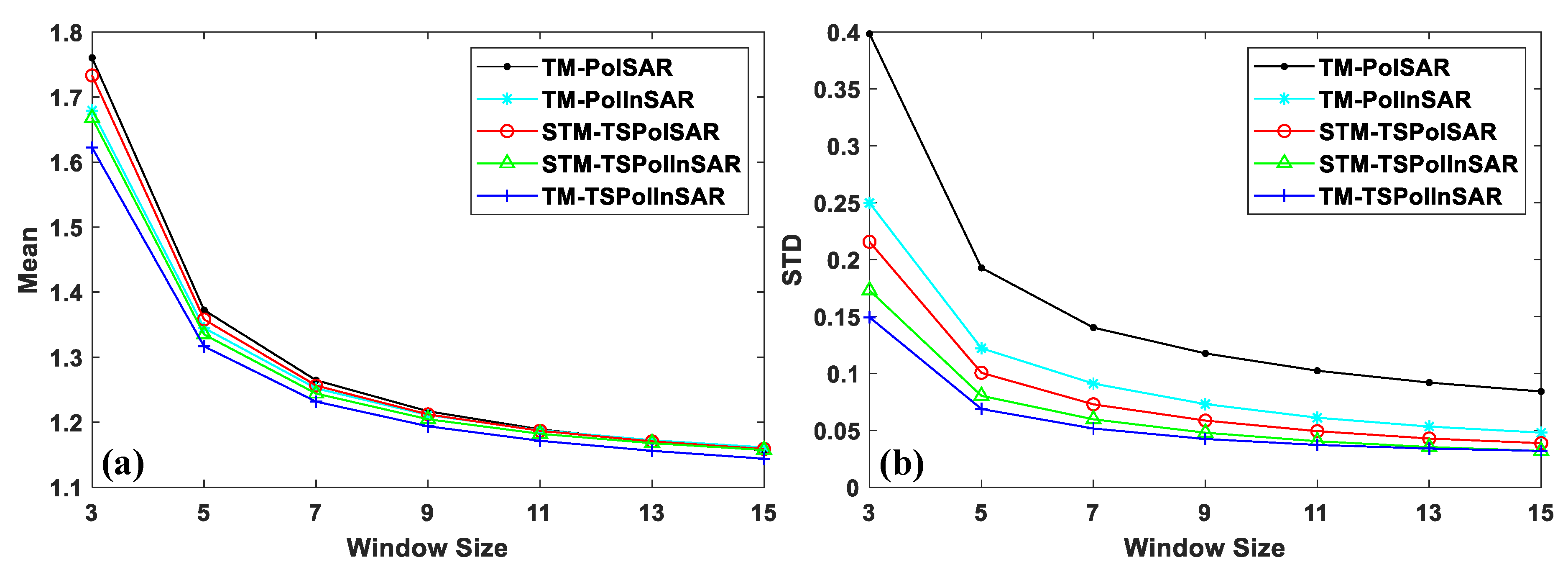
6.1. Comparison of Statistical Characteristics Based on The Homogeneous Areas

The ENL can describe the speckle noise level in the SAR data model, and hence the following is to analyze the statistical characteristics of different ENL estimators in detail. The overall image of C-band RADARSAT-2 TSPolSAR data is processed by both traditional TM-PolSAR and proposed STM-TSPolSAR estimator with a sliding window size set $\left\{k\times k|k=3,5,7,9,11,13,15\right\}$ and multiple series size set $\left\{1,2,3,4,5,6,7,8\right\}$. As shown in Figure 11, both ENL images of ROI-I marked by the dotted box in Figure 5 are estimated with a sliding window size 7 × 7. The proposed STM-TSPolSAR estimator effectively detects the round boundary of central farmland shown in Figure 11c, but the traditional TM-PolSAR estimator fails shown in Figure 11b. For performing quantitative analysis based on the homogeneous area, we make statistics of both mean and STD indicators on the red ellipse marked area (5463 pixels) under multiple window and series sizes shown in Figure 12 and Figure 13, respectively. With the increase of sliding window size, all statistical values of both estimators decreases. The proposed STM-TSPolSAR estimator has more robust statistical characteristics, and both estimated mean and STD indicators are always less than that of TM-PolSAR estimator regardless of window size. Besides, with the increase of series size, the STD reduces down, but the mean decreases first, then increases, and finally tends to be stable. The ENL estimation is easily affected by the degree of heterogeneity between the selected pixels. For the crop with time-varying polarimetric characteristics, at first, with the increase of SAR observation number, the changes between the observed pixels in the selected farmland are slightly different, and the estimated mean leads to a significant decrease. However, as the number of time-series observations increases to a certain extent, the temporal variation of the observed pixels is stable, the corresponding estimated mean rises and, finally, tends to be stable.

The following is based on P-band E-SAR TSPolInSAR data to analyze the statistical characteristics of different ENL estimators under multiple parameters. Specifically, the full image is processed by these estimators with a sliding window size set $\left\{k\times k|k=3,5,7,9,11,13,15\right\}$ and multiple series size set $\left\{1,2,3,4,5,6\right\}$. Figure 14 shows the estimated ENL images of ROI-III (190 × 190 pixels) under different estimators with a sliding window size 7 × 7. There exist some large fluctuations in the grassland using the traditional TM-PolSAR estimator, while other estimated results look smoother, especially of STM-TSPolInSAR and TM-TSPolInSAR estimators. Based on a homogeneous area marked by the red polygon (3674 pixels) in Figure 14, both mean and STD indicators are computed under multiple window and series sizes for analyzing the statistical characteristics, as shown in Figure 15 and Figure 16. In all estimated results with multiple window sizes, as shown in Figure 15, the numerical ranking of the estimated means is TM-PolSAR > STM-TSPolSAR > TM-PolInSAR > STM-TSPolInSAR > TM-TSPolInSAR, and the numerical ranking of the estimated STDs is TM-PolSAR > TM-PolInSAR > STM-TSPolSAR > STM-TSPolInSAR > TM-TSPolInSAR. In case of multiple series sizes, as shown in Figure 16, the numerical ranking of the estimated means is STM-TSPolInSAR > STM-TSPolSAR > TM-TSPolInSAR, and the numerical ranking of the estimated STDs is STM-TSPolSAR $\approx$ STM-TSPolInSAR > TM-TSPolInSAR. Additionally, the window or series size increases, and the estimated mean and STD decrease. It can be seen from the aforementioned estimates that the estimated effect of ENL is similar to the simulated experimental results because the P-band E-SAR TSPolInSAR data acquired with a short-term observation interval maintains the polarimetric stationarity in time.

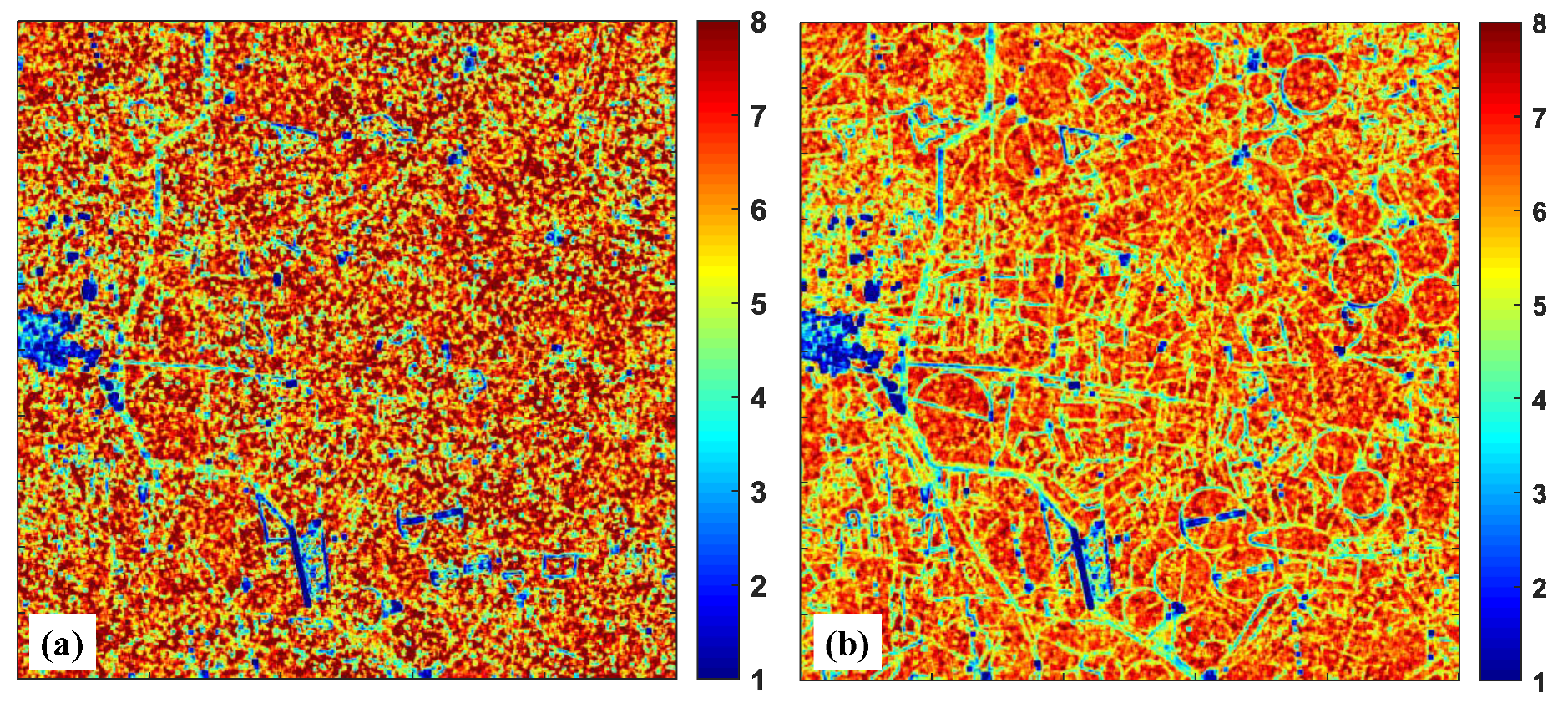
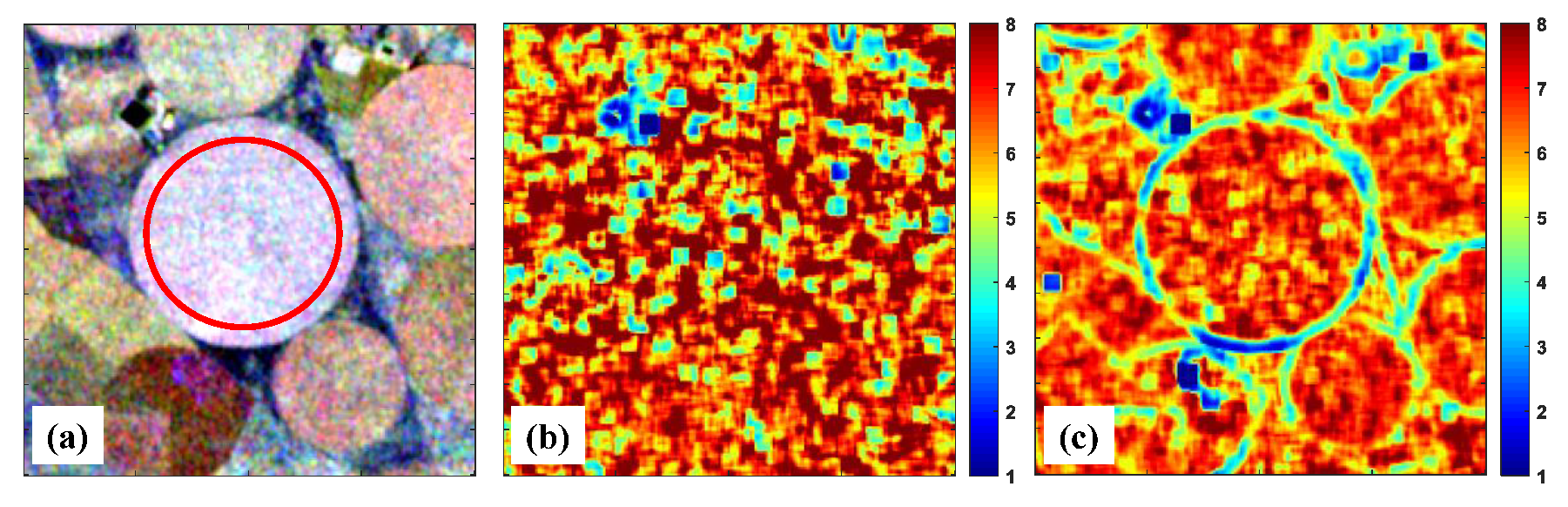
6.2. Comparison of Homogeneity Evaluation Performance Based on the Textured Areas

The ENL estimator can evaluate the region homogeneity level, and hence the following is to make a detailed analysis of the homogeneity evaluation performance of different ENL estimators. For C-band RADARSAT TSPolSAR data, traditional TM-PolSAR and proposed STM-TSPolSAR estimators with a sliding window size 7 × 7 estimate the ENL images of ROI-II marked by the dotted box in Figure 5. It is seen from Figure 17a that many edges cannot be detected by the TM-PolSAR estimator in Figure 17b. In contrast, as shown in Figure 17c, the estimated ENL image of the proposed STM-TSPolSAR estimator contains most boundaries, because this proposed method is different from the traditional method in that the time-varying polarimetric characteristics of the crop is taken into consideration. Then, the estimated ENL profiles along the red line marked in Figure 17a with three window sizes are shown in Figure 18 for quantitatively analyzing the edge detection capability. As shown in Figure 18, taking the manually judged edges marked by the gray dotted lines as the reference, in case of all window sizes, the proposed STM-TSPolSAR estimator detects the third edge but the traditional TM-PolSAR estimator cannot. With the increase of sliding window size, the position of the detected edges change and blur in the case of a large window. It is seen from Figure 18a that the proposed estimator has an excellent performance on region homogeneity evaluation even in the case of small windows, but traditional estimated result easily occurs some false edge. Obviously, the estimated result of the classical estimator with a large sliding window has blurred the second edge significantly, as seen in Figure 18c. Therefore, it has been demonstrated that the proposed STM-TSPolSAR estimator has detected the edge more accurately and robustly that the traditional TM-PolSAR estimator.

The following experiment is based on the P-band E-SAR TSPolInSAR data to estimate the ENL results in the ROI-IV marked by the dotted box in Figure 8 for analyzing the performance of region homogeneity evaluation. Obviously, as shown in Figure 19a, the ROI-IV contains many clear edges and is suitable for evaluating the edge detection ability of different estimators. The estimated ENL images of ROI-IV, with a sliding window size of 7 × 7, are shown in Figure 19b–f. Taking the averaged PauliRGB image as the reference, most of the edges are detected by all estimators effectively, and it shows a similar estimation performance. Then, for further detailed analysis of the edge detection capability, the estimated ENL profiles along the red line marked in Figure 19a with three window sizes are shown in Figure 20. According to the manually judged edges, all estimators can effectively detect the edges in case of three window sizes, but the corresponding position has deviated from the real place as the window size increases. However, it is seen from Figure 20b that the traditional TM-PolSAR estimated results are unstable in the homogeneous area, and it means the appearance probability of false edge is much higher than the proposed four ENL estimators. Therefore, these proposed ENL estimators have a more robust estimation performance, and it also can enhance the capability of region homogeneity evaluation, especially STM-TSPolSAR, STM-TSPolInSAR, and TM-TSPolInSAR estimators.

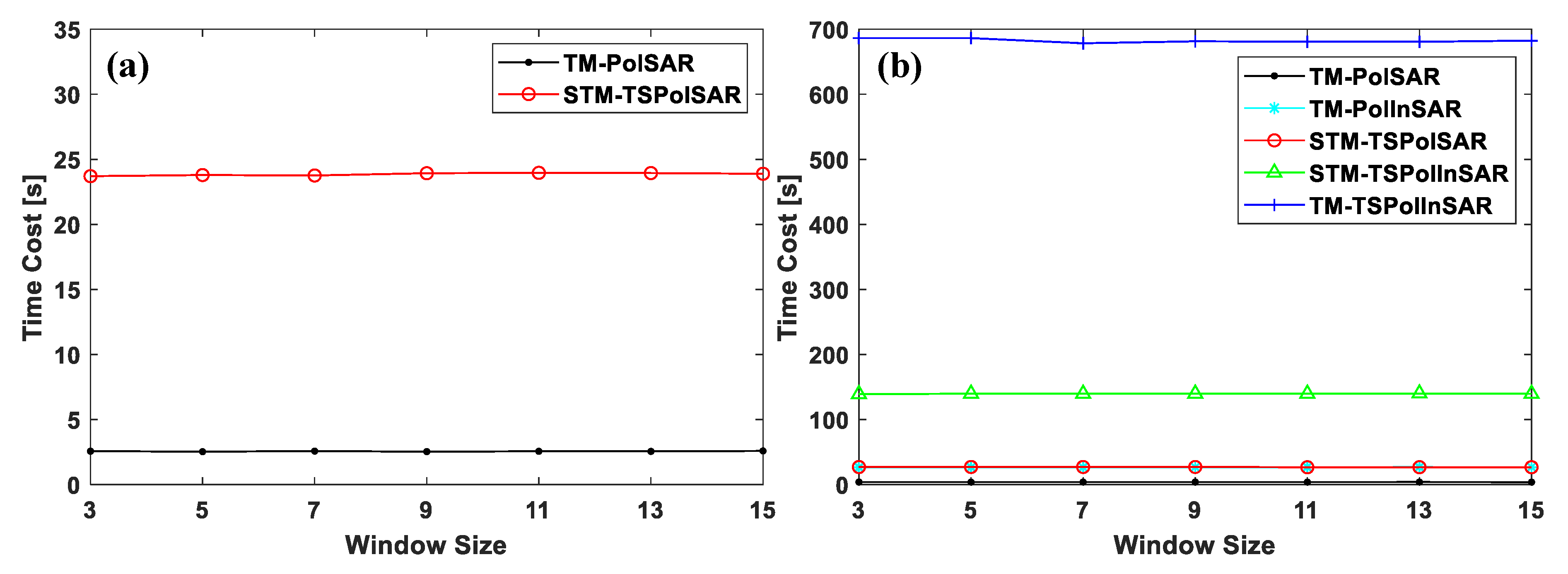
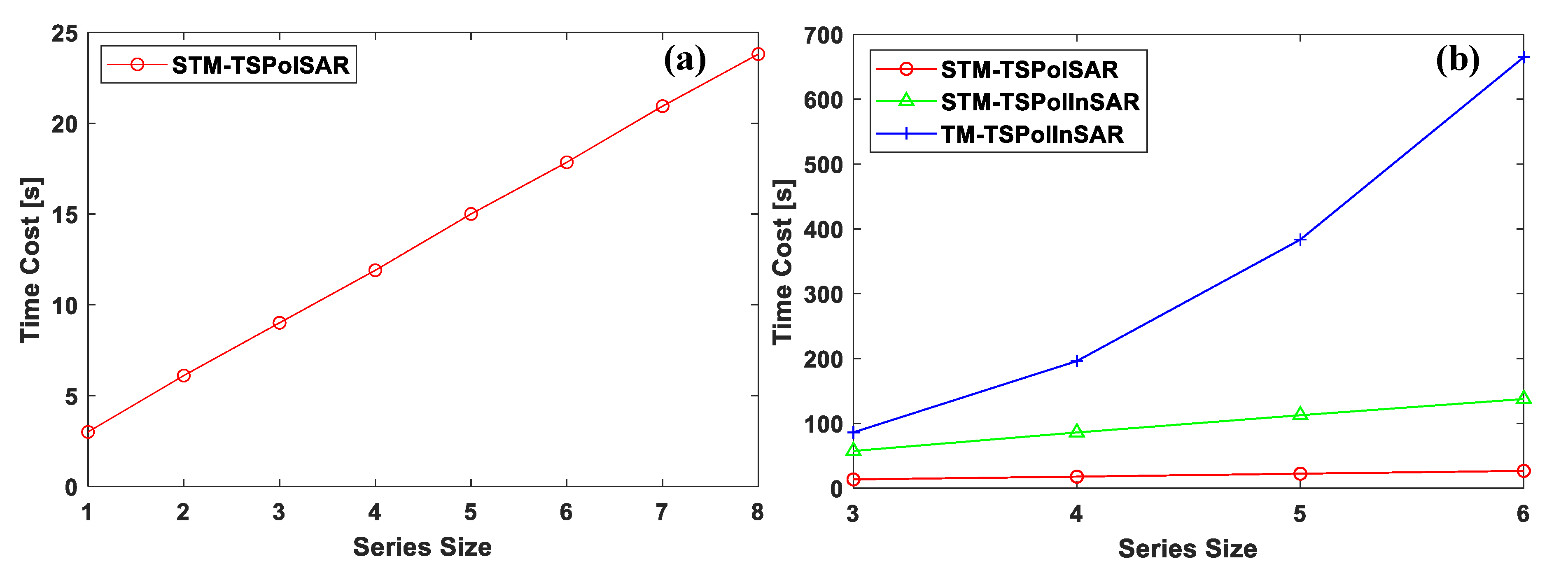
6.3. Efficiency Comparison Based on Two TSPol(In)SAR Datasets

We finally present the efficiency comparison of different ENL estimators in terms of memory size and time cost. All ENL estimation processing is implemented by MATLAB programming software under the hardware configuration of a single-core 3.4GHz CPU and 80 GB RAM. Supposing an image of I × J size with P polarization channels acquired by N observations,

Table 1. Memory sizes of processing data in different ENL estimators.

Estimator	TM-PolSAR	TM-PolInSAR	STM-TSPolSAR	STM-TSPolInSAR	TM-TSPolInSAR
Memory Size	IJP2	IJ(2P)2	IJP2N	IJ(2P)2(N−1)	IJ(PN)2

displays the memory sizes of data to be processed in different ENL estimators. It can be seen in Table 1 that the memory size of processing data increases exponentially as the number of observations increases. The memory size of both STM-TSPolSAR and STM-TSPolInSAR estimators is one order of magnitude lower than that of the TM-TSPolInSAR estimator. Based on two TSPol(In)SAR data used above, we compute the time cost of different estimators with multiple window and series sizes shown in Figure 21 and Figure 22, respectively. The time costs of all estimators are independent of the window size in Figure 21, and the numerical ranking is TM-PolSAR < TM-PolInSAR $\approx$ STM-TSPolSAR < STM-TSPolInSAR < TM-TSPolInSAR. Additionally, as shown in Figure 22, with the series size increases, the time cost of the STM-TSPolSAR estimator grows slowly, the STM-PolInSAR estimator approaches linear growth, but the TM-TSPolInSAR estimator grows rapidly, similar to the exponential growth.

7. Conclusions

To overcome the limitation of the inadequate observation information in traditional estimators, this paper is based on the TSPol(In)SAR data and proposes four novel ENL estimators, including TM-PolInSAR, STM-TSPolSAR, STM-TSPolInSAR, and TM-TSPolInSAR estimators. These proposed ENL estimators take the temporal characteristics or interferometric coherence into consideration and satisfy the requirement of most TSPol(In)SAR data types in the practical applications [36].

Three experimental TSPol(In)SAR datasets are selected for detailed comparison and quantitative analysis on the estimation performance, including simulated 10-look TSPolInSAR data, C-band RADARSAT-2 TSPolSAR data, and P-band E-SAR TSPolInSAR data. It has been demonstrated that the proposed four estimators show more accurate and robust statistical characteristics under multiple window and series sizes than that of the traditional TM-PolSAR estimator. According to the estimated bias or mean and STD, both STM-TSPolSAR and STM-TSPolInSAR estimators have similar estimation performance, and the TM-TSPolInSAR estimator shows the best effect due to the full use of the observation information of ground objects. It is worth noting that the proposed STM-TSPolSAR estimator has a more effective capability of region homogeneity evaluation and detects many edges that the traditional TM-PolSAR estimator cannot discover. Because this proposed method utilizes polarimetric coherency matrices of all observation and considers the time-varying polarimetric characteristics of the crop. Finally, referring to the efficiency comparison of different ENL estimators in terms of both memory size and time cost aspects, we apply these estimators to the following TSPol(In)SAR data type:

(1)

The TM-PolInSAR estimator can be applied to PolInSAR data;

(2)

The ENL of TSPolSAR data can be estimated by the STM-TSPolSAR estimator;

(3)

The STM-TSPolInSAR estimator can be applied to TSPolInSAR data with single reference or small baseline set.

(4)

In case of fewer observations, the proposed TM-TSPolInSAR estimator estimates the ENL of standard TSPolInSAR data.

This paper is based on the complex Wishart distributed coherency matrix and extends the TM estimator to multiple types of TSPol(In)SAR data. The spatial resolution of SAR images gets higher and higher, and a resolution cell can have the opportunity to observe much thinner spatial features that cause a higher scene heterogeneity in the SAR clutter. Therefore, a non-Gaussian model should be considered, and the corresponding estimator also can be easily applied to high-resolution TSPol(In)SAR data according to the same strategy in this paper, which will obtain a better estimation performance. In the future, these improved ENL estimators with the superior estimation performance will be widely used in TSPol(In)SAR application, such as multitemporal polarimetric (interferometric) SAR filter, multi-temporal crop classification, and superpixel generation.