Direction-of-Departure and Direction-of-Arrival Estimation Algorithm Based on Compressive Sensing: Data Fitting
Abstract
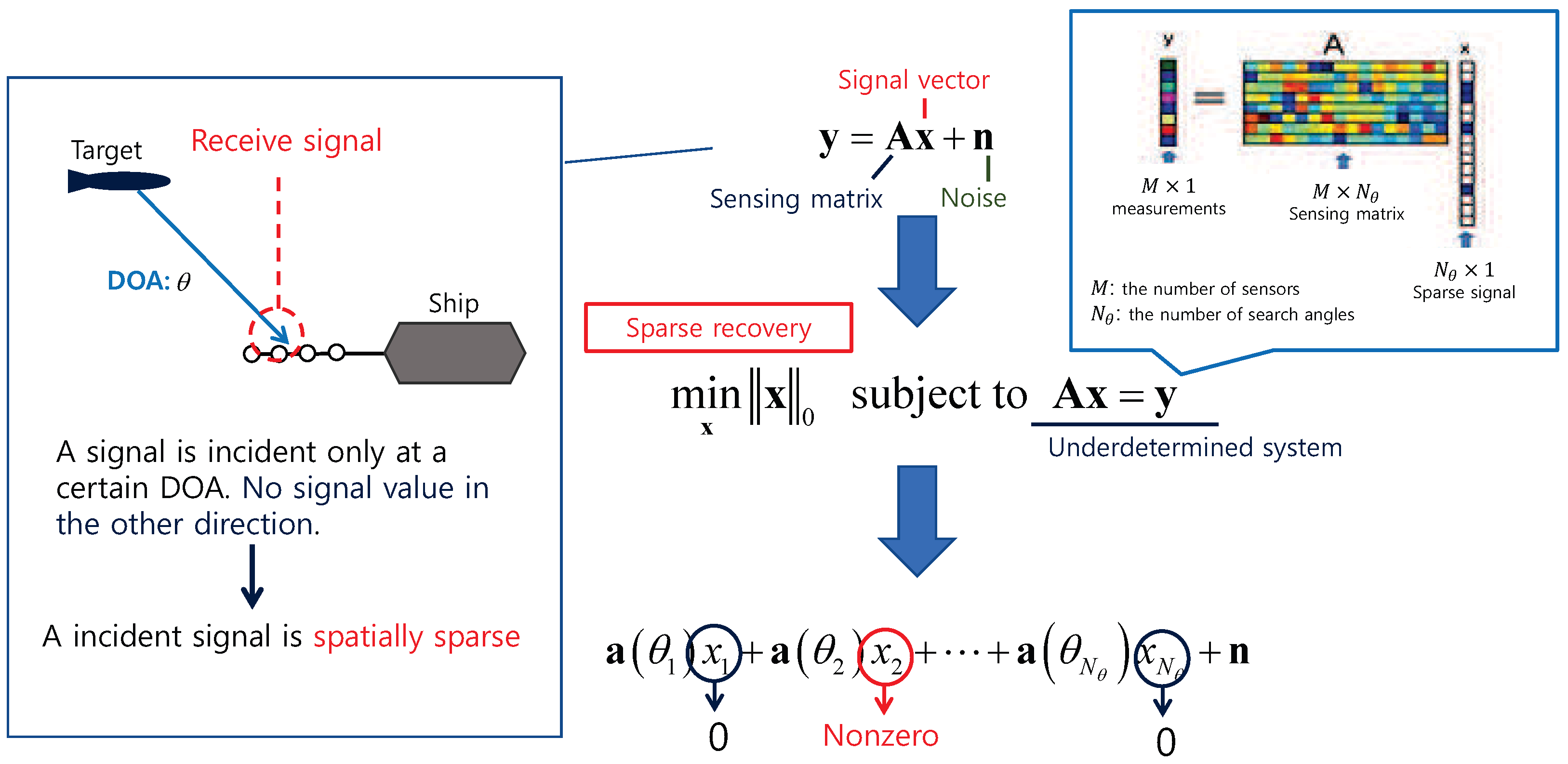
:1. Introduction
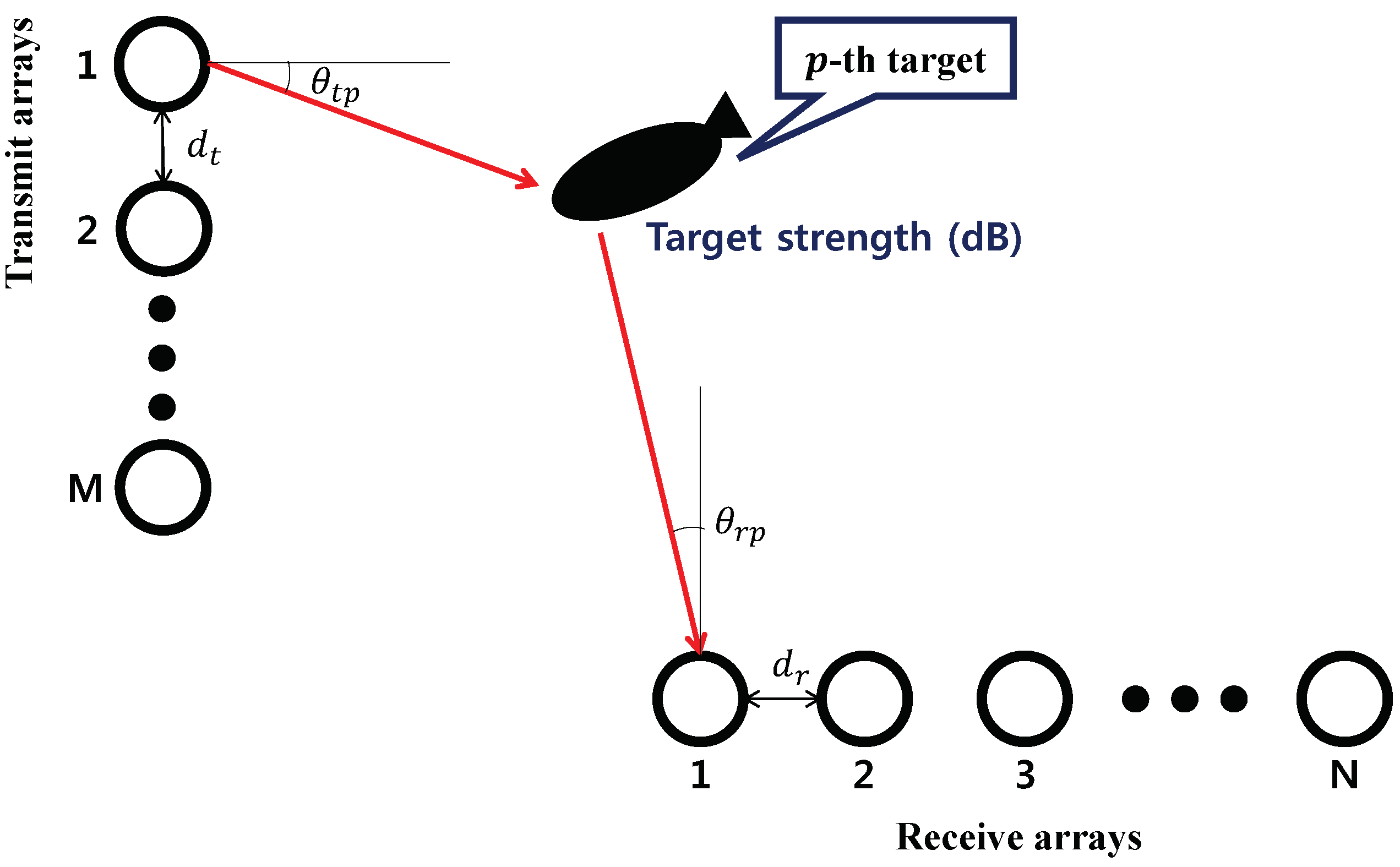
2. Signal Modeling of Bistatic MIMO Sonar System
3. Bistatic Data Fitting DOD/DOA Estimation Algorithm
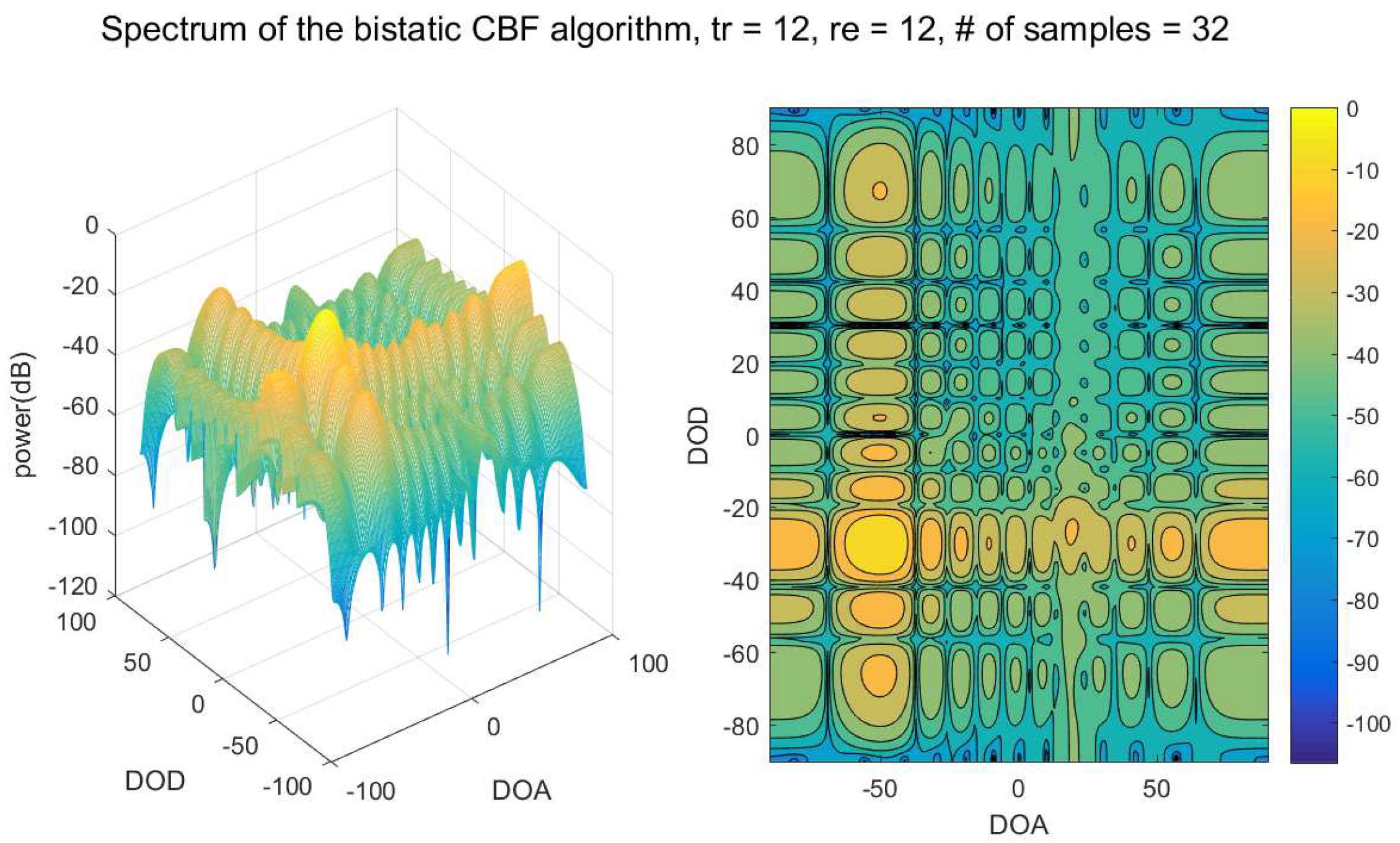
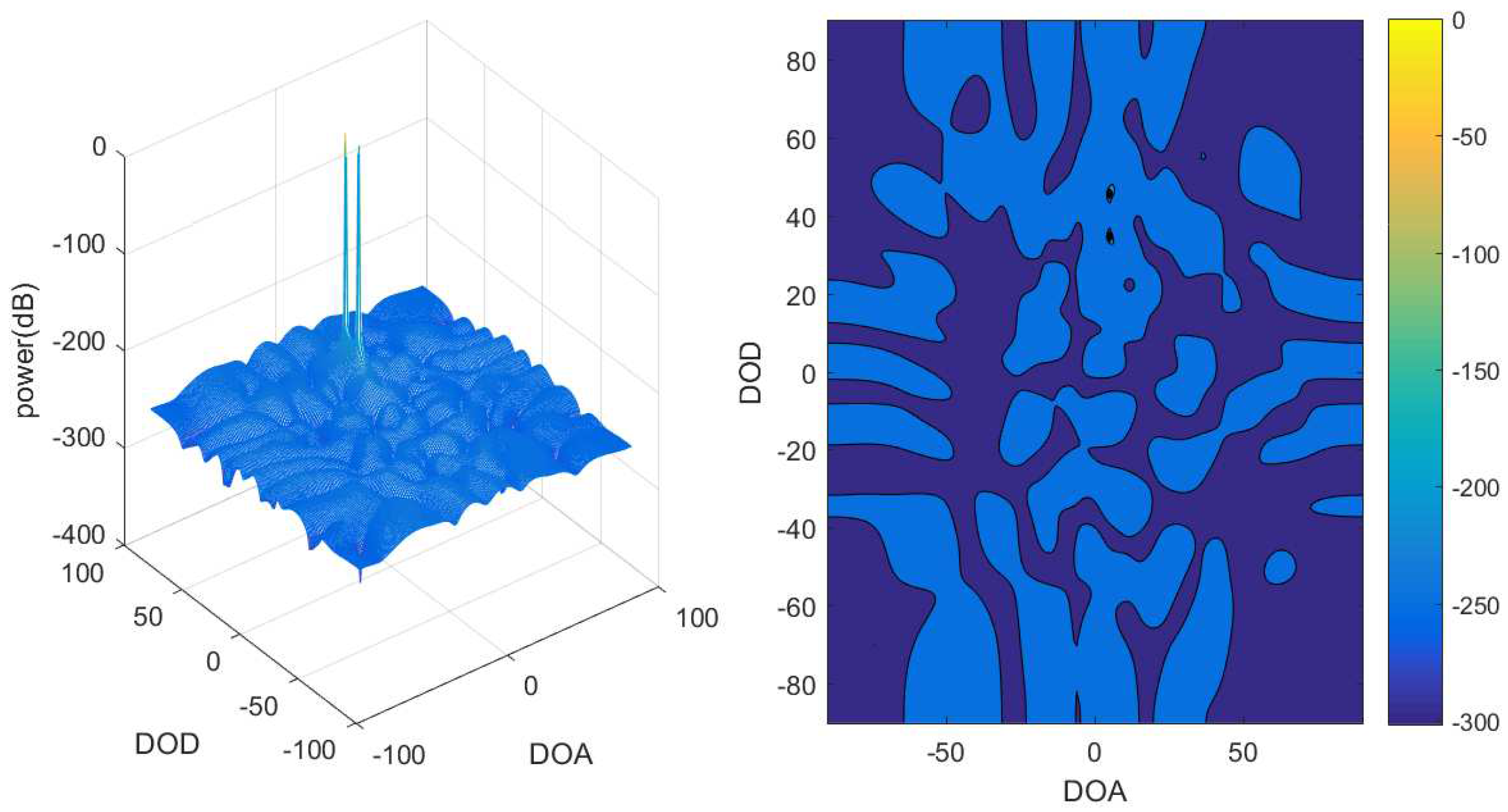
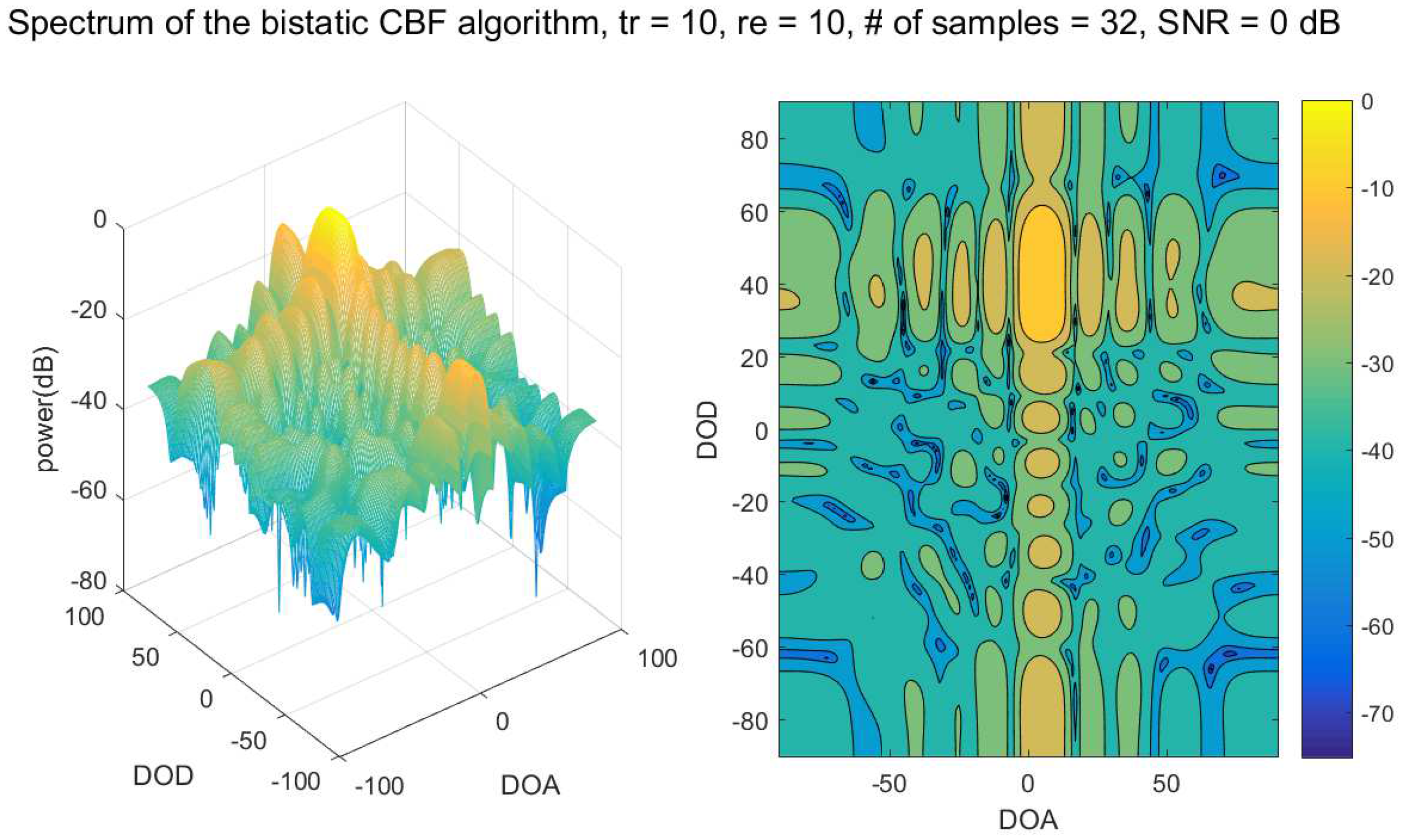
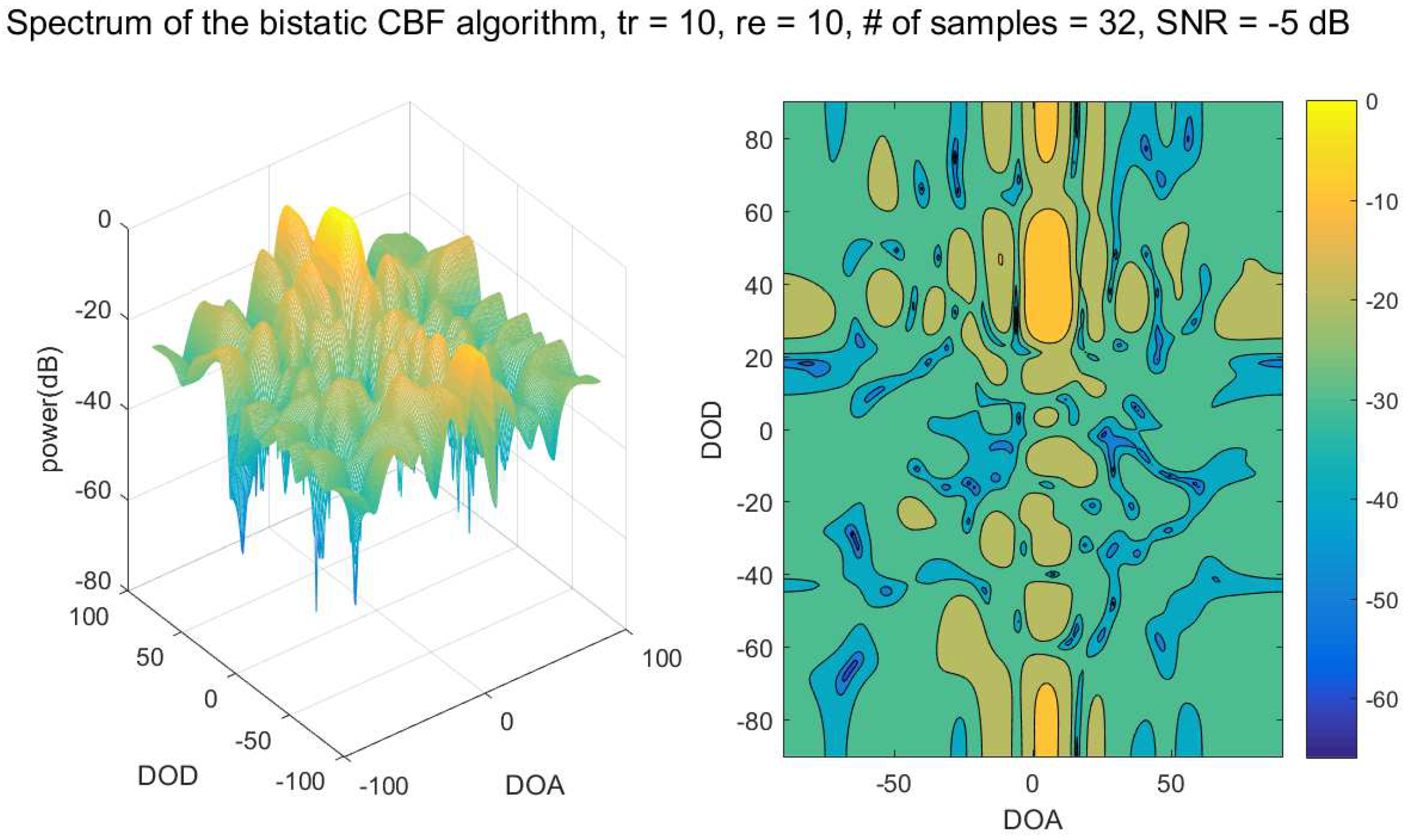
4. Numerical Results
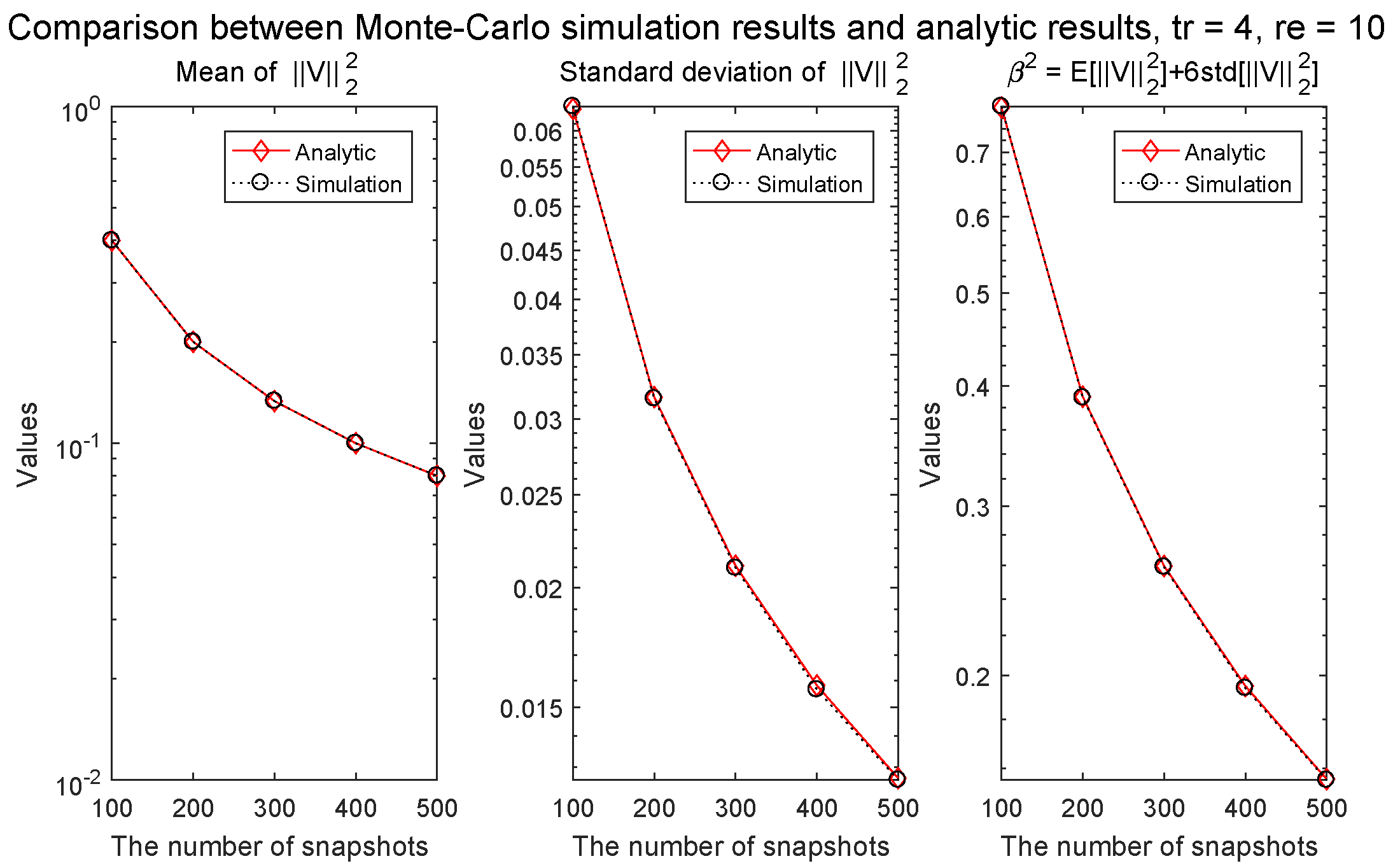
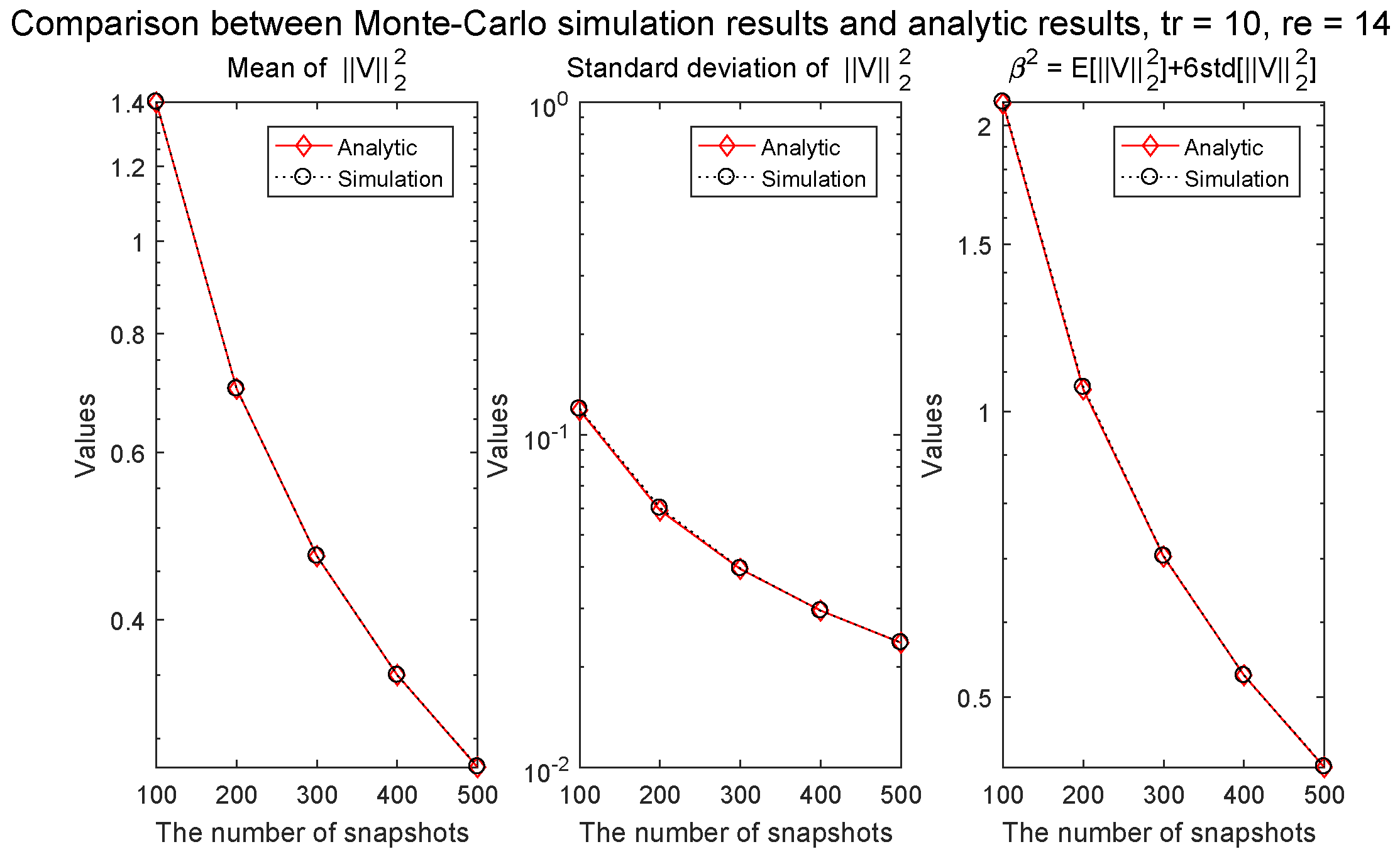
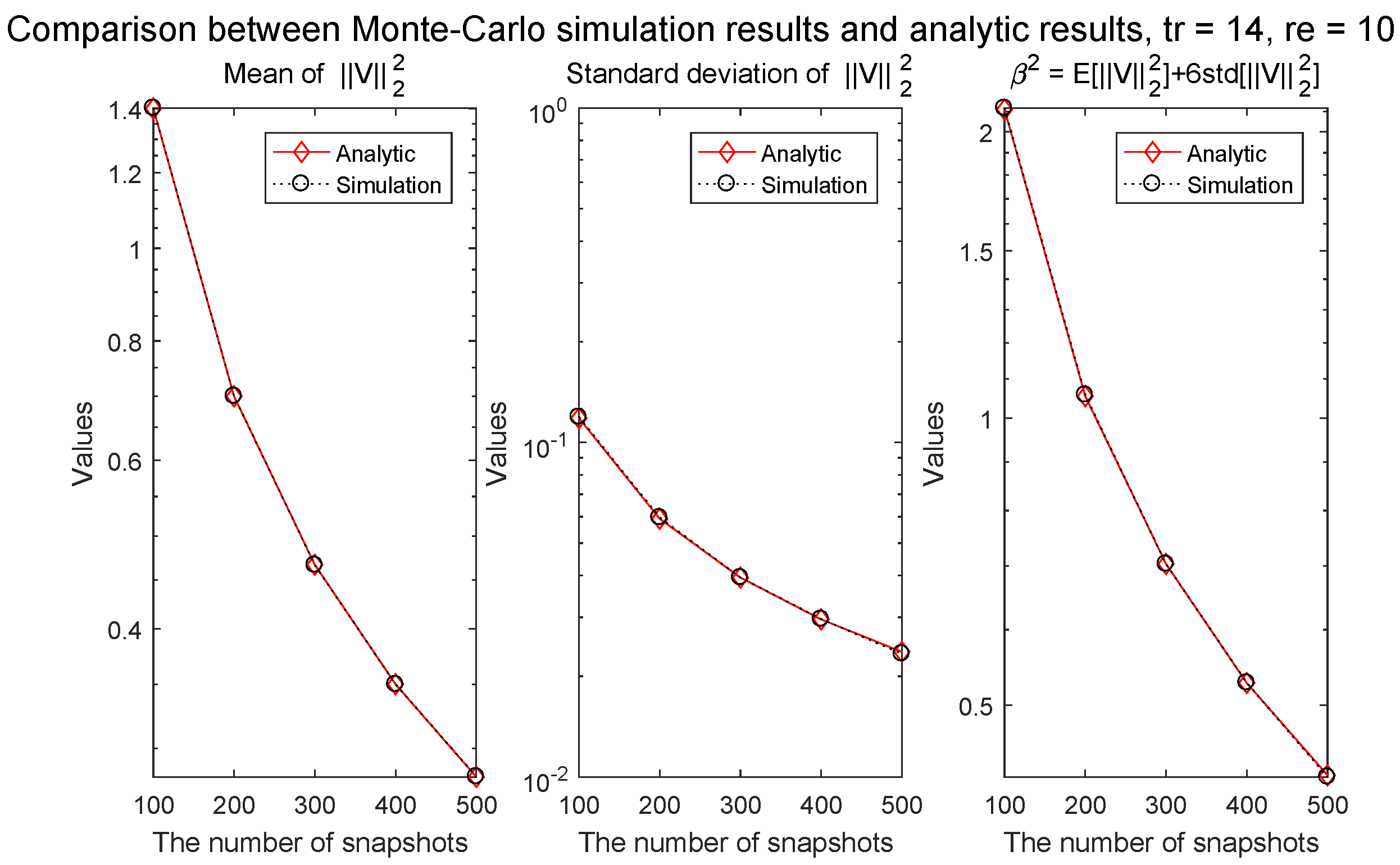
4.1. Checking the Analytically Derived Parameter of the Constraint Condition
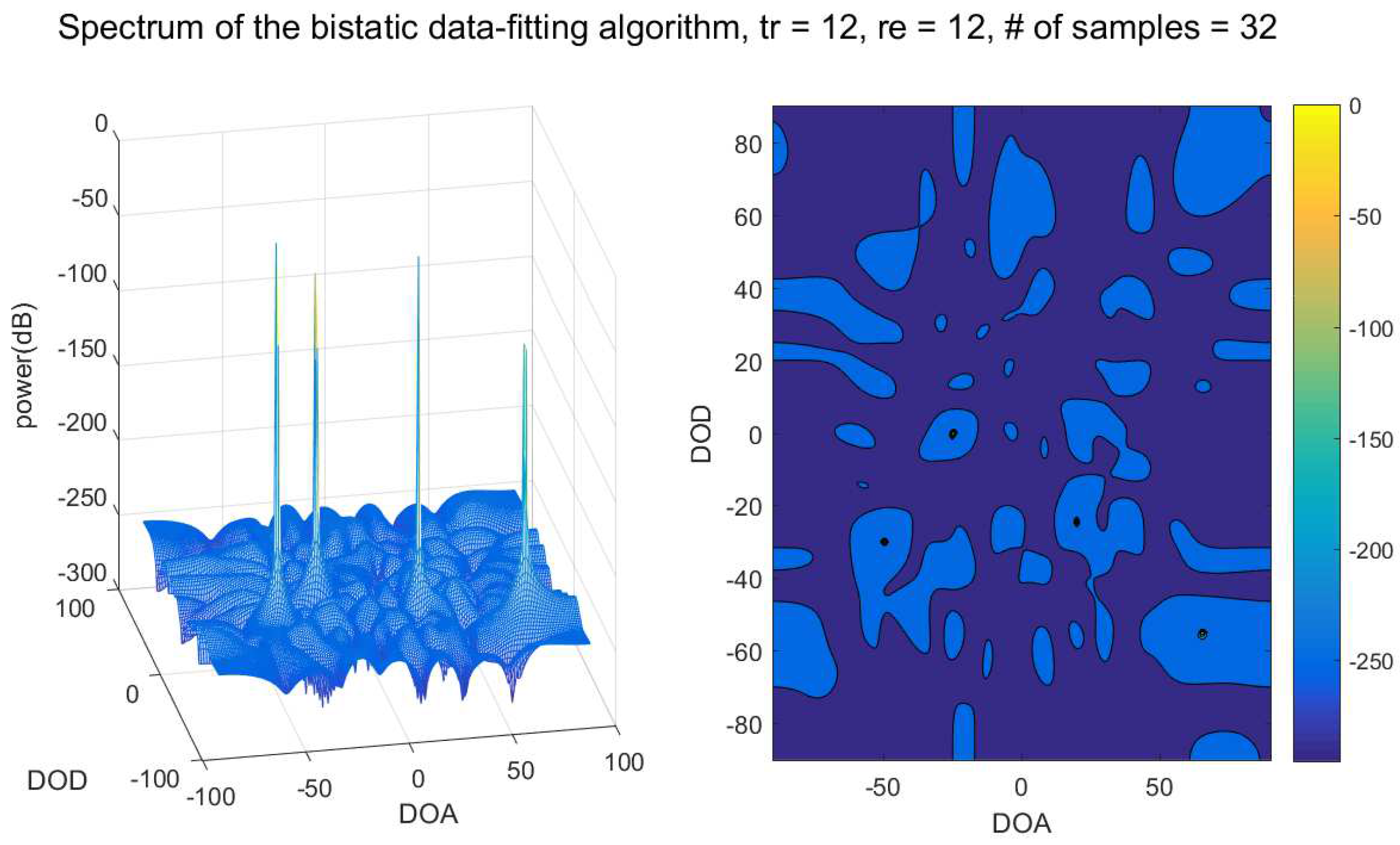
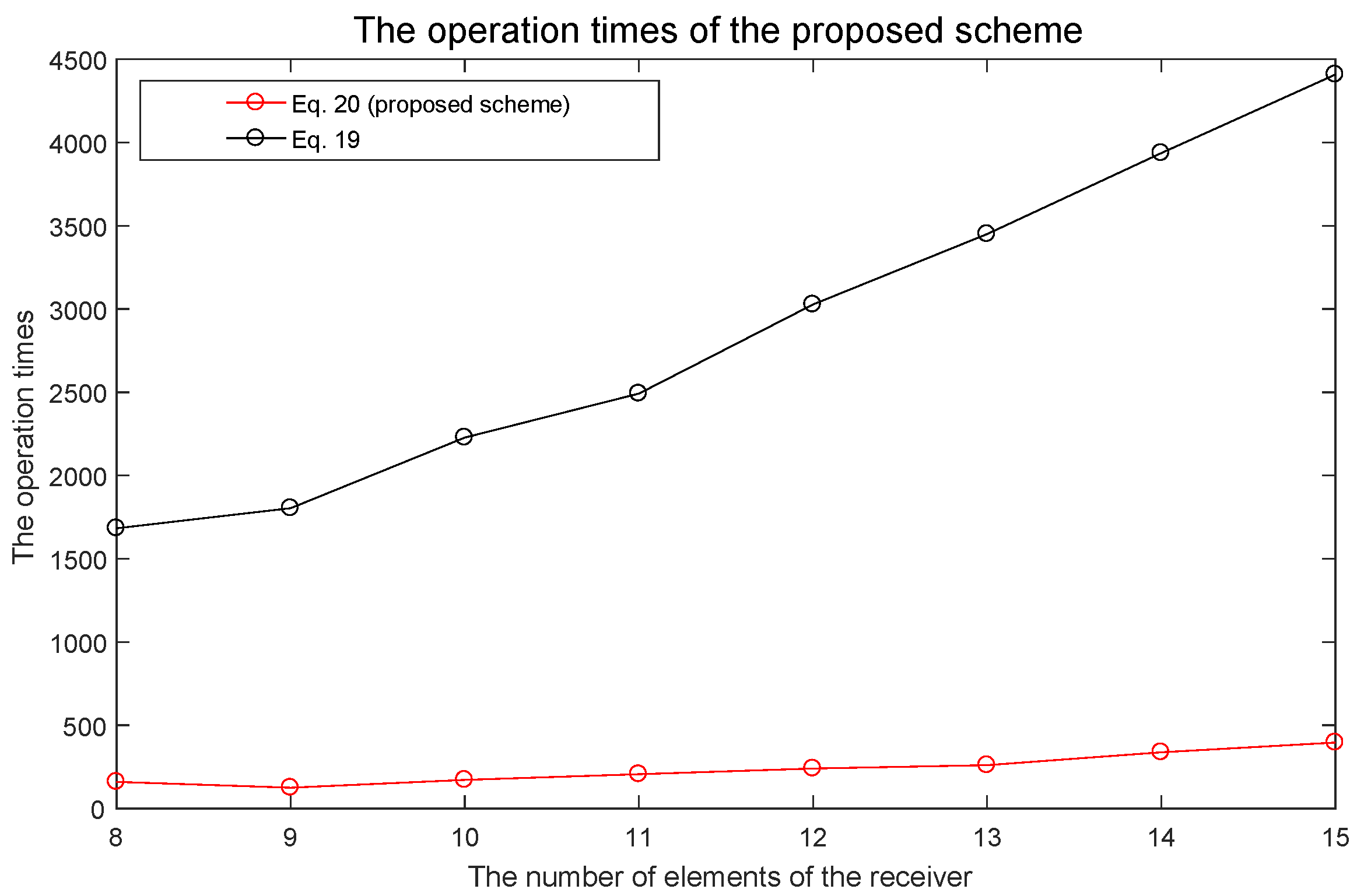
4.2. Performance of the Bistatic Data Fitting DOD/DOA Estimation Algorithm
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Parameter of the Constraint Condition β2
Appendix A.1. Mean of
Appendix A.2. Standard Deviation of
Appendix A.2.1. Part 1
Derivation of E [A2]
Derivation of
Derivation of
Appendix A.2.2. Part 2
References
- Krim, H.; Viberg, M. Two decades of array signal processing research—The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Capon, J. High resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Malioutov, D.; Cetin, M.; Willsky, A. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef] [Green Version]
- Mohimani, H.; Babaie-Zadeh, M. A Fast Approach for Overcomplete Sparse Decomposition Based on Smoothed l0 Norm. IEEE Trans. Signal Process. 2009, 57, 289–301. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Kaveh, M.; Tsuji, H. Sparse spectral fitting for direction of arrival and power estimation. In Proceedings of the 2009 IEEE/SP 15th Workshop on Statistical Signal Processing, Cardiff, UK, 31 August–3 September 2009. [Google Scholar]
- Picard, J.; Weiss, A. Direction finding of multiple emitters by spatial sparsity and linear programming. In Proceedings of the 2009 9th International Symposium on Communications and Information Technology (ISCIT), Icheon, Korea, 28–30 September 2009; pp. 1258–1262. [Google Scholar]
- Zheng, J.; Kaveh, M. Directions-of-arrival estimation using a sparse spatial spectrum model with uncertainty. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP’11), Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- Stoica, P.; Babu, P.; Li, J. Spice: A sparse covariance-based estimation method for array processing. IEEE Trans. Signal Process. 2011, 59, 629–638. [Google Scholar] [CrossRef]
- Zheng, J.; Kaveh, M. Sparse Spatial Spectral Estimation: A Covariance Fitting Algorithm, Performance and Regularization. IEEE Trans. Signal Process. 2013, 61, 2767–2777. [Google Scholar] [CrossRef]
- Paik, J.W.; Hong, W.; Ahn, J.-K.; Lee, J.-H. Statistics on noise covariance matrix for covariance fitting-based compressive sensing direction-of-arrival estimation algorithm: For use with optimization via regularization. J. Acoust. Soc. Am. 2018, 143, 3883–3890. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Zhang, X.; Chen, P. Compressed Sensing-Based DOA Estimation with Antenna Phase Errors. Electronics 2019, 2019, 294. [Google Scholar] [CrossRef] [Green Version]
- Salama, A.A.; Ahmad, M.O.; Swamy, M.N.S. Compressed Sensing DOA Estimation in the Presence of Unknown Noise. Prog. Electromagn. Res. C 2020, 102, 47–62. [Google Scholar] [CrossRef]
- Jin, M.; Liao, G.; Li, J. Joint DOD and DOA estimation for bistatic MIMO radar. Signal Process. 2009, 89, 244–251. [Google Scholar] [CrossRef]
- Liu, F.; Wang, J. AD-MUSIC for jointly DOA and DOD Estimation in Bistatic MIMO Radar System. In Proceedings of the International Conference on Computer Design and Appliations (ICCDA 2010), Qinhuangdao, China, 25–27 June 2010. [Google Scholar]
- Li, L.; Chen, F.; Dai, J. Separate DOD and DOA Estimation for Bistatic MIMO Radar. Int. J. Antennas Propag. 2016, 2016. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.L.; Gu, H.; Su, W.M. A new method for joint DOD and DOA estimation in bistatic MIMO radar. Signal Process. 2010, 90, 714–718. [Google Scholar] [CrossRef]
- Zheng, G.; Tang, J. DOD and DOA estimation in bistatic MIMO radar for nested and coprime array with closed-form DOF. Int. J. Electron. 2017, 104, 885–897. [Google Scholar] [CrossRef]
- Ali, H.; Ahmad, S.; Sharawi, M.S.; Alouini, M.S. Reduced complexity DOA and DOD estimation for a single moving target in bistatic MIMO radar. Signal Process. 2019, 166, 1–11. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, P. Compressed sensing-based DOA and DOD estimation in bistatic co-prime MIMO arrays. In Proceedings of the 2017 IEEE Conference on Antenna Measurements and Applications (CAMA), Ibaraki, Japan, 4–6 December 2017. [Google Scholar]

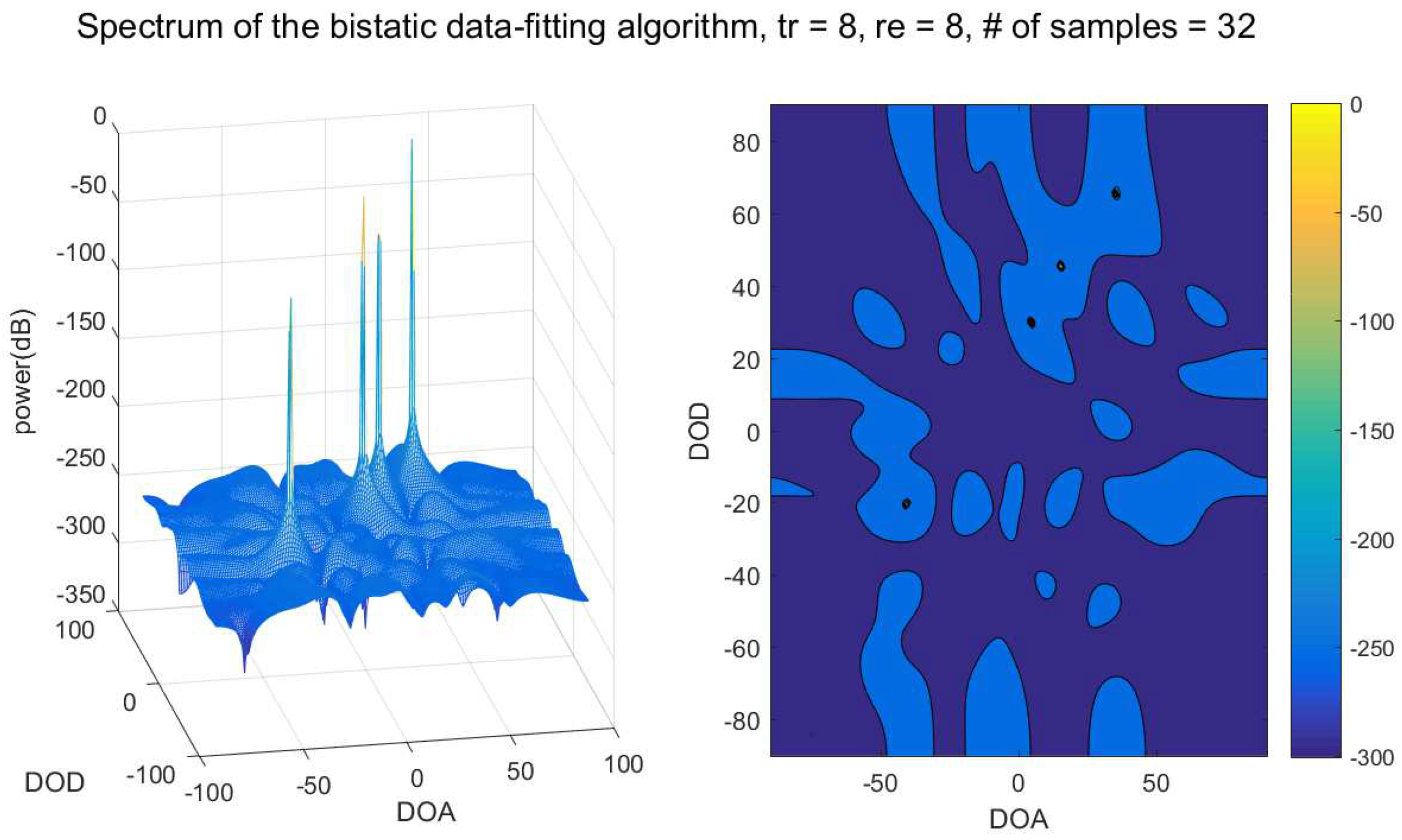
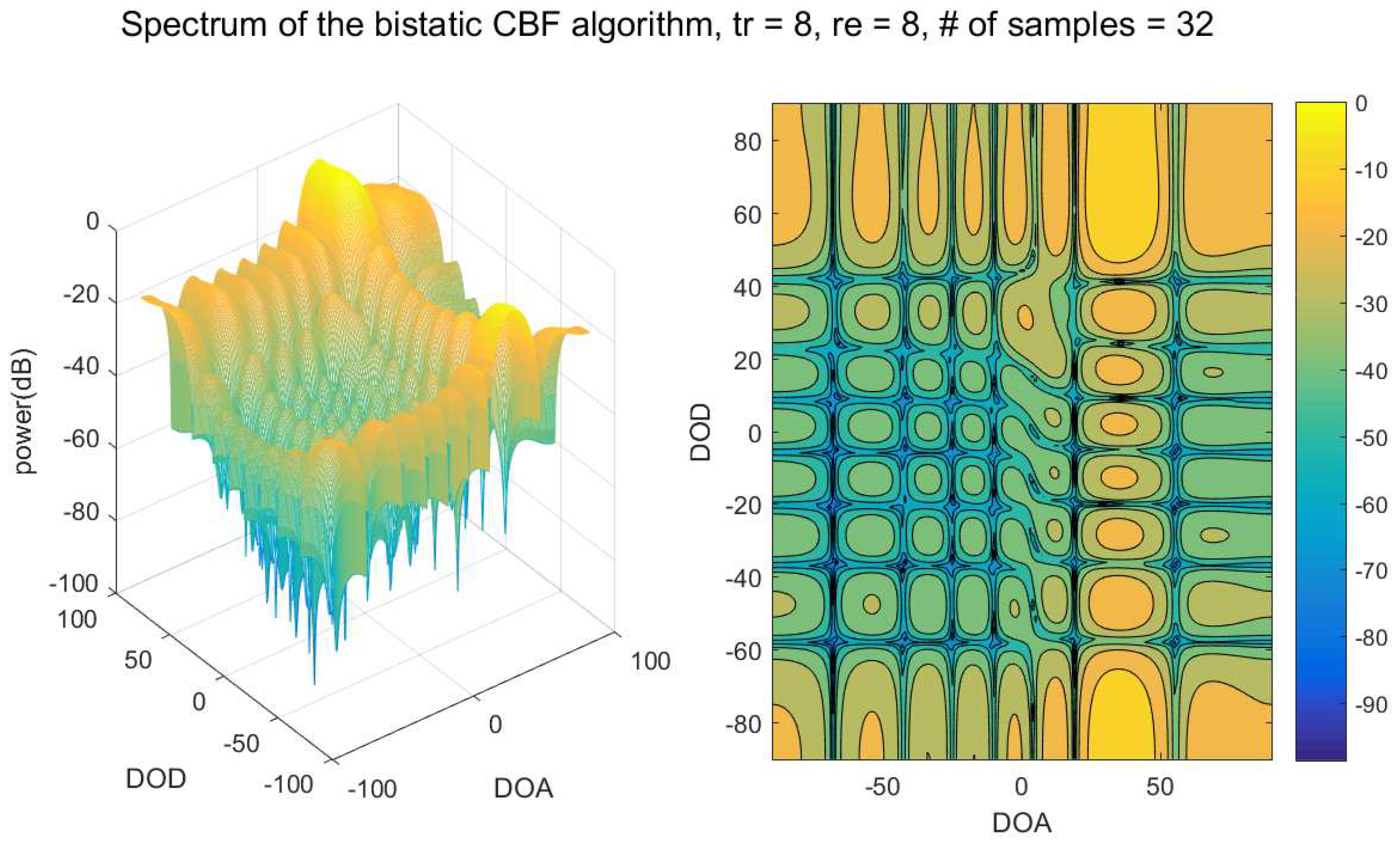

| Parameter | Value |
|---|---|
| The number of elements of the transmitter | 8 |
| The number of elements of the receiver | 8 |
| The number of samples | 32 |
| The number of targets | 4 |
| The wavelength | m |
| Inter-elements spacing at the receiver | wavelength |
| Inter-elements spacing at the transmitter | wavelength |
| Search range of DOD and DOA | :: |
| True DOD and DOA of the target 1 (SNR = −5 dB) | , |
| True DOD and DOA of the target 2 (SNR = 15 dB) | , |
| True DOD and DOA of the target 3 (SNR = 0 dB) | , |
| True DOD and DOA of the target 4 (SNR = 25 dB) | , |
| Parameter | Value |
|---|---|
| The number of elements of the transmitter | 12 |
| The number of elements of the receiver | 12 |
| The number of samples | 32 |
| The number of targets | 4 |
| The wavelength | m |
| Inter-elements spacing at the receiver | wavelength |
| Inter-elements spacing at the transmitter | wavelength |
| Search range of DOD and DOA | :: |
| True DOD and DOA of the target 1 (SNR = 25 dB) | , |
| True DOD and DOA of the target 2 (SNR = 15 dB) | , |
| True DOD and DOA of the target 3 (SNR = −5 dB) | , |
| True DOD and DOA of the target 4 (SNR = 5 dB) | , |
| Parameter | Value |
|---|---|
| The number of elements of the transmitter | 10 |
| The number of elements of the receiver | 10 |
| The number of samples | 32 |
| The number of targets | 2 |
| The wavelength | m |
| Inter-elements spacing at the receiver | wavelength |
| Inter-elements spacing at the transmitter | wavelength |
| Search range of DOD and DOA | :: |
| True DOD and DOA of the target 1 | , |
| True DOD and DOA of the target 2 | , |
| Parameter | Value |
|---|---|
| The number of elements of the transmitter | 8 |
| The number of elements of the receiver | 8:15 |
| The number of samples | 32 |
| The number of targets | 4 |
| The wavelength | m |
| The number of weight parameters | 10 |
| Inter-elements spacing at the receiver | wavelength |
| Inter-elements spacing at the transmitter | wavelength |
| Search range of DOD and DOA | :: |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paik, J.W.; Hong, W.; Lee, J.-H. Direction-of-Departure and Direction-of-Arrival Estimation Algorithm Based on Compressive Sensing: Data Fitting. Remote Sens. 2020, 12, 2773. https://doi.org/10.3390/rs12172773
Paik JW, Hong W, Lee J-H. Direction-of-Departure and Direction-of-Arrival Estimation Algorithm Based on Compressive Sensing: Data Fitting. Remote Sensing. 2020; 12(17):2773. https://doi.org/10.3390/rs12172773
Chicago/Turabian StylePaik, Ji Woong, Wooyoung Hong, and Joon-Ho Lee. 2020. "Direction-of-Departure and Direction-of-Arrival Estimation Algorithm Based on Compressive Sensing: Data Fitting" Remote Sensing 12, no. 17: 2773. https://doi.org/10.3390/rs12172773
APA StylePaik, J. W., Hong, W., & Lee, J.-H. (2020). Direction-of-Departure and Direction-of-Arrival Estimation Algorithm Based on Compressive Sensing: Data Fitting. Remote Sensing, 12(17), 2773. https://doi.org/10.3390/rs12172773






