Validation of Sentinel-3A Based Lake Level over US and Canada
Abstract
:1. Introduction
2. Material and Methods
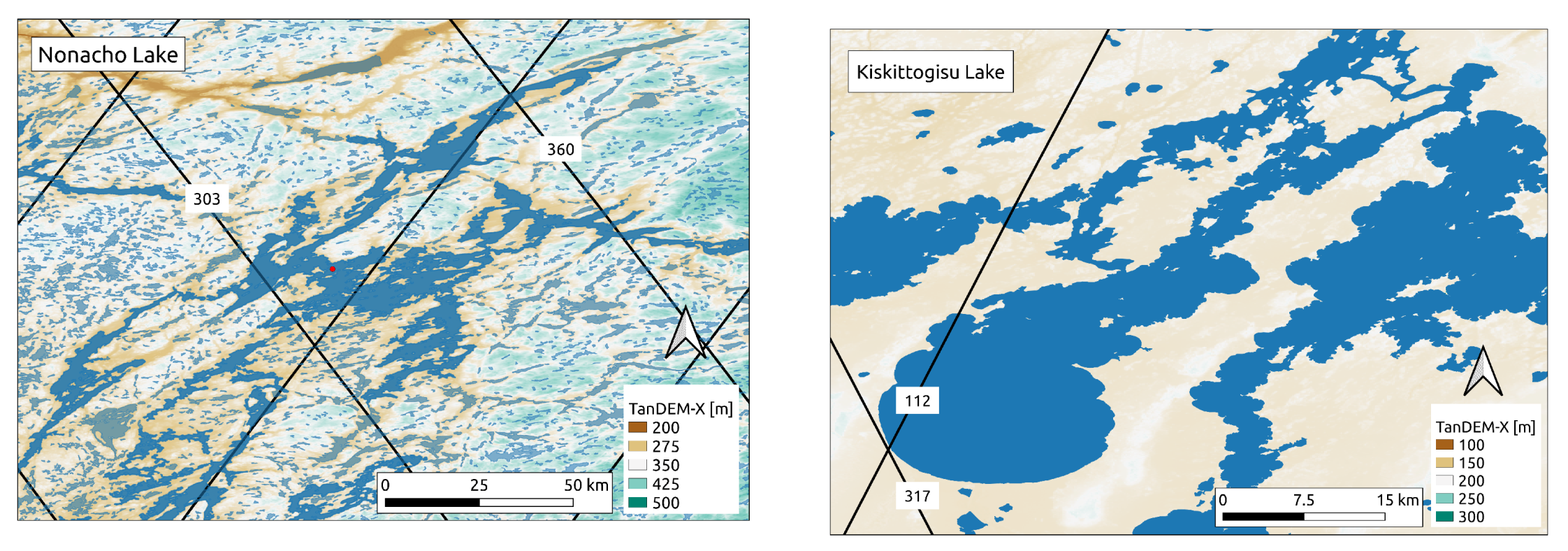
2.1. Data Sets and Study Area
2.2. Construction of Sentinel-3A Surface Water Elevations
2.3. Generation of Sentinel-3A Lake Level Time Series
2.4. Validation Measures
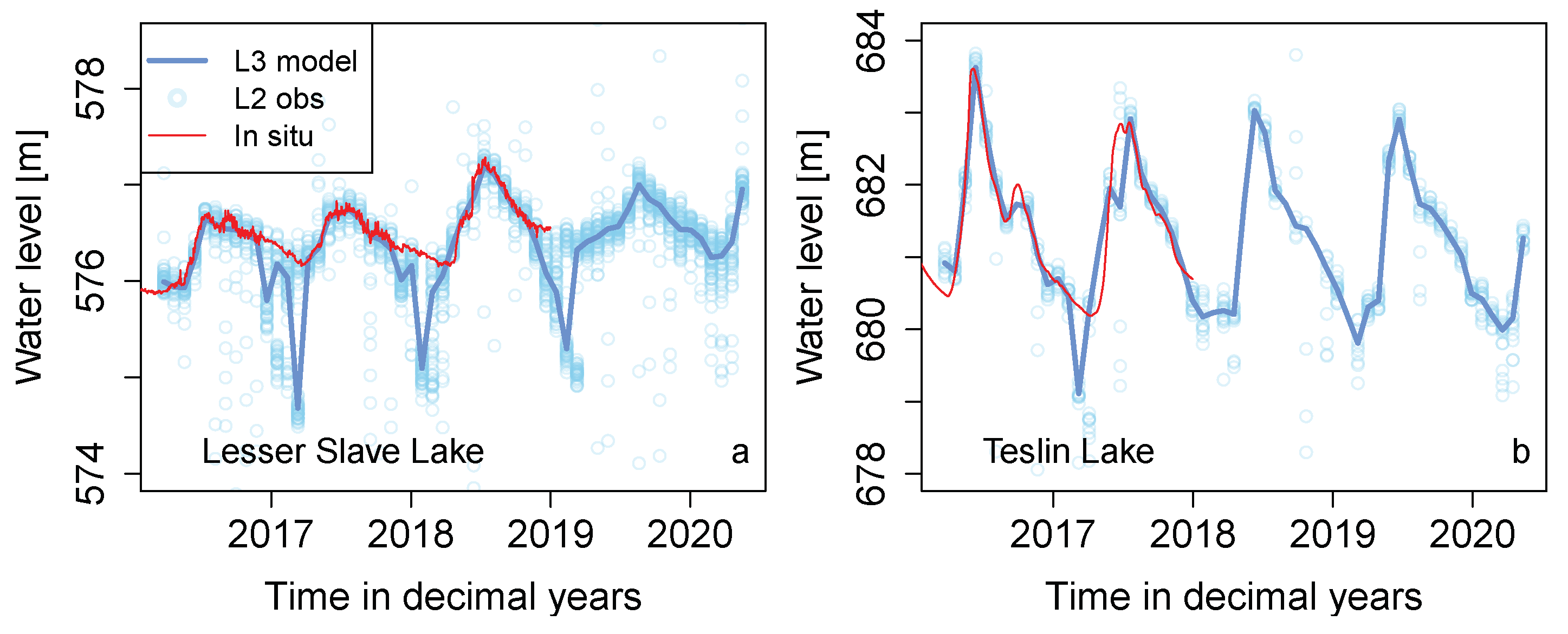
3. Results
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A





References
- Berry, P.A.M.; Garlick, J.D.; Freeman, J.A.; Mathers, E.L. Global inland water monitoring from multi-mission altimetry. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Frappart, F.; Seyler, F.; Martinez, J.M.; Leon, J.G.; Cazenave, A. Floodplain water storage in the Negro River basin estimated from microwave remote sensing of inundation area and water levels. Remote Sens. Environ. 2005, 99, 387–399. [Google Scholar] [CrossRef] [Green Version]
- Villadsen, H.; Andersen, O.B.; Stenseng, L.; Nielsen, K.; Knudsen, P. CryoSat-2 altimetry for river level monitoring—Evaluation in the Ganges–Brahmaputra River basin. Remote Sens. Environ. 2015, 168, 80–89. [Google Scholar] [CrossRef]
- Jiang, L.; Nielsen, K.; Andersen, O.B.; Bauer-Gottwein, P. Monitoring recent lake level variations on the Tibetan Plateau using CryoSat-2 SARIn mode data. J. Hydrol. 2017, 544, 109–124. [Google Scholar] [CrossRef] [Green Version]
- Biancamaria, S.; Frappart, F.; Leleu, A.S.; Marieu, V.; Blumstein, D.; Desjonquères, J.D.; Boy, F.; Sottolichio, A.; Valle-Levinson, A. Satellite radar altimetry water elevations performance over a 200 m wide river: Evaluation over the Garonne River. Adv. Space Res. 2017, 59, 128–146. [Google Scholar] [CrossRef] [Green Version]
- Zakharova, E.; Nielsen, K.; Kamenev, G.; Kouraev, A. River discharge estimation from radar altimetry: Assessment of satellite performance, river scales and methods. J. Hydrol. 2020, 583, 124561. [Google Scholar] [CrossRef]
- Birkett, C.M.B. The contribution of TOPEX/POSEIDON to the global monitoring of climatically sensitive lakes. J. Geophys. Res. 1995, 100204, 25179–25204. [Google Scholar] [CrossRef]
- Koblinsky, C.J.; Clarke, R.T.; Brenner, A.C.; Frey, H. Measurement of river level variations with satellite altimetry. Water Resour. Res. 1993, 29, 1839–1848. [Google Scholar] [CrossRef]
- Schwatke, C.; Dettmering, D.; Bosch, W.; Seitz, F. DAHITI—An innovative approach for estimating water level time series over inland waters using multi-mission satellite altimetry. Hydrol. Earth Syst. Sci. 2015, 19, 4345–4364. [Google Scholar] [CrossRef] [Green Version]
- Crétaux, J.F.; Jelinski, W.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.C.; Nino, F.; Del Rio, R.A.; Cazenave, A.; et al. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- Birkett, C.; Reynolds, C.; Beckley, B.; Doorn, B. From research to operations: The USDA global reservoir and lake monitor. In Coastal Altimetry; Springer: Berlin/Heidelberg, Germany, 2011; pp. 19–50. [Google Scholar]
- Villadsen, H.; Deng, X.; Andersen, O.B.; Stenseng, L.; Nielsen, K.; Knudsen, P. Improved inland water levels from SAR altimetry using novel empirical and physical retrackers. J. Hydrol. 2016, 537, 234–247. [Google Scholar] [CrossRef] [Green Version]
- Boergens, E.; Nielsen, K.; Andersen, O.; Dettmering, D.; Seitz, F. River Levels Derived with CryoSat-2 SAR Data Classification—A Case Study in the Mekong River Basin. Remote Sens. 2017, 9, 1238. [Google Scholar] [CrossRef] [Green Version]
- Jiang, L.; Nielsen, K.; Dinardo, S.; Andersen, O.B.; Bauer-Gottwein, P. Evaluation of Sentinel-3 SRAL SAR altimetry over Chinese rivers. Remote Sens. Environ. 2020, 237. [Google Scholar] [CrossRef]
- Dinardo, S.; Fenoglio-Marc, L.; Becker, M.; Scharroo, R.; Fernandes, M.J.; Staneva, J.; Grayek, S.; Benveniste, J. A RIP-based SAR retracker and its application in North East Atlantic with Sentinel-3. Adv. Space Res. 2020. [Google Scholar] [CrossRef]
- Raney, R.K. The delay/Doppler radar altimeter. Geosci. Remote Sens. IEEE Trans. 1998, 36, 1578–1588. [Google Scholar] [CrossRef]
- Nielsen, K.; Stenseng, L.; Andersen, O.; Knudsen, P. The Performance and Potentials of the CryoSat-2 SAR and SARIn Modes for Lake Level Estimation. Water 2017, 9, 374. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Santi, E.; Tourian, M.J.; Filippucci, P.; Amarnath, G.; Brocca, L. Daily River Discharge Estimates by Merging Satellite Optical Sensors and Radar Altimetry Through Artificial Neural Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 329–341. [Google Scholar] [CrossRef]
- Jiang, L.; Madsen, H.; Bauer-Gottwein, P. Simultaneous calibration of multiple hydrodynamic model parameters using satellite altimetry observations of water surface elevation in the Songhua River. Remote Sens. Environ. 2019, 225, 229–247. [Google Scholar] [CrossRef]
- Gao, Q.; Makhoul Varona, E.; Escorihuela, M.J.; Zribi, M.; Quintana-Seguí, P. Comparision of retrackers’ performances over inland water bodies. In International Geoscience and Remote Sensing Symposium (IGARSS); Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018; pp. 9296–9299. [Google Scholar] [CrossRef]
- Quartly, G.D.; Nencioli, F.; Raynal, M.; Bonnefond, P.; Nilo Garcia, P.; Garcia-Mondéjar, A.; Flores de la Cruz, A.; Cretaux, J.F.; Taburet, N.; Frery, M.L.; et al. The Roles of the S3MPC: Monitoring, Validation and Evolution of Sentinel-3 Altimetry Observations. Remote Sens. 2020, 12, 1763. [Google Scholar] [CrossRef]
- Ray, C.; Martin-Puig, C.; Clarizia, M.P.; Ruffini, G.; Dinardo, S.; Gommenginger, C.; Benveniste, J. SAR Altimeter Backscattered Waveform Model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 911–919. [Google Scholar] [CrossRef]
- Wingham, D.J.; Rapley, C.G.; Griffiths, H. New techniques in satellite altimeter tracking systems. In Proceedings of the 1986 International Geoscience and Remote Sensing Symposium(IGARSS’86) on Remote Sensing: Today’s Solutions for Tomorrow’s Information Needs, Zurich, Switzerland, 8–11 September 1986; Volume 3. [Google Scholar]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Le Gac, S.; Boy, F.; Blumstein, D.; Lasson, L.; Picot, N. Benefits of the Open-Loop Tracking Command (OLTC): Extending conventional nadir altimetry to inland waters monitoring. Adv. Space Res. 2019. [Google Scholar] [CrossRef]
- Ray, C.; Roca, M.; Martin-Puig, C.; Escolà, R.; Garcia, A. Amplitude and Dilation Compensation of the SAR Altimeter Backscattered Power. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2473–2476. [Google Scholar] [CrossRef]
- Brown, G.S. The average impulse response of a rough surface and its applications. Antennas Propag. IEEE Trans. 1977, 25, 67–74. [Google Scholar] [CrossRef]
- Bamber, J.L. Ice sheet altimeter processing scheme. Int. J. Remote Sens. 1994, 15, 925–938. [Google Scholar] [CrossRef]
- Frappart, F.; Calmant, S.; Cauhopé, M.; Seyler, F.; Cazenave, A. Preliminary results of ENVISAT RA-2-derived water levels validation over the Amazon basin. Remote Sens. Environ. 2006, 100, 252–264. [Google Scholar] [CrossRef] [Green Version]
- Cheng, K.C.; Calmant, S.; Kuo, C.Y.; Tseng, H.Z.; Shum, C.K.; Seyler, F.; Silva, J.S.D. Branco River Stage Gradient Determination and Amazon Hydrologic Studies Using GPS Water Level Measurements. Mar. Geod. 2009, 32, 267–283. [Google Scholar] [CrossRef]
- Santos da Silva, J.; Calmant, S.; Seyler, F.; Rotunno Filho, O.C.; Cochonneau, G.; Mansur, W.J. Water levels in the Amazon basin derived from the ERS 2 and ENVISAT radar altimetry missions. Remote Sens. Environ. 2010, 114, 2160–2181. [Google Scholar] [CrossRef]
- Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Lehner, B.; Verdin, K.; Jarvis, A. New global hydrography derived from spaceborne elevation data. Eos 2008, 89, 93–94. [Google Scholar] [CrossRef]
- Robinson, N.; Regetz, J.; Guralnick, R.P. EarthEnv-DEM90: A nearly-global, void-free, multi-scale smoothed, 90m digital elevation model from fused ASTER and SRTM data. ISPRS J. Photogramm. Remote Sens. 2014, 87, 57–67. [Google Scholar] [CrossRef]
- Nielsen, K.; Stenseng, L.; Andersen, O.B.; Villadsen, H.; Knudsen, P. Validation of CryoSat-2 SAR mode based lake levels. Remote Sens. Environ. 2015, 171, 162–170. [Google Scholar] [CrossRef] [Green Version]
- Beckers, J.F.; Casey, J.A.; Haas, C. Retrievals of lake ice thickness from great slave lake and great bear lake using cryoSat-2. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3708–3720. [Google Scholar] [CrossRef]
- Shu, S.; Liu, H.; Beck, R.A.; Frappart, F.; Korhonen, J.; Xu, M.; Yang, B.; Hinkel, K.M.; Huang, Y.; Yu, B. Analysis of Sentinel-3 SAR altimetry waveform retracking algorithms for deriving temporally consistent water levels over ice-covered lakes. Remote Sens. Environ. 2020, 239, 111643. [Google Scholar] [CrossRef]





| RMSE [m] | 95% Conf | Cor | 95% Conf | % Outliers | 95% Conf | # Cycles | |
|---|---|---|---|---|---|---|---|
| US ocean | 0.25 | [0.19 0.31] | 0.86 | [0.75 0.94] | 11.3 | [8.2 15.5] | 56 |
| US OCOG | 0.19 | [0.16 0.23] | 0.93 | [0.84 0.97] | 11.2 | [7.7 14.5] | 57 |
| CA ocean | 0.32 | [0.28 0.36] | 0.77 | [0.72 0.85] | 14.7 | [13.6 16.6] | 38 |
| CA OCOG | 0.25 | [0.20 0.30] | 0.84 | [0.76 0.90] | 17.2 | [15.1 18.8] | 38 |
| CA ocean | 0.12 | [0.11 0.14] | 0.87 | [0.83 0.93] | - | - | 17 |
| CA OCOG | 0.09 | [0.08 0.10] | 0.95 | [0.91 0.97] | - | - | 17 |
| RMSE [m] | 95% Conf | Cor | 95% Conf | % Outliers | 95% Conf | # Cycles | |
|---|---|---|---|---|---|---|---|
| US | 0.021 | [0.008 0.046] | −0.013 | [−0.036 −0.003] | −0.001 | [−0.007 0.021] | 57 |
| CA | 0.053 | [0.045 0.066] | −0.027 | [−0.041 −0.014] | −0.007 | [−0.018 0.003] | 38 |
| CA | 0.026 | [0.020 0.037] | −0.023 | [−0.028 −0.015] | - | - | 17 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nielsen, K.; Andersen, O.B.; Ranndal, H. Validation of Sentinel-3A Based Lake Level over US and Canada. Remote Sens. 2020, 12, 2835. https://doi.org/10.3390/rs12172835
Nielsen K, Andersen OB, Ranndal H. Validation of Sentinel-3A Based Lake Level over US and Canada. Remote Sensing. 2020; 12(17):2835. https://doi.org/10.3390/rs12172835
Chicago/Turabian StyleNielsen, Karina, Ole Baltazar Andersen, and Heidi Ranndal. 2020. "Validation of Sentinel-3A Based Lake Level over US and Canada" Remote Sensing 12, no. 17: 2835. https://doi.org/10.3390/rs12172835





