A New Compact Delay, Doppler Stretch and Phase Estimation CRB with a Band-Limited Signal for Generic Remote Sensing Applications
Abstract
:1. Introduction
- The first contribution is a general compact closed-form CRB expression for the delay-Doppler estimation of a generic band-limited signal which is only supposed to have a finite number on non-zero samples, thus encompassing all existing CRB expressions.
- A second contribution is the introduction of a general compact closed-form CRB expression for the amplitude and phase.
- The compact CRBs obtained are expressed in terms of the baseband signal samples, making it especially easy to use whatever the baseband signal considered. This allows to exploit such expressions in a plethora of remote sensing applications.
- The validity of the new CRB expressions is assessed in the context of GNSS, both using synthetic and real data.
2. Signal Model
3. Maximum Likelihood and Ambiguity Function
4. New Compact CRB for Delay, Doppler Stretch and Phase Estimation with a Band-limited Signal
4.1. Background on CRB for the Single Source CSM
4.2. A Preliminary Compact CRB for the Single Band-Limited Source CSM
4.3. Comparison with Existing Literature
4.4. A Versatile Compact CRB for Delay, Doppler Stretch and Phase Estimation with a Band-Limited Signal
4.5. Standard Narrowband Signal Model
4.6. Further Insights and Outlooks
5. Validation and Discussion
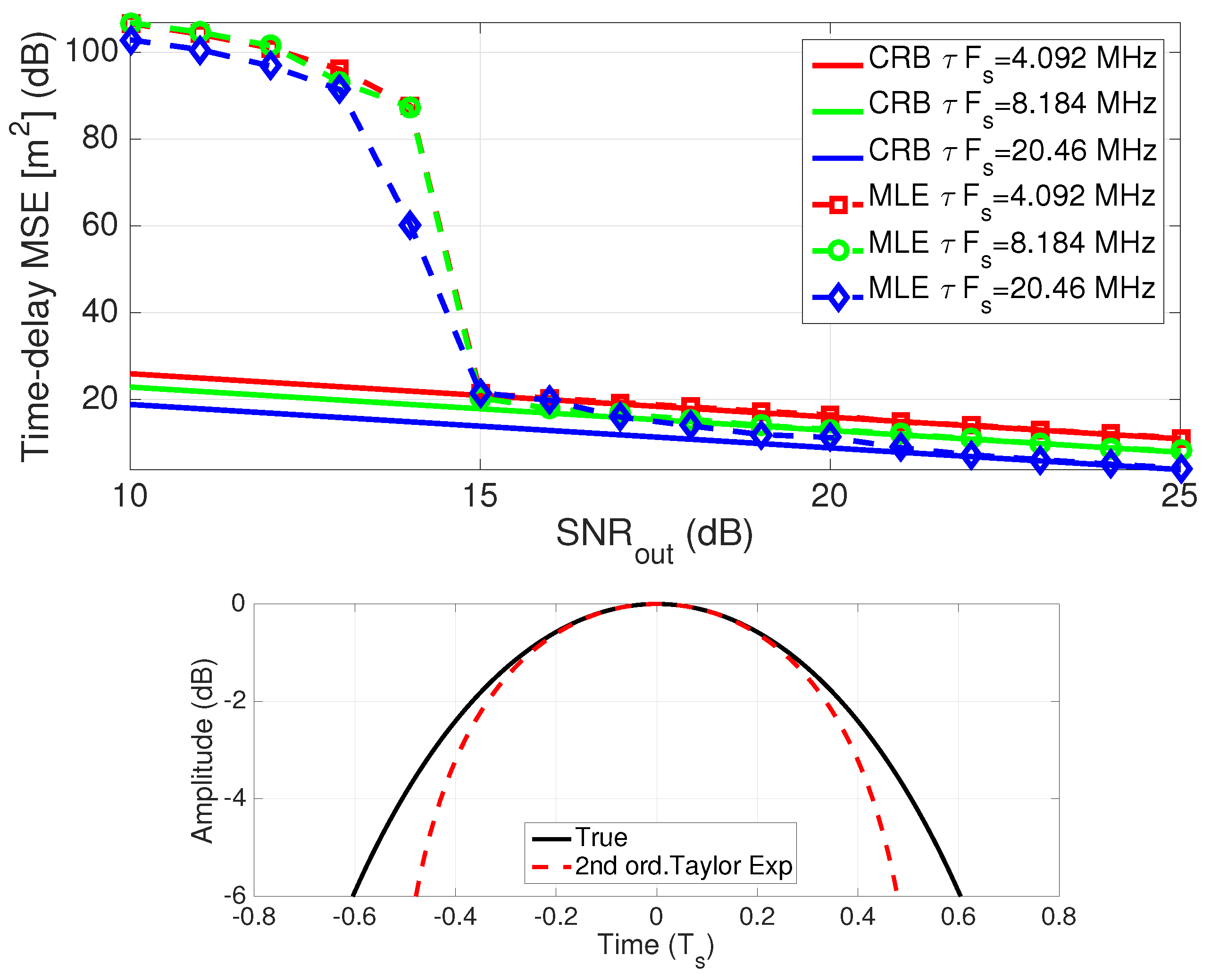
5.1. Synthetic Signal
5.2. Real-Life GPS Data Experiment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Analytic (Compact) Expression of ℜ {Φ (η)}
Appendix A.1. Computing the Terms in
Appendix A.2. Integral Form of the Inner Terms in (A3) and (A4)
Appendix A.3. Rewriting (24) in Terms of W
Appendix A.4. Computing and
Appendix A.5. Analytic Expression of
Appendix A.6. Analytic Expression of when s(t) is a Real Signal
Appendix B. Computation of the Different Terms in the CRB Expression (25)–(26)
References
- Woodward, P.M. Probability and Information Theory with Application to Radar; Artech House: Norwood, MA, USA, 1953. [Google Scholar]
- Rihaczek, A.W. Delay-Doppler ambiguity function for wideband signals. IEEE Trans. Aerosp. Electron. Syst. 1967, 3, 705–711. [Google Scholar] [CrossRef]
- Swick, D.A. A Review of Wideband Ambiguity Functions; Technical Report 6994; Naval Res. Lab.: Washington, DC, USA, 1969. [Google Scholar]
- Trees, H.L.V. Detection, Estimation, and Modulation Theory, Part III: Radar—Sonar Signal Processing and Gaussian Signals in Noise; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Mengali, U.; D’Andrea, A.N. Synchronization Techniques for Digital Receivers; Plenum Press: New York, NY, USA, 1997. [Google Scholar]
- Trees, H.L.V. Optimum Array Processing; Wiley-Interscience: New York, NY, USA, 2002. [Google Scholar]
- Ricker, D.W. Echo Signal Processing; Kluwer Academic; Springer: New York, NY, USA, 2003. [Google Scholar]
- Chen, J.; Huang, Y.A.; Benesty, J. Time Delay Estimation. In Audio Signal Processing for Next-Generation Multimedia Communication Systems; Huang, Y., Benesty, J., Eds.; Springer: Boston, MA, USA, 2004; Chapter 8; pp. 197–227. [Google Scholar]
- Levy, B.C. Principles of Signal Detection and Parameter Estimation; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Munoz, D.; Lara, F.B.; Vargas, C.; Enriquez, R. Position Location Techniques and Applications; Academic Press: Oxford, UK, 2009. [Google Scholar]
- Yan, J.; Tiberius, C.C.J.M.; Janssen, G.J.M.; Teunissen, P.J.G.; Bellusci, G. Review of range-based positioning algorithms. IEEE Trans. Aerosp. Electron. Syst. 2013, 28, 2–27. [Google Scholar] [CrossRef] [Green Version]
- Zavorotny, V.U.; Gleason, S.; Cardellach, E.; Camps, A. Tutorial on remote sensing using GNSS bistatic radar of opportunity. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–45. [Google Scholar] [CrossRef] [Green Version]
- Trees, H.L.V.; Bell, K.L. (Eds.) Bayesian Bounds for Parameter Estimation and Nonlinear Filtering/Tracking; Wiley/IEEE Press: New York, NY, USA, 2007. [Google Scholar]
- Trees, H.L.V. Detection, Estimation, and Modulation Theory: Part I; Wiley: New York, NY, USA, 1968. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Stoica, P.; Nehorai, A. Performances study of conditional and unconditional direction of arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1783–1795. [Google Scholar] [CrossRef]
- Renaux, A.; Forster, P.; Chaumette, E.; Larzabal, P. On the High-SNR Conditional Maximum-Likelihood Estimator Full Statistical Characterization. IEEE Trans. Signal Process. 2006, 54, 4840–4843. [Google Scholar] [CrossRef] [Green Version]
- Jin, Q.; Wong, K.M.; Luo, Z.Q. The estimation of time delay and Doppler stretch of wideband signals. IEEE Trans. Signal Process. 1995, 43, 904–916. [Google Scholar] [CrossRef]
- Niu, X.X.; Ching, P.C.; Chan, Y. Wavelet based approach for joint time delay and Doppler stretch measurements. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 1111–1119. [Google Scholar] [CrossRef]
- Dogandzic, A.; Nehorai, A. Cramér-Rao Bounds for Estimating Range, Velocity, and Direction with an Active Array. IEEE Trans. Signal Process. 2001, 49, 1122–1137. [Google Scholar] [CrossRef] [Green Version]
- Noels, N.; Wymeersch, H.; Steendam, H.; Moeneclaey, M. True Cramér-Rao bound for timing recovery from a bandlimited linearly Modulated waveform with unknown carrier phase and frequency. IEEE Trans. Commun. 2004, 52, 473–483. [Google Scholar] [CrossRef]
- He-Wen, W.; Shangfu, Y.; Qun, W. Influence of random carrier phase on true Cramer-Rao lower bound for time delay estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Honolulu, HI, USA, 15–20 April 2007. [Google Scholar]
- Wei, H.; Ye, S.; Wan, Q. Influence of phase on Cramer-Rao lower bounds for joint time delay and Doppler stretch estimation. In Proceedings of the IEEE International Symposium on Signal Processing and Its Applications (ISSPA), Sharjah, UAE, 12–15 February 2007. [Google Scholar]
- Johnson, J.; Fowler, M. Cramer-Rao lower bound on Doppler frequency of coherent pulse trains. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Las Vegas, NV, USA, 31 March–4 April 2008. [Google Scholar]
- Closas, P.; Fernández-Prades, C.; Fernández-Rubio, J.A. Cramér-Rao bound analysis of positioning approaches in GNSS receivers. IEEE Trans. Signal Process. 2009, 57, 3775–3786. [Google Scholar] [CrossRef]
- Enneking, C.; Stein, M.; Castañeda, M.; Antreich, F.; Nossek, J.A. Multi-satellite time-delay estimation for reliable high-resolution GNSS receivers. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Myrtle Beach, SC, USA, 23–26 April 2012. [Google Scholar]
- Pourhomayoun, M.; Fowler, M. Cramer-Rao lower bound for frequency estimation for coherent pulse train with unknown pulse. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1304–1312. [Google Scholar] [CrossRef]
- Nan, Z.; Zhao, T.; Huang, T. Cramer-Rao lower bounds of joint time delay and Doppler-stretch estimation with random stepped-frequency signals. In Proceedings of the IEEE International Conference on Digital Signal Processing (DSP), Beijing, China, 16–18 October 2016. [Google Scholar]
- Zhao, T.; Huang, T. Cramer-Rao Lower Bounds for the Joint Delay-Doppler Estimation of an Extended Target. IEEE Trans. Signal Process. 2016, 64, 1562–1573. [Google Scholar] [CrossRef] [Green Version]
- Gogolev, I.; Yashin, G. Cramer-Rao Lower Bound of Doppler Stretch and Delay in Wideband Signal Model. In Proceedings of the IEEE Conference of Russian Young Researchers in EEE (EIConRus), St. Petersburg, Russia, 1–3 February 2017. [Google Scholar]
- Chen, Y.; Blum, R.S. On the Impact of Unknown Signals on Delay, Doppler, Amplitude, and Phase Parameter Estimation. IEEE Trans. Signal Process. 2019, 67, 431–443. [Google Scholar] [CrossRef]
- Medina, D.; Ortega, L.; Vilà-Valls, J.; Closas, P.; Vincent, F.; Chaumette, E. Compact CRB for Delay, Doppler, and Phase Estimation—Application to GNSS SPP and RTK Performance Characterisation. IET Radar Sonar Navig. 2020. accepted for publication. [Google Scholar] [CrossRef]
- Bartov, A.; Messer, H. Lower bound on the achievable DSP performance for localizing step-like continuous signals in noise. IEEE Trans. Signal Process. 1998, 46, 2195–2201. [Google Scholar] [CrossRef]
- Yau, S.F.; Bresler, Y. A Compact Cramér-Rao Bound Expression for Parametric Estimation of Superimposed Signals. IEEE Trans. Signal Process. 1992, 40, 1226–1230. [Google Scholar] [CrossRef]
- Ottersten, B.; Viberg, M.; Stoica, P.; Nehorai, A. Exact and Large Sample Maximum Likelihood Techniques for Parameter Estimation and Detection in Array Processing. In Radar Array Processing; Haykin, S., Litva, J., Shepherd, T.J., Eds.; Springer: Heidelberg, Germany, 1993; Chapter 4; pp. 99–151. [Google Scholar]
- Menni, T.; Chaumette, E.; Larzabal, P.; Barbot, J. New Results on Deterministic Cramér–Rao Bounds for Real and Complex Parameters. IEEE Trans. Signal Process. 2012, 60, 1032–1049. [Google Scholar] [CrossRef]
- Speiser, J.M. Wideband ambiguity functions. IEEE Trans. Inf. Theory 1967, 13, 122–123. [Google Scholar] [CrossRef]
- Lin, Z.B. Wideband ambiguity function of broadband signals. J. Acoust. Soc. Am. 1988, 83, 2108–2116. [Google Scholar] [CrossRef]
- Dawood, M.; Narayanan, R. Generalised wideband ambiguity function of a coherent ultrawideband random noise radar. IEE Proc. Radar Sonar Navig. 2003, 150, 379–386. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Montenbruck, O. (Eds.) Handbook of Global Navigation Satellite Systems; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Lestarquit, L.; Peyrezabes, M.; Darrozes, J.; Motte, E.; Roussel, N.; Wautelet, G.; Frappart, F.; Ramillien, G.; Biancale, R.; Zribi, M. Reflectometry With an Open-Source Software GNSS Receiver: Use Case With Carrier Phase Altimetry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4843–4853. [Google Scholar] [CrossRef]
- Cardellach, E.; Li, W.; Rius, A.; Semmling, M.; Wickert, J.; Zus, F.; Ruf, C.S.; Buontempo, C. First Precise Spaceborne Sea Surface Altimetry With GNSS Reflected Signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 13, 102–112. [Google Scholar] [CrossRef]
- Skolnik, M.I. Radar Handbook, 3rd ed.; McGraw-Hill: New York, NY, USA, 1990. [Google Scholar]
- Das, P.; Vilà-Valls, J.; Chaumette, E.; Vincent, F.; Davain, L.; Bonnabel, S. On the Accuracy Limit of Time-delay Estimation with a Band-limited Signal. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019. [Google Scholar]
- Sussman, S. Least-square synthesis of radar ambiguity functions. IRE Trans. Inf. Theory 2009, 8, 246–254. [Google Scholar] [CrossRef]
- Arlery, F.; Kassab, R.; Tan, U.; Lehmann, F. Efficient Gradient Method for Locally Optimizing the Periodic/Aperiodic Ambiguity Function. In Proceedings of the IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016. [Google Scholar]
- Sebt, M.A.; Sheikhi, A.; Cheikhi, M.N. Orthogonal frequency-division multiplexing radar signal design with optimised ambiguity function and low peak-to-average power ratio. IET Radar Sonar Navig. 2009, 3, 122–132. [Google Scholar] [CrossRef]
- Cavazzuti, M. Optimization Methods: From Theory to Design Scientific and Technological Aspects in Mechanics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Dréao, J.; Chatterjee, A.; Pétrowski, A.; Siarry, P.; Taillard, E. Metaheuristics for Hard Optimization: Methods and Case Studies; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Fernández-Prades, C.; Lo Presti, L.; Falletti, E. Satellite radiolocalization from GPS to GNSS and beyond: Novel technologies and applications for civil mass market. Proc. IEEE 2011, 99, 1882–1904. [Google Scholar] [CrossRef]
- Kaplan, E.D. (Ed.) Understanding GPS: Principles and Applications, 2nd ed.; Artech House: Norwood, MA, USA, 2006. [Google Scholar]
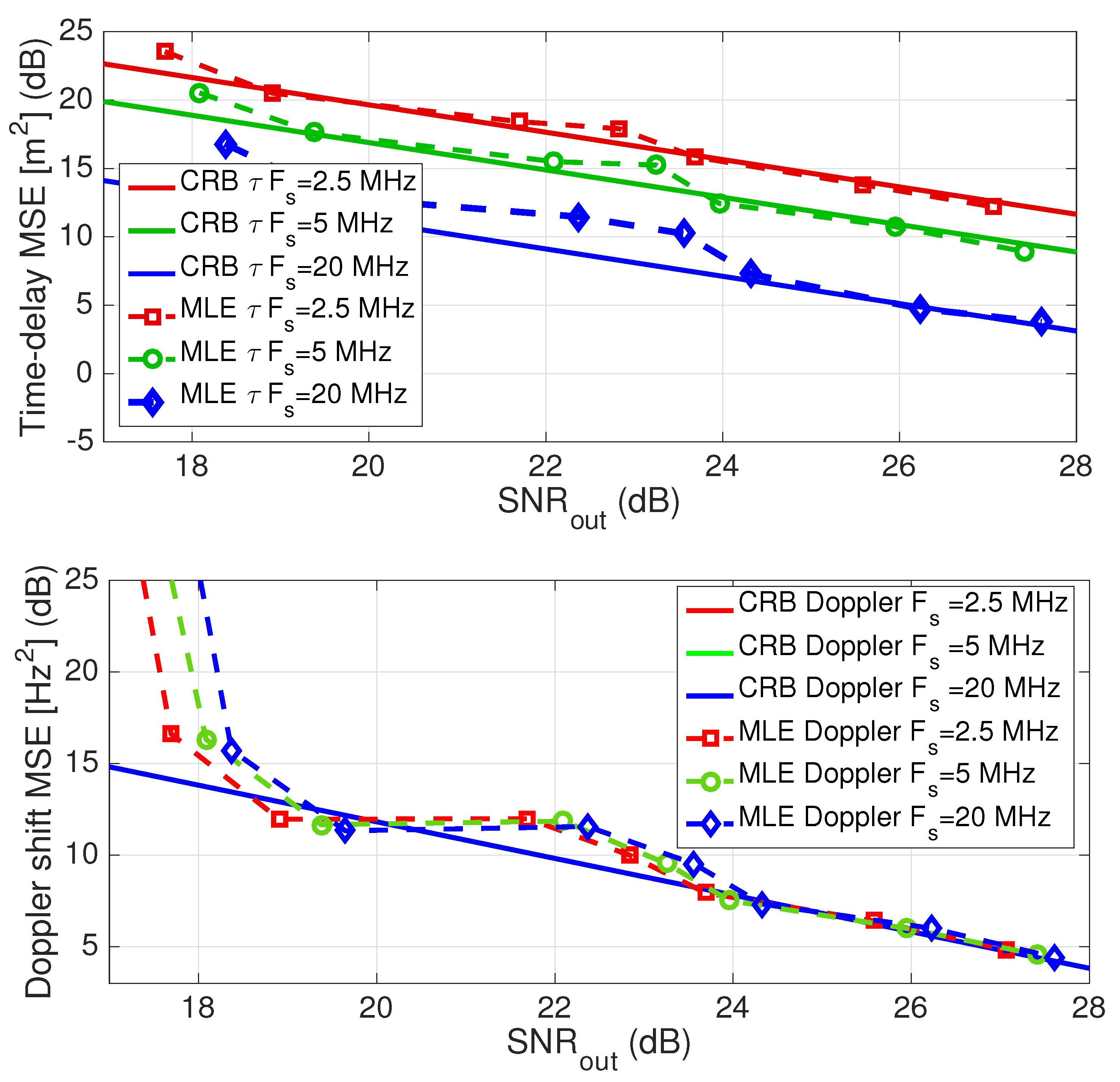
| PRN Id | Doppler | Elev | Azim | |
|---|---|---|---|---|
| 31 | 17.7 | 3170 | 19.3 | −50.6 |
| 14 | 18.9 | −490 | 44.8 | −95.3 |
| 2 | 21.7 | 930 | 28.6 | 86.7 |
| 24 | 22.8 | −2950 | 34.1 | 133 |
| 25 | 23.7 | 480 | 70.7 | −41.7 |
| 29 | 25.6 | 2480 | 51.3 | −162.7 |
| 12 | 27.1 | −1780 | 53.9 | 56 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, P.; Vilà-Valls, J.; Vincent, F.; Davain, L.; Chaumette, E. A New Compact Delay, Doppler Stretch and Phase Estimation CRB with a Band-Limited Signal for Generic Remote Sensing Applications. Remote Sens. 2020, 12, 2913. https://doi.org/10.3390/rs12182913
Das P, Vilà-Valls J, Vincent F, Davain L, Chaumette E. A New Compact Delay, Doppler Stretch and Phase Estimation CRB with a Band-Limited Signal for Generic Remote Sensing Applications. Remote Sensing. 2020; 12(18):2913. https://doi.org/10.3390/rs12182913
Chicago/Turabian StyleDas, Priyanka, Jordi Vilà-Valls, François Vincent, Loïc Davain, and Eric Chaumette. 2020. "A New Compact Delay, Doppler Stretch and Phase Estimation CRB with a Band-Limited Signal for Generic Remote Sensing Applications" Remote Sensing 12, no. 18: 2913. https://doi.org/10.3390/rs12182913
APA StyleDas, P., Vilà-Valls, J., Vincent, F., Davain, L., & Chaumette, E. (2020). A New Compact Delay, Doppler Stretch and Phase Estimation CRB with a Band-Limited Signal for Generic Remote Sensing Applications. Remote Sensing, 12(18), 2913. https://doi.org/10.3390/rs12182913







