Evaluation of Different Radiative Transfer Models for Microwave Backscatter Estimation of Wheat Fields
Abstract
1. Introduction
- investigate different RT model combinations and asses their advantages and disadvantages;
- evaluate if different radar acquisition geometries are modeled adequately with the used RT models; and
- serve as preliminary work for future synergistic retrieval approaches of SAR and optical sensors with a focus on high spatial and temporal resolutions.
2. Datasets
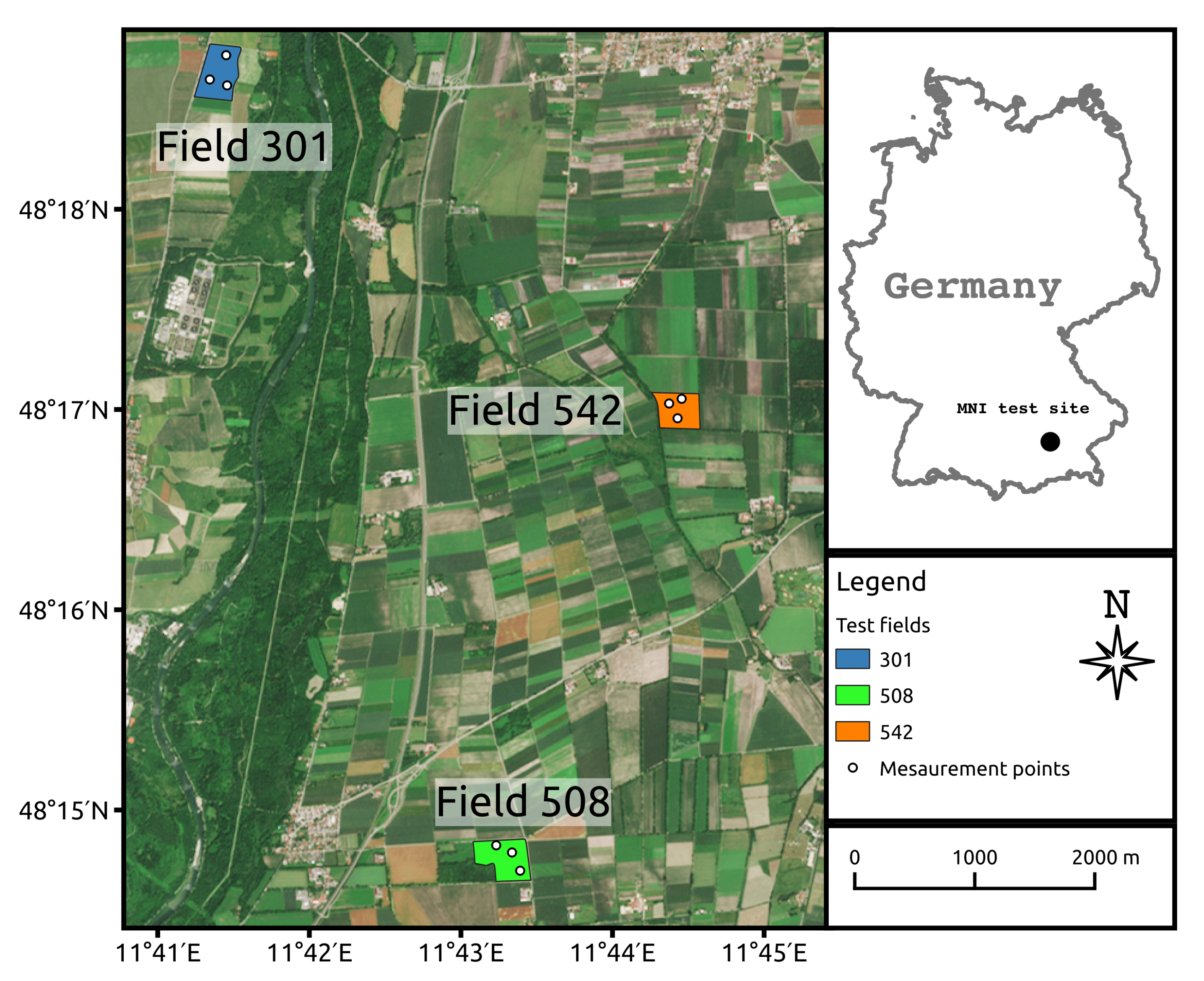
2.1. Study Area
2.2. Field Data
2.3. Satellite Data
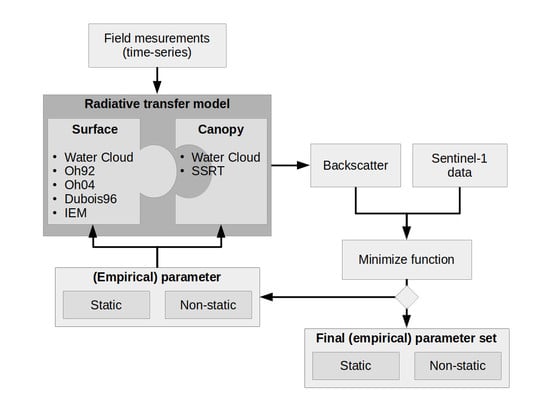
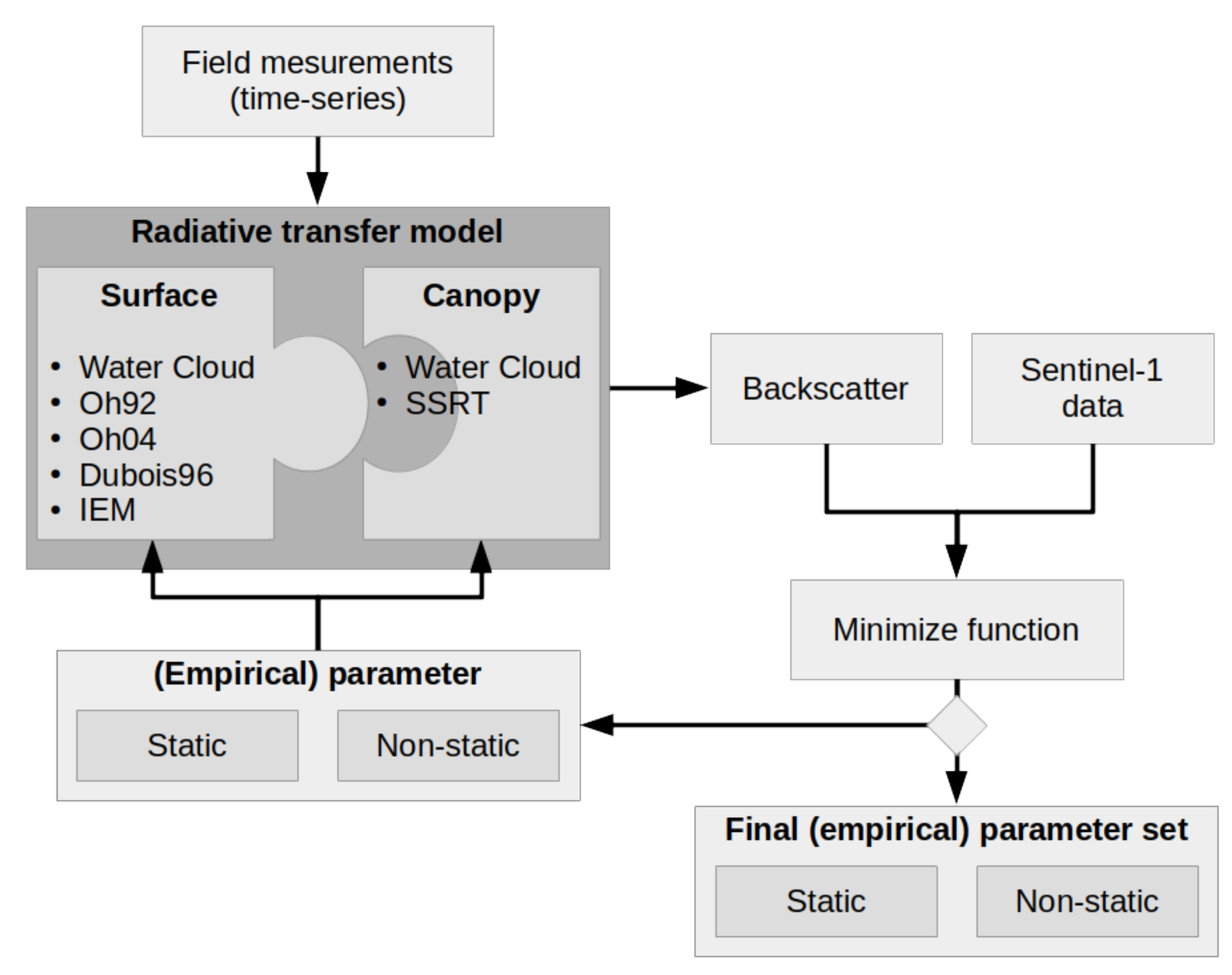
3. Microwave Radiative Transfer Models
3.1. Surface RT Models
3.1.1. Empirical Water Cloud Model (WCM Surface Part)
3.1.2. Semi-Empirical Oh Model 1992 (Oh92)
3.1.3. Semi-Empirical Oh Model 2004 (Oh04)
3.1.4. Semi-Empirical Dubois Model (Dubois95)
3.1.5. Physical Integral Equation Model (IEM)
3.2. Surface and Canopy RT Models
3.2.1. Empirical Water Cloud Model (WCM)
3.2.2. Semi-Empirical Single Scattering Radiative Transfer (SSRT) Model
3.3. Practical Considerations
3.4. Differences between Applied Models
4. Results and Discussion
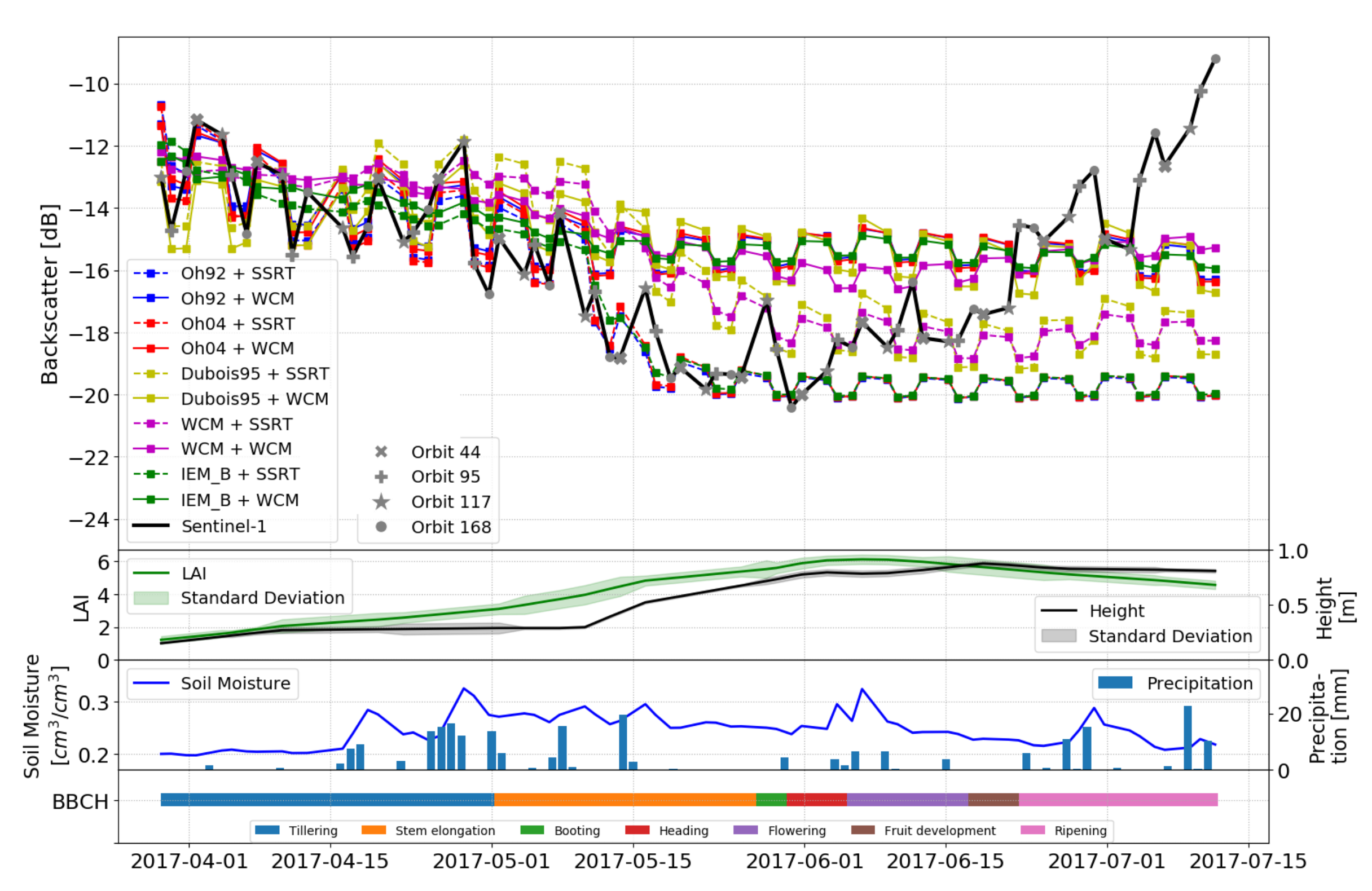
4.1. Model Calibration Results
4.1.1. Static Empirical Parameters
4.1.2. Non-Static Empirical Parameters
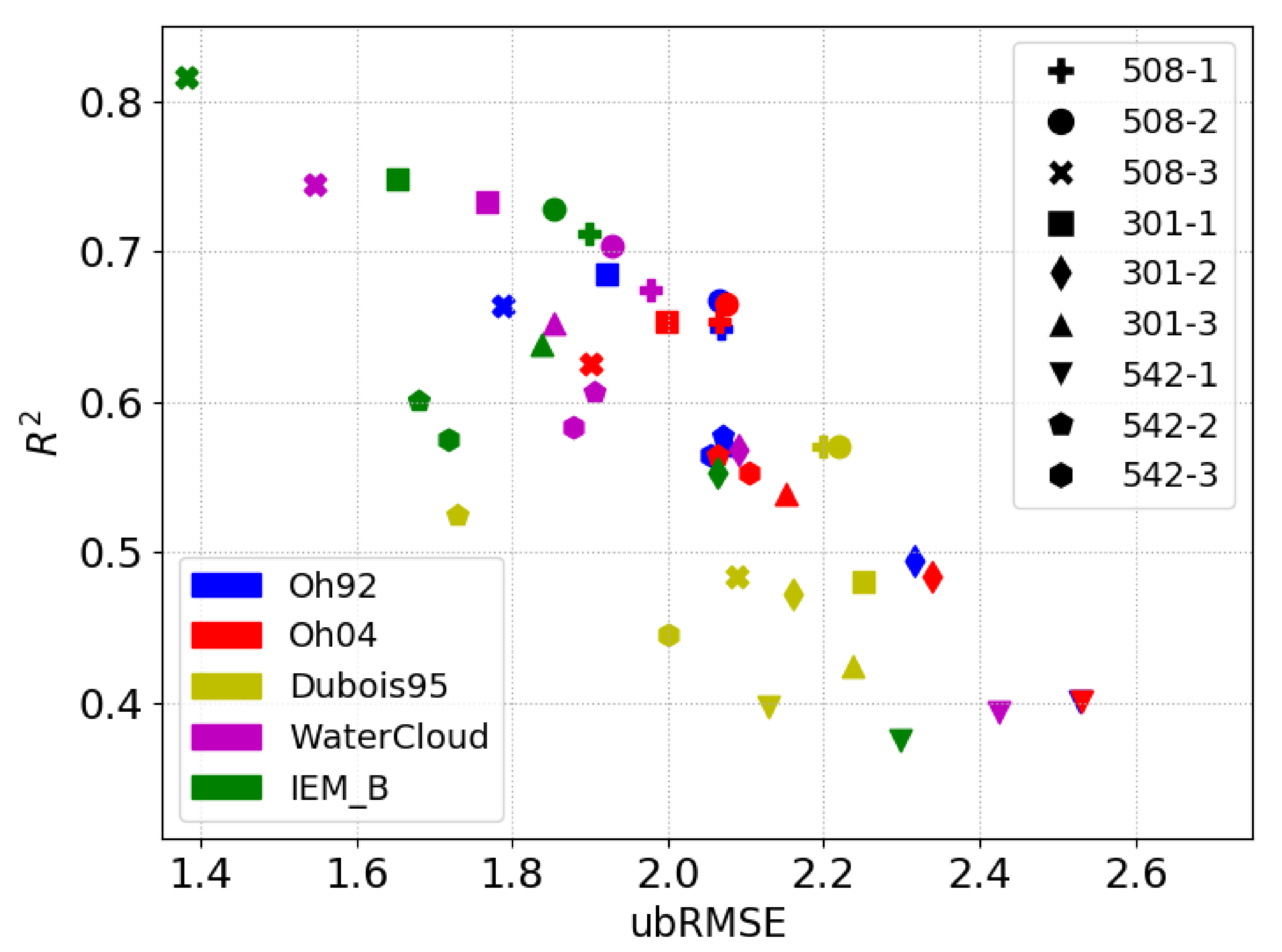
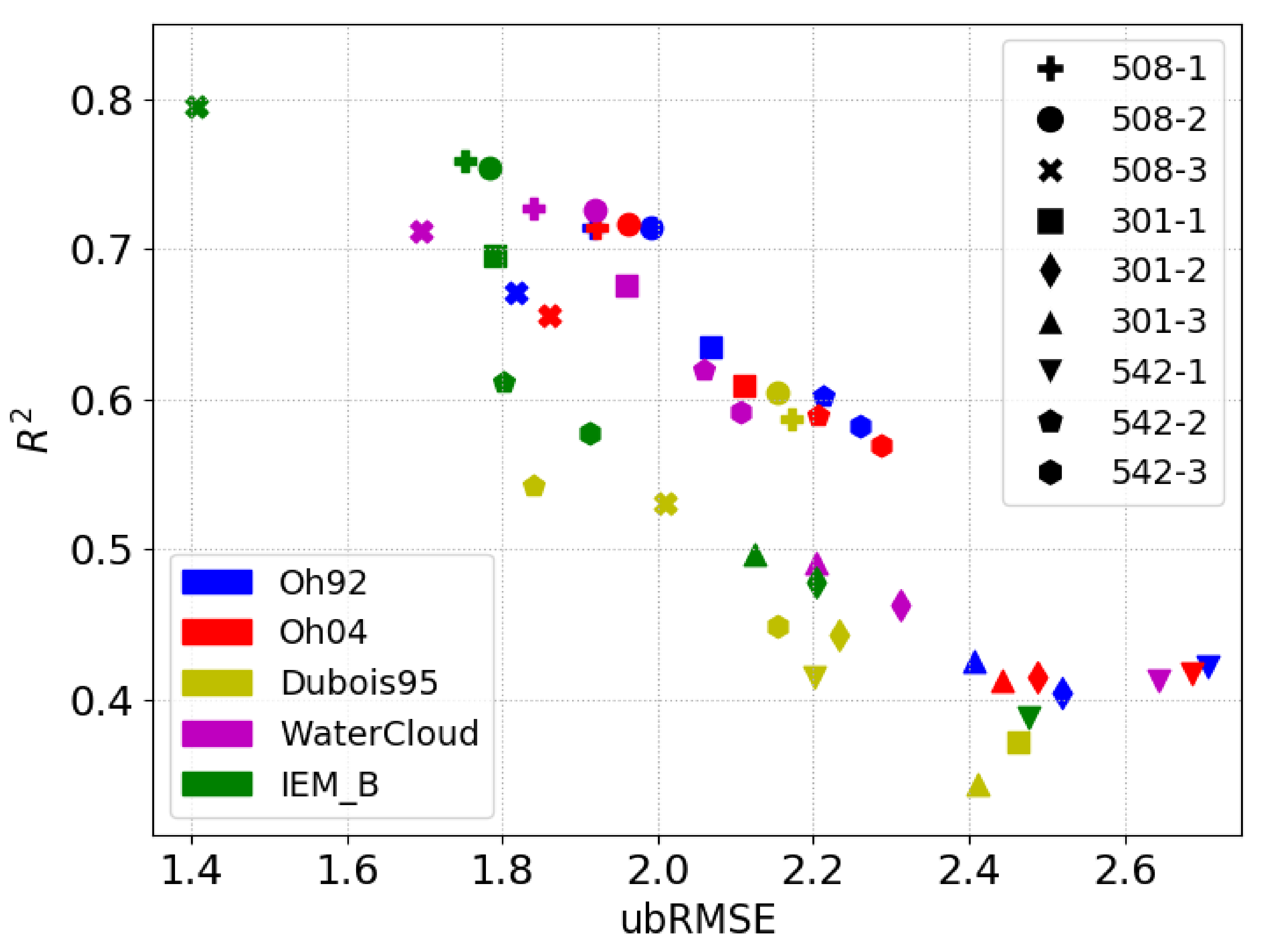
4.2. Model Validation Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hollmann, R.; Merchant, C.J.; Saunders, R.; Downy, C.; Buchwitz, M.; Cazenave, A.; Chuvieco, E.; Defourny, P.; de Leeuw, G.; Forsberg, R.; et al. The ESA Climate Change Initiative: Satellite Data Records for Essential Climate Variables. Bull. Am. Meteorol. Soc. 2013, 94, 1541–1552. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil Moisture for Hydrological Applications: Open Questions and New Opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Hochschild, V.; Thiel, C.; Grünler, S. Derivation of Land Cover and Soil Moisture from Airborne Polarimetric SAR-Data. Sao/NASA Astrophys. Data Syst. 2001, 475, 355–358. [Google Scholar]
- Zribi, M.; Muddu, S.; Bousbih, S.; Al Bitar, A.; Tomer, S.K.; Baghdadi, N.; Bandyopadhyay, S. Analysis of L-Band SAR Data for Soil Moisture Estimations over Agricultural Areas in the Tropics. Remote Sens. 2019, 11, 1122. [Google Scholar] [CrossRef]
- Oldak, A.; Jackson, T.J.; Starks, P.; Elliott, R. Mapping Near-Surface Soil Moisture on Regional Scale Using ERS-2 SAR Data. Int. J. Remote Sens. 2003, 24, 4579–4598. [Google Scholar] [CrossRef]
- Baghdadi, N.; Aubert, M.; Cerdan, O.; Franchistéguy, L.; Viel, C.; Martin, E.; Zribi, M.; Desprats, J.F. Operational Mapping of Soil Moisture Using Synthetic Aperture Radar Data: Application to the Touch Basin (France). Sensors 2007, 7, 2458–2483. [Google Scholar] [CrossRef]
- Kornelsen, K.C.; Coulibaly, P. Advances in Soil Moisture Retrieval from Synthetic Aperture Radar and Hydrological Applications. J. Hydrol. 2013, 476, 460–489. [Google Scholar] [CrossRef]
- Engman, E. The Potential of SAR in Hydrology. In Proceedings of the IGARSS ’94-1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; Volume 1, pp. 283–285. [Google Scholar] [CrossRef]
- Le Hegarat-Mascle, S.; Zribi, M.; Alem, F.; Weisse, A.; Loumagne, C. Soil Moisture Estimation from ERS/SAR Data: Toward an Operational Methodology. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2647–2658. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for Improved Earth System Understanding: State-of-the Art and Future Directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Amitrano, D.; Martino, G.D.; Iodice, A.; Riccio, D.; Ruello, G.; Ciervo, F.; Papa, M.N.; Koussoubé, Y. Effectiveness of High-Resolution SAR for Water Resource Management in Low-Income Semi-Arid Countries. Int. J. Remote Sens. 2014, 35, 70–88. [Google Scholar] [CrossRef]
- Holtgrave, A.K.; Förster, M.; Greifeneder, F.; Notarnicola, C.; Kleinschmit, B. Estimation of Soil Moisture in Vegetation-Covered Floodplains with Sentinel-1 SAR Data Using Support Vector Regression. PFG J. Photogramm. Remote. Sens. Geoinf. Sci. 2018, 86, 85–101. [Google Scholar] [CrossRef]
- Urban, M.; Berger, C.; Mudau, T.E.; Heckel, K.; Truckenbrodt, J.; Onyango Odipo, V.; Smit, I.P.J.; Schmullius, C. Surface Moisture and Vegetation Cover Analysis for Drought Monitoring in the Southern Kruger National Park Using Sentinel-1, Sentinel-2, and Landsat-8. Remote Sens. 2018, 10, 1482. [Google Scholar] [CrossRef]
- Bousbih, S.; Zribi, M.; El Hajj, M.; Baghdadi, N.; Lili-Chabaane, Z.; Gao, Q.; Fanise, P. Soil Moisture and Irrigation Mapping in A Semi-Arid Region, Based on the Synergetic Use of Sentinel-1 and Sentinel-2 Data. Remote Sens. 2018, 10, 1953. [Google Scholar] [CrossRef]
- Barrett, B.W.; Dwyer, E.; Whelan, P. Soil Moisture Retrieval from Active Spaceborne Microwave Observations: An Evaluation of Current Techniques. Remote Sens. 2009, 1, 210–242. [Google Scholar] [CrossRef]
- Ulaby, F. Radar Measurement of Soil Moisture Content. IEEE Trans. Antennas Propag. 1974, 22, 257–265. [Google Scholar] [CrossRef]
- Ulaby, F.; Long, D.; Blackwell, W.; Elachi, C.; Fung, A.; Ruf, C.; Sarabandi, K.; Zyl, J.; Zebker, H. Microwave Radar and Radiometric Remote Sensing; University of Michigan Press: Ann Arbor, MI, USA, 2014. [Google Scholar]
- Baghdadi, N.; King, C.; Bourguignon, A.; Remond, A. Potential of ERS and Radarsat Data for Surface Roughness Monitoring over Bare Agricultural Fields: Application to Catchments in Northern France. Int. J. Remote Sens. 2002, 23, 3427–3442. [Google Scholar] [CrossRef]
- Holah, N.; Baghdadi, N.; Zribi, M.; Bruand, A.; King, C. Potential of ASAR/ENVISAT for the Characterization of Soil Surface Parameters over Bare Agricultural Fields. Remote Sens. Environ. 2005, 96, 78–86. [Google Scholar] [CrossRef]
- Wickel, A.J.; Jackson, T.J.; Wood, E.F. Multitemporal Monitoring of Soil Moisture with RADARSAT SAR during the 1997 Southern Great Plains Hydrology Experiment. Int. J. Remote Sens. 2001, 22, 1571–1583. [Google Scholar] [CrossRef]
- Mathieu, R.; Sbih, M.; Viau, A.A.; Anctil, F.; Parent, L.E.; Boisvert, J. Relationships between Radarsat SAR Data and Surface Moisture Content of Agricultural Organic Soils. Int. J. Remote Sens. 2003, 24, 5265–5281. [Google Scholar] [CrossRef]
- Attema, E.P.W.; Ulaby, F.T. Vegetation Modeled as a Water Cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Prévot, L.; Champion, I.; Guyot, G. Estimating Surface Soil Moisture and Leaf Area Index of a Wheat Canopy Using a Dual-Frequency (C and X Bands) Scatterometer. Remote Sens. Environ. 1993, 46, 331–339. [Google Scholar] [CrossRef]
- Champion, I.; Prevot, L.; Guyot, G. Generalized Semi-Empirical Modelling of Wheat Radar Response. Int. J. Remote Sens. 2000, 21, 1945–1951. [Google Scholar] [CrossRef]
- Dabrowska-Zielinska, K.; Inoue, Y.; Kowalik, W.; Gruszczynska, M. Inferring the Effect of Plant and Soil Variables on C- and L-Band SAR Backscatter over Agricultural Fields, Based on Model Analysis. Adv. Space Res. 2007, 39, 139–148. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F. An Empirical Model and an Inversion Technique for Radar Scattering from Bare Soil Surfaces. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
- Oh, Y. Quantitative Retrieval of Soil Moisture Content and Surface Roughness from Multipolarized Radar Observations of Bare Soil Surfaces. IEEE Trans. Geosci. Remote Sens. 2004, 42, 596–601. [Google Scholar] [CrossRef]
- Dubois, P.; van Zyl, J.; Engman, T. Measuring Soil Moisture with Imaging Radars. IEEE Trans. Geosci. Remote Sens. 1995, 33, 915–926. [Google Scholar] [CrossRef]
- Fung, A.; Li, Z.; Chen, K. Backscattering from a Randomly Rough Dielectric Surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Baghdadi, N.; King, C.; Chanzy, A.; Wigneron, J.P. An Empirical Calibration of the Integral Equation Model Based on SAR Data, Soil Moisture and Surface Roughness Measurement over Bare Soils. Int. J. Remote Sens. 2002, 23, 4325–4340. [Google Scholar] [CrossRef]
- Baghdadi, N.; Abou Chaaya, J.; Zribi, M. Semiempirical Calibration of the Integral Equation Model for SAR Data in C-Band and Cross Polarization Using Radar Images and Field Measurements. IEEE Geosci. Remote Sens. Lett. 2011, 8, 14–18. [Google Scholar] [CrossRef]
- Chen, K.; Wu, T.D.; Tsang, L.; Li, Q.; Shi, J.; Fung, A. Emission of Rough Surfaces Calculated by the Integral Equation Method with Comparison to Three-Dimensional Moment Method Simulations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Sarabandi, K.; McDonald, K.; Whitt, M.; Dobson, M.C. Michigan Microwave Canopy Scattering Model. Int. J. Remote Sens. 1990, 11, 1223–1253. [Google Scholar] [CrossRef]
- Ferrazzoli, P.; Guerriero, L. Radar Sensitivity to Tree Geometry and Woody Volume: A Model Analysis. IEEE Trans. Geosci. Remote Sens. 1995, 33, 360–371. [Google Scholar] [CrossRef]
- De Roo, R.; Du, Y.; Ulaby, F.; Dobson, M. A Semi-Empirical Backscattering Model at L-Band and C-Band for a Soybean Canopy with Soil Moisture Inversion. IEEE Trans. Geosci. Remote Sens. 2001, 39, 864–872. [Google Scholar] [CrossRef]
- Quast, R.; Wagner, W. Analytical Solution for First-Order Scattering in Bistatic Radiative Transfer Interaction Problems of Layered Media. Appl. Opt. 2016, 55, 5379–5386. [Google Scholar] [CrossRef] [PubMed]
- Quast, R.; Albergel, C.; Calvet, J.C.; Wagner, W. A Generic First-Order Radiative Transfer Modelling Approach for the Inversion of Soil and Vegetation Parameters from Scatterometer Observations. Remote Sens. 2019, 11, 285. [Google Scholar] [CrossRef]
- Zribi, M.; Taconet, O.; Le Hégarat-Mascle, S.; Vidal-Madjar, D.; Emblanch, C.; Loumagne, C.; Normand, M. Backscattering Behavior and Simulation Comparison over Bare Soils Using SIR-C/X-SAR and ERASME 1994 Data over Orgeval. Remote Sens. Environ. 1997, 59, 256–266. [Google Scholar] [CrossRef]
- Baghdadi, N.; Zribi, M. Evaluation of Radar Backscatter Models IEM, OH and Dubois Using Experimental Observations. Int. J. Remote Sens. 2006, 27, 3831–3852. [Google Scholar] [CrossRef]
- Khabazan, S.; Motagh, M.; Hosseini, M. Evaluation of Radar Backscattering Models IEM, OH, and Dubois Using L and C-Bands SAR Data over Different Vegetation Canopy Covers and Soil Depths. In ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; Copernicus GmbH: Göttingen, Germany, 2013; Volume XL-1-W3, pp. 225–230. [Google Scholar] [CrossRef]
- Choker, M.; Baghdadi, N.; Zribi, M.; El Hajj, M.; Paloscia, S.; Verhoest, N.E.C.; Lievens, H.; Mattia, F. Evaluation of the Oh, Dubois and IEM Backscatter Models Using a Large Dataset of SAR Data and Experimental Soil Measurements. Water 2017, 9, 38. [Google Scholar] [CrossRef]
- Ezzahar, J.; Ouaadi, N.; Zribi, M.; Elfarkh, J.; Aouade, G.; Khabba, S.; Er-Raki, S.; Chehbouni, A.; Jarlan, L. Evaluation of Backscattering Models and Support Vector Machine for the Retrieval of Bare Soil Moisture from Sentinel-1 Data. Remote Sens. 2020, 12, 72. [Google Scholar] [CrossRef]
- Kweon, S.K.; Oh, Y. A Modified Water-Cloud Model With Leaf Angle Parameters for Microwave Backscattering From Agricultural Fields. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2802–2809. [Google Scholar] [CrossRef]
- Pierdicca, N.; Pulvirenti, L.; Pace, G. A Prototype Software Package to Retrieve Soil Moisture From Sentinel-1 Data by Using a Bayesian Multitemporal Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 153–166. [Google Scholar] [CrossRef]
- Baghdadi, N.; El Hajj, M.; Zribi, M.; Bousbih, S. Calibration of the Water Cloud Model at C-Band for Winter Crop Fields and Grasslands. Remote Sens. 2017, 9, 969. [Google Scholar] [CrossRef]
- Graham, A.J.; Harris, R. Estimating Crop and Waveband Specific Water Cloud Model Parameters Using a Theoretical Backscatter Model. Int. J. Remote Sens. 2002, 23, 5129–5133. [Google Scholar] [CrossRef]
- Liu, C.; Shi, J. Estimation of Vegetation Parameters of Water Cloud Model for Global Soil Moisture Retrieval Using Time-Series L-Band Aquarius Observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5621–5633. [Google Scholar] [CrossRef]
- Kumar, K.; Prasad, K.S.H.; Arora, M.K. Estimation of Water Cloud Model Vegetation Parameters Using a Genetic Algorithm. Hydrol. Sci. J. 2012, 57, 776–789. [Google Scholar] [CrossRef]
- Kumar, K.; Rao, H.P.S.; Arora, M.K. Study of Water Cloud Model Vegetation Descriptors in Estimating Soil Moisture in Solani Catchment. Hydrol. Process. 2015, 29, 2137–2148. [Google Scholar] [CrossRef]
- Song, X.; Ma, J.; Li, X.; Leng, P.; Zhou, F.; Li, S. First Results of Estimating Surface Soil Moisture in the Vegetated Areas Using ASAR and Hyperion Data: The Chinese Heihe River Basin Case Study. Remote Sens. 2014, 6, 12055–12069. [Google Scholar] [CrossRef]
- Van Emmerik, T.; Steele-Dunne, S.C.; Judge, J.; van de Giesen, N. Impact of Diurnal Variation in Vegetation Water Content on Radar Backscatter From Maize During Water Stress. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3855–3869. [Google Scholar] [CrossRef]
- Xu, C.; Qu, J.J.; Hao, X.; Wu, D. Monitoring Surface Soil Moisture Content over the Vegetated Area by Integrating Optical and SAR Satellite Observations in the Permafrost Region of Tibetan Plateau. Remote Sens. 2020, 12, 183. [Google Scholar] [CrossRef]
- Lievens, H.; Verhoest, N.E.C. On the Retrieval of Soil Moisture in Wheat Fields From L-Band SAR Based on Water Cloud Modeling, the IEM, and Effective Roughness Parameters. IEEE Geosci. Remote Sens. Lett. 2011, 8, 740–744. [Google Scholar] [CrossRef]
- Bai, X.; He, B. Potential of Dubois Model for Soil Moisture Retrieval in Prairie Areas Using SAR and Optical Data. Int. J. Remote Sens. 2015, 36, 5737–5753. [Google Scholar] [CrossRef]
- Xing, M.; He, B.; Ni, X.; Wang, J.; An, G.; Shang, J.; Huang, X. Retrieving Surface Soil Moisture over Wheat and Soybean Fields during Growing Season Using Modified Water Cloud Model from Radarsat-2 SAR Data. Remote Sens. 2019, 11, 1956. [Google Scholar] [CrossRef]
- He, B.; Xing, M.; Bai, X. A Synergistic Methodology for Soil Moisture Estimation in an Alpine Prairie Using Radar and Optical Satellite Data. Remote Sens. 2014, 6, 10966–10985. [Google Scholar] [CrossRef]
- Qiu, J.; Crow, W.T.; Wagner, W.; Zhao, T. Effect of Vegetation Index Choice on Soil Moisture Retrievals via the Synergistic Use of Synthetic Aperture Radar and Optical Remote Sensing. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 47–57. [Google Scholar] [CrossRef]
- Tao, L.; Wang, G.; Chen, W.; Chen, X.; Li, J.; Cai, Q. Soil Moisture Retrieval From SAR and Optical Data Using a Combined Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 637–647. [Google Scholar] [CrossRef]
- Zhao, X.; Huang, N.; Niu, Z.; Raghavan, V.; Song, X. Soil Moisture Retrieval in Farmland Using C-Band SAR and Optical Data. Spat. Inf. Res. 2017, 25, 431–438. [Google Scholar] [CrossRef]
- Attarzadeh, R.; Amini, J.; Notarnicola, C.; Greifeneder, F. Synergetic Use of Sentinel-1 and Sentinel-2 Data for Soil Moisture Mapping at Plot Scale. Remote Sens. 2018, 10, 1285. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Bazzi, H. Synergic Use of Sentinel-1 and Sentinel-2 Images for Operational Soil Moisture Mapping at High Spatial Resolution over Agricultural Areas. Remote Sens. 2017, 9, 1292. [Google Scholar] [CrossRef]
- Gao, F.; Morisette, J.T.; Wolfe, R.E.; Ederer, G.; Pedelty, J.; Masuoka, E.; Myneni, R.; Tan, B.; Nightingale, J. An Algorithm to Produce Temporally and Spatially Continuous MODIS-LAI Time Series. IEEE Geosci. Remote Sens. Lett. 2008, 5, 60–64. [Google Scholar] [CrossRef]
- Dhakar, R.; Sehgal, V.K.; Chakraborty, D.; Sahoo, R.N.; Mukherjee, J. Field Scale Wheat LAI Retrieval from Multispectral Sentinel 2A-MSI and LandSat 8-OLI Imagery: Effect of Atmospheric Correction, Image Resolutions and Inversion Techniques. Geocarto Int. 2019, 1–21. [Google Scholar] [CrossRef]
- Xie, Q.; Dash, J.; Huete, A.; Jiang, A.; Yin, G.; Ding, Y.; Peng, D.; Hall, C.C.; Brown, L.; Shi, Y.; et al. Retrieval of Crop Biophysical Parameters from Sentinel-2 Remote Sensing Imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 187–195. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; Wocher, M.; Mauser, W.; Hank, T. Modellbasierte Selektion Hyperspektraler EnMAP Kanäle Zur Optimalen Invertierung von Strahlungstransfermodellen Für Landwirtschaftliche Kulturen. PFG J. Photogramm. Remote Sens. Geoinf. Sci. 2018, 86, 263–272. [Google Scholar] [CrossRef]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Retrieval of Biophysical Crop Variables from Multi-Angular Canopy Spectroscopy. Remote Sens. 2017, 9, 726. [Google Scholar] [CrossRef]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Fitted PROSAIL Parameterization of Leaf Inclinations, Water Content and Brown Pigment Content for Winter Wheat and Maize Canopies. Remote Sens. 2019, 11, 1150. [Google Scholar] [CrossRef]
- Wocher, M.; Berger, K.; Danner, M.; Mauser, W.; Hank, T. Physically-Based Retrieval of Canopy Equivalent Water Thickness Using Hyperspectral Data. Remote Sens. 2018, 10, 1924. [Google Scholar] [CrossRef]
- Kellndorfer, J.; Pierce, L.; Dobson, M.; Ulaby, F. Toward Consistent Regional-to-Global-Scale Vegetation Characterization Using Orbital SAR Systems. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1396–1411. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Belaud, G.; Cheviron, B.; Courault, D.; Charron, F. Soil Moisture Retrieval over Irrigated Grassland Using X-Band SAR Data. Remote Sens. Environ. 2016, 176, 202–218. [Google Scholar] [CrossRef]
- Fung, A.; Liu, W.; Chen, K.; Tsay, M. An Improved Iem Model for Bistatic Scattering From Rough Surfaces. J. Electromagn. Waves Appl. 2002, 16, 689–702. [Google Scholar] [CrossRef]
- Marzahn, P.; Ludwig, R. Using Multi-Dimensional Microwave Remote Sensing Information for the Retrieval of Soil Surface Roughness. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 1257–1262. [Google Scholar] [CrossRef]
- Marzahn, P.; Rieke-Zapp, D.; Ludwig, R. Assessment of Soil Surface Roughness Statistics for Microwave Remote Sensing Applications Using a Simple Photogrammetric Acquisition System. ISPRS J. Photogramm. Remote Sens. 2012, 72, 80–89. [Google Scholar] [CrossRef]
- Wegmüller, U.; Santoro, M.; Mattia, F.; Balenzano, A.; Satalino, G.; Marzahn, P.; Fischer, G.; Ludwig, R.; Floury, N. Progress in the Understanding of Narrow Directional Microwave Scattering of Agricultural Fields. Remote Sens. Environ. 2011, 115, 2423–2433. [Google Scholar] [CrossRef]
- Jia, M.; Tong, L.; Zhang, Y.; Chen, Y. Multitemporal Radar Backscattering Measurement of Wheat Fields Using Multifrequency (L, S, C, and X) and Full-Polarization. Radio Sci. 2013, 48, 471–481. [Google Scholar] [CrossRef]
- Mattia, F.; Le Toan, T.; Picard, G.; Posa, F.; D’Alessio, A.; Notarnicola, C.; Gatti, A.; Rinaldi, M.; Satalino, G.; Pasquariello, G. Multitemporal C-Band Radar Measurements on Wheat Fields. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1551–1560. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Kerr, Y.; Waldteufel, P.; Saleh, K.; Escorihuela, M.J.; Richaume, P.; Ferrazzoli, P.; de Rosnay, P.; Gurney, R.; Calvet, J.C.; et al. L-Band Microwave Emission of the Biosphere (L-MEB) Model: Description and Calibration against Experimental Data Sets over Crop Fields. Remote Sens. Environ. 2007, 107, 639–655. [Google Scholar] [CrossRef]
- Davidson, M.; Toan, T.L.; Mattia, F.; Satalino, G.; Manninen, T.; Borgeaud, M. On the Characterization of Agricultural Soil Roughness for Radar Remote Sensing Studies. IEEE Trans. Geosci. Remote Sens. 2000, 38, 630–640. [Google Scholar] [CrossRef]
- Picard, G.; Le Toan, T.; Mattia, F. Understanding C-Band Radar Backscatter from Wheat Canopy Using a Multiple-Scattering Coherent Model. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1583–1591. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-rayes, M.A. Microwave Dielectric Behavior of Wet Soil-Part II: Dielectric Mixing Models. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 35–46. [Google Scholar] [CrossRef]
- Khabbazan, S.; Vermunt, P.; Steele-Dunne, S.; Ratering Arntz, L.; Marinetti, C.; van der Valk, D.; Iannini, L.; Molijn, R.; Westerdijk, K.; van der Sande, C. Crop Monitoring Using Sentinel-1 Data: A Case Study from The Netherlands. Remote Sens. 2019, 11, 1887. [Google Scholar] [CrossRef]
- Allen, S.T.; Whitsell, M.L.; Keim, R.F. Leaf Area Allometrics and Morphometrics in Baldcypress. Can. J. For. Res. 2015, 45, 963–969. [Google Scholar] [CrossRef]
- He, L.; Tong, L.; Li, Y.; Chen, Y.; Tan, L.; Guo, C. Polarimetric Analysis of Radar Backscatter from Ground-Based Scatterometers and Wheat Biomass Monitoring with Advanced Synthetic Aperture Radar Images. J. Appl. Remote Sens. 2016, 10, 026008. [Google Scholar] [CrossRef]
- Meier, U.; Bleiholder, H.; Buhr, L.; Feller, C.; Hack, H.; Heß, M.; Lancashire, P.D.; Schnock, U.; Stauß, R.; van den Boom, T.; et al. The BBCH System to Coding the Phenological Growth Stages of Plants–History and Publications. J. FÜr Kult. 2009, 61, 41–52. [Google Scholar] [CrossRef]
- Riedel, T.; Liebeskind, P.; Schmullius, C. Seasonal and Diurnal Changes of Polarimetric Parameters from Crops Derived by the Cloude Decomposition Theorem at L-Band. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 5, pp. 2714–2716. [Google Scholar] [CrossRef]
- Riedel, T.; Pathe, C.; Thiel, C.; Herold, M.; Schmullius, C. Systematic Investigation on the Effect of Dew and Interception on Multifrequency and Multipolarimetric Radar Backscatter Signals. Sao/NASA Astrophys. Data Syst. 2002, 475, 99–104. [Google Scholar]
- Way, J.; Paris, J.; Dobson, M.; McDonals, K.; Ulaby, F.; Weber, J.; Ustin, L.; Vanderbilt, V.; Kasischke, E. Diurnal Change in Trees as Observed by Optical and Microwave Sensors: The EOS Synergism Study. IEEE Trans. Geosci. Remote Sens. 1991, 29, 807. [Google Scholar] [CrossRef]
- Hornbuckle, B.K.; Rowlandson, T.L.; Russell, E.; Kaleita, A.; Logsdon, S.; Kruger, A.; Yueh, S.; De Roo, R.D. Howdoes Dew Affect L-Band Backscatter? Analysis of Pals Data at the Iowa Validation Site and Implications for Smap. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 4835–4838. [Google Scholar] [CrossRef]
- Konings, A.G.; Piles, M.; Rötzer, K.; McColl, K.A.; Chan, S.K.; Entekhabi, D. Vegetation Optical Depth and Scattering Albedo Retrieval Using Time Series of Dual-Polarized L-Band Radiometer Observations. Remote Sens. Environ. 2016, 172, 178–189. [Google Scholar] [CrossRef]

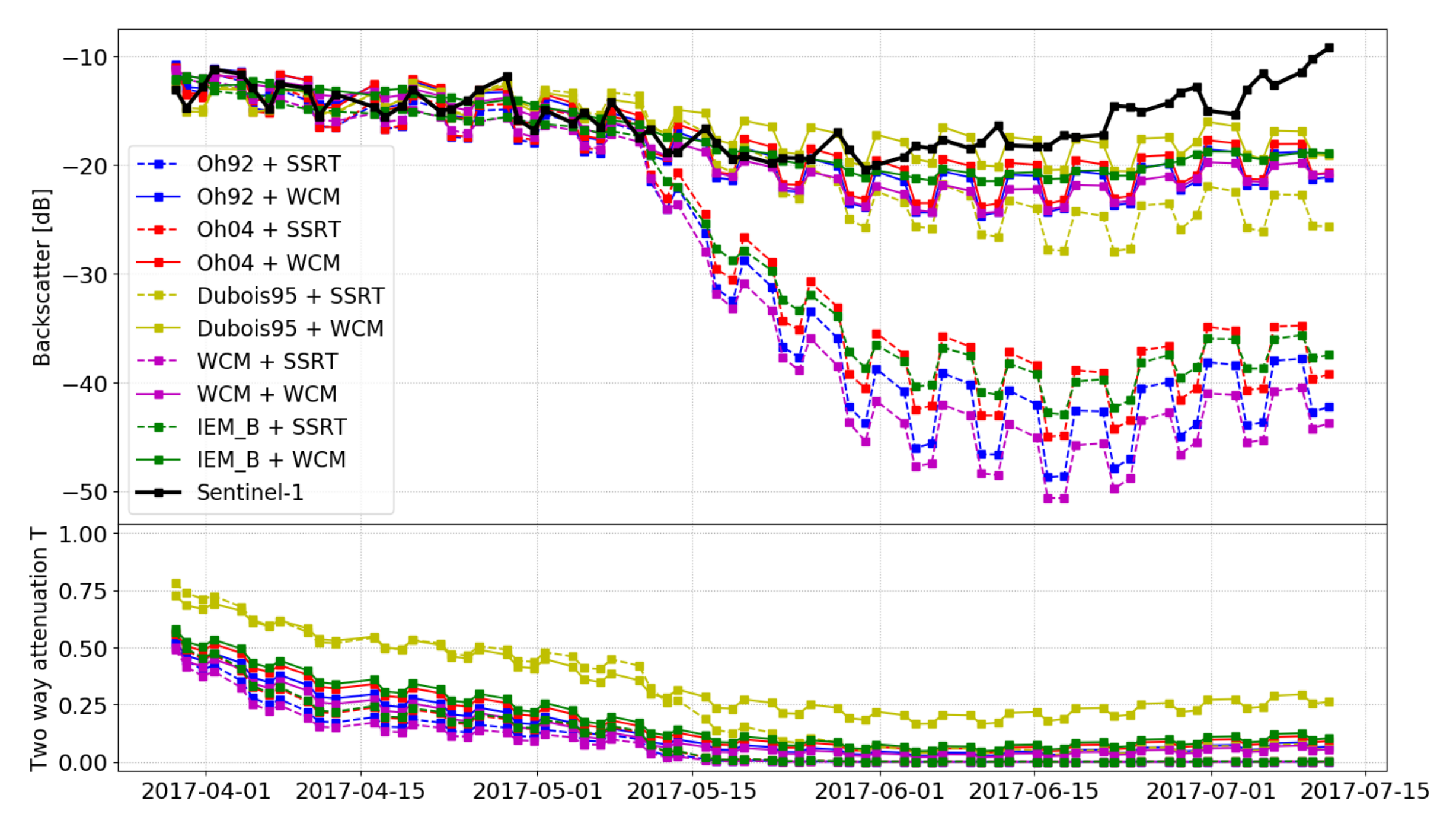
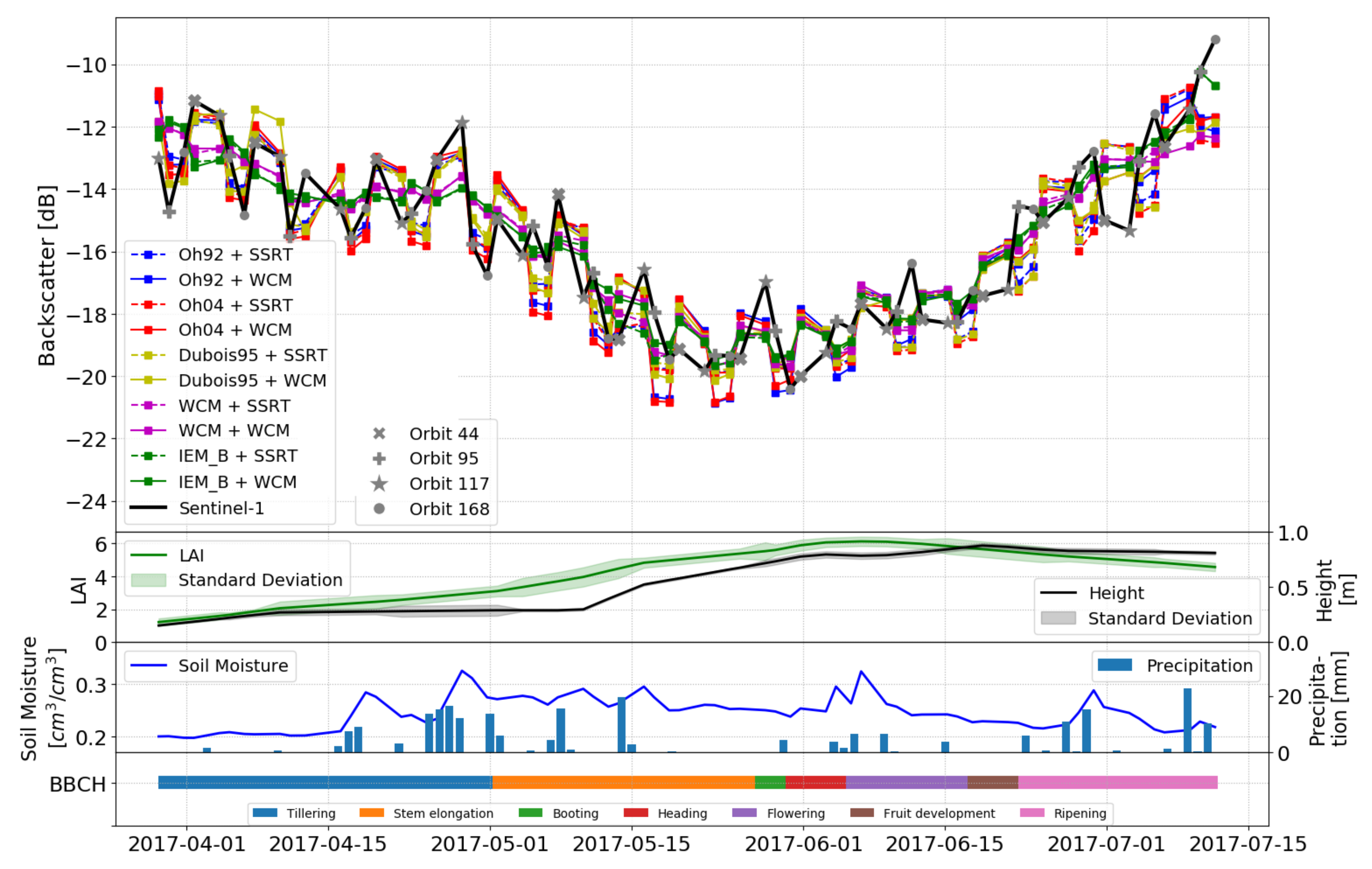

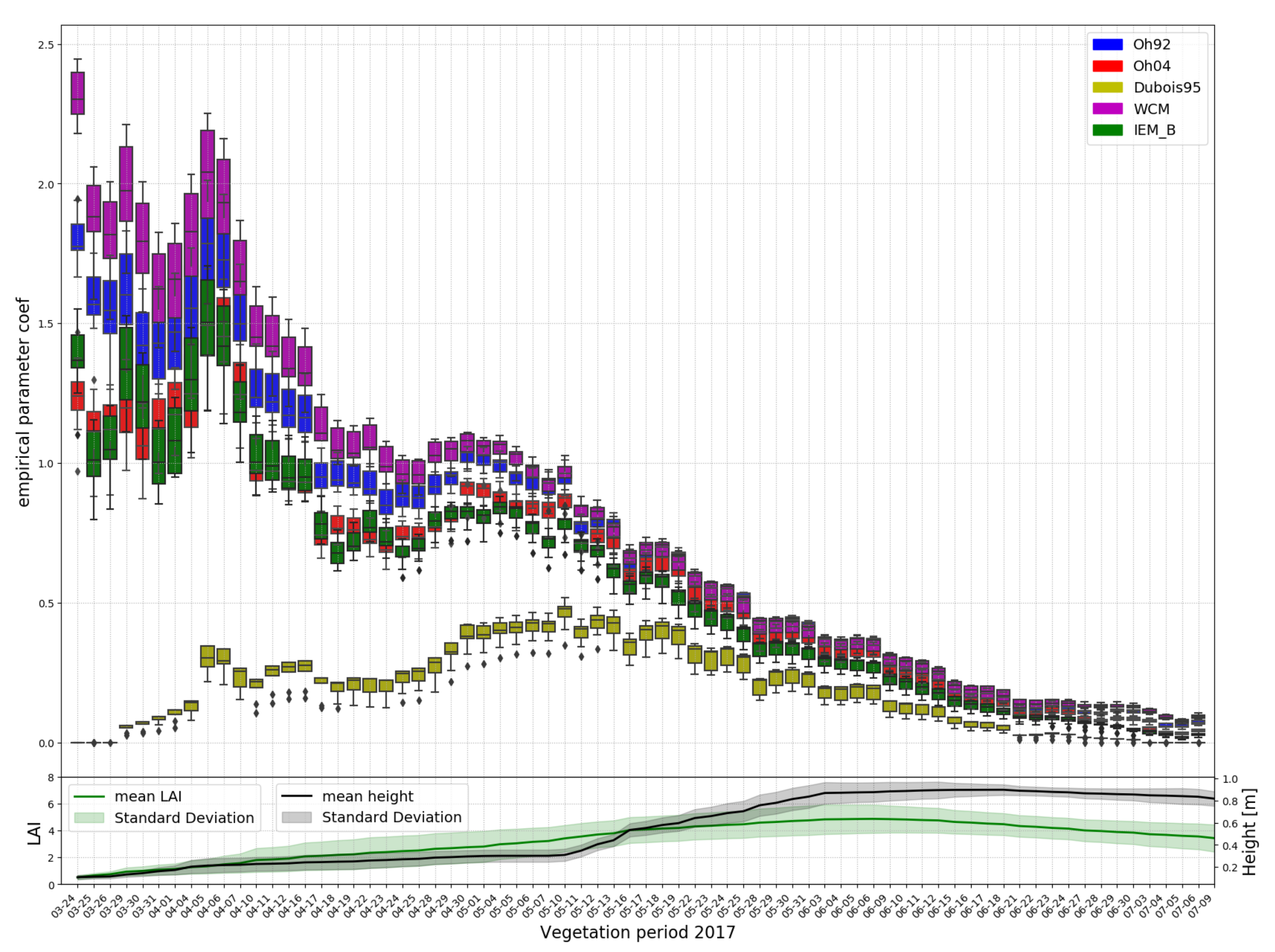
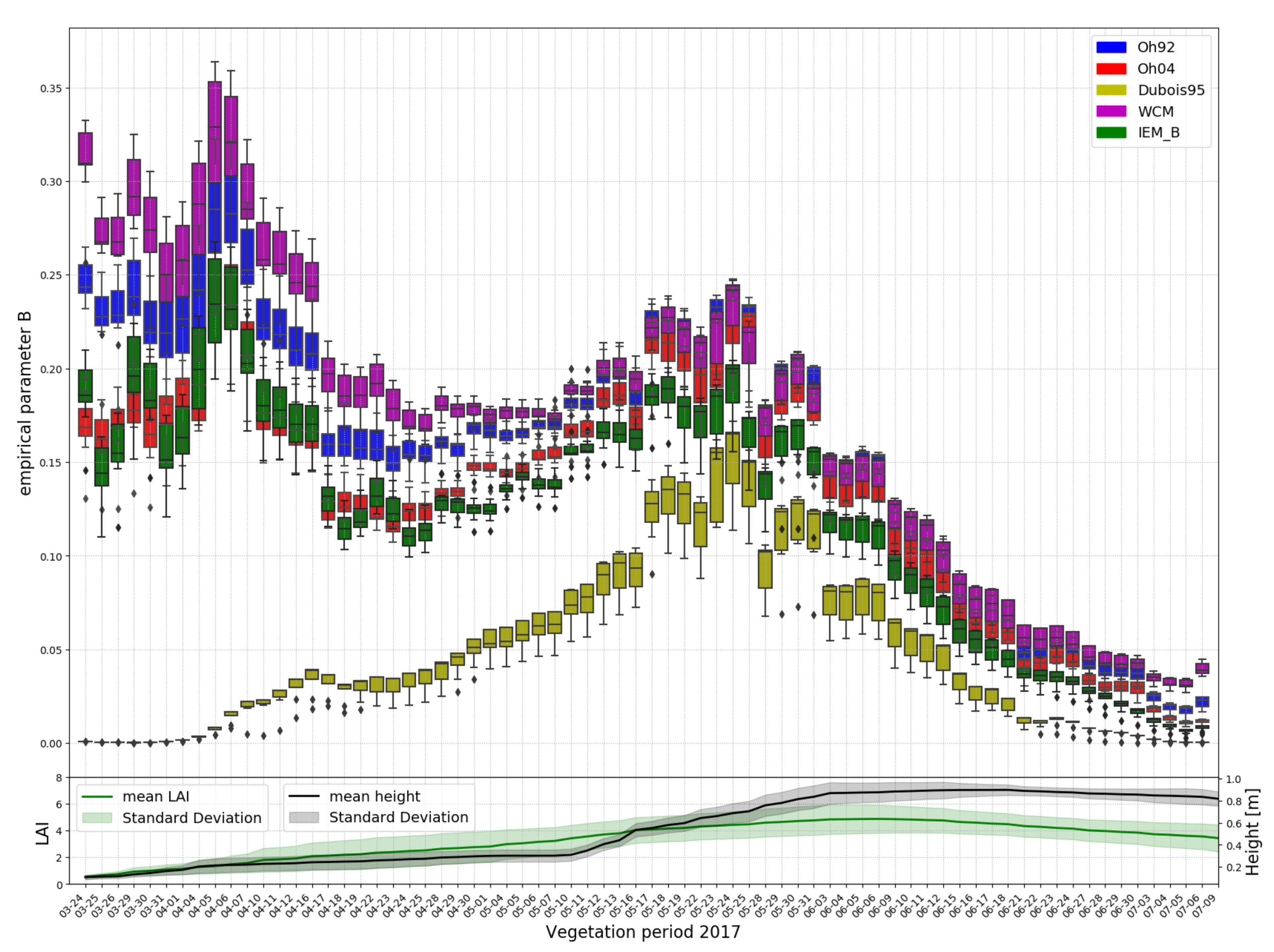
| Variable | Acquisition Time | Time Interval | Range |
|---|---|---|---|
| Canopy height [cm] | 03/24–07/17/2017 | weekly | 7–105 |
| LAI | 03/24–07/17/2017 | weekly | 0.35–6.25 |
| Soil moisture [m3/m3] | 03/24–07/17/2017 | continues | 0.09–0.38 |
| Variable | Time Interval | Mean | Std |
|---|---|---|---|
| Soil sand content [%] | once (several locations) | 24.08 | 10.46 |
| Soil clay content [%] | once (several locations) | 7.38 | 1.80 |
| Bulk density [g/cm3] | once (several locations) | 1.45 | 0.13 |
| Asc./Desc. | Incidence Angle [] | Relative Orbit | Amount | Revisit Time [Days] | Acquisition Time |
|---|---|---|---|---|---|
| Ascending | 36 | 44 | 19 | 6 | 4:58 p.m. |
| 45 | 117 | 19 | 6 | 5:06 p.m. | |
| Descending | 43 | 95 | 20 | 6 | 5:17 a.m. |
| 35 | 168 | 20 | 6 | 5:25 a.m. |
| Type | Validity Range | Site Dependent | Required Parameters | Pol. | ||
|---|---|---|---|---|---|---|
| Fitted | Field Measurements or Literature Values | |||||
| WCM surface | empi. | Yes | C, D | , | HH, VV VH | |
| Oh92 | semi-empi. | No | s, k, , (, , , ) | HH, VV VH | ||
| Oh04 | semi-empi. | No | s, k, , | HH, VV VH | ||
| Dubois95 | semi-empi. | No | s, k, , (, , , ) | HH, VV | ||
| IEM_B | theoretical | No | s, k, l, , (, , , ) | HH, VV VH | ||
| SSRT | semi-empi. | Yes | () | H, , , | HH, VV VH | |
| WCM canopy | empi. | Yes | A, B | (), (), | HH, VV VH | |
| k | s | C | D | A | |
|---|---|---|---|---|---|
| [cm−1] | [cm] | [dB] | [dB] | ||
| 1.13 | 1.2 | 0.03 | −14.61 | 12.88 | 0.0029 |
| Model | Calibration | |
|---|---|---|
| Surface + Canopy | RMSE [dB] | R |
| Oh92 + SSRT | 2.11 | 0.20 |
| Oh92 + WCM | 1.97 | 0.26 |
| Oh04 + SSRT | 2.02 | 0.18 |
| Oh04 + WCM | 1.92 | 0.23 |
| Dubois95 + SSRT | 2.09 | 0.08 |
| Dubois95 + WCM | 2.03 | 0.08 |
| WCM + SSRT | 2.25 | 0.22 |
| WCM + WCM | 2.08 | 0.34 |
| IEM_B + SSRT | 2.24 | 0.15 |
| IEM_B + WCM | 2.13 | 0.24 |
| Model | Calibration | Validation | |||
|---|---|---|---|---|---|
| Surface + Canopy | RMSE [dB] | R | RMSE [dB] | ubRMSE [dB] | R |
| Oh92 + SSRT | 1.24 | 0.73 | 2.82 | 2.10 | 0.59 |
| Oh92 + WCM | 1.22 | 0.73 | 2.75 | 2.21 | 0.57 |
| Oh04 + SSRT | 1.33 | 0.69 | 2.87 | 2.14 | 0.57 |
| Oh04 + WCM | 1.32 | 0.68 | 2.81 | 2.22 | 0.57 |
| Dubois95 + SSRT | 1.55 | 0.49 | 3.06 | 2.11 | 0.49 |
| Dubois95 + WCM | 1.60 | 0.45 | 3.06 | 2.18 | 0.48 |
| WCM + SSRT | 1.16 | 0.82 | 2.65 | 1.93 | 0.63 |
| WCM + WCM | 1.13 | 0.81 | 2.57 | 2.08 | 0.60 |
| IEM_B + SSRT | 1.32 | 0.78 | 2.62 | 1.82 | 0.64 |
| IEM_B + WCM | 1.34 | 0.77 | 2.54 | 1.92 | 0.62 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weiß, T.; Ramsauer, T.; Löw, A.; Marzahn, P. Evaluation of Different Radiative Transfer Models for Microwave Backscatter Estimation of Wheat Fields. Remote Sens. 2020, 12, 3037. https://doi.org/10.3390/rs12183037
Weiß T, Ramsauer T, Löw A, Marzahn P. Evaluation of Different Radiative Transfer Models for Microwave Backscatter Estimation of Wheat Fields. Remote Sensing. 2020; 12(18):3037. https://doi.org/10.3390/rs12183037
Chicago/Turabian StyleWeiß, Thomas, Thomas Ramsauer, Alexander Löw, and Philip Marzahn. 2020. "Evaluation of Different Radiative Transfer Models for Microwave Backscatter Estimation of Wheat Fields" Remote Sensing 12, no. 18: 3037. https://doi.org/10.3390/rs12183037
APA StyleWeiß, T., Ramsauer, T., Löw, A., & Marzahn, P. (2020). Evaluation of Different Radiative Transfer Models for Microwave Backscatter Estimation of Wheat Fields. Remote Sensing, 12(18), 3037. https://doi.org/10.3390/rs12183037