Optical Remote Sensing Image Registration Using Spatial-Consistency and Average Regional Information Divergence Minimization via Quantum-Behaved Particle Swarm Optimization
Abstract
:1. Introduction
2. Average Regional Information Divergence
3. SC-ARID-QPSO
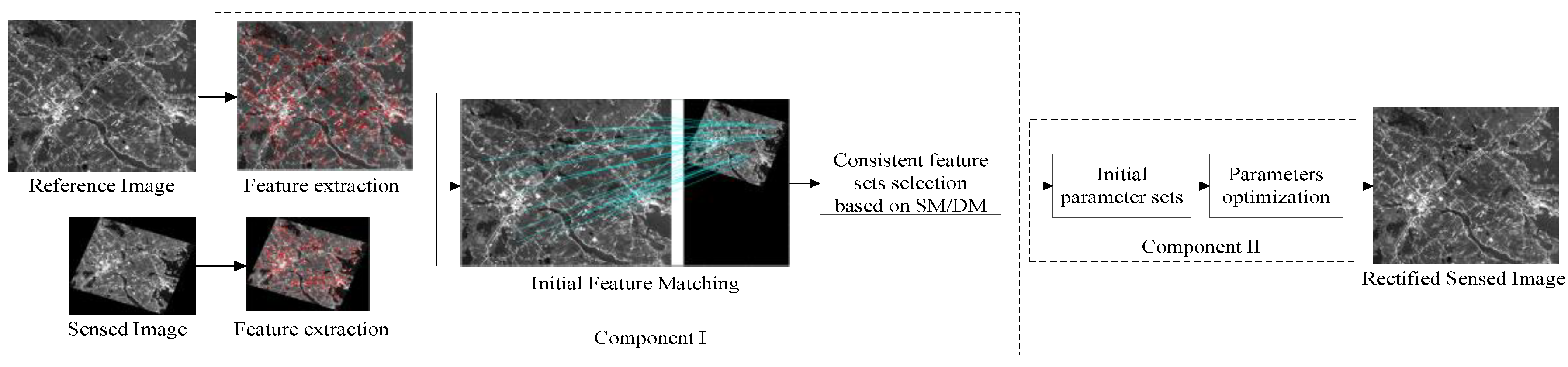
3.1. Component I: Consistent Feature Set Selection
3.1.1. Feature Extraction and Matching
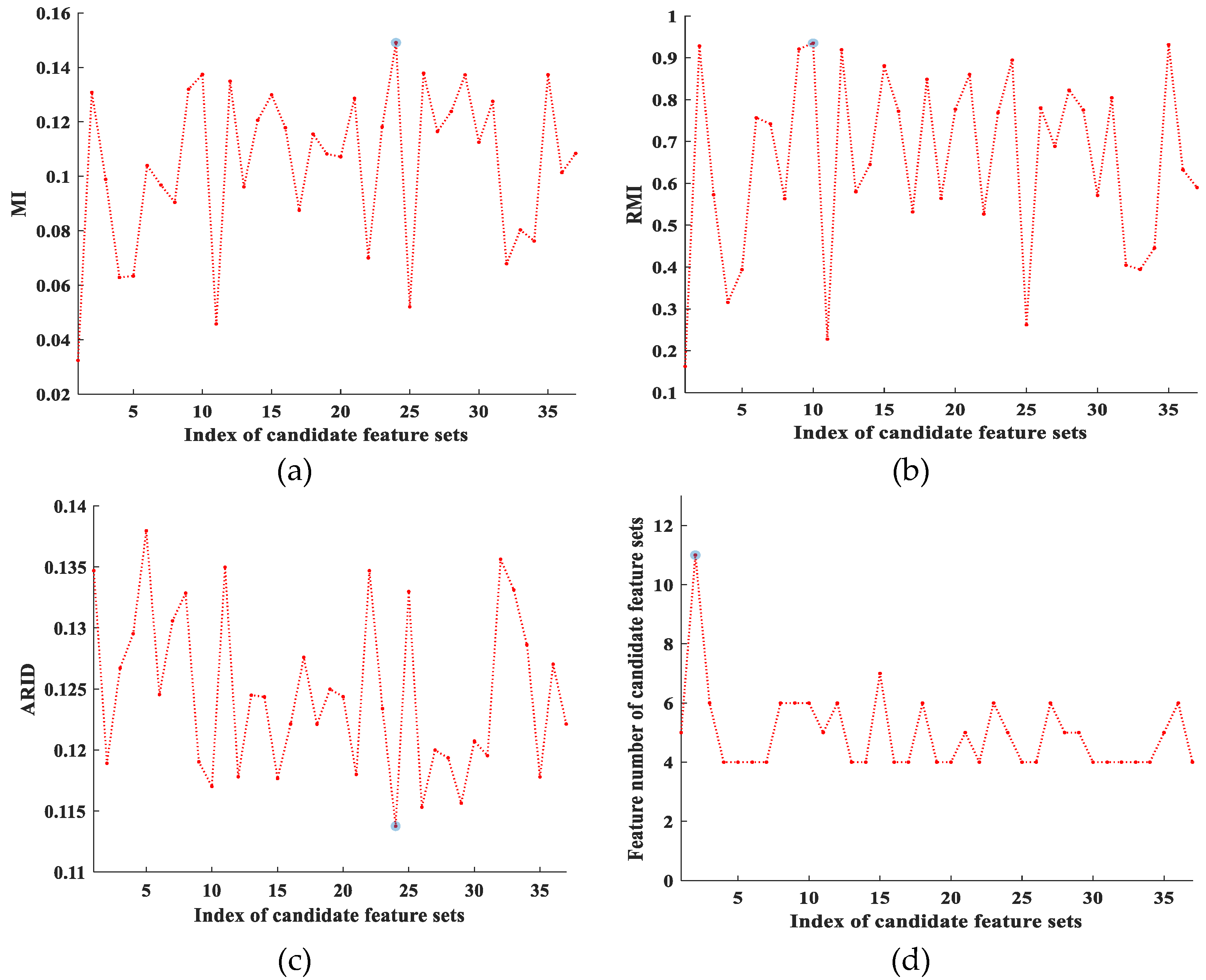
3.1.2. Consistent Feature Set Selection Based on ARID
- Implement SIFT and random sample consensus on reference image and sensed image to obtain initial consistent feature point sets where is the jth initial consistent feature point set and M0 is the number of initial consistent feature point sets.
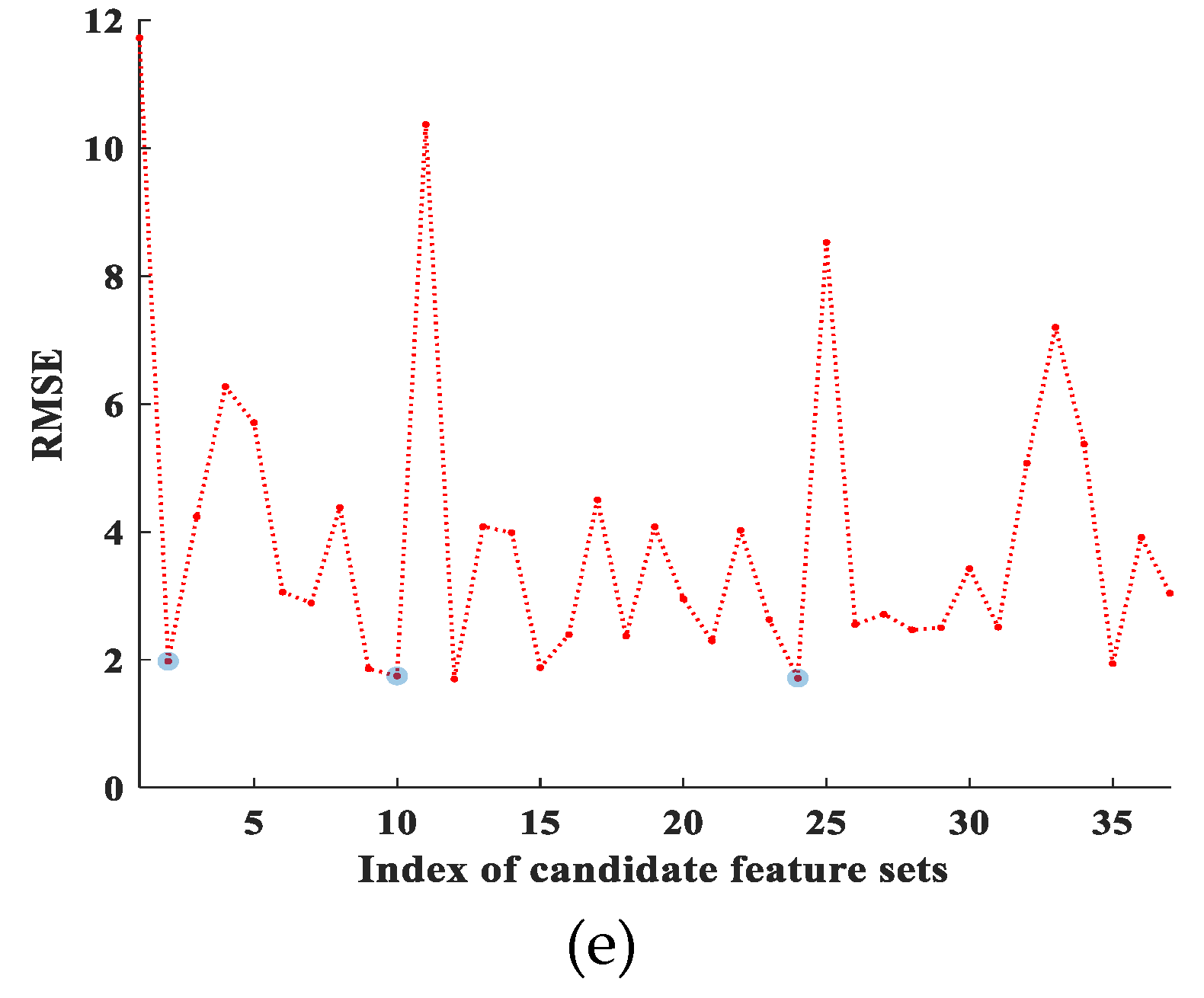
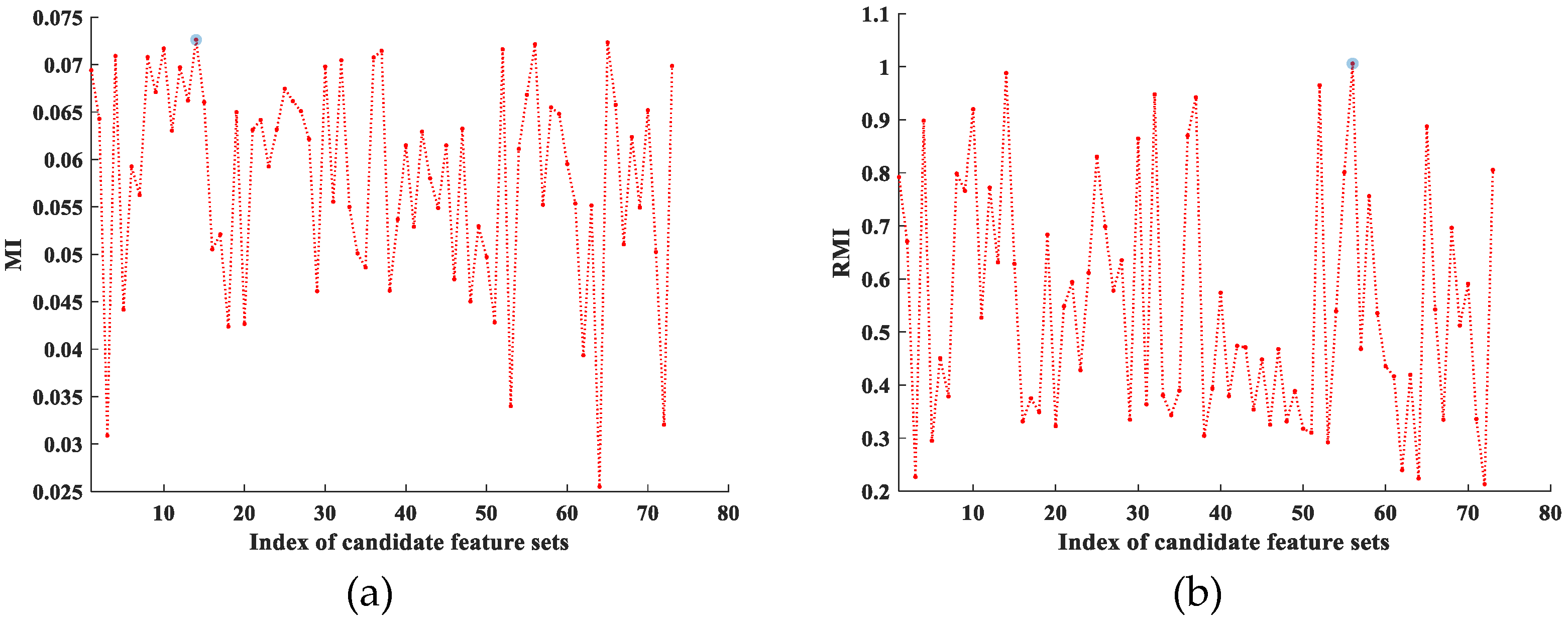
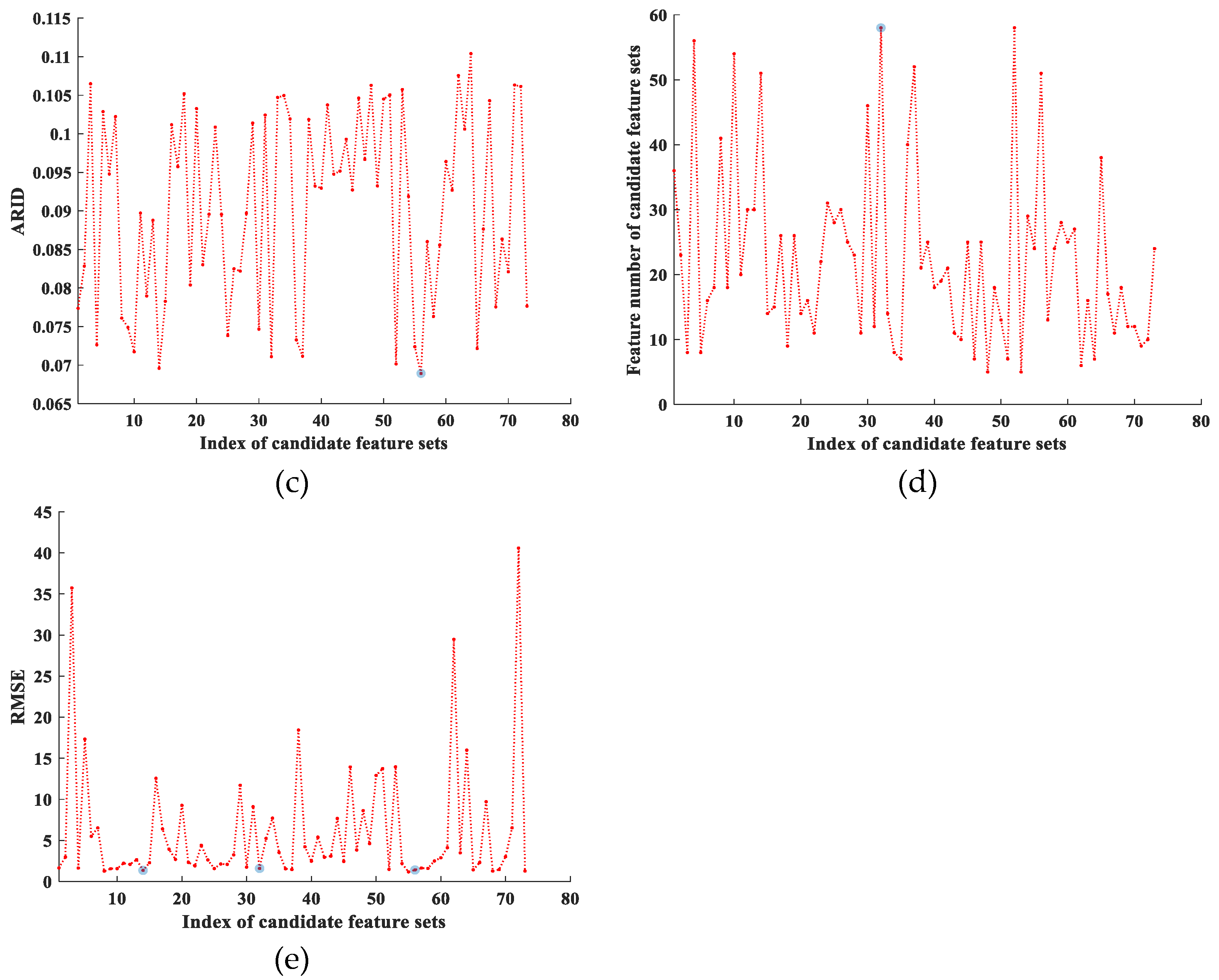
- Adopt to calculate registration parameters set where is the jth initial registration parameter and discrepancy values DVs set for image and rectified sensed image based on . The initial consistent feature point set is selected based on minimum ARID, denoted by , where .
3.2. Component II: Fine Registration by Minimizing Average Regional Information Divergence (ARID) via QPSO
3.2.1. Initial Parameters of QPSO Generated by the Consistent Feature Set Obtained in Component I
- Find the coordinate of feature points in by randomly tuning parameter b to generate tuned feature point sets .
- Adopt to calculate a registration parameters set and corresponding DVs set . The first M particles, which have smaller DVs than , are used as initial particle swarms . If there are not M particle satisfying the DVs are less than , the number of tuned feature set should be increased. The initial particle swarms are also used as initial local optimum particles and the corresponding ARID is denoted by .
- Select the particle corresponding minimum ARID among , denoted by , as the global optimum particle .
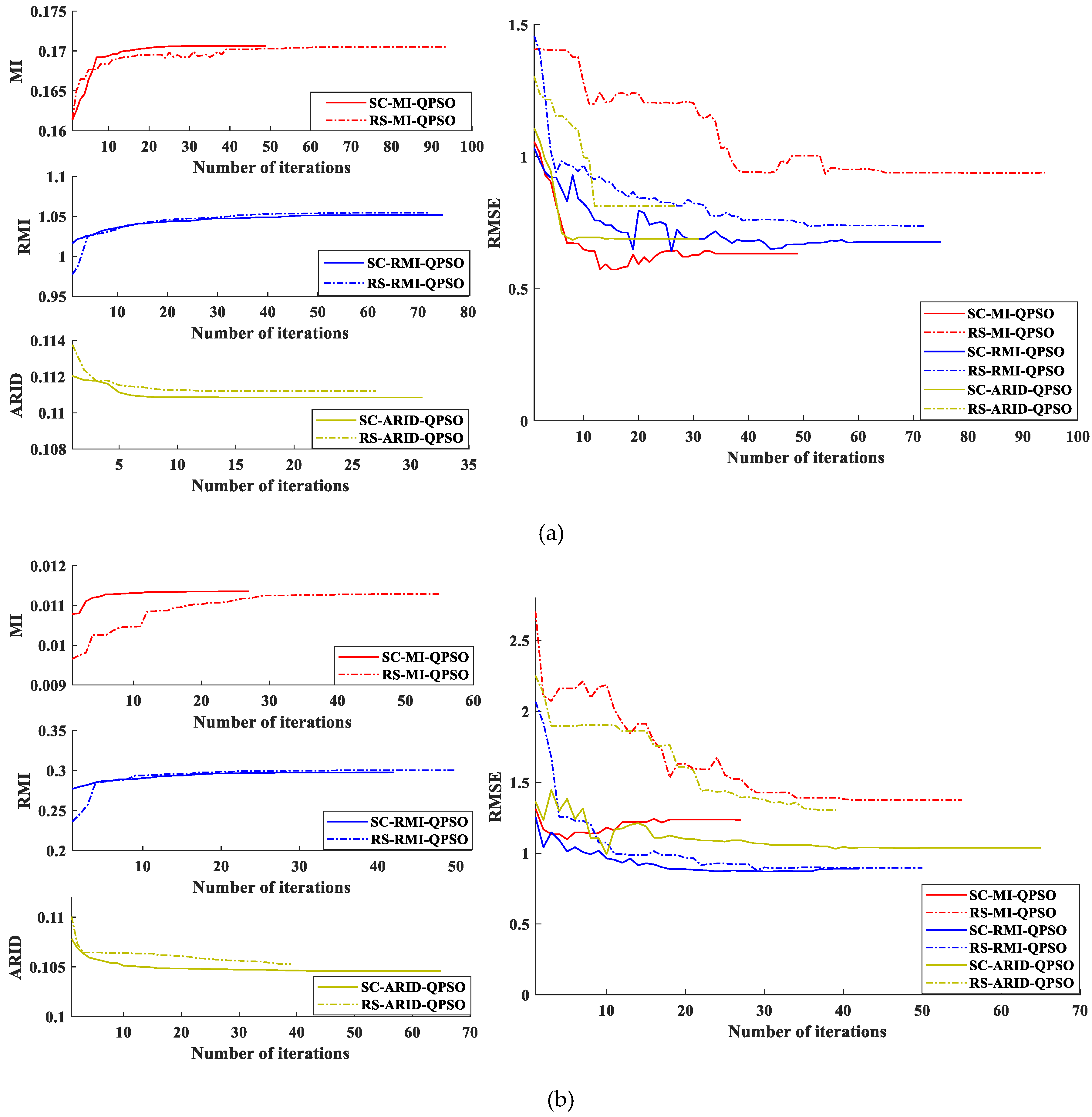
3.2.2. Parameters Optimized by Minimizing ARID via QPSO
| Algorithm1. SC-ARID-QPSO |
| Input: reference image , sensed image , the number of iterations, k, the number of no updating, n, maximum iterative number = 100, threshold τ = 10−4 and nτ = 15, coordinate tuning parameter b, particle population M = 20, Particle dimension D = 6 (for affine model) or 8 (for projective model) control parameters α0 and α1, initial particle swarm (i = 1, 2, …, M), tuning range . |
| Output: Final registration parameters |
| 1. Initialize: , and k = 0, n = 0. |
| 2. Initialization of initial local optimum particle and global optimum particle . |
| 3. Implement QPSO to optimize registration parameters: |
| While k < do; |
| Calculate β using Equation (7) and using Equation (4). |
| For m = 1:M do |
| For d = 1:D do |
| Calculate and using Equation (5) and Equation (6). |
| End for |
| Calculate based on using (2) and (3). |
| If then , , End if |
| End for |
| If then , , End if |
| If then n = n + 1 |
| If then Break, End if |
| End if |
| End while |
| 4. Return as final registration parameters |
4. Novelties of SC-ARID-QPSO
- The first novelty is introduction of ARID, which considers a neighboring region as a random variable. Such ARID is quite different from RMI and RIRMI in the sense that the latter was calculated under the assumption that high-dimensional distribution is approximately normally distributed, while the former defines the desired probability distribution by normalizing its neighborhood region histogram to unity. The discrepancy between the overlapped regions of reference image and rectified sensed image is calculated by averaging the values of RID of all pixels in the overlapped region without a need of calculating their joint probability distribution.
- The Second novelty is to develop a two-component cascaded registration method which optimizes spatial-consistency and ARID registration parameters. In contrast to most AFBMs [36,37] which only uses the pre-registration as initial parameters for the fine registration, SC-ARID-QPSO uses pre-registration based on SC and ARID to initialize the parameters for fine registration. The process of ARID-constrained parameter initialization guarantees the quality of initialized parameter set. In particular, it is quite different from an AFBM developed in [41], called iterative SIFT (ISIFT) which replaces the sensed image via a feedback loop to re-implement registration process. More specifically, ISIFT iteratively feeds a rectified image to replace the current sensed images, while SC-ARID-QPSO iteratively optimizes the registration parameters using an ARID-based objective function with the ARID-constrained initialized parameter set from the same set of the reference and sensed images.
- The last and most important novelty is fundamental different concepts used to derive ISIFT and SC-ARID-QPSO. Despite the fact that both ISIFT and SC-ARID-QPSO use an iterative process, the ISIFT feeds back rectified images to update the input sensed images as opposed to SC-ARID-QPSO, which uses QPSO iteratively to optimize parameter sets. So, ISIFT [41] and SC-ARID-QPSO are designed based on different uses of iterative processes since they both use spatial-consistency and intensity-similarity to perform different tasks. However, it is worth noting that there are several key differences between ISIFT and SC-ARID-QPSO. First of all, SC-ARID-QPSO takes advantage of QPSO to optimize registration parameter by minimizing ARID via optimization algorithm, while ISIFT does not. Second of all, SC-ARID-QPSO develops ARID as a novel discrepancy metric compared to ISIFT which uses traditional similarity metrics. Third of all, although the experimental datasets used in this paper are the same as the datasets in reference [41], their purposes are different. In this paper, the experimental results are used to demonstrate the effectiveness of ARID and the performance of SC-ARID-QPSO as opposed to ISIFT which used the data sets to show effectiveness of consistent feature selection strategy and iterative performance of ISIFT. Specifically, in Component I, the designed experiments are used for validating the accuracy and effectiveness of ARID. In Component II, the designed experiments are used to demonstrate the iterative process of parameter optimization by minimizing ARID via QPSO as well as the effective selection of initialized parameter set. In addition, the comparative experiments further show the superior performance of SC-ARID-QPSO to compared methods.
5. Experimental Setting
5.1. Data Sets
5.2. Parameter Setting
5.3. Evaluation Criteria
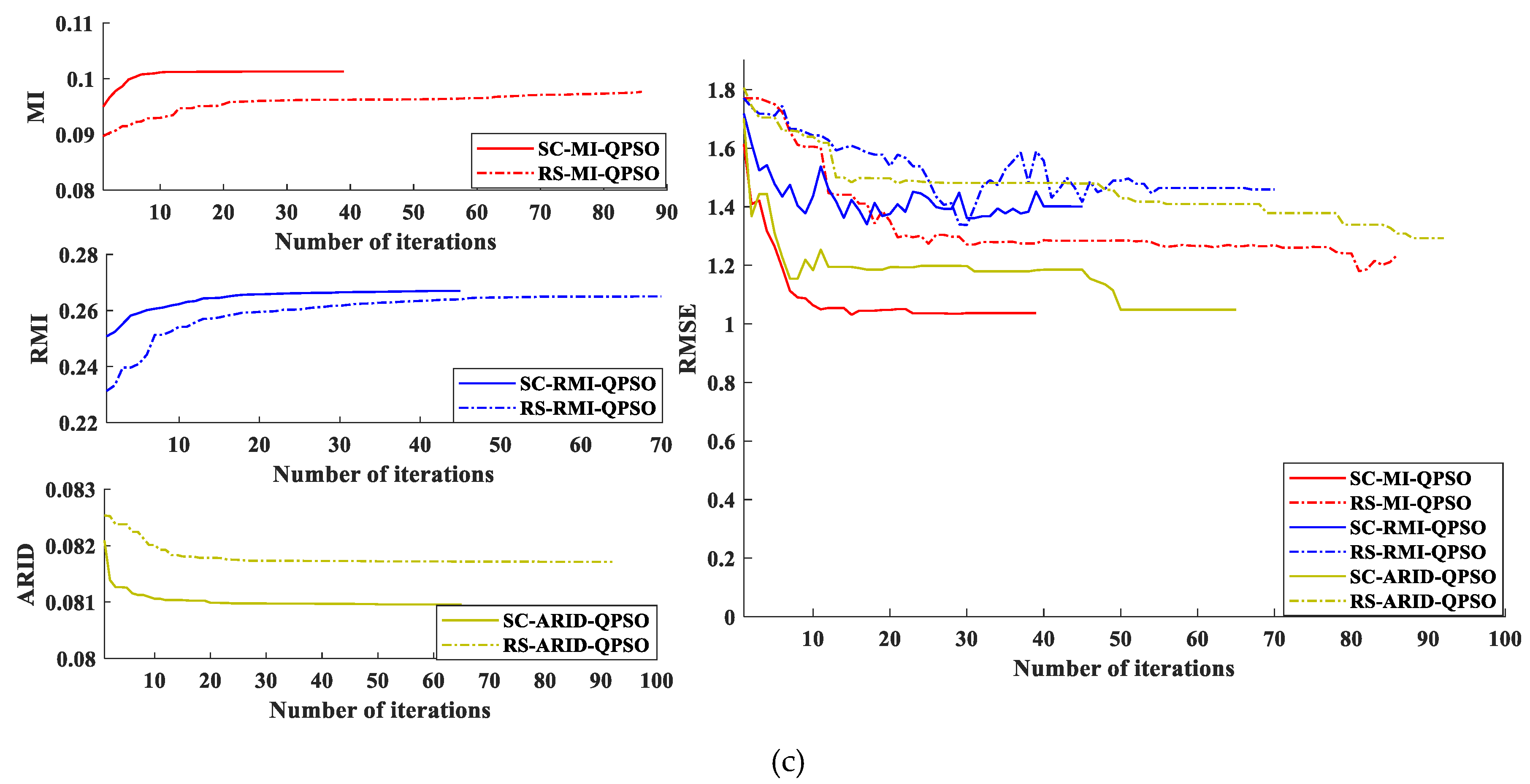
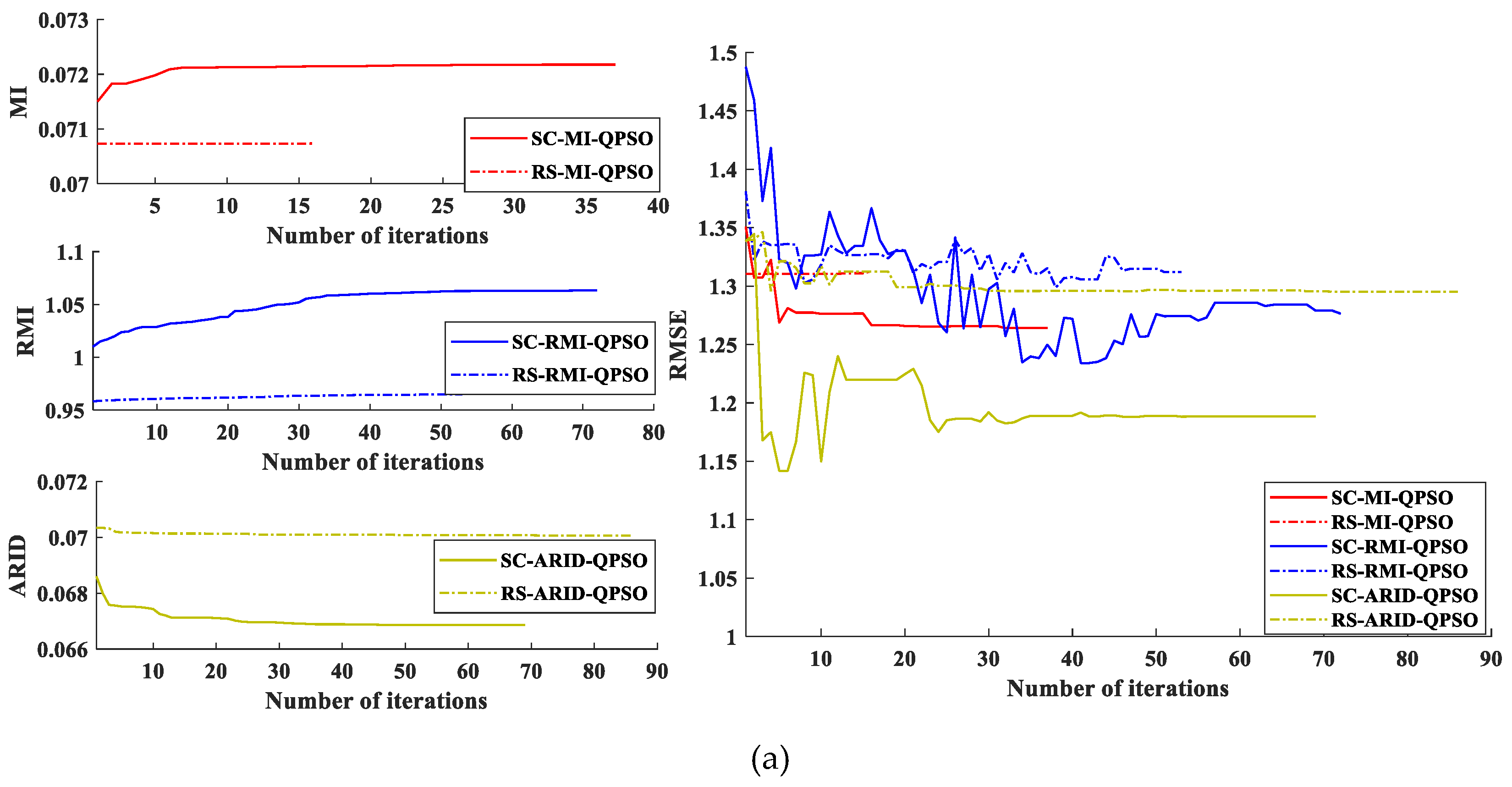
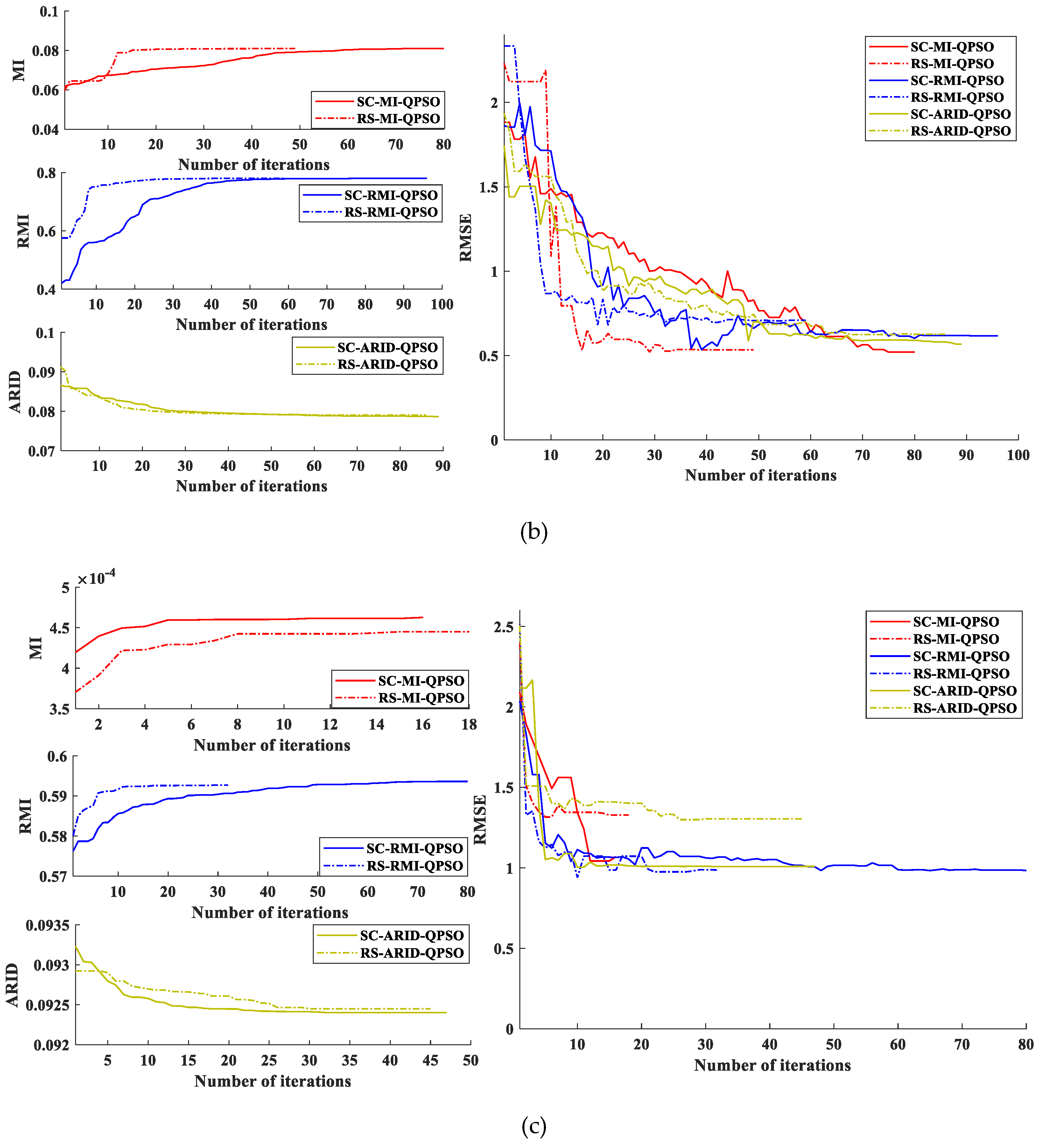
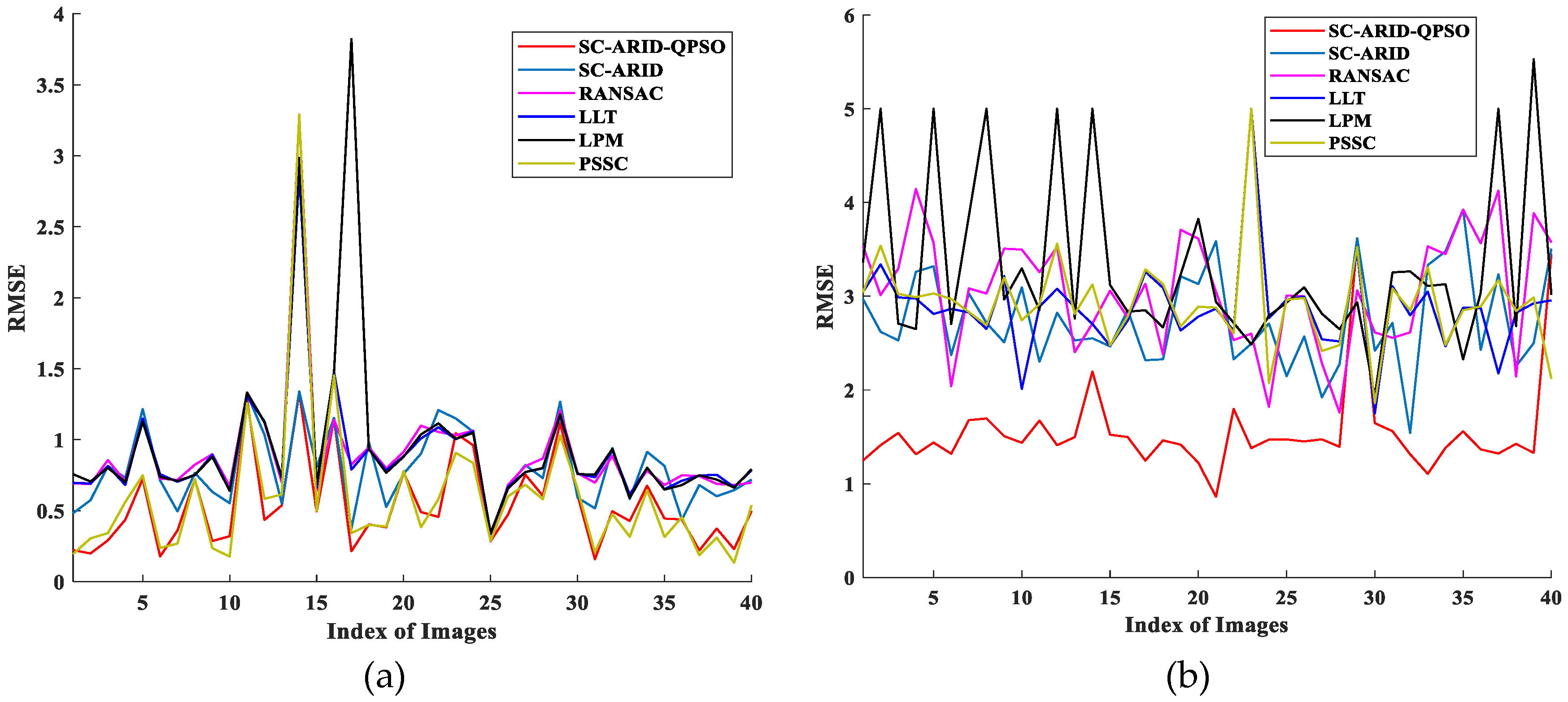
6. Experimental Results
6.1. Simulated Datasets Experiments
6.2. Real Datasets Experiments
6.3. Comparative Analysis on Registration Performance
7. Discussion
8. Conclusions
- A new measure, called average regional information divergency (ARID), is specifically designed to calculate the discrepancy between the registration parameters.
- SC-ARID-QPSO, using ARID to select a consistent feature set in Component I as well as to optimize registration parameters in Component II, provides a novel approach as a new AFBM.
- The feature extraction method and parameter optimization algorithm used in SC-ARID-QPSO can be replaced by better feature extraction methods and optimization algorithms. Under certain extreme situations, where there are no more than three or more pairs of correctly matched feature pairs among initial SIFT feature pairs, other modified better feature extraction methods can be used to replace SIFT. In this case, the framework of SC-ARID-QPSO is still applicable.
Author Contributions
Funding
Conflicts of Interest
List of Acronyms
| ARID | average regional information divergence |
| DM | discrepancy metric |
| DV | discrepancy value |
| OR | overlapped region in the reference image and rectified images |
| QPSO | quantum-behaved particle swarm optimization |
| SC | spatial consistency |
| SIFT | scale-invariant feature transform |
| SM | similarity metric |
| SC | spatial consistency |
| SM | similarity metric |
| SV | similarity value |
List of Symbols
| pixel in the region of reference image overlapped with rectified sensed image | |
| pixel in the region of rectified sensed image overlapped with reference image | |
| probability vector corresponding | |
| probability vector corresponding | |
| R | reference image |
| S | sensed image |
| consistent feature set | |
| registration parameter set | |
| Srec | rectified sensed image |
| the intensity vectors of local neighborhood region for | |
| ARID value set | |
| the intensity vectors of local neighborhood region for |
References
- Zitová, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef] [Green Version]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Sedaghat, A.; Mokhtarzade, M.; Ebadi, H. Uniform robust scale-invariant feature matching for optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4516–4527. [Google Scholar] [CrossRef]
- Paul, S.; Pati, U.C. Remote sensing optical image registration using modified uniform robust SIFT. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1300–1304. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, F.; You, H. OS-SIFT: A robust SIFT-like algorithm for high-resolution optical-to-SAR image registration in suburban areas. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3078–3090. [Google Scholar] [CrossRef]
- Chang, H.; Wu, G.; Chiang, M. Remote sensing image registration based on modified SIFT and feature slope grouping. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1363–1367. [Google Scholar] [CrossRef]
- Sedaghat, A.; Mohammadi, N. Uniform competency-based local feature extraction for remote sensing images. ISPRS J. Photogramm. Remote Sens. 2018, 135, 142–157. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Gool, L.V. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2007, 110, 346–359. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. A performance evaluation of local descriptors. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1615–1630. [Google Scholar] [CrossRef] [Green Version]
- Tola, E.; Lepetit, V.; Fua, P. DAISY: An efficient dense descriptor applied to wide-baseline stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 815–830. [Google Scholar] [CrossRef] [Green Version]
- Sedaghat, A.; Ebadi, H. Remote sensing image matching based on adaptive binning SIFT descriptor. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5283–5293. [Google Scholar] [CrossRef]
- Chen, J.; Tian, J.; Lee, N.; Zheng, J.; Smith, R.T.; Laine, A.F. A partial intensity invariant feature descriptor for multimodal retinal image registration. IEEE Trans. Biomed. Eng. 2010, 57, 1707–1718. [Google Scholar] [CrossRef] [Green Version]
- Sedaghat, A.; Ebadi, H. Distinctive order based self-similarity descriptor for multi-Sensor remote sensing image matching. ISPRS J. Photogramm. Remote Sens. 2015, 108, 62–71. [Google Scholar] [CrossRef]
- Sedaghat, A.; Mohammadi, N. Illumination-robust remote sensing image matching based on oriented self-similarity. ISPRS J. Photogramm. Remote Sens. 2019, 153, 21–35. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1980, 24, 381–395. [Google Scholar] [CrossRef]
- Song, Z.; Zhou, S.; Guan, J. A novel image registration algorithm for remote sensing under affine transformation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4895–4912. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, W.P.; Gong, M.G.; Su, L.Z.; Jiao, L.C. A novel point-matching algorithm based on fast sample consensus for image registration. IEEE Geosci. Remote Sens. Lett. 2015, 12, 43–47. [Google Scholar] [CrossRef]
- Ma, J.Y.; Zhou, H.B.; Zhao, J.; Gao, Y.; Jiang, J.J.; Tian, J.W. Robust feature matching for remote sensing image registration via locally linear transforming. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6469–6481. [Google Scholar] [CrossRef]
- Ma, J.Y.; Zhao, J.; Jiang, J.J.; Zhou, H.B. Locality preserving matching. Int J. Comput. Vis. 2019, 127, 512–531. [Google Scholar] [CrossRef]
- Ma, J.Y.; Zhao, J.; Jiang, J.J.; Zhou, H.B. Locality preserving matching. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Melbourne, VIC, Australia, 19–25 August 2017; pp. 4492–4498. [Google Scholar]
- Ma, Y.; Wang, J.; Xu, H.; Zhang, S.; Mei, X.; Ma, J. Robust image feature matching via progressive sparse spatial consensus. IEEE Access 2017, 5, 24568–24579. [Google Scholar] [CrossRef]
- Maes, F.; Collignon, A.; Vandermeulen, D.; Marchal, G.; Suetens, P. Multimodality image registration by maximization of mutual information. IEEE Trans. Med. Imaging 1997, 16, 187–198. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yi, Z.; Cao, Z.G.; Yang, X. Multi-spectral remote image registration based on SIFT. Electron. Lett. 2008, 44, 107–108. [Google Scholar] [CrossRef]
- Liang, J.; Liu, X.P.; Huang, K.N.; Li, X.; Wang, D.G.; Wang, X.W. Automatic registration of multisensor images using an integrated spatial and mutual information (SMI) metric. IEEE Trans. Geosci. Remote Sens. 2014, 52, 603–615. [Google Scholar] [CrossRef]
- Russakoff, D.B.; Tomasi, G.; Rohlfing, T. Image similarity using mutual information of regions. Eur. Conf. Comput. Vis. 2004, 3023, 596–607. [Google Scholar]
- Li, L.X. The Registration and Fusion of Multi-sensor Images Based on Mutual Information. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2013. [Google Scholar]
- Wong, A.; Clausi, D.A. ARRSI: Automatic registration of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1483–1493. [Google Scholar] [CrossRef]
- Navy, P.; Page, V.; Grandchamp, E.; Desachy, J. Matching two clusters of points extracted from satellite images. Pattern Recognit. Lett. 2006, 27, 268–274. [Google Scholar] [CrossRef] [Green Version]
- Rueckert, D.; Clarkson, M.J.; Hill, D.L.G.; Hawkes, D.J. Non-rigid registration using higher-order mutual information. In Proceedings of the Medical Imaging 2000: Image Processing Proceedings SPIE, San Diego, CA, USA, 14 February 2000; Volume 3979, pp. 438–447. [Google Scholar]
- Pluim, J.P.W.; Maintz, J.B.A.; Viergever, M.A. Image registration by maximization of combined mutual information and gradient information. IEEE Trans. Med. Imaging 2000, 19, 809–814. [Google Scholar] [CrossRef]
- Cole-Rhodes, A.A.; Johnson, K.L.; LeMoigne, J.; Zavorin, I. Multiresolution registration of remote sensing imagery by optimization of mutual information using a stochastic gradient. IEEE Trans. Image Process. 2003, 12, 1495–1511. [Google Scholar] [CrossRef]
- Kern, J.P.; Pattichis, M.S. Robust multispectral image registration using mutual-information models. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1494–1505. [Google Scholar] [CrossRef]
- Chen, H.M.; Varshney, P.K.; Arora, M.K. Performance of mutual information similarity measure for registration of multitemporal remote sensing images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2445–2454. [Google Scholar] [CrossRef]
- Studholme, C.; Hill, D.L.G.; Hawkes, D.J. An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognit. 1999, 32, 71–86. [Google Scholar] [CrossRef]
- Johnson, K.; Cole-Rhodes, A.; Zavorin, I.; Moigne, J.L. Mutual information as a similarity measure for remote sensing image registration. Proc. SPIE 2001, 4383, 51–61. [Google Scholar]
- Gong, M.G.; Zhao, S.M.; Jiao, L.C.; Tian, D.Y.; Wang, S. A novel coarse-to-fine scheme for automatic image registration based on SIFT and mutual information. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4328–4438. [Google Scholar] [CrossRef]
- Zhao, L.Y.; Lv, B.Y.; Li, X.R.; Chen, S.H. Multi-source remote sensing image registration based on scale-invariant feature transform and optimization of regional mutual information. Acta Phys. Sin. Chin. Ed. 2015, 64, 124204. [Google Scholar]
- Chen, S.H.; Li, X.R.; Zhao, L.Y.; Yang, H. Medium-low resolution multisource remote sensing image registration based on SIFT and robust regional mutual information. Int. J. Remote Sens. 2018, 39, 3215–3242. [Google Scholar] [CrossRef]
- Ye, Y.X.; Shan, J. A local descriptor based registration method for multispectral remote sensing images with non-linear intensity differences. ISPRS J. Photogramm. Remote Sens. 2014, 90, 83–95. [Google Scholar] [CrossRef]
- Yang, H.; Li, X.R.; Zhao, L.Y.; Chen, S.H. A novel coarse-to-fine scheme for remote sensing image registration based on SIFT and phase correlation. Remote Sens. 2019, 11, 1833. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.H.; Zhong, S.W.; Xue, B.; Li, X.R.; Zhao, L.Y.; Chang, C.-I. Iterative Scale-Invariant Feature Transform for Remote Sensing Image Registration. IEEE Trans. Geosci. Remote Sens. 2020, 1–22. [Google Scholar] [CrossRef]
- Gharbia, R.; Ahmed, S.A.; Hassanien, A.E. Remote Sensing Image Registration Based on Particle Swarm Optimization and Mutual Information; Springer: New Delhi, India, 2015; Volume 127, pp. 399–408. [Google Scholar]
- Zhuang, Y.W.; Gao, K.; Miu, X.H.; Han, L.; Gong, X.M. Infrared and visual image registration based on mutual information with a combined particle swarm optimization Powell search algorithm. Opt. Int. J. Light Electron. Opt. 2016, 127, 188–191. [Google Scholar] [CrossRef]
- Xia, K.M.; Chen, X.Z.; Guo, G.G. Fast Algorithm for Simulated Annealing Applied to Registering of Noisy Images. J. Shanghai Univ. 2003, 9, 392. [Google Scholar]
- Liu, P.; Zhou, J.; Luo, D.Z.; Kai, D.U. Research on IR and Visual Image Registration Based on Mutual Information and Ant Colony Algorithm. Microcomput. App. 2008, 29, 53–58. [Google Scholar]
- Sun, T.H. Applying particle swarm optimization algorithm to roundness measurement. Expert Syst. Appl. 2009, 36, 3428–3438. [Google Scholar] [CrossRef]
- Sun, J.; Feng, B.; Xu, W.B. Particle swarm optimization with particles having quantum behavior. In Proceedings of the 2004 Congress on Evolutionary Computation CEC2004, Portland, OR, USA, 19–23 June 2004; pp. 325–331. [Google Scholar]
- Sun, J.; Feng, B.; Xu, W.B. Adaptive Parameter Control for Quantum-behaved Particle Swarm Optimization on Individual Level. In Proceedings of the 2005 IEEE International Conference on Systems, Man and Cybernetics, Hawaii, HI, USA, 10–12 October 2005; p. 30493054. [Google Scholar]
- Chang, C.-I. Hyperspectral Imaging: Techniques for Spectral Detection and Classification; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2003. [Google Scholar]
- Chang, C.-I. An information-theoretic approach to spectral variability, similarity, and discrimination for hyperspectral image analysis. IEEE Trans. Inf. Theory 2000, 46, 1927–1932. [Google Scholar] [CrossRef] [Green Version]
- ENVI Image Analysis Software (5.2 version). L3HARRIS Geospatial. Available online: https://www.harrisgeospatial.com/Software-Technology/ENVI (accessed on 15 October 2014).
- UC Merced Land Use Dataset. Available online: http://140.112.27.140/wp-content/uploads/2018/12/Datasets.zip (accessed on 5 December 2018).
- High-Resolution Orthoimagery Data. Available online: http://weegee.vision.ucmerced.edu/datasets/landuse.html (accessed on 28 October 2010).
- USGS. Earth Explorer. Available online: https://earthexplorer.usgs.gov/ (accessed on 28 August 2016).
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (ACM GIS), San Jose, CA, USA, 2–5 November 2010. [Google Scholar]
- Matlab Code of LLT. Available online: https://github.com/jiayi-ma/LLT (accessed on 29 September 2018).
- Matlab Code of LPM. Available online: https://github.com/jiayi-ma/LPM (accessed on 16 March 2019).
- Matlab Code of PSSC. Available online: https://github.com/JiahaoPlus/PSSC (accessed on 31 December 2018).




| Data Sets | Component I | Component II | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RANSAC | SC-MI | SC-RMI | SC-ARID | RS-MI-QPSO | RS-RMI-QPSO | RS-ARID-QPSO | SC-MI-QPSO | SC-RMI-QPSO | SC-ARID-QPSO | |
| 1 | 1.9764 | 1.7120 | 1.7456 | 1.7120 | 0.9395 | 0.7682 | 0.8129 | 0.6335 | 0.6777 | 0.6894 |
| 2 | 1.9361 | 1.4554 | 1.4554 | 1.4554 | 1.3761 | 0.8978 | 1.3046 | 1.2344 | 0.8905 | 1.0383 |
| 3 | 1.7709 | 1.7647 | 1.7647 | 1.7647 | 1.2656 | 1.4589 | 1.2925 | 1.0370 | 1.4006 | 1.0483 |
| Data Sets | Component I | Component II | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RANSAC | SC-MI | SC-RMI | SC-ARID | RS-MI-QPSO | RS-RMI-QPSO | RS-ARID-QPSO | SC-MI-QPSO | SC-RMI-QPSO | SC-ARID-QPSO | |
| 1 | 1.5920 | 1.3550 | 1.4010 | 1.4010 | 1.3126 | 1.3119 | 1.2952 | 1.2639 | 1.2764 | 1.1883 |
| 2 | 2.9361 | 2.1332 | 2.1332 | 2.1332 | 0.5342 | 0.7087 | 0.6264 | 0.5203 | 0.6174 | 0.5676 |
| 3 | 2.4050 | 2.2640 | 2.2640 | 2.2640 | 1.3266 | 0.9868 | 1.3052 | 1.0700 | 0.9835 | 1.0093 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Xue, B.; Yang, H.; Li, X.; Zhao, L.; Chang, C.-I. Optical Remote Sensing Image Registration Using Spatial-Consistency and Average Regional Information Divergence Minimization via Quantum-Behaved Particle Swarm Optimization. Remote Sens. 2020, 12, 3066. https://doi.org/10.3390/rs12183066
Chen S, Xue B, Yang H, Li X, Zhao L, Chang C-I. Optical Remote Sensing Image Registration Using Spatial-Consistency and Average Regional Information Divergence Minimization via Quantum-Behaved Particle Swarm Optimization. Remote Sensing. 2020; 12(18):3066. https://doi.org/10.3390/rs12183066
Chicago/Turabian StyleChen, Shuhan, Bai Xue, Han Yang, Xiaorun Li, Liaoying Zhao, and Chein-I Chang. 2020. "Optical Remote Sensing Image Registration Using Spatial-Consistency and Average Regional Information Divergence Minimization via Quantum-Behaved Particle Swarm Optimization" Remote Sensing 12, no. 18: 3066. https://doi.org/10.3390/rs12183066
APA StyleChen, S., Xue, B., Yang, H., Li, X., Zhao, L., & Chang, C.-I. (2020). Optical Remote Sensing Image Registration Using Spatial-Consistency and Average Regional Information Divergence Minimization via Quantum-Behaved Particle Swarm Optimization. Remote Sensing, 12(18), 3066. https://doi.org/10.3390/rs12183066









