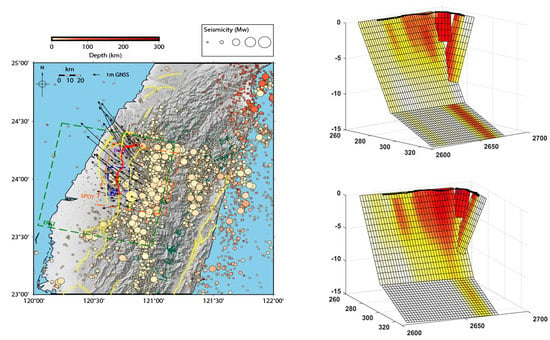
Joint Inversion of Geodetic Observations and Relative Weighting—The 1999 Mw 7.6 Chi-Chi Earthquake Revisited
Abstract
:1. Introduction
2. Geodetic Data Sets and Processing
2.1. GPS Measurements
2.2. Levelling Data
2.3. InSAR: ERS-2 Interferometric Processing Chain
2.4. Sub-Pixel Correlation of SPOT Images
3. Earthquake Modelling
3.1. Generalized Akaike’s Bayesian Information Criterion (gABIC)
- : Nx1 vector containing 5 data types (total N observations);
- NxM coefficient matrix;
- : coefficient matrix containing Prior constraints
- a is a M dimensional model parameter vector that varies with the time windows;
- : are vectors of the Gaussian-distributed uncertainties of observations and constraints, respectively.
- is the smoothness parameter;
- is a hyperparameter representing the weight of the constraint;
- .
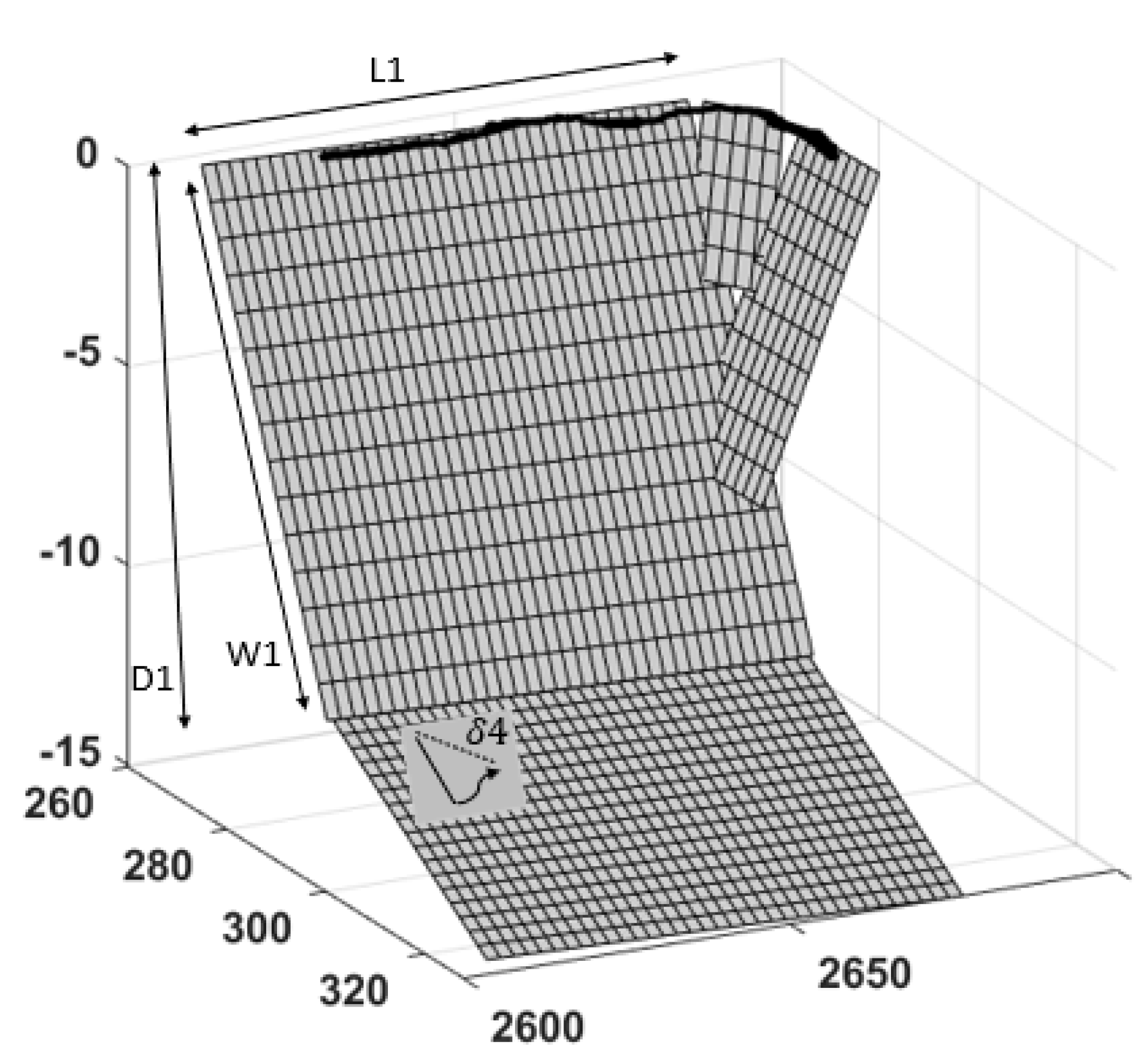
3.2. Modelling Strategy: Fault Geometry and Slip Distribution
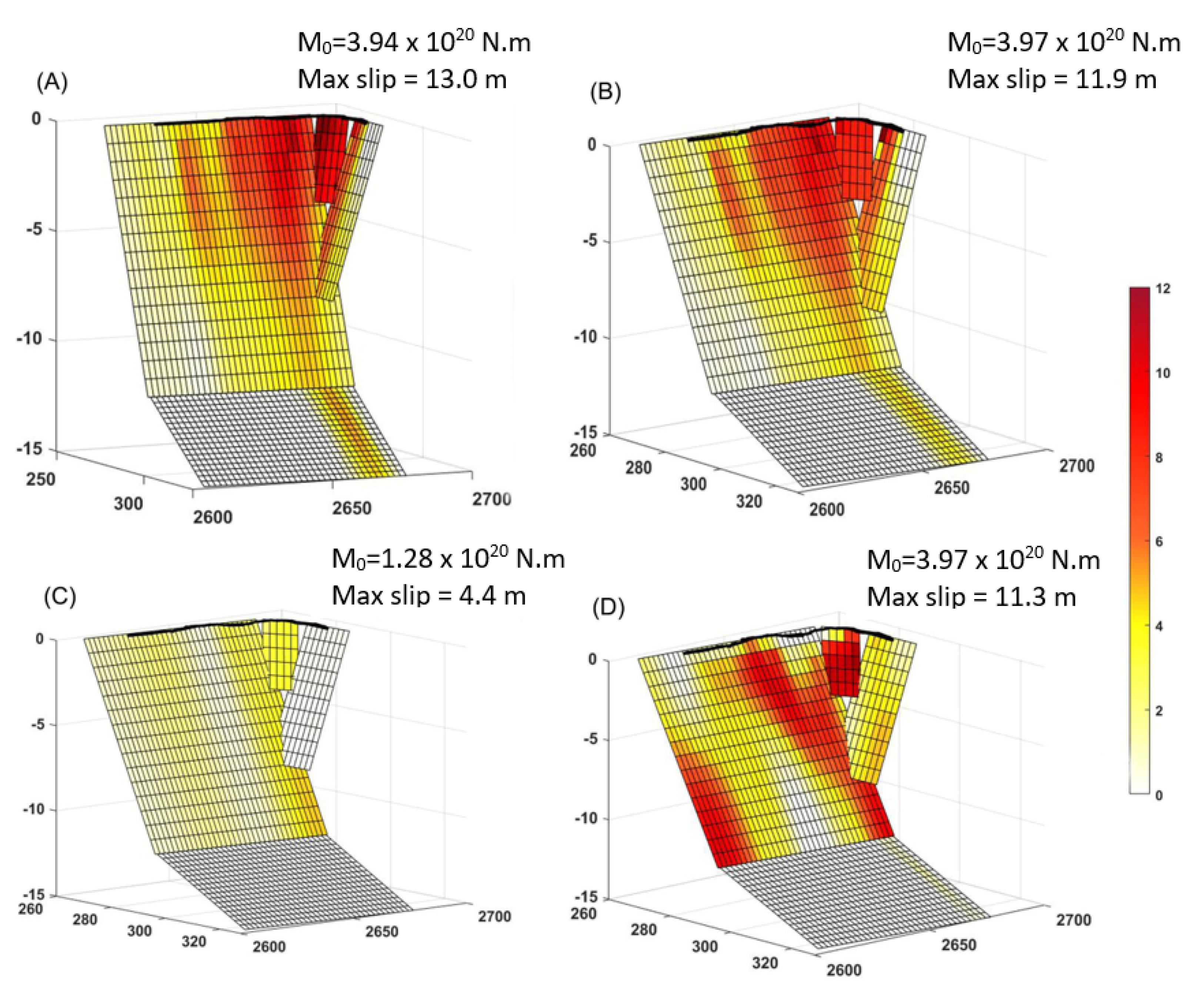
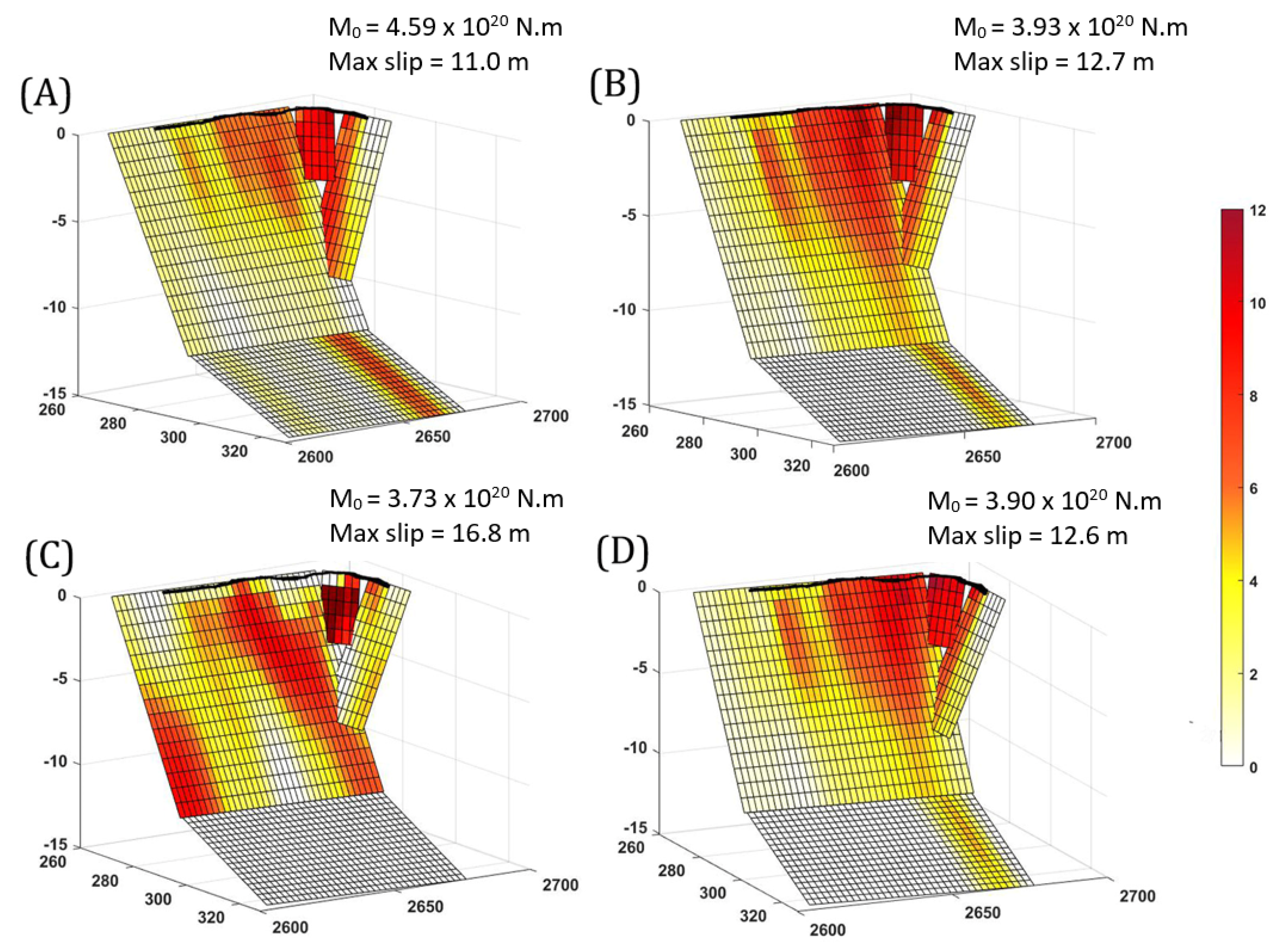
4. Data Set Weighting
4.1. Benefit of Multiple Data Sets
4.2. gABIC Impact
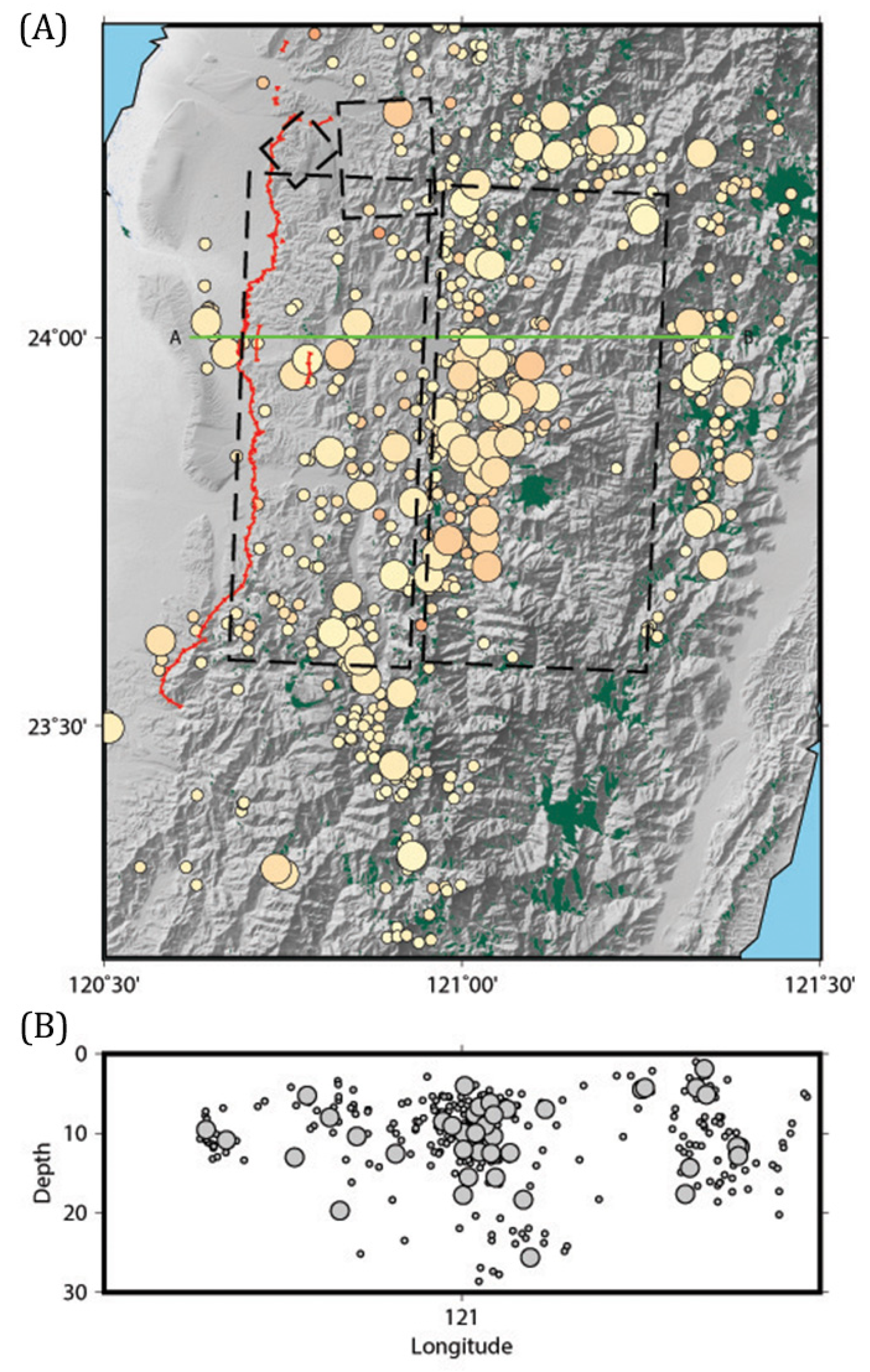
5. Seismic Hazard
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CGS | Central Geological Survey |
| COSI-Corr | Co-registration of Optically Sensed Images and Correlation |
| CSC | Coulomb Stress Change |
| CWB | Central Weather Bureau |
| DEM | Digital Elevation Model |
| ENVI | Environment for Visualizing Images |
| ERS | European Remote-Sensing Satellite |
| ESA | European Space Agency |
| gABIC | Generalized Akaike’s Bayesian Information Criterion |
| GCP | Ground Control Point |
| GPS | Global Positioning System |
| IDL | Interactive Data Language |
| IESAS | Institute of Earth Sciences, Academia Sinica |
| InSAR | Interferometric Synthetic Aperture Radar |
| MOEA | Ministry of Economic Affairs |
| MOI | Ministry of Interior |
| M-PSO | Multi-peak Particle Swarm Optimization |
| PSOKINV | Particle Swarm Optimization and Okada Inversion package |
| RMS | Root Mean Square |
| SNAP | Sentinel Application Platform |
| SNAPHU | Statistical-cost, Network-flow Algorithm for Phase Unwrapping |
| SNR | Signal-To-Noise Ratio |
| SPOT | Satellite Pour l’Observation de la Terre |
| SRTM | Shuttle Radar Topography Mission |
| TWD67 | Transverse Mercator Two-degree Grid 1967 |
| USGS | United States Geological Survey |
| WGS84 | World Geodetic System 1984 |
References
- Ching, K.E.; Hsieh, M.L.; Johnson, K.; Chen, K.; Rau, R.J.; Yang, M. Modern vertical deformation rates and mountain building in Taiwan from precise leveling and continuous GPS observations, 2000–2008. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Ma, K.F.; Mori, J.; Lee, S.J.; Yu, S.B. Spatial and Temporal Distribution of Slip for the 1999 Chi-Chi, Taiwan, Earthquake. Bull. Seismol. Soc. Am. 2001, 91, 1069–1087. [Google Scholar]
- Wang, J.H. Studies of Earthquake Energies in Taiwan: A Review. Terr. Atmos. Ocean. Sci. 2016, 27, 1–19. [Google Scholar] [CrossRef]
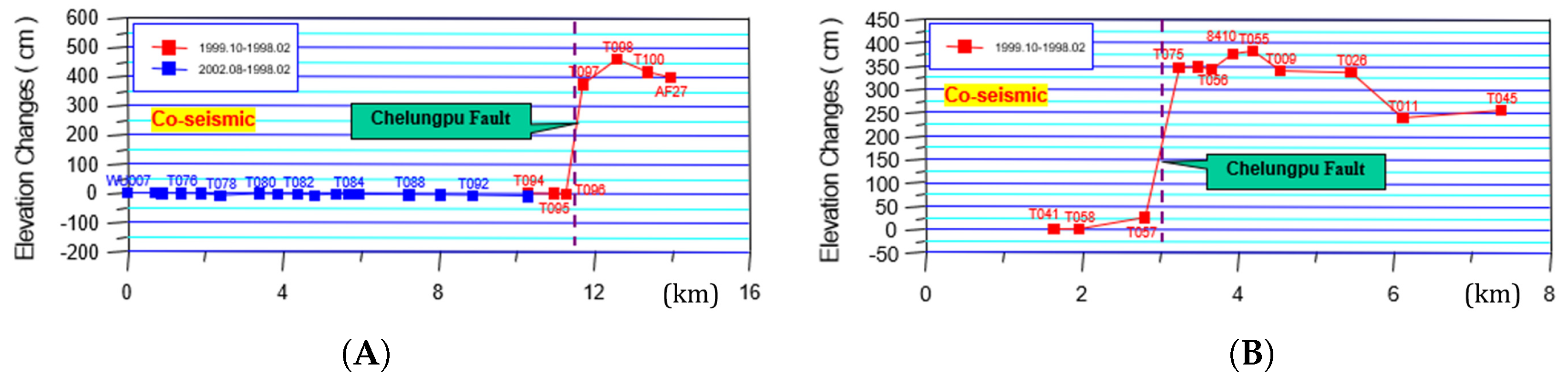
- Lee, Y.H.; Shih, Y.X. Coseismic displacement, bilateral rupture, and structural characteristics at the southern end of the 1999 Chi-Chi earthquake rupture, central Taiwan. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Lee, J.C.; Chen, Y.G.; Sieh, K.; Mueller, K.; Chen, W.S.; Chu, H.T.; Chan, Y.C.; Rubin, C.; Yeats, R. A Vertical Exposure of the 1999 Surface Rupture of the Chelungpu Fault at Wufeng, Western Taiwan: Structural and Paleoseismic Implications for an Active Thrust Fault. Bull. Seismol. Soc. Am. 2001, 91, 914–929. [Google Scholar] [CrossRef]
- Pathier, E.; Fruneau, B.; Deffontaines, B.; Angelier, J.; Chang, C.; Yu, S.; Lee, C. Coseismic displacements of the footwall of the Chelungpu fault caused by the 1999, Taiwan, Chi-Chi earthquake from InSAR and GPS data. Earth Planet. Sci. Lett. 2003, 212, 73–88. [Google Scholar] [CrossRef]
- Lee, J.C.; Chan, Y.C. Structure of the 1999 Chi-Chi earthquake rupture and interaction of thrust faults in the active fold belt of western Taiwan. J. Asian Earth Sci. 2007, 31, 226–239. [Google Scholar] [CrossRef]
- Angelier, J.; Lee, J.C.; Chu, H.T.; Hu, J.C.; Lu, C.Y.; Chan, Y.C.; Tin-Jai, L.; Font, Y.; Deffontaines, B.; Yi-Ben, T. Le séisme de Chi-Chi (1999) et sa place dans l’orogène de Taiwan. Comptes Rendus de l’Academie de Sciences Serie IIa: Sciences de la Terre et des Planetes 2001, 333, 5–21. [Google Scholar] [CrossRef]
- Yu, S.B.; Kuo, L.C.; Hsu, Y.J.; Su, H.H.; Liu, C.C.; Hou, C.S.; Lee, J.F.; Lai, T.C.; Liu, C.C.; Liu, C.L.; et al. Preseismic Deformation and Coseismic Displacements Associated with the 1999 Chi-Chi, Taiwan, Earthquake. Bull. Seismol. Soc. Am. 2001, 91, 995–1012. [Google Scholar] [CrossRef]
- Dominguez, S.; Avouac, J.P.; Michel, R. Horizontal coseismic deformation of the 1999 Chi-Chi earthquake measured from SPOT satellite images: Implications for the seismic cycle along the western foothills of central Taiwan. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Kuo, Y.; Ayoub, F.; Leprince, S.; Chen, Y.; Avouac, J.; Shyu, J.; Lai, K.; Kuo, Y. Coseismic thrusting and folding in the 1999 Mw 7.6 Chi-Chi earthquake: A high-resolution approach by aerial photos taken from Tsaotun, central Taiwan. J. Geophys. Res. Solid Earth 2014, 119, 645–660. [Google Scholar] [CrossRef] [Green Version]
- Loevenbruck, A.; Cattin, R.; Le Pichon, X.; Courty, M.; Yu, S. Seismic cycle in Taiwan derived from GPS measurements. Comptes rendus de l’Académie des Sciences serie II Fascicule A-Sciences de la terre et des planètes 2001, 333, 57–64. [Google Scholar] [CrossRef]
- Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar]
- Johnson, K.; Segall, P. Imaging the ramp–decollement geometry of the Chelungpu fault using coseismic GPS displacements from the 1999 Chi-Chi, Taiwan earthquake. Tectonophysics 2004, 378, 123–139. [Google Scholar]
- Zhang, L.; Wu, J.C.; Ge, L.L.; Ding, X.L.; Chen, Y.L. Determining fault slip distribution of the Chi-Chi Taiwan earthquake with GPS and InSAR data using triangular dislocation elements. J. Geodyn. 2008, 45, 163–168. [Google Scholar] [CrossRef]
- Hsu, Y.J.; Avouac, J.P.; Yu, S.B.; Chang, C.H.; Wu, Y.M.; Woessner, J. Spatio-temporal Slip, and Stress Level on the Faults within the Western Foothills of Taiwan: Implications for Fault Frictional Properties. Pure Appl. Geophys. 2009, 166, 1853–1884. [Google Scholar] [CrossRef] [Green Version]
- Johnson, K.M.; Hsu, Y.J.; Segall, P.; Yu, S.B. Fault geometry and slip distribution of the 1999 Chi-Chi Taiwan earthquake imaged from inversion of GPS data. Geophys. Res. Lett. 2001, 28, 2285–2288. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Chan, Y.C.; Hu, J.C.; Angelier, J.; Lee, J.C. Detailed surface co-seismic displacement of the 1999 Chi-Chi earthquake in western Taiwan and implication of fault geometry in the shallow subsurface. J. Struct. Geol. 2008, 30, 1167–1176. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Network approaches to two-dimensional phase unwrapping: Intractability and two new algorithms. J. Opt. Soc. Am. 2000, 17, 401–414. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J. Opt. Soc. Am. 2001, 18, 338–351. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, C.W.; Zebker, H.A. Phase unwrapping for large SAR interferograms: Statistical segmentation and generalized network models. IEEE Trans. Geosci. Remote. Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, R.; Werner, C. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef] [Green Version]
- Van Puymbroeck, N.; Michel, R.; Binet, R.; Avouac, J.; Taboury, J. Measuring earthquakes from optical satellite images. Appl. Opt. 2000, 39, 3486–3494. [Google Scholar] [CrossRef] [PubMed]
- Michel, R.; Avouac, J.; Taboury, J. Measuring near field coseismic displacements from SAR images: Application to the Landers earthquake. Geophys. Res. Lett. 1999, 26, 3017–3020. [Google Scholar] [CrossRef] [Green Version]
- Leprince, S.; Barbot, S.; Ayoub, F.; Avouac, J. Automatic and Precise Ortho-rectification, Coregistration, and Subpixel Correlation of Satellite Images, Application to Ground Deformation Measurements. IEEE Trans. Goesci. Rmote Sens. 2007, 45, 1529–1558. [Google Scholar] [CrossRef] [Green Version]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Jonsson, S.; Zebker, H.; Segall, P.; Amelung, F. Fault Slip Distribution of the 1999 Mw 7.1 Hector Mine, California, Earthquake, Estimated from Satellite Radar and GPS Measurements. Bull. Seismol. Soc. Am. 2002, 92, 1377–1389. [Google Scholar] [CrossRef]
- Funning, G.; Fukahata, Y.; Yagi, Y.; Parsons, B. A method for the joint inversion of geodetic and seismic waveform data using ABIC: Application to the 1997 Manyi, Tibet, earthquake. Geophys. J. Int. 2014, 196, 1564–1579. [Google Scholar] [CrossRef] [Green Version]
- Yi, L.; Xu, C.; Zhang, X.; Wen, Y.; Jiang, G.; Li, M.; Wang, Y. Joint inversion of GPS, InSAR and teleseismic data sets for the rupture process of the 2015 Gorkha, Nepal, earthquake using a generalized ABIC method. J. Asian Earth Sci. 2017, 148, 121–130. [Google Scholar] [CrossRef]
- Yi, L.; Xu, C.; Wen, Y.; Zhang, X.; Jiang, G. Rupture process of the 2016 Mw 7.8 Ecuador earthquake from joint inversion of InSAR data and teleseismic P waveforms. Tectonophysics 2018, 722, 163–174. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike; Springer: New York, NY, USA, 1973; pp. 267–281. [Google Scholar]
- Yabuki, T.; Matu’ura, M. Geodetic data inversion using a Bayesian information criterion for spatial distribution of fault slip. Geophys. J. Int. 1992, 109, 363–375. [Google Scholar] [CrossRef]
- Yue, L.F.; Suppe, J.; Hung, J.H. Structural geology of a classic thrust belt earthquake: The 1999 Chi-Chi earthquake Taiwan (Mw = 7.6). J. Struct. Geol. 2005, 27, 2058–2083. [Google Scholar] [CrossRef]
- Maerten, F.; Maerten, L.; Pollard, D. iBem3D, a three-dimensional iterative boundary element method using angular dislocations for modeling geologic structures. Comput. Geosci. 2014, 72, 1–17. [Google Scholar] [CrossRef]
- Feng, W.; Li, Z.; Elliott, J.; Fukushima, Y.; Hoey, T.; Singleton, A.; Cook, R.; Xu, Z. The 2011 Mw 6.8 Burma earthquake: Fault constraints provided by multiple SAR techniques. Geophys. J. Int. 2013, 195, 650–660. [Google Scholar] [CrossRef] [Green Version]
- Feng, W.; Li, Z. A novel hybrid PSO/simplex algorithm for determining earthquake source parameters using InSAR observations. Diqiu Wulixue Jinzhan Progress Geophys. 2010, 25, 1550–1559. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Richards-Dinger, K.; Bozkurt, S. Forecasting the evolution of seismicity in southern California: Animations built on earthquake stress transfer. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Lin, J.; Stein, R. Stress triggering in thrust and subduction earthquakes, and stress interaction between the southern San Andreas and nearby thrust and strike-slip faults. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Wessel, P.; Smith, W. New, improved version of Generic Mapping Tools released. EOS Trans. Am. Geophys. Union 1998, 79, 579. [Google Scholar] [CrossRef]


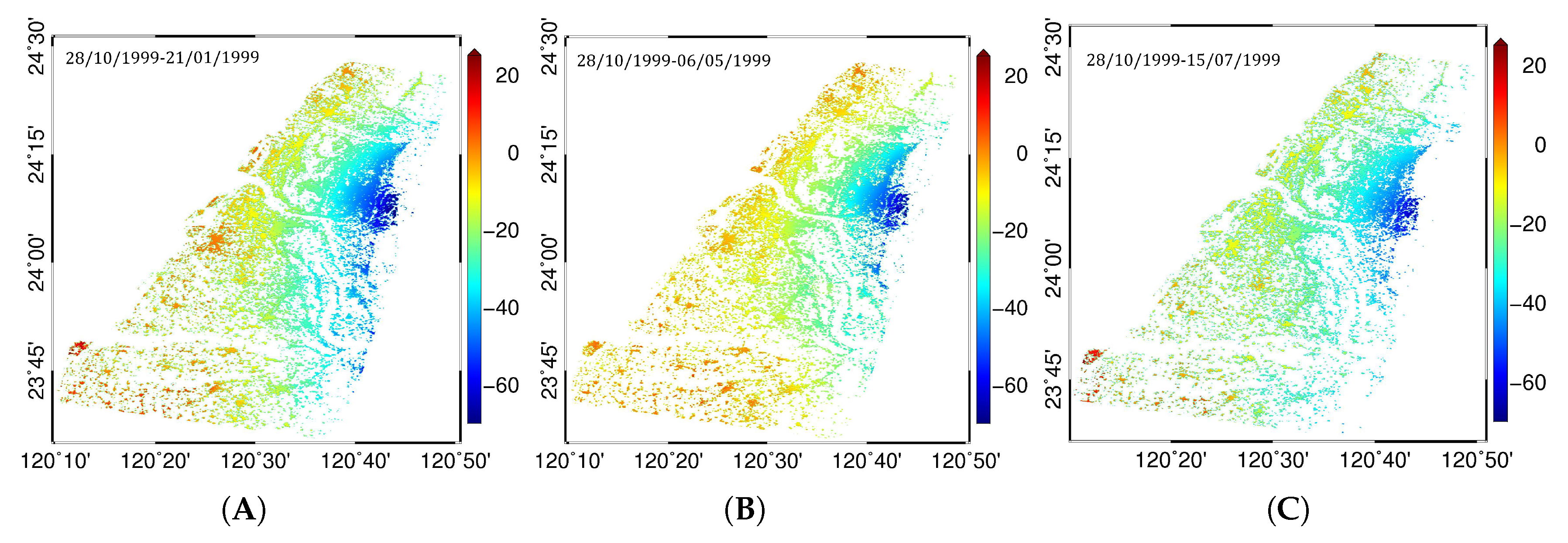
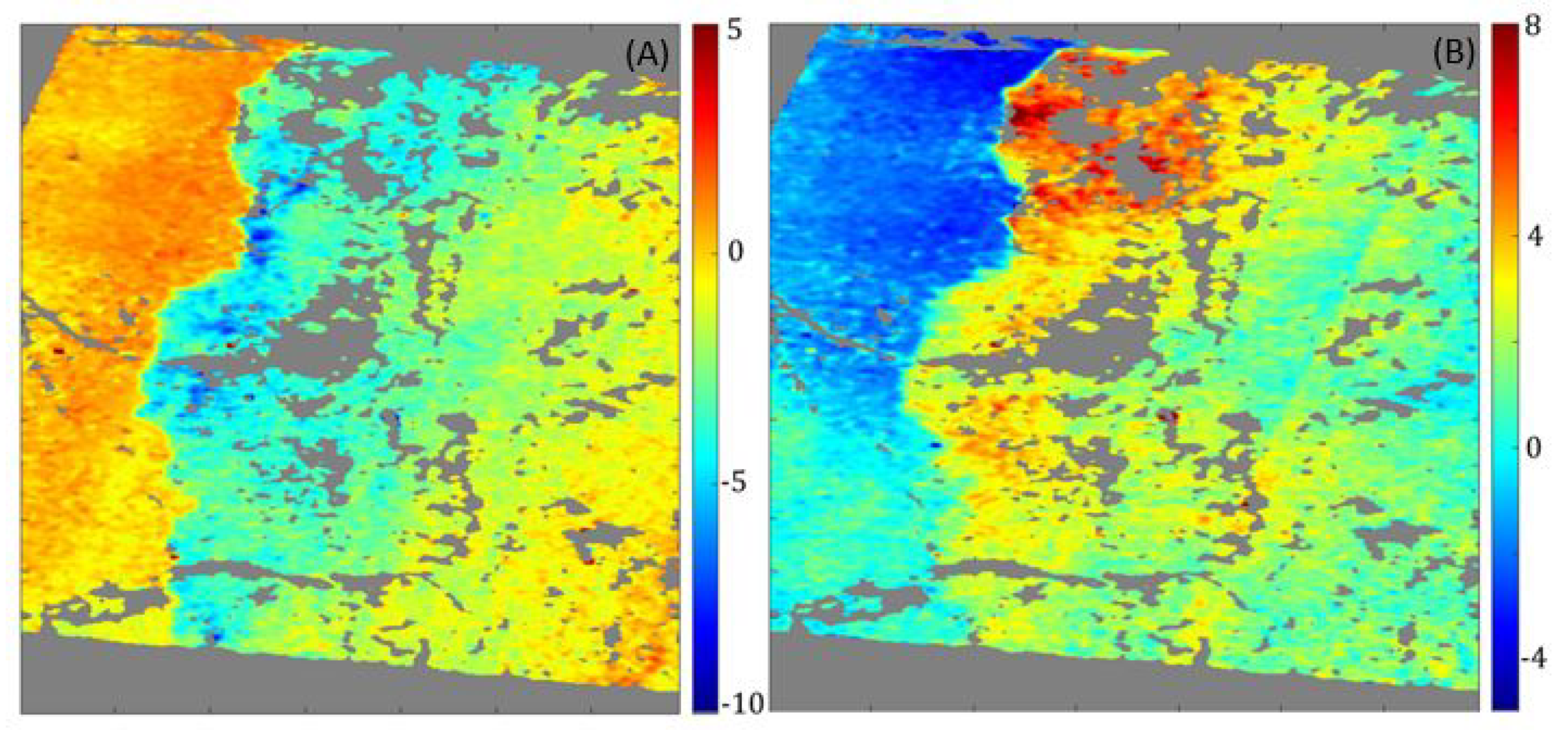


| Acquisition Date | Track | Frame | Orbit | Temporal Baseline [Days] | Perp. Baseline [m] | Height Ambiguity [m] |
|---|---|---|---|---|---|---|
| 28 October 1999 | 232 | 3123 | 23633 | - | - | - |
| 21 January 1999 | 232 | 3123 | 19625 | 280.00 | −92.89 | 102.07 |
| 06 May 1999 | 232 | 3123 | 21128 | 175.00 | 20.08 | −469.46 |
| 15 July 1999 | 232 | 3123 | 22130 | 105.00 | −247.71 | 38.28 |
| Acquisition Date | Satellite/Orient. | Cloud Cover | Incidence Angle | Orient. Angle | Sun Elevation | Sun Azimuth |
|---|---|---|---|---|---|---|
| 29 January 1999 | SPOT2/Right | 2.9° | 9.4° | 42.9° | 151.0° | |
| 23 November 1999 | SPOT1/Right | 2.5° | 9.4° | 43.4° | 159.7° |
| This Study | Length | Width | Depth | Dip | Strike | Rake |
|---|---|---|---|---|---|---|
| Segment 1 | 71.45 km | 30 km | 0 km | 3.3° | 62° | |
| Segment 2 | 10 km | 10 km | 0 km | 22° | 50° | 90° |
| Segment 3 | 15 km | 20 km | 0 km | 24° | 88° | 90° |
| Segment 4 | 70 km | 34 km | 11.7 km | 5.7° | 3.3° | 54° |
| [14,17] | ||||||
| (SRCMOD) | ||||||
| Segment 1 | 70 km | 30 km | 0 km | 23° [22–31] | 3.3° | ? |
| Segment 2 | 8.6 km | 30 km | 0 km | 23° [13–30] | 35° | ? |
| Segment 3 | 27 km [22–35] | 30 km | 0 km | 21° [14–41] | 88° [49–94] | ? |
| Segment 4 | 70 km | ? | [5.8–8.6] km | [0–7]° | 88° | ? |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roger, M.; Li, Z.; Clarke, P.; Song, C.; Hu, J.-C.; Feng, W.; Yi, L. Joint Inversion of Geodetic Observations and Relative Weighting—The 1999 Mw 7.6 Chi-Chi Earthquake Revisited. Remote Sens. 2020, 12, 3125. https://doi.org/10.3390/rs12193125
Roger M, Li Z, Clarke P, Song C, Hu J-C, Feng W, Yi L. Joint Inversion of Geodetic Observations and Relative Weighting—The 1999 Mw 7.6 Chi-Chi Earthquake Revisited. Remote Sensing. 2020; 12(19):3125. https://doi.org/10.3390/rs12193125
Chicago/Turabian StyleRoger, Marine, Zhenhong Li, Peter Clarke, Chuang Song, Jyr-Ching Hu, Wanpeng Feng, and Lei Yi. 2020. "Joint Inversion of Geodetic Observations and Relative Weighting—The 1999 Mw 7.6 Chi-Chi Earthquake Revisited" Remote Sensing 12, no. 19: 3125. https://doi.org/10.3390/rs12193125
APA StyleRoger, M., Li, Z., Clarke, P., Song, C., Hu, J.-C., Feng, W., & Yi, L. (2020). Joint Inversion of Geodetic Observations and Relative Weighting—The 1999 Mw 7.6 Chi-Chi Earthquake Revisited. Remote Sensing, 12(19), 3125. https://doi.org/10.3390/rs12193125