A Spatially Transferable Drought Hazard and Drought Risk Modeling Approach Based on Remote Sensing Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Geo-Data
2.3. Methodology
2.3.1. Drought Hazard Analysis
2.3.2. Vulnerability and Risk Analysis
3. Results
3.1. Drought Hazard Analysis in the USA, South Africa and Zimbabwe
3.1.1. Drought Hazard in the Missouri Basin (USA)
3.1.2. Applicability of the Developed Hazard Model for South Africa
3.1.3. Applicability of the Developed Hazard Model in Zimbabwe
3.1.4. Evaluation of the Logistic Regression Model for South Africa and Zimbabwe
3.1.5. Comparison between the Drought Hazard Model and the Global Drought Observatory of the Joint Research Center (JRC)
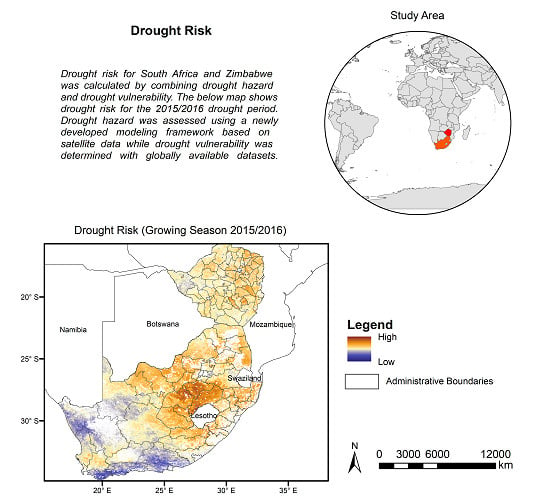
3.2. Drought Vulnerability and Risk Analysis in South Africa and Zimbabwe
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wilhite, D.A. (Ed.) Drought: A Global Assessment, 2nd ed.; Routledge: London, UK, 2000; ISBN 9780415168335. [Google Scholar]
- Sivakumar, M.V.K.; Motha, R.P.; Wilhite, D.A.; Wood, D.A. Agricultural Drought Indices. In Proceedings of the WMO/UNISDR Expert Group Meeting on Agricultural Drought Indices, Murcia, Spain, 2–4 June 2010. [Google Scholar]
- UN-Spider. Drought. 2019. Available online: http://www.un-spider.org/risks-and-disasters/natural-hazards/drought (accessed on 3 December 2019).
- IPCC (Ed.) Summary for Policymakers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Pachauri, R K.; Mayer, L. (Eds.) Climate Change 2014, Synthesis Report; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2015; ISBN 978-92-9169-143-2. [Google Scholar]
- Wilhite, D.A. (Ed.) Preparing for Drought: A Methodology. In Drought: A Global Assessment, 2nd ed.; Routledge: London, UK, 2000; pp. 89–104. ISBN 9780415168335. [Google Scholar]
- Owrangi, M.A.; Adamowski, J.; Rahnemaei, M.; Mohammadzadeh, A.; Sharifan, R.A. Drought Monitoring Methodology Based on AVHRR Images and SPOT Vegetation Maps. JWARP 2011, 3, 325–334. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Zhou, L.; Liu, M.; Zhang, J.; Leng, S.; Diao, C. Establishing and assessing the Integrated Surface Drought Index (ISDI) for agricultural drought monitoring in mid-eastern China. Int. J. Appl. Earth Obs. Geoinf. 2012, 23, 397–410. [Google Scholar] [CrossRef]
- Zhou, L.; Wu, J.; Zhang, J.; Leng, S.; Liu, M.; Zhang, J.; Zhao, L.; Zhang, F.; Shi, Y. The Integrated Surface Drought Index (ISDI) as an Indicator for Agricultural Drought Monitoring: Theory, Validation, and Application in Mid-Eastern China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1254–1262. [Google Scholar] [CrossRef]
- Gulácsi, A.; Kovács, F. Drought Monitoring With Spectral Indices Calculated From Modis Satellite Images in Hungary. J. Environ. Geogr. 2015, 8. [Google Scholar] [CrossRef] [Green Version]
- Zhuo, W.; Huang, J.; Zhang, X.; Sun, H.; Zhu, D.; Su, W.; Zhang, C.; Liu, Z. Comparison of five drought indices for agricultural drought monitoring and impacts on winter wheat yields analysis. In Proceedings of the 2016 Fifth International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Tianjin, China, 18–20 July 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Di, W.; Qu, J.J.; Hao, X. Agricultural drought monitoring using MODIS-based drought indices over the USA Corn Belt. Int. J. Remote Sens. 2015, 36, 5403–5425. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, C.; Li, W.; Fang, X.; Zhang, T.; Zhu, Q.; Chen, H.; Zhao, P. Monitoring and estimating drought-induced impacts on forest structure, growth, function, and ecosystem services using remote-sensing data: Recent progress and future challenges. Environ. Rev. 2013, 21, 103–115. [Google Scholar] [CrossRef]
- Hazaymeh, K.; Hassan, Q.K. Remote sensing of agricultural drought monitoring: A state of art review. AIMS Environ. Sci. 2016, 3, 604–630. [Google Scholar] [CrossRef]
- Peng, C.; Deng, M.; Di, L. Relationships between Remote-Sensing-Based Agricultural Drought Indicators and Root Zone Soil Moisture: A Comparative Study of Iowa. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4572–4580. [Google Scholar] [CrossRef]
- Park, S.; Im, J.; Park, S.; Rhee, J. Drought monitoring using high resolution soil moisture through multi-sensor satellite data fusion over the Korean peninsula. Agric. For. Meteorol. 2017, 237–238, 257–269. [Google Scholar] [CrossRef]
- Zhang, Q.; Yu, H.; Sun, P.; Singh, V.P.; Shi, P. Multisource data based agricultural drought monitoring and agricultural loss in China. Glob. Planet. Chang. 2019, 172, 298–306. [Google Scholar] [CrossRef]
- Bayissa, Y.A.; Tadesse, T.; Svoboda, M.; Wardlow, B.; Poulsen, C.; Swigart, J.; van Andel, S.J. Developing a satellite-based combined drought indicator to monitor agricultural drought: A case study for Ethiopia. GIScience Remote Sens. 2019, 56, 718–748. [Google Scholar] [CrossRef]
- Zhang, X.; Obringer, R.; Wei, C.; Chen, N.; Niyogi, D. Droughts in India from 1981 to 2013 and Implications to Wheat Production. Sci. Rep. 2017, 7, 44552. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sur, C.; Park, S.-Y.; Kim, T.-W.; Lee, J.-H. Remote Sensing-based Agricultural Drought Monitoring using Hydrometeorological Variables. KSCE J. Civ. Eng. 2019, 23, 5244–5256. [Google Scholar] [CrossRef]
- Qu, C.; Hao, X.; Qu, J.J. Monitoring Extreme Agricultural Drought over the Horn of Africa (HOA) Using Remote Sensing Measurements. Remote Sens. 2019, 11, 902. [Google Scholar] [CrossRef] [Green Version]
- Caccamo, G.; Chisholm, L.A.; Bradstock, R.A.; Puotinen, M.L. Assessing the sensitivity of MODIS to monitor drought in high biomass ecosystems. Remote Sens. Environ. 2011, 115, 2626–2639. [Google Scholar] [CrossRef]
- Chang, C.-T.; Wang, H.-C.; Huang, C.-Y. Assessment of MODIS-derived indices (2001–2013) to drought across Taiwan’s forests. Int. J. Biometeorol. 2017, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.; Wang, P.; Li, X. Using MODIS Land Surface Temperature and Normalized Difference Vegetation Index products for monitoring drought in the southern Great Plains, USA. Int. J. Remote Sens. 2004, 25, 61–72. [Google Scholar] [CrossRef]
- Wang, S.; Davidson, A.; Latifovic, R.; Trishchenko, A. The impact of drought on land surface albedo. Am. Geophys. Union 2004, 85. [Google Scholar]
- Vogt, J.V.; Naumann, G.; Masante, D.; Spinoni, J.; Cammalleri, C.; Erian, W.; Pischke, F.; Pulwarty, R.; Barbosa, P. Drought Risk Assessment. A Conceptual Framework; Publications Office of the European Union: Luxembourg, 2018; ISBN 978-92-79-97469-4. [Google Scholar]
- Huntington, J.L.; Hegewisch, K.C.; Daudert, B.; Morton, C.G.; Abatzoglou, J.T.; McEvoy, D.J.; Erickson, T. Climate Engine: Cloud Computing and Visualization of Climate and Remote Sensing Data for Advanced Natural Resource Monitoring and Process Understanding. Bull. Am. Meteorol. Soc. 2017, 98, 2397–2410. [Google Scholar] [CrossRef]
- Chen, D.; Chen, H.W. Using the Köppen classification to quantify climate variation and change: An example for 1901–2010. Environ. Dev. 2013, 6, 69–79. [Google Scholar] [CrossRef]
- FAO. Faostat. 2019. Available online: http://www.fao.org/faostat/en/#data (accessed on 10 January 2019).
- Homer, C.; Dewitz, J.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N.; Wickham, J.; Megown, K. Completion of the 2011 National Land Cover Database for the Conterminous United States—Representing a Decade of Land Cover Change Information. Photogramm. Eng. Remote Sens. 2015, 81, 345–354. [Google Scholar]
- ESA Climate Change Initiative—Land Cover project 2017. CCI Land Cover—S2 Prototype Land Cover 20M Map of Africa. 2016. Available online: http://2016africalandcover20m.esrin.esa.int/ (accessed on 14 March 2019).
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vermote, E.F.; Roger, J.C.; Ray, J.P. MODIS Surface Reflectance User’s Guide—Collection 6. 2018. Available online: http://modis-sr.ltdri.org/guide/MOD09_UserGuide_v1.4.pdf (accessed on 20 April 2018).
- Wan, Z.; Hook, S.; Hulley, G. MOD11A2 MODIS/Terra Land Surface Temperature/Emissivity 8-Day L3 Global 1 km SIN Grid V006 [Data]; NASA EOSDIS Land Processes DAAC; U.S. Geological Survey: Reston, VA, USA, 2015. [CrossRef]
- Schaaf, C.; Wang, Z. MCD43A3 MODIS/Terra + Aqua BRDF/Albedo Daily L3 Global—500 m V006; NASA EOSDIS Land Processes DAAC; U.S. Geological Survey: Reston, VA, USA, 2015. [CrossRef]
- CIESIN. Gridded Population of the World, Version 4 (GPWv4): Population Density, Revision 10. Available online: https://catalog.data.gov/dataset/gridded-population-of-the-world-version-4-gpwv4-population-density-revision-10 (accessed on 10 January 2019).
- Kummu, M.; Taka, M.; Guillaume, J.H.A. Gridded global datasets for Gross Domestic Product and Human Development Index over 1990–2015. Sci. Data 2018, 5, 180004. [Google Scholar] [CrossRef] [Green Version]
- Landmann, T.; Eidmann, D.; Cornish, N.; Franke, J.; Siebert, S. Optimizing harmonics from Landsat time series data: The case of mapping rainfed and irrigated agriculture in Zimbabwe. Remote Sens. Lett. 2019, 10, 1038–1046. [Google Scholar] [CrossRef]
- Gilbert, M.; Nicolas, G.; Cinardi, G.; van Boeckel, T.P.; Vanwambeke, S.O.; Wint, G.R.W.; Robinson, T.P. Global distribution data for cattle, buffaloes, horses, sheep, goats, pigs, chickens and ducks in 2010. Sci. Data 2018, 5, 180227. [Google Scholar] [CrossRef] [Green Version]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. Eighth Conf. Appl. Climatol. 1993, 22, 179–184. [Google Scholar]
- Rouse, J.W.; Hass, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. In Proceedings of the 3rd Earth Resources Technology Satellite-1 Symposium, Greenbelt, MD, USA, 10–14 December 1973; pp. 309–317. [Google Scholar]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Wan, Z. MODIS Land Surface Temperature Products Users’ Guide: Collection-6. 2019. Available online: https://icess.eri.ucsb.edu/modis/LstUsrGuide/MODIS_LST_products_Users_guide_Collection-6.pdf (accessed on 26 March 2019).
- Zeileis, A.; Kleiber, C.; Krämer, W.; Hornik, K. Testing and dating of structural changes in practice. Comput. Stat. Data Anal. 2003, 44, 109–123. [Google Scholar] [CrossRef] [Green Version]
- Muggeo, V.M.R. Segmented: An R package to fit regression models with broken-line relationships. R News 2008, 8, 20–25. [Google Scholar]
- Abdel-Rahman, E.; Landmann, T.; Kyalo, R.; Ong’amo, G.; Mwalusepo, S.; Sulieman, S.; Le Ru, B. Predicting stem borer density in maize using RapidEye and generalized linear models. Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 61–74. [Google Scholar] [CrossRef]
- Mosomtai, G.; Evander, M.; Sandström, P.; Ahlm, C.; Sang, R.; Hassan, O.A.; Affognon, H.; Landmann, T. Association of ecological factors with Rift Valley fever occurrence and mapping of risk zones in Kenya. Int. J. Infect. Dis. 2016, 46, 49–55. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning. With Applications in R, 6th ed.; Springer: New York, NY, USA, 2015; ISBN 978-1-4614-7137-0. [Google Scholar]
- Veall, M.R.; Zimmermann, K.F. Pseudo-R² Measures for Some Common Limited Dependent Variable Models. J. Econ. Surv. 1996, 10, 241–259. [Google Scholar] [CrossRef] [Green Version]
- McFadden, D. Quantitative Methods for Analyzing Travel Behavior of Individuals: Some Recent Developments; Institute of Transportation Studies, University of California: Berkeley, CA, USA, 1977. [Google Scholar]
- Baldenhofer, K.G. Das ENSO-Phänomen: Der El Niño von 2015/16. 2015. Available online: http://www.enso.info/anhang/El_Nino_2015_16.pdf (accessed on 10 January 2019).
- Zhong, S.; Wang, C.; Yang, Y.; Huang, Q. Risk assessment of drought in Yun-Gui-Guang of China jointly using the Standardized Precipitation Index and vulnerability curves. Geomat. Nat. Hazards Risk 2018, 9, 892–918. [Google Scholar] [CrossRef]
- Hagenlocher, M.; Meza, I.; Anderson, C.C.; Min, A.; Renaud, F.G.; Walz, Y.; Siebert, S.; Sebesvari, Z. Drought vulnerability and risk assessments: State of the art, persistent gaps, and research agenda. Environ. Res. Lett. 2019, 14, 83002. [Google Scholar] [CrossRef]
- Dijkstra, L.; Poelman, H. Regional Working Papter 2014: A harmonised definition of cities and rural areas: The new degree of urbanisation. In European Commission’s Directorate General (DG) for Regional and Urban Policy: Working Papers; European Commission: Brussels, Belgium, 2014; pp. 1–24. [Google Scholar]
- NOAA Climate Government. El Niño Climate Impacts. 2019. Available online: https://www.climate.gov/news-features/featured-images/global-impacts-el-ni%C3%B1o-and-la-ni%C3%B1a (accessed on 14 March 2019).
- Baldenhofer, K.G. Das ENSO-Phänomen: ENSO-Lexikon. 2019. Available online: http://www.enso.info/enso-lexikon/index.html (accessed on 23 January 2019).
- BBC News. South Africa Grapples with Worst Drought in 30 Years. 2019. Available online: https://www.bbc.com/news/world-africa-34884135 (accessed on 23 January 2019).
- Al, J. South Africa in Midst of ‘Epic Drought’. 2019. Available online: https://www.aljazeera.com/news/2015/11/south-africa-midst-epic-drought-151104070934236.html (accessed on 23 January 2019).
- News24. Extreme Drought Persists Across SA. 2019. Available online: https://www.news24.com/SouthAfrica/News/extreme-drought-persists-across-sa-20160117 (accessed on 23 January 2019).
- BBC News. Zimbabwe’s Robert Mugabe Declares Drought Disaster. 2019. Available online: https://www.bbc.com/news/world-africa-35500820 (accessed on 23 January 2019).
- ReliefWeb. Zimbabwe: 2016–2017 Drought Disaster Domestic and International Appeal for Assistance. 2019. Available online: https://reliefweb.int/report/zimbabwe/zimbabwe-2016-2017-drought-disaster-domestic-and-international-appeal-assistance (accessed on 23 January 2019).
- Kogan, F. Remote Sensing for Food Security; Springer International Publishing: Cham, Switzerland, 2019; ISBN 978-3-319-96255-9. [Google Scholar]
- Onyia, N.; Balzter, H.; Berrio, J.-C. Normalized Difference Vegetation Vigour Index: A New Remote Sensing Approach to Biodiversity Monitoring in Oil Polluted Regions. Remote Sens. 2018, 10, 897. [Google Scholar] [CrossRef] [Green Version]
- Wilhelmi, O.V.; Wilhite, D.A. Assessing Vulnerability to Agricultural Drought: A Nebraska Case Study. Nat. Hazards 2002, 25, 37–58. [Google Scholar] [CrossRef]
- Ebi, K.L.; Bowen, K. Extreme events as sources of health vulnerability: Drought as an example. Weather Clim. Extrem. 2016, 11, 95–102. [Google Scholar] [CrossRef] [Green Version]






| Data | Product | Spatial Resolution | Period | Spatial Coverage | Data Source |
|---|---|---|---|---|---|
| Land use classification | |||||
| Land use | NLCD | 30 m | 2011 | USA | [30] |
| Land use | CCI | 20 m | 2016 | Africa | [31] |
| Definition of drought periods | |||||
| Crop yield | FAOSTAT | National statistics | 2001–2016 | Global | [29] |
| Predictors for logistic regression model | |||||
| Precipitation | CHIRPS | 0.05° | 1981–2018 | 50°S–50°N | [32] |
| Surface reflectance | MOD09A1 | 500 m | 2000–today | Global | [33] |
| LST | MOD11A2 | 1 km | 2000–today | Global | [34] |
| Albedo | MOD43A3 | 500 m | 2000–today | Global | [35] |
| Data for drought vulnerability and drought risk analysis | |||||
| Population density | GPWv4 | 30 arc–sec | 2015 | Global | [36] |
| Gross domestic product | GDP_PPP_30arcsec_v2 | 30 arc–sec | 2015 | Global | [37] |
| Farming systems | Farming Systems | 30 m | 2017 | Zimbabwe | [38] |
| Livestock density | - | ~0.08° | 2010 | Global | [39] |
| SPI3 | NDII | NDVI | Albedo | |
|---|---|---|---|---|
| NDII | 0.41 | - | - | - |
| NDVI | 0.45 | 0.71 | - | - |
| Albedo | −0.3 | −0.07 | −0.24 | - |
| LST | −0.56 | −0.53 | −0.49 | 0.22 |
| Condition Index | Albedo | LST | NDII | NDVI | SPI3 |
|---|---|---|---|---|---|
| 1 | - | - | - | - | - |
| 1.75 | - | - | - | - | - |
| 3.15 | 0.49 | 0.57 | - | - | - |
| 4.23 | - | - | - | - | 0.96 |
| 10.66 | - | - | 0.93 | 0.94 | - |
| Coefficient | z-Value | |
|---|---|---|
| (constant) | −0.20 | −35.6 |
| Albedo | 0.13 | 22.6 |
| LST | 0.43 | 66.6 |
| NDII | −0.83 | −111.7 |
| SPI3 | −0.12 | −17.6 |
| Coefficient | z-Value | |
|---|---|---|
| (constant) | −0.17 | −31.5 |
| Albedo | 0.25 | 40.0 |
| LST | 0.48 | 59.8 |
| NDII | −0.35 | −40.2 |
| NDVI | 0.61 | 70.0 |
| SPI3 | −0.93 | −118.1 |
| Coefficient | z-Value | |
|---|---|---|
| (constant) | −0.03 | −6.3 |
| Albedo | 0.19 | −35.4 |
| LST | 0.07 | −10.1 |
| NDII | −0.46 | −67.4 |
| NDVI | 0.10 | 18.2 |
| SPI3 | −0.38 | −57.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schwarz, M.; Landmann, T.; Cornish, N.; Wetzel, K.-F.; Siebert, S.; Franke, J. A Spatially Transferable Drought Hazard and Drought Risk Modeling Approach Based on Remote Sensing Data. Remote Sens. 2020, 12, 237. https://doi.org/10.3390/rs12020237
Schwarz M, Landmann T, Cornish N, Wetzel K-F, Siebert S, Franke J. A Spatially Transferable Drought Hazard and Drought Risk Modeling Approach Based on Remote Sensing Data. Remote Sensing. 2020; 12(2):237. https://doi.org/10.3390/rs12020237
Chicago/Turabian StyleSchwarz, Maximilian, Tobias Landmann, Natalie Cornish, Karl-Friedrich Wetzel, Stefan Siebert, and Jonas Franke. 2020. "A Spatially Transferable Drought Hazard and Drought Risk Modeling Approach Based on Remote Sensing Data" Remote Sensing 12, no. 2: 237. https://doi.org/10.3390/rs12020237
APA StyleSchwarz, M., Landmann, T., Cornish, N., Wetzel, K.-F., Siebert, S., & Franke, J. (2020). A Spatially Transferable Drought Hazard and Drought Risk Modeling Approach Based on Remote Sensing Data. Remote Sensing, 12(2), 237. https://doi.org/10.3390/rs12020237