Precipitation Regime Classification Based on Cloud-Top Temperature Time Series for Spatially-Varied Parameterization of Precipitation Models
Abstract
:1. Introduction
2. Datasets
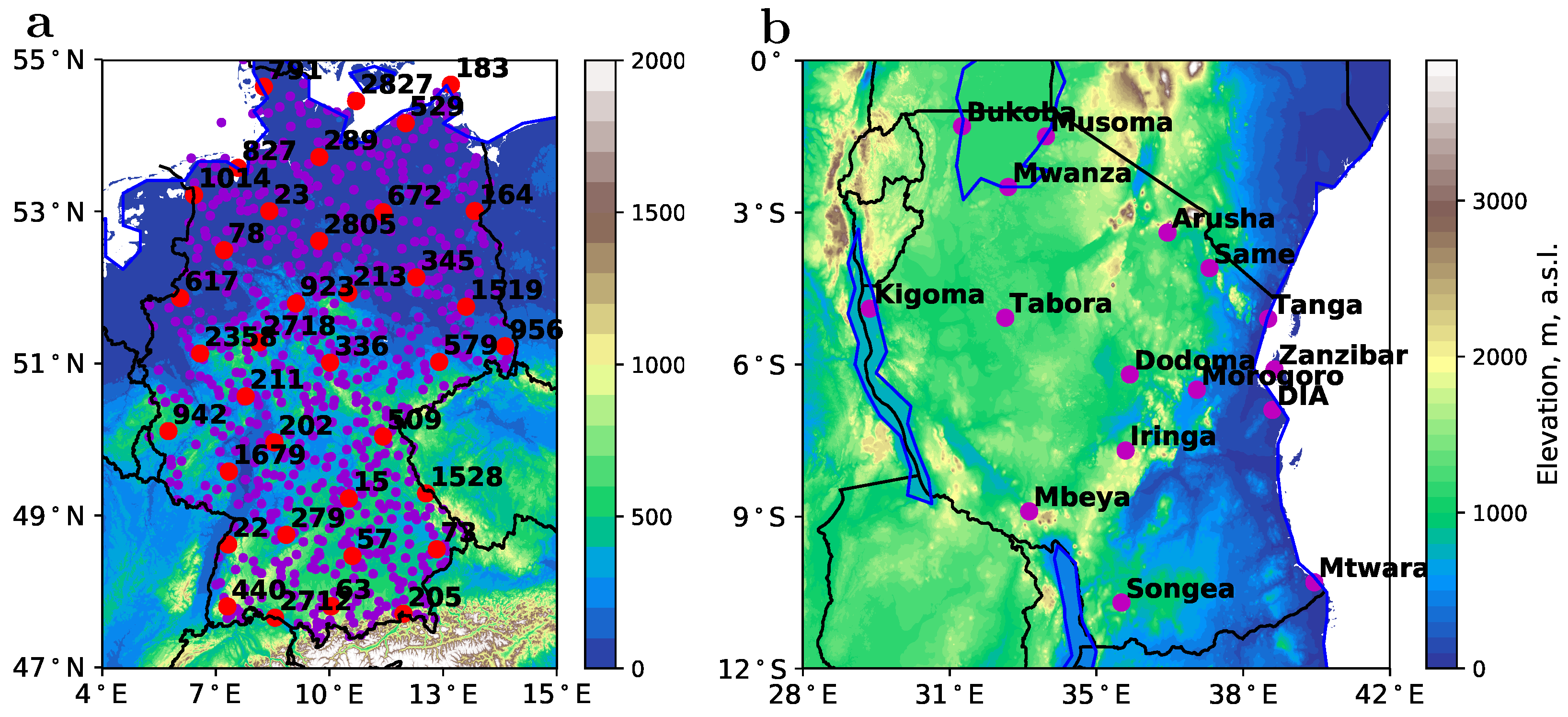
2.1. Precipitation Climatology and Data for the Two Study Regions
2.2. Data Preprocessing
3. Methodology
3.1. Methodological Framework
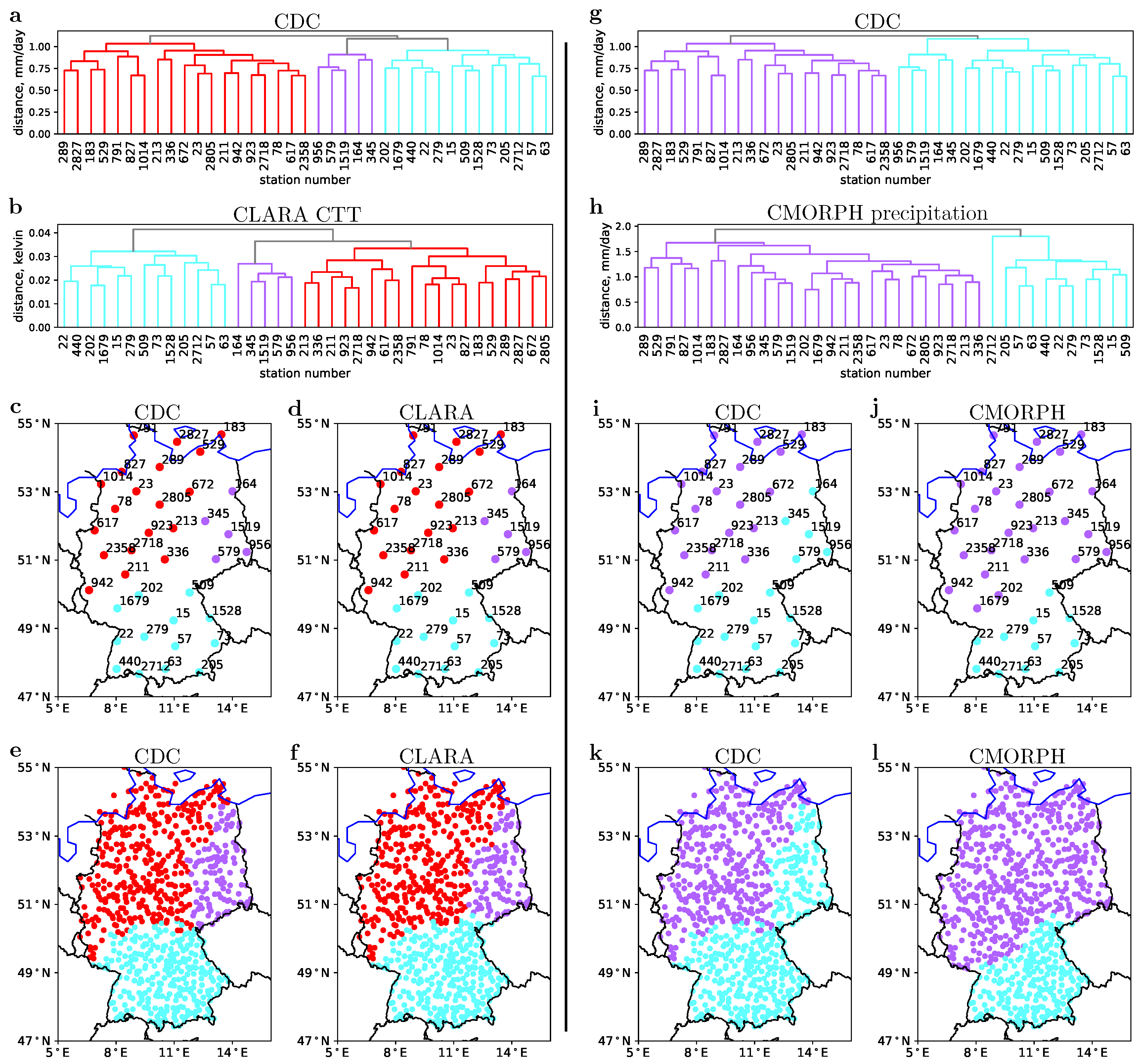
3.2. Clustering of Stations and Classification of Satellite Grid Cells
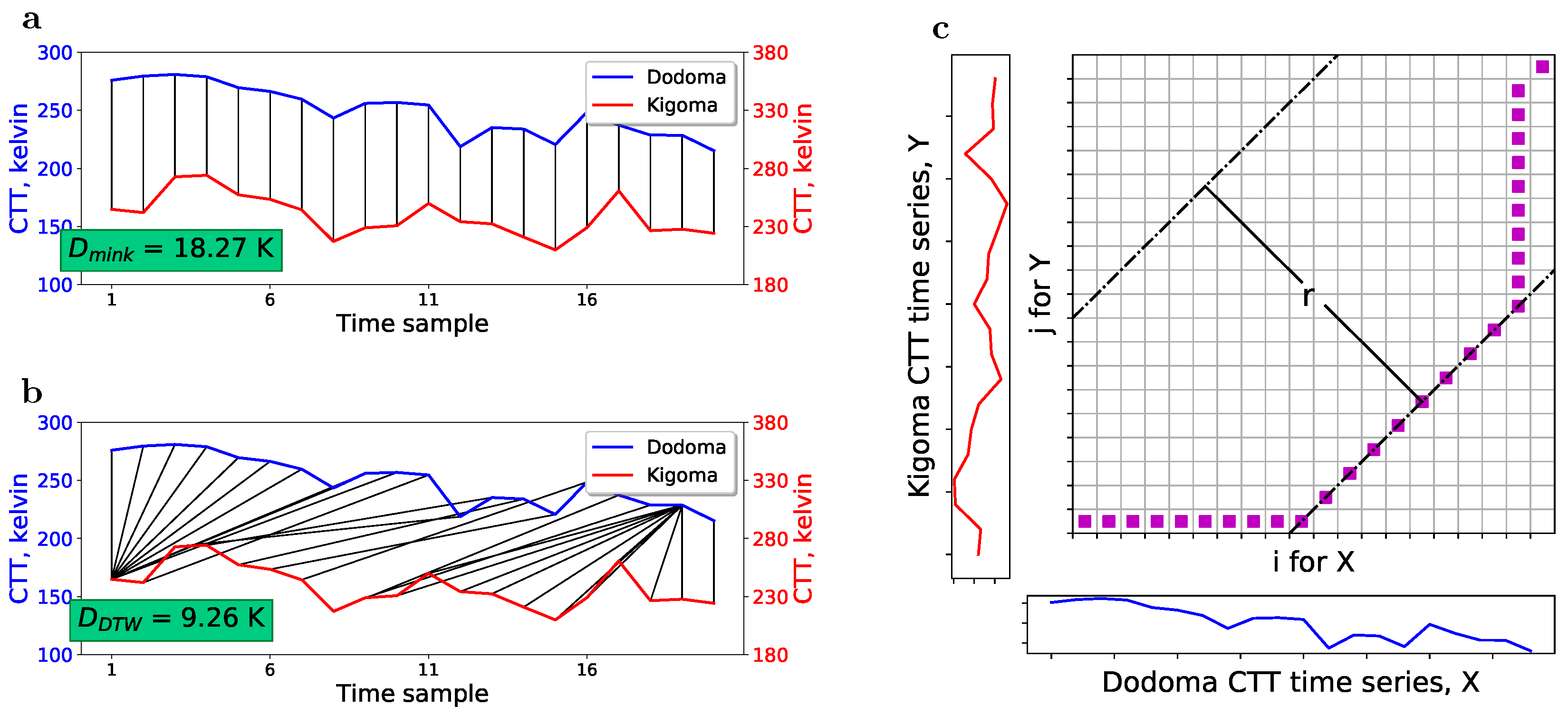
3.3. Time Series Distance Using Dynamic Time Warping
3.4. Selection of Temporal Scale
3.5. Selection of Number of Clusters
4. Results and Analysis
4.1. Validation over Germany
4.2. Application over Tanzania, a Data-Scarce Environment
4.3. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. IPCC, 2014: Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; Technical report; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations–the CRU TS3. 10 Dataset. Int. J. Clim. 2014, 34, 623–642. [Google Scholar] [CrossRef] [Green Version]
- Schamm, K.; Ziese, M.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Schneider, U.; Schröder, M.; Stender, P. Global gridded precipitation over land: A description of the new GPCC First Guess Daily product. Earth Syst. Sci. Data 2014, 6, 49–60. [Google Scholar] [CrossRef] [Green Version]
- Xie, P.; Chen, M.; Shi, W. CPC unified gauge-based analysis of global daily precipitation. In Proceedings of the 4th Conference on Hydrology, Atlanta, GA, USA, 17–21 January 2010. [Google Scholar]
- Dee, D.P.; Uppala, S.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Ame. Meteorol. Soci. 2010, 91, 1015–1058. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Morrissey, M.M.; Bolvin, D.T.; Curtis, S.; Joyce, R.; McGavock, B.; Susskind, J. Global precipitation at one-degree daily resolution from multisatellite observations. J. Hydrometeorol. 2001, 2, 36–50. [Google Scholar] [CrossRef] [Green Version]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG); Algorithm Theoretical Basis Document (ATBD) Version 4.5, NASA/GSFC, NASA/GSFC Code 612; NASA: Greenbelt, MD, USA, 2015.
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Beck, H.E.; Van Dijk, A.I.; Levizzani, V.; Schellekens, J.; Gonzalez Miralles, D.; Martens, B.; De Roo, A. MSWEP: 3-hourly 0.25 global gridded precipitation (1979-2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef] [Green Version]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—a new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [Green Version]
- Van de Giesen, N.; Hut, R.; Selker, J. The Trans-African Hydro-Meteorological Observatory (TAHMO). Wiley Interdiscip. Rev. Water 2014, 1, 341–348. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef] [Green Version]
- Le Coz, C.; van de Giesen, N. Comparison of rainfall products over sub-Sahara Africa. J. Hydrometeorol. 2019. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. Discuss. 2007, 4, 439–473. [Google Scholar] [CrossRef] [Green Version]
- Herrmann, S.M.; Mohr, K.I. A continental-scale classification of rainfall seasonality regimes in Africa based on gridded precipitation and land surface temperature products. J. Appl. Meteorol. Clim. 2011, 50, 2504–2513. [Google Scholar] [CrossRef]
- Arkin, P.A.; Meisner, B.N. The relationship between large-scale convective rainfall and cold cloud over the western hemisphere during 1982-84. Mon. Weather Rev. 1987, 115, 51–74. [Google Scholar] [CrossRef] [Green Version]
- Adler, R.F.; Negri, A.J.; Keehn, P.R.; Hakkarinen, I.M. Estimation of monthly rainfall over Japan and surrounding waters from a combination of low-orbit microwave and geosynchronous IR data. J. Appl. Meteorol. 1993, 32, 335–356. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Gao, X.; Sorooshian, S.; Arkin, P.A.; Imam, B. A microwave infrared threshold technique to improve the GOES precipitation index. J. Appl. Meteorol. 1999, 38, 569–579. [Google Scholar] [CrossRef]
- Vicente, G.A.; Scofield, R.A.; Menzel, W.P. The operational GOES infrared rainfall estimation technique. Bull. Am. Meteorol. Soc. 1998, 79, 1883–1898. [Google Scholar] [CrossRef]
- Maidment, R.I.; Grimes, D.; Black, E.; Tarnavsky, E.; Young, M.; Greatrex, H.; Allan, R.P.; Stein, T.; Nkonde, E.; Senkunda, S.; et al. A new, long-term daily satellite-based rainfall dataset for operational monitoring in Africa. Sci. Data 2017, 4, 170063. [Google Scholar] [CrossRef]
- Hsu, K.l.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.L.; Sorooshian, S.; Gao, X. Precipitation estimation from remotely sensed imagery using an artificial neural network cloud classification system. J. Appl. Meteorol. 2004, 43, 1834–1853. [Google Scholar] [CrossRef] [Green Version]
- Salvador, S.; Chan, P. Toward accurate dynamic time warping in linear time and space. Intell. Data Anal. 2007, 11, 561–580. [Google Scholar] [CrossRef] [Green Version]
- Hofstätter, M.; Lexer, A.; Homann, M.; Blöschl, G. Large-scale heavy precipitation over central Europe and the role of atmospheric cyclone track types. Int. J. Clim. 2018, 38, e497–e517. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scofield, R.A. The NESDIS operational convective precipitation-estimation technique. Mon. Weather Rev. 1987, 115, 1773–1793. [Google Scholar] [CrossRef]
- Kaspar, F.; Müller-Westermeier, G.; Penda, E.; Mächel, H.; Zimmermann, K.; Kaiser-Weiss, A.; Deutschländer, T. Monitoring of climate change in Germany - data, products and services of Germany’s National Climate Data Centre. Adv. Sci. Res. 2013, 10, 99–106. [Google Scholar] [CrossRef] [Green Version]
- Karlsson, K.G.; Anttila, K.; Trentmann, J.; Stengel, M.; Meirink, J.F.; Devasthale, A.; Hanschmann, T.; Kothe, S.; Jääskeläinen, E.; Sedlar, J.; et al. CLARA-A2: the second edition of the CM SAF cloud and radiation data record from 34 years of global AVHRR data. Atmos. Chem. Phy. 2017, 17, 5809–5828. [Google Scholar] [CrossRef] [Green Version]
- Torres, C.E.; Barba, L.A. Fast radial basis function interpolation with Gaussians by localization and iteration. J. Comput. Phys. 2009, 228, 4976–4999. [Google Scholar] [CrossRef]
- Sakoe, H. Dynamic programming algorithm optimization for spoken word recognition. IEEE Tran. Acoust. Speech Signal Process. 1978, 26, 43–49. [Google Scholar] [CrossRef] [Green Version]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, S.; ten Veldhuis, M.-c.; van de Giesen, N.; Heemink, A.; Verlaan, M. Precipitation Regime Classification Based on Cloud-Top Temperature Time Series for Spatially-Varied Parameterization of Precipitation Models. Remote Sens. 2020, 12, 289. https://doi.org/10.3390/rs12020289
Lu S, ten Veldhuis M-c, van de Giesen N, Heemink A, Verlaan M. Precipitation Regime Classification Based on Cloud-Top Temperature Time Series for Spatially-Varied Parameterization of Precipitation Models. Remote Sensing. 2020; 12(2):289. https://doi.org/10.3390/rs12020289
Chicago/Turabian StyleLu, Sha, Marie-claire ten Veldhuis, Nick van de Giesen, Arnold Heemink, and Martin Verlaan. 2020. "Precipitation Regime Classification Based on Cloud-Top Temperature Time Series for Spatially-Varied Parameterization of Precipitation Models" Remote Sensing 12, no. 2: 289. https://doi.org/10.3390/rs12020289
APA StyleLu, S., ten Veldhuis, M.-c., van de Giesen, N., Heemink, A., & Verlaan, M. (2020). Precipitation Regime Classification Based on Cloud-Top Temperature Time Series for Spatially-Varied Parameterization of Precipitation Models. Remote Sensing, 12(2), 289. https://doi.org/10.3390/rs12020289





