A Novel Approach for the Determination of the Height of the Tropopause from Ground-Based GNSS Observations
Abstract
:1. Introduction
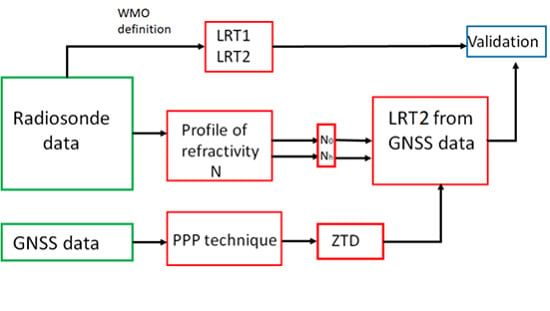
2. Materials and Methods
2.1. Description of GNSS Data Sources
2.2. Description of Radiosonde Data
2.3. Methodology
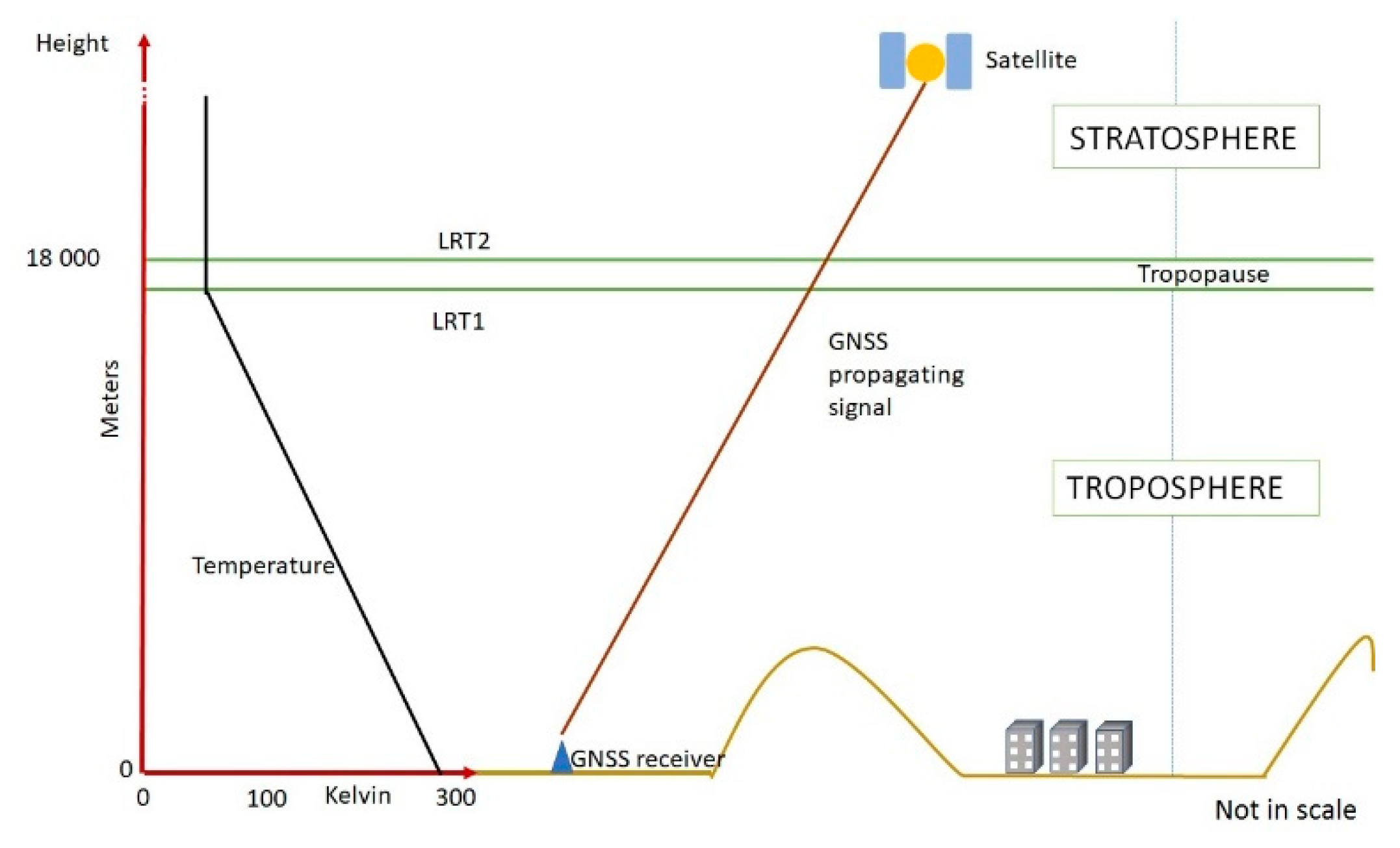
2.3.1. LRT1 and LRT2 from Radiosonde Data
2.3.2. Profile of the Refractivity of the Troposphere
2.3.3. Profile of the Refractivity
2.3.4. Estimation of ZTD
2.3.5. Computing LRT2 from GNSS Data
3. Results
3.1. Annual Cycle of the Refractivity Profile
Diurnal Cycle of N0 and Nh
3.2. D1 Parameter
3.3. Results of Proposed Algorithm
3.4. Validation of Results
4. Discussion of Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Santer, B.D.; Sausen, R.; Wigley, T.M.L.; Boyle, J.S.; AchutaRao, K.; Doutriaux, C.; Hansen, J.E.; Meehl, G.A.; Roeckner, E.; Ruedy, R.; et al. Behavior of tropopause height and atmospheric temperature in models, reanalyses, an d observations: Decadal changes. J. Geophys. Res. 2003, 108, 22. [Google Scholar] [CrossRef] [Green Version]
- Santer, B.D.; Wehner, M.F.; Wigley, T.M.L.; Sausen, R.; Meehl, G.A.; Taylor1, K.E.; Ammann, C.; Arblaster, J.; Washington, W.M.; Boyle1, J.S.; et al. Contribution of anthropogenic and natural forcing to recent tropopause height changes. Sci. Mag. 2003, 301, 479–483. [Google Scholar] [CrossRef] [Green Version]
- Santer, B.D.; Wigley, T.M.L.; Simmons, A.J.; Kållberg, P.W.; Kelly, G.A.; Uppala, S.M.; Ammann, C.; Boyle, J.S.; Brüggemann, W.; Doutriaux, C.; et al. Identification of anthropogenic climate change using a second-generation reanalysis. J. Geophys. Res. 2004, 109, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, T.; Beyerle, G.; Heise, S.; Wickert, J.; Rothaucher, M. A climatology of multiple tropopauses derived from GPS radio occultations with CHAMP and SAC-C. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Holton, J.R.; Haynes, P.H.; McIntyre, M.E.; Douglass, A.R.; Rood, R.B.; Pfister, L. Stratosphere-Troposphere Exchange. Rev. Geophys. 1995, 33, 403–439. [Google Scholar] [CrossRef]
- Feng, S.; Fu, Y.; Xiao, Q. Trends in the global tropopause thickness revealed by radiosondes. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- WMO. Meteorology: A three-dimensional science: Second session of the Commission for Aerology. WMO Bull. 1957, 4, 134–138. [Google Scholar]
- Seidel, D.J.; Randel, W.J. Variability and trends in the global tropopause estimated from radiosonde data. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Rieckh, T.; Scherllin-Pirscher, B.; Ladstädter, F.; Foelsche, U. Characteristics of tropopause parameters as observed with GPS radio occultation. Atmos. Meas. Tech. 2014, 7, 2014–3958. [Google Scholar] [CrossRef] [Green Version]
- Añel, J.A.; Gimeno, L.; de la Torre, L.; Nieto, R. Changes in tropopause height for the Eurasian region determined from CARDS radiosonde data. Naturwissenschaften 2006, 93, 2006–2609. [Google Scholar] [CrossRef]
- Hall, C.M.; Hansen, G.; Sigernes, F.; Ruiz, K.M.K. Tropopause height at 78N 16E: Average seasonal variation 2007–2010. Atmos. Chem. Phys. 2011, 11, 2011–5490. [Google Scholar] [CrossRef] [Green Version]
- Arai, K.; Liang, X.M. Sensitivity analysis for air temperature profile estimation methods around the tropopause using simulated Aqua/AIRS data. Adv. Space Res. 2009, 43, 2009–2851. [Google Scholar] [CrossRef]
- Lerner, J.A.; Weisz, E.; Kirchengast, G. Temperature and humidity retrieval from simulated Infrared Atmospheric Sounding Interferometer (IASI) measurements. J. Geophys. Res. Atmos. 2002, 107, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Lau, L.; Cross, P. Phase Multipath Mitigation Techniques for High Precision Positioning in All Conditions and Environments. J. Navig. 2007, 60, 457–482. [Google Scholar] [CrossRef]
- Lau, L.; Tateshita, H.; Sato, K. Impact of Multi-GNSS on Positioning Accuracy and Multipath Errors in High-Precision Single-Epoch Solutions -A Case Study in Ningbo China. J. Navig. 2015, 68, 999–1017. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Miao, L.; Wang, S.; Shen, J. A constrained LAMBDA method for GPS attitude determination. GPS Solut. 2009, 13, 97–107. [Google Scholar] [CrossRef]
- Lau, L.; Cross, P.; Steen, M. Flight Tests of Error-Bounded Heading and Pitch Determination with Two GPS Receivers. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 388–404. [Google Scholar] [CrossRef]
- Awange, J.L. Environmental Monitoring Using GNSS: Global Navigation Satellite Systems; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Astudillo, J.M.; Lau, L.; Tang, Y.-T.; Moore, T. Analysing the Zenith Tropospheric Delay Estimates in On-line Precise Point Positioning (PPP) Services and PPP Software Packages. Sensors 2018, 18, 580. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mathew, S.S.; Kumar, K. Estimation of zonally resolved edges of the tropical belt using GPS-RO measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2555–2561. [Google Scholar] [CrossRef]
- Hoinka, K.P. Statistics of the Global Tropopause Pressure. Mon. Weather Rev. 1998, 126, 3303–3325. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS-Global Navigation Satellite Systems GPS, GLONASS, GALILEO and More; Springer: Wien, Austria, 2008. [Google Scholar]
- Thayer, G. An improved equation for the radio refractive index of air. Radio Sci. 1974, 9, 803–807. [Google Scholar] [CrossRef]
- Essen, L.; Froome, K.D. The refractive indices and dielectric constants of air and its principal constituents at 24,000 Mc/s. Proc. Phys. Soc. Sect. B 1951, 64, 862. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Thomson, G.W. The Antoine Equation for Vapor Pressure Data. Chem. Rev. 1946, 38, 1–39. [Google Scholar] [CrossRef]
- Gao, Y. GNSS Solutions: Precise Point Positioning and Its Challenges. InsideGNSS 2006, November/December, 16–18. [Google Scholar]
- Heroux, P.; Kouba, J. GPS Precise Point Positioning Using IGS Orbit Products. Phys. Chem. Earth 2001, 26, 573–578. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the effcient and robust analysis of GPS data from large networks. Geophys. Res. 1997, 12, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Tolman, B.W. GPS Precise Absolute Positioning via Kalman Filtering. In Proceedings of the ION GNSS 21st International Technical Meeting of the Satellite Division, Savannah, GA, USA, 16–19 September 2008. [Google Scholar]
- Takasu, T. Real-time PPP with RTKLIB and IGS real-time satellite orbit and clock. In Proceedings of the IGS Workshop 2010, Newcastle upon Tyne, UK, 28 June–2 July 2010. [Google Scholar]











| GNSS Stations | |||||
|---|---|---|---|---|---|
| Code | Lat (°) | Long (°) | Height (m) | Location | Country |
| JPLM | 34.2 | −118.17 | 423.99 | Pasadena | United States |
| GMSD | 30.56 | 131.02 | 142.65 | Nakatane town | Japan |
| TWTF | 24.95 | 121.16 | 203.12 | Taoyuan | Taiwan |
| MKEA | 19.8 | −155.46 | 3754.7 | Mauna Kea | United States |
| CNMR | 15.23 | 145.74 | 64.4 | Saipan | United States |
| DJIG | 11.53 | 42.85 | 711.41 | Djibouti | Djibouti |
| KOUG | 5.09 | −52.64 | 107.25 | Kourou | French Guiana |
| NAUR | −0.55 | 166.93 | 46.3 | Nauru, Yaren District | Nauru |
| SEYG | −4.68 | 55.53 | −37.09 | Pointe Larue | Seychelles |
| XMIS | −10.45 | 105.69 | 261.58 | Christmas Island | Australia |
| ZAMB | −15.46 | 28.31 | 1324.91 | Lusaka | Zambia |
| VACS | −20.3 | 57.5 | 420.4 | Vacoas | Mauritius |
| UFPR | −25.45 | −49.23 | 925.8 | Curitiba | Brazil |
| NNOR | −31.05 | 116.19 | 234.98 | New Norcia | Australia |
| STR1 | −35.31 | 149.01 | 800.03 | Canberra | Australia |
| Radiosonde Stations | ||||
|---|---|---|---|---|
| Code | Lat (°) | Lon (°) | Height (m) | City |
| USM00072376 | 35.23 | −111.82 | 2179 | AZ FLAGSTAFF, USA |
| IRM00040841 | 30.25 | 56.97 | 1748 | KERMAN, IRAN |
| CHM00056778 | 25.01 | 102.68 | 1892 | KUNMING, CHINA |
| CHM00059758 | 20 | 110.25 | 64 | HAIKOU, CHINA |
| INM00043192 | 15.48 | 73.82 | 58.4 | GOA/PANJIM, INDIA |
| RPM00098646 | 10.32 | 123.98 | 23 | MACTAN, THE PHILIPINES |
| MYM00048601 | 5.3 | 100.27 | 3 | PENANG, MALASYA |
| BRM00082099 | 0.05 | −51.07 | 16 | MACAPA (AERO), BRAZIL |
| IDM00097180 | −5.07 | 119.55 | 14 | UJUNG PANDANG, INDONESIA |
| BRM00082917 | −10 | −67.8 | 142 | RIO BRANCO (AERO), BRAZIL |
| BRM00083378 | −15.87 | −47.93 | 1061 | BRASILIA (AERO), BRAZIL |
| BRM00083650 | −20.5 | −29.317 | 5 | TRINDADE (ILHA), BRAZIL |
| MAM00067197 | −25.03 | 46.95 | 8 | TAOLAGNARO, MADAGASCAR |
| BRM00083971 | −30 | −51.18 | 3 | PORTO ALEGRE (AERO), BRAZIL |
| ASM00094910 | −35.16 | 147.46 | 220.7 | WAGGA AMO, AUSTRALIA |
| Station | Latitude [°] | LRT2_RS [km] | LRT2_GNSS [km] | Mean_dlrt2 [km] | STD_DLRT2 [km] | dlrt2_Max [km] | dlrt2_Min [km] | Median_dlrt2 [km] | RMSE [km] |
|---|---|---|---|---|---|---|---|---|---|
| JPLM | 35 | 17.6 | 17.25 | 0.35 | 3.16 | 10.18 | −6.76 | −0.50 | 3.16 |
| GMSD | 30 | 17.9 | 18.79 | −0.89 | 3.36 | 12.42 | −6.66 | −0.31 | 3.37 |
| TWTF | 25 | 18 | 19.53 | −1.53 | 2.56 | 10.52 | −6.00 | −0.10 | 2.57 |
| MKEA | 20 | 18 | 19.72 | −1.72 | 2.36 | 6.30 | −1.74 | 0.21 | 2.09 |
| CNMR | 15 | 18.1 | 19.81 | −1.71 | 1.98 | 10.12 | −2.56 | 0.44 | 1.24 |
| DJIG | 10 | 18.5 | 19.91 | −1.41 | 1.69 | 5.96 | −3.20 | 0.57 | 1.84 |
| KOUG | 5 | 19 | 19.95 | −0.95 | 1.00 | 7.54 | −0.12 | 1.68 | 2.50 |
| NAUR | 0 | 19 | 20.36 | −1.36 | 2.12 | 10.52 | −0.99 | 2.30 | 3.36 |
| SEYG | −5 | 18.9 | 19.70 | −0.80 | 2.30 | 12.42 | −0.12 | 2.08 | 2.99 |
| XMIS | −10 | 18.5 | 17.95 | 0.55 | 2.40 | 6.30 | −1.21 | 1.89 | 3.13 |
| ZAMB | −15 | 18.1 | 19.22 | −1.12 | 2.31 | 9.62 | −2.15 | 1.57 | 3.28 |
| VACS | −20 | 18 | 19.30 | −1.30 | 2.01 | 10.12 | −1.99 | 0.54 | 2.51 |
| UFPR | −25 | 17.8 | 18.59 | −0.79 | 2.00 | 12.42 | −0.88 | 0.34 | 2.00 |
| NNOR | −30 | 17.7 | 17.55 | 0.15 | 2.30 | 7.31 | −4.05 | 0.13 | 2.34 |
| STR1 | −35 | 17.7 | 19.33 | −1.63 | 3.10 | 5.96 | −1.10 | −0.14 | 3.10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendez Astudillo, J.; Lau, L.; Tang, Y.-T.; Moore, T. A Novel Approach for the Determination of the Height of the Tropopause from Ground-Based GNSS Observations. Remote Sens. 2020, 12, 293. https://doi.org/10.3390/rs12020293
Mendez Astudillo J, Lau L, Tang Y-T, Moore T. A Novel Approach for the Determination of the Height of the Tropopause from Ground-Based GNSS Observations. Remote Sensing. 2020; 12(2):293. https://doi.org/10.3390/rs12020293
Chicago/Turabian StyleMendez Astudillo, Jorge, Lawrence Lau, Yu-Ting Tang, and Terry Moore. 2020. "A Novel Approach for the Determination of the Height of the Tropopause from Ground-Based GNSS Observations" Remote Sensing 12, no. 2: 293. https://doi.org/10.3390/rs12020293
APA StyleMendez Astudillo, J., Lau, L., Tang, Y. -T., & Moore, T. (2020). A Novel Approach for the Determination of the Height of the Tropopause from Ground-Based GNSS Observations. Remote Sensing, 12(2), 293. https://doi.org/10.3390/rs12020293