Classification of 3D Point Clouds Using Color Vegetation Indices for Precision Viticulture and Digitizing Applications
Abstract
:1. Introduction
2. Materials and Methods
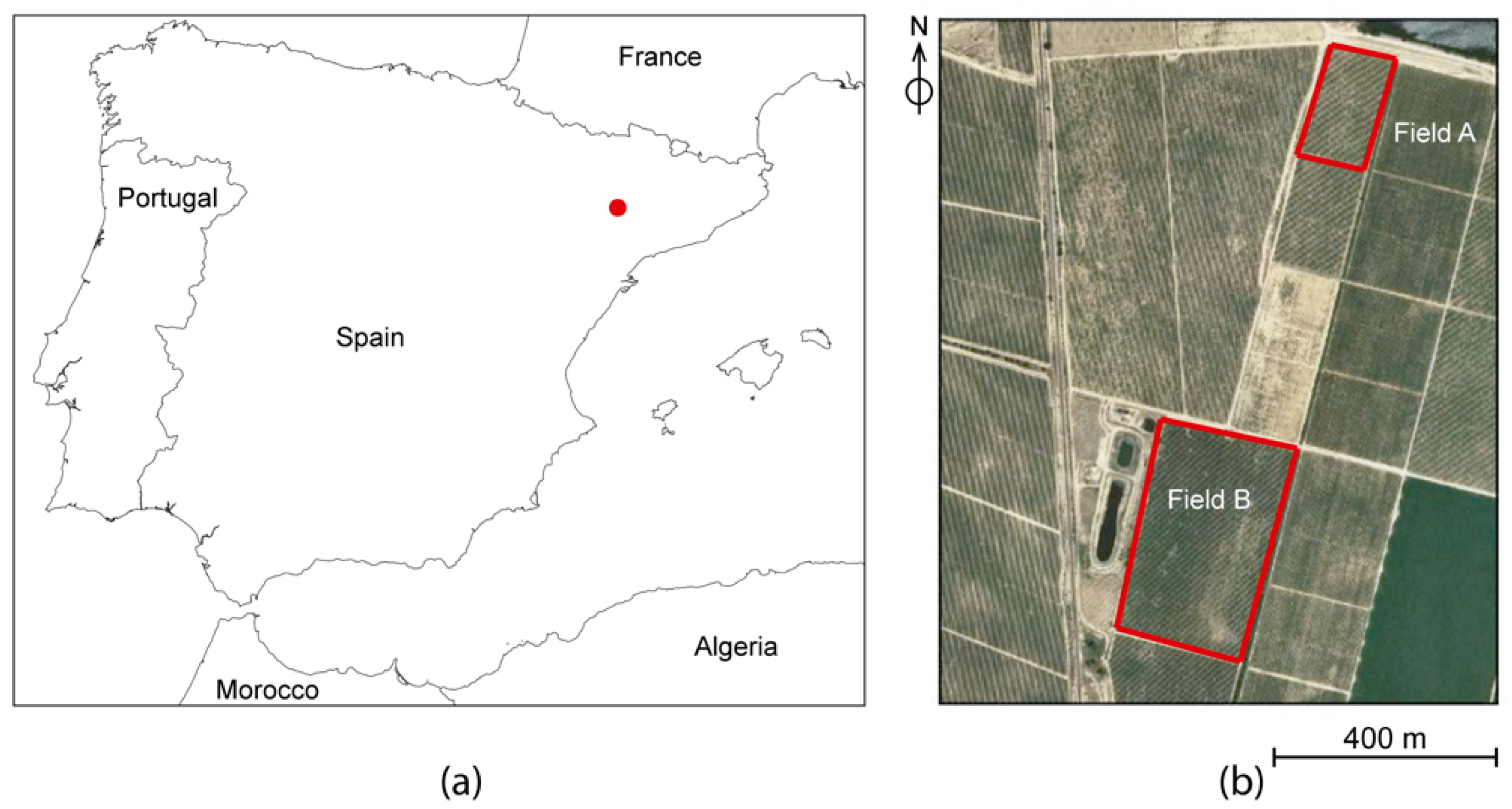
2.1. Study Field and UAV Flights
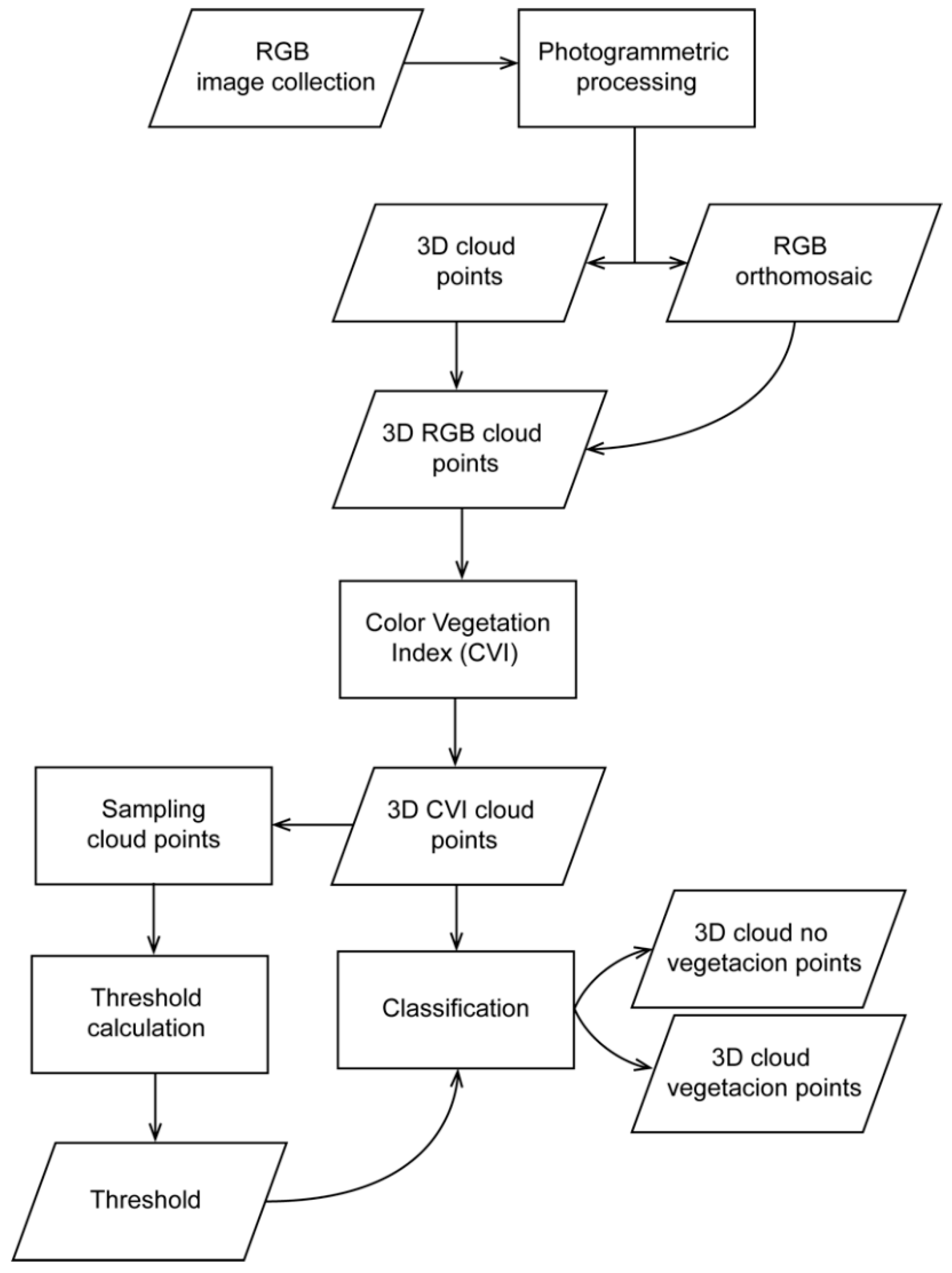
2.2. Point Cloud Classification
2.3. Validation of Vineyard Height Estimation
3. Results
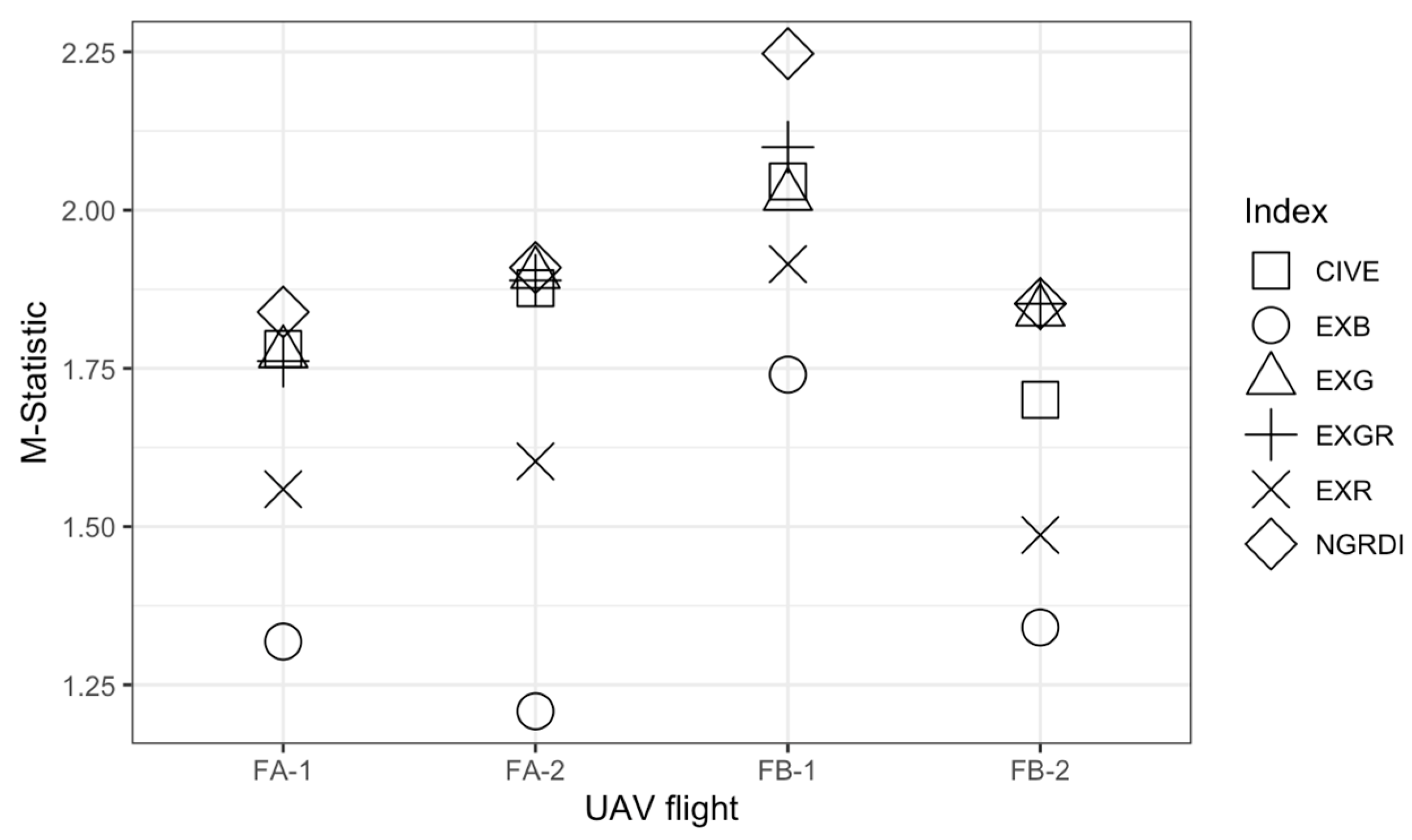
3.1. Color Vegetation Index Selection
3.2. Point Cloud Classification
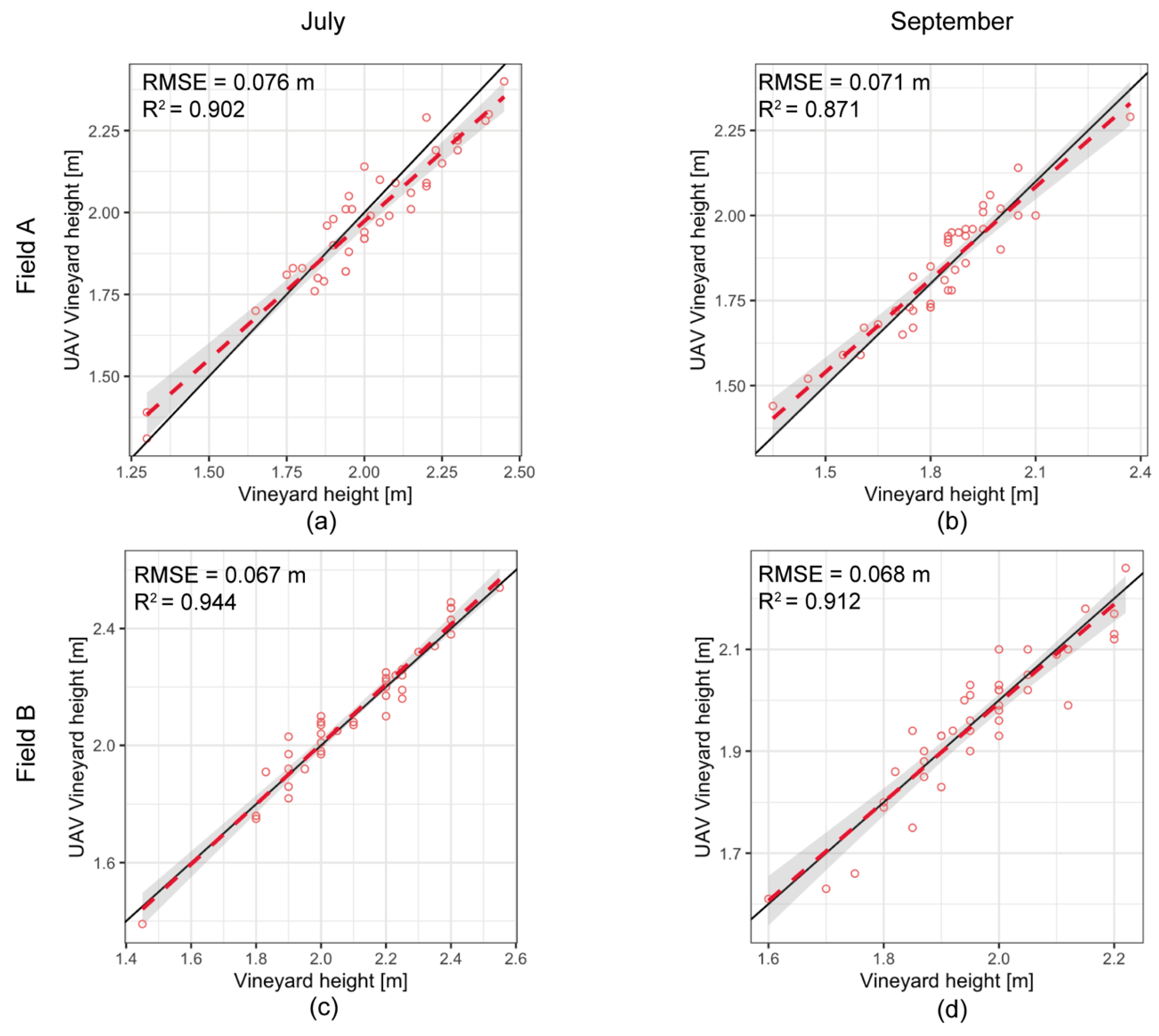
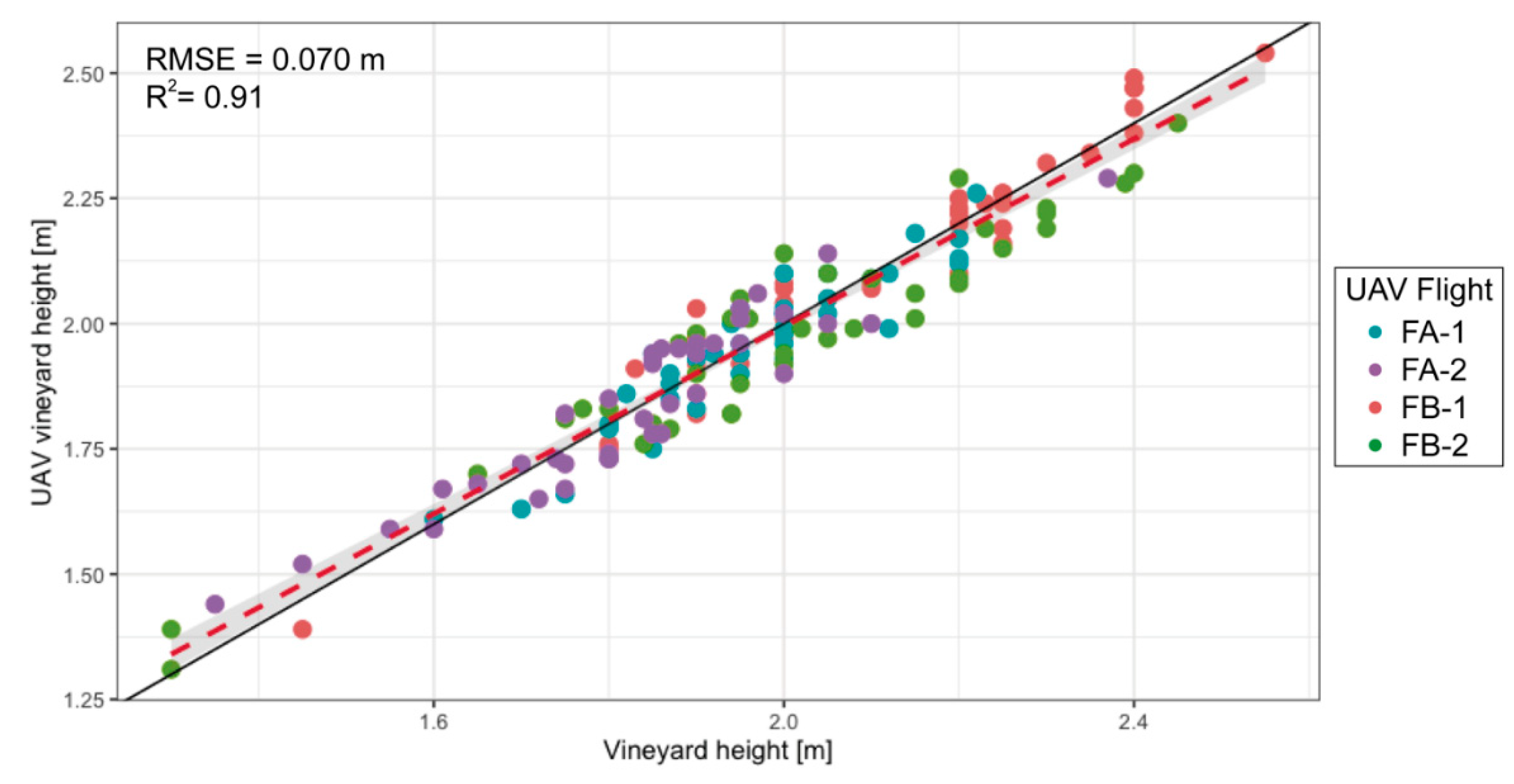
3.3. Vine Height Quantification
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cook, S.E.; Bramley, R.G.V. Precision agriculture—opportunities, benefits and pitfalls of site-specific crop management in Australia. Aust. J. Exp. Agric. 1998, 38, 753–763. [Google Scholar] [CrossRef]
- Whelan, B.M.; McBratney, A.B. The “Null Hypothesis” of Precision Agriculture Management. Precis. Agric. 2000, 2, 265–279. [Google Scholar] [CrossRef]
- Bramley, R.G.V.; Hamilton, R.P. Understanding variability in winegrape production systems. 1. Within vineyard variation in yield over several vintages. Aust. J. Grape Wine Res. 2004, 10, 32–45. [Google Scholar] [CrossRef]
- Schieffer, J.; Dillon, C. The economic and environmental impacts of precision agriculture and interactions with agro-environmental policy. Precis. Agric. 2015, 16, 46–61. [Google Scholar] [CrossRef]
- Bramley, R.; Pearse, B.; Chamberlain, P. Being profitable precisely—A case study of precision viticulture from Margaret River. Aust. N. Zealand Grapegrow. Winemak. Available online: http://www.nwvineyards.net/docs/PVProfitabiltyPaper.pdf (accessed on 1 October 2019).
- Llorens, J.; Gil, E.; Llop, J.; Escolà, A. Variable rate dosing in precision viticulture: Use of electronic devices to improve application efficiency. Crop Prot. 2010, 29, 239–248. [Google Scholar] [CrossRef] [Green Version]
- Ballesteros, R.; Ortega, J.F.; Hernández, D.; Moreno, M.Á. Characterization of Vitis vinifera L. Canopy Using Unmanned Aerial Vehicle-Based Remote Sensing and Photogrammetry Techniques. Am. J. Enol. Vitic. 2015, 66, 120. [Google Scholar] [CrossRef]
- Boomsma, C.R.; Santini, J.B.; West, T.D.; Brewer, J.C.; McIntyre, L.M.; Vyn, T.J. Maize grain yield responses to plant height variability resulting from crop rotation and tillage system in a long-term experiment. Soil Tillage Res. 2010, 106, 227–240. [Google Scholar] [CrossRef]
- Tilly, N.; Hoffmeister, D.; Cao, Q.; Huang, S.; Lenz-Wiedemann, V.; Miao, Y.; Bareth, G. Multitemporal crop surface models: Accurate plant height measurement and biomass estimation with terrestrial laser scanning in paddy rice. J. Appl. Remote Sens. 2014, 8, 1–23. [Google Scholar] [CrossRef]
- Pereira, A.R.; Green, S.; Villa Nova, N.A. Penman–Monteith reference evapotranspiration adapted to estimate irrigated tree transpiration. Agric. Water Manag. 2006, 83, 153–161. [Google Scholar] [CrossRef]
- Cohen, S.; Fuchs, M.; Moreshet, S.; Cohen, Y. The distribution of leaf area, radiation, photosynthesis and transpiration in a Shamouti orange hedgerow orchard. Part II. Photosynthesis, transpiration, and the effect of row shape and direction. Agric. Meteorol. 1987, 40, 145–162. [Google Scholar] [CrossRef]
- Fuchs, M.; Cohen, Y.; Moreshet, S. Determining transpiration from meteorological data and crop characteristics for irrigation management. Irrig. Sci. 1987, 8, 91–99. [Google Scholar] [CrossRef]
- Stanton, C.; Starek, M.J.; Elliott, N.; Brewer, M.; Maeda, M.M.; Chu, T. Unmanned aircraft system-derived crop height and normalized difference vegetation index metrics for sorghum yield and aphid stress assessment. J. Appl. Remote Sens. 2017, 11, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Sio-Se Mardeh, A.; Ahmadi, A.; Poustini, K.; Mohammadi, V. Evaluation of drought resistance indices under various environmental conditions. Field Crop. Res. 2006, 98, 222–229. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Dempewolf, J.; Nagol, J.; Hein, S.; Thiel, C.; Zimmermann, R. Measurement of within-season tree height growth in a mixed forest stand using UAV imagery. Forest. 2017, 8, 231. [Google Scholar] [CrossRef] [Green Version]
- Birdal, A.C.; Avdan, U.; Türk, T. Estimating tree heights with images from an unmanned aerial vehicle. Geomat. Nat. Hazards Risk 2017, 8, 1144–1156. [Google Scholar] [CrossRef] [Green Version]
- Johansen, K.; Raharjo, T.; McCabe, M. Using multi-spectral UAV imagery to extract tree crop structural properties and assess pruning effects. Remote. Sens. 2018, 10, 854. [Google Scholar] [CrossRef] [Green Version]
- Del-Campo-Sanchez, A.; Ballesteros, R.; Hernandez-Lopez, D.; Ortega, J.F.; Moreno, M.A.; Agroforestry and Cartography Precision Research Group. Quantifying the effect of Jacobiasca lybica pest on vineyards with UAVs by combining geometric and computer vision techniques. PLoS ONE 2019, 14, e0215521. [Google Scholar] [CrossRef] [Green Version]
- Lin, G.; Tang, Y.; Zou, X.; Li, J.; Xiong, J. In-field citrus detection and localisation based on RGB-D image analysis. Biosyst. Eng. 2019, 186, 34–44. [Google Scholar] [CrossRef]
- Lin, G.; Tang, Y.; Zou, X.; Xiong, J.; Li, J. Guava detection and pose estimation using a low-cost RGB-D sensor in the field. Sensors 2019, 19, 428. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.-H.; Ehsani, R. A Laser Scanner Based Measurement System for Quantification of Citrus Tree Geometric Characteristics. Appl. Eng. Agric. 2009, 25, 777–788. [Google Scholar] [CrossRef]
- Bongers, F. Methods to assess tropical rain forest canopy structure: An overview. In Tropical Forest Canopies: Ecology and Management: Proceedings of ESF Conference, Oxford University, 12–16 December 1998; Linsenmair, K.E., Davis, A.J., Fiala, B., Speight, M.R., Eds.; Springer: Dordrecht, The Netherlands, 2001; pp. 263–277. [Google Scholar] [CrossRef]
- Côté, J.-F.; Fournier, R.A.; Verstraete, M.M. Canopy Architectural Models in Support of Methods Using Hemispherical Photography. In Hemispherical Photography in Forest Science: Theory, Methods, Applications; Fournier, R.A., Hall, R.J., Eds.; Springer: Dordrecht, The Netherlands, 2017; pp. 253–286. [Google Scholar] [CrossRef]
- Phattaralerphong, J.; Sinoquet, H. A Method for 3D Reconstruction of Tree Canopy Volume from Photographs: Assessment from 3D Digitised Plants. Available online: https://www.researchgate.net/publication/281471747_A_method_for_3D_reconstruction_of_tree_canopy_volume_photographs_assessment_from_3D_digitised_plants (accessed on 1 October 2019).
- Giuliani, R.; Magnanini, E.; Fragassa, C.; Nerozzi, F. Ground monitoring the light–shadow windows of a tree canopy to yield canopy light interception and morphological traits. Plantcell Environ. 2000, 23, 783–796. [Google Scholar] [CrossRef]
- Kise, M.; Zhang, Q. Development of a stereovision sensing system for 3D crop row structure mapping and tractor guidance. Biosyst. Eng. 2008, 101, 191–198. [Google Scholar] [CrossRef]
- Schumann, A.W.; Zaman, Q.U. Software development for real-time ultrasonic mapping of tree canopy size. Comput. Electron. Agric. 2005, 47, 25–40. [Google Scholar] [CrossRef]
- Llorens, J.; Gil, E.; Llop, J. Ultrasonic and LIDAR sensors for electronic canopy characterization in vineyards: Advances to improve pesticide application methods. Sensors 2011, 11, 2177–2194. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rosell, J.R.; Sanz, R. A review of methods and applications of the geometric characterization of tree crops in agricultural activities. Comput. Electron. Agric. 2012, 81, 124–141. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Sarría, A.; Martínez, L.; Velázquez-Martí, B.; Sajdak, M.; Estornell, J.; Recio, J.A. Different methodologies for calculating crown volumes of Platanus hispanica trees using terrestrial laser scanner and a comparison with classical dendrometric measurements. Comput. Electron. Agric. 2013, 90, 176–185. [Google Scholar] [CrossRef]
- Llorens, J.; Gil, E.; Llop, J.; Queraltó, M. Georeferenced LiDAR 3D vine plantation map generation. Sensors 2011, 11, 6237–6256. [Google Scholar] [CrossRef]
- Andújar, D.; Moreno, H.; Bengochea-Guevara, J.M.; de Castro, A.; Ribeiro, A. Aerial imagery or on-ground detection? An economic analysis for vineyard crops. Comput. Electron. Agric. 2019, 157, 351–358. [Google Scholar] [CrossRef]
- Díaz-Varela, R.; de la Rosa, R.; León, L.; Zarco-Tejada, P. High-resolution airborne UAV imagery to assess olive tree crown parameters using 3D photo reconstruction: Application in breeding trials. Remote Sens. 2015, 7, 4213–4232. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Mesas-Carrascosa, F.; Rumbao, I.; Berrocal, J.; Porras, A. Positional quality assessment of orthophotos obtained from sensors onboard multi-rotor UAV platforms. Sensors 2014, 14, 22394–22407. [Google Scholar] [CrossRef] [PubMed]
- Mesas-Carrascosa, F.-J.; Notario García, M.; Meroño de Larriva, J.; García-Ferrer, A. An analysis of the influence of flight parameters in the generation of unmanned aerial vehicle (UAV) orthomosaicks to survey archaeological areas. Sensors 2016, 16, 1838. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sankaran, S.; Khot, L.R.; Espinoza, C.Z.; Jarolmasjed, S.; Sathuvalli, V.R.; Vandemark, G.J.; Miklas, P.N.; Carter, A.H.; Pumphrey, M.O.; Knowles, N.R.; et al. Low-altitude, high-resolution aerial imaging systems for row and field crop phenotyping: A review. Eur. J. Agron. 2015, 70, 112–123. [Google Scholar] [CrossRef]
- Guo, Q.; Su, Y.; Hu, T.; Zhao, X.; Wu, F.; Li, Y.; Liu, J.; Chen, L.; Xu, G.; Lin, G.; et al. An integrated UAV-borne lidar system for 3D habitat mapping in three forest ecosystems across China. Int. J. Remote Sens. 2017, 38, 2954–2972. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; López-Granados, F.; Serrano, N.; Arquero, O.; Peña, J.M. High-Throughput 3-D Monitoring of Agricultural-Tree Plantations with Unmanned Aerial Vehicle (UAV) Technology. PLoS ONE 2015, 10, e0130479. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mesas-Carrascosa, F.-J.; Pérez-Porras, F.; Meroño de Larriva, J.; Mena Frau, C.; Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P.; García-Ferrer, A. Drift correction of lightweight microbolometer thermal sensors on-board unmanned aerial vehicles. Remote Sens. 2018, 10, 615. [Google Scholar] [CrossRef] [Green Version]
- Candiago, S.; Remondino, F.; De Giglio, M.; Dubbini, M.; Gattelli, M. Evaluating multispectral images and vegetation indices for precision farming applications from UAV images. Remote Sens. 2015, 7, 4026–4047. [Google Scholar] [CrossRef] [Green Version]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J. Hyperspectral imaging: A review on UAV-based sensors, data processing and applications for agriculture and forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef] [Green Version]
- Jozkow, G.; Totha, C.; Grejner-Brzezinska, D. UAS Topographic Mapping with Velodyne Lidar Sensor. Available online: https://www.researchgate.net/profile/Grzegorz_Jozkow/publication/307536902_UAS_TOPOGRAPHIC_MAPPING_WITH_VELODYNE_LiDAR_SENSOR/links/57f7ddf608ae280dd0bcc8e8/UAS-TOPOGRAPHIC-MAPPING-WITH-VELODYNE-LiDAR-SENSOR.pdf (accessed on 1 October 2019).
- Nagai, M.; Chen, T.; Shibasaki, R.; Kumagai, H.; Ahmed, A. UAV-Borne 3-D Mapping System by Multisensor Integration. IEEE Trans. Geosci. Remote Sens. 2009, 47, 701–708. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; Peña, J.M.; de Castro, A.I.; López-Granados, F. Multi-temporal mapping of the vegetation fraction in early-season wheat fields using images from UAV. Comput. Electron. Agric. 2014, 103, 104–113. [Google Scholar] [CrossRef]
- Jakubowski, M.; Li, W.; Guo, Q.; Kelly, M. Delineating individual trees from LiDAR data: A comparison of vector-and raster-based segmentation approaches. Remote Sens. 2013, 5, 4163–4186. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Tang, Y.; Zou, X.; Huang, K.; Li, L.; He, Y. High-accuracy multi-camera reconstruction enhanced by adaptive point cloud correction algorithm. Opt. Lasers Eng. 2019, 122, 170–183. [Google Scholar] [CrossRef]
- Tang, Y.; Li, L.; Wang, C.; Chen, M.; Feng, W.; Zou, X.; Huang, K. Real-time detection of surface deformation and strain in recycled aggregate concrete-filled steel tubular columns via four-ocular vision. Robot. Comput. Integr. Manuf. 2019, 59, 36–46. [Google Scholar] [CrossRef]
- Whiteside, T.G.; Boggs, G.S.; Maier, S.W. Comparing object-based and pixel-based classifications for mapping savannas. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 884–893. [Google Scholar] [CrossRef]
- Guo, Q.; Kelly, M.; Gong, P.; Liu, D. An Object-Based Classification Approach in Mapping Tree Mortality Using High Spatial Resolution Imagery. Gisci. Remote Sens. 2007, 44, 24–47. [Google Scholar] [CrossRef]
- Chang, A.; Eo, Y.; Kim, Y.; Kim, Y. Identification of individual tree crowns from LiDAR data using a circle fitting algorithm with local maxima and minima filtering. Remote Sens. Lett. 2013, 4, 29–37. [Google Scholar] [CrossRef]
- Hyyppa, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners. IEEE Trans. Geosci. Remote Sens. 2001, 39, 969–975. [Google Scholar] [CrossRef]
- Kwak, D.-A.; Lee, W.-K.; Lee, J.-H.; Biging, G.S.; Gong, P. Detection of individual trees and estimation of tree height using LiDAR data. J. Res. 2007, 12, 425–434. [Google Scholar] [CrossRef]
- Jing, L.; Hu, B.; Li, J.; Noland, T. Automated Delineation of Individual Tree Crowns from Lidar Data by Multi-Scale Analysis and Segmentation. Photogramm. Eng. Remote Sens. 2012, 78, 1275–1284. [Google Scholar] [CrossRef]
- Jiménez-Brenes, F.M.; López-Granados, F.; de Castro, A.I.; Torres-Sánchez, J.; Serrano, N.; Peña, J.M. Quantifying pruning impacts on olive tree architecture and annual canopy growth by using UAV-based 3D modelling. Plant Methods 2017, 13, 55. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Castro, A.; Jiménez-Brenes, F.; Torres-Sánchez, J.; Peña, J.; Borra-Serrano, I.; López-Granados, F. 3-D characterization of vineyards using a novel UAV imagery-based OBIA procedure for precision viticulture applications. Remote Sens. 2018, 10, 584. [Google Scholar] [CrossRef] [Green Version]
- Suárez, J.C.; Ontiveros, C.; Smith, S.; Snape, S. Use of airborne LiDAR and aerial photography in the estimation of individual tree heights in forestry. Comput. Geosci. 2005, 31, 253–262. [Google Scholar] [CrossRef]
- Lee, H.; Slatton, K.C.; Roth, B.E.; Cropper, W.P. Adaptive clustering of airborne LiDAR data to segment individual tree crowns in managed pine forests. Int. J. Remote Sens. 2010, 31, 117–139. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef] [Green Version]
- De Castro, A.; Torres-Sánchez, J.; Peña, J.; Jiménez-Brenes, F.; Csillik, O.; López-Granados, F. An automatic random forest-OBIA algorithm for early weed mapping between and within crop rows using UAV imagery. Remote Sens. 2018, 10, 285. [Google Scholar] [CrossRef] [Green Version]
- Chang, A.; Jung, J.; Maeda, M.M.; Landivar, J. Crop height monitoring with digital imagery from Unmanned Aerial System (UAS). Comput. Electron. Agric. 2017, 141, 232–237. [Google Scholar] [CrossRef]
- Eckstein, W.; Muenkelt, O. Extracting Objects from Digital Terrain Models. Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/2572/0000/Extracting-objects-from-digital-terrain-models/10.1117/12.216942.short (accessed on 15 October 2019).
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. Isprs J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Axelsson, P. Processing of laser scanner data—Algorithms and applications. Isprs J. Photogramm. Remote Sens. 1999, 54, 138–147. [Google Scholar] [CrossRef]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the World from Internet Photo Collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef] [Green Version]
- Mesas-Carrascosa, F.-J.; Torres-Sánchez, J.; Clavero-Rumbao, I.; García-Ferrer, A.; Peña, J.-M.; Borra-Serrano, I.; López-Granados, F. Assessing optimal flight parameters for generating accurate multispectral orthomosaicks by UAV to support site-specific crop management. Remote Sens. 2015, 7, 12793–12814. [Google Scholar] [CrossRef] [Green Version]
- Mao, W.; Wang, Y.; Wang, Y. Real-time detection of between-row weeds using machine vision. In Proceedings of the 2003 ASAE Annual Meeting, Las Vegas, NV, USA, 27–30 July 2003; p. 1. [Google Scholar]
- Woebbecke, D.; Meyer, G.; Von Bargen, K.; Mortensen, D. Shape features for identifying young weeds using image analysis. Trans. ASAE-Am. Soc. Agric. Eng. 1995, 38, 271–282. [Google Scholar] [CrossRef]
- Meyer, G.E.; Hindman, T.W.; Laksmi, K. Machine Vision Detection Parameters for Plant Species Identification. In Proceedings of the Precision Agriculture and Biological Quality, Boston, MA, USA, 14 January 1999; Volume 3543, pp. 327–335. [Google Scholar]
- Camargo Neto, J. A Combined Statistical-Soft Computing APPROACH for Classification and Mapping Weed Species in Minimum-TILLAGE Systems. 2004. Available online: https://search.proquest.com/openview/c9d042c0b775871973b4494b3233002c/1?cbl=18750&diss=y&pq-origsite=gscholar (accessed on 1 October 2019).
- Kataoka, T.; Kaneko, T.; Okamoto, H.; Hata, S. Crop growth estimation system using machine vision. In Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2003), Kobe, Japan, 20–24 July 2003; Volume1072, pp. b1079–b1083. [Google Scholar]
- Woebbecke, D.M.; Meyer, G.E.; Bargen, K.V.; Mortensen, D.A. Plant Species Identification, Size, and Enumeration Using Machine Vision Techniques on Near-Binary Images. In Proceedings of the Applications in Optical Science and Engineering, Boston, MA, USA, 12 May 1993. [Google Scholar]
- Gée, C.; Bossu, J.; Jones, G.; Truchetet, F. Crop/weed discrimination in perspective agronomic images. Comput. Electron. Agric. 2008, 60, 49–59. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Remer, L.A. Detection of forests using mid-IR reflectance: An application for aerosol studies. IEEE Trans. Geosci. Remote Sens. 1994, 32, 672–683. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray level histogram. IEEE Trans. Syst. Man Cybern. 1979, 9, 66–166. [Google Scholar] [CrossRef] [Green Version]
- Fox, J. The R commander: A basic-statistics graphical user interface to R. J. Stat. Softw. 2005, 14, 1–42. [Google Scholar] [CrossRef] [Green Version]
- Pádua, L.; Marques, P.; Hruška, J.; Adão, T.; Peres, E.; Morais, R.; Sousa, J. Multi-Temporal Vineyard Monitoring through UAV-Based RGB Imagery. Remote Sens. 2018, 10, 1907. [Google Scholar] [CrossRef] [Green Version]
- Caruso, G.; Tozzini, L.; Rallo, G.; Primicerio, J.; Moriondo, M.; Palai, G.; Gucci, R.J.V. Estimating biophysical and geometrical parameters of grapevine canopies (‘Sangiovese’) by an unmanned aerial vehicle (UAV) and VIS-NIR cameras. Vitis 2017, 56, 63–70. [Google Scholar]
- Madec, S.; Baret, F.; de Solan, B.; Thomas, S.; Dutartre, D.; Jezequel, S.; Hemmerlé, M.; Colombeau, G.; Comar, A. High-Throughput Phenotyping of Plant Height: Comparing Unmanned Aerial Vehicles and Ground LiDAR Estimates. Front. Plant Sci. 2017, 8. [Google Scholar] [CrossRef] [Green Version]
- Weiss, M.; Baret, F. Using 3D point clouds derived from UAV RGB imagery to describe vineyard 3D macro-structure. Remote Sens. 2017, 9, 111. [Google Scholar] [CrossRef] [Green Version]
- Comba, L.; Biglia, A.; Ricauda Aimonino, D.; Gay, P. Unsupervised detection of vineyards by 3D point-cloud UAV photogrammetry for precision agriculture. Comput. Electron. Agric. 2018, 155, 84–95. [Google Scholar] [CrossRef]





| Color Index | Equation 1,2 |
|---|---|
| Excess of Blue | |
| Excess of Green | |
| Excess of Red | |
| Excess of Green minus excess Red | |
| Color Index of Vegetation Extraction | |
| Normal Green–Red Difference Index |
| Field | Date | Vegetation [Number Points] | Non-Vegetation [Number Points] |
|---|---|---|---|
| A | July | 28,623 | 28,419 |
| A | September | 26,561 | 27,134 |
| B | July | 29,359 | 29,670 |
| B | September | 31,894 | 31,050 |
| Field—UAV Flight Date | Vegetation | Non-Vegetation | ||||
|---|---|---|---|---|---|---|
| CVI | Mean | SD | Mean | SD | M-Statistic | |
| A-July | EXG | 0.32473 | 0.15767 | 0.0086 | 0.02055 | 1.77385 |
| EXR | 0.04268 | 0.07627 | 0.21251 | 0.03267 | 1.55906 | |
| EXB | −0.14404 | 0.11568 | 0.04441 | 0.02727 | 1.31834 | |
| EXGR | 0.28206 | 0.22842 | −0.20391 | 0.04747 | 1.76143 | |
| CIVE | 18.66369 | 0.0635 | 18.7923 | 0.00873 | 1.78067 | |
| NGRDI | 0.11897 | 0.07445 | −0.07587 | 0.0315 | 1.83896 | |
| A-September | EXG | −0.003 | 0.02099 | 0.21128 | 0.09185 | 1.89905 |
| EXR | 0.21739 | 0.03187 | 0.09187 | 0.04643 | 1.60307 | |
| EXB | 0.05267 | 0.02171 | −0.06466 | 0.0754 | 1.20829 | |
| EXGR | −0.2204 | 0.04935 | 0.11941 | 0.13054 | 1.88897 | |
| CIVE | 18.79697 | 0.00906 | 18.70938 | 0.03758 | 1.87791 | |
| NGRDI | −0.08266 | 0.03015 | 0.06504 | 0.04723 | 1.90891 | |
| B–July | EXG | 0.00393 | 0.01493 | 0.27952 | 0.12134 | 2.02242 |
| EXR | 0.22984 | 0.02356 | 0.08768 | 0.05069 | 1.91471 | |
| EXB | 0.03238 | 0.02103 | −0.1378 | 0.10041 | 1.40132 | |
| EXGR | −0.22591 | 0.03361 | 0.19184 | 0.16538 | 2.09936 | |
| CIVE | 18.7948 | 0.00628 | 18.68292 | 0.04843 | 2.04517 | |
| NGRDI | −0.09258 | 0.02186 | 0.07311 | 0.05187 | 2.24719 | |
| B–September | EXG | 0.0111 | 0.01794 | 0.21911 | 0.09513 | 1.8397 |
| EXR | 0.20106 | 0.01717 | 0.12787 | 0.03742 | 1.34068 | |
| EXB | 0.05303 | 0.01948 | −0.10953 | 0.08987 | 1.4867 | |
| EXGR | −0.18996 | 0.03012 | 0.09123 | 0.12171 | 1.85206 | |
| CIVE | 18.78438 | 0.00726 | 18.7079 | 0.03759 | 1.7051 | |
| NGRDI | −0.06546 | 0.01514 | 0.03075 | 0.03644 | 1.86511 | |
| Factor | F | p |
|---|---|---|
| Field | 3.735 | 0.1075 |
| Flight date | 0.157 | 0.6929 |
| Field: Flight date | 2.784 | 0.1972 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mesas-Carrascosa, F.-J.; de Castro, A.I.; Torres-Sánchez, J.; Triviño-Tarradas, P.; Jiménez-Brenes, F.M.; García-Ferrer, A.; López-Granados, F. Classification of 3D Point Clouds Using Color Vegetation Indices for Precision Viticulture and Digitizing Applications. Remote Sens. 2020, 12, 317. https://doi.org/10.3390/rs12020317
Mesas-Carrascosa F-J, de Castro AI, Torres-Sánchez J, Triviño-Tarradas P, Jiménez-Brenes FM, García-Ferrer A, López-Granados F. Classification of 3D Point Clouds Using Color Vegetation Indices for Precision Viticulture and Digitizing Applications. Remote Sensing. 2020; 12(2):317. https://doi.org/10.3390/rs12020317
Chicago/Turabian StyleMesas-Carrascosa, Francisco-Javier, Ana I. de Castro, Jorge Torres-Sánchez, Paula Triviño-Tarradas, Francisco M. Jiménez-Brenes, Alfonso García-Ferrer, and Francisca López-Granados. 2020. "Classification of 3D Point Clouds Using Color Vegetation Indices for Precision Viticulture and Digitizing Applications" Remote Sensing 12, no. 2: 317. https://doi.org/10.3390/rs12020317
APA StyleMesas-Carrascosa, F.-J., de Castro, A. I., Torres-Sánchez, J., Triviño-Tarradas, P., Jiménez-Brenes, F. M., García-Ferrer, A., & López-Granados, F. (2020). Classification of 3D Point Clouds Using Color Vegetation Indices for Precision Viticulture and Digitizing Applications. Remote Sensing, 12(2), 317. https://doi.org/10.3390/rs12020317








