Next Article in Journal
Integrating Remote Sensing and Street View Images to Quantify Urban Forest Ecosystem Services
Previous Article in Journal
Online Semantic Subspace Learning with Siamese Network for UAV Tracking
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 12
Issue 2
10.3390/rs12020328
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Letter

Greening Trends of Southern China Confirmed by GRACE

by
Le Chang
and
Wenke Sun
*
Key Laboratory of Computational Geodynamics, University of Chinese Academy of Sciences, Beijing 100049, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2020, 12(2), 328; https://doi.org/10.3390/rs12020328
Submission received: 5 December 2019 / Revised: 14 January 2020 / Accepted: 16 January 2020 / Published: 19 January 2020
(This article belongs to the Section Remote Sensing Communications)
Browse Figures
Versions Notes

Abstract

:
As reported by the National Aeronautics and Space Administration (NASA), the world has been greening over the last two decades, with the highest greening occurring in China and India. The increasing vegetation will increase plant tissue accumulation and water storage capacity, and all of these variations will cause mass change. In this study, we found that the mass change related to greening in Southern China could be confirmed by Gravity Recovery and Climate Experiment (GRACE) observations. The mean mass change rate detected by GRACE is 6.7 ± 0.8 mm/yr in equivalent water height during 2003–2016 in our study region. This is consistent with the sum of vegetation tissue, soil water and groundwater change calculated using multi-source data. The vegetation accumulation is approximately 3.8 ± 1.3 mm/yr, which is the major contribution to region mass change. We also found that the change of water storage capacity related to vegetation can be detected by GRACE.

Graphical Abstract

1. Introduction

Vegetation is essential for the subsistence of all life on Earth, as it provides oxygen through photosynthesis and consumes greenhouse gases to slow the rate of global warming. Vegetation change has a large influence on water resources, and this has been highly recognized by the Intergovernmental Panel on Climate Change (IPCC) [1]. Glacial ice is the largest source of freshwater on the Earth. However, it was reported in recent studies that ice sheets and high mountain glaciers are decreasing in area in response to global warming [2,3], which will affect the global trends of freshwater availability [4]. Surface runoff is a major component of the water cycle which affects land water storage change. Wei et al. [5] found that the variation of vegetation cover has a strong effect on the annual global average variation of runoff, and the greater the forest losses, the greater the annual runoff variation. According to Bhanja et al. [6], groundwater storage change is associated with vegetation cover, because groundwater supports the growth of natural vegetation and biota. The vegetation water content (VWC) has also been widely used in agriculture and forestry studies. Chen et al. [7] reported that the change of vegetation and VWC have a positive linear relationship according to moderate-resolution imaging spectroradiometer (MODIS) data and ground-measured VWC data. The increase in vegetation will increase soil infiltration, and the high infiltration rate of water into the soil will improve soil water availability [8]. Zheng [9] found that the change of vegetation can also affect soil erosion, using field survey data from Loess Plateau in 2005. Puigdefábregas [10] found that vegetation affects the sediment fluxes in dry lands using field observations and numerical simulation experiments.
The amount of plants on the Earth has increased over the last two decades, and China and India lead the increase in greening on land according to data from the National Aeronautics and Space Administration (NASA) Earth Observatory. This was first reported by Chen et al. [11] based on MODIS measurements. This greening could be expressed as the increase of the leaf area index (LAI). We found that all these mass changes mentioned above related to vegetation changes can be detected by NASA’s Gravity Recovery and Climate Experiment (GRACE) gravity satellite.
The GRACE satellite mission has been accurately mapping the variations in Earth’s gravity field since its launch in March 2002. The time-varying gravity field solved by GRACE can be used for many applications, for example, in increasing our understanding of climate change and related natural phenomena [12]. The gravity variations studied by GRACE include the mass changes of terrestrial water reserves at large scales (global, regional, and watershed scales) as follows [13,14]: Co-seismic gravitation field variation of large subduction earthquakes [15,16]; global high mountain glacier and polar ice sheet mass change [17,18,19]; global mean sea level budget and sea level change caused by deep ocean warming [20,21]; and sediment accumulation rate change in coastal areas [22]. However, GRACE has not been used to study vegetation mass change.
In the present study, we found that the greening pattern in Southern China is consistent with the mass trend pattern detected by GRACE in Southern China, and we confirmed the greening by GRACE. We analyzed the contribution of each factor and the intra-annual change relationship between vegetation and mass in Southern China using multi-source data.

2. Data and Methods

2.1. Leaf Area Index

In this study, we used the MCD15A2H version 6 /level 4 product [23] and MOD17A3 V055 [24] provided by the NASA Land Processes Distributed Active Center Distribution Server hosted at the U.S. Geological Survey Earth Resources Observation and Science Center (https://e4ftl01.cr.usgs.gov/MOTA/). The MCD15A2H product includes the LAI band from the combination of Terra MODIS and Aqua MODIS with a spatiotemporal resolution of 500 m and 8 d. The MODIS LAI products use a sinusoidal projection to grid the data and divide the world into areas measuring approximately 10° by 10°. We used the MODIS Reprojection Tool to mosaic the grid areas together and resampled to 0.005° and converted to geographical projections with the WGS84 datum; we then converted them to GeoTIFF files.

2.2. GRACE Data

The GRACE satellite affords researchers an important geodetic method by which to detect the gravity changes on the Earth. It has provided monthly global gravity solutions for more than 10 years since it launched in 2002. We used the monthly Release 06 solutions (spherical harmonic coefficients expanded up to degree 60) provided by the Center for Space Research of the University of Texas at Austin (http://icgem.gfz-potsdam.de/series/01_GRACE_monthly/CSR% 20Release%2006). The DDK4 filter was used to process the GRACE coefficients [25]. We added back the degree-1 coefficients according to GRACE Technical Note 13, which were computed based on the data of Sun et al. [26] and replaced the C20s coefficients calculated by the satellite laser-ranging solutions [27]. The glacial isostatic adjustment (GIA) affects all regions of the world, so it should be considered. The GIA effect is corrected by a three-dimensional Geruo13 model [28].

2.3. Precipitation Data

Global precipitation data were obtained from the Global Precipitation Climatology Project (GPCP). GPCP is part of the global energy and water cycle exchange activity operating under the auspices of the world climate research program [29]. The global precipitation product was analyzed by integrating the various satellite datasets of ocean and land and a gauge analysis over land [30]. We used the monthly gridded version 2.3 data from 2003 to 2017, which have 2.5° by 2.5° spatial resolutions on global ocean and land (http://gpcp.umd.edu/).

2.4. Fitting Method

We used the least-squares method to fit the time series to obtain the trend. The semiannual and annual cycles are also considered in the following equation.
y = a + b · x + c · cos ( 2 π T 1 · x + φ 1 ) + d · cos ( 2 π T 2 · x + φ 2 ) + ε
where a is constant; b is the trend; c and d are annual and semiannual amplitudes; x is the time; T1 and T2 are the semiannual and annual cycles; φ 1 and φ 2 are the initial phases, respectively; and ε is the residual error.

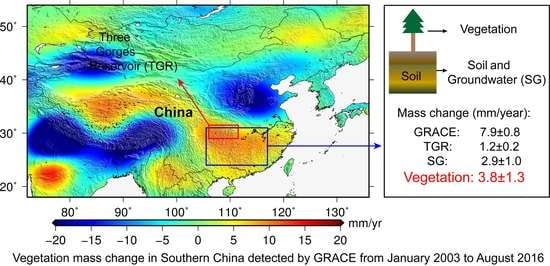
3. Mass Change Trend Related to Greening Detected by GRACE

We calculated the LAI trend for China from January 2003 to August 2016; this is shown in Figure 1a. It can be seen that most parts of Eastern China are greening. According to the research of Chen et al. [11], the greening of Southern China is predominantly a result of tree planting programs. The increase of vegetation will bring many benefits to those areas, such as increased biomass accumulation, soil water, ground water, and VWC, and a decrease of soil erosion and sediment. All of these variations will cause a mass change in those areas, which could be detected by GRACE. The trend of mass change from January 2003 to August 2016 in the study area was calculated using GRACE data, as shown in Figure 1b. There are obvious increasing mass signals in Southern China. The statistical significance analysis of the trends within our study region were analyzed and are shown in the Section 2 of the supporting information files (Figure S1). There are also obvious mass decreasing signals caused by excessive depletion of groundwater in north China [13], as shown in Figure 1b. These large decreasing signals affect our research of vegetation variation. Therefore, we selected the area within the blue box (105.5° E—117° E, 24° N—31° N, with approximately 9.86 × 105 km2) in Figure 1 as our study region, which is not affected by the large decreasing signal.

3.1. Effects of the Three Gorges Reservoir and Lakes on the Mass Signals

The mass signals detected by GRACE comprise the overall effects of all the mass changes in this region, and it also includes signals of water level changes of Three Gorges Reservoir and lakes; these sources of noise should be removed using other data.
Wang et al. [31] reported that the water storage changes in the Three Gorges Reservoir of China could be detected by GRACE. Therefore, the reservoir effect should be taken into account. In our study, we used the in situ data to remove the contribution of water storage changes in the Three Gorges Reservoir from the original GRACE data. Solving this problem requires the knowledge of the water level change and its pattern of change. As shown in Figure 2b, the water level can be obtained from the China Three Gorges Corporation (https://www.ctg.com.cn/), and we converted those data to a monthly mean water level. The reservoir spans approximately 600 km along the Yangtze River, from the dam to Chongqing City (Figure 2a), and the maximum water level can reach 175 m. Hence, it is difficult to determine the shape and depth of the reservoir. To obtain the water-surface changing pattern with increasing water levels, we used Shuttle Radar Topography Mission (STRM) 90 m digital elevation data to determine the boundary of the water surface; these data are provided by the Consultative Group for International Agricultural Research Consortium for Spatial Information (CGIAR-CSI, http://srtm.csi.cgiar.org/). According to the monthly mean water level and digital elevation data of the reservoir, we determined the extent of the water surface every month. Thus, the monthly mean water level of every grid point (90 by 90 m) within our study period was calculated. We then calculated the trend of water level change at every grid point within the reservoir from January 2003 to August 2016, and expanded them to the spherical harmonic coefficients up to degree 60. We then, smoothed them with the DDK4 filter, which is consistent with the GRACE process, as shown in Figure 2c. Therefore, the signals caused by the Three Gorges Reservoir were removed from the GRACE solutions.
According to the study of Yi et al. [32], the water levels of Dongting Lake and Poyang Lake (see Figure S2) increased in our study period, but the data collection period was from 2003 to 2011, which was shorter than our study period. They found that the levels of Dongting Lake and Poyang Lake are increasing at a rate of 0.02 ± 0.07 and 0.02 ± 0.08 m/yr, respectively, and we assumed that the increased rates of both lakes were 0.02 ± 0.08 m/yr from January 2003 to August 2016; this signal was also removed from the GRACE solutions. When this signal was expanded to the spherical harmonic coefficients up to degree 60 and smoothed with DDK4 filter, the contribution of the two lakes is pretty small. As the influence of these lakes is much smaller than that of Three Gorges Reservoir, we do not show it here. The mean mass change rate of Three Gorges Reservoir and the two lakes is 1.2 ± 0.2 mm/yr in our study region. The mass change pattern shown in Figure 2d with the effects of the reservoir and lakes removed.

3.2. Contribution of Each Factor

After removing the noise signals, the mass change in our study region was related to the vegetation variations. The mean mass change rate in our study region was 6.7 ± 0.8 mm/yr from January 2003 to August 2016, as detected by GRACE, which includes the changes of vegetation alone, soil water, and groundwater. The uncertainty of GRACE includes the measurement noise and trend fitting error within a 95% confidence interval. The measurement error was calculated using the method proposed by Wahr et al. [33], and the error of region mean mass trend was obtained by propagating the stokes coefficient errors and trends fitting error.
The annual mass change of carbon in plants was represented by net primary productivity (NPP, the annual accumulation of carbon) which is related to the LAI [34]. Schiesinger and Bernhardt [35] reported that the carbon content of plants is typically approximately 45%–50% (we use the mean value 47.5% ± 2.5%) of the plant tissue (dry). However, the plants contain a lot of water. According to the research of Kramer [36], the water content of herbaceous plants is approximately 80%–90% of the fresh weight, while it is over 50% for woody plants. In our study region, most plants are trees according to the supplementary material of Chen et al. [11], as shown in Figure S3. Thus, the water content of vegetation should be greater than 50%. We used the MOD17A3 data to calculate the mean annual NPP during 2003–2014. As the interannual variation of NPP is very small within our study period, we only show the pattern of NPP in 2014 (Figure 3). The unit of NPP is kg/m2, so we can convert it to equivalent water height using the water density of 1000 kg/m3 (NPP/1000, unit: m). Then, we expanded it to the spherical harmonic coefficients up to degree 60 and smoothed with DDK4 filter. The mean NPP in our study region is approximately 0.6 mm/yr. Therefore, the total contribution of vegetation ( N P P c a r b o n   c o n t e n t   ×   w a t e r   c o n t e n t = 0.6 ( 47.5 ± 2.5 % )   ×   ( ≥ 50 % ) ) will be larger than 2.5 ± 0.2 mm/yr.
The increase of vegetation will improve the soil water storage capacity. We used the mean value of four versions of the Global Land Data Assimilation System (GLDAS) hydrological model from NASA and the Climate Prediction Center (CPC) model from National Oceanic and Atmospheric Administration (NOAA) to study the trend of soil moisture. The method of calculation is described in the supporting information, and the region mean time series of the five models is shown in Figure S4. The regional mean rate is 2.3 ± 1.0 mm/yr.
We also studied groundwater change using the groundwater stress indicators dataset [37] provided by Goethe University, Frankfurt (Germany); the data introduction and data processing methods are described in the supporting information file. The data period was 2001–2010, but we can see that the linear change of groundwater is stable (Figure 4 and Figure S5), so we assumed that the region’s mean groundwater increase rates remained the same until August 2016. The groundwater change rate in our region is approximately 0.6 ± 0.1 mm/yr.
The time series and corresponding linear change rate of each factor are shown in Figure 4. We can see that the vegetation mass change is the main factor in our study region (black line). We summarized the change rates of all factors in Table 1. The total change rate of vegetation alone, soil water, and groundwater is approximately ≥ 5.4 ± 1.0 mm/yr, which is consistent with that of GRACE. After removing the contribution of soil water and groundwater, we found that the contribution of vegetation is approximately 3.8 ± 1.3 mm/yr. The change of vegetation is a relatively large quantity that should not be neglected in Southern China.

4. Discussion

4.1. Challenge of Calculating Mass Change of All Greening Regions

As mentioned above, large mass redistribution on the Earth can be detected by GRACE, since the mass signal detected by GRACE is the combination of all the mass changes, and the signals from adjacent regions affect each other. The gravity signals are complicated in China, as shown in Figure 1b, and the large decrease of groundwater in northern China affects a large part of the region [38]. For instance, the same problem has been encountered in previous studies of Asia high mountain glacial changes, for example, Matsuo and Heki [39] obtained an ice melting rate of −47 Gt/yr, which is overestimated due to the underestimation of Indian groundwater. Jacob et al. [40] obtained the rate −4 ± 20 Gt/yr, which is underestimated due to the neglect of the positive signal from the interior of the Tibetan Plateau. Yi and Sun [41] reported that the glacier change of high mountain Asia is −35.0 ± 5.8 Gt/yr, calculated using a space domain inverse method. They considered the signals of northern India and the interior of the Tibetan Plateau around the glacier. Therefore, the signals around the target are very important to the research results. The exact geographic position and mass change of groundwater in northern China are not available, so it is difficult to remove them from the GRACE data. It then becomes difficult to calculate the mass change of every greening area.

4.2. Relation between Intra-Annual Change of Mass and Vegetation

The LAI data were transferred to the spherical harmonic coefficients up to degree 60, and then converted to grid data that are the same as those of GRACE. The mean value of the same month was calculated as shown in Figure 5, in which the blue line is the mass change and the red line the LAI change. According to Figure 5, it can be seen that the LAI and mass increased from January to July and decreased from August to December. However, the LAI is almost the same in July and August and decreased from September to December. Blanken et al. [42] studied the seasonal water exchange above and within a boreal aspen forest using in situ measurement data. They also obtained the seasonal change of water and LAI, and their results are very similar to those of our study. They used the water balance equation (P = E + D + ∆S, where P is precipitation, E evapotranspiration, D vertical drainage, and ∆S is soil water storage variation) to study water exchange. They found that the value of P–E and soil water storage increase before the LAI reaches its maximum value, and those values start to decrease when the LAI reaches the plateau of maximum value, because evapotranspiration becomes the dominant factor. This is consistent with the mass and LAI change in our study region.
The large seasonal mass change must be related to the rainfall and the seasonal fluctuation of vegetation water content. The mean rainfall of every month in our study region is shown in Figure 5. From January to April, the region rainfall increased much more than the region’s mean mass change. This means that most part of the rainwater ran away due to the low soil water storage capacity, which may be related to the low LAI. As the LAI increases, the water storage capacity increases, and the mass increases. When the rainfall starts to decrease, the water storage capacity still increases with LAI increase in June. Thus, we speculate that vegetation has an important effect on the region’s water storage capacity, and, moreover, that it can be detected by GRACE. According to the research of Nemani and Running [43], the LAI and soil available water capacity are positively correlated, and an LAI change of 1 m2/m2 corresponds to a change of approximately 100 mm of soil available water capacity, which is consistent with our study.

5. Conclusions

In this study, we investigated the detectability of mass change related to variation of vegetation using GRACE data. We used the MODIS LAI dataset to represent vegetation change. The change trends of LAI from January 2003 to August 2016 were large in Southern China. The greening trends in Southern China could be detected by GRACE after removing the effects of the Three Gorges Reservoir and nearby lakes. The mass change in our study region was 6.7 ± 0.8 mm/yr from January 2003 to August 2016 detected by GRACE, and the sum of each factor calculated by multi-source data is consistent with GRACE. Therefore, the greening of Southern China was confirmed by GRACE. The mass change of vegetation is approximately 3.8 ± 1.3 mm/yr calculated by GRACE, and thus, non-negligible in the study of other scientific problems. We also analyzed the intra-annual change of vegetation and mass, and we determined that there is a strong positive correlation between the intra-annual change of mass and vegetation. Furthermore, the change of vegetation could regulate the water storage capacity of land, a feature was also detected by GRACE.

Supplementary Materials

The following are available online at https://www.mdpi.com/2072-4292/12/2/328/s1, Figure S1: Distribution of p-values across our study region, Figure S2: Positions and water levels of two lakes in southeastern China, Figure S3: Map of vegetation classes aggregated from 2007 MCD12C1 product, Figure S4: Time series of regional mean soil water change, Figure S5: Time series of regional mean groundwater change from 2003 to 2010.

Author Contributions

L.C. conceived the original experiment; W.S. helped improve experimental design; L.C. analyzed the data, performed the experiments, and wrote the manuscript; W.S. revised the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported financially by the National Natural Science Foundation of China (41974093, 41774088, 41331066 and 41474059), the Key Research Program of Frontier Sciences Chinese Academy of Sciences (QYZDY-SSWSYS003).

Acknowledgments

We thank three anonymous referees and editor for thorough, thoughtful reviews that helped to improve the paper. The MODIS data were provided by the NASA Land Processes Distributed Active Center Distribution Server hosted at the U.S. Geological Survey Earth Resources Observation and Science Center (https://e4ftl01.cr.usgs.gov/MOTA/). The GRACE data were provided by the Center for Space Research of the University of Texas at Austin (http://icgem.gfz-potsdam.de/series/01_GRACE_monthly/CSR% 20Release%2006). The global precipitation data were obtained from the Global Precipitation Climatology Project (http://gpcp.umd.edu/). The water level data of Three Gorges Reservoir were obtained from the China Three Gorges Corporation (https://www.ctg.com.cn/). STRM data were provided by the Consultative Group for International Agricultural Research Consortium for Spatial Information (CGIAR-CSI, http://srtm.csi.cgiar.org/). The groundwater data were provided by Goethe University, Frankfurt (Germany, http://www.uni-frankfurt.de/77679007/9__GW_Stress_Indicators).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kundzewicz, Z.; Mata, L.; Arnell, N.; Döll, P.; Kabat, P.; Jiménez, B.; Miller, K.; Oki, T.; Sen, Z.; Shiklomanov, I. Freshwater resources and their management. In Climate Change 2007: Impacts, Adaptation and Vulnerability Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Parry, M.L., Canziani, O.F., Palutikof, J.P., van der Linden, P.J., Hanson, C.E., Eds.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
  2. Mackintosh, A.N.; Anderson, B.M.; Lorrey, A.M.; Renwick, J.A.; Frei, P.; Dean, S.M. Regional cooling caused recent New Zealand glacier advances in a period of global warming. Nat. Commun. 2017, 8, 14202. [Google Scholar] [CrossRef] [PubMed]
  3. Stocker, T.; Qin, D.; Plattner, G.; Tignor, M.; Allen, S.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P. IPCC 2013: Summary for Policymakers In Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
  4. Kaser, G.; Großhauser, M.; Marzeion, B. Contribution potential of glaciers to water availability in different climate regimes. Proc. Natl. Acad. Sci. USA 2010, 107, 20223–20227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  5. Wei, X.; Li, Q.; Zhang, M.; Giles-Hansen, K.; Liu, W.; Fan, H.; Wang, Y.; Zhou, G.; Piao, S.; Liu, S. Vegetation cover—Another dominant factor in determining global water resources in forested regions. Glob. Chang. Biol. 2018, 24, 786–795. [Google Scholar] [CrossRef] [PubMed]
  6. Bhanja, S.N.; Malakar, P.; Mukherjee, A.; Rodell, M.; Mitra, P.; Sarkar, S. Using satellite-based vegetation cover as indicator of groundwater storage in natural vegetation areas. Geophys. Res. Lett. 2019, 46, 8082–8092. [Google Scholar] [CrossRef]
  7. Chen, D.; Huang, J.; Jackson, T. Vegetation water content estimation for corn and soybeans using spectral indices derived from MODIS near-and short-wave infrared bands. Remote Sens. Environ. 2005, 98, 225–236. [Google Scholar] [CrossRef]
  8. Dekker, S.C.; Rietkerk, M.; Bierkens, M.F. Coupling microscale vegetation–soil water and macroscale vegetation–precipitation feedbacks in semiarid ecosystems. Glob. Chang. Biol. 2007, 13, 671–678. [Google Scholar] [CrossRef] [Green Version]
  9. Zheng, F.-L. Effect of vegetation changes on soil erosion on the loess plateau. Pedosphere 2006, 16, 420–427. [Google Scholar] [CrossRef]
  10. Puigdefábregas, J. The role of vegetation patterns in structuring runoff and sediment fluxes in drylands. Earth Surf. Process. Landf. 2005, 30, 133–147. [Google Scholar] [CrossRef]
  11. Chen, C.; Park, T.; Wang, X.; Piao, S.; Xu, B.; Chaturvedi, R.K.; Fuchs, R.; Brovkin, V.; Ciais, P.; Fensholt, R. China and India lead in greening of the world through land-use management. Nat. Sustain. 2019, 2, 122–129. [Google Scholar] [CrossRef]
  12. Chen, J. Satellite gravimetry and mass transport in the earth system. Geod. Geodyn. 2019, 10, 402–415. [Google Scholar] [CrossRef]
  13. Feng, W.; Zhong, M.; Lemoine, J.M.; Biancale, R.; Hsu, H.T.; Xia, J. Evaluation of groundwater depletion in north china using the gravity recovery and climate experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
  14. Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  15. Matsuo, K.; Heki, K. Coseismic gravity changes of the 2011 Tohoku-Oki earthquake from satellite gravimetry. Geophys. Res. Lett. 2011, 38, L00G12. [Google Scholar] [CrossRef] [Green Version]
  16. Heki, K.; Matsuo, K. Coseismic gravity changes of the 2010 earthquake in central Chile from satellite gravimetry. Geophys. Res. Lett. 2010, 37, L24306. [Google Scholar] [CrossRef] [Green Version]
  17. Zemp, M.; Huss, M.; Thibert, E.; Eckert, N.; McNabb, R.; Huber, J.; Barandun, M.; Machguth, H.; Nussbaumer, S.; Gärtner-Roer, I. Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016. Nature 2019, 568, 382–386. [Google Scholar] [CrossRef] [PubMed]
  18. Rignot, E.; Mouginot, J.; Scheuchl, B.; van den Broeke, M.; van Wessem, M.J.; Morlighem, M. Four decades of Antarctic ice sheet mass balance from 1979–2017. Proc. Natl. Acad. Sci. USA 2019, 116, 1095–1103. [Google Scholar] [CrossRef] [Green Version]
  19. Li, J.; Chen, J.; Ni, S.; Tang, L.; Hu, X. Long-term and inter-annual mass changes of Patagonia ice field from GRACE. Geod. Geodyn. 2019, 10, 100–109. [Google Scholar] [CrossRef]
  20. Chang, L.; Tang, H.; Wang, Q.; Sun, W. Global thermosteric sea level change contributed by the deep ocean below 2000 m estimated by Argo and CTD data. Earth Planet. Sci. Lett. 2019, 524, 115727. [Google Scholar] [CrossRef]
  21. Yi, S.; Heki, K.; Qian, A. Acceleration in the global mean sea level rise: 2005–2015. Geophys. Res. Lett. 2017, 44, 11905–11913. [Google Scholar] [CrossRef] [Green Version]
  22. Chang, L.; Tang, H.; Yi, S.; Sun, W. The trend and seasonal change of sediment in the East China Sea detected by GRACE. Geophys. Res. Lett. 2019, 46, 1250–1258. [Google Scholar] [CrossRef]
  23. Myneni, R.; Knyazikhin, Y.; Park, T. MCD15A2H MODIS/Terra+ Aqua Leaf Area Index/FPAR 8-day L4 Global 500 m SIN Grid V006. NASA EOSDIS Land Processes DAAC. 2015. Available online: https://modis.gsfc.nasa.gov/data/dataprod/mod15.php (accessed on 5 June 2019).
  24. Running, S.; Mu, Q.; Zhao, M. MOD17A3 MODIS/Terra Net Primary Production Yearly L4 Global 1km SIN Grid V055. NASA EOSDIS Land Processes DAAC. 2011. Available online: https://cmr.earthdata.nasa.gov/search/concepts/C198653829-LPDAAC_ECS.html (accessed on 5 June 2019).
  25. Kusche, J.; Schmidt, R.; Petrovic, S.; Rietbroek, R. Decorrelated GRACE time-variable gravity solutions by GFZ, and their validation using a hydrological model. J. Geod. 2009, 83, 903–913. [Google Scholar] [CrossRef] [Green Version]
  26. Sun, Y.; Riva, R.; Ditmar, P. Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models. J. Geophys. Res. Solid Earth 2016, 121, 8352–8370. [Google Scholar] [CrossRef] [Green Version]
  27. Cheng, M.; Ries, J.C.; Tapley, B.D. Variations of the earth’s figure axis from satellite laser ranging and GRACE. J. Geophys. Res. Solid Earth 2011, 116, B01409. [Google Scholar] [CrossRef] [Green Version]
  28. Geruo, A.; Wahr, J.; Zhong, S. Computations of the viscoelastic response of a 3-D compressible earth to surface loading: An application to glacial isostatic adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar]
  29. Adler, R.; Sapiano, M.; Huffman, G.; Wang, J.-J.; Gu, G.; Bolvin, D.; Chiu, L.; Schneider, U.; Becker, A.; Nelkin, E. The global precipitation climatology project (GPCP) monthly analysis (new version 2.3) and a review of 2017 global precipitation. Atmosphere 2018, 9, 138. [Google Scholar] [CrossRef] [Green Version]
  30. Huffman, G.J.; Adler, R.F.; Arkin, P.; Chang, A.; Ferraro, R.; Gruber, A.; Janowiak, J.; McNab, A.; Rudolf, B.; Schneider, U. The global precipitation climatology project (GPCP) combined precipitation dataset. Bull. Am. Meteorol. Soc. 1997, 78, 5–20. [Google Scholar] [CrossRef]
  31. Wang, X.; de Linage, C.; Famiglietti, J.; Zender, C.S. Gravity recovery and climate experiment (GRACE) detection of water storage changes in the three gorges reservoir of China and comparison with in situ measurements. Water Resour. Res. 2011, 47, W12502. [Google Scholar] [CrossRef]
  32. Yi, S.; Wang, Q.; Sun, W. Basin mass dynamic changes in China from GRACE based on a multibasin inversion method. J. Geophys. Res. Solid Earth 2016, 121, 3782–3803. [Google Scholar] [CrossRef] [Green Version]
  33. Wahr, J.; Swenson, S.; Velicogna, I. Accuracy of GRACE mass estimates. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
  34. Gholz, H.L. Environmental limits on aboveground net primary production, leaf area, and biomass in vegetation zones of the pacific northwest. Ecology 1982, 63, 469–481. [Google Scholar] [CrossRef]
  35. Schlesinger, W.H.; Bernhardt, E.S. Biogeochemistry: An Analysis of Global Change; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
  36. Kramer, P.J. Water Relations of Plants; Academic Press: Cambridge, MA, USA, 1983. [Google Scholar]
  37. Herbert, C.; Döll, P. Global assessment of current and future groundwater stress with a focus on transboundary aquifers. Water Resour. Res. 2019, 55, 4760–4784. [Google Scholar] [CrossRef]
  38. Feng, W.; Shum, C.; Zhong, M.; Pan, Y. Groundwater storage changes in china from satellite gravity: An overview. Remote Sens. 2018, 10, 674. [Google Scholar] [CrossRef] [Green Version]
  39. Matsuo, K.; Heki, K.J.E.; Letters, P.S. Time-variable ice loss in Asian high mountains from satellite gravimetry. Earth Planet. Sci. Lett. 2010, 290, 30–36. [Google Scholar] [CrossRef]
  40. Jacob, T.; Wahr, J.; Pfeffer, W.T.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef] [PubMed]
  41. Yi, S.; Sun, W. Evaluation of glacier changes in high-mountain Asia based on 10 year GRACE RL05 models. J. Geophys. Res. Solid Earth 2014, 119, 2504–2517. [Google Scholar] [CrossRef]
  42. Blanken, P.; Black, T.; Neumann, H.; Den Hartog, G.; Yang, P.; Nesic, Z.; Lee, X. The seasonal water and energy exchange above and within a boreal aspen forest. J. Hydrol. 2001, 245, 118–136. [Google Scholar] [CrossRef]
  43. Nemani, R.R.; Running, S.W. Testing a theoretical climate-soil-leaf area hydrologic equilibrium of forests using satellite data and ecosystem simulation. Agric. For. Meteorol. 1989, 44, 245–260. [Google Scholar] [CrossRef]
Remotesensing 12 00328 g001 550
Figure 1. Trends in patterns of leaf area index (LAI) (a, unit: 10−1m2/m2/yr) and mass (b, unit: mm/yr) in equivalent water heights from January 2003 to August 2016, as measured by moderate-resolution imaging spectroradiometer (MODIS) and Gravity Recovery and Climate Experiment (GRACE). The blue box denotes our study region.
Figure 1. Trends in patterns of leaf area index (LAI) (a, unit: 10−1m2/m2/yr) and mass (b, unit: mm/yr) in equivalent water heights from January 2003 to August 2016, as measured by moderate-resolution imaging spectroradiometer (MODIS) and Gravity Recovery and Climate Experiment (GRACE). The blue box denotes our study region.
Remotesensing 12 00328 g001
Remotesensing 12 00328 g002 550
Figure 2. Influence of the Three Gorges Reservoir: (a) map of the reservoir; (b) the water level change of the reservoir; (c) trend of the water change from January 2003 to August 2016 after truncating the order to 60 and filtering by DDK4; and (d) mass change after removing the effects of reservoir and lakes.
Figure 2. Influence of the Three Gorges Reservoir: (a) map of the reservoir; (b) the water level change of the reservoir; (c) trend of the water change from January 2003 to August 2016 after truncating the order to 60 and filtering by DDK4; and (d) mass change after removing the effects of reservoir and lakes.
Remotesensing 12 00328 g002
Remotesensing 12 00328 g003 550
Figure 3. Net primary productivity in 2014, converted to equivalent water heights.
Figure 3. Net primary productivity in 2014, converted to equivalent water heights.
Remotesensing 12 00328 g003
Remotesensing 12 00328 g004 550
Figure 4. The time series and their corresponding linear change of each factor after a one-year filter. The dotted lines are the extension of trends.
Figure 4. The time series and their corresponding linear change of each factor after a one-year filter. The dotted lines are the extension of trends.
Remotesensing 12 00328 g004
Remotesensing 12 00328 g005 550
Figure 5. Monthly change of LAI, mass, and rainfall in our study region calculated using mean values of the same month. The blue line is the mass change measured by GRACE, the red line is the LAI measured by MODIS, and the yellow bar is the rainfall from Global Precipitation Climatology Project (GPCP).
Figure 5. Monthly change of LAI, mass, and rainfall in our study region calculated using mean values of the same month. The blue line is the mass change measured by GRACE, the red line is the LAI measured by MODIS, and the yellow bar is the rainfall from Global Precipitation Climatology Project (GPCP).
Remotesensing 12 00328 g005
Table
Table 1. Mass change rate of each factor within the study region.
Table 1. Mass change rate of each factor within the study region.
NumberFactorsAmplitude (mm)Rate (mm/yr)
SeasonalInterannual
1GRACE56.153.9+7.9 ± 0.8
2Three Gorges Reservoir, lakes4.52.7+1.2 ± 0.2
3Soil water52.345.8+2.3 ± 1.0
4Groundwater28.45.4+0.6 ± 0.1
5Vegetation estimated by MODIS----≥2.5 ± 0.2
6Vegetation estimated by GRACE (1–2–3–4)----+3.8 ± 1.3
7Mass changed relate to vegetation variation estimated (1–2)60.653.9+6.7 ± 0.8
8Soil water, groundwater, and Vegetation (3 + 4 + 5)----≥5.4 ± 1.0

Share and Cite

MDPI and ACS Style

Chang, L.; Sun, W. Greening Trends of Southern China Confirmed by GRACE. Remote Sens. 2020, 12, 328. https://doi.org/10.3390/rs12020328

AMA Style

Chang L, Sun W. Greening Trends of Southern China Confirmed by GRACE. Remote Sensing. 2020; 12(2):328. https://doi.org/10.3390/rs12020328

Chicago/Turabian Style

Chang, Le, and Wenke Sun. 2020. "Greening Trends of Southern China Confirmed by GRACE" Remote Sensing 12, no. 2: 328. https://doi.org/10.3390/rs12020328

APA Style

Chang, L., & Sun, W. (2020). Greening Trends of Southern China Confirmed by GRACE. Remote Sensing, 12(2), 328. https://doi.org/10.3390/rs12020328

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop