Mitigation of Arctic Tundra Surface Warming by Plant Evapotranspiration: Complete Energy Balance Component Estimation Using LANDSAT Satellite Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Study Sites
2.2. Data Description
2.3. Calculation of Surface Functional Parameters
2.4. Calculation of Net Radiation Components
2.5. Calculation of Surface Energy Balance Components
3. Results
3.1. Mid-Seasonal Radiation Balance
3.2. Mid-Seasonal Surface Functional Parameters and Surface Energy Balance Components
3.3. Radiation Balance during the 2016 Vegetation Season
3.4. Surface Functional Parameters and Surface Energy Balance Components during the 2016 Vegetation Season
4. Discussion
4.1. Radiation Balance
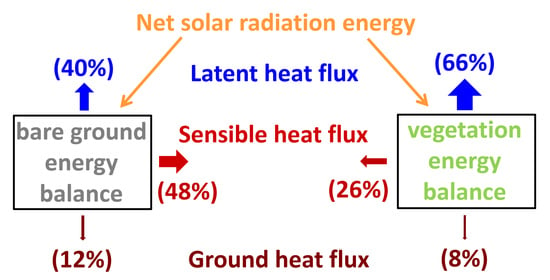
4.2. Surface Energy Balance Components
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Serreze, M.C.; Walsh, J.E.; Chapin, F.S., III; Osterkamp, T.; Dyurgerov, M.; Romanovsky, V.; Oechel, W.C.; Morison, J.; Zhang, T.; Barry, R.G. Observational Evidence of Recent Change in the Northern High-Latitude Environment. Clim. Change 2000, 46, 159–207. [Google Scholar] [CrossRef]
- Chapin, F.S., III; Sturm, M.; Serreze, M.C.; McFadden, J.P.; Key, J.R.; Lloyd, A.H.; McGuire, A.D.; Rupp, T.S.; Lynch, A.H.; Schimel, J.P.; et al. Role of Land-Surface Changes in Arctic Summer Warming. Science 2005, 310, 657–660. [Google Scholar] [CrossRef]
- Serreze, M.C.; Barry, R.G. Processes and impacts of Arctic amplification: A research synthesis. Glob. Planet Change 2011, 77, 85–96. [Google Scholar] [CrossRef]
- Walker, D.A.; Epstein, H.E.; Jia, G.J.; Balser, A.; Copass, C.; Edwards, E.J.; Gould, W.A.; Hollingsworth, J.; Knudson, J.; Maier, H.A.; et al. Phytomass, LAI, and NDVI in northern Alaska: Relationships to summer warmth, soil pH, plant functional types, and extrapolation to the circumpolar Arctic. J. Geophys. Res. Atmos. 2003, 108, 8169. [Google Scholar] [CrossRef]
- Vegetation and the Atmosphere; Monteith, J.L. (Ed.) Principles; Academic Press Inc.: London, UK, 1975; Volume 1, pp. 13–150. [Google Scholar]
- Gates, D.M. Biophysical Ecology; Dover Publications Inc.: Mineola, NY, USA, 1980; pp. 12–54. [Google Scholar]
- Monteith, J.L.; Unsworth, M. Principles of Environmental Physics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1990; pp. 177–217. [Google Scholar]
- Jones, H.G. Plants and Microclimate, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992; pp. 106–131. [Google Scholar]
- Pokorný, J. Dissipation of solar energy in landscape—Controlled by management of water and vegetation. Renew. Energ. 2001, 24, 641–645. [Google Scholar] [CrossRef]
- Brom, J.; Pokorný, J. Temperature and humidity characteristics of two willow stands, a peaty meadow and a drained pasture and their impact on landscape functioning. Boreal Environ. Res. 2009, 14, 389–403. [Google Scholar]
- Hesslerová, P.; Pokorný, J.; Brom, J.; Rejšková-Procházková, A. Daily dynamics of radiation surface temperature of different land cover types in a temperate cultural landscape: Consequences for the local climate. Ecol. Eng. 2013, 54, 145–154. [Google Scholar] [CrossRef]
- Oke, T.R. The heat island of the urban boundary layer: Characteristics, causes and effects. In Wind Climate in Cities; Cermak, J.E., Davenport, A.G., Plate, E.J., Domingos, X.V., Eds.; Springer: Dordrecht, The Netherlands, 1995; pp. 81–107. [Google Scholar]
- Armson, D.; Stringer, P.; Ennos, A.R. The effect of tree shade and grass on surface and globe temperatures in an urban area. Urban For. Urban Green. 2012, 11, 245–255. [Google Scholar] [CrossRef]
- Rahman, M.A.; Armson, D.; Ennos, A.R. A comparison of the growth and cooling effectiveness of five commonly planted urban tree species. Urban Ecosyst. 2015, 18, 371–389. [Google Scholar] [CrossRef]
- Mariani, L.; Parisi, S.G.; Cola, G.; Lafortezza, R.; Colangelo, G.; Sanesi, G. Climatological analysis of the mitigating effect of vegetation on the urban heat island of Milan, Italy. Sci. Total Environ. 2016, 569–570, 762–773. [Google Scholar] [CrossRef] [PubMed]
- Pielke, R.A.; Avissar, R. Influence of landscape structure on local and regional climate. Landsc. Ecol. 1990, 4, 133–155. [Google Scholar] [CrossRef]
- Kalnay, E.; Cai, M. Impact of urbanization and land-use change on climate. Nature 2003, 423, 528–531. [Google Scholar] [CrossRef] [PubMed]
- Makarieva, A.M.; Gorshkov, V.G. The Biotic Pump: Condensation, atmospheric dynamics and climate. Int. J. Water 2010, 5, 365–385. [Google Scholar] [CrossRef]
- Hesslerová, P.; Pokorný, J. Forest clearing, water loss, and land surface heating as development costs. Int. J. Water 2010, 5, 401–418. [Google Scholar] [CrossRef]
- Nedbal, V.; Brom, J. Impact of highway construction on land surface energy balance and local climate derived from LANDSAT satellite data. Sci. Total Environ. 2018, 633, 658–667. [Google Scholar] [CrossRef] [PubMed]
- Westermann, S.; Langer, M.; Boike, J. Spatial and temporal variations of summer surface temperatures of high-arctic tundra on Svalbard—Implications for MODIS LST based permafrost monitoring. Remote Sens. Environ. 2011, 115, 908–922. [Google Scholar] [CrossRef]
- Hachem, S.; Duguay, C.R.; Allard, M. Comparison of MODIS-derived land surface temperatures with ground surface and air temperature measurements in continuous permafrost terrain. Cryosphere 2012, 6, 51–69. [Google Scholar] [CrossRef] [Green Version]
- Vourlitis, G.L.; Oechel, W.C. Eddy covariance measurements of CO2 and energy fluxes of an Alaskan tussock tundra ecosystem. Ecology 1999, 80, 686–701. [Google Scholar] [CrossRef]
- Westermann, S.; Lüers, J.; Langer, M.; Piel, K.; Boike, J. The annual surface energy budget of a high-arctic permafrost site on Svalbard, Norway. Cryosphere 2009, 3, 245–263. [Google Scholar] [CrossRef] [Green Version]
- Lüers, J.; Bareiss, J. Direct near-surface measurements of sensible heat fluxes in the Arctic tundra applying eddy covariance and laser scintillometry—The Arctic Turbulence Experiment 2006 on Svalbard (ARCTEX-2006). Theor. Appl. Climatol. 2011, 105, 387–402. [Google Scholar] [CrossRef]
- Brázdil, R.; Chmal, H.; Kida, J.; Klementowski, J.; Konečný, M.; Pereyma, J.; Piasecki, J.; Prošek, P.; Sobik, M.; Szczepankiewicz-Szmyrka, A. Results of Investigation of the Geographical Research Expedition Spitsbergen 1985; University of J.E. Purkyně: Brno, Czech Republic, 1988; pp. 152–178. [Google Scholar]
- McFadden, J.P.; Chapin, F.S., III; Hollinger, D.Y. Subgrid-scale variability in the surface energy balance of arctic tundra. J. Geophys. Res. Atmos. 1988, 103, 28947–28961. [Google Scholar] [CrossRef]
- Lloyd, C.R.; Harding, R.J.; Friborg, T.; Aurela, M. Surface fluxes of heat and water vapour from sites in the European Arctic. Theor. Appl. Climatol. 2001, 70, 9–33. [Google Scholar] [CrossRef]
- Johansen, B.; Karlsen, S.; Tømmervik, H. Vegetation mapping of Svalbard utilising Landsat TM/ETM data. Polar Rec. 2012, 48, 47–63. [Google Scholar] [CrossRef]
- Nordli, Ø.; Przybylak, R.; Ogilvie, A.E.J.; Isaksen, K. Long-term temperature trends and variability on Spitsbergen: The extended Svalbard Airport temperature series, 1898–2012. Polar Res. 2014, 33, 21349. [Google Scholar] [CrossRef] [Green Version]
- Láska, K.; Witoszová, D.; Prošek, P. Weather patterns of the coastal zone of Petuniabukta, central Spitsbergen in the period 2008–2010. Pol. Polar Res. 2012, 33, 297–318. [Google Scholar] [CrossRef]
- USGS. LANDSAT 8 (L8) Data Users Handbook; Department of the Interior U.S. Geological Survey: Sioux Falls, SD, USA, 2016; pp. 9–98.
- USGS. Product Guide. LANDSAT 8 Surface Reflectance Code (LaSRC) Product; Department of the Interior U.S. Geological Survey: Sioux Fall, SD, USA, 2018; pp. 13–27.
- Barsi, J.A.; Schott, J.R.; Palluconi, F.D.; Hook, S.J. Validation of a Web-Based Atmospheric Correction Tool for Single Thermal Band Instruments. Proc. SPIE 2005, 58820. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- NASA. Atmospheric Correction Parameter Calculator. 2019. Available online: https://atmcorr.gsfc.nasa.gov/ (accessed on 5 September 2020).
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Paolini, L. Land surface temperature retrieval from LANDSAT TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Arya, S.P. Introduction to Micrometeorology, 2nd ed.; Academic Press: London, UK, 2001; pp. 28–45. [Google Scholar]
- Kumar, L.; Skidmore, A.K.; Knowles, E. Modelling topographic variation in solar radiation in a GIS environment. Int. J. Geogr. Inf. Sci. 1997, 11, 475–497. [Google Scholar] [CrossRef]
- Tasumi, M.; Allen, R.G.; Trezza, R. At-Surface Reflectance and Albedo from Satellite for Operational Calculation of Land Surface Energy Balance. J. Hydrol. Eng. 2008, 13, 51–63. [Google Scholar] [CrossRef]
- Brutsaert, W. Evapotranspiration into the Atmosphere. Theory, History and Applications; Kluwer Academic publishers: Dordrecht, The Netherlands, 1982; pp. 138–141. [Google Scholar]
- Buck, A.L. New Equations for Computing Vapor Pressure and Enhancement Factor. J. Appl. Meteor. 1981, 20, 1527–1532. [Google Scholar] [CrossRef] [Green Version]
- Bastiaanssen, W.G.M. SEBAL-based sensible and latent heat fluxes in the irrigated Gediz Basin, Turkey. J. Hydrol. 2000, 229, 87–100. [Google Scholar] [CrossRef]
- Lhomme, J.-P.; Elguero, E. Examination of evaporative fraction diurnal behaviour using a soil-vegetation model coupled with a mixed-layer model. Hydrol. Earth Syst. Sci. 1999, 3, 259–270. [Google Scholar] [CrossRef]
- Suleiman, A.; Crago, R. Hourly and Daytime Evapotranspiration from Grassland Using Radiometric Surface Temperatures. Agron. J. 2004, 96, 384–390. [Google Scholar] [CrossRef]
- Harding, R.J.; Lloyd, C.R. Fluxes of Water and Energy from Three High Latitude Tundra Sites in Svalbard. Hydrol. Res. 1998, 29, 267–284. [Google Scholar] [CrossRef]
- Hrbáček, F.; Kňažková, M.; Nývlt, D.; Láska, K.; Mueller, C.W.; Ondruch, J. Active layer monitoring at CALM-S site near J.G.Mendel Station, James Ross Island, eastern Antarctic Peninsula. Sci. Total Environ. 2017, 601–602, 987–997. [Google Scholar] [CrossRef]
- Rott, H.; Obleitner, F. The Energy Balance of Dry Tundra in West Greenland. Arct. Antarct. Alp. Res. 1992, 24, 352–362. [Google Scholar] [CrossRef]
- Migała, K.; Wojtuń, B.; Szymański, W.; Muskała, P. Soil moisture and temperature variation under different types of tundra vegetation during the growing season: A case study from the Fuglebekken catchment, SW Spitsbergen. Catena 2014, 116, 10–18. [Google Scholar] [CrossRef]
- Ambrožová, K.; Hrbáček, F.; Láska, K. The Summer Surface Energy Budget of the Ice-Free Area of Northern James Ross Island and Its Impact on the Ground Thermal Regime. Atmosphere 2020, 11, 877. [Google Scholar] [CrossRef]
- Epstein, H.E.; Raynolds, M.K.; Walker, D.A.; Bhatt, U.S.; Tucker, C.J.; Pinzon, J.E. Dynamics of aboveground phytomass of the circumpolar Arctic tundra during the past three decades. Environ. Res. Lett. 2012, 7, 015506. [Google Scholar] [CrossRef]
- Johansen, B.; Tømmervik, H. The relationship between phytomass, NDVI and vegetation communities on Svalbard. Int. J. Appl. Earth Obs. Geoinf. 2014, 27, 20–30. [Google Scholar] [CrossRef]
- Larcher, W. Physiological Plant Ecology, 4th ed.; Springer Verlag: Berlin, Germany, 2003. [Google Scholar]
- Kirkham, M.B. Principles of Soil and Plant Water Relations; Academic Press: Amsterdam, The Netherlands, 2004; pp. 67–240. [Google Scholar]
- Jaksic, V.; Kiely, G.; Albertson, J.; Oren, R.; Katul, G.; Leahy, P.; Byrne, K.A. Net ecosystem exchange of grassland in contrasting wet and dry years. Agric. For. Meteor. 2006, 139, 323–334. [Google Scholar] [CrossRef]
- Wang, K.; Wang, P.; Li, Z.; Cribb, M.; Sparrow, M. A simple method to estimate actual evapotranspiration from a combination of net radiation, vegetation index, and temperature. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Arora, V. Modeling Vegetation as a Dynamic Component in Soil-Vegetation-Atmosphere Transfer Schemes and Hydrological Models. Rev. Geophys. 2002, 40, 3-1–3-26. [Google Scholar] [CrossRef] [Green Version]
- Opała-Owczarek, M.; Pirożnikow, E.; Owczarek, P.; Szymański, W.; Luks, B.; Kępski, D.; Szymanowski, M.; Wojtuń, B.; Migała, K. The influence of abiotic factors on the growth of two vascular plant species (Saxifraga oppositifolia and Salix polaris) in the High Arctic. Catena 2018, 163, 219–232. [Google Scholar] [CrossRef]
- Zeng, Z.; Piao, S.; Li, L.Z.X.; Wang, T.; Ciais, P.; Lian, X.; Yang, Y.; Mao, J.; Shi, X.; Myneni, R.B. Impact of Earth Greening on the Terrestrial Water Cycle. J. Climate 2018, 31, 2633–2650. [Google Scholar] [CrossRef]





| Satellite Image Acquisition Time | Air Temperature (°C) | Air Relative Humidity (%) | Wind Speed (ms−1) | Primary Incident Shortwave Radiation (Wm−2) |
|---|---|---|---|---|
| 15 July 2014 | 10.7 | 69.4 | 3.2 | 517.4 |
| 9 July 2015 | 11.0 | 52.4 | 5.4 | 529.5 |
| 14 June 2016 | 7.5 | 55.2 | 3.6 | 560.8 |
| 2 July 2016 | 12.6 | 67.8 | 6.2 | 538.9 |
| 9 July 2016 | 11.3 | 49.7 | 4.6 | 530.6 |
| 27 July 2016 | 9.6 | 73.1 | 2.9 | 495.5 |
| 10 August 2016 | 5.5 | 73.3 | 8.1 | 378.2 |
| 10 July 2017 | 8.8 | 72.9 | 4.2 | 552.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nedbal, V.; Láska, K.; Brom, J. Mitigation of Arctic Tundra Surface Warming by Plant Evapotranspiration: Complete Energy Balance Component Estimation Using LANDSAT Satellite Data. Remote Sens. 2020, 12, 3395. https://doi.org/10.3390/rs12203395
Nedbal V, Láska K, Brom J. Mitigation of Arctic Tundra Surface Warming by Plant Evapotranspiration: Complete Energy Balance Component Estimation Using LANDSAT Satellite Data. Remote Sensing. 2020; 12(20):3395. https://doi.org/10.3390/rs12203395
Chicago/Turabian StyleNedbal, Václav, Kamil Láska, and Jakub Brom. 2020. "Mitigation of Arctic Tundra Surface Warming by Plant Evapotranspiration: Complete Energy Balance Component Estimation Using LANDSAT Satellite Data" Remote Sensing 12, no. 20: 3395. https://doi.org/10.3390/rs12203395
APA StyleNedbal, V., Láska, K., & Brom, J. (2020). Mitigation of Arctic Tundra Surface Warming by Plant Evapotranspiration: Complete Energy Balance Component Estimation Using LANDSAT Satellite Data. Remote Sensing, 12(20), 3395. https://doi.org/10.3390/rs12203395