Effects of the High-Order Ionospheric Delay on GPS-Based Tropospheric Parameter Estimations in Turkey
Abstract
1. Introduction
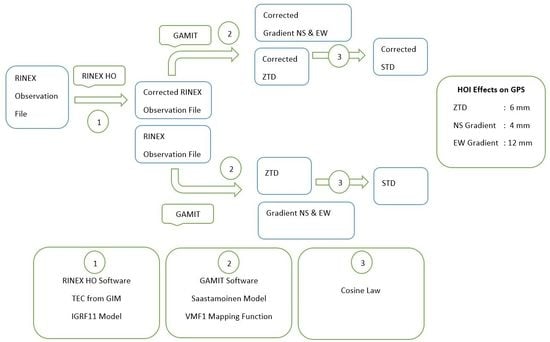
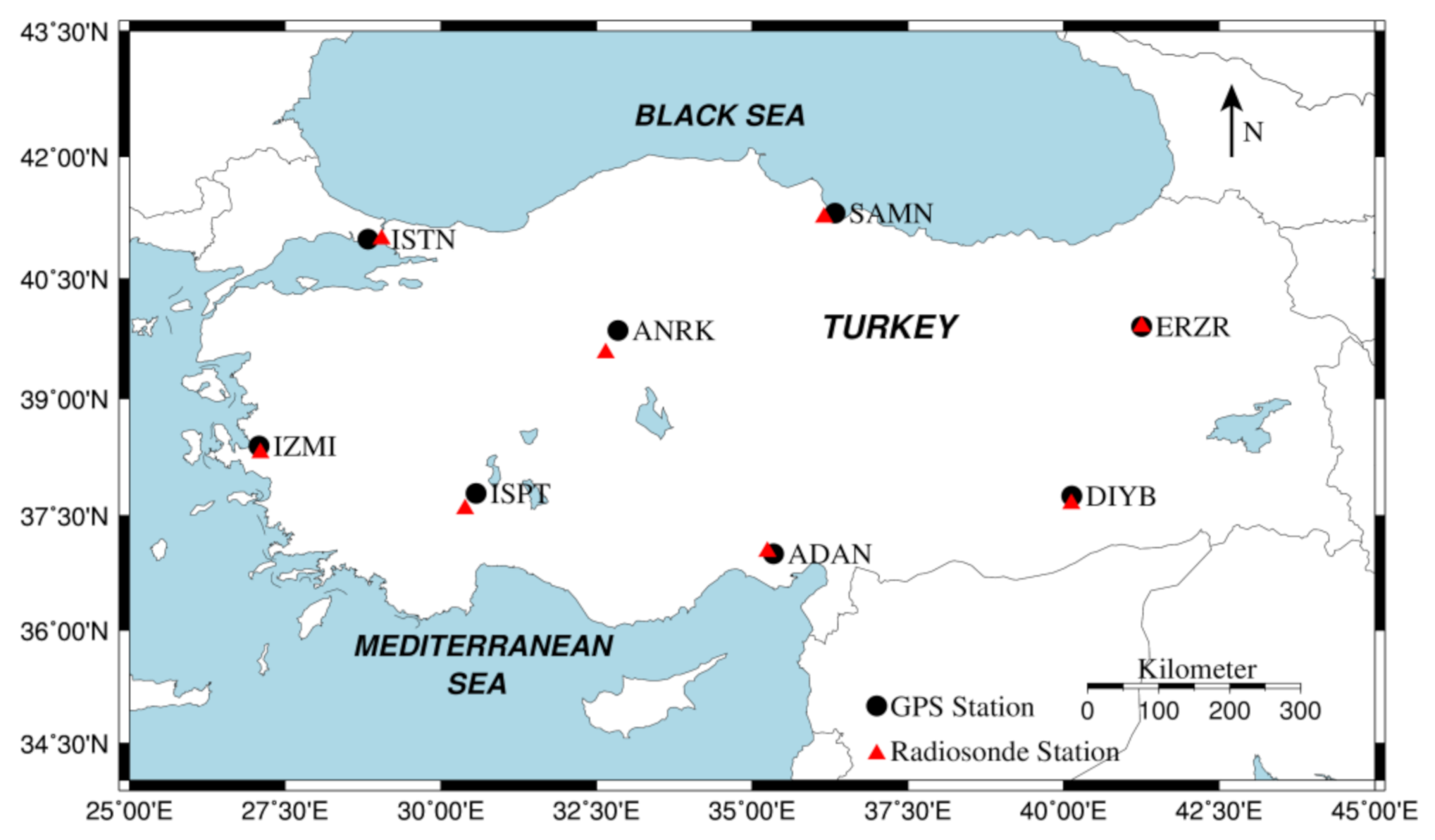
2. GPS Data Analysis and Methods
3. Results and Discussion
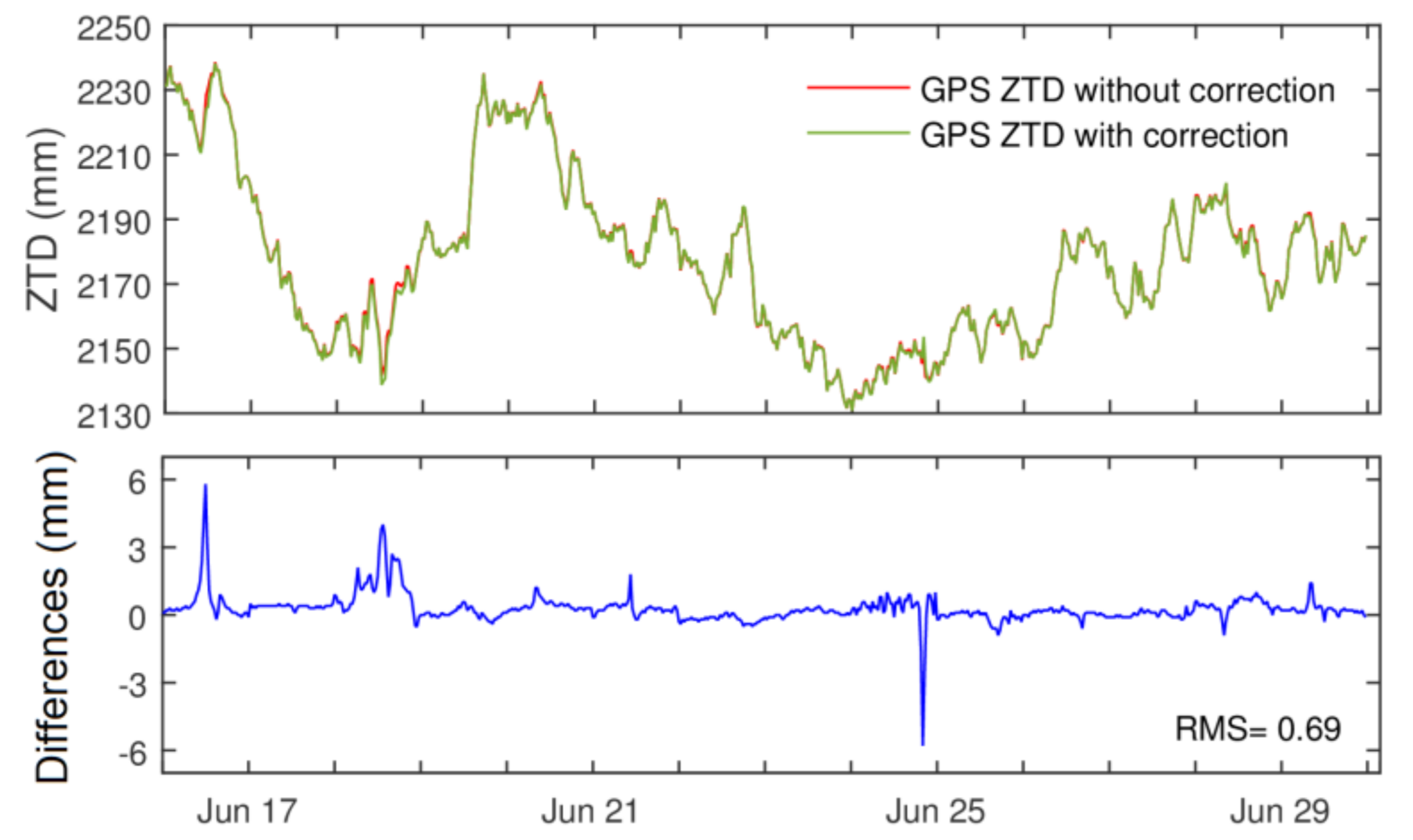
3.1. HOI Effects on GPS ZTD and Gradients
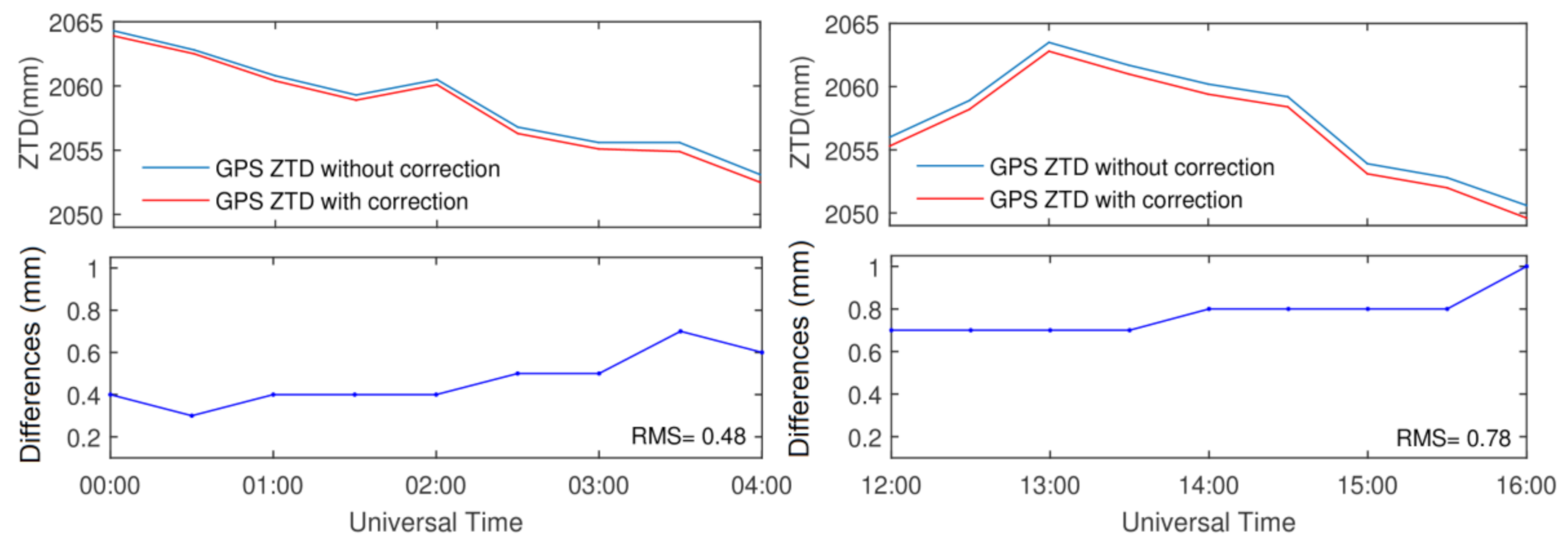
3.2. HOI Effects During the Daytime and Nighttime
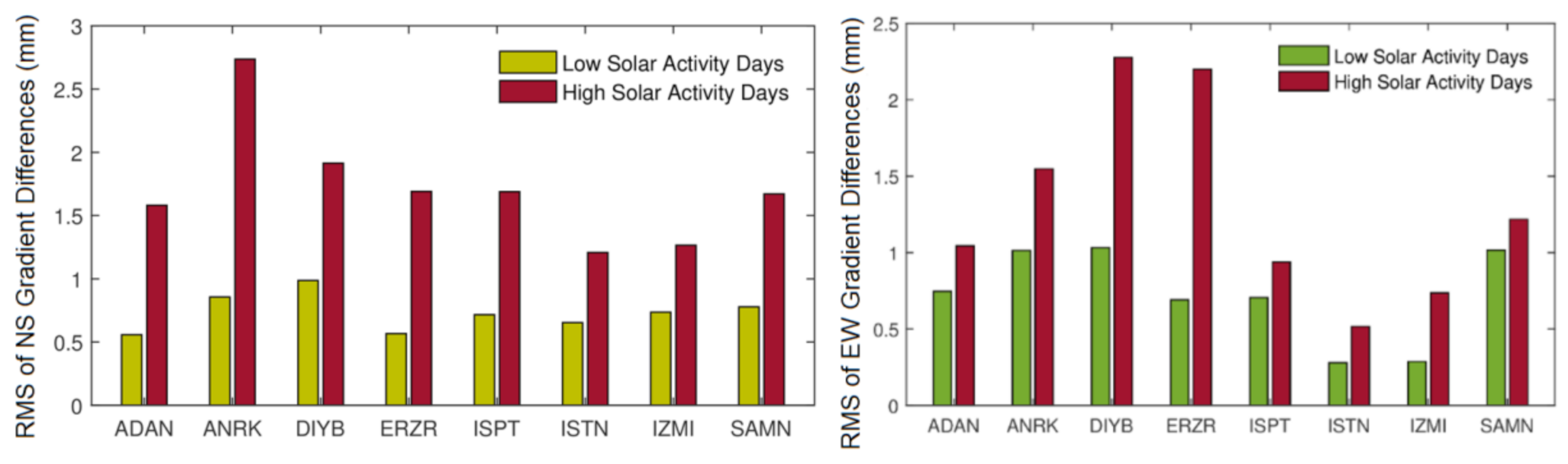
3.3. HOI Effects during the High and Low Solar Activities
3.4. HOI Effect on Slant Tropospheric Delay
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. Space Phys. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water. J. Appl. Meteorol. Climatol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Businger, S.; Chiswell, S.R.; Bevis, M.; Duan, J.; Anthes, R.A.; Rocken, C.; Ware, R.; Exner, M.; Vanhove, T.; Solheim, F.S. The Promise of GPS in Atmospheric Monitoring. Bull. Am. Meteorol. Soc. 1996, 77, 5–18. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, K.; Rohm, W.; Choy, S.; Norman, R.; Wang, C.S. Real-time retrieval of precipitable water vapor from GPS precise point positioning. J. Geophys. Res. Atmos. 2014, 119, 10044–10057. [Google Scholar] [CrossRef]
- Gurbuz, G.; Jin, S. Long-time variations of precipitable water vapour estimated from GPS, MODIS and radiosonde observations in Turkey. Int. J. Clim. 2017, 37, 5170–5180. [Google Scholar] [CrossRef]
- Rocken, C.; van Hove, T.; Johnson, J.; Solheim, F.; Ware, R.; Bevis, M.; Chiswell, S.; Businger, S. GPS/STORM—GPS Sensing of Atmospheric Water Vapor for Meteorology. J. Atmos. Ocean. Technol. 1995, 12, 468–478. [Google Scholar] [CrossRef]
- Jin, S.; Park, J.U.; Cho, J.H.; Park, P.H. Seasonal variability of GPS-derived zenith tropospheric delay (1994–2006) and climate implications. J. Geophys. Res. Space Phys. 2007, 112. [Google Scholar] [CrossRef]
- Jin, S.; Li, Z.; Cho, J. Integrated Water Vapor Field and Multiscale Variations over China from GPS Measurements. J. Appl. Meteorol. Clim. 2008, 47, 3008–3015. [Google Scholar] [CrossRef]
- Jin, S.; Luo, O. Variability and Climatology of PWV from Global 13-Year GPS Observations. IEEE Trans. Geosci. Remote. Sens. 2009, 47, 1918–1924. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orús, R. Second-order ionospheric term in GPS: Implementation and impact on geodetic estimates. J. Geophys. Res. Space Phys. 2007, 112. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Aragón-Ángel, À.; Defraigne, P.; Bergeot, N.; Prieto-Cerdeira, R.; García-Rigo, A. Distribution and mitigation of higher-order ionospheric effects on precise GNSS processing. J. Geophys. Res. Solid Earth 2014, 119, 3823–3837. [Google Scholar] [CrossRef]
- Petrie, E.J.; King, M.A.; Moore, P.; Lavallée, D.A. Higher-order ionospheric effects on the GPS reference frame and velocities. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Hadas, T.; Krypiak-Gregorczyk, A.; Hernández-Pajares, M.; Kapłon, J.; Paziewski, J.; Wielgosz, P.; García-Rigo, A.; Kazmierski, K.; Sośnica, K.; Kwasniak, D.; et al. Impact and Implementation of Higher-Order Ionospheric Effects on Precise GNSS Applications. J. Geophys. Res. Solid Earth 2017, 122, 9420–9436. [Google Scholar] [CrossRef]
- Zus, F.; Deng, Z.; Wickert, J. The impact of higher-order ionospheric effects on estimated tropospheric parameters in Precise Point Positioning. Radio Sci. 2017, 52, 963–971. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, F.; Zhang, X. The Effects of Higher-Order Ionospheric Terms on GPS Tropospheric Delay and Gradient Estimates. Remote Sens. 2018, 10, 1561. [Google Scholar] [CrossRef]
- Zhang, S.; Fang, L.; Wang, G.; Li, W. The impact of second-order ionospheric delays on the ZWD estimation with GPS and BDS measurements. GPS Solut. 2020, 24, 1–11. [Google Scholar] [CrossRef]
- Jin, S.; Occhipinti, G.; Jin, R. GNSS ionospheric seismology: Recent observation evidences and characteristics. Earth Sci. Rev. 2015, 147, 54–64. [Google Scholar] [CrossRef]
- Jin, S.; Jin, R.; Li, D. Assessment of BeiDou differential code bias variations from multi-GNSS network observations. Ann. Geophys. 2016, 34, 259–269. [Google Scholar] [CrossRef]
- Li, J.; Jin, S. High-order ionospheric effects on electron density estimation from Fengyun-3C GPS radio occultation. Ann. Geophys. 2017, 35, 403–411. [Google Scholar] [CrossRef][Green Version]
- Bassiri, S.; Hajj, G.A. Higher-order ionospheric effects on the global positioning system observables and means of modeling them. Manuscr. Geod. 1993, 18, 280–289. [Google Scholar]
- Kedar, S.; Hajj, G.A.; Wilson, B.D.; Heflin, M.B. The effect of the second order GPS ionospheric correction on receiver positions. Geophys. Res. Lett. 2003, 30, 1829. [Google Scholar] [CrossRef]
- Brunner, F.K.; Gu, M. An improved model for the dual frequency ionospheric correction of GPS observations. Manuscr. Geod. 1991, 16, 205–214. [Google Scholar]
- Marques, H.A.; Monico, J.F.G.; Aquino, M. RINEX_HO: Second- and third-order ionospheric corrections for RINEX observation files. GPS Solut. 2011, 15, 305–314. [Google Scholar] [CrossRef]
- King, R.W.; Collins, J.; Masters, E.M.; Rizos, C.; Stolz, A. Surveying with GPS; Monograph No. 9; School of Surveying, University of New South Wales: Kensington, NSW, Australia, 1985. [Google Scholar]
- Mandea, M.; Macmillan, S. International Geomagnetic Reference Field—The eighth generation. Earth Planets Space 2000, 52, 1119–1124. [Google Scholar] [CrossRef]
- Arfken, G. Mathematical Methods for Physicists; Elsevier: Amsterdam, The Netherlands, 1985. [Google Scholar]
- Odijk, D. Fast Precise GPS Positioning in the Presence of Ionospheric Delays. Ph.D. Thesis, Faculty of Civil Engineering and Geosciences, Delft University of Technology, Delft, The Netherlands, 2002. [Google Scholar]
- Hoque, M.M.; Jakowski, N. Higher order ionospheric effects in precise GNSS positioning. J. Geod. 2006, 81, 259–268. [Google Scholar] [CrossRef]
- Hartmann, G.K.; Leitinger, R. Range errors due to ionospheric and tropospheric effects for signal frequencies above 100 MHz. J. Geod. 1984, 58, 109–136. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; McClusky, S.C. Introduction to GAMIT/GLOBK 10.6; Massachusetts Institute of Technology: Cambridge, MA, USA, 2015. [Google Scholar]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging of satellites. In The Use of Artificial Satellites for Geodesy; Geophysical monograph series 15; American Geophysical Union: Washington, DC, USA, 1972; pp. 247–251. [Google Scholar] [CrossRef]
- Boehm, J. Vienna mapping functions in VLBI analyses. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean. Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- McCarthy, D.D.; Petit, G. IERS Conventions (2003); IERS Technical Note 32; Verlag des Budesamts fur Kartographie und Geodasie: Frankfurt, Germany, 2004. [Google Scholar]
- Springer, T.A.; Beutler, G.; Rothacher, M. A New Solar Radiation Pressure Model for GPS Satellites. GPS Solut. 1999, 2, 50–62. [Google Scholar] [CrossRef]
- Davis, J.L.; Elgered, G.; Niell, A.E.; Kuehn, C.E. Ground-based measurement of gradients in the “wet” radio refractivity of air. Radio Sci. 1993, 28, 1003–1018. [Google Scholar] [CrossRef]
- Teke, K.; Böhm, J.; Nilsson, T.; Schuh, H.; Steigenberger, P.; Dach, R.; Heinkelmann, R.; Willis, P.; Haas, R.; García-Espada, S.; et al. Multi-technique comparison of troposphere zenith delays and gradients during CONT08. J. Geod. 2011, 85, 395–413. [Google Scholar] [CrossRef]
- Tapping, K.F. The 10.7 cm solar radio flux (F10.7). Space Weather 2013, 11, 394–406. [Google Scholar] [CrossRef]






| Stations | Mean (mm) | RMS (mm) |
|---|---|---|
| ADAN | 0.24 | 0.48 |
| ANRK | 0.26 | 0.56 |
| DIYB | 0.27 | 0.69 |
| ERZR | 0.27 | 0.56 |
| ISPT | 0.24 | 0.45 |
| ISTN | 0.22 | 0.45 |
| IZMI | 0.23 | 0.47 |
| SAMN | 0.24 | 0.45 |
| GPS | NS Gradient (mm) | EW Gradient (mm) | ||
|---|---|---|---|---|
| Stations | Mean | RMS | Mean | RMS |
| ADAN | 1.00 | 1.09 | 0.43 | 1.39 |
| ANRK | 0.78 | 1.17 | 0.02 | 1.58 |
| DIYB | 1.02 | 1.29 | −0.03 | 2.12 |
| ERZR | 0.82 | 1.01 | 0.86 | 1.83 |
| ISPT | 0.99 | 1.11 | 0.14 | 0.70 |
| ISTN | 0.92 | 1.06 | −0.02 | 0.52 |
| IZMI | 0.83 | 1.09 | 0.13 | 0.77 |
| SAMN | 0.99 | 1.04 | 0.55 | 1.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akgul, V.; Gurbuz, G.; Kutoglu, S.H.; Jin, S. Effects of the High-Order Ionospheric Delay on GPS-Based Tropospheric Parameter Estimations in Turkey. Remote Sens. 2020, 12, 3569. https://doi.org/10.3390/rs12213569
Akgul V, Gurbuz G, Kutoglu SH, Jin S. Effects of the High-Order Ionospheric Delay on GPS-Based Tropospheric Parameter Estimations in Turkey. Remote Sensing. 2020; 12(21):3569. https://doi.org/10.3390/rs12213569
Chicago/Turabian StyleAkgul, Volkan, Gokhan Gurbuz, Senol Hakan Kutoglu, and Shuanggen Jin. 2020. "Effects of the High-Order Ionospheric Delay on GPS-Based Tropospheric Parameter Estimations in Turkey" Remote Sensing 12, no. 21: 3569. https://doi.org/10.3390/rs12213569
APA StyleAkgul, V., Gurbuz, G., Kutoglu, S. H., & Jin, S. (2020). Effects of the High-Order Ionospheric Delay on GPS-Based Tropospheric Parameter Estimations in Turkey. Remote Sensing, 12(21), 3569. https://doi.org/10.3390/rs12213569