Multi-Granularity Mission Negotiation for a Decentralized Remote Sensing Satellite Cluster
Abstract
1. Introduction
2. Proposed Methods
2.1. Mission Preprocess for All Levels of Granularity
2.1.1. Time Window Calculation
2.1.2. Profit Calculation
2.1.3. Cost Calculation
2.2. Multi-Granularity Partition of the Multi-Agent Negotiation Model
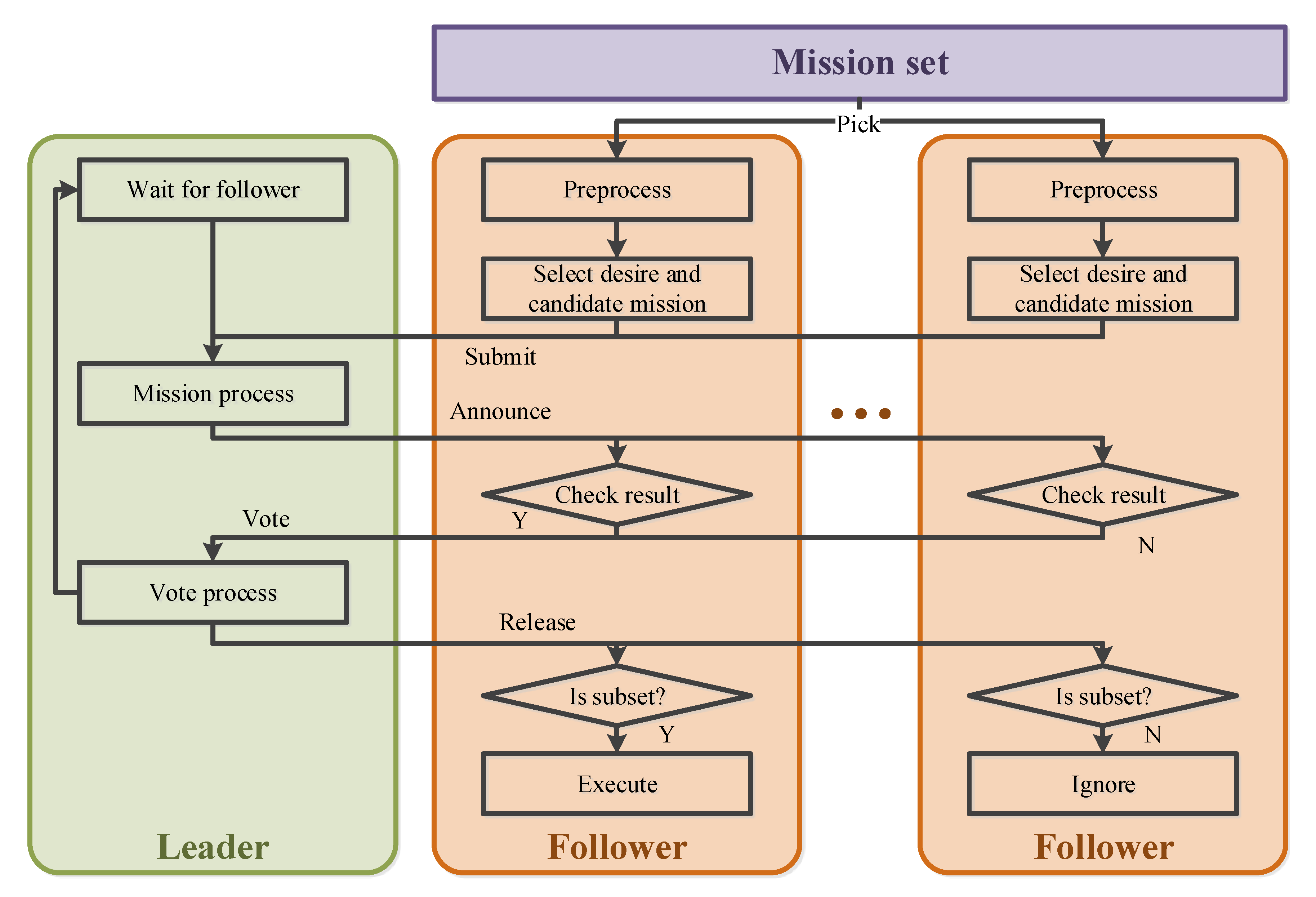
2.2.1. Low-Level Granularity
- Step 1: Preprocessing the missions. The Follower first preprocesses the missions by calculating the time window, profit, and cost.
- Step 2: Select a set of desired mission stages. The desired mission stages are selected by decision algorithm in Follower.
- Step 3: Transmit the mission set. The set of desired mission stages and their cost is broadcast, and the Leader records the mission set.
- Step 4: Leader process. The Leader finishes the mission assignment using a greedy algorithm. According to the profit calculation model, the profits of each mission stage are the same. That means the mission stages are assigned to the satellite with less cost.
- Step 5: Announce temporary result. The Leader announces a temporary result to all Followers.
- Step 6: Result check and national vote. The Follower logs and checks the result. If the assigned missions are all in the desired mission set submitted, the Follower votes in favor, and if not votes against. The national vote result can be expressed as:
- Step 7: Result release. The Leader records the selection from the Follower who votes in favor. Then the Leader releases the final negotiation result.
- Step 8: Execute. The Follower checks the result again, then picks the intersection of the set of assigned missions and the set of desired mission stages , and then executes the mission stages in the intersection.
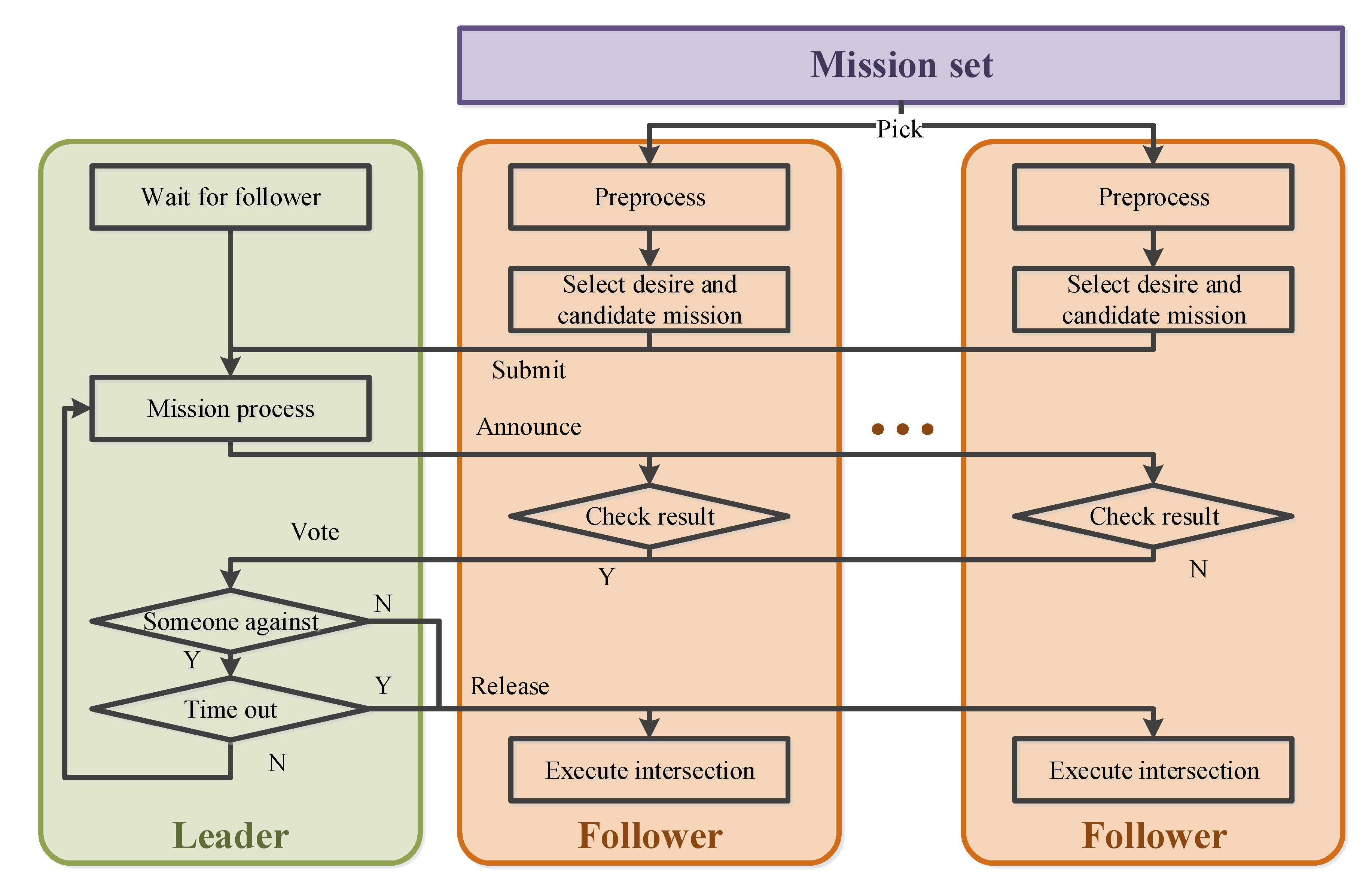
2.2.2. Middle-Level Granularity Model
- Step 1: Preprocessing the missions. Same as the Step 1 in low-level granularity.
- Step 2: Select a set of mission stages. Differently from the Step 2 in low-level granularity, the set of mission stages contains both desired and candidate mission stages.
- Step 3: Transmit the mission set. Differently from the Step 3 in low-level granularity, these mission stages broadcast include their execution costs and time windows, and the Leader records the set.
- Step 4: Leader process. Same as Step 4 in low-level granularity.
- Step 5: Announce temporary result. Same as Step 5 in low-level granularity
- Step 6: Result check and vote. The Followers working in the middle-level granularity are responsible for their own mission set. The assigned missions must all be in the submitted mission set. The total cost of the mission set is less than satellite’s capability . Besides, the assigned mission set must contain enough missions. The Follower votes in favor if the above two constraints are satisfied. If not, the Follower votes against. The vote result V is expressed as:
- Step 7: Vote process. If all Followers vote in favor or number of negotiation failures is too high, the Leader stops negotiation and goes to Step 8. If not, the Leader adjusts the set of mission stages while still using a greedy algorithm, and then goes to Step 5.
- Step 8: Result release. The Leader releases the final negotiation result.
- Step 9: Execute. Same as the Step 8 in low-level granularity.
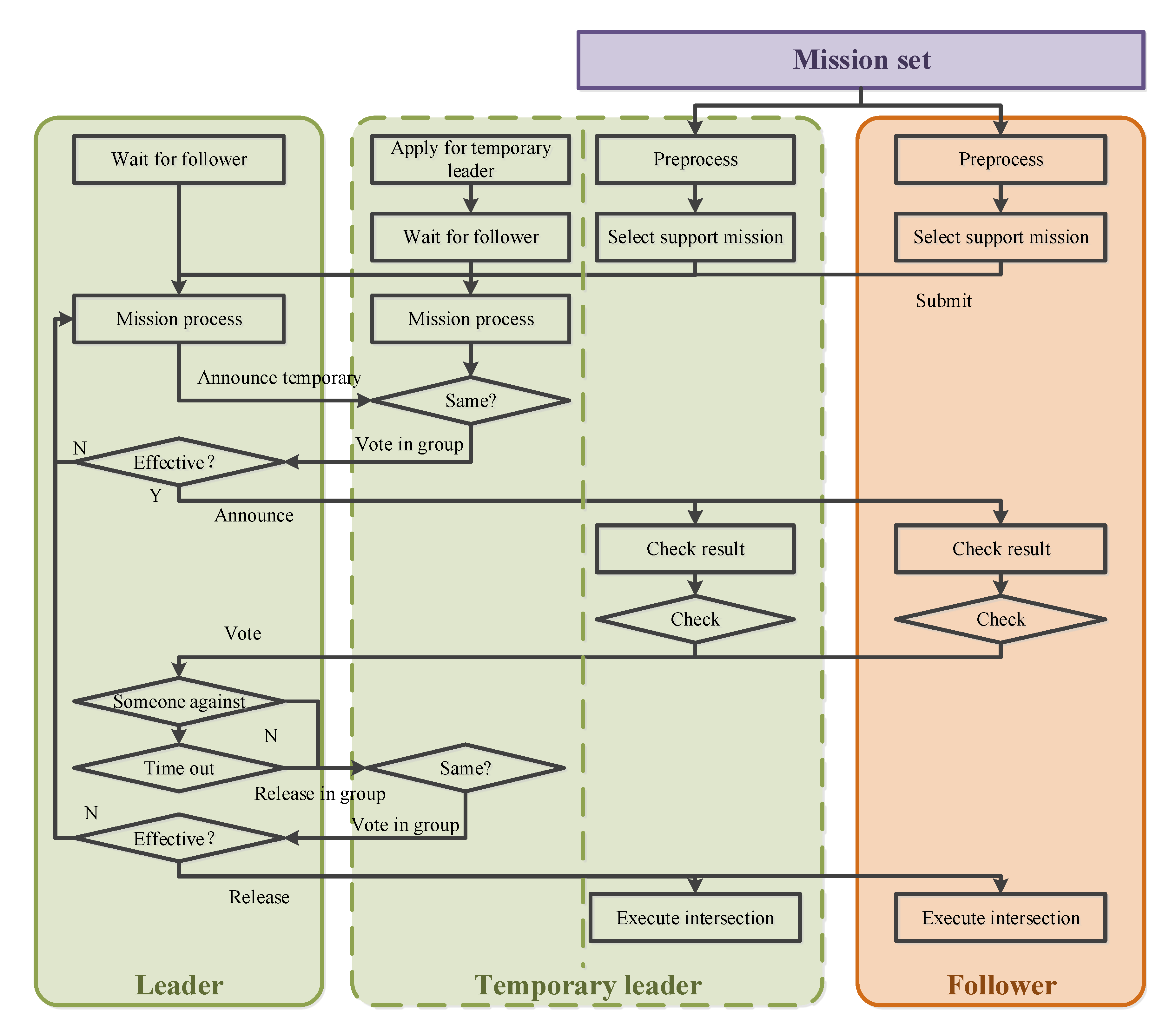
2.2.3. High-Level Granularity Model
- Step 1: Apply to join the Leader group. There exists one Leader in the system as the Leader for all levels of granularity. In order to increase the fault tolerance rate, the Follower with a direct connection (only one hop to the Leader) applies to join the Leader group. After being authorized by the Leader, it becomes a TLeader.
- Step 2: Preprocessing the missions. Same as before.
- Step 3: Select a set of mission stages. The set of mission stages, which contains all the supported mission stages, is selected by decision algorithm in Followers and TLeaders.
- Step 4: Transmit the mission set. These mission stages are broadcast, including their execution cost and time window, and both the Leader and TLeaders record the set.
- Step 5: Leader Process. The Leader and TLeaders assign missions using a greedy algorithm, considering an extra constraint of the maximum cost of each Follower.
- Step 6: Announce temporary result. The Leader firstly announces a temporary result in the Leader group and votes for the result. Then the temporary result is announced if confirmed by most TLeaders. If not they go to Step 5 to process again.
- Step 7: Result check and vote. Same as before.
- Step 8: Vote process. If all Followers vote in favor or negotiation fails times too much, the Leader stops negotiations and goes to Step 9. If not, the Leader adjusts the set of mission stages still using a greedy algorithm and then goes to Step 6.
- Step 9: Result release. Same as Step 6, the Leader releases the final negotiation result first in the leader group. After being confirmed, the negotiation results are released to all nodes.
- Step 10: Execute. Same as before.
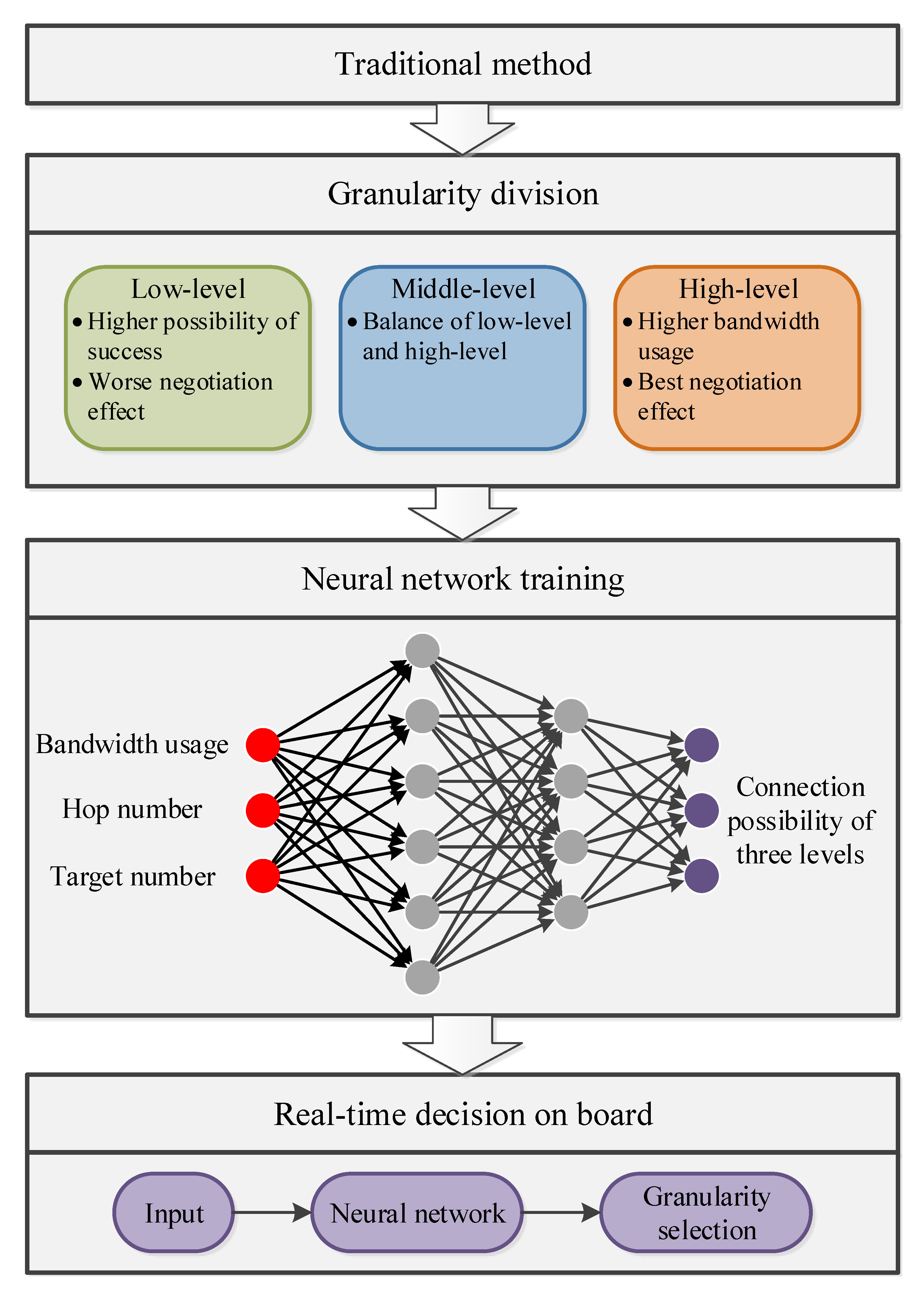
2.3. Real-Time Level Selection of Negotiation Granularity
2.3.1. Neural Network Description
2.3.2. Neural Network Training
3. Experiments and Analyses
3.1. Experimental Data
3.1.1. Targets and Mission Status
3.1.2. Imaging Satellite
3.2. Neural Network Training
3.2.1. Sample Collection
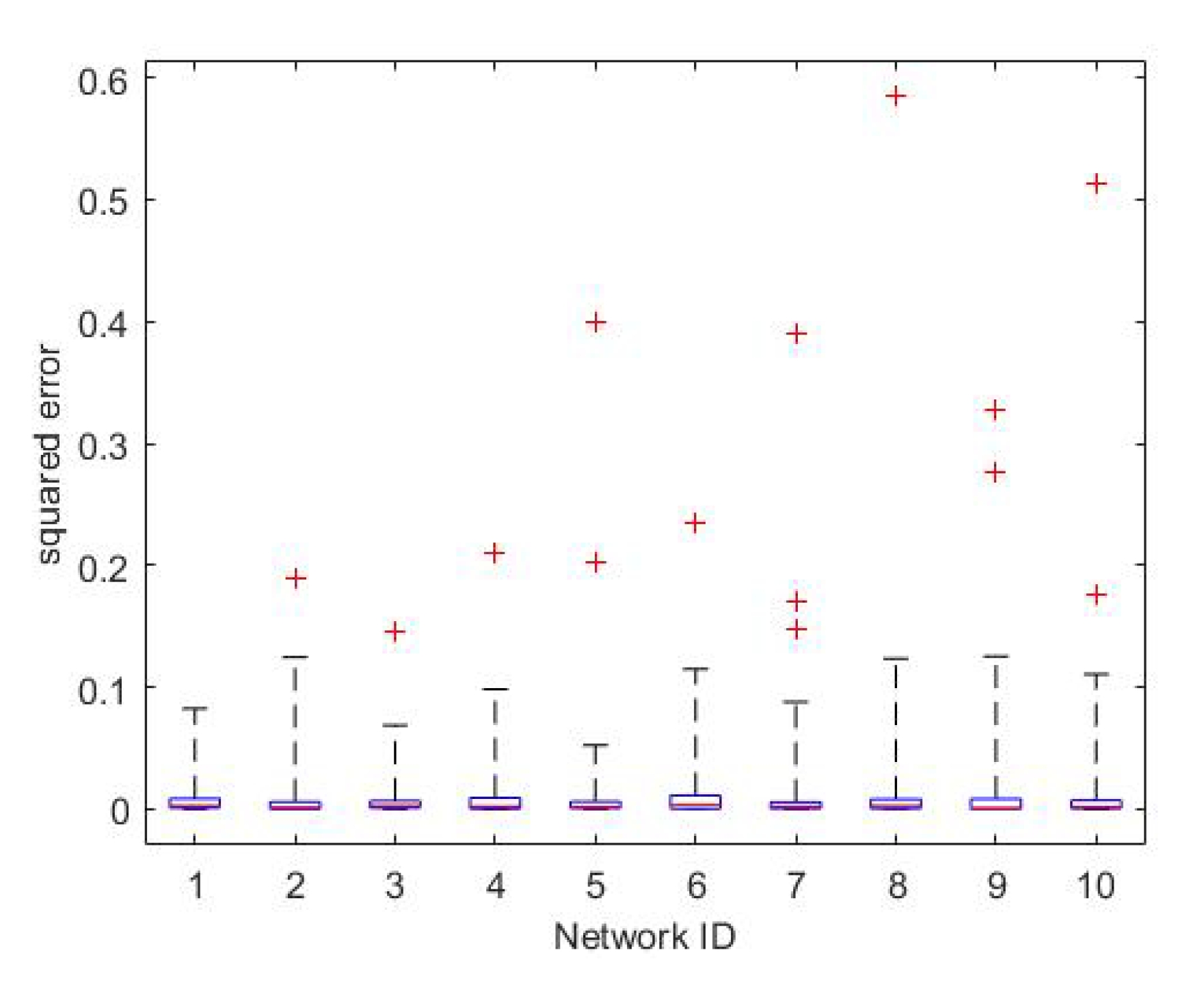
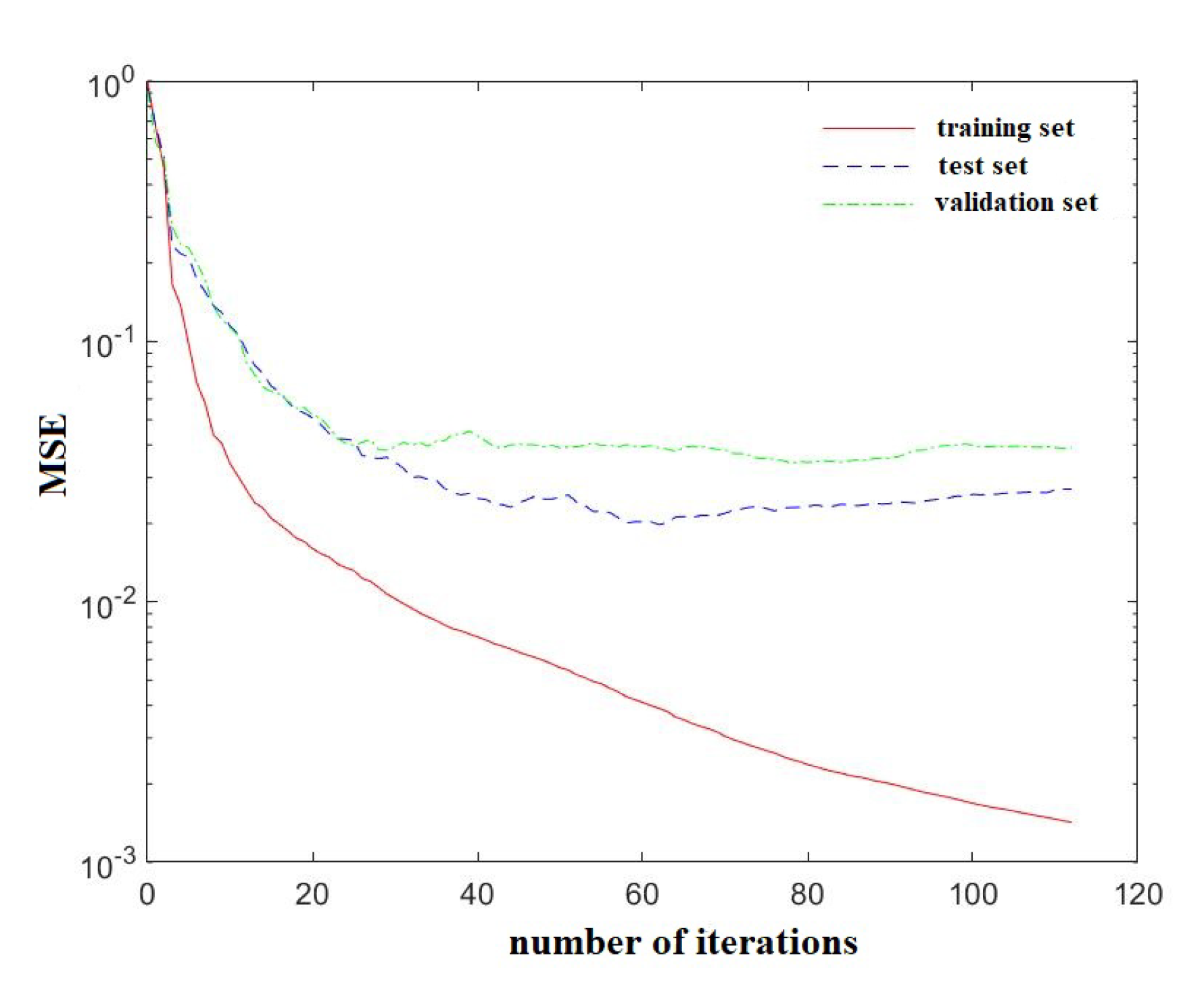
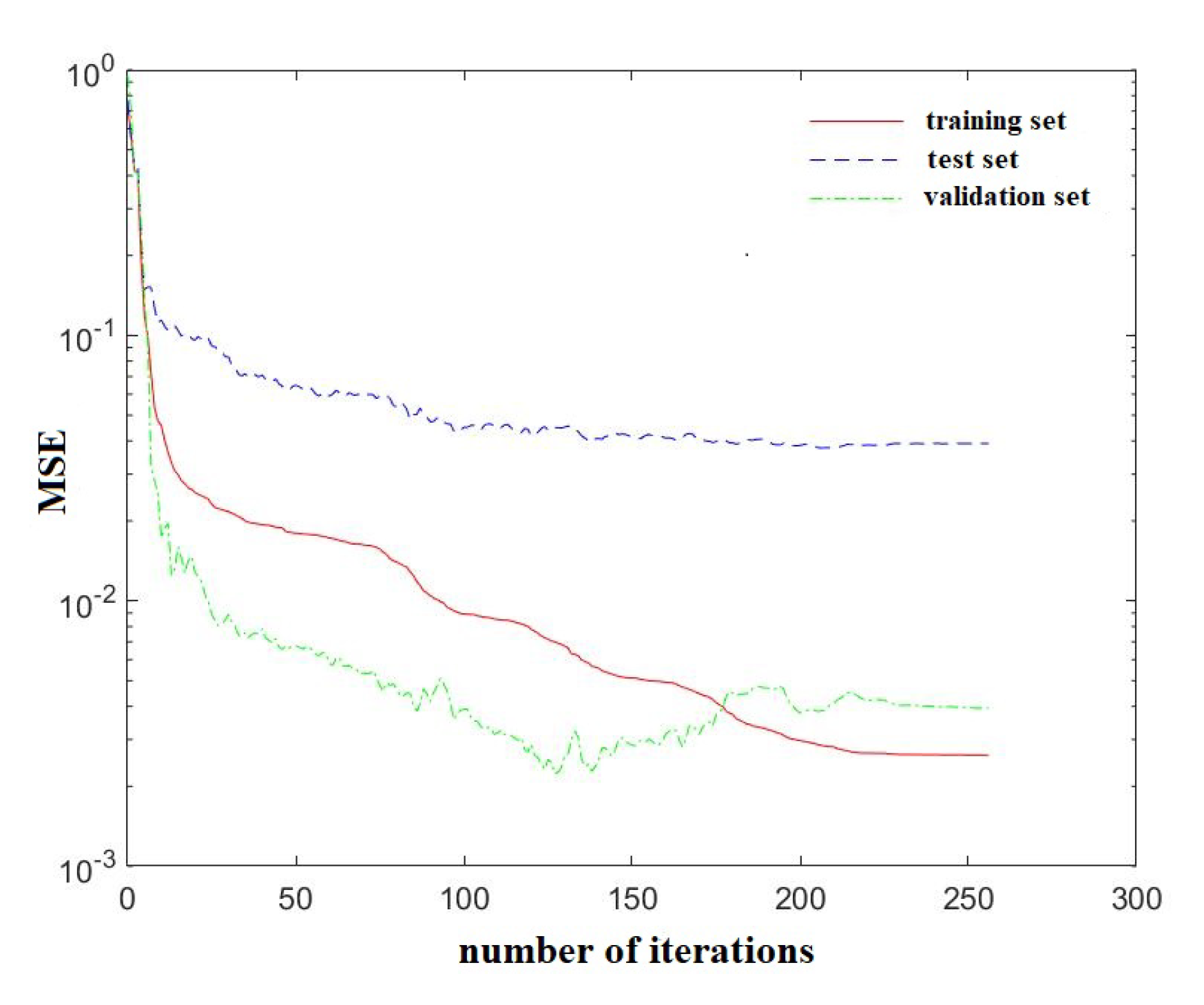
3.2.2. Training Result
3.3. Experimental Results
4. Discussion
5. Conclusions
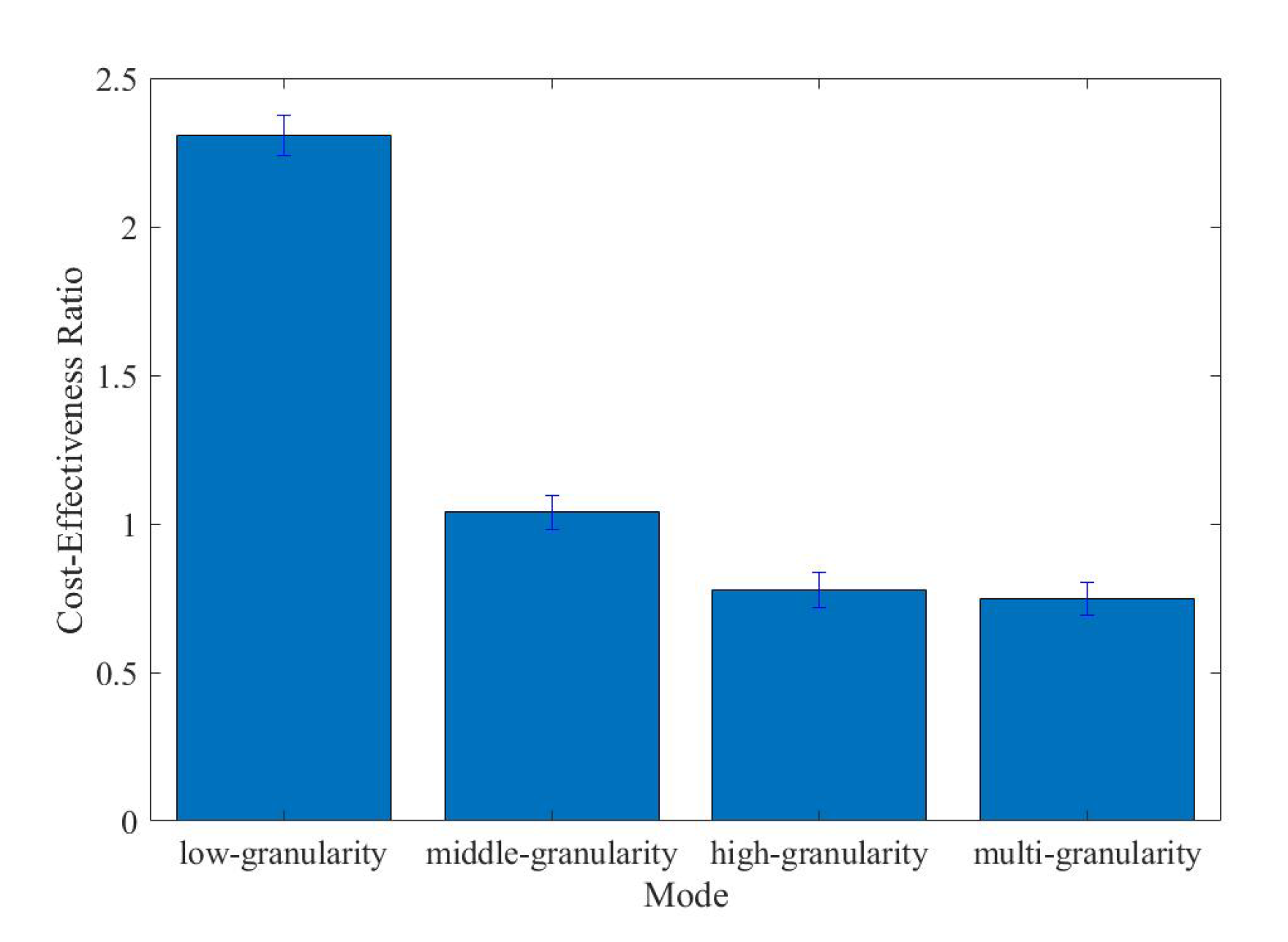
- The three levels of granularity we allocated work for different situations. We combine the advantages of the levels and use the best level of granularity according to the situation, which brings about better profits and a higher cost-effectiveness ratio.
- Complex situation analysis for granularity selection also brings about time delay; therefore, a neural network is trained for granularity selection in real-time.
- The framework of satellites is decentralization, which means it is suitable for a large satellite cluster containing failure nodes and malicious nodes.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Target ID | Position | Course Angle | Velocity | Mission Status |
|---|---|---|---|---|
| 1 | 46.78 E, 0.16 N | 13 | 3.2 | 3 |
| 2 | 135.27 E, 1.05 S | 78 | 16.3 | 1 |
| 3 | 148.65 E, 1.62 N | −51 | 8.6 | 0 |
| 4 | 105.82 E, 1.14 N | −133.97 | 24.12 | 2 |
| 5 | 22.83 W, 1.58 S | −100.56 | 29.78 | 0 |
| 6 | 170.52 W, 1.71 N | 10.64 | 2.11 | 1 |
| 7 | 117.21 W, 1.63 N | 39.89 | 11.31 | 3 |
| 8 | 155.38 W, 0.74 N | −71.28 | 7.25 | 3 |
| 9 | 97.38 E, 0.82 S | −145.84 | 6.68 | 0 |
| 10 | 126.06 E, 1.98 S | 2.46 | 9.55 | 0 |
| 11 | 105.34 W, 0.4 N | −25.63 | 13.69 | 4 |
| 12 | 77.51 E, 0.86 S | 168.43 | 26.08 | 1 |
| 13 | 135.86 E, 0.35 S | 106.17 | 25.44 | 3 |
| 14 | 2.22 E, 1.64 N | −67.71 | 22.44 | 4 |
| 15 | 70.67 W, 0.56 N | −16.66 | 22.43 | 1 |
| 16 | 17.6 E, 0.68 N | −76.47 | 27.61 | 3 |
| 17 | 126.7 E, 0.43 S | 90.43 | 11.53 | 2 |
| 18 | 112.02 E, 0.3 S | −23.47 | 3.07 | 1 |
| 19 | 41.83 E, 0.19 N | −173.1 | 14.92 | 3 |
| 20 | 95.34 E, 0.67 S | 153.94 | 12.87 | 2 |
| 21 | 79.91 E, 1.81 S | −33.18 | 14.69 | 1 |
| 22 | 93.55 W, 0.25 S | 151.94 | 8.31 | 3 |
| 23 | 67.62 E, 1.14 N | −23.34 | 0.76 | 3 |
| 24 | 137.7 W, 1.35 N | 151.97 | 6.76 | 4 |
| 25 | 2.81 E, 0.24 N | −32.75 | 13.52 | 3 |
| 26 | 129 E, 0.07 N | 116.76 | 21.59 | 2 |
| 27 | 43.86 E, 0.48 S | −85.93 | 21.44 | 4 |
| 28 | 36.48 W, 1.31 N | 41.81 | 6.89 | 4 |
| 29 | 97.03 E, 1.09 S | 29.79 | 8.49 | 2 |
| 30 | 113.56 W, 0.49 N | −169.45 | 17.23 | 0 |
| 31 | 133.4 E, 1.63 S | 10.05 | 22.34 | 3 |
| 32 | 19.59 W, 1.05 S | 53.3 | 20.34 | 3 |
| 33 | 8.16 W, 0.71 S | 93.46 | 1.85 | 4 |
| 34 | 1.83 W, 0.59 N | −162.03 | 27.42 | 3 |
| 35 | 12.1 E, 1.21 S | −75.38 | 6.97 | 5 |
| 36 | 38.86 W, 1.61 N | −144.91 | 16.06 | 1 |
| 37 | 162.48 E, 0.09 S | −10.36 | 1.36 | 3 |
| 38 | 19.94 W, 0.49 N | −66.05 | 1.89 | 3 |
| 39 | 135.58 E, 0.59 S | 5.57 | 4.11 | 3 |
| 40 | 148.4 E, 0.92 S | −152.6 | 3.02 | 0 |
| 41 | 66.06 W, 1.62 S | −0.55 | 17.06 | 3 |
| 42 | 27.49 W, 1.47 N | 178.75 | 23.1 | 3 |
| 43 | 152.13 E, 1.88 S | 82.93 | 14.51 | 1 |
| 44 | 116.76 E, 0.43 N | −160.38 | 29.13 | 4 |
| 45 | 35.72 E, 0.95 S | −47.87 | 21.9 | 1 |
| 46 | 130.59 W, 0.77 N | −72.46 | 3.6 | 4 |
| 47 | 153.51 E, 0.68 S | −179.4 | 17.78 | 4 |
| 48 | 112.79 E, 1.31 N | −151.89 | 14.86 | 5 |
| 49 | 163.11 E, 1.76 S | 84.84 | 12.45 | 4 |
| 50 | 126.49 E, 0.94 N | 87.96 | 18.17 | 3 |
| 51 | 60.67 W, 1.37 S | 135.86 | 18.85 | 2 |
| 52 | 22.05 E, 1.45 N | −88.89 | 14.6 | 1 |
| 53 | 70.15 W, 1.28 N | 10.91 | 13.85 | 2 |
| 54 | 102.21 E, 0.24 N | 62.43 | 24.97 | 1 |
| 55 | 22.49 W, 0.06 S | 92.65 | 14.14 | 3 |
| 56 | 73.21 E, 1.43 N | 112.86 | 3.76 | 2 |
| 57 | 72.99 E, 1.56 S | −150.73 | 7.81 | 0 |
| 58 | 97.73 E, 0.07 N | −160.3 | 24.27 | 2 |
| 59 | 120.5 E, 1.01 N | −101.32 | 18.42 | 3 |
| 60 | 83.49 E, 0.89 N | −143.76 | 22.46 | 1 |
| 61 | 42.29 E, 0.54 S | −165.52 | 22.5 | 4 |
| 62 | 119.69 E, 1.59 N | −49.59 | 13.76 | 3 |
| 63 | 137.64 E, 0.16 N | 109.7 | 20.11 | 0 |
| 64 | 44.04 E, 0.9 N | 145.48 | 17.54 | 3 |
| 65 | 34.77 E, 1.94 N | 93.66 | 10.2 | 4 |
| 66 | 16.9 E, 1.71 S | −172.48 | 9.42 | 1 |
| 67 | 166.71 E, 1.4 N | 54.01 | 26.03 | 1 |
| 68 | 8.43 W, 1.62 S | 66.33 | 16.09 | 2 |
| 69 | 9.69 E, 1.17 S | −136.29 | 6.59 | 0 |
| 70 | 25.3 E, 1.55 N | 133.45 | 21.39 | 4 |
| 71 | 162.65 W, 0.72 S | 45.93 | 22.26 | 5 |
| 72 | 71.92 E, 0.75 S | −48.13 | 18.14 | 2 |
| 73 | 126.34 W, 1.3 S | −59.5 | 11.53 | 4 |
| 74 | 129.3 E, 1.21 S | 96.87 | 12.91 | 1 |
| 75 | 148.87 E, 0.6 N | −75.96 | 28.33 | 4 |
| 76 | 175.76 E, 1.89 S | −7.35 | 21.8 | 2 |
| 77 | 51.35 W, 1.51 N | −96.73 | 5.56 | 0 |
| 78 | 82.54 W, 1.26 S | 149.41 | 19.72 | 2 |
| 79 | 88.86 W, 0.78 S | −19.87 | 19.76 | 2 |
| 80 | 143.25 E, 1.43 S | −21.42 | 15.94 | 1 |
| 81 | 34.11 E, 0.25 S | 111.23 | 22.74 | 4 |
| 82 | 66.3 E, 1.43 N | 125.25 | 14.13 | 1 |
| 83 | 88.45 W, 1.37 N | −42.87 | 18.76 | 3 |
| 84 | 166.84 W, 0.1 S | 17.65 | 1.04 | 3 |
| 85 | 114.67 W, 1.96 N | 29.31 | 20.07 | 5 |
| 86 | 137.9 W, 1.33 S | −119.95 | 24.72 | 2 |
| 87 | 135.84 W, 0.78 S | −91.32 | 2.48 | 4 |
| 88 | 130.55 E, 1.93 S | 154.1 | 2.58 | 5 |
| 89 | 65.21 W, 0.01 N | 21.85 | 13.07 | 1 |
| 90 | 155.26 W, 1.65 N | −112.8 | 29.73 | 2 |
| 91 | 129.67 W, 1.78 N | −36.53 | 7.34 | 4 |
| 92 | 99.27 W, 0.41 S | 52.87 | 15.02 | 3 |
| 93 | 33.13 E, 1.37 N | −139.99 | 6.01 | 1 |
| 94 | 168.98 W, 0.99 N | 170.18 | 7.95 | 2 |
| 95 | 74.4 W, 1.4 N | 19.14 | 9.08 | 2 |
| 96 | 137.41 E, 0.36 N | 165.85 | 20.56 | 4 |
| 97 | 62.26 E, 1.99 S | 83.51 | 16.07 | 2 |
| 98 | 177.51 W, 1.49 N | −125.73 | 9.44 | 2 |
| 99 | 34.16 W, 0.31 S | −102.79 | 7.26 | 5 |
| 100 | 173.14 W, 1.55 N | 167.35 | 22.78 | 5 |
References
- Van der Werf, G.R.; Randerson, J.T.; Giglio, L.; Collatz, G.J.; Mu, M.; Kasibhatla, P.S.; Morton, D.C.; DeFries, R.S.; Jin, Y.; van Leeuwen, T.T. Global fire emissions and the contribution of deforestation, savanna, forest, agricultural, and peat fires. Atmos. Chem. Phys. 2010, 10, 11707–11735. [Google Scholar] [CrossRef]
- Opgenoorth, H.J.; Lockwood, M.; Alcaydé, D.; Donovan, E.; Engebretson, M.J.; Van Eyken, A.P.; Kauristie, K.; Lester, M.; Moen, J.; Waterman, J.; et al. Coordinated ground-based, low altitude satellite and Cluster observations on global and local scales during a transient post-noon sector excursion of the magnetospheric cusp. Ann. Geophys. 2001, 19, 1367–1398. [Google Scholar] [CrossRef]
- Lockwood, M.; Opgenoorth, H.; Van Eyken, A.P.; Fazakerley, A.; Bosqued, J.M.; Denig, W.; Wild, J.A.; Cully, C.; Greenwald, R.; Lu, G.; et al. Coordinated Cluster, ground-based instrumentation and low-altitude satellite observations of transient poleward-moving events in the ionosphere and in the tail lobe. Ann. Geophys. 2001, 19, 1589–1612. [Google Scholar] [CrossRef]
- Rabideau, G.; Knight, R.; Chien, S.; Fukunaga, A.; Govindjee, A. Iterative Repair Planning for Spacecraft Operations in the ASPEN System. ISAIRAS 1999, 440, 99. [Google Scholar]
- Rayman, M.D.; Varghese, P.; Lehman, D.H.; Livesay, L.L. Results from the Deep Space 1 Technology Validation Mission. ACTA Astronaut. 2000, 47, 475–487. [Google Scholar] [CrossRef]
- Campbell, M.; Schetter, T. Comparison of multiple agent-based organizations for satellite constellations. J. Spacecr. Rockets 2002, 39, 274–283. [Google Scholar] [CrossRef]
- Schetter, T.; Campbell, M.; Surka, D. Agent Systems, Mobile Agents, and Applications. In Multiple Agent-Based Autonomy for Satellite Constellations; Elsevier Science Publishers Ltd.: Cambridge, UK, 2003. [Google Scholar]
- Schetter, T.; Campbell, M.; Surka, D. Multiple agent-based autonomy for satellite constellations. Artif. Intell. 2003, 145, 147–180. [Google Scholar] [CrossRef]
- He, Y.; Chen, Y.; Lu, J.; Chen, C.; Wu, G. Scheduling multiple agile earth observation satellites with an edge computing framework and a constructive heuristic algorithm. J. Syst. Archit. 2019, 95, 205–208. [Google Scholar] [CrossRef]
- Si-wei, C.; Jing, C.; Lin-Cheng, S. A MAS-based negotiation model and its application to multiple observation collaborative satellite planning. In Proceedings of the 2010 The 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010; pp. 205–208. [Google Scholar]
- Chong, W.; Ning, J.; Jun, L.; Jun, W.; Hao, C. Cooperative Co-evolutionary Algorithm in Satellite Imaging Scheduling of Cooperative Multiple Centers. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010. [Google Scholar]
- Iacopino, C.; Palmer, P.; Brewer, A.; Policella, N.; Donati, A. EO Constellation MPS based on ant colony optimization algorithms. In Proceedings of the International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 12–14 June 2013; pp. 159–164. [Google Scholar]
- Zhao, Y.; Liu, Y.; Wen, G.; Ren, W.; Chen, G. Designing Distributed Specified-Time Consensus Protocols for Linear Multiagent Systems Over Directed Graphs. IEEE Trans. Autom. Control 2019, 64, 2945–2952. [Google Scholar] [CrossRef]
- Buzzi, P.G.; Selva, D.; Hitomi, N.; Blackwell, W.J. Assessment of constellation designs for earth observation: Application to the TROPICS mission. Acta Astronaut. 2019, 161, 166–182. [Google Scholar] [CrossRef]
- Globus, A.; Crawford, J.; Lohn, J.; Pryor, A. A comparison of techniques for scheduling earth observing satellites. In Proceedings of the Conference on Nineteenth National Conference on Artificial Intelligence, San Jose, CA, USA, 25–29 July 2004. [Google Scholar]
- Araguz, C.; Closa, M.; Bou-Balust, E.; Alarcon, E. A Design-Oriented Characterization Framework for Decentralized, Distributed, Autonomous Systems: The Nano-Satellite Swarm Case. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019. [Google Scholar]
- Gallud, X.; Selva, D. Agent-based simulation framework and consensus algorithm for observing systems with adaptive modularity. Syst. Eng. 2018, 21, 432–454. [Google Scholar] [CrossRef]
- He, L.; Li, G.; Xin, L.; Chen, Y. An autonomous multi-sensor satellite system based on multi-agent blackboard model. Eksploat. Niezawodn. Maint. Reliab. 2017, 19, 447–458. [Google Scholar] [CrossRef]
- Nag, S.; Li, A.S.; Merrick, J.H. Scheduling algorithms for rapid imaging using agile Cubesat constellations. Adv. Space Res. 2018, 61, 891–913. [Google Scholar] [CrossRef]
- Wang, J.; Demeulemeester, E.; Qiu, D. A pure proactive scheduling algorithm for multiple earth observation satellites under uncertainties of clouds. Comput. Oper. Res. 2016, 74, 1–13. [Google Scholar] [CrossRef]
- Wang, J.; Demeulemeester, E.; Hu, X.; Wu, G. Expectation and SAA Models and Algorithms for Scheduling of Multiple Earth Observation Satellites Under the Impact of Clouds. IEEE Syst. J. 2020, 1–12. [Google Scholar] [CrossRef]
- Ongaro, D.; Ousterhout, J. In search of an understandable consensus algorithm. USENIX Annu. Tech. Conf. 2014, 14, 305–319. [Google Scholar]
- Castro, M.; Liskov, B. Practical Byzantine fault tolerance. OSDI 1999, 99, 173–186. [Google Scholar]
- Dhillon, V.; Metcalf, D.; Hooper, M. Recent Developments in Blockchain. Blockchain Enabled Appl. 2017, 11, 151–181. [Google Scholar]
- Jakobsson, M.; Juels, A. Proofs of Work and Bread Pudding Protocols. In Secure Information Networks; Springer: Boston, MA, USA, 1999; pp. 258–272. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Environ. Sci. Technol. 2003, 37, 1–9. [Google Scholar]


| Stages | Discovery | Identification | Confirmation | Tracking | Monitoring |
|---|---|---|---|---|---|
| profit | 0.25 | 0.1 | 0.15 | 0.25 | 0.25 |
| Mission Status ID | Mission Status |
|---|---|
| 0 | not discovered |
| 1 | discovered |
| 2 | identified |
| 3 | confirmed |
| 4 | tracking |
| 5 | monitoring |
| Target ID | Position | Course Angle | Velocity | Mission Status |
|---|---|---|---|---|
| 1 | 46.78 E, 0.16 N | 13 | 3.2 | 3 |
| 2 | 135.27 E, 1.05 S | 78 | 16.3 | 1 |
| 3 | 148.65 E, 1.62 N | −51 | 8.6 | 0 |
| ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| Category | Parameter | Value |
|---|---|---|
| Orbit Parameter | Semimajor Axis (m) | 6,878,000 |
| Eccentricity | 0 | |
| Inclination () | 0 | |
| RAAN () | 0 | |
| Argument of Perigee () | 0 | |
| True Anomaly () | 230 | |
| Attitude Parameter | Agile | Y |
| Max. Maneuver Angle | 45 | |
| Angular Velocity | 1 | |
| Angular Acceleration | 0.1 | |
| Maneuver Mode | Trapezoid Method | |
| Payload Parameter | Imaging Width (km) | 4 |
| Image Size per Frame (Mb) | 6.4 | |
| Communication Parameter | Frequency Band | S |
| Antenna Number | 4 | |
| Bandwidth (M) | 10 | |
| Modulation Mode (M) | PSK | |
| Spread Spectrum Mode (M) | CDMA |
| Group ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| bandwidth usage | 60% | 65% | 70% | 75% | 80% | 85% | 90% |
| Group ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| target number | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Network ID | First Layer | Second Layer | ||
|---|---|---|---|---|
| Activation Function | Nodes Number | Activation Function | Nodes Number | |
| 1 | radbas | 32 | purelin | 3 |
| 2 | softmax | 32 | purelin | 3 |
| 3 | satlin | 32 | purelin | 3 |
| 4 | softmax | 256 | purelin | 3 |
| 5 | satlin | 64 | purelin | 3 |
| 6 | radbas | 32 | purelin | 3 |
| 7 | poslin | 32 | purelin | 3 |
| 8 | tansig | 32 | purelin | 3 |
| 9 | logsig | 32 | purelin | 3 |
| 10 | radbasn | 32 | purelin | 3 |
| Network ID | First Layer | Second Layer | Third Layer | |||
|---|---|---|---|---|---|---|
| Activation Function | Nodes Number | Activation Function | Nodes Number | Activation Function | Nodes Number | |
| 1 | satlin | 8 | softmax | 16 | purelin | 3 |
| 2 | satlin | 128 | radbas | 16 | purelin | 3 |
| 3 | satlin | 16 | radbas | 64 | purelin | 3 |
| 4 | satlin | 16 | softmax | 64 | purelin | 3 |
| 5 | satlin | 64 | softmax | 256 | purelin | 3 |
| 6 | softmax | 32 | radbas | 64 | purelin | 3 |
| 7 | softmax | 32 | satlin | 16 | purelin | 3 |
| 8 | satlin | 32 | satlin | 32 | purelin | 3 |
| 9 | satlin | 64 | softmax | 128 | purelin | 3 |
| 10 | softmax | 64 | softmax | 256 | purelin | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, X.; Dong, Y.; Xie, S. Multi-Granularity Mission Negotiation for a Decentralized Remote Sensing Satellite Cluster. Remote Sens. 2020, 12, 3595. https://doi.org/10.3390/rs12213595
Deng X, Dong Y, Xie S. Multi-Granularity Mission Negotiation for a Decentralized Remote Sensing Satellite Cluster. Remote Sensing. 2020; 12(21):3595. https://doi.org/10.3390/rs12213595
Chicago/Turabian StyleDeng, Xuelei, Yunfeng Dong, and Shucong Xie. 2020. "Multi-Granularity Mission Negotiation for a Decentralized Remote Sensing Satellite Cluster" Remote Sensing 12, no. 21: 3595. https://doi.org/10.3390/rs12213595
APA StyleDeng, X., Dong, Y., & Xie, S. (2020). Multi-Granularity Mission Negotiation for a Decentralized Remote Sensing Satellite Cluster. Remote Sensing, 12(21), 3595. https://doi.org/10.3390/rs12213595





