A Deep Learning-Based Method for Quantifying and Mapping the Grain Size on Pebble Beaches
Abstract
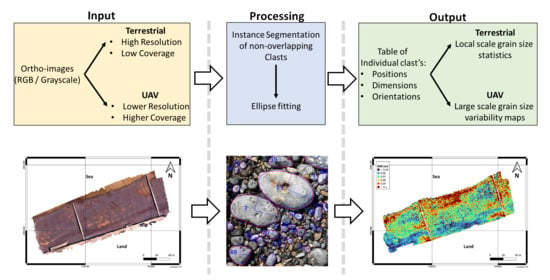
1. Introduction
2. Data and Methodology
2.1. Data
2.2. Mask R-CNN Segmentation
2.3. Clast Size Measurement and Validation
3. Example of Applications
3.1. Study Sites
3.2. Influence of the Hydrodynamics on Etretat Pebbles’ Size
3.3. Clast Size Mapping at Etretat and Hautot-Sur-Mer
3.3.1. Validation
3.3.2. Results and Discussion
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Buscombe, D.; Masselink, G. Concepts in gravel beach dynamics. Earth-Science Rev. 2006, 79, 33–52. [Google Scholar] [CrossRef]
- Finkl, C.W. Coastal classification: Systematic approaches to consider in the development of a comprehensive scheme. J. Coast. Res. 2004, 20, 166–213. [Google Scholar] [CrossRef]
- Gomez, B. Temporal variations in bedload transport rates: The effect of progressive bed armouring. Earth Surf. Process. Landforms 1983, 8, 41–54. [Google Scholar] [CrossRef]
- Klingeman, P.C.; Emmett, W.W. Gravel bedload transport processes. In Gravel Bed Rivers; Hey, R.D., Bathurst, J.C., Thorne, C.R., Eds.; Wiley: Chichester, UK, 1982; pp. 141–179. [Google Scholar]
- Mason, T.; Coates, T.T. Sediment transport processes on mixed beaches: A review for shoreline management. J. Coast. Res. 2001, 17, 645–657. [Google Scholar]
- Rubin, D.M.; Topping, D.J. Quantifying the relative importance of flow regulation and grain size regulation of suspended sediment transport α and tracking changes in grain size of bed sediment β (Water Resources Research (2008) 44, (W09701) DOI: 10.1029/2008WR006819). Water Resour. Res. 2008, 44, 133–146. [Google Scholar] [CrossRef]
- Bergillos, R.J.; Masselink, G.; McCall, R.T.; Ortega-Sánchez, M. Modelling overwash vulnerability along mixed sand-gravel coasts with xbeach-g: Case study of playa granada, southern Spain. Proc. Coast. Eng. Conf. 2016, 35, 1–9. [Google Scholar]
- Masselink, G.; Poate, T.; McCall, R.; van Geer, P. Modelling storm response on gravel beaches using XBeach-G. Proc. Inst. Civ. Eng. Marit. Eng. 2014, 167, 173–191. [Google Scholar] [CrossRef]
- Dal Cin, R. “Pebble clusters”: Their origin and utilization in the study of palaeocurrents. Sediment. Geol. 1968, 2, 233–241. [Google Scholar] [CrossRef]
- Butt, T.; Russell, P.; Turner, I. The influence of swash infiltration–exfiltration on beach face sediment transport: Onshore or offshore? Coast. Eng. 2001, 42, 35–52. [Google Scholar] [CrossRef]
- Kondolf, G.M.; Wolman, M.G. The sizes of salmonid spawning gravels. Water Resour. Res. 1993, 29, 2275–2285. [Google Scholar] [CrossRef]
- Adams, J. Gravel Size Analysis from Photographs. J. Hydraul. Div. 1979, 105, 1247–1255. [Google Scholar]
- Kellerhals, R.; Bray, D.I. Sampling Procedures for Coarse Fluvial Sediments. J. Hydraul. Div. 1971, 97, 1165–1180. [Google Scholar]
- Barnard, P.L.; Rubin, D.M.; Harney, J.; Mustain, N. Field test comparison of an autocorrelation technique for determining grain size using a digital “beachball” camera versus traditional methods. Sediment. Geol. 2007, 201, 180–195. [Google Scholar] [CrossRef]
- Graham, D.J.; Rice, S.P.; Reid, I. A transferable method for the automated grain sizing of river gravels. Water Resour. Res. 2005, 41, 1–12. [Google Scholar] [CrossRef]
- Fehr, R. Einfache Bestimmung der Korngrös¬senverteilung von Geschiebematerial mit Hilfe der Linienzahlanalyse (Simple detection of grain size distribution of sediment material using line-count analysis). Schweizer Ing. und Archit. 1987, 105, 1104–1109. [Google Scholar]
- Leopold, L.B. An Improved Method for Size Distribution of Stream Bed Gravel. Water Resour. Res. 1970, 6, 1357–1366. [Google Scholar] [CrossRef]
- Wolman, M.G. A method of sampling coarse river-bed material. Trans. Am. Geophys. Union 1954, 35, 951–956. [Google Scholar] [CrossRef]
- Ibbeken, H.; Schleyer, R. Photo-sieving: A method for grain-size analysis of coarse-grained, unconsolidated bedding surfaces. Earth Surf. Process. Landforms 1986, 11, 59–77. [Google Scholar] [CrossRef]
- Buscombe, D.; Masselink, G. Grain-size information from the statistical properties of digital images of sediment. Sedimentology 2009, 56, 421–438. [Google Scholar] [CrossRef]
- Buscombe, D. SediNet: A configurable deep learning model for mixed qualitative and quantitative optical granulometry. Earth Surf. Process. Landforms 2020, 45, 638–651. [Google Scholar] [CrossRef]
- Buscombe, D. Transferable wavelet method for grain-size distribution from images of sediment surfaces and thin sections, and other natural granular patterns. Sedimentology 2013, 60, 1709–1732. [Google Scholar] [CrossRef]
- Carbonneau, P.E.; Lane, S.N.; Bergeron, N.E. Catchment-scale mapping of surface grain size in gravel bed rivers using airborne digital imagery. Water Resour. Res. 2004, 40, 1–11. [Google Scholar] [CrossRef]
- Rubin, D.M. A simple autocorrelation algorithm for determining grain size from digital images of sediment. J. Sediment. Res. 2004, 74, 160–165. [Google Scholar] [CrossRef]
- Verdú, J.M.; Batalla, R.J.; Martínez-Casasnovas, J.A. High-resolution grain-size characterisation of gravel bars using imagery analysis and geo-statistics. Geomorphology 2005, 72, 73–93. [Google Scholar] [CrossRef]
- Butler, J.B.; Lane, S.N.; Chandler, J.H. Automated extraction of grain-size data from gravel surfaces using digital image processing. J. Hydraul. Res. 2001, 39, 519–529. [Google Scholar] [CrossRef]
- Graham, D.J.; Reid, I.; Rice, S.P. Automated sizing of coarse-grained sediments: Image-processing procedures. Math. Geol. 2005, 37, 1–28. [Google Scholar] [CrossRef]
- Purinton, B.; Bookhagen, B. Introducing PebbleCounts: A grain-sizing tool for photo surveys of dynamic gravel-bed rivers. Earth Surf. Dyn. 2019, 7, 859–877. [Google Scholar] [CrossRef]
- Sime, L.C.; Ferguson, R.I. Information on Grain Sizes in Gravel-Bed Rivers By Automated Image Analysis. J. Sediment. Res. 2003, 73, 630–636. [Google Scholar] [CrossRef]
- Detert, M.; Weibrecht, V. User Guide to Gravelometric image Analysis by Basegrain; Fukuoka, S., Nakagawa, H., Sumi, T., Zhang, H., Eds.; CRC Press: Boca Raton, FL, USA, 2013; ISBN 9781138000629. [Google Scholar]
- Le, Q.V. Building high-level features using large scale unsupervised learning. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 8595–8598. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollar, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar] [CrossRef]
- Heikkila, J.; Silven, O. A four-step camera calibration procedure with implicit image correction. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, Puerto Rico, USA, 17–19 June 1997; IEEE: New York, NY, USA, 1997; pp. 1106–1112. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef]
- Shelhamer, E.; Long, J.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar] [CrossRef] [PubMed]
- Perez, L.; Wang, J. The Effectiveness of Data Augmentation in Image Classification using Deep Learning. Available online: https://arxiv.org/abs/1712.04621 (accessed on 13 December 2017).
- Detert, M.; Kadinski, L.; Weitbrecht, V. On the way to airborne gravelometry based on 3D spatial data derived from images. Int. J. Sediment Res. 2018, 33, 84–92. [Google Scholar] [CrossRef]
- Letortu, P. Le recul des falaises crayeuses haut-normandes et les inondations par la mer en Manche centrale et orientale: De la qualification de l’aléa à la caracterisation des risques induits (Retreat of the High-Normandy Chalk Cliffs and Flooding by the Sea in the Central and Eastern Channel: From the Identification of Hazards to the Characterization of the Induced Risks). Ph.D. Thesis, University of Caen Normandy, Caen, France, 2013. [Google Scholar]
- Cerema. Fiches synthétiques de mesure des états de mer Tome 1—Mer du Nord, Manche et Atlantique; Cerema: Bron, France, 2020; ISBN 9782371804333. [Google Scholar]
- Costa, S.; Maquaire, O.; Letortu, P.; Thirard, G.; Compain, V.; Roulland, T.; Medjkane, M.; Davidson, R.; Graff, K.; Lissak, C.; et al. Sedimentary Coastal Cliffs of Normandy: Modalities and Quantification of Retreat. J. Coast. Res. 2019, 88, 46–60. [Google Scholar] [CrossRef]
- Jennings, R.; Shulmeister, J. A field based classification scheme for gravel beaches. Mar. Geol. 2002, 186, 211–228. [Google Scholar] [CrossRef]
- Laboratoire Central d’Hydraulique de France (LCHF). Étude de la Production des Galets sur le Littoral Haut-Normand (Study of the Pebble Production on the Shorelines of High-Normandy); Sitecmo: Dieppe, France, 1972. [Google Scholar]
- Bujan, N.; Cox, R.; Lin, L.C.; Ducrocq, C.; Hwung, H.H. Semiautomatic Digital Clast Sizing of a Cobble Beach, Nantian, Taiwan. J. Coast. Res. 2018, 34, 1367–1381. [Google Scholar] [CrossRef]
- Costa, S.; Lageat, Y.; Hénaff, A. The gravel beaches of north-west France and their contribution to the dynamic of the coastal cliff-shore platform system. Ann. Geomorphol. 2006, 144, 199–214. [Google Scholar]
- Bertoni, D.; Dean, S.; Trembanis, A.C.; Sarti, G. Multi-month sedimentological characterization of the backshore of an artificial coarse-clastic beach in Italy. Rend. Lincei 2020, 31, 65–77. [Google Scholar] [CrossRef]
- Masselink, G.; Evans, D.; Hughes, M.G.; Russell, P. Suspended sediment transport in the swash zone of a dissipative beach. Mar. Geol. 2006, 216, 169–189. [Google Scholar] [CrossRef]
- Guza, R.T.; Thornton, E.B. Swash oscillations on a natural beach. J. Geophys. Res. Ocean. 1982, 87, 483–491. [Google Scholar] [CrossRef]
- Holman, R.A. Edge waves and the configuration of the shoreline. In Handbook of Coastal Processes and Erosion; CRC Press: Boca Raton, FL, USA, 2018; pp. 21–34. [Google Scholar]
- Aagaard, T. Swash oscillations on dissipative beaches-Implications for beach erosion. J. Coast. Res. 1990, 738–752. Available online: www.jstor.org/stable/44868669 (accessed on 7 November 2020).
- Sarti, G.; Bertoni, D. Monitoring backshore and foreshore gravel deposits on a mixed sand and gravel beach (Apuane-Versilia coast, Tuscany, Italy). GeoActa 2007, 6, 73–81. [Google Scholar]
- Ciavola, P.; Castiglione, E. Sediment dynamics of mixed sand and gravel beaches at short timescales. J. Coast. Res. 2009, II, 1751–1755. [Google Scholar]
- Zingg, T. Beitrag zur schotteranalyse (Contribution to Ballast Analysis). Ph.D. Thesis, University of Zurich, Zurich, Switzerland, 1935. [Google Scholar]
- Wadell, H. Volume, shape, and roundness of rock particles. J. Geol. 1932, 40, 443–451. [Google Scholar] [CrossRef]















| Date | Profile | Quantile | p-Value | Tau | Slope |
|---|---|---|---|---|---|
| 2020/03/05 | A n = 6 | D10 | 0.06 | –0.73 | –0.55 |
| D50 | 0.13 | –0.60 | –1.26 | ||
| D90 | 0.71 | –0.20 | –0.95 | ||
| D n = 6 | D10 | 0.85 | –0.07 | –0.64 | |
| D50 | 0.45 | –0.33 | –1.21 | ||
| D90 | 0.85 | –0.07 | –0.47 | ||
| F n = 10 | D10 | 0.07 | –0.47 | –1.01 | |
| D50 | 0.03 | –0.56 | –1.54 | ||
| D90 | 0.11 | –0.42 | –1.63 | ||
| 2020/03/13 | B n = 6 | D10 | 0.26 | 0.47 | 1.08 |
| D50 | 0.06 | 0.73 | 2.53 | ||
| D90 | 0.06 | 0.73 | 4.76 | ||
| C n = 3 | D10 | 0.60 | –0.33 | –0.35 | |
| D50 | 0.60 | –0.33 | –0.15 | ||
| D90 | 0.60 | 0.33 | 1.01 | ||
| E n = 7 | D10 | 0.55 | 0.24 | 0.29 | |
| D50 | 0.07 | 0.62 | 0.80 | ||
| D90 | 0.23 | 0.43 | 1.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soloy, A.; Turki, I.; Fournier, M.; Costa, S.; Peuziat, B.; Lecoq, N. A Deep Learning-Based Method for Quantifying and Mapping the Grain Size on Pebble Beaches. Remote Sens. 2020, 12, 3659. https://doi.org/10.3390/rs12213659
Soloy A, Turki I, Fournier M, Costa S, Peuziat B, Lecoq N. A Deep Learning-Based Method for Quantifying and Mapping the Grain Size on Pebble Beaches. Remote Sensing. 2020; 12(21):3659. https://doi.org/10.3390/rs12213659
Chicago/Turabian StyleSoloy, Antoine, Imen Turki, Matthieu Fournier, Stéphane Costa, Bastien Peuziat, and Nicolas Lecoq. 2020. "A Deep Learning-Based Method for Quantifying and Mapping the Grain Size on Pebble Beaches" Remote Sensing 12, no. 21: 3659. https://doi.org/10.3390/rs12213659
APA StyleSoloy, A., Turki, I., Fournier, M., Costa, S., Peuziat, B., & Lecoq, N. (2020). A Deep Learning-Based Method for Quantifying and Mapping the Grain Size on Pebble Beaches. Remote Sensing, 12(21), 3659. https://doi.org/10.3390/rs12213659