Reconstruction of Spatiotemporally Continuous MODIS-Band Reflectance in East and South Asia from 2012 to 2015
Abstract
:1. Introduction
2. Model and Method
2.1. BRDF Model
2.2. Algorithm for the Reconstruction of MODIS-Band Reflectance
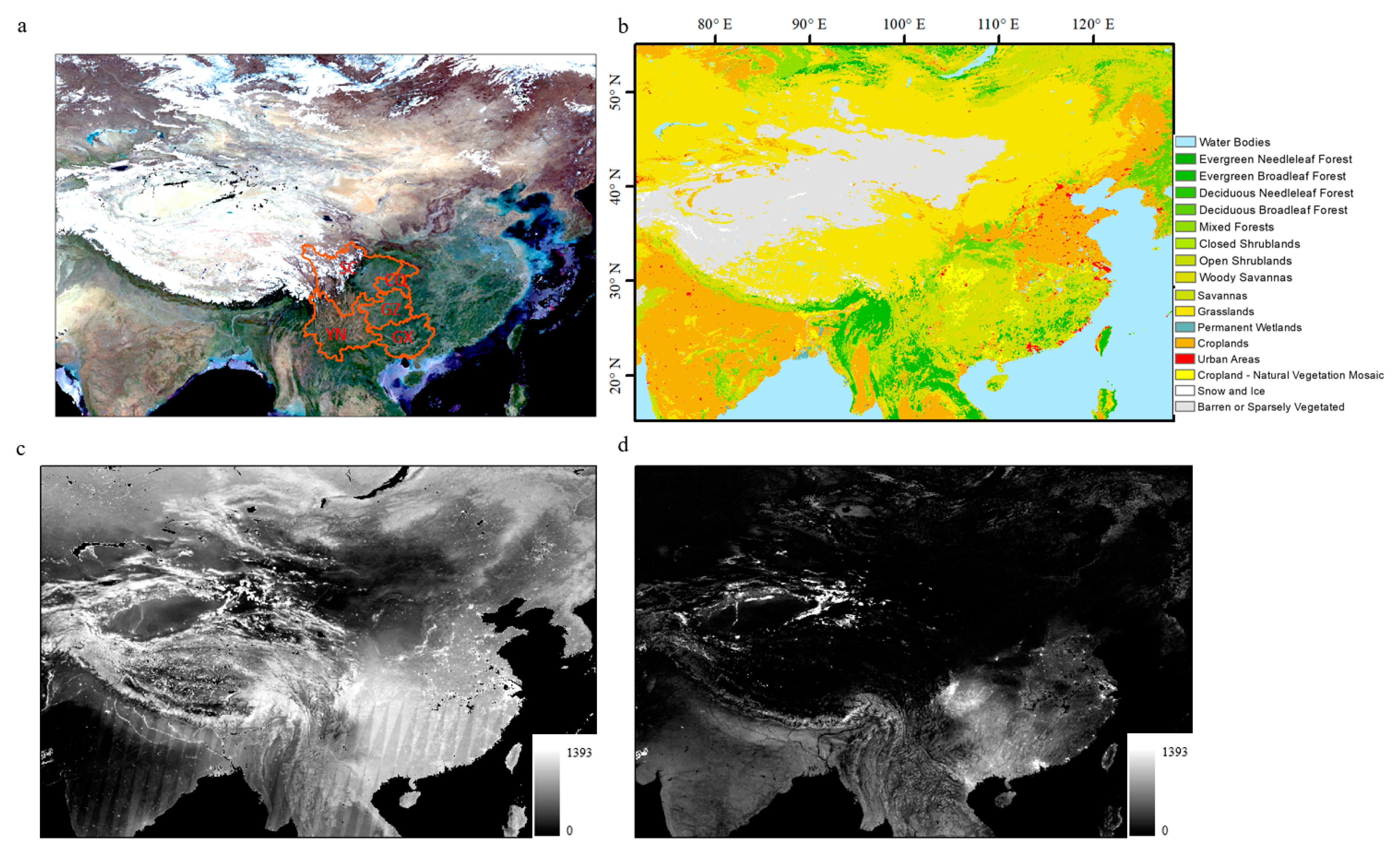
3. Experimental Area and Data
4. Result
4.1. Retrieval of MODIS Band Reflectance Based on the BRDF Models
4.2. Performance in the Reconstruction of Spatiotemporally Continuous MODIS-Band Reflectance
5. Discussion
5.1. Spatiotemporal Distribution of the Precision of the Derived MODIS Band Reflectance based on the BRDF Models
5.2. Evaluation of Derived Shortwave Reflectance based on the Three BRDF Models
5.3. Quantification of the Improvement in Spatiotemporal Continuity for the Reconstruction of MODIS-Band Reflectance
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wulder, M.A.; Loveland, T.R.; Roy, D.P.; Crawford, C.J.; Masek, J.G.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Belward, A.S.; Cohen, W.B.; et al. Current status of Landsat program, science, and applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef] [PubMed]
- Claverie, M.; Vermote, E.; Franch, B.; Masek, J.G. Evaluation of the Landsat-5 TM and Landsat-7 ETM+ surface reflectance products. Remote Sens. Environ. 2015, 169, 390–403. [Google Scholar] [CrossRef]
- Mira, M.; Weiss, M.; Baret, F.; Courault, D.; Hagolle, O.; Gallego-Elvira, B.; Olioso, A. The MODIS (collection V006) BRDF/albedo product MCD43D: Temporal course evaluated over agricultural landscape. Remote Sens. Environ. 2015, 170, 216–228. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Wang, T.; Shi, J.; Yu, Y.; Husi, L.; Gao, B.; Zhou, W.; Ji, D.; Zhao, T.; Xiong, C.; Chen, L. Cloudy-sky land surface longwave downward radiation (LWDR) estimation by integrating MODIS and AIRS/AMSU measurements. Remote Sens. Environ. 2018, 205, 100–111. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.P. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Jia, L.; Menenti, M. Reconstruction of global MODIS NDVI time series: Performance of Harmonic ANalysis of Time Series (HANTS). Remote Sens. Environ. 2015, 163, 217–228. [Google Scholar] [CrossRef]
- Tavakol, A.; Rahmani, V.; Quiring, S.M.; Kumar, S.V. Evaluation analysis of NASA SMAP L3 and L4 and SPoRT-LIS soil moisture data in the United States. Remote Sens. Environ. 2019, 229, 234–246. [Google Scholar] [CrossRef]
- Justice, C.; Townshend, J.; Vermote, E.; Masuoka, E.; Wolfe, R.; Saleous, N.; Roy, D.; Morisette, J. An overview of MODIS Land data processing and product status. Remote Sens. Environ. 2002, 83, 3–15. [Google Scholar] [CrossRef]
- Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Tao, S.; Fang, J.; Ma, S.; Cai, Q.; Xiong, X.; Tian, D.; Zhao, X.; Fang, L.; Zhang, H.; Zhu, J. Changes in China’s lakes: Climate and human impacts. Natl. Sci. Rev. 2020, 7, 132–140. [Google Scholar] [CrossRef] [Green Version]
- Ronghua, M. A half-century of changes in China’s lakes: Global warming or human influence? Geophysical Research Letters 2010. [Google Scholar] [CrossRef]
- Wang, M.; Du, L.; Ke, Y.; Huang, M.; Zhang, J.; Zhao, Y.; Li, X.; Gong, H. Impact of Climate Variabilities and Human Activities on Surface Water Extents in Reservoirs of Yongding River Basin, China, from 1985 to 2016 Based on Landsat Observations and Time Series Analysis. Remote Sens. 2019, 11, 560. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Yao, T.; Chen, W.; Zheng, G.; Shum, C.K.; Yang, K.; Piao, S.; Sheng, Y.; Yi, S.; Li, J. Regional differences of lake evolution across China during 1960s-2015 and its natural and anthropogenic causes. Remote Sens. Environ. 2018, 221, 386–404. [Google Scholar] [CrossRef]
- Cover, M.L.; Change, L.-C. MODIS Land Cover Product Algorithm Theoretical Basis Document (ATBD) Version 5.0; 1999. Available online: https://modis.gsfc.nasa.gov/data/atbd/atbd_mod12.pdf (accessed on 5 November 2020).
- Cui, Y.; Zeng, C.; Zhou, J.; Xie, H.; Wan, W.; Hu, L.; Xiong, W.; Chen, X.; Fan, W.; Hong, Y. A spatio-temporal continuous soil moisture dataset over the Tibet Plateau from 2002 to 2015. Sci. Data 2019, 6, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Anderson, M.; Daughtry, C.; Johnson, D. Assessing the variability of corn and soybean yields in central Iowa using high spatiotemporal resolution multi-satellite imagery. Remote Sens. 2018, 10, 1489. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.H.; Lai, K.H.; Chen, Z.B.; Chen, J.Y. Patch-Based Information Reconstruction of Cloud-Contaminated Multitemporal Images. IEEE Trans. Geosci. Remote. Sens. 2014, 52, 163–174. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z.-L. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote. Sens. 1997, 35, 980–996. [Google Scholar]
- Huete, A.; Justice, C.; Van Leeuwen, W. MODIS vegetation index (MOD13). In Algorithm Theor. Basis Doc.; 1999; 4. Available online: https://modis.gsfc.nasa.gov/data/atbd/atbd_mod13.pdf (accessed on 5 November 2020).
- Strahler, A.H.; Muller, J.; Lucht, W.; Schaaf, C.; Tsang, T.; Gao, F.; Li, X.; Lewis, P.; Barnsley, M.J. MODIS BRDF/albedo product: Algorithm theoretical basis document version 5.0. MODIS Doc. 1999, 23, 42–47. [Google Scholar]
- Tang, X.; Bullock, E.L.; Olofsson, P.; Woodcock, C.E. Can VIIRS continue the legacy of MODIS for near real-time monitoring of tropical forest disturbance. Remote Sens. Environ. 2020, 249, 112024. [Google Scholar] [CrossRef]
- Strugnell, N.C.; Lucht, W.; Hyman, A.H.; Meister, G. Continental-scale albedo inferred from land cover class, field observations of typical BRDFs and AVHRR data. In Proceedings of the IGARSS’98. Sensing and Managing the Environment. 1998 IEEE International Geoscience and Remote Sensing. Symposium Proceedings, (Cat. No. 98CH36174), Seattle, WA, USA, 6–10 July 1998; pp. 595–597. [Google Scholar]
- Strugnell, N.C.; Lucht, W. An algorithm to infer continental-scale albedo from AVHRR data, land cover class, and field observations of typical BRDFs. J. Clim. 2001, 14, 1360–1376. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.O.; Bréon, F.-M. Towards a generalized approach for correction of the BRDF effect in MODIS directional reflectances. IEEE Trans. Geosci. Remote. Sens. 2008, 47, 898–908. [Google Scholar] [CrossRef]
- Zhang, H.; Jiao, Z.T.; Chen, L.; Dong, Y.D.; Zhang, X.N.; Lian, Y.; Qian, D.; Cui, T.J. Quantifying the Reflectance Anisotropy Effect on Albedo Retrieval from Remotely Sensed Observations Using Archetypal BRDFs. Remote Sens. 2018, 10, 1628. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Jiao, Z.T.; Dong, Y.D.; Du, P.; Li, Y.; Lian, Y.; Cui, T.J. Analysis of Extracting Prior BRDF from MODIS BRDF Data. Remote Sens. 2016, 8, 1004. [Google Scholar] [CrossRef] [Green Version]
- Jiao, Z.T.; Hill, M.J.; Schaaf, C.B.; Zhang, H.; Wang, Z.S.; Li, X.W. An Anisotropic Flat Index (AFX) to derive BRDF archetypes from MODIS. Remote Sens. Environ. 2014, 141, 168–187. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.F.; Sobrino, J.A.; Julien, Y. Retrieval of Surface Albedo on a Daily Basis: Application to MODIS Data. IEEE Trans. Geosci. Remote. Sens. 2014, 52, 7549–7558. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.F.; Claverie, M. Intercomparison of Landsat albedo retrieval techniques and evaluation against in situ measurements across the US SURFRAD network. Remote Sens. Environ. 2014, 152, 627–637. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.; Skakun, S.; Roger, J.; Masek, J.G.; Ju, J.; Villaescusanadal, J.L.; Santamariaartigas, A. A Method for Landsat and Sentinel 2 (HLS) BRDF Normalization. Remote Sens. 2019, 11, 632. [Google Scholar] [CrossRef] [Green Version]
- Franch, B.; Vermote, E.; Skakun, S.; Roger, J.C.; Santamaria-Artigas, A.; Villaescusa-Nadal, J.L.; Masek, J. Toward Landsat and Sentinel-2 BRDF Normalization and Albedo Estimation: A Case Study in the Peruvian Amazon Forest. Front. Earth Sci. 2018, 6. [Google Scholar] [CrossRef] [Green Version]
- Gao, B.; Gong, H.; Wang, T.; Zhou, J. An Improved Bidirectional Reflectance Distribution Function (BRDF) Model that Considers Soil Moisture and the Normalized Difference Vegetation Index (NDVI). IEEE Trans. Geosci. Remote. Sens. 2020. (under review). [Google Scholar]
- Zeng, J.Y.; Chen, K.S.; Bi, H.Y.; Chen, Q. A Preliminary Evaluation of the SMAP Radiometer Soil Moisture Product Over United States and Europe Using Ground-Based Measurements. IEEE Trans. Geosci. Remote. Sens. 2016, 54, 4929–4940. [Google Scholar] [CrossRef]
- Roujean, J.L. A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data. J. Geophys. Res. 1992, 97, 20455–420468. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Strahler, A.H. Solar Zenith Angle Effects on Forest Canopy Hemispherical Reflectances Calculated with a Geometric-Optical Bidirectional Reflectance Model. IEEE Trans. Geosci. Remote. Sens. 1993, 31, 921–927. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Strahler, A.H. Simulating the Bidirectional and Hemispherical Reflectance of Mountainous and Forested Scenes with a Geometric-Optical Model. In Proceedings of the Seventh Conference on Satellite Meteorology and Oceanography, Monterey, CA, USA, 6–10 June 1994; pp. 602–604. [Google Scholar]
- Wanner, W.; Li, X.; Strahler, A.H. On the Derivation of Kernels for Kernel-Driven Models of Bidirectional Reflectance. J. Geophys. Res.-Atmos. 1995, 100, 21077–21089. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H. Geometric-optical bidirectional reflectance modeling of a conifer forest canopy. IEEE Trans. Geosci. Remote Sens. 1986, 906–919. [Google Scholar] [CrossRef]
- Cui, C.Y.; Xu, J.; Zeng, J.Y.; Chen, K.S.; Bai, X.J.; Lu, H.; Chen, Q.; Zhao, T.J. Soil Moisture Mapping from Satellites: An Intercomparison of SMAP, SMOS, FY3B, AMSR2, and ESA CCI over Two Dense Network Regions at Different Spatial Scales. Remote Sens. 2018, 10, 33. [Google Scholar] [CrossRef] [Green Version]
- Wagner, W.; Dorigo, W.; de Jeu, R.; Fernandez, D.; Benveniste, J.; Haas, E.; Ertl, M. Fusion of active and passive microwave observations to create an essential climate variable data record on soil moisture. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2012, 7, 315–321. [Google Scholar]
- Jin, Y.F.; Schaaf, C.B.; Woodcock, C.E.; Gao, F.; Li, X.W.; Strahler, A.H.; Lucht, W.; Liang, S.L. Consistency of MODIS surface bidirectional reflectance distribution function and albedo retrievals: 2. Validation. J. Geophys. Res.-Atmos. 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Cescatti, A.; Marcolla, B.; Vannan, S.K.S.; Pan, J.Y.; Román, M.O.; Yang, X.; Ciais, P.; Cook, R.B.; Law, B.E.; Matteucci, G. Intercomparison of MODIS albedo retrievals and in situ measurements across the global FLUXNET network. Remote Sens. Environ. 2012, 121, 323–334. [Google Scholar] [CrossRef] [Green Version]
- Román, M.O.; Gatebe, C.K.; Shuai, Y.; Wang, Z.; Gao, F.; Masek, J.G.; He, T.; Liang, S.; Schaaf, C.B. Use of in situ and airborne multiangle data to assess MODIS-and Landsat-based estimates of directional reflectance and albedo. IEEE Trans. Geosci. Remote. Sens. 2013, 51, 1393–1404. [Google Scholar] [CrossRef]
- Shuai, Y.M.; Masek, J.G.; Gao, F.; Schaaf, C.B. An algorithm for the retrieval of 30-m snow-free albedo from Landsat surface reflectance and MODIS BRDF. Remote Sens. Environ. 2011, 115, 2204–2216. [Google Scholar] [CrossRef]
- Qu, Y.; Liu, Q.; Liang, S.L.; Wang, L.Z.; Liu, N.F.; Liu, S.H. Direct-Estimation Algorithm for Mapping Daily Land-Surface Broadband Albedo From MODIS Data. IEEE Trans. Geosci. Remote. Sens. 2013, 52, 907–919. [Google Scholar] [CrossRef]
- Liang, S.L.; Strahler, A.H.; Walthall, C. Retrieval of land surface albedo from satellite observations: A simulation study. J. Appl. Meteorol. 1999, 38, 712–725. [Google Scholar] [CrossRef]
- Wang, Z.; Schaaf, C.B.; Strahler, A.H.; Chopping, M.J.; Román, M.O.; Shuai, Y.; Woodcock, C.E.; Hollinger, D.Y.; Fitzjarrald, D.R. Evaluation of MODIS albedo product (MCD43A) over grassland, agriculture and forest surface types during dormant and snow-covered periods. Remote Sens. Environ. 2014, 140, 60–77. [Google Scholar] [CrossRef] [Green Version]









| Data | Data Set Name | Spatiotemporal Coverage | Resolution |
|---|---|---|---|
| Soil moisture | EVC soil moisture Interpolated by GRNN | UL: 70°E, 55°N, DR: 130°E, 15°N; and from 2012 to 2015 | 0.05° and daily |
| NDVI | MOD09CMG V006 Interpolated by HANTS | UL: 70°E, 55°N, DR: 130°E, 15°N; and from 2012 to 2015 | 0.05° and daily |
| Spectral reflectance | MOD09 CMG V006 | UL: 70°E, 55°N, DR: 130°E, 15°N; and from 2012 to 2015 | 0.05° and daily |
| BRDF parameters | MCD43C1 V006 | UL: 70°E, 55°N, DR: 130°E, 15°N; and from 2012 to 2015 | 0.05° and daily |
| Land cover | MCD12Q1 V006 | UL: 70°E, 55°N, DR: 130°E, 15°N; and from 2012 to 2015 | 0.05° and yearly |
| Band | Band 1 | Band 2 | Band 3 | Band 4 | Band 5 | Band 6 | Band 7 | Shortwave | |
|---|---|---|---|---|---|---|---|---|---|
| Bandwidth (NM) | 620–670 | 841–876 | 459–479 | 545–565 | 1230–1250 | 1628–1652 | 2105–2155 | 400–2500 | |
| 268 day | RTLSR | 34.6 | 18.9 | 64.1 | 40.4 | 8.2 | 10.9 | 16.4 | 19.6 |
| Gao | 16.7 | 11.4 | 27.7 | 18.3 | 7.0 | 7.6 | 11.0 | 9.8 | |
| Adjusted BF | 26.3 | 16.5 | 52.8 | 33.1 | 7.1 | 9.3 | 12.9 | 16.4 | |
| 188 day | RTLSR | 34.4 | 16.6 | 53.8 | 33.8 | 7.6 | 9.6 | 14.6 | 17.9 |
| Gao | 15.5 | 10.7 | 26.6 | 17.2 | 6.5 | 7.0 | 9.9 | 9.7 | |
| Adjusted BF | 25.1 | 13.7 | 44.0 | 27.7 | 6.4 | 7.7 | 10.7 | 14.7 | |
| 108 day | RTLSR | 28.0 | 14.4 | 45.8 | 28.7 | 6.6 | 8.3 | 12.3 | 15.4 |
| Gao | 13.8 | 9.3 | 24.2 | 15.6 | 5.7 | 6.2 | 8.7 | 9.7 | |
| Adjusted BF | 19.2 | 10.6 | 36.2 | 22.8 | 5.3 | 6.5 | 8.9 | 12.5 | |
| Band 1 | Band 2 | Band 3 | Band 4 | Band 5 | Band 6 | Band 7 | ||
|---|---|---|---|---|---|---|---|---|
| Bandwidth (NM) | 620–670 | 841–876 | 459–479 | 545–565 | 1230–1250 | 1628–1652 | 2105–2155 | |
| 268 day | MCD43C1 | 9.6 | 6.7 | 21.4 | 14.0 | 5.2 | 5.4 | 8.5 |
| RTLSR | 33.8 | 18.1 | 60.7 | 39.0 | 8.1 | 10.4 | 21.6 | |
| Gao | 16.7 | 11.6 | 28.1 | 18.4 | 7.1 | 7.6 | 12.8 | |
| Adjusted BF | 24.9 | 15.4 | 49.4 | 31.1 | 7.0 | 8.8 | 17.3 | |
| 188 day | MCD43C1 | 9.5 | 6.7 | 21.3 | 13.9 | 5.1 | 5.4 | 7.3 |
| RTLSR | 31.3 | 16.8 | 54.5 | 34.5 | 7.5 | 9.7 | 14.7 | |
| Gao | 15.7 | 10.7 | 26.7 | 17.3 | 6.6 | 7.1 | 10.0 | |
| Adjusted BF | 23.2 | 13.4 | 44.1 | 27.7 | 6.3 | 7.9 | 10.9 | |
| 108 day | MCD43C1 | 9.3 | 6.5 | 20.2 | 13.3 | 5.1 | 5.3 | 7.2 |
| RTLSR | 23.2 | 13.9 | 42.3 | 26.7 | 6.5 | 8.2 | 12.1 | |
| Gao | 13.7 | 9.1 | 23.6 | 15.3 | 5.6 | 6.2 | 8.6 | |
| Adjusted BF | 17.5 | 10.2 | 34.2 | 21.5 | 5.2 | 6.4 | 8.8 |
| Band 1 | Band 2 | Band 3 | Band 4 | Band 5 | Band 6 | Band 7 | Shortwave | |
|---|---|---|---|---|---|---|---|---|
| Bandwidth (NM) | 620–670 | 841–876 | 459–479 | 545–565 | 1230–1250 | 1628–1652 | 2105–2155 | 400–2500 |
| MODIS | 0.3973 | 0.2382 | 0.3489 | −0.2655 | 0.1604 | −0.0138 | 0.0682 | 0.0036 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, B.; Gong, H.; Zhou, J.; Wang, T.; Liu, Y.; Cui, Y. Reconstruction of Spatiotemporally Continuous MODIS-Band Reflectance in East and South Asia from 2012 to 2015. Remote Sens. 2020, 12, 3674. https://doi.org/10.3390/rs12213674
Gao B, Gong H, Zhou J, Wang T, Liu Y, Cui Y. Reconstruction of Spatiotemporally Continuous MODIS-Band Reflectance in East and South Asia from 2012 to 2015. Remote Sensing. 2020; 12(21):3674. https://doi.org/10.3390/rs12213674
Chicago/Turabian StyleGao, Bo, Huili Gong, Jie Zhou, Tianxing Wang, Yuanyuan Liu, and Yaokui Cui. 2020. "Reconstruction of Spatiotemporally Continuous MODIS-Band Reflectance in East and South Asia from 2012 to 2015" Remote Sensing 12, no. 21: 3674. https://doi.org/10.3390/rs12213674
APA StyleGao, B., Gong, H., Zhou, J., Wang, T., Liu, Y., & Cui, Y. (2020). Reconstruction of Spatiotemporally Continuous MODIS-Band Reflectance in East and South Asia from 2012 to 2015. Remote Sensing, 12(21), 3674. https://doi.org/10.3390/rs12213674






