1. Introduction
Spatially explicit information about tree species distribution and other forest parameters, such as height, crown cover, and biomass, are valuable for various ecological applications, the parametrization of land surface models, and forest management. Forests regulate climate and biogeochemical cycles and represent an important terrestrial carbon reservoir [
1]. As a result of climate change, Europe will likely experience higher temperatures and more frequent and severe droughts in the future [
2]. The combination of increased heat and drought may lead to higher fire risk in Mediterranean Europe but also in temperate and boreal ecosystems in Europe [
3]. Fire spread and severity depend largely on fuel flammability, which in forest ecosystems is among other factors dependent on the dominant tree species. Different tree species vary in crown openness, wood moisture content, and litter flammability, factors driving fuel flammability, and fire behaviour in forests [
4,
5]. Knowing the tree species distribution in a particular area is thus helpful for forest fire prevention and management. Besides the use of detailed tree species distribution maps in forest fire prevention, such maps would be useful for other ecological applications and fields, for example, sustainable forest management, which aims to conserve biological diversity in forests [
6], as well as close-to-nature forest management, in which monospecific plantations are transformed to heterogeneous mixed-species stands that more closely resemble natural forests [
7]. However, the sheer number of trees present in a particular forest limits the manual identification and classification of individual trees in detailed maps and asks for an automated approach.
Remote sensing is particularly useful for data acquisition needed for large scale forest monitoring, since it enables the acquisition of data over large areas at a high level of detail with a synoptic view. In this way, remote sensing has the potential to complement field inventories [
8].
For the classification of individual trees at the species level, both high spatial and high spectral resolution data are desired [
9,
10]. Tree species and forest types classifications have used remote sensing datasets with different spectral resolutions [
11,
12,
13,
14,
15]. Multispectral data are nowadays widely and freely available and have shown potential for classification of tree species and forest types at individual tree level, e.g., [
10,
11,
12,
13,
14,
15,
16,
17,
18,
19]. These studies, however, require manual delineation of individual tree crowns, which is quite labour-intensive and thus cannot be easily applied over large areas [
20].
Species classification at individual tree level can be challenging due to the fact that the spectral signature retrieved from trees is, amongst others, influenced by its biochemical properties, canopy structure, forest maturity, and acquisition conditions [
21]. The spectral signature that satellites measure is composed of the combination of reflectance from tree crown, tree crown shadows, illuminated and shadowed parts of tree crowns, and from the understory, e.g., soil, herbaceous vegetation, and litter [
22]. The understory reflectance thus has an effect on the identification of tree species in open forests when pixel classification is used [
11]. Object-based classification, which in this case is the classification of individual tree crowns as separate objects, minimizes the spectral mixture of tree and understory reflectance by grouping pixels that belong to the same tree crown [
22,
23,
24,
25]. For each tree crown, spectral and crown structural information, the latter describing the geometrical properties of a tree crown, can be extracted and included in classification algorithms [
12].
To classify tree species, both parametric and non-parametric classification algorithms have been used [
7,
12,
22]; parametric algorithms include maximum likelihood and Bayesian methods [
11]. Non-parametric classifiers do not make any assumptions about the shape of the model function. The non-parametric classifier random forest (RF) is robust against noise, and the setup is simple when compared to other non-parametric methods [
26,
27]. Previous studies have applied the RF model to classify tree species using multispectral satellite data [
28] or crown structural data derived from airborne laser scanning (ALS) data as explanatory variables or features in the model. Furthermore, RF models have previously been used on crown structural and spectral data combined in a single classification [
29,
30], which has shown to improve the classification accuracy [
31] compared to using only structural data. Another potential layer of information that could be utilized in an RF or similar model is the phenological variation between tree species. In temperate forests, biophysical and structural properties of the tree canopy change with the changing seasons as a result of flowering, leaf-onset, and, in winter, deciduous trees by leaf senescence. These phenological changes vary widely among different tree species [
32], and species variation can be captured with multitemporal imagery [
15,
33,
34].
The aim of our study is to develop a new method to automatically map tree crowns and to classify those crowns to species level using multitemporal Sentinel-2 imagery from four consecutive seasons (autumn 2018–summer 2019) and crown structural variables derived from ALS data. To the best of our knowledge, we are the first to combine fully automatic tree crown segmentation with a tree species classification model in a single method. We applied our method to map individual trees in a mixed temperate forest area in The Netherlands and classified these trees at species and phylum level (angiosperm vs. gymnosperm).
2. Materials and Methods
2.1. Study Area
The study area is situated in the Veluwe, the largest contiguous forest in The Netherlands (52°11′–52°24′ N, 5°71′–5°92′ E, WGS84). Our study area covers the central part of the Veluwe and is located west of the town Apeldoorn and north of the Nationaal Park De Hoge Veluwe. The Netherlands have a temperate oceanic climate with an average annual precipitation of 832.5 mm and average air temperature of 14.1 °C [
35].
The Veluwe is characterized by the presence of push moraines and other glacial geomorphological landscape elements. The landscape was formed during the second last glacial, the Saale glaciation (300—130 kyr BP). In the last ice age, the Weichselian glaciation (115—11.7 kyr BP), aeolian coversands were deposited. Due to deforestation and subsequent overgrazing since the 12th century, more than half of the Veluwe was converted from forest to open heathlands and drift sands by the 19th century [
36]. As the soil in these areas deteriorated and the heathlands largely lost their agricultural use by the end of the 19th century, large tracts of unproductive heathland were planted with mostly coniferous tree species. Scots pine (
Pinus sylvestris) was planted in poor heathland areas, while on more fertile soils, forests of broadleaved trees and Douglas fir (
Pseudotsuga menziesii) were preferred [
37]. The eight most common species in our study area were found to be European beech (
Fagus sylvatica), Douglas fir (
Pseudotsuga menziesii), Japanese larch (
Larix kaempferi), northern red oak (
Quercus rubra), Scots pine (
Pinus sylvestris), silver birch (
Betula pendula), Norway spruce (
Picea abies), and common oak (
Quercus robur) (
Appendix A Figure A1 and
Figure A2).
Our study area covers approximately 140 km
2 of broadleaved, coniferous, and mixed forests, large unvegetated drift sands areas, and heathlands, but also anthropogenic structures such as buildings and roads (
Figure 1).
2.2. Field Data
Two field surveys of 12 days were conducted, one in May 2019 and a subsequent survey in December 2019 (
Figure 1). Trees were measured separately (n = 1743) and in plots (n = 479). The location of sample sites was selected based on the vegetation structure and the species composition being representative for the larger study area and by bike accessibility. In total, 17 plots of 30 by 30 m were established and measured in May 2019. The plots were located in heterogeneous forest stands located more than 3 m away from roads and distributed over the entire study area (
Figure 1). For each individual tree, the location of the trees was logged using a Trimble Geo 7X Handheld Data Collector (1–100 cm accuracy), which used more than 50 independent and differentially corrected GPS recordings to determine the final position. The horizontal position of the samples had a final average uncertainty of 0.5–1 m. Furthermore, for each tree, the diameter at breast height (DBH, range 1.9–129.9 cm) was measured using a measuring tape. Finally, the average crown width was determined as the average of four perpendicular radii of the tree branches. The length of the four radii were assessed by visually determining the crown extent and then measuring the distance between the maximum crown extent and the tree trunk with a Bosch laser PLR 50 C (±2 mm accuracy). The tree crown area (range: 1.1–352.9 m
2) was then calculated from these data as the surface of an ellipse (crown area = π ∗ a ∗ b; in which a and b are the mean of the two largest and two smallest radii, respectively).
The number of trees per plot ranged between 13 and 53, with an average of 27 trees. During the field campaign in May 2019, we sampled 268 individual trees and collected data of 26 different tree species. The number of trees per species are shown in
Table 1. The samples of the eight most common species were used for the classification on tree species level. All 26 species were used for the classification on phylum, angiosperm or gymnosperm, level.
In December 2019, two days of additional field data collection were carried out to survey another 1475 individual trees of the eight most common species (
Table 1). The location of homogeneous stands was determined by aerial photograph interpretation. During this survey, only the tree species and location were determined.
To exclude anthropogenic features from the tree species and phylum analysis, polygons overlapping houses, roads, or other human made features were identified as anthropogenic features (n = 238). This classification was based on the interpretation of Sentinel-2 imagery.
2.3. Digital Elevation Model and Pre-Processing
We used the national digital elevation model (DEM) of The Netherlands (Actueel Hoogtebestand Nederland, AHN) to construct a canopy height model (CHM) for the study area. The AHN is a collaboration between the regional water authorities, provinces, and Directorate-General for Public Works and Water Management that has resulted in an ALS derived high resolution DEM of The Netherlands over multiple years [
38]. The ALS acquisition flights over our study area were carried out between December and March 2017/2018, when winter deciduous trees do not have leaves.
The recording resulted in a point cloud, which was calibrated and classified by the Directorate-General for Public Works and Water Management, leading to two different datasets. The digital terrain model (DTM) consists of points that were classified as ground level. For every pixel of 50 cm by 50 cm, the value that represents the centre of the cell was calculated with the squared inverse distance weighting method. The other dataset is the digital surface model (DSM). This dataset contains points that do not represent the ground level but instead vegetation or buildings [
39]. Both the DTM and the DSM were freely downloaded from the portal of Publieke Dienstverlening Op de Kaart (PDOK). Eleven tiles that were recorded in 2018 covered the entire study area. The error in height was 5 cm, and the horizontal resolution was 50 cm. The average point density was 6–10 points per m
2. For cells with no data, we calculated the height values using inverse distance weighting [
40] within a search radius of 60 m for the DTM and 160 m for the DSM. The CHM was constructed as the difference between the DSM and the DTM, thereby representing the actual height of the tree crowns at the same resolution of the DTM (
Figure 2).
2.4. Satellite Imagery and Pre-Processing
The spectral information of the individual tree crowns was extracted from Sentinel-2 imagery. The Sentinel-2 satellite program is part of Copernicus, an Earth observation program of the European Union. Sentinel-2 consists of two satellites that have a sun-synchronous polar orbit at 786 km altitude. Both satellites carry a multi-spectral instrument (MSI) with 13 spectral bands, covering the visible (VIS), the near infra-red (NIR), and the short wave infra-red (SWIR) at different spatial resolutions ranging from 10 to 60 m. The MSI is a passive, optical push-broom sensor with a swath width of 290 km. This results in a short revisit time of around five days, increasing the chance to get cloud free images [
41].
For image selection, we used two criteria, (1) images should be free of any cloud/haze cover in the study area, and (2) image acquisition time should be close to the date of the field data collection. The Sentinel images used were from 18 September 2018, 17 November 2018, 21 April 2019, and 26 August 2019 to enable the detection of phenological changes. We assumed that no significant changes in forest cover had taken place between the different acquisition dates.
The Sentinel-2 10 m resolution bands were downloaded via the external Semi-Automatic Classification Plugin (SCP, version 6.4.0.2) within Quantum GIS (QGIS, version 3.6.3). We included the blue (band 2, 490 nm), the green (band 3, 560 nm), the red (band 4, 665 nm), and the near infrared (band 8, 842 nm) bands (
Table 2). Subsequently, the Dark Object Subtraction 1 (DOS1) atmospheric correction within the SCP was performed on all images [
42]. A total of 16 images, 4 bands for each date, were clipped to the extent of the research area and subsequently stacked. The geographic coordinate system used during the analysis was set to EPSG:28992—Amersfoort/RD New—Projected.
2.5. Delineation of Tree Crowns
For tree species and phylum classification, we applied an object-based approach using automatically delineated tree crowns as spatial polygons (
Figure 2). The data processing and analyses were performed in R (version 3.6.0) and QGIS (version 3.6.3). The classification models were used to predict the species and phyla of all trees present in the entire study area.
We applied the method described by Popescu and Wyne [
43] to detect tree tops and delineate tree crowns. In the CHM, tree tops were detected using the R-package lidR (version 2.0.3) [
44]. This function applies a variable window technique with a local maximum (LM) filter. A pixel is identified as a local maximum when its neighbouring pixels have a lower height value [
45]. The LM filter has a circular or a square search window. The former was used in this study, since a circular window is a better approximation of a tree crown compared to a square [
43]. The search window size should be adjusted to a size that corresponds to the tree crown present on the CHM. The algorithm from lidR records the height of each pixel and calculates the search window size for the local maximum filter based on a predefined function that describes the relationship between tree height and crown area. The R-package ForestTools (version 0.2.0) [
46] was applied to delineate tree crowns from the tree top data and the CHM. This function implements a watershed segmentation to outline crowns from a CHM. It extends a region from the highest point, as long as the neighbouring pixels have a lower height value [
47].
The field-estimated crown area data allowed us to fit a tree crown area–height relationship to prescribe the search window size for the LM filter. We tested both linear (Crown area = a + b ∗ Height) and quadratic functions (Crown area = a + b ∗ Height
2), in which a and b represent the intercept and the slope of the relationship, respectively. The tree crown area–height relationship that best described our data was:
First, the root mean square error (RMSE) was calculated for the number of trees in each plot. The number of trees measured in the field were compared to the number of trees derived from the LM filter, for which a and b parameters were modified. The values of a and b of both the linear and the quadratic function that gave the lowest RMSE in the grid-search were chosen. The RMSE results with the different variables are shown in
Appendix A Figure A3 and
Table A1 and
Table A2. The linear function 1.2 + 0.3 ∗ Height resulted in a RMSE value of 11.47 trees. The RMSE value of the function 3.1 + 0.0091 ∗ Height
2 was 10.65 trees.
Second, the field-measured crown area was compared with the crown area derived from the automatically delineated tree crowns. The measured tree and the nearest derived tree top were coupled using distance matrix. This matrix measures the distance between the GPS location of the trees measured in the field and the coordinates of the derived tree tops. The RMSE of the tree crowns of the eight most common species are tabulated in
Appendix A Table A3. The function that gave the lowest RMSE for tree crowns was the linear function, which was chosen to delineate all tree tops and crowns in the study area, for which we applied a minimum threshold of 2 m tree height and 2 m
2 crown area.
2.6. Crown Structural and Spectral Information
For each delineated tree crown, we extracted several crown structural features from the CHM. These included minimum, maximum, sum, mean, median, standard deviation, range, and variance of tree height and crown projected surface area.
From the Sentinel-2 imagery, the mean spectral values for all downloaded bands were extracted to the delineated tree crowns using the R-package velox (version 0.2.0) [
48]. Centroids from the Sentinel-2 pixels that overlapped with the tree crowns were averaged for each individual crown. For small tree crowns that did not intersect with any Sentinel-2 pixel centroid, the spectral values of the nearest pixel centroid were assigned.
The location of the trees measured in the field were connected to the nearest centre of a delineated tree crown by using a distance matrix. The nearest distance ranged between 0.1 m and 16.8 m, and the mean distance was 2.4 m. Trees with a nearest distance larger than 6 m were excluded from the analysis. The mean crown area for those trees was 30.7 m2 (SD = 20.1 m2).
Delineated tree crowns sometimes covered multiple sampled trees, and those trees were connected to the same centre of the crown. In this case, we assigned the field-measured tree with the most similar crown area as from the delineated tree crown to this crown. This procedure slightly reduced the sample size (
Table 3).
2.7. Random Forest Classification
The random forest (RF) model, a non-parametric algorithm, has previously shown to perform well in tree species and group classifications [
26]. The RF model consists of an ensemble of decision trees. Each tree is constructed by taking an individual bootstrap sample randomly from the original training dataset. The tree consists of multiple nodes. At each node, the data are split according to the features, for instance, the maximum height or the value of a spectral band. At each node, a subset of features is randomly selected. The best-splitting feature is determined by the Gini criterion and subsequently chosen.
The classification error is estimated by using the samples that are not present in the bootstrap sample (out-of-bag data, OOB). The samples in the OOB dataset are classified by the corresponding decision tree. For each sample in the original dataset, the majority vote in classification outcomes of the decision trees is compared to the true label. This gives an estimate of the misclassification rate.
The explanatory power of the input variables is calculated by the mean decrease in accuracy (MDA) and the mean decrease in Gini (MDG). The MDA of a variable is assessed by randomly converting the values of the variable for the OOB data, while values of the other variables are kept constant. The misclassification rate is compared with the randomly commuted rate, resulting in the importance of the variable. The decreases in the splitting criterion Gini are summarised and normalized by the number of trees in the forest to calculate the MDG of a variable [
49].
In this study, we performed classifications based on different combinations of crown structural and spectral features. We tested the classification suitability of the following combinations of features: (1) both the crown structural variables and the spectral data from four seasons; (2) only the spectral data from four seasons; (3) only the crown structural variables; and (4) the crown structural variables in combination with spectral data from only one season.
We used the R-package randomForest (version 4.6.14) [
49,
50] for tree species and phylum classification. The RF model requires two parameters: (1) the number of input variables randomly split at each node, and (2) the number of classification trees or bootstrap iterations. The number of split variables (mtry) was optimised, which searches the optimal value of mtry compared to the OOB error. The number of trees (ntree) was set to 500. Using the VSURF R-package (version 1.1.0) [
51,
52] and the established mtry and ntree values, we selected uncorrelated and most relevant variables from the dataset. The data for each sampled tree species and anthropogenic features were randomly split; two thirds of each class were used to train the RF model on all classification combinations and levels. The remaining one third of the data were used to validate the RF model and to calculate the classification accuracies. The classification accuracies were based on the label (species or phylum) the delineated tree crown should have had based on field observations and what it was predicted to be by the RF model. Finally, for each automatically delineated tree crown in the entire research area, we predicted its species and phylum using the best performing RF model.
5. Conclusions
In this study, we developed a novel method to automatically delineate individual tree crowns and subsequently classify these crowns to the species level using freely available Sentinel-2 satellite imagery and ALS data. Using this method, we created a detailed tree species distribution map of eight dominant tree species for a 140 km2 mixed temperate forest in the Veluwe, The Netherlands. Trees were sampled in heterogeneous field plots or as individual trees, resulting in a sample size of 2460 trees. We delineated tree crowns automatically from a constructed canopy height model on which tree tops were detected with a local maximum filter. The local maximum filter used a linear tree crown area–height relationship fitted from our field data, and tree crowns were delineated using a watershed segmentation. The local maximum filter and the watershed segmentation performed well for gymnosperm trees but experienced difficulties with large angiosperm trees with a complex crown structure. The automatic crown delineation method was also not able to detect small understory trees beneath a closed canopy.
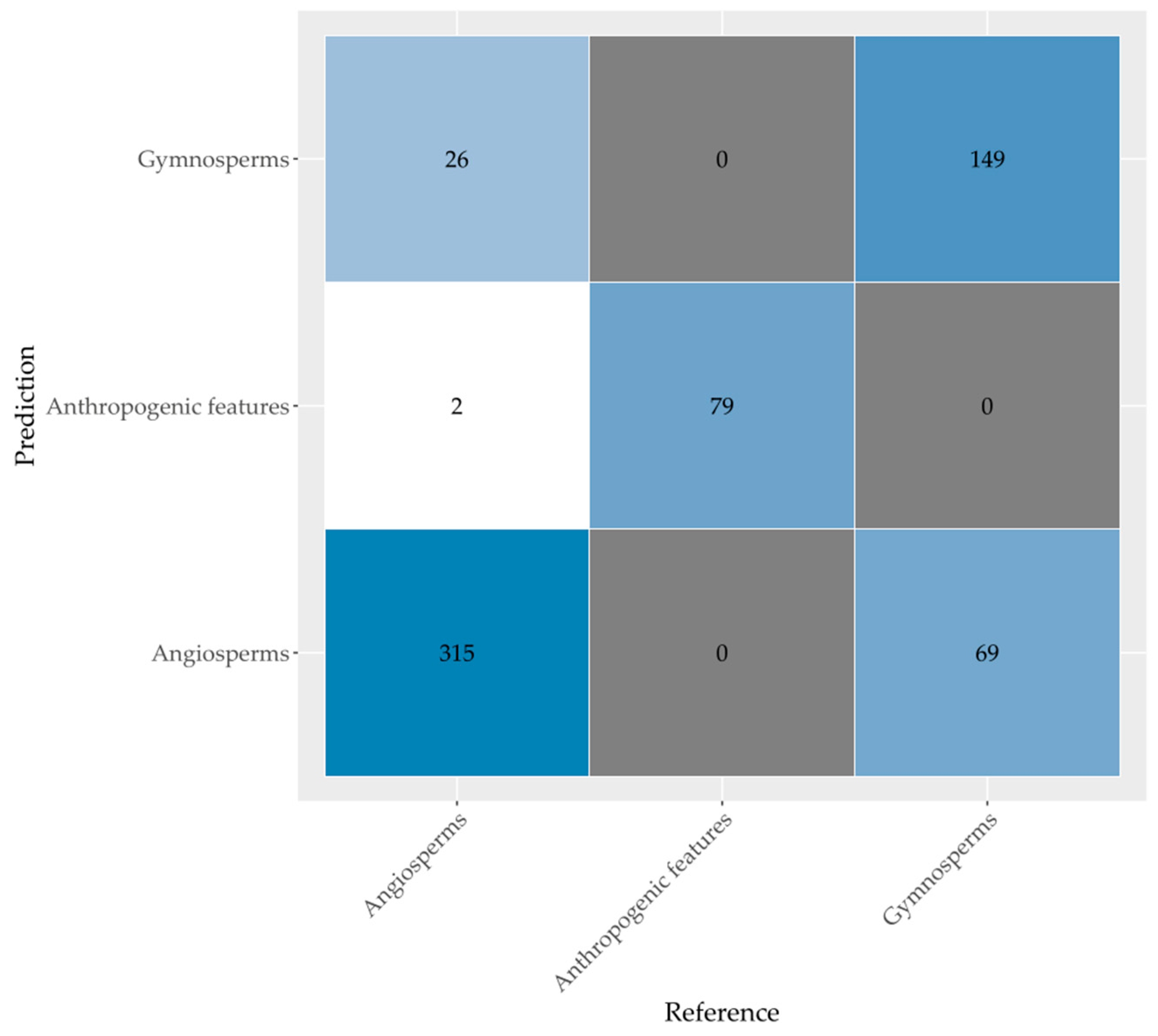
We used reference data in an object-based random forest model, and the results were validated with an independent dataset. Different combinations of feature sets were tested. The features included spectral variables of the 10 m resolution bands of Sentinel-2 images and crown structural variables calculated from the ALS derived canopy height model dataset. Sentinel-2 imagery was acquired for 18 September 2018, 17 November 2018, 21 April 2019, and 26 August 2019 to cover phenological changes. After variable reduction, the model obtained the highest accuracies for the classification with spectral and crown structural variables combined (78.5%, Kappa value 0.75 for tree species; and 85.5%, Kappa value 0.73 for tree phyla). Adding phenological and crown structural information thus improved classification results. Still, misclassifications occurred, probably due to mixing of understory reflectance, clustered trees from different species due to the coarse resolution of Sentinel-2 imagery, and unequal distribution of samples over the classes.
We extrapolated the RF models over the entire 140 km2 study area to generate tree species and tree phyla maps of individual trees. These maps of detailed tree species distributions can be a highly valuable tool for forest management, ecological surveys, and forest fire management. Our classification models can also be extended to other forest areas that are characterised by the presence of the same species and by a comparable forest structure.