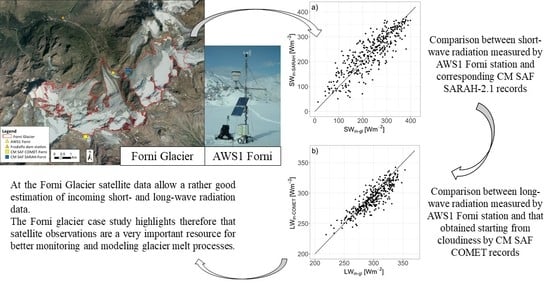
Comparing Measured Incoming Shortwave and Longwave Radiation on a Glacier Surface with Estimated Records from Satellite and Off-Glacier Observations: A Case Study for the Forni Glacier, Italy
Abstract
:1. Introduction
2. Study Area and Data
2.1. Forni Glacier and the Meteorological Stations
2.2. Incoming Shortwave Radiation Satellite Data
2.3. Cloudiness Satellite Data
3. Methods
3.1. Error Measures
3.2. Cloud Transmissivity at AWS1 Forni
3.3. Cloud Transmissivity Parametrization from Daily Temperature Range
3.4. Cloud Transmissivity and Cloudiness
3.5. Estimated Incoming Shortwave and Longwave Records
3.6. Glacier Melting
3.7. Comparison of Glacier Melt Amount from Observed and Estimated SWin and LWin
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brunetti, M.; Lentini, G.; Maugeri, M.; Nanni, T.; Auer, I.; Böhm, R.; Schöner, W. Climate variability and change in the Greater Alpine Region over the last two centuries based on multi-variable analysis. Int. J. Clim. 2009, 29, 2197–2225. [Google Scholar] [CrossRef]
- Haeberli, W.; Beniston, M. Climate change and its impacts on glaciers and permafrost in the Alps. Ambio 1998, 27, 258–265. [Google Scholar]
- Gobiet, A.; Kotlarski, S.; Beniston, M.; Heinrich, G.; Rajczak, J.; Stoffel, M. 21st century climate change in the European Alps—A review. Sci. Total Environ. 2014, 493, 1138–1151. [Google Scholar] [CrossRef] [PubMed]
- Hock, R. Glacier melt: A review of processes and their modelling. Prog. Phys. Geogr. Earth Environ. 2005, 29, 362–391. [Google Scholar] [CrossRef]
- Oerlemans, J.; Oerlemansutrecht, J. Analysis of a 3 year meteorological record from the ablation zone of Morteratschgletscher, Switzerland: Energy and mass balance. J. Glaciol. 2000, 46, 571–579. [Google Scholar] [CrossRef] [Green Version]
- Senese, A.; Diolaiuti, G.; Mihalcea, C.; Smiraglia, C. Energy and mass balance of Forni Glacier (Stelvio National Park, Italian Alps) from a 4-year meteorological data record. Arct. Antarct. Alp. Res. 2012, 44, 122–134. [Google Scholar] [CrossRef] [Green Version]
- Manara, V.; Brunetti, M.; Celozzi, A.; Maugeri, M.; Sanchez-Lorenzo, A.; Wild, M. Detection of dimming/brightening in Italy from homogenized all-sky and clear-sky surface solar radiation records and underlying causes (1959–2013). Atmos. Chem. Phys. Discuss. 2016, 16, 11145–11161. [Google Scholar] [CrossRef] [Green Version]
- Manara, V.; Bassi, M.; Brunetti, M.; Cagnazzi, B.; Maugeri, M. 1990–2016 surface solar radiation variability and trend over the Piedmont region (northwest Italy). Theor. Appl. Clim. 2019, 136, 849–862. [Google Scholar] [CrossRef]
- Pellicciotti, F.; Raschle, T.; Huerlimann, T.; Carenzo, M.; Burlando, P. Transmission of solar radiation through clouds on melting glaciers: A comparison of parameterizations and their impact on melt modelling. J. Glaciol. 2011, 57, 367–381. [Google Scholar] [CrossRef] [Green Version]
- Müller, H. On the radiation budget in the alps. J. Clim. 1985, 5, 445–462. [Google Scholar] [CrossRef]
- Granger, R.J.; Gray, D.M. A Net Radiation Model for Calculating Daily Snowmelt in Open Environments. Hydrol. Res. 1990, 21, 217–234. [Google Scholar] [CrossRef]
- Conway, J.P.; Cullen, N.J. Cloud effects on surface energy and mass balance in the ablation area of Brewster Glacier, New Zealand. Cryosphere 2016, 10, 313–328. [Google Scholar] [CrossRef] [Green Version]
- Iziomon, M.; Mayer, H.; Matzarakis, A. Downward atmospheric longwave irradiance under clear and cloudy skies: Measurement and parameterization. J. Atmos. Sol. Terr. Phys. 2003, 65, 1107–1116. [Google Scholar] [CrossRef]
- Choi, M.; Jacobs, J.M.; Kustas, W.P. Assessment of clear and cloudy sky parameterizations for daily downwelling longwave radiation over different land surfaces in Florida, USA. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Stamnes, K.; Bowling, S.A. Impact of Clouds on Surface Radiative Fluxes and Snowmelt in the Arctic and Subarctic. J. Clim. 1996, 9, 2110–2123. [Google Scholar] [CrossRef]
- Hock, R.; Noetzli, C. Areal melt and discharge modeling of Storgläciaren, Sweden. Ann. Glaciol. 1997, 24, 997. [Google Scholar] [CrossRef] [Green Version]
- Senese, A.; Maugeri, M.; Ferrari, S.; Confortola, G.; Soncini, A.; Bocchiola, D.; Diolaiuti, G. 2016: Modelling shortwave and longwave downward radiation and air temperature driving ablation at the Forni Glacier (Stelvio National Park, Italy). Geogr. Fis. Dinam. Quat. 2016, 39, 89–100. [Google Scholar]
- Iqbal, M. An Introduction to Solar Radiation; Academic Press: Orlando, FL, USA, 1983. [Google Scholar]
- Frederick, J.E.; Steele, H.D. The Transmission of Sunlight through Cloudy Skies: An Analysis Based on Standard Meteorological Information. J. Appl. Meteorol. 1995, 34, 2755–2761. [Google Scholar] [CrossRef] [Green Version]
- Xu, K.M.; Randall, D.A. A semiempirical cloudiness parameterization for use in climate models. J. Atmos. Sci. 1996, 53, 3084–3102. [Google Scholar] [CrossRef] [Green Version]
- Shonk, J.K.; Hogan, R.J.; Edwards, J.M.; Mace, G.G. Effect of improving representation of horizontal and vertical cloud structure on the Earth’s global radiation budget. Part I: Review and parametrization. Q. J. R. Meteorol. Soc. 2010, 136, 1191–1204. [Google Scholar] [CrossRef] [Green Version]
- Morcrette, C.J.; O’Connor, E.J.; Petch, J.C. Evaluation of two cloud parametrization schemes using ARM and Cloud-Net observations. Q. J. R. Meteorol. Soc. 2012, 138, 964–979. [Google Scholar] [CrossRef]
- Bristow, K.L.; Campbell, G.S. On the relationship between incoming solar radiation and daily maximum and minimum temperature. Agric. For. Meteorol. 1984, 31, 159–166. [Google Scholar] [CrossRef]
- Campbell, G.G.; Haar, T.H.V. Comparison of surface temperature minimum and maximum and satellite measured cloudiness and radiation budget. J. Geophys. Res. Space Phys. 1997, 102, 16639–16645. [Google Scholar] [CrossRef]
- Thornton, P.E.; Running, S.W. An improved algorithm for estimating incident daily solar radiation from measurements of temperature, humidity, and precipitation. Agric. For. Meteorol. 1999, 93, 211–228. [Google Scholar] [CrossRef]
- Paul, F.; Kääb, A.; Maisch, M.; Kellenberger, T.W.; Haeberli, W. The new remote-sensing-derived Swiss glacier inventory I. Methods. Ann. Glaciol. 2002, 34, 355–361. [Google Scholar] [CrossRef] [Green Version]
- Paul, F.; Frey, H.; Le Bris, R. A new glacier inventory for the European Alps from Landsat TM scenes of 2003: Challenges and results. Ann. Glaciol. 2011, 52, 144–152. [Google Scholar] [CrossRef] [Green Version]
- Paul, F.; Barrand, N.; Baumann, S.; Berthier, E.; Bolch, T.; Casey, K.; Frey, H.; Joshi, S.; Konovalov, V.; Le Bris, R.; et al. On the accuracy of glacier outlines derived from remote-sensing data. Ann. Glaciol. 2013, 54, 171–182. [Google Scholar] [CrossRef] [Green Version]
- Paul, F.; Bolch, T.; Briggs, K.; Kääb, A.; McMillan, M.; McNabb, R.; Nagler, T.; Nuth, C.; Rastner, P.; Strozzi, T.; et al. Error sources and guidelines for quality assessment of glacier area, elevation change, and velocity products derived from satellite data in the Glaciers_cci project. Remote Sens. Environ. 2017, 203, 256–275. [Google Scholar] [CrossRef] [Green Version]
- Pellikka, P.; Rees, W.G. Remote sensing of glaciers: Techniques for topographic, spatial, and thematic mapping of glaciers. In Remote Sensing of Glacier, 1st ed.; CRC Press: Cleveland, OH, USA, 2009. [Google Scholar]
- Racoviteanu, A.E.; Paul, F.; Raup, B.; Khalsa, S.J.S.; Armstrong, R. Challenges in glacier mapping from space: Recommendations from the Global Land Ice Measurements from Space (GLIMS) initiative. Ann. Glaciol. 2009, 50, 53–69. [Google Scholar] [CrossRef] [Green Version]
- Fischer, M.; Huss, M.; Barboux, C.; Hoelzle, M. The New Swiss Glacier Inventory SGI2010: Relevance of Using High-Resolution Source Data in Areas Dominated by Very Small Glaciers. Arct. Antarct. Alp. Res. 2014, 46, 933–945. [Google Scholar] [CrossRef] [Green Version]
- Kääb, A.; Winsvold, S.H.; Altena, B.; Nuth, C.; Nagler, T.; Wuite, J. Glacier Remote Sensing Using Sentinel-2. Part I: Radiometric and Geometric Performance, and Application to Ice Velocity. Remote Sens. 2016, 8, 598. [Google Scholar] [CrossRef] [Green Version]
- Minora, U.; Bocchiola, D.; D’Agata, C.; Maragno, D.; Mayer, C.; Lambrecht, A.; Vuillermoz, E.; Senese, A.; Compostella, C.; Smiraglia, C.; et al. Glacier area stability in the Central Karakoram National Park (Pakistan) in 2001–2010: The “Karakoram Anomaly” in the spotlight. Prog. Phys. Geogr. Earth Environ. 2016, 40, 629–660. [Google Scholar] [CrossRef]
- Mölg, N.; Bolch, T.; Rastner, P.; Strozzi, T.; Paul, F. A consistent glacier inventory for Karakoram and Pamir derived from Landsat data: Distribution of debris cover and mapping challenges. Earth Syst. Sci. Data 2018, 10, 1807–1827. [Google Scholar] [CrossRef] [Green Version]
- Azzoni, R.S.; Sarıkaya, M.A.; Fugazza, D. Turkish glacier inventory and classification from high-resolution satellite data. Mediterr. Geosci. Rev. 2020, 2, 153–162. [Google Scholar] [CrossRef]
- Rabatel, A.; Francou, B.; Soruco, A.; Gomez, J.; Cáceres, B.; Ceballos, J.L.; Basantes, R.; Vuille, M.; Sicart, J.-E.; Huggel, C.; et al. Current state of glaciers in the tropical Andes: A multi-century perspective on glacier evolution and climate change. Cryosphere 2013, 7, 81–102. [Google Scholar] [CrossRef] [Green Version]
- Rabatel, A.; Ceballos, J.L.; Micheletti, N.; Jordan, E.; Braitmeier, M.; González, J.; Mölg, N.; Ménégoz, M.; Huggel, C.; Zemp, M. Toward an imminent extinction of Colombian glaciers? Geogr. Ann. Ser. A Phys. Geogr. 2018, 100, 75–95. [Google Scholar] [CrossRef]
- Gardent, M.; Rabatel, A.; Dedieu, J.-P.; Deline, P. Multitemporal glacier inventory of the French Alps from the late 1960s to the late 2000s. Glob. Planet. Chang. 2014, 120, 24–37. [Google Scholar] [CrossRef]
- Diolaiuti, G.A.; Azzoni, R.S.; D’Agata, C.; Maragno, D.; Fugazza, D.; Vagliasindi, M.; Mortara, G.; Perotti, L.; Bondesan, A.; Carton, A.; et al. Present extent, features and regional distribution of Italian glaciers. LHB 2019, 159–175. [Google Scholar] [CrossRef]
- Paul, F.; Rastner, P.; Azzoni, R.S.; Diolaiuti, G.A.; Fugazza, D.; Le Bris, R.; Nemec, J.; Rabatel, A.; Ramusovic, M.; Schwaizer, G.; et al. Glacier shrinkage in the Alps continues unabated as revealed by a new glacier inventory from Sentinel-2. Earth Syst. Sci. Data 2020, 12, 1805–1821. [Google Scholar] [CrossRef]
- Paul, F.; Winsvold, S.H.; Kääb, A.; Nagler, T.; Schwaizer, G. Glacier Remote Sensing Using Sentinel-2. Part II: Mapping Glacier Extents and Surface Facies, and Comparison to Landsat 8. Remote Sens. 2016, 8, 575. [Google Scholar] [CrossRef] [Green Version]
- Millan, R.; Mouginot, J.; Rabatel, A.; Jeong, S.; Cusicanqui, D.; Derkacheva, A.; Chekki, M. Mapping Surface Flow Velocity of Glaciers at Regional Scale Using a Multiple Sensors Approach. Remote Sens. 2019, 11, 2498. [Google Scholar] [CrossRef] [Green Version]
- Oerlemans, J.; Giesen, R.; Broeke, M.V.D. Retreating alpine glaciers: Increased melt rates due to accumulation of dust (Vadret da Morteratsch, Switzerland). J. Glaciol. 2009, 55, 729–736. [Google Scholar] [CrossRef] [Green Version]
- Mihalcea, C.; Brock, B.W.; Diolaiuti, G.A.; D’Agata, C.; Citterio, M.; Kirkbride, M.; Cutler, M.E.J.; Smiraglia, C. Using ASTER satellite and ground-based surface temperature measurements to derive supraglacial debris cover and thickness patterns on Miage Glacier (Mont Blanc Massif, Italy). Cold Reg. Sci. Technol. 2008, 52, 341–354. [Google Scholar] [CrossRef]
- Mihalcea, C.; Mayer, C.; Diolaiuti, G.A.; D’Agata, C.; Smiraglia, C.; Lambrecht, A.; Vuillermoz, E.; Tartari, G. Spatial distribution of debris thickness and melting from remote-sensing and meteorological data, at debris-covered Baltoro glacier, Karakoram, Pakistan. Ann. Glaciol. 2008, 48, 49–57. [Google Scholar] [CrossRef] [Green Version]
- Azzoni, R.S.; Fugazza, D.; Zerboni, A.; Senese, A.; D’Agata, C.; Maragno, D.; Carzaniga, A.; Cernuschi, M.; Diolaiuti, G.A. Evaluating high-resolution remote sensing data for reconstructing the recent evolution of supra glacial debris. Prog. Phys. Geogr. Earth Environ. 2018, 42, 3–23. [Google Scholar] [CrossRef] [Green Version]
- Klok, E.J.; Greuell, W.; Oerlemans, J. Temporal and spatial variation of the surface albedo of Morteratschgletscher, Switzerland, as derived from 12 Landsat images. J. Glaciol. 2003, 49, 491–502. [Google Scholar] [CrossRef] [Green Version]
- Fugazza, D.; Senese, A.; Azzoni, R.S.; Maugeri, M.; Diolaiuti, G.A. Spatial distribution of surface albedo at the Forni Glacier (Stelvio National Park, Central Italian Alps). Cold Reg. Sci. Technol. 2016, 125, 128–137. [Google Scholar] [CrossRef]
- Traversa, G.; Fugazza, D.; Senese, A.; Diolaiuti, G.A. Preliminary results on Antarctic albedo from remote sensing observations. Geogr. Fis. Din. Quat. 2019, 42, 245–254. [Google Scholar]
- Fugazza, D.; Senese, A.; Azzoni, R.S.; Maugeri, M.; Maragno, D.; Diolaiuti, G.A. New evidence of glacier darkening in the Ortles-Cevedale group from Landsat observations. Glob. Planet. Chang. 2019, 178, 35–45. [Google Scholar] [CrossRef]
- Brown, M.E.; Racoviteanu, A.; Tarboton, D.; Gupta, A.S.; Nigro, J.; Policelli, F.; Habib, S.; Tokay, M.; Shrestha, M.; Bajracharya, S.; et al. An integrated modeling system for estimating glacier and snow melt driven streamflow from remote sensing and earth system data products in the Himalayas. J. Hydrol. 2014, 519, 1859–1869. [Google Scholar] [CrossRef] [Green Version]
- Minora, U.; Godone, D.; Lorenzini, S.; D’agata, C.; Bocchiola, D.; Barcaza Sepulveda, G.; Smiraglia, C.; Diolaiuti, G.A. 2008–2011 snow cover area (SCA) variability over 18 watersheds of the central Chile through MODIS data. Geogr. Fis. Dinam. Quat. 2015, 38. [Google Scholar] [CrossRef]
- Dong, C.; Menzel, L. Producing cloud-free MODIS snow cover products with conditional probability interpolation and meteorological data. Remote Sens. Environ. 2016, 186, 439–451. [Google Scholar] [CrossRef]
- Hall, D.; Kelly, R.E.J.; Riggs, G.A.; Chang, A.T.C.; Foster, J.L. Assessment of the relative accuracy of hemispheric-scale snow-cover maps. Ann. Glaciol. 2002, 34, 24–30. [Google Scholar] [CrossRef] [Green Version]
- Tsai, Y.-L.S.; Dietz, A.J.; Oppelt, N.; Kuenzer, C. Remote Sensing of Snow Cover Using Spaceborne SAR: A Review. Remote Sens. 2019, 11, 1456. [Google Scholar] [CrossRef] [Green Version]
- De Gregorio, L.; Callegari, M.; Marin, C.; Zebisch, M.; Bruzzone, L.; Demir, B.; Strasser, U.; Marke, T.; Günther, D.; Nadalet, R.; et al. A Novel Data Fusion Technique for Snow Cover Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2862–2877. [Google Scholar] [CrossRef] [Green Version]
- Gascoin, S.; Grizonnet, M.; Bouchet, M.; Salgues, G.; Hagolle, O. Theia Snow collection: High-resolution operational snow cover maps from Sentinel-2 and Landsat-8 data. Earth Syst. Sci. Data 2019, 11, 493–514. [Google Scholar] [CrossRef] [Green Version]
- Touzi, R.; Hong, G.; Motohka, T.; Shinichi, S.; De Lisle, D. Investigation of Compact SAR L and C band Complementarity for Permafrost Characterization In Arctic Regions. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 4665–4667. [Google Scholar]
- Fugazza, D.F.; Shaw, T.E.; Mashtayeva, S.; Brock, B.W. Inter-annual variability in snow cover depletion patterns and atmospheric circulation indices in the Upper Irtysh basin, Central Asia. Hydrol. Process. 2020, 34, 3738–3757. [Google Scholar] [CrossRef]
- Pfeifroth, U.; Sanchez-Lorenzo, A.; Manara, V.; Trentmann, J.; Hollmann, R. Trends and Variability of Surface Solar Radiation in Europe Based on Surface- and Satellite-Based Data Records. J. Geophys. Res. Atmos. 2018, 123, 1735–1754. [Google Scholar] [CrossRef]
- Pfeifroth, U.; Kothe, S.; Trentmann, J.; Hollmann, R.; Fuchs, P.; Kaiser, J.; Werscheck, M. Surface Radiation Data Set—Heliosat (SARAH)—Edition 2.1. Satell. Appl. Facil. Clim. Monit. 2019. [Google Scholar] [CrossRef]
- Stöckli, R.; Duguay–Tetzlaff, A.; Bojanowski, J.; Hollmann, R.; Fuchs, P.; Werscheck, M. CM SAF ClOud Fractional Cover dataset from METeosat First and Second Generation—Edition 1 (COMET Ed. 1). Satell. Appl. Facil. Clim. Monit. 2017. [Google Scholar] [CrossRef]
- Bojanowski, J.; Stöckli, R.; Duguay-Tetzlaff, A.; Finkensieper, S.; Hollmann, R. Performance Assessment of the COMET Cloud Fractional Cover Climatology across Meteosat Generations. Remote Sens. 2018, 10, 804. [Google Scholar] [CrossRef] [Green Version]
- Manara, V.; Brunetti, M.; Gilardoni, S.; Landi, T.C.; Maugeri, M. 1951–2017 changes in the frequency of days with visibility higher than 10 km and 20 km in Italy. Atmos. Environ. 2019, 214, 116861. [Google Scholar] [CrossRef]
- Haiden, T.; Trentmann, J. Verification of cloudiness and radiation forecasts in the greater Alpine region. Meteorol. Z. 2016, 25, 3–15. [Google Scholar] [CrossRef]
- Senese, A.; Diolaiuti, G.; Verza, G.P.; Smiraglia, C. Surface energy budget and melt amount for the years 2009 and 2010 at the Forni Glacier (Italian Alps, Lombardy). Geogr. Fis. Din. Quat. 2012, 35, 69–77. [Google Scholar]
- Gambelli, S.; Senese, A.; D’agata, C.; Smiraglia, C.; Diolaiuti, G. Preliminary analysis for distribution of the surface energy budget of the Forni Glacier, Valtellina (Ortles-Cevedale Group, Italy). Geogr. Fis. Din. Quat. 2014, 37, 15–22. [Google Scholar] [CrossRef]
- Azzoni, R.S.; Senese, A.; Zerboni, A.; Maugeri, M.; Smiraglia, C.; Diolaiuti, G.A. Estimating ice albedo from fine debris cover quantified by a semi-automatic method: The case study of Forni Glacier, Italian Alps. Cryosphere 2016, 10, 665–679. [Google Scholar] [CrossRef] [Green Version]
- Senese, A.; Maugeri, M.; Meraldi, E.; Verza, G.P.; Azzoni, R.S.; Compostella, C.; Diolaiuti, G.A. Estimating the snow water equivalent on a glacierized high elevation site (Forni Glacier, Italy). Cryosphere 2018, 12, 1293–1306. [Google Scholar] [CrossRef] [Green Version]
- Garen, D.C.; Marks, D. Spatially distributed energy balance snowmelt modelling in a mountainous river basin: Estimation of meteorological inputs and verification of model results. J. Hydrol. 2005, 315, 126–153. [Google Scholar] [CrossRef]
- Anslow, F.S.; Hostetler, S.; Bidlake, W.R.; Clark, P.U. Distributed energy balance modeling of South Cascade Glacier, Washington and assessment of model uncertainty. J. Geophys. Res. Space Phys. 2008, 113, 02019. [Google Scholar] [CrossRef] [Green Version]
- Sauberer, F. Zur Abschätzung der Globalstrahlung in verschiedenen Höhenstufen der Ostalpen. Wetter Leben 1955, 7, 22–29. (In German) [Google Scholar]
- Konzelmann, T.; Van De Wal, R.S.; Greuell, W.; Bintanja, R.; Henneken, E.A.; Abe-Ouchi, A. Parameterization of global and longwave incoming radiation for the Greenland Ice Sheet. Glob. Planet. Chang. 1994, 9, 143–164. [Google Scholar] [CrossRef]
- Greuell, W.; Knap, W.H.; Smeets, P.C. Elevational changes in meteorological variables along a midlatitude glacier during summer. J. Geophys. Res. Space Phys. 1997, 102, 25941–25954. [Google Scholar] [CrossRef]
- Wexler, A. Vapor pressure formulation for water in range 0 to 100 C. A revision. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1976, 80A, 775–785. [Google Scholar] [CrossRef] [PubMed]
- Senese, A.; Maugeri, M.; Vuillermoz, E.; Smiraglia, C.; Diolaiuti, G.A. Using daily air temperature thresholds to evaluate snow melting occurrence and amount on Alpine glaciers by T-index models: The case study of the Forni Glacier (Italy). Cryosphere 2014, 8, 1921–1933. [Google Scholar] [CrossRef] [Green Version]
- Minora, U.; Senese, A.; Bocchiola, D.; Soncini, A.; D’Agata, C.; Ambrosini, R.; Mayer, C.; Lambrecht, A.; Vuillermoz, E.; Smiraglia, C.; et al. A simple model to evaluate ice melt over the ablation area of glaciers in the Central Karakoram National Park, Pakistan. Ann. Glaciol. 2015, 56, 202–216. [Google Scholar] [CrossRef] [Green Version]
- Senese, A.; Maragno, D.; Fugazza, D.F.; Soncini, A.; D’Agata, C.; Azzoni, R.S.; Minora, U.; Ul-Hassan, R.; Vuillermoz, E.; Khan, M.A.; et al. Inventory of glaciers and glacial lakes of the Central Karakoram National Park (CKNP—Pakistan). J. Maps 2018, 14, 189–198. [Google Scholar] [CrossRef]
- Bocchiola, D.; Soncini, A.; Senese, A.; Diolaiuti, G.A. Modelling Hydrological Components of the Rio Maipo of Chile, and Their Prospective Evolution under Climate Change. Climate 2018, 6, 57. [Google Scholar] [CrossRef] [Green Version]
- Bajracharya, S.R.; Maharjan, S.B.; Shrestha, F.; Guo, W.-Q.; Liu, S.; Immerzeel, W.; Shrestha, B. The glaciers of the Hindu Kush Himalayas: Current status and observed changes from the 1980s to 2010. Int. J. Water Resour. Dev. 2015, 31, 161–173. [Google Scholar] [CrossRef] [Green Version]
- Luckman, B.H. The Geomorphic Activity of Snow Avalanches. Geograf. Ann. Ser. A 1977, 59, 31–48. [Google Scholar] [CrossRef]
- Ling, F.; Zhang, T. Impact of the timing and duration of seasonal snow cover on the active layer and permafrost in the Alaskan Arctic. Permafr. Periglac. Process. 2003, 14, 141–150. [Google Scholar] [CrossRef]



| Model | Equation |
|---|---|
| Linear | |
| Polynomial | |
| Exponential | |
| Gaussian |
| MBE | MAE | RMSE | BRRMSE | R2 | |
|---|---|---|---|---|---|
| SWin-SARAH (W m−2) | 2.0 | 34.9 | 44.4 | 44.4 | 0.73 |
| SWin-∆T (W m−2) | 10.8 | 47.5 | 60.6 | 59.7 | 0.51 |
| SWin-COMET (W m−2) | 8.1 | 42.0 | 52.2 | 51.6 | 0.66 |
| LWin-∆T (W m−2) | −9.4 | 14.8 | 19.5 | 17.0 | 0.51 |
| LWin-COMET (W m−2) | −6.9 | 10.7 | 13.6 | 11.8 | 0.76 |
| Cumulative Melting (m w.e.) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| MBE | MAE | RMSE | BRRMSE | R2 | 2006 | 2007 | 2008 | 2009 | |
| M(SWin-gl,LWin-gl) | 3.64 | 3.54 | 3.85 | 3.66 | |||||
| M(SWin-gl,LWin-COMET) | −0.002 | 0.003 | 0.003 | 0.003 | 0.98 | 3.49 | 3.34 | 3.71 | 3.52 |
| M(SWin-gl,LWin-∆T) | −0.002 | 0.004 | 0.005 | 0.004 | 0.96 | 3.39 | 3.26 | 3.72 | 3.46 |
| M(SWin-SARAH,LWin-gl) | 0.001 | 0.008 | 0.011 | 0.011 | 0.75 | 3.83 | 3.68 | 3.77 | 3.80 |
| M(SWin-COMET,LWin-gl) | 0.003 | 0.011 | 0.013 | 0.013 | 0.58 | 3.73 | 3.89 | 4.09 | 3.81 |
| M(SWin-∆T,LWin-gl) | 0.003 | 0.012 | 0.016 | 0.015 | 0.44 | 3.93 | 4.00 | 3.98 | 3.87 |
| M(SWin-SARAH,LWin-COMET) | 0.000 | 0.008 | 0.010 | 0.010 | 0.73 | 3.67 | 3.49 | 3.63 | 3.65 |
| M(SWin-COMET,LWin-COMET) | 0.001 | 0.010 | 0.012 | 0.012 | 0.62 | 3.57 | 3.69 | 3.95 | 3.66 |
| M(SWin-∆T,LWin-∆T) | 0.001 | 0.011 | 0.013 | 0.013 | 0.55 | 3.67 | 3.71 | 3.85 | 3.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senese, A.; Manara, V.; Maugeri, M.; Diolaiuti, G.A. Comparing Measured Incoming Shortwave and Longwave Radiation on a Glacier Surface with Estimated Records from Satellite and Off-Glacier Observations: A Case Study for the Forni Glacier, Italy. Remote Sens. 2020, 12, 3719. https://doi.org/10.3390/rs12223719
Senese A, Manara V, Maugeri M, Diolaiuti GA. Comparing Measured Incoming Shortwave and Longwave Radiation on a Glacier Surface with Estimated Records from Satellite and Off-Glacier Observations: A Case Study for the Forni Glacier, Italy. Remote Sensing. 2020; 12(22):3719. https://doi.org/10.3390/rs12223719
Chicago/Turabian StyleSenese, Antonella, Veronica Manara, Maurizio Maugeri, and Guglielmina Adele Diolaiuti. 2020. "Comparing Measured Incoming Shortwave and Longwave Radiation on a Glacier Surface with Estimated Records from Satellite and Off-Glacier Observations: A Case Study for the Forni Glacier, Italy" Remote Sensing 12, no. 22: 3719. https://doi.org/10.3390/rs12223719
APA StyleSenese, A., Manara, V., Maugeri, M., & Diolaiuti, G. A. (2020). Comparing Measured Incoming Shortwave and Longwave Radiation on a Glacier Surface with Estimated Records from Satellite and Off-Glacier Observations: A Case Study for the Forni Glacier, Italy. Remote Sensing, 12(22), 3719. https://doi.org/10.3390/rs12223719