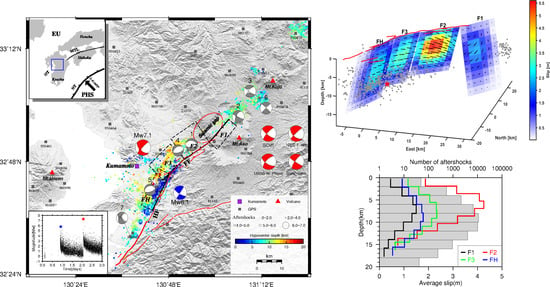
Multi-Segment Rupture Model of the 2016 Kumamoto Earthquake Revealed by InSAR and GPS Data
Abstract
:1. Introduction
2. Coseismic Surface Displacements from InSAR and GPS Data
2.1. InSAR Data
2.2. GPS Data
3. Model
3.1. Determination of the Fault Geometry with the jRi Method
3.2. Distributed Slip Model
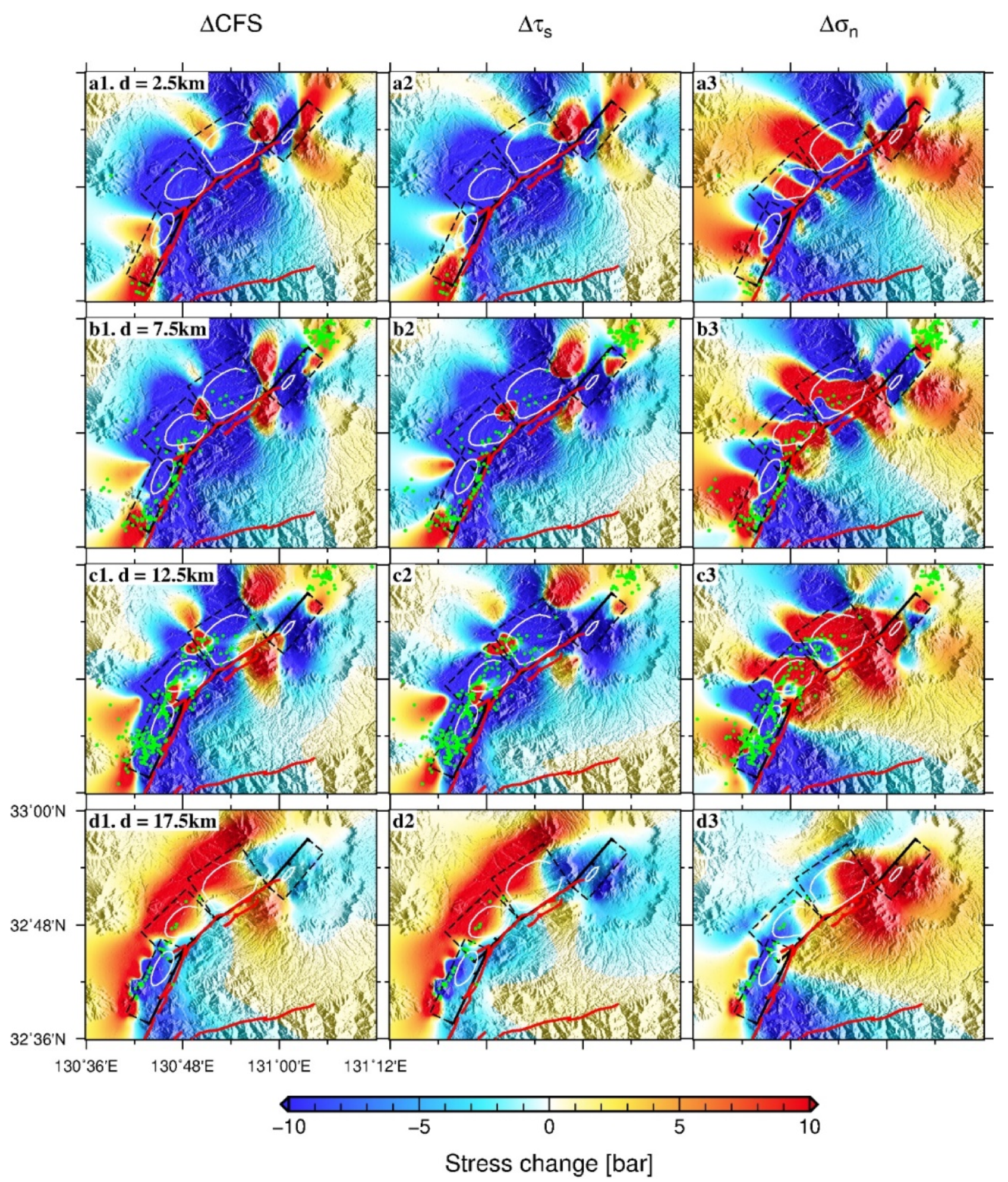
4. Coulomb Stress Change Analysis
5. Discussion
5.1. Seismogenic Fault Geometry
5.2. Comparison with Previous Slip Distribution Models
5.3. Shallow Slip Deficit
5.4. Sensitivity Analysis of Coulomb Stress Change
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Checkerboard and Jackknife Tests
References
- Yagi, Y.; Okuwaki, R.; Enescu, B.; Kasahara, A.; Miyakawa, A.; Otsubo, M. Rupture process of the 2016 Kumamoto earthquake in relation to the thermal structure around Aso volcano. Earth Planets Space 2016, 68, 118. [Google Scholar] [CrossRef] [Green Version]
- Asano, K.; Iwata, T. Source rupture processes of the foreshock and mainshock in the 2016 Kumamoto earthquake sequence estimated from the kinematic waveform inversion of strong motion data. Earth Planets Space 2016, 68, 147. [Google Scholar] [CrossRef] [Green Version]
- Yue, H.; Ross, Z.E.; Liang, C.; Michel, S.; Fattahi, H.; Fielding, E.; Moore, A.; Liu, Z.; Jia, B. The 2016 Kumamoto Mw = 7.0 Earthquake: A significant event in a fault–volcano system. J. Geophys. Res. Solid Earth 2017, 122, 9166–9183. [Google Scholar] [CrossRef]
- Global Centroid Moment Tensor Catalogue (GCMT). Available online: http://www.globalcmt.org/CMTsearch.html (accessed on 30 June 2020).
- United States Geological Survey (USGS). Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us20005iis/moment-tensor (accessed on 30 June 2020).
- National Research Institute for Earth Science and Disaster Resilience (NIED). Available online: https://www.fnet.bosai.go.jp/event/tdmt.php?_id=20160415162400&LANG=en (accessed on 30 June 2020).
- Shirahama, Y.; Yoshimi, M.; Awata, Y.; Maruyama, T.; Azuma, T.; Miyashita, Y.; Mori, H.; Imanishi, K.; Takeda, N.; Ochi, T.; et al. Characteristics of the surface ruptures associated with the 2016 Kumamoto earthquake sequence, central Kyushu, Japan. Earth Planets Space 2016, 68, 191. [Google Scholar] [CrossRef] [Green Version]
- Matsumoto, S.; Nakao, S.; Ohkura, T.; Miyazaki, M.; Shimizu, H.; Abe, Y.; Inoue, H.; Nakamoto, M.; Yoshikawa, S.; Yamashita, Y.; et al. Spatial heterogeneities in tectonic stress in Kyushu, Japan and their relation to a major shear zone Seismology. Earth Planets Space 2015, 67, 172. [Google Scholar] [CrossRef] [Green Version]
- Kato, A.; Nakamura, K.; Hiyama, Y. The 2016 Kumamoto earthquake sequence. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2016, 92, 358–371. [Google Scholar] [CrossRef] [Green Version]
- Kubo, H.; Suzuki, W.; Aoi, S.; Sekiguchi, H. Source rupture processes of the 2016 Kumamoto, Japan, earthquakes estimated from strong-motion waveforms. Earth Planets Space 2016, 68, 161. [Google Scholar] [CrossRef] [Green Version]
- Hao, J.; Ji, C.; Yao, Z. Slip history of the 2016 Mw 7.0 Kumamoto earthquake: Intraplate rupture in complex tectonic environment. Geophys. Res. Lett. 2017, 44, 743–750. [Google Scholar] [CrossRef]
- Fukahata, Y.; Hashimoto, M. Simultaneous estimation of the dip angles and slip distribution on the faults of the 2016 Kumamoto earthquake through a weak nonlinear inversion of InSAR data. Earth Planets Space 2016, 68, 204. [Google Scholar] [CrossRef] [Green Version]
- Ozawa, T.; Fujita, E.; Ueda, H. Crustal deformation associated with the 2016 Kumamoto Earthquake and its effect on the magma system of Aso volcano. Earth Planets Space 2016, 68, 186. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, K.; Miyakoshi, K.; Somei, K.; Irikura, K. Source process of the 2016 Kumamoto earthquake (Mj7.3) inferred from kinematic inversion of strong-motion records. Earth Planets Space 2017, 69, 64. [Google Scholar] [CrossRef]
- Zhang, Y.; Shan, X.; Zhang, G.; Gong, W.; Liu, X.; Yin, H.; Zhao, D.; Wen, S.; Qu, C. Source model of the 2016 Kumamoto, Japan, earthquake constrained by InSAR, GPS, and strong-motion data: Fault slip under extensional stress. Bull. Seismol. Soc. Am. 2018, 108, 2675–2686. [Google Scholar] [CrossRef]
- Yague-Martinez, N.; Prats-Iraola, P.; Gonzalez, F.R.; Brcic, R.; Shau, R.; Geudtner, D.; Eineder, M.; Bamler, R. Interferometric Processing of Sentinel-1 TOPS Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2220–2234. [Google Scholar] [CrossRef] [Green Version]
- Werner, C.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. GAMMA SAR and interferometric processing software. In Proceedings of the ERS ENVISAT Symposium, Gothenburg, Sweden, 16–20 October 2000. [Google Scholar]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.W.; Zebker, H.A. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J. Opt. Soc. Am. A 2001, 18, 338. [Google Scholar] [CrossRef] [Green Version]
- He, P.; Wen, Y.; Xu, C.; Chen, Y. Complete three-dimensional near-field surface displacements from imaging geodesy techniques applied to the 2016 Kumamoto earthquake. Remote Sens. Environ. 2019, 232, 111321. [Google Scholar] [CrossRef]
- Wen, Y.; Xu, C.; Liu, Y.; Jiang, G. Deformation and source parameters of the 2015 Mw 6.5 earthquake in Pishan, Western China, from Sentinel-1A and ALOS-2 data. Remote Sens. 2016, 8, 134. [Google Scholar] [CrossRef] [Green Version]
- Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar]
- Jónsson, S.; Zebker, H.; Segall, P.; Amelung, F. Fault slip distribution of the 1999 Mw 7.1 Hector Mine, California, earthquake, estimated from satellite radar and GPS measurements. Bull. Seismol. Soc. Am. 2002, 92, 1377–1389. [Google Scholar] [CrossRef]
- Burgmann, R.; Ayhan, M.E.; Fielding, E.J.; Wright, T.J.; McClusky, S.; Aktug, B.; Demir, C.; Lenk, O.; Turkezer, A. Deformation during the 12 November 1999 Duzce, Turkey, earthquake, from GPS and InSAR data. Bull. Seismol. Soc. Am. 2002, 92, 161–171. [Google Scholar] [CrossRef]
- Fukahata, Y.; Wright, T.J. A non-linear geodetic data inversion using ABIC for slip distribution on a fault with an unknown dip angle. Geophys. J. Int. 2008, 173, 353–364. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Newman, A.V.; Feng, L.; Fritz, H.M. Slip distribution from the 1 April 2007 Solomon Islands earthquake: A unique image of near-trench rupture. Geophys. Res. Lett. 2009, 36, 6–11. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Liu, Y.; Wen, Y.; Wang, R. Coseismic slip distribution of the 2008 Mw 7.9 Wenchuan earthquake from joint inversion of GPS and InSAR data. Bull. Seismol. Soc. Am. 2010, 100, 2736–2749. [Google Scholar] [CrossRef]
- Barnhart, W.D.; Lohman, R.B. Automated fault model discretization for inversions for coseismic slip distributions. J. Geophys. Res. Solid Earth 2010, 115, 1–17. [Google Scholar] [CrossRef]
- Luo, H.; Chen, T.; Xu, C.; Sha, H. Fault dip angle determination with the jRi criterion and coulomb stress changes associated with the 2015 Mw 7.9 Gorkha Nepal earthquake revealed by InSAR and GPS data. Tectonophysics 2017, 714, 55–61. [Google Scholar] [CrossRef]
- Stark, P.; Parker, R. Bounded-variable least-squares: An algorithm and applications. Comput. Stat. 1995, 1–13. [Google Scholar]
- Fujiwara, S.; Morishita, Y.; Nakano, T.; Kobayashi, T.; Yarai, H. Non-tectonic liquefaction-induced large surface displacements in the Aso Valley, Japan, caused by the 2016 Kumamoto earthquake, revealed by ALOS-2 SAR. Earth Planet. Sci. Lett. 2017, 474, 457–465. [Google Scholar] [CrossRef]
- Reasenberg, P.A.; Simpson, R.W. Response of regional seismicity to the static stress change produced by the Loma Prieta earthquake. Science 1992, 255, 1687–1690. [Google Scholar] [CrossRef]
- King, G.C.P.; Stein, R.S.; Lin, J. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 1994, 84, 935–953. [Google Scholar]
- Freed, A.M. Earthquake triggering by static, dynamic, and postseismic stress transfer. Annu. Rev. Earth Planet. Sci. 2005, 33, 335–367. [Google Scholar] [CrossRef] [Green Version]
- Toda, S.; Stein, R.S.; Reasenberg, P.A.; Dieterich, J.H.; Yoshida, A. Stress transferred by the 1995 Mw = 6.9 Kobe, Japan, shock: Effect on aftershocks and future earthquake probabilities. J. Geophys. Res. Solid Earth 1998, 103, 24543–24565. [Google Scholar] [CrossRef] [Green Version]
- Toda, S.; Stein, R.S.; Sevilgen, V.; Lin, J. Coulomb 3.3 Graphic-Rich Deformation and Stress-Change Software for Earthquake, Tectonic, and Volcano Research and Teaching—User Guide; U.S. Geological Survey Open-File Report 2011–1060; U.S. Geological Survey: Reston, VA, USA, 2011; 63p.
- Kobayashi, H.; Koketsu, K.; Miyake, H. Rupture processes of the 2016 Kumamoto earthquake sequence: Causes for extreme ground motions. Geophys. Res. Lett. 2017, 44, 6002–6010. [Google Scholar] [CrossRef]
- Himematsu, Y.; Furuya, M. Fault source model for the 2016 Kumamoto earthquake sequence based on ALOS-2/PALSAR-2 pixel-offset data: Evidence for dynamic slip partitioning. Earth Planets Space 2016, 68, 169. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; Feng, G.; Wang, T.; Bürgmann, R. Toward full exploitation of coherent and incoherent information in Sentinel-1 TOPS data for retrieving surface displacement: Application to the 2016 Kumamoto (Japan) earthquake. Geophys. Res. Lett. 2017, 44, 1758–1767. [Google Scholar] [CrossRef] [Green Version]
- Scott, C.; Champenois, J.; Klinger, Y.; Nissen, E.; Maruyama, T.; Chiba, T.; Arrowsmith, R. The 2016 M7 Kumamoto, Japan, earthquake slip field derived from a joint inversion of differential lidar topography, optical correlation, and InSAR surface displacements. Geophys. Res. Lett. 2019, 46, 6341–6351. [Google Scholar] [CrossRef] [Green Version]
- Tse, S.T.; Rice, J.R. Crustal earthquake instability in relation to the depth variation of frictional slip properties. J. Geophys. Res. 1986, 91, 9452. [Google Scholar] [CrossRef] [Green Version]
- Marone, C. Laboratory-derived friction laws and their application to seismic faulting. Annu. Rev. Earth Planet. Sci. 1998, 26, 643–696. [Google Scholar] [CrossRef] [Green Version]
- Fialko, Y.; Sandwell, D.; Simons, M.; Rosen, P. Three-dimensional deformation caused by the Bam, Iran, earthquake and the origin of shallow slip deficit. Nature 2005, 435, 295–299. [Google Scholar] [CrossRef]
- Kaneko, Y.; Fialko, Y. Shallow slip deficit due to large strike-slip earthquakes in dynamic rupture simulations with elasto-plastic off-fault response. Geophys. J. Int. 2011, 186, 1389–1403. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Tong, X.; Sandwell, D.T.; Milliner, C.W.D.; Dolan, J.F.; Hollingsworth, J.; Leprince, S.; Ayoub, F. Refining the shallow slip deficit. Geophys. J. Int. 2016, 204, 1867–1886. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.H.; Fielding, E.J.; Dickinson, H.; Sun, J.; Gonzalez-Ortega, J.A.; Freed, A.M.; Bürgmann, R. Fault geometry inversion and slip distribution of the 2010 Mw 7.2 El Mayor-Cucapah earthquake from geodetic data. J. Geophys. Res. Solid Earth 2017, 122, 607–621. [Google Scholar] [CrossRef] [Green Version]
- Moore, J.D.P.; Yu, H.; Tang, C.H.; Wang, T.; Barbot, S.; Peng, D.; Masuti, S.; Dauwels, J.; Hsu, Y.J.; Lambert, V.; et al. Imaging the distribution of transient viscosity after the 2016 Mw 7.1 Kumamoto earthquake. Science 2017, 356, 163–167. [Google Scholar] [CrossRef] [PubMed]
- Perfettini, H.; Avouac, J.P. Postseismic relaxation driven by brittle creep: A possible mechanism to reconcile geodetic measurements and the decay rate of aftershocks, application to the Chi-Chi earthquake, Taiwan. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Nissen, E.; Elliott, J.R.; Sloan, R.A.; Craig, T.J.; Funning, G.J.; Hutko, A.; Parsons, B.E.; Wright, T.J. Limitations of rupture forecasting exposed by instantaneously triggered earthquake doublet. Nat. Geosci. 2016, 9, 330–336. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.; Wobbe, F. Generic mapping tools: Improved version released. Eos Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef] [Green Version]
- Melgar, D.; Ganas, A.; Geng, J.; Liang, C.; Fielding, E.J.; Kassaras, I. Source characteristics of the 2015 Mw 6.5 Lefkada, Greece, strike-slip earthquake. J. Geophys. Res. Solid Earth 2017, 122, 2260–2273. [Google Scholar]







| Track | Sensor | Orbit | Mode | Primary Image (yyyy/mm/dd) | Secondary Image (yyyy/mm/dd) | (m) | (days) | (cm) | Np |
|---|---|---|---|---|---|---|---|---|---|
| P023D | ALOS-2 | Descending | Strip-map | 2016/03/07 | 2016/04/18 | 81.5 | 42 | 2.3 | 657 |
| T163D | Sentinel-1A | Descending | IW | 2016/03/27 | 2016/04/20 | 1.9 | 24 | 2.5 | 549 |
| T156A | Sentinel-1A | Ascending | IW | 2016/04/08 | 2016/04/20 | 65.4 | 12 | 3.2 | 568 |
| Segment | Latitude (°) | Longitude (°) | Depth (km) | Length (km) | Width (km) | Strike (°) | Dip (°) | Max Slip (m) | Moment (Nm) | Mw |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 131.0178 | 32.9088 | 0.2 | 12 | 18 | 40 | 77 | 2.3 | 4.89 × 1019 | 7.09 |
| F2 | 130.9222 | 32.8386 | 0.2 | 12 | 18 | 236 | 57 | 5.6 | ||
| F3 | 130.8216 | 32.7722 | 0.2 | 12 | 18 | 226 | 63 | 3.3 | ||
| FH | 130.7672 | 32.6918 | 0.2 | 16 | 18 | 205 | 74 | 3.0 |
| ID | Origin Time (UTC) | Hypocenter | Mw | Nodal Plane 1 | Nodal Plane 2 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| yyyy/mm/dd | dd:mm | Latitude (°) | Longitude (°) | Depth (km) | Strike/Dip/Rake | Strike/Dip/Rake | ||||
| 1 | 2016/04/15 | 16:45 | 32.8632 | 130.8990 | 10.55 | 5.7 | 286/35/–70 | −18.15 | 81/57/–104 | –20.11 |
| 2 | 2016/04/15 | 18:03 | 32.9638 | 131.0868 | 6.89 | 5.5 | 209/60/–174 | 7.35 | 116/85/–30 | 7.79 |
| 3 | 2016/04/15 | 18:55 | 33.0265 | 131.1910 | 10.89 | 5.5 | 220/72/–167 | 1.09 | 126/78/–19 | 2.02 |
| 4 | 2016/04/16 | 00:48 | 32.8470 | 130.8350 | 15.91 | 5.2 | 230/38/–112 | −4.43 | 77/55/–73 | 6.95 |
| 5 | 2016/04/16 | 07:02 | 32.6992 | 130.7200 | 12.30 | 5.1 | 255/30/–88 | 3.24 | 72/60/–91 | –2.78 |
| 6 | 2016/04/18 | 11:41 | 33.0020 | 131.1998 | 8.64 | 5.4 | 314/86/3 | 2.38 | 224/87/176 | 1.07 |
| 7 | 2016/04/19 | 08:52 | 32.5352 | 130.6353 | 9.96 | 5.3 | 221/60/–169 | 2.45 | 126/81/–30 | 1.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Chen, T.; Wang, M.; Li, Y. Multi-Segment Rupture Model of the 2016 Kumamoto Earthquake Revealed by InSAR and GPS Data. Remote Sens. 2020, 12, 3721. https://doi.org/10.3390/rs12223721
He Z, Chen T, Wang M, Li Y. Multi-Segment Rupture Model of the 2016 Kumamoto Earthquake Revealed by InSAR and GPS Data. Remote Sensing. 2020; 12(22):3721. https://doi.org/10.3390/rs12223721
Chicago/Turabian StyleHe, Zhongqiu, Ting Chen, Mingce Wang, and Yanchong Li. 2020. "Multi-Segment Rupture Model of the 2016 Kumamoto Earthquake Revealed by InSAR and GPS Data" Remote Sensing 12, no. 22: 3721. https://doi.org/10.3390/rs12223721
APA StyleHe, Z., Chen, T., Wang, M., & Li, Y. (2020). Multi-Segment Rupture Model of the 2016 Kumamoto Earthquake Revealed by InSAR and GPS Data. Remote Sensing, 12(22), 3721. https://doi.org/10.3390/rs12223721