FPGA-Based On-Board Hyperspectral Imaging Compression: Benchmarking Performance and Energy Efficiency against GPU Implementations
Abstract
:1. Introduction
2. Materials and Methods
2.1. HyperLCA Algorithm
2.1.1. General Notation
2.1.2. HyperLCA Initialization
2.1.3. HyperLCA Transform
| Algorithm 1 HyperLCA Transform. |
| Inputs: |
| , |
| Outputs: |
| ; ; ; |
| Algorithm: |
| 1: {Additional stopping condition initialization.} |
| 2: Average pixel: ; |
| 3: Centralized image: ; |
| 4: for to do |
| 5: for to do |
| 6: Brightness Calculation: ; |
| 7: end for |
| 8: Maximum Brightness: argmax(); |
| 9: Extracted pixels: ; |
| 10: ; |
| 11: ; |
| 12: Projection vector: ; |
| 13: Information Subtraction: ; |
| 14: {Additional stopping condition checking.} |
| 15: end for |
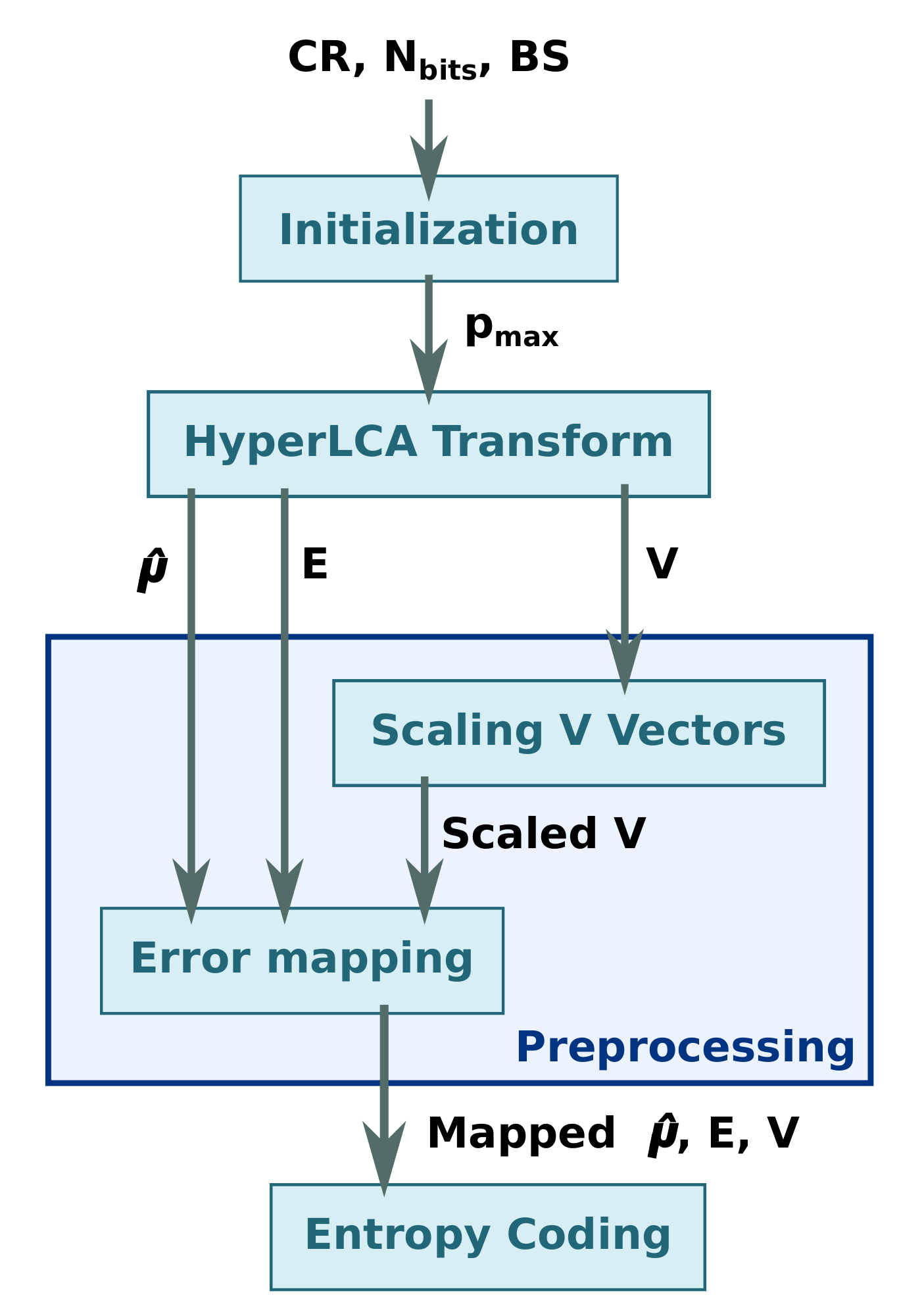
2.1.4. HyperLCA Preprocessing
Scaling V Vectors
Error Mapping
2.1.5. HyperLCA Entropy Coding
2.1.6. HyperLCA Data Types and Precision Evaluation
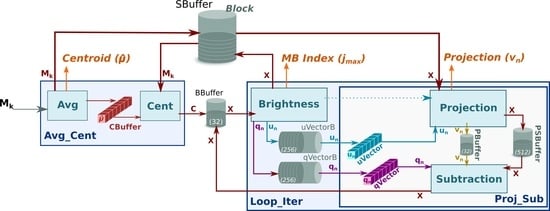
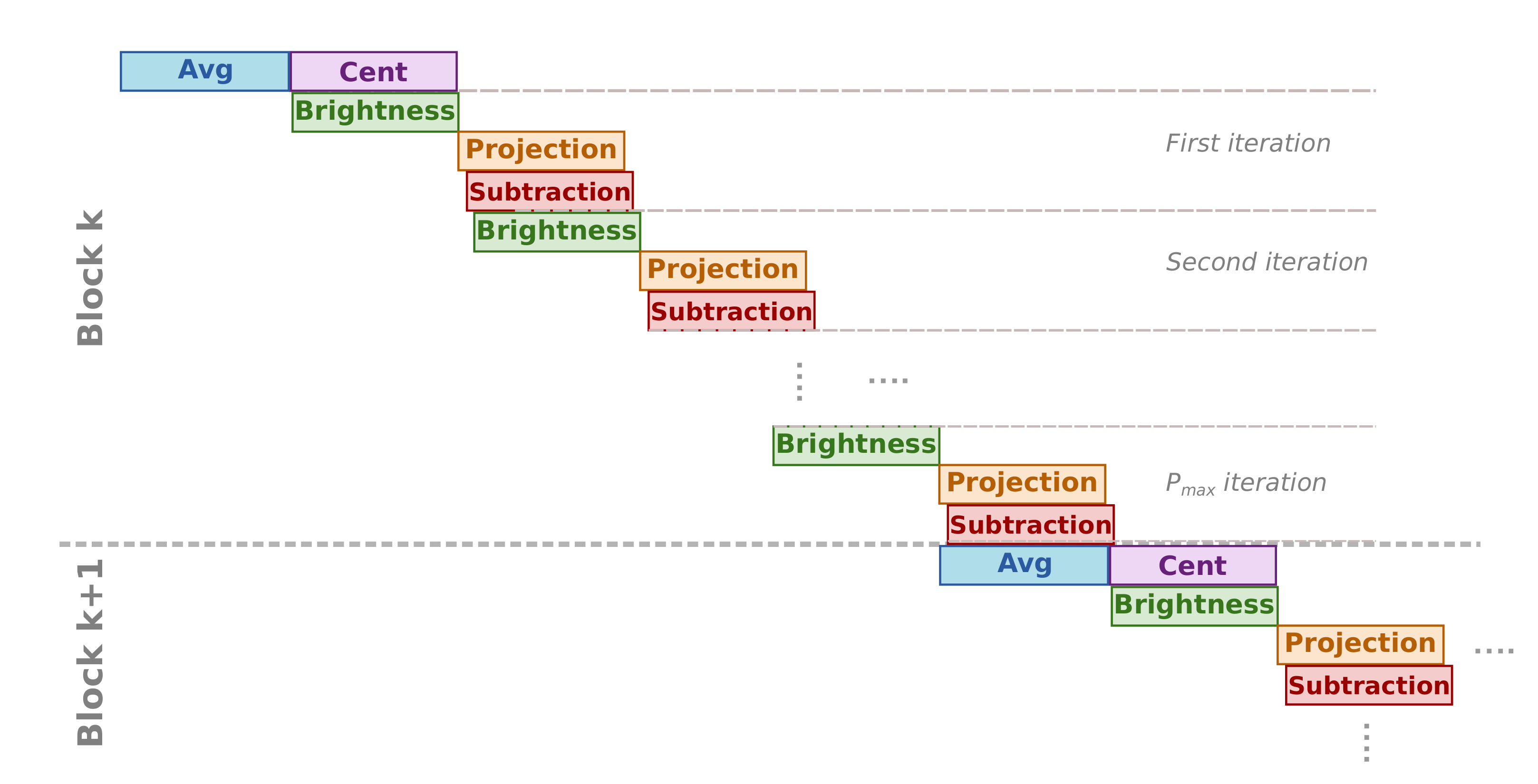
2.2. FPGA Implementation of the HyperLCA Algorithm
2.2.1. HyperLCA Transform
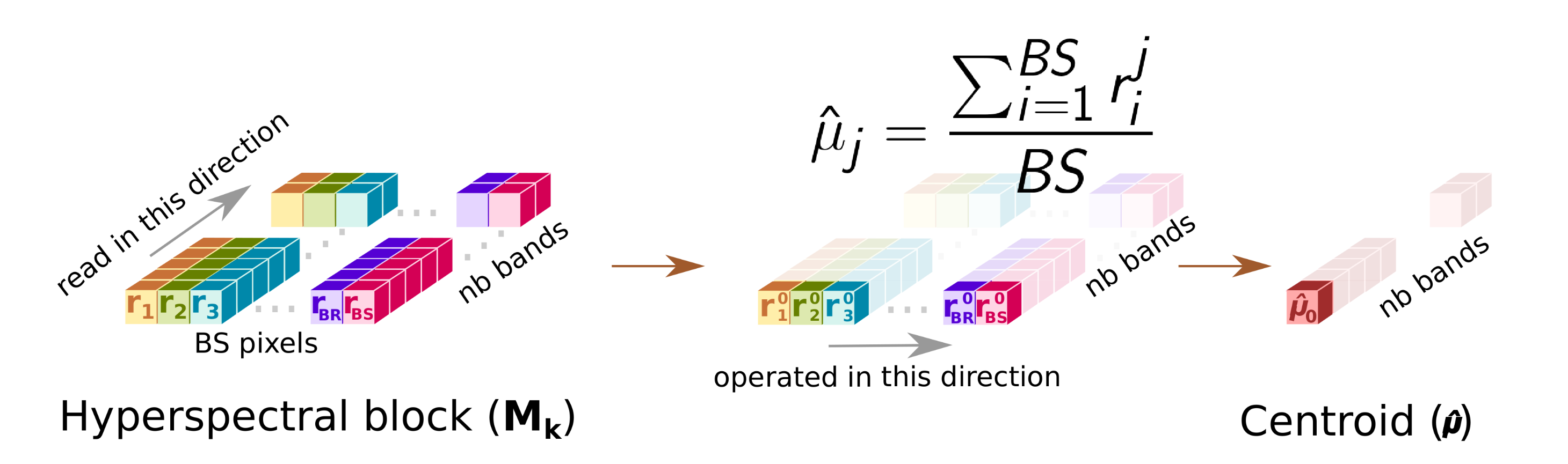
- Avg
- This sub-module computes the centroid or average pixel, , of the original hyperspectral block, , following line 2 of Algorithm 1, and stores it in CBuffer, a buffer that shares with Cent sub-module. During this operation, Avg forwards a copy of the centroid to the HyperLCA Coder via a dedicated port (orange arrow). At the same time, the Avg sub-module writes all the pixels of the into the SBuffer. A copy of the original hyperspectral block, , will be available once Avg finishes, ready to be consumed as a stream by Cent, which reduces the latency.Figure 3 shows in detail the functioning of the Avg stage. The main problem in this stage is the way the hyperspectral data is stored. In our case, the hyperspectral block, , is ordered by the bands that make up a hyperspectral pixel. However, to obtain the centroid, , the hyperspectral block must be read by bands (in-width reading) instead of by pixels (in-depth reading). We introduce an optimization that handles the data as it is received (in-depth), avoiding the reordering of the data to maintain a stream-like processing. This optimization consists of an accumulate vector, whose depth is equal to the number of bands that stores partial results of the summation for each band, i.e., the first position of this vector contains the partial results of the first band, the second position the partial results of the second band and so on. The use of this vector removes the loop-carry dependency in the HLS loop that models the behavior of the Avg sub-module, saving processing cycles. The increase in resources is minimal, which is justified by the gain in performance.
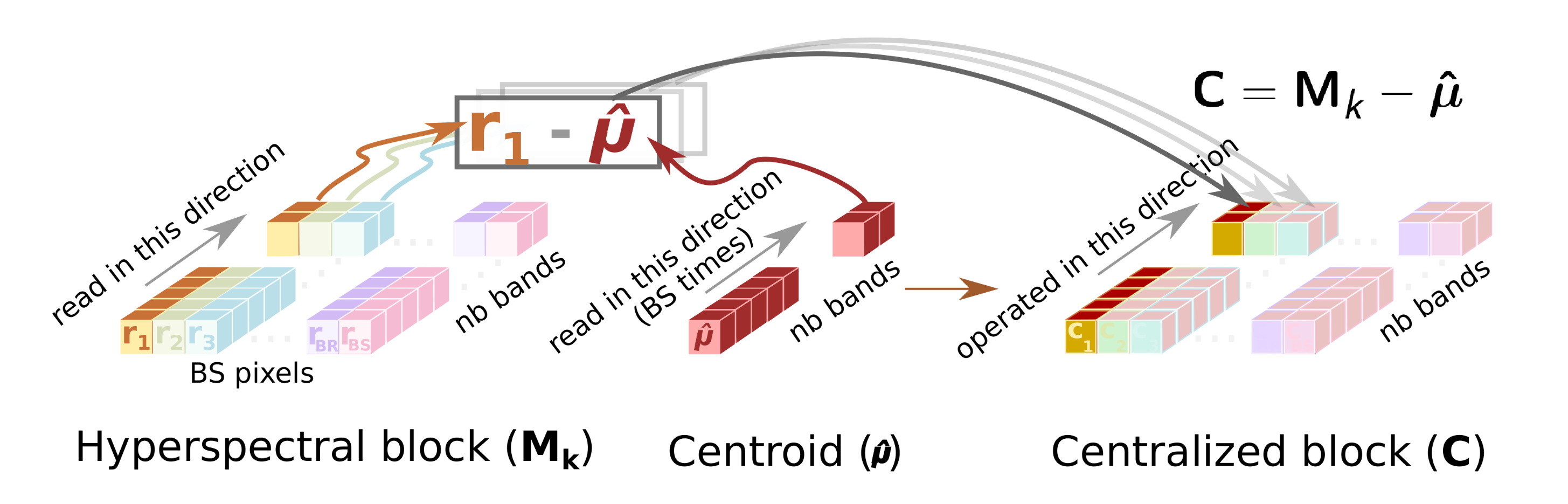
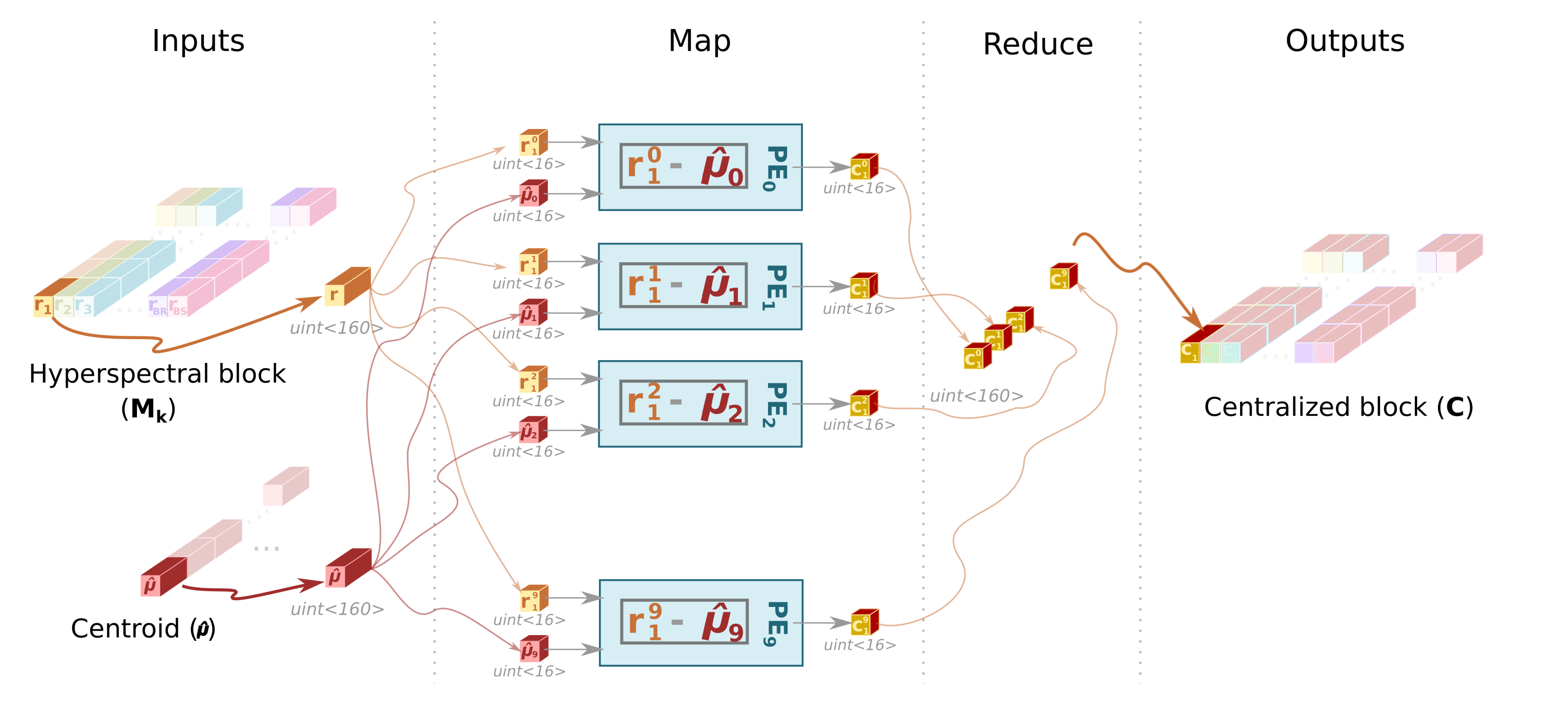
- Cent
- This sub-module reads the original hyperspectral block, , from the SBuffer to centralize it (). This operation consists of subtracting the average pixel, calculated in the previous stage, from each hyperspectral pixel of the block (line 3 of Algorithm 1). Figure 4 shows this process, highlighting the elements that are involved in the centralization of the first hyperspectral pixel. Thus, the Cent block reads the centroid, , which is stored in the CBuffer, as many times hyperspectral pixels have the original block (i.e., times in the example illustrated in Figure 4). Therefore, CBuffer is an addressable buffer that permanently stores the centroid of the current hyperspectral block that is being processed. The result of this stage is written into the BBuffer FIFO, which makes unnecessary an additional copy of the centralized image, . As soon as the centralized components of the hyperspectral pixels are computed, the data is ready at the input of the Loop_Iter module and, therefore, it can start to perform its operations without waiting for the block to be completely centralized.
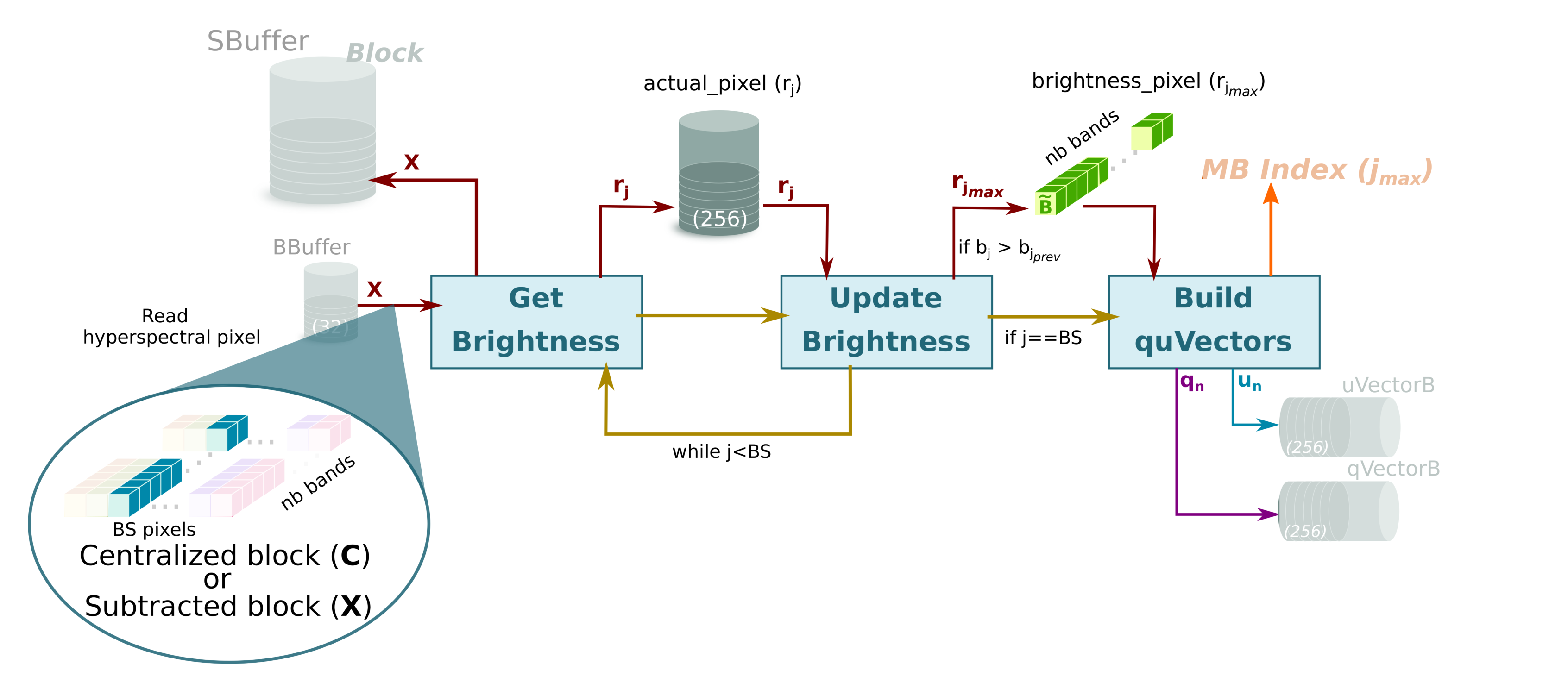
- Brightness
- This sub-module starts as soon as there is data in the BBuffer. In this sense, Brightness sub-module works in parallel with the rest of the system; the input of the Brightness module is the output of Cent module in the first iteration, i.e., the centralized image, , while the input for all other iterations is the output of Subtraction sub-module that corresponds to the image for being subtracted, depicted as for the sake of clarity (see brown arrows in Figure 2).Brightness sub-module has been optimized to achieve a dataflow behavior that takes the same time regardless of the location of the brightest hyperspectral pixel. Figure 5 shows how the orthogonal projection vectors and are obtained by the three sub-modules in Brightness. First, the Get Brightness sub-module reads in order the hyperspectral pixel of the block from the BBuffer ( or , it depends on the loop iteration) and calculates its brightness () as specified in line 6 of Algorithm 1. Get Brightness also makes a copy of the hyperspectral pixel in an internal buffer (actual_pixel) and in SBuffer. Thus, actual_pixel contains the current hyperspectral pixel whose brightness is being calculated, while SBuffer will contain a copy of the hyperspectral block with transformations (line 6 and assignment in line 13 of Algorithm 1).Once the brightness of the current hyperspectral pixel is calculated, the Update Brightness sub-module will update the internal vector brightness_pixel if the current brightness is greater than the previous one. Regardless of such condition, the module will empty the content of actual_pixel in order to keep the dataflow with the Get Brightness sub-module. The operations of both sub-modules are performed until all hyperspectral pixels of the block are processed (inner loop, lines 5 to 7 of Algorithm 1). The reason to use a vector to store the brightest pixel instead of a FIFO is because the HLS tool would stall the dataflow otherwise.Finally, the orthogonal projection vectors and are accordingly obtained from the brightest pixel (lines 10 and 11 of Algorithm 1) by the module Build quVectors. Both are written in separate FIFOs: qVectorB and uVectorB, respectively. Furthermore, the contents of these FIFOs are copied in qVector and uVector arrays in order to get a double space memory that does not deadlock the system and allows Proj_Sub sub-module to read several times (concretely times) the orthogonal projection vectors and to obtain the projected image vector, , and transform the current hyperspectral block. This module also returns the index of the brightest pixel, , so that the HyperLCA Coder stage reads the original pixel from the external memory, such as DDR, where the hyperspectral image is stored in order to build the compressed bitstream.
- Proj_Sub
- Although this sub-module is represented by separate Projection and Subtraction boxes in Figure 2, it must be mentioned that both perform their computations in parallel. The Proj_Sub sub-module reads just once the hyperspectral block that was written in SBuffer by the Brightness sub-module (). Figure 6 shows an example of Projection and Subtraction stages. First, each hyperspectral pixel of the block is read by the Projection sub-module to obtain the projected image vector according to line 12 of Algorithm 1. At the same time, the hyperspectral pixel is written in PSBuffer, which can store two hyperspectral pixels. Two is the number of pixels because the Subtraction stage begins right after the first projection on the first hyperspectral pixel is ready, i.e., the executions of Projection and Subtraction are shifted by one pixel. Figure 6 shows such behavior. While pixel is being consumed by Subtraction, pixel is being written in PSBuffer. During the projection of the second hyperspectral pixel (), the subtraction of the first one () can be performed since all the input operands, included the projection , are available, following the expression in line 13 of Algorithm 1.The output of the Projection sub-module is the projected image vector, , which is forwarded to the HyperLCA Coder accelerator (through the Projection port) and to the Subtration sub-module (via the PBuffer FIFO). At the same time, the output of the Subtraction stage feeds the Loop_Iter block (see purple arrow, labeled as , in Figure 2) with the pixels of the transformed block in the iteration. It means that Brightness stage can start the next iteration without waiting to get the complete image subtracted. Thus, the initialization interval between loop-iterations is reduced as much as possible because the Brightness starts when the first subtracted data is ready.
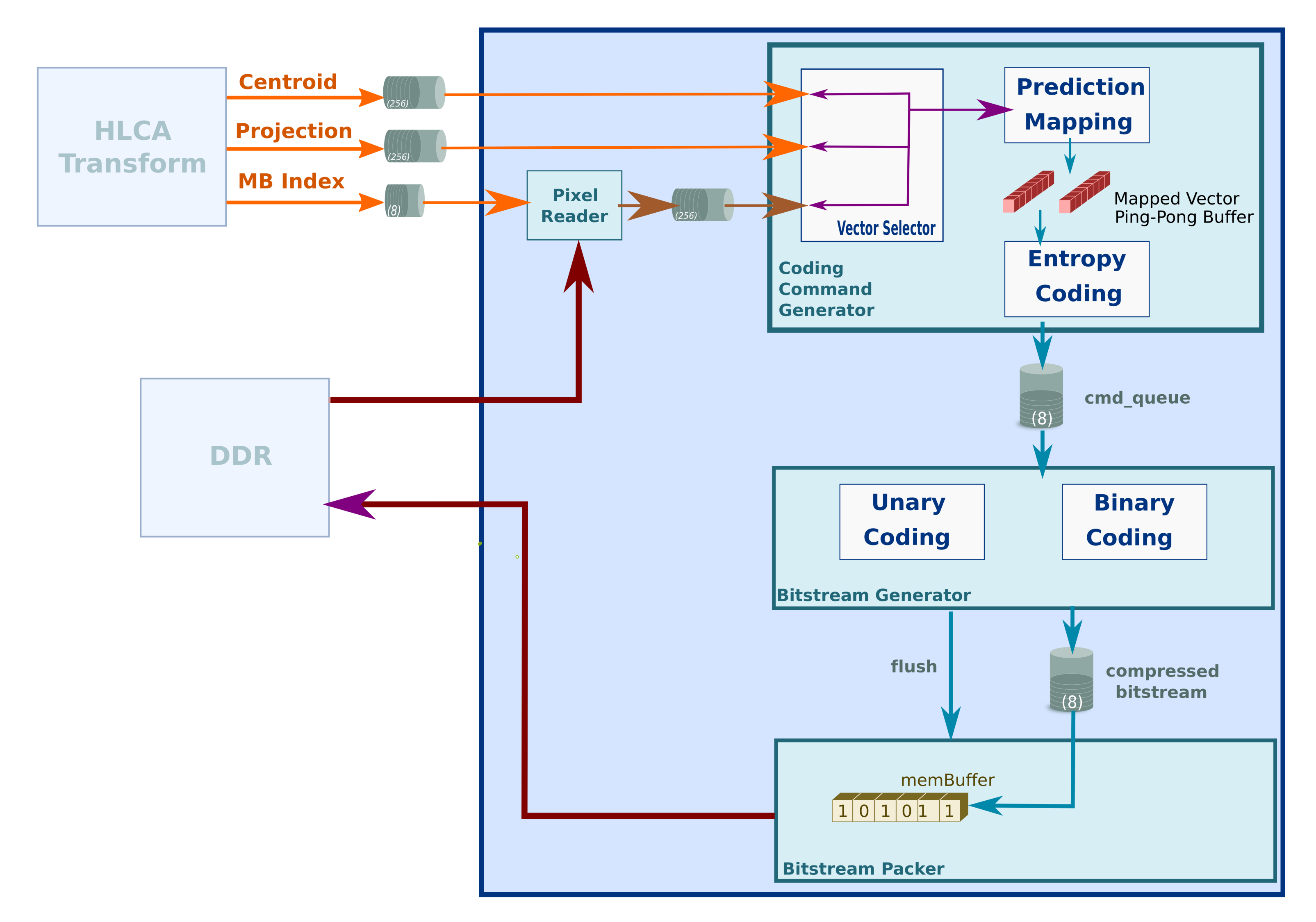
2.2.2. Coder
| 1 //Original code 2 b = log2(M) + 1; 3 difference = pow(2,b) − M; 4 5 //FPGA optimization 6 b = (32 − __builtin_clz(M)); 7 difference = (1<<b) − M; |
2.3. Reference Hyperspectral Data
3. Results
3.1. Evaluation of the HyperLCA Compression Performance
3.2. Evaluation of the HyperLCA Hardware Accelerator
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| BS | CR | Cycles per Block | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Max Frame Rate) | |||||||||||||||
| 1 PE | 2 PEs | 4 PEs | 6 PEs | 10 PEs | 12 PEs | ||||||||||
| 100 MHz | 150 MHz | 100 MHz | 150 MHz | 100 MHz | 150 MHz | 100 MHz | 150 MHz | 100 MHz | 150 MHz | 100 MHz | 150 MHz | ||||
| 12 | 12 | 2,666,775 | 1,388,085 | 763,648 | 563,553 | 404,613 | 364,594 | 12 | |||||||
| 37 | 56 | 72 | 108 | 131 | 196 | 178 | 266 | 248 | 370 | 275 | 411 | ||||
| 1024 | 16 | 2,093,523 | 1,088,779 | 599,742 | 445,886 | 323,820 | 293,101 | 9 | |||||||
| 47 | 71 | 91 | 137 | 167 | 250 | 225 | 336 | 310 | 463 | 343 | 511 | ||||
| 20 | 1,711,355 | 889,312 | 490,447 | 367,439 | 269,887 | 245,360 | 7 | ||||||||
| 58 | 87 | 112 | 168 | 204 | 305 | 273 | 408 | 373 | 555 | 410 | 611 | ||||
| 12 | 1,145,407 | 596,547 | 328,928 | 244,157 | 176,829 | 159,901 | 10 | ||||||||
| 43 | 65 | 83 | 125 | 152 | 228 | 205 | 307 | 284 | 424 | 314 | 469 | ||||
| 512 | 16 | 953,703 | 496,418 | 273,941 | 204,570 | 149,589 | 135,691 | 8 | |||||||
| 52 | 78 | 100 | 151 | 183 | 273 | 245 | 366 | 336 | 501 | 370 | 552 | ||||
| 20 | 761,999 | 396,125 | 218,877 | 165,082 | 122,367 | 111,546 | 6 | ||||||||
| 69 | 98 | 126 | 189 | 229 | 342 | 304 | 454 | 411 | 612 | 452 | 672 | ||||
| 12 | 479,335 | 250,030 | 138,409 | 103,597 | 76,005 | 69,030 | 8 | ||||||||
| 52 | 78 | 100 | 149 | 181 | 270 | 242 | 361 | 330 | 493 | 364 | 543 | ||||
| 256 | 16 | 382,863 | 199,499 | 110,479 | 83,400 | 62,056 | 56,649 | 6 | |||||||
| 65 | 97 | 125 | 187 | 227 | 339 | 301 | 449 | 405 | 604 | 444 | 661 | ||||
| 20 | 286,391 | 148,931 | 82,691 | 63,382 | 48,200 | 44,265 | 4 | ||||||||
| 87 | 130 | 167 | 251 | 303 | 453 | 397 | 591 | 523 | 778 | 570 | 847 | ||||
| 8 | 12 | 3,622,195 | 1,886,981 | 1,036,739 | 759,669 | 539,143 | 483,832 | 17 | |||||||
| 27 | 41 | 53 | 79 | 96 | 144 | 131 | 197 | 186 | 278 | 207 | 310 | ||||
| 1024 | 16 | 2,857,859 | 1,487,981 | 818,201 | 602,802 | 431,461 | 388,391 | 13 | |||||||
| 34 | 52 | 67 | 100 | 122 | 183 | 166 | 248 | 232 | 347 | 258 | 386 | ||||
| 20 | 2,284,607 | 1,188,572 | 654,337 | 485,088 | 350,730 | 316,731 | 10 | ||||||||
| 43 | 65 | 84 | 126 | 153 | 229 | 206 | 309 | 286 | 427 | 317 | 473 | ||||
| 12 | 1,528,815 | 797,038 | 438,876 | 323,247 | 231,359 | 208,129 | 14 | ||||||||
| 32 | 49 | 62 | 94 | 114 | 170 | 155 | 232 | 217 | 324 | 241 | 360 | ||||
| 512 | 16 | 1,145,407 | 596,571 | 328,949 | 244,100 | 176,809 | 159,834 | 10 | |||||||
| 43 | 65 | 83 | 125 | 152 | 227 | 205 | 307 | 284 | 424 | 370 | 469 | ||||
| 20 | 953,703 | 496,495 | 274,002 | 204,592 | 149,566 | 135,748 | 8 | ||||||||
| 52 | 78 | 100 | 151 | 183 | 273 | 245 | 366 | 336 | 501 | 370 | 552 | ||||
| 12 | 575,808 | 300,575 | 166,183 | 123,677 | 89,908 | 81,374 | 10 | ||||||||
| 43 | 65 | 83 | 124 | 150 | 225 | 202 | 303 | 279 | 417 | 309 | 460 | ||||
| 256 | 16 | 431,099 | 224,781 | 124,409 | 93,463 | 68,997 | 62,850 | 7 | |||||||
| 57 | 86 | 111 | 166 | 201 | 301 | 268 | 401 | 364 | 543 | 400 | 596 | ||||
| 20 | 382,863 | 199,486 | 110,540 | 83,520 | 62,093 | 56,658 | 6 | ||||||||
| 65 | 97 | 125 | 187 | 227 | 339 | 301 | 448 | 405 | 603 | 444 | 661 | ||||
References
- Plaza, A.; Benediktsson, J.A.; Boardman, J.W.; Brazile, J.; Bruzzone, L.; Camps-Valls, G.; Chanussot, J.; Fauvel, M.; Gamba, P.; Gualtieri, A.; et al. Recent advances in techniques for hyperspectral image processing. Remote. Sens. Environ. 2009, 113, S110–S122. [Google Scholar] [CrossRef]
- Noor, N.R.M.; Vladimirova, T. Integer KLT design space exploration for hyperspectral satellite image compression. In International Conference on Hybrid Information Technology; Springer: Berlin, Germany, 2011; pp. 661–668. [Google Scholar]
- Radosavljević, M.; Brkljač, B.; Lugonja, P.; Crnojević, V.; Trpovski, Ž.; Xiong, Z.; Vukobratović, D. Lossy Compression of Multispectral Satellite Images with Application to Crop Thematic Mapping: A HEVC Comparative Study. Remote Sens. 2020, 12, 1590. [Google Scholar] [CrossRef]
- Villafranca, A.G.; Corbera, J.; Martín, F.; Marchán, J.F. Limitations of hyperspectral earth observation on small satellites. J. Small Satell. 2012, 1, 19–29. [Google Scholar]
- Valentino, R.; Jung, W.S.; Ko, Y.B. A Design and Simulation of the Opportunistic Computation Offloading with Learning-Based Prediction for Unmanned Aerial Vehicle (UAV) Clustering Networks. Sensors 2018, 18, 3751. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lopez, S.; Vladimirova, T.; Gonzalez, C.; Resano, J.; Mozos, D.; Plaza, A. The promise of reconfigurable computing for hyperspectral imaging onboard systems: A review and trends. Proc. IEEE 2013, 101, 698–722. [Google Scholar] [CrossRef]
- George, A.D.; Wilson, C.M. Onboard processing with hybrid and reconfigurable computing on small satellites. Proc. IEEE 2018, 106, 458–470. [Google Scholar] [CrossRef]
- Fu, S.; Chang, R.; Couture, S.; Menarini, M.; Escobar, M.; Kuteifan, M.; Lubarda, M.; Gabay, D.; Lomakin, V. Micromagnetics on high-performance workstation and mobile computational platforms. J. Appl. Phys. 2015, 117, 17E517. [Google Scholar] [CrossRef]
- Ortenberg, F.; Thenkabail, P.; Lyon, J.; Huete, A. Hyperspectral sensor characteristics: Airborne, spaceborne, hand-held, and truck-mounted; Integration of hyperspectral data with Lidar. Hyperspectral Remote Sens. Veg. 2011, 4, 39–68. [Google Scholar]
- Board, N.S.; Council, N.R. Autonomous Vehicles in Support of Naval Operations; National Academies Press: Washington DC, USA, 2005. [Google Scholar]
- Gómez, C.; Green, D.R. Small unmanned airborne systems to support oil and gas pipeline monitoring and mapping. Arab. J. Geosci. 2017, 10, 202. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef] [Green Version]
- Keymeulen, D.; Aranki, N.; Hopson, B.; Kiely, A.; Klimesh, M.; Benkrid, K. GPU lossless hyperspectral data compression system for space applications. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012; pp. 1–9. [Google Scholar]
- Huang, B. Satellite Data Compression; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Consultative Committee for Space Data Systems (CCSDS). Image Data Compression.CCSDS, Green Book 120.1-G-2. Available online: https://public.ccsds.org/Pubs/120x1g2.pdf (accessed on 10 July 2020).
- Motta, G.; Rizzo, F.; Storer, J.A. Hyperspectral Data Compression; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Penna, B.; Tillo, T.; Magli, E.; Olmo, G. Transform coding techniques for lossy hyperspectral data compression. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1408–1421. [Google Scholar] [CrossRef]
- Marcellin, M.W.; Taubman, D.S. JPEG2000: Image compression fundamentals, standards, and practice. In International Series in Engineering and Computer Science, Secs 642; Springer: New York, NY, USA, 2002. [Google Scholar]
- Chang, L.; Cheng, C.M.; Chen, T.C. An efficient adaptive KLT for multispectral image compression. In Proceedings of the 4th IEEE Southwest Symposium on Image Analysis and Interpretation, Austin, TX, USA, 2–4 April 2000; pp. 252–255. [Google Scholar]
- Hao, P.; Shi, Q. Reversible integer KLT for progressive-to-lossless compression of multiple component images. In Proceedings of the 2003 International Conference on Image Processing (Cat. No. 03CH37429), Barcelona, Spain, 14–17 September 2003; Volume 1, pp. 1–633. [Google Scholar]
- Abrardo, A.; Barni, M.; Magli, E. Low-complexity predictive lossy compression of hyperspectral and ultraspectral images. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 797–800. [Google Scholar]
- Kiely, A.B.; Klimesh, M.; Blanes, I.; Ligo, J.; Magli, E.; Aranki, N.; Burl, M.; Camarero, R.; Cheng, M.; Dolinar, S.; et al. The new CCSDS standard for low-complexity lossless and near-lossless multispectral and hyperspectral image compression. In Proceedings of the 2018 Onboard Payload Data Compression Workshop, Matera, Italy, 20–21 September 2018; pp. 1–7. [Google Scholar]
- Auge, E.; Santalo, J.; Blanes, I.; Serra-Sagrista, J.; Kiely, A. Review and implementation of the emerging CCSDS recommended standard for multispectral and hyperspectral lossless image coding. In Proceedings of the 2011 First International Conference on Data Compression, Communications and Processing, Palinuro, Italy, 21–24 June 2011; pp. 222–228. [Google Scholar]
- Augé, E.; Sánchez, J.E.; Kiely, A.B.; Blanes, I.; Serra-Sagrista, J. Performance impact of parameter tuning on the CCSDS-123 lossless multi-and hyperspectral image compression standard. J. Appl. Remote Sens. 2013, 7, 074594. [Google Scholar] [CrossRef] [Green Version]
- Santos, L.; Magli, E.; Vitulli, R.; López, J.F.; Sarmiento, R. Highly-parallel GPU architecture for lossy hyperspectral image compression. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 670–681. [Google Scholar] [CrossRef]
- Barrios, Y.; Sánchez, A.J.; Santos, L.; Sarmiento, R. SHyLoC 2.0: A Versatile Hardware Solution for On-Board Data and Hyperspectral Image Compression on Future Space Missions. IEEE Access 2020, 8, 54269–54287. [Google Scholar] [CrossRef]
- Santos, L.; López, J.F.; Sarmiento, R.; Vitulli, R. FPGA implementation of a lossy compression algorithm for hyperspectral images with a high-level synthesis tool. In Proceedings of the 2013 NASA/ESA Conference on Adaptive Hardware and Systems (AHS-2013), Torino, Italy, 24–27 June 2013; pp. 107–114. [Google Scholar]
- Guerra, R.; Barrios, Y.; Díaz, M.; Santos, L.; López, S.; Sarmiento, R. A New Algorithm for the On-Board Compression of Hyperspectral Images. Remote Sens. 2018, 10, 428. [Google Scholar] [CrossRef] [Green Version]
- Díaz, M.; Guerra, R.; Horstrand, P.; Martel, E.; López, S.; López, J.F.; Roberto, S. Real-Time Hyperspectral Image Compression Onto Embedded GPUs. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 1–18. [Google Scholar] [CrossRef]
- Guerra, R.; Santos, L.; López, S.; Sarmiento, R. A new fast algorithm for linearly unmixing hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6752–6765. [Google Scholar] [CrossRef]
- Díaz, M.; Guerra, R.; López, S.; Sarmiento, R. An algorithm for an accurate detection of anomalies in hyperspectral images with a low computational complexity. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1159–1176. [Google Scholar] [CrossRef]
- Díaz, M.; Guerra, R.; Horstrand, P.; López, S.; Sarmiento, R. A Line-by-Line Fast Anomaly Detector for Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2019, 8968–8982. [Google Scholar] [CrossRef]
- Diaz, M.; Guerra Hernández, R.; Lopez, S. A Novel Hyperspectral Target Detection Algorithm For Real-Time Applications With Push-Broom Scanners. In Proceedings of the 10th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands; 24–26 September 2019, 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Díaz, M.; Guerra, R.; Horstrand, P.; López, S.; López, J.F.; Sarmiento, R. Towards the Concurrent Execution of Multiple Hyperspectral Imaging Applications by Means of Computationally Simple Operations. Remote Sens. 2020, 12, 1343. [Google Scholar] [CrossRef] [Green Version]
- Consultative Committee for Space Data Systems (CCSDS). Blue Books: Recommended Standards. Available online: https://public.ccsds.org/Publications/BlueBooks.aspx (accessed on 11 March 2019).
- Howard, P.G.; Vitter, J.S. Fast and Efficient Lossless Image Compression. In Proceedings of the DCC ‘93: Data Compression Conference, Snowbird, UT, USA, 30 March–2 April 1993; pp. 351–360. [Google Scholar]
- Guerra Hernández, R.; Barrios, Y.; Diaz, M.; Baez, A.; Lopez, S.; Sarmiento, R. A Hardware-Friendly Hyperspectral Lossy Compressor for Next-Generation Space-Grade Field Programmable Gate Arrays. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 1–17. [Google Scholar] [CrossRef]
- Oberstar, E.L. Fixed-point representation & fractional math. Oberstar Consult. 2007, 9. Available online: https://www.superkits.net/whitepapers/Fixed%20Point%20Representation%20&%20Fractional%20Math.pdf (accessed on 15 March 2019).
- Hu, C.; Feng, L.; Lee, Z.; Davis, C.; Mannino, A.; Mcclain, C.; Franz, B. Dynamic range and sensitivity requirements of satellite ocean color sensors: Learning from the past. Appl. Opt. 2012, 51, 6045–6062. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, A.; Mehta, S.; Paul, S.; Parmar, R.; Samudraiah, R. Dynamic Range Enhancement of Remote Sensing Electro-Optical Imaging Systems. In Proceeding of the Symposium at Indian Society of Remote Sensing, Bhopal, India; 2012. [Google Scholar]
- Xilinx Inc. UltraFast Vivado HLS Methodology Guide; Technical Report; Xilinx Inc.: San Jose, CA, USA, 2020. [Google Scholar]
- Cong, J.; Liu, B.; Neuendorffer, S.; Noguera, J.; Vissers, K.; Zhang, Z. High-Level Synthesis for FPGAs: From Prototyping to Deployment. IEEE Trans. Comput.-Aided Design Integr. Circuits Syst. 2011, 30, 473–491. [Google Scholar] [CrossRef] [Green Version]
- Bailey, D.G. The Advantages and Limitations of High Level Synthesis for FPGA Based Image Processing. In Proceedings of the 9th International Conference on Distributed Smart Cameras, September 2015; pp. 134–139. [Google Scholar] [CrossRef]
- de Fine Licht, J.; Meierhans, S.; Hoefler, T. Transformations of High-Level Synthesis Codes for High-Performance Computing. arXiv 2018, arXiv:1805.08288. [Google Scholar]
- Dean, J.; Ghemawat, S. MapReduce: Simplified Data Processing on Large Clusters. Commun. ACM 2008, 51, 107–113. [Google Scholar] [CrossRef]
- Caba, J.; Rincón, F.; Dondo, J.; Barba, J.; Abaldea, M.; López, J.C. Testing framework for on-board verification of HLS modules using grey-box technique and FPGA overlays. Integration 2019, 68, 129–138. [Google Scholar] [CrossRef]
- Caba, J.; Cardoso, J.M.P.; Rincón, F.; Dondo, J.; López, J.C. Rapid Prototyping and Verification of Hardware Modules Generated Using HLS. In Proceedings of the Applied Reconfigurable Computing, Architectures, Tools, and Applications-14th International Symposium, ARC 2018, Santorini, Greece, 2–4 May 2018; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2018; Volume 10824, pp. 446–458. [Google Scholar] [CrossRef]
- Horstrand, P.; Guerra, R.; Rodríguez, A.; Díaz, M.; López, S.; López, J.F. A UAV platform based on a hyperspectral sensor for image capturing and on-board processing. IEEE Access 2019, 7, 66919–66938. [Google Scholar] [CrossRef]
- NVIDIA Corporation. NVIDIA Jetson Linux Developer Guide 32.4.3 Release. Power Management for Jetson Nano and Jetson TX1 Devices. Available online: https://docs.nvidia.com/jetson/l4t/index.html#page/Tegra%20Linux%20Driver%20Package%20Development%20Guide/power_management_nano.html (accessed on 7 September 2019).
- NVIDIA Corporation. NVIDIA Jetson Linux Driver Package Software Features Release 32.3. Power Management for Jetson TX2 Series Devices. Available online: https://docs.nvidia.com/jetson/archives/l4t-archived/l4t-3231/index.html#page/Tegra%20Linux%20Driver%20Package%20Development%20Guide/power_management_tx2_32.html (accessed on 7 September 2019).
- NVIDIA Corporation. NVIDIA Jetson Linux Developer Guide 32.4.3 Release. Power Management for Jetson Xavier NX and Jetson AGX Xavier Series Device. Available online: https://docs.nvidia.com/jetson/l4t/index.html#page/Tegra%20Linux%20Driver%20Package%20Development%20Guide/power_management_jetson_xavier.html (accessed on 7 September 2019).




| Variable | Integer Part | Decimal Part | Total | ||||||
|---|---|---|---|---|---|---|---|---|---|
| I32 | I16 | I12 | I32 | I16 | I12 | I32 | I16 | I12 | |
| C | 20 | 16 | 14 | 12 | 0 | 2 | 32 | 16 | 16 |
| b | 48 | 48 | 48 | 16 | 16 | 16 | 64 | 64 | 64 |
| q | 20 | 20 | 20 | 12 | 12 | 12 | 32 | 32 | 32 |
| u | 2 | 2 | 2 | 30 | 30 | 30 | 32 | 32 | 32 |
| v | 2 | 2 | 2 | 30 | 30 | 30 | 32 | 32 | 32 |
| 16 | 16 | 12 | 0 | 0 | 0 | 16 | 16 | 12 | |
| Nbits | BS | CR | SNR | MAD | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I12 | I16 | I32 | F32 | I12 | I16 | I32 | F32 | I12 | I16 | I32 | F32 | |||
| 12 | 12 | 43.01 | 38.01 | 43.12 | 42.75 | 24.50 | 39.00 | 25.00 | 25.50 | 3.12 | 5.55 | 3.08 | 3.22 | |
| 1024 | 16 | 42.27 | 38.57 | 42.27 | 41.97 | 32.25 | 41.50 | 32.25 | 32.50 | 3.40 | 5.21 | 3.40 | 3.52 | |
| 20 | 41.31 | 39.13 | 41.31 | 41.06 | 41.25 | 46.50 | 41.25 | 41.25 | 3.73 | 4.88 | 3.80 | 3.91 | ||
| 12 | 42.99 | 38.95 | 43.03 | 42.68 | 26.25 | 34.50 | 25.00 | 25.00 | 3.13 | 4.98 | 3.12 | 3.24 | ||
| 512 | 16 | 42.45 | 39.36 | 42.47 | 42.14 | 30.75 | 38.00 | 30.00 | 30.50 | 3.33 | 4.75 | 3.33 | 3.45 | |
| 20 | 41.50 | 39.92 | 41.48 | 41.24 | 39.50 | 43.75 | 39.50 | 40.00 | 3.72 | 4.46 | 3.72 | 3.83 | ||
| 12 | 43.03 | 40.00 | 43.02 | 42.67 | 25.00 | 34.50 | 25.00 | 25.50 | 3.12 | 4.42 | 3.12 | 3.25 | ||
| 256 | 16 | 42.33 | 40.51 | 42.32 | 42.02 | 34.75 | 37.25 | 34.75 | 35.00 | 3.38 | 4.16 | 3.38 | 3.50 | |
| 20 | 40.94 | 40.59 | 40.59 | 40.73 | 54.75 | 57.75 | 54.75 | 54.75 | 3.96 | 4.13 | 3.97 | 4.06 | ||
| 8 | 12 | 41.80 | 36.91 | 42.19 | 41.68 | 23.25 | 41.50 | 22.00 | 22.25 | 3.62 | 6.32 | 3.47 | 3.69 | |
| 1024 | 16 | 41.63 | 37.42 | 41.73 | 41.27 | 25.50 | 41.25 | 25.50 | 26.50 | 3.69 | 5.95 | 3.65 | 3.86 | |
| 20 | 41.20 | 37.89 | 41.20 | 40.79 | 32.25 | 42.00 | 32.50 | 32.25 | 3.87 | 5.64 | 3.87 | 4.07 | ||
| 12 | 42.49 | 37.99 | 42.70 | 42.26 | 23.00 | 38.00 | 22.75 | 22.25 | 3.33 | 5.57 | 3.25 | 3.42 | ||
| 512 | 16 | 42.07 | 38.64 | 42.09 | 41.69 | 27.50 | 36.00 | 26.50 | 26.75 | 3.49 | 5.17 | 3.48 | 3.65 | |
| 20 | 41.61 | 39.01 | 41.60 | 41.25 | 31.25 | 39.50 | 30.50 | 31.75 | 3.68 | 4.95 | 3.68 | 3.84 | ||
| 12 | 42.79 | 39.35 | 42.82 | 42.39 | 24.75 | 35.50 | 25.00 | 25.00 | 3.20 | 4.76 | 3.19 | 3.36 | ||
| 256 | 16 | 42.15 | 39.96 | 42.13 | 41.76 | 30.00 | 37.00 | 29.75 | 29.75 | 3.45 | 4.43 | 3.46 | 3.61 | |
| 20 | 41.80 | 40.21 | 41.78 | 41.44 | 35.75 | 37.00 | 35.75 | 36.00 | 3.59 | 4.31 | 3.60 | 3.74 | ||
| BS | CR | Min SBuffer Depth | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 PE | 2 PEs | 4 PEs | 6 PEs | 10 PEs | 12 PEs | ||||
| 12 | 12 | 12 | |||||||
| 1024 | 16 | 184,320 | 92,160 | 46,080 | 30,720 | 18,432 | 15,360 | 9 | |
| 20 | 7 | ||||||||
| 12 | 10 | ||||||||
| 512 | 16 | 92,160 | 46,080 | 30,720 | 18,432 | 15,360 | 7680 | 8 | |
| 20 | 6 | ||||||||
| 12 | 8 | ||||||||
| 256 | 16 | 46,080 | 30,720 | 18,432 | 5,360 | 7680 | 3840 | 6 | |
| 20 | 4 | ||||||||
| 8 | 12 | 17 | |||||||
| 1024 | 16 | 184,320 | 92,160 | 46,080 | 30,720 | 18,432 | 15,360 | 13 | |
| 20 | 10 | ||||||||
| 12 | 14 | ||||||||
| 512 | 16 | 92,160 | 46,080 | 30,720 | 18,432 | 15,360 | 7680 | 10 | |
| 20 | 8 | ||||||||
| 12 | 10 | ||||||||
| 256 | 16 | 46,080 | 30,720 | 18,432 | 15,360 | 7680 | 3840 | 7 | |
| 20 | 6 | ||||||||
| Data Width (bits) | 16 | 32 | 64 | 96 | 160 | 192 | |||
| BS | Num. PEs | BRAM18K | DSP48E | FlipFlops | LUTs | ||||
|---|---|---|---|---|---|---|---|---|---|
| 256 | 1 | 56 | (20.0%) | 9 | (4.09%) | 6942 | (6.52%) | 5194 | (9.76%) |
| 2 | 59 | (21.07%) | 16 | (7.27%) | 9112 | (8.56%) | 8735 | (16.42%) | |
| 4 | 71 | (25.36%) | 30 | (13.64%) | 20,171 | (18.96%) | 15,811 | (29.72%) | |
| 6 | 71 | (25.36%) | 62 | (28.18%) | 29,368 | (27.6%) | 23,530 | (44.23%) | |
| 10 | 84 | (30.0%) | 102 | (46.36%) | 47,350 | (44.5%) | 38,221 | (71.84%) | |
| 12 | 71 | (25.36%) | 122 | (55.45%) | 56,297 | (52.91%) | 45,867 | (86.22%) | |
| 512 | 1 | 101 | (36.07%) | 9 | (4.09%) | 6988 | (6.57%) | 5270 | (9.91%) |
| 2 | 102 | (36.43%) | 16 | (7.27%) | 9159 | (8.61%) | 8820 | (16.58%) | |
| 4 | 113 | (40.36%) | 30 | (13.64%) | 20,215 | (19.0%) | 16,040 | (30.15%) | |
| 6 | 113 | (40.36%) | 62 | (28.18%) | 29,406 | (27.64%) | 23,761 | (44.66%) | |
| 10 | 124 | (44.29%) | 102 | (46.36%) | 47,420 | (44.57%) | 38,352 | (72.09%) | |
| 12 | 113 | (40.36%) | 122 | (55.45%) | 56,342 | (52.95%) | 45,857 | (86.20%) | |
| 1024 | 1 | 192 | (68.57%) | 9 | (4.09%) | 7114 | (6.69%) | 5468 | (10.28%) |
| 2 | 190 | (67.86%) | 16 | (7.27%) | 9278 | (8.72%) | 8969 | (16.86%) | |
| 4 | 198 | (70.71%) | 30 | (13.64%) | 20,301 | (19.08%) | 16,210 | (30.47%) | |
| 6 | 199 | (71.07%) | 62 | (28.18%) | 29,524 | (27.75%) | 23,916 | (44.95%) | |
| 10 | 204 | (72.86%) | 102 | (46.36%) | 47,514 | (44.66%) | 38,485 | (72.34%) | |
| 12 | 199 | (71.07%) | 122 | (55.45%) | 56,463 | (53.07%) | 46,116 | (86.68%) | |
| BS | BRAM18K | DSP48E | FlipFlops | LUTs | ||||
|---|---|---|---|---|---|---|---|---|
| 2,565,121,024 | 7 | (2.5%) | 1 | (0.45%) | 3464 | (3.25%) | 4106 | (7.71%) |
| Max Frame Rate | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BS | CR | 1 PE | 2 PEs | 4 PEs | 6 PEs | 10 PEs | 12 PEs | |||||||
| 12 | 12 | 37 | 56 | 72 | 108 | 131 | 196 | 178 | 266 | 248 | 370 | 275 | 411 | |
| 1024 | 16 | 47 | 71 | 91 | 137 | 167 | 250 | 225 | 336 | 310 | 463 | 343 | 511 | |
| 20 | 58 | 87 | 112 | 168 | 204 | 305 | 273 | 408 | 373 | 555 | 410 | 611 | ||
| 12 | 43 | 65 | 83 | 125 | 152 | 228 | 205 | 307 | 284 | 424 | 314 | 469 | ||
| 512 | 16 | 52 | 78 | 100 | 151 | 183 | 273 | 245 | 366 | 336 | 501 | 370 | 552 | |
| 20 | 69 | 98 | 126 | 189 | 229 | 342 | 304 | 454 | 411 | 612 | 452 | 672 | ||
| 12 | 52 | 78 | 100 | 149 | 181 | 270 | 242 | 361 | 330 | 493 | 364 | 543 | ||
| 256 | 16 | 65 | 97 | 125 | 187 | 227 | 339 | 301 | 449 | 405 | 604 | 444 | 661 | |
| 20 | 87 | 130 | 167 | 251 | 303 | 453 | 397 | 591 | 523 | 778 | 570 | 847 | ||
| 8 | 12 | 27 | 41 | 53 | 79 | 96 | 144 | 131 | 197 | 186 | 278 | 207 | 310 | |
| 1024 | 16 | 34 | 52 | 67 | 100 | 122 | 183 | 166 | 248 | 232 | 347 | 258 | 386 | |
| 20 | 43 | 65 | 84 | 126 | 153 | 229 | 206 | 309 | 286 | 427 | 317 | 473 | ||
| 12 | 32 | 49 | 62 | 94 | 114 | 170 | 155 | 232 | 217 | 324 | 241 | 360 | ||
| 512 | 16 | 43 | 65 | 83 | 125 | 152 | 227 | 205 | 307 | 284 | 424 | 370 | 469 | |
| 20 | 52 | 78 | 100 | 151 | 183 | 273 | 245 | 366 | 336 | 501 | 370 | 552 | ||
| 12 | 43 | 65 | 83 | 124 | 150 | 225 | 202 | 303 | 279 | 417 | 309 | 460 | ||
| 256 | 16 | 57 | 86 | 111 | 166 | 201 | 301 | 268 | 401 | 364 | 543 | 400 | 596 | |
| 20 | 65 | 97 | 125 | 187 | 227 | 339 | 301 | 448 | 405 | 603 | 444 | 661 | ||
| BS | CR | Cycles per Block | |||
|---|---|---|---|---|---|
| Transform Delay (12 PEs) | Coder Delay | ||||
| 12 | 12 | 364,594 | 184,999 | 12 | |
| 1024 | 16 | 293,101 | 137,379 | 9 | |
| 20 | 245,360 | 105,836 | 7 | ||
| 12 | 159,901 | 88,235 | 10 | ||
| 512 | 16 | 135,691 | 70,468 | 8 | |
| 20 | 111,546 | 52,593 | 6 | ||
| 12 | 69,030 | 44,095 | 8 | ||
| 256 | 16 | 56,649 | 33,294 | 6 | |
| 20 | 44,265 | 22,587 | 4 | ||
| 8 | 12 | 483,832 | 194,170 | 17 | |
| 1024 | 16 | 388,391 | 147,055 | 13 | |
| 20 | 316,731 | 111,919 | 10 | ||
| 12 | 208,129 | 94,584 | 14 | ||
| 512 | 16 | 159,834 | 67,697 | 10 | |
| 20 | 135,748 | 54,037 | 8 | ||
| 12 | 81,374 | 44,579 | 10 | ||
| 256 | 16 | 62,850 | 31,424 | 7 | |
| 20 | 56,658 | 27,163 | 6 | ||
| Jetson Nano | |
| LPGPU | GPU NVIDIA Maxwell architecture with 128 NVIDIA CUDA cores |
| CPU | Quad-core ARM Cortex-A57 MPCore processor |
| Memory | 4 GB LPDDR4, 1600MHz 25.6 GB/s |
| Jetson TX2 | |
| LPGPU | GPU NVIDIA Pascal with 256 CUDA cores |
| CPU | HMP Dual Denver 2/2 MB L2 + Quad ARM A57/2 MB L2 |
| Memory | 8 GB LPDDR4, 128 bits bandwidth, 59.7 GB/s |
| Jetson Xavier NX | |
| LPGPU | GPU NVIDIA Volta with 384 NVIDIA CUDA cores and 48 Tensor cores |
| CPU | 6-core NVIDIA Carmel ARM®v8.2 64-bit CPU 6 MB L2 + 4 MB L3 |
| Memory | 8 GB 128-bit LPDDR4x @ 51.2GB/s |
| Max Frame Rate | |||||||
|---|---|---|---|---|---|---|---|
| FPGA | GPU | ||||||
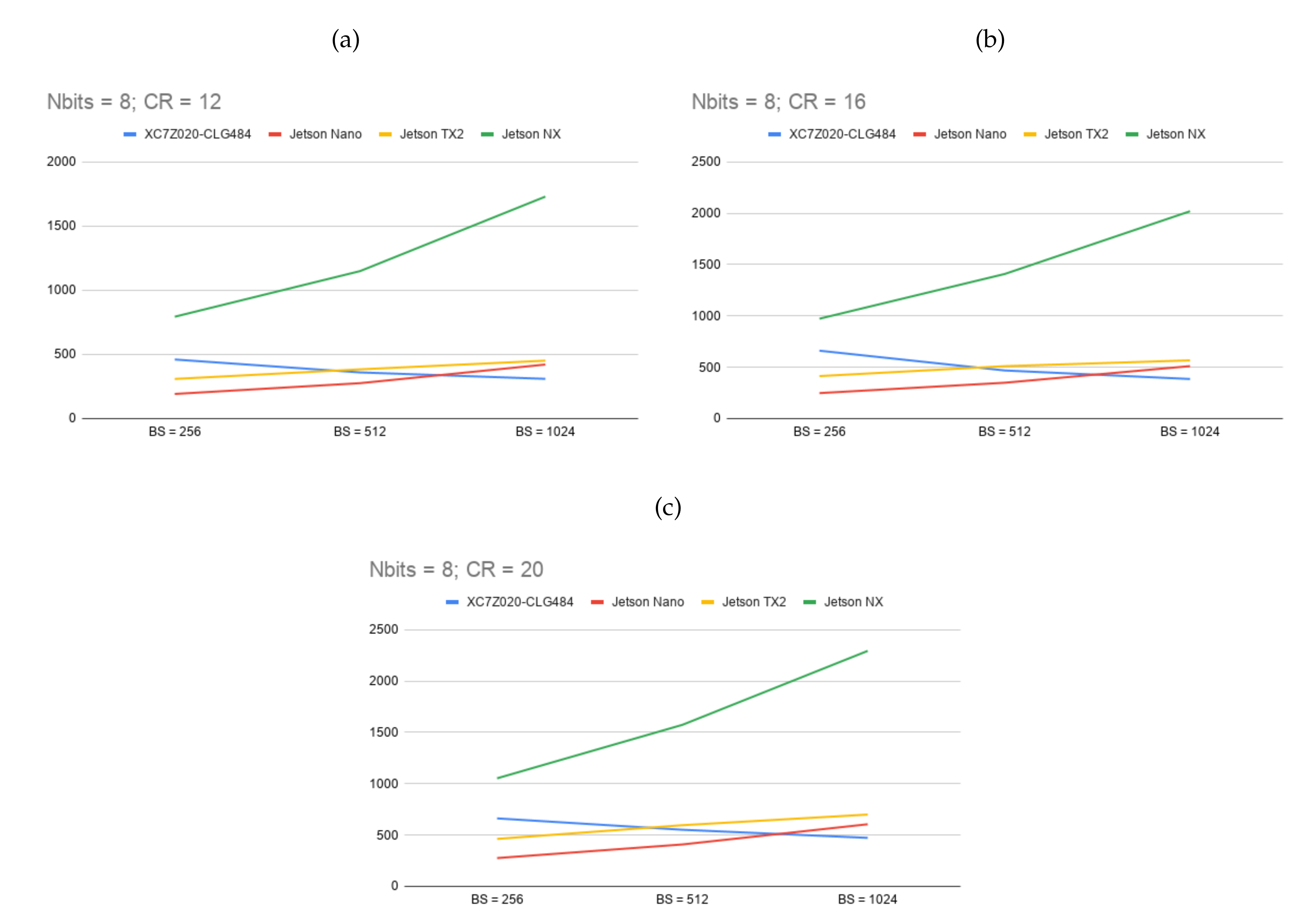
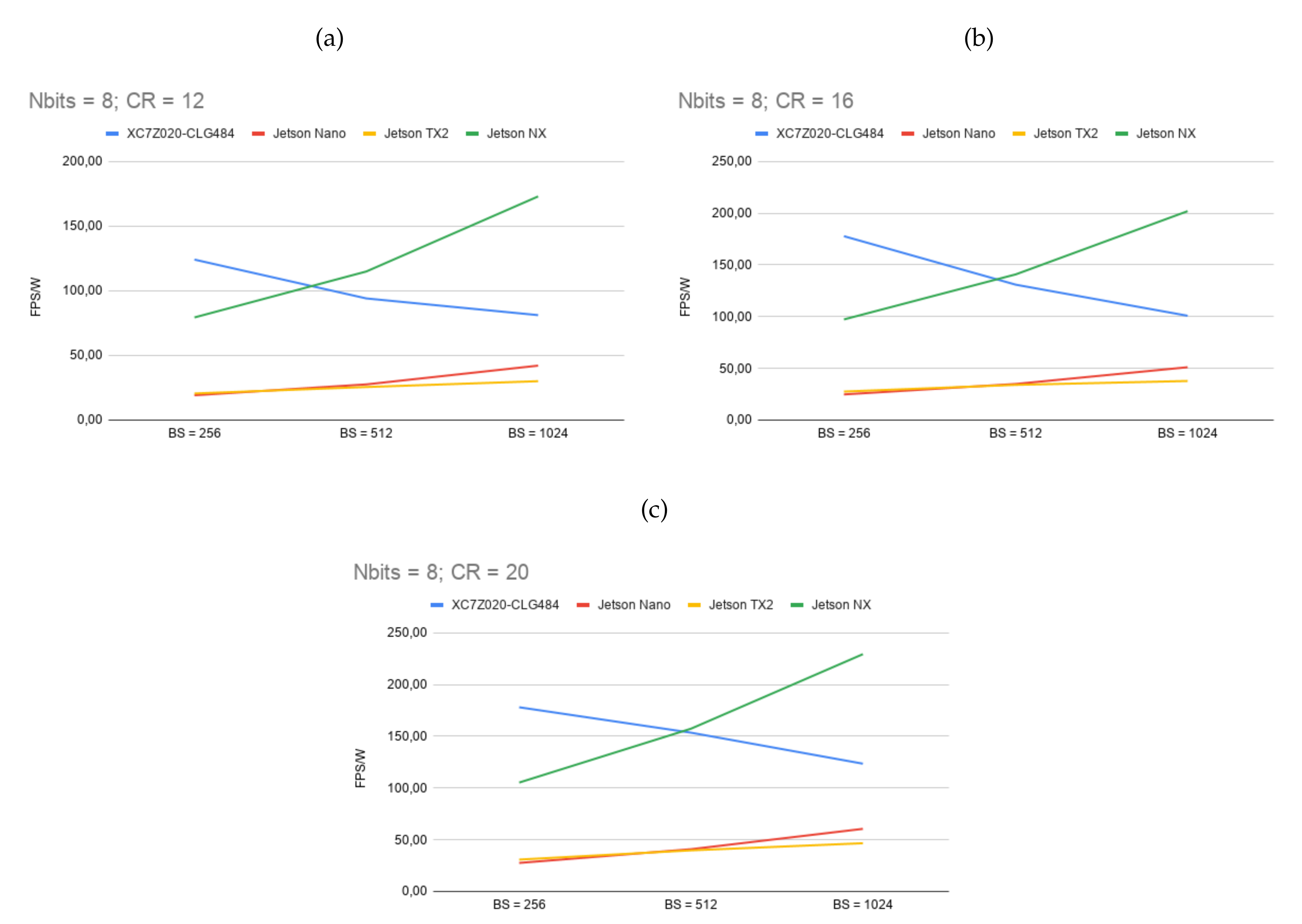
| BS | CR | XC7Z020-CLG484 (MicroZed) | Jetson Nano | Jetson TX2 | Jetson Xavier NX | ||
| 100 MHz | 150 MHz | 921.6 MHz | 1.12 GHz | 800 MHz | |||
| 3.12 W | 3.74 W | 10 W | 15 W | 10 W | |||
| 12 | 12 | 275 | 411 | 533 | 558 | 2062 | |
| 1024 | 16 | 343 | 511 | 638 | 762 | 2422 | |
| 20 | 410 | 611 | 729 | 923 | 2682 | ||
| 12 | 315 | 469 | 351 | 506 | 1405 | ||
| 512 | 16 | 371 | 553 | 408 | 599 | 1582 | |
| 20 | 452 | 672 | 487 | 748 | 1767 | ||
| 12 | 365 | 543 | 225 | 372 | 909 | ||
| 256 | 16 | 445 | 662 | 275 | 465 | 1052 | |
| 20 | 570 | 847 | 357 | 620 | 1251 | ||
| 8 | 12 | 207 | 310 | 421 | 452 | 1730 | |
| 1024 | 16 | 258 | 386 | 511 | 568 | 2020 | |
| 20 | 317 | 473 | 606 | 700 | 2294 | ||
| 12 | 241 | 360 | 276 | 384 | 1149 | ||
| 512 | 16 | 371 | 469 | 350 | 511 | 1409 | |
| 20 | 371 | 552 | 409 | 596 | 1574 | ||
| 12 | 309 | 461 | 192 | 309 | 794 | ||
| 256 | 16 | 401 | 662 | 249 | 414 | 973 | |
| 20 | 444 | 663 | 276 | 463 | 1053 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caba, J.; Díaz, M.; Barba, J.; Guerra, R.; López, J.A.d.l.T.a. FPGA-Based On-Board Hyperspectral Imaging Compression: Benchmarking Performance and Energy Efficiency against GPU Implementations. Remote Sens. 2020, 12, 3741. https://doi.org/10.3390/rs12223741
Caba J, Díaz M, Barba J, Guerra R, López JAdlTa. FPGA-Based On-Board Hyperspectral Imaging Compression: Benchmarking Performance and Energy Efficiency against GPU Implementations. Remote Sensing. 2020; 12(22):3741. https://doi.org/10.3390/rs12223741
Chicago/Turabian StyleCaba, Julián, María Díaz, Jesús Barba, Raúl Guerra, and Jose A. de la Torre and Sebastián López. 2020. "FPGA-Based On-Board Hyperspectral Imaging Compression: Benchmarking Performance and Energy Efficiency against GPU Implementations" Remote Sensing 12, no. 22: 3741. https://doi.org/10.3390/rs12223741
APA StyleCaba, J., Díaz, M., Barba, J., Guerra, R., & López, J. A. d. l. T. a. (2020). FPGA-Based On-Board Hyperspectral Imaging Compression: Benchmarking Performance and Energy Efficiency against GPU Implementations. Remote Sensing, 12(22), 3741. https://doi.org/10.3390/rs12223741