1. Introduction
Object detection in aerial images is an important research direction in the field of computer vision [
1], and its development has great significance in both the civilian and military fields. In the civilian field, aerial image object detection technology is widely used in the real-time update of urban spatial database, urban planning, disaster detection, etc. In the military field, this technology has become an important means of military reconnaissance and early warning in the modern army. Despite many advanced methods based on deep learning [
2,
3] have succeeded in the natural image object detection, the development of object detection in aerial images is relatively slow because of the complicated backgrounds, overlooking views, and variations in scale and shape of the objects [
4,
5].
To detect the special objects of the different scales, the multi-scale image pyramid [
6] is usually adopted. However, this method requires many calculations and memories, hence many object detectors have avoided the multi-scale image pyramid representation. From this, some researchers built the multi-scale pyramids based on the internal structure of the convolutional neural network (CNN) [
7] to detect multi-scale targets, which only request a small number of additional computational cost. Some typical methods based on this idea are as follows. The feature pyramid network (FPN) [
8] adopts a top-down structure and lateral connections for fusing the shallow layer features with low-level semantic information and the deep layer features with high-level semantic information, which enriches the features of the different scales. The single-shot multibox detector (SSD) [
9] fuses the different scale features from the different layers to obtain the multi-scale features without additional calculation. The scale-aware trident network (TridentNet) [
10] can generate the specific feature maps with different scales through a parallel multi-branch framework for which each branch owns the different receptive fields. YOLOv3 (You only look once) [
3] is inspired by the FPN structure and introduces a similar feature pyramid structure to detect the objects with multi-scale. Although these advanced methods can improve the general multi-scale object detection effect to a certain extent, they are still unable to completely solve the huge differences in object scales and that in object shapes under complex background, thus cannot achieve the optimal effect in aerial image object detection. Generally speaking, aerial images are generally acquired from vertical vision with the different equipment and distance, variational weather and lighting conditions, so the background of the aerial image is generally very complex, and there are targets with vast differences in scale and that in shape. There are also some scholars who have proposed corresponding solutions for many objects with different shapes in aerial images. Qiu et al. [
11] leveraged an aspect ratio attention network to select the region of interest (RoI) features that match the shapes of objects. Based on this, many objects with large aspect ratio differences in aerial images can also be referred to as multi-shape objects in object detection. In addition to Reference [
11], Xu et al. [
12] developed an aspect ratio constrained non-maximum suppression (arcNMS), and Yan et al. [
13] proposed the class aspect ratio constrained non-maximum suppression (CARC-NMS) to remove the line like false region proposals (LFRP) during non-maximum suppression (NMS) process. But these two methods afore-mentioned are only suitable for removing the false detect results with abnormal aspect ratio caused by deformable convolution [
14] in the network.
Figure 1 displays some concrete examples of aerial images. From
Figure 1, the scale of the bus in
Figure 1c is much larger than that in
Figure 1a. Moreover, the scales of the ships in
Figure 1b,d are much smaller than the scales of the bridges and harbors. Moreover, the shapes of the bridges and harbors are also quite different from that of ordinary objects. It can be clearly seen from
Figure 1b,d that the aspect ratios of the bridges and harbors are relatively large.
To solve the multi-scale object detection problems further better, in addition to the complex multi-scale network structures mentioned above, there are some well-designed modules that are embedded into the network to fuse the multi-scale features and can effectively detect the multi-scale objects.
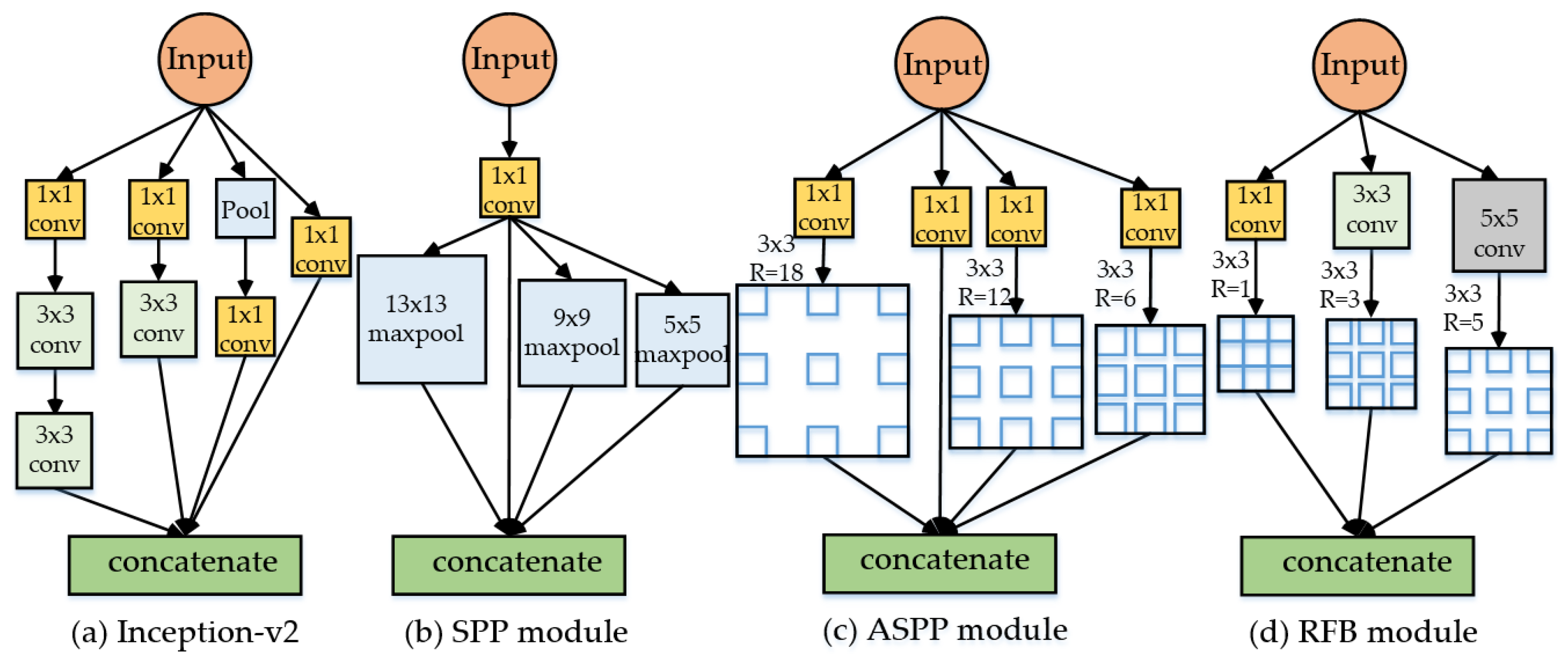
Figure 2 shows the details of four typical multi-scale fusion modules. The inception-v2 module [
15] (a) uses the different convolutional kernels to extract multi-scale feature information. The spatial pyramid pooling (SPP) module [
16] (
Figure 2b) utilizes the pooling layers of the different sizes for fusing the multi-scale features. The atrous spatial pyramid pooling (ASPP) module [
17] (
Figure 2c) exploits multiple parallel atrous convolutional layers with different rates for extracting multi-scale feature information. Furthermore, the receptive field block (RFB) [
18] (
Figure 2d) uses multi-scale atrous convolutional layers to adapt to the different scale kernels of CNN, which can cover the different scale receptive fields and is very useful for obtaining multi-scale features. With reasonable design, these modules can effectively increase the multi-scale feature extraction capability of neural networks and further improve the effect of multi-scale object detection. However, the objects in aerial images generally not only differ in the scale, but also their shapes may also vary widely. As mentioned above, the aspect ratio of the bridge and harbor is very large, as shown in
Figure 1b,d. Therefore, it is necessary to design more effective modules for realizing the more effective detection of the multi-scale and multi-shape targets in aerial images.
Moreover, when fusing the multi-scale or the multi-shape features, either by fusing the different scale features of different layers or by fusing the different scale or shape features of the different branches of the same layer, most of the existing methods [
3,
8] usually ignore the importance of each merged parts that are treated equally and through direct concatenation or addition on the channels with the uniform weights to merge the different features of the different layers or the different branches of the same layer. Therefore, this is not conducive to the neural network for making full use of the different features.
In addition, due to the complex background and the diversity of object scales and shapes in aerial images, a larger and more complex network model is usually required for obtaining more excellent detection accuracy. However, the larger network model is often large in volume, which will affect detection efficiency and make it difficult to deploy the network model on the resource-limited devices for real-time detection and practical applications. Besides, it is empirically known that larger network models generally contain many redundant information, thus some researchers [
19,
20,
21,
22,
23,
24] have proposed some model compression methods for reducing model volume and speeding up object detection. Among these model compression methods, the structural pruning [
19,
20,
21,
22,
23], especially channel pruning [
19,
21,
23], is widely used to reduce the number of model parameters and computing complexity. Nevertheless, the existing methods usually design a predefined global threshold [
19,
21] for all layers or the independent local threshold for each layer [
23] to pruning unimportant channels for saving memory and decreasing inference time. It is worth noting that the absolute value of the scale factors in batch normalization (BN) [
25] layers are generally used to measure the importance of each channel in the model, and the channel pruning threshold is also designed according to the scale factors [
19,
21,
23]. But when designing the channel pruning threshold, the above-mentioned methods either only consider the value distribution of the global scale factors or only consider the value distribution of the local scale factors in the corresponding layers, so they cannot reach both the global optimality of all layers and the local optimality of each layer at the same time, and their performances are usually not optimal. Therefore, it is an urgent problem that how to propose a more suitable channel pruning method with the superior pruning threshold for achieving more efficient model compression and improving the object detection speed of aerial images without affecting the model accuracy.
In this paper, to solve the above problems, we propose a slimmer network for more efficient object detection in aerial images. Firstly, we design a polymorphic module (PM) to simultaneously learn the characteristics of great differences in the object scales and that in the object shapes, so it can better detect the hugely different targets in aerial images. The well-designed PM can also enable the network to focus better on the key information of the objects from the background for achieving more accurate detection. Considering the concatenation of the different features using unified weights may not be able to utilize the feature information suitably and efficiently, we then design a group attention module (GAM) for better learning the different concatenate features in the network. Specifically, the GAM can assign different importance to the different concatenation layers. Based on the designed modules, we further propose a fast and accurate network called PG-YOLO (P, G represent the PM and GAM, respectively), which also employs multiple detection headers with adaptive anchors for the aerial image object detection. The baseline of this network is the currently excellent YOLOv3 [
3]. Because we have devised a more reasonable and efficient network structure, the proposed PG-YOLO can achieve higher detection accuracy for multi-scale and multi-shape objects in aerial images. In addition, considering that the large network model tends to have a large model volume with some redundant information, which will affect detection efficiency and make it difficult to deploy the network model on the resource-limited devices for practical applications, we propose an efficient channel pruning method with a superior layer-wise weighted threshold to slim the network model and realize higher detection efficiency nearly without accuracy loss for real-time detection.
Our main contributions in this paper are as follows:
We design a polymorphic module (PM) for learning the multi-scale and multi-shape object features simultaneously in aerial images. The PM is also able to make the network focus better on the key feature of the objects for achieving more accurate detection. Moreover, a group attention module (GAM) is designed for better utilizing the different concatenate features in the network.
By devising multiple detection headers with adaptive anchors and the designed two modules, we propose a one-stage network called PG-YOLO for realizing the higher detection accuracy in aerial images.
We propose a more efficient channel pruning method for model compression, which can achieve higher detection efficiency for real-time detection and practical applications. Specifically, we can slim the network parameters from 63.7 million (M) to 3.3M, which decreases the parameter size by 94.8%. Theoretically, our proposed channel pruning idea could also be used for slimming the network model in other fields.
The rest part of this work is summarized as follows.
Section 2 briefly reviews the most or some related works. In
Section 3, we detail the proposed method.
Section 4 illustrates the experimental datasets, procedures, and evaluation criteria. In
Section 5, we verify the effectiveness of the proposed method, and compare the results on three public datasets. Finally, the discussions and conclusions of this paper are provided in
Section 6 and
Section 7.
4. Experiments
4.1. Datasets
For proving the effectiveness of the proposed method, we execute the comparative experiments of object detection in aerial images on public VisDrone-DET [
5], DIOR [
1], and DOTA [
36] datasets.
Table 1 lists the general information on these datasets. Noting that the size in
Table 1 refers to the maximum size in the corresponding dataset.
VisDrone-DET dataset contains 10.209 images (6471 for training, 548 for validation, 1580 for testing, and 1610 in the test-dev subset) captured by the different heights with the different drones equipped with cameras across 14 different cities in China, which consists of 10 categories: Pedestrian, people, bicycle, car, van, truck, tricycle, awning-tricycle, bus, and motor. These images are annotated by more than 2.5 million bounding boxes of instances. Furthermore, the static images are obtained with different weather and lighting conditions, which is beneficial for enhancing the robustness of the model.
DIOR dataset covers 23.463 images with 192.472 instances. Moreover, it is divided into 20 categories: Airplane (APL), airport (AP), baseball field (BF), basketball court (BC), bridge (BR), chimney (CH), dam (DA), expressway service area (ESA), expressway toll station (ETS), golf course (GC), ground track field (GTF), harbor (HA), overpass (OP), ship (SH), stadium (SD), storage tank (ST), tennis court (TC), train station (TS), vehicle (VH), and windmill (WM). Each category has about 1200 images. DIOR reaches a great larger scale in categories, instances, and total images comparing to precious aerial datasets. The image size is 800 × 800 pixels in this dataset, and the range of spatial resolution is 0.5-30m. These images were obtained under different conditions, due to the variability of the weather, the season, and the quality of imaging equipment, so the specific contents are very different even if the image depicts the same place, which makes DIOR a more challenging task to detect. The annotation of DIOR is the horizontal bounding box. Besides, the distribution of training data and testing data are very close to ensure a good balance.
DOTA dataset consists of 2806 aerial images and 188.282 annotated object instances in 15 categories, which are plane (PL), baseball diamond (BD), bridge (BR), ground track field (GTF), small vehicle (SV), large vehicle (LV), ship (SH), tennis court (TC), basketball court (BC), storage tank (ST), soccer ball field (SBF), roundabout (RA), harbor (HA), swimming pool (SP), and helicopter (HC). The instances are annotated in two forms: The horizontal bounding boxes (HBB) and the oriented bounding boxes (OBB). Note that this work focuses on detecting the horizontal bounding boxes. Besides, for training and validation, the images are chipped into 1024 × 1024 pixels with an overlap value 200 pixels, due to the large size of these images.
4.2. Experimental Procedures
4.2.1. Normal Training
Following the training strategies provided by the Darknet [
3] in PyTorch repository, our proposed detector is trained on an Nvidia GTX 1080Ti GPU with 11-GB RAM in an end-to-end manner, and the synchronized stochastic gradient descent (SGD) with a weight decay of 1e-4 and momentum of 0.9 is used to optimize our detector. When the input images are resized to 608 pixels for avoiding using much memory, the mini-batch is set to 7. But when the input size is 832 pixels to obtain higher accuracy, these are only four input images for each mini-batch. Note that for the DIOR and DOTA datasets, the input images are resized to 608 pixels in all experiments. We train a total of 200 epochs with a learning rate of 1e-3 for the first 140 epochs, 1e-4 for the next 40 epochs, and 1e-5 for the remaining 20 epochs.
4.2.2. Training with Sparsity
When our network model reaches the ideal precision, the sparse training with sparse channel regularization will be implemented. Specifically, we execute channel-wise sparsity training on the PG-YOLO for 200 epochs. Moreover, we choose the optimal penalty factor
of the training loss function as 1e-3 in the experiments. Furthermore, the residual parameters of sparse training are the same as those in the normal training. In addition, the histograms of scale factors before and after sparse training are shown in
Figure 9. In
Figure 9, the vertical axis represents the ordinal number of the convolutional layer, and the horizontal axis represents the corresponding distribution of scale factors
(gamma) for each layer. As can be seen from
Figure 9, after sparse training, the scale factor of the unimportant channel tends to be near zero, which is more conducive to channel pruning.
4.2.3. Pruning
After sparsity training, we apply the proposed layer-wise weighted threshold for determining whether a channel should be pruned or not in each layer. Moreover, we set
to 1e-4 in our experiments. Compared with [
19], the proposed method cannot appear to prune all the channels of a layer, because our designed pruning threshold for each layer is reasonably distributed between the maximum and minimum values of scale factors. Especially, we generally utilize the normal pruning method, which ignores the convolutional layer of residual shortcut connection to execute channel pruning, because it usually has little effect on accuracy. In addition, for further reducing the unimportant parameters of the model, we also carry out extreme shortcut pruning for which the pruning layer include the convolutional layer of residual shortcut connection, and the pruning results are shown in
Section 5.
4.2.4. Fine-Tuning
After channel pruning, the detection accuracy of the neural network model may be decreased. Therefore, we usually need to fine-tune the model after pruning to improve accuracy. It is worth noting that since our normal pruning has little impact on detection accuracy, we only fine-tune the model after extreme shortcut pruning. More specifically, the weights of the shortcut pruned PG-YOLO are used to initialize this slimmed network when fine-tuning, and other training hyper-parameters are the same as the normal training.
4.3. Evaluation Criteria
In this paper, to ensure the fairness of the experiments, the experimental data and the parameter settings are strictly consistent. In the experiments, the evaluation metrics used to quantitatively evaluate the model performance mainly include: (1) Precision, (2) recall, (3) F1 score, (4) mean average precision (mAP), (5) model parameters, (6) model volume, (7) compression rate (CR): The percentage of parameter reduction, (8) average run time per image, and (9) precision-recall curve (PRC).
The precision value, recall rate, and
F1 score can be formulated as:
where
TP,
FP, and
FN represent the number of true positives, false positives, and false negatives, respectively. The PRC illuminates the correlation between precision and recall. When the particular detector maintains high precision with the increase of the recall rate, it is considered to be excellent in performance. The region area under the PRC is AP, which is the average precision of all recall values from 0 to 1. The mean average precision (mAP) represents the average precision value for all categories. It is worth noting that the higher the value of mAP, the better the performance of the detector.
6. Discussion
By analyzing the characteristics of the objects concretely in arial images, this paper proposes an effective network PG-YOLO to improve the object detection accuracy of arial images. Based on the proposed network, we further propose an effective channel pruning method with the layer-wise weighted threshold to compress the network model to further reduce the model parameters and improve the detection speed. The design of the layer-wise weighted threshold both considers the global scale factors distribution of all layers and the local scale factors distribution of each layer, which means the proposed layer-wise weighted threshold integrates the importance distribution of each layer and the importance distribution of each channel in each layer. Therefore, the proposed channel pruning method is more reasonable and efficient when pruning the unimportant channels, and it can slim the model, while keeping high detection accuracy. The effectiveness of each component of the proposed method is proved by the ablation experiments. Especially, without fine-tuning, we can prune the model from 63.7M to 10.1M by the normal pruning on the VisDrone-DET dataset with the input size of 832 × 832 pixels. Moreover, after the extreme shortcut pruning with fine-tuning, the model parameters can be reduced from 63.7M to 3.3M, which decreases parameter size by 94.8%.
In addition, the proposed layer-wise weighted threshold for channel pruning can not only be applied to the object detection network proposed in this paper, but also the scholars in other fields can use it to compress their network models to reduce the model parameters and increase the model inference speed for practical application, such as classification, segmentation, etc. Although our method achieves higher object detection accuracy and the detection speed is also very fast, especially after the channel pruning for model compression, the methods with the baseline YOLOv3 have a common problem; that is, to pursue faster detection speed, it usually causes a certain degree of the detection accuracy loss. In the future, our work will focus on further improving detection accuracy, while maintaining a fast detection speed.