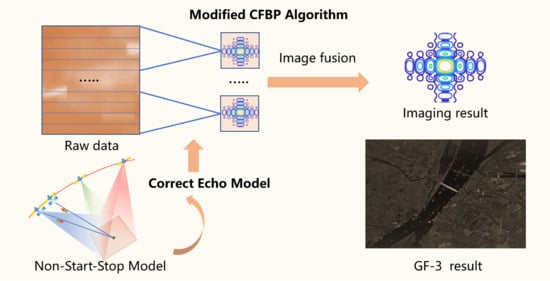
A Modified Cartesian Factorized Backprojection Algorithm Integrating with Non-Start-Stop Model for High Resolution SAR Imaging
Abstract
:1. Introduction
2. Materials and Methods
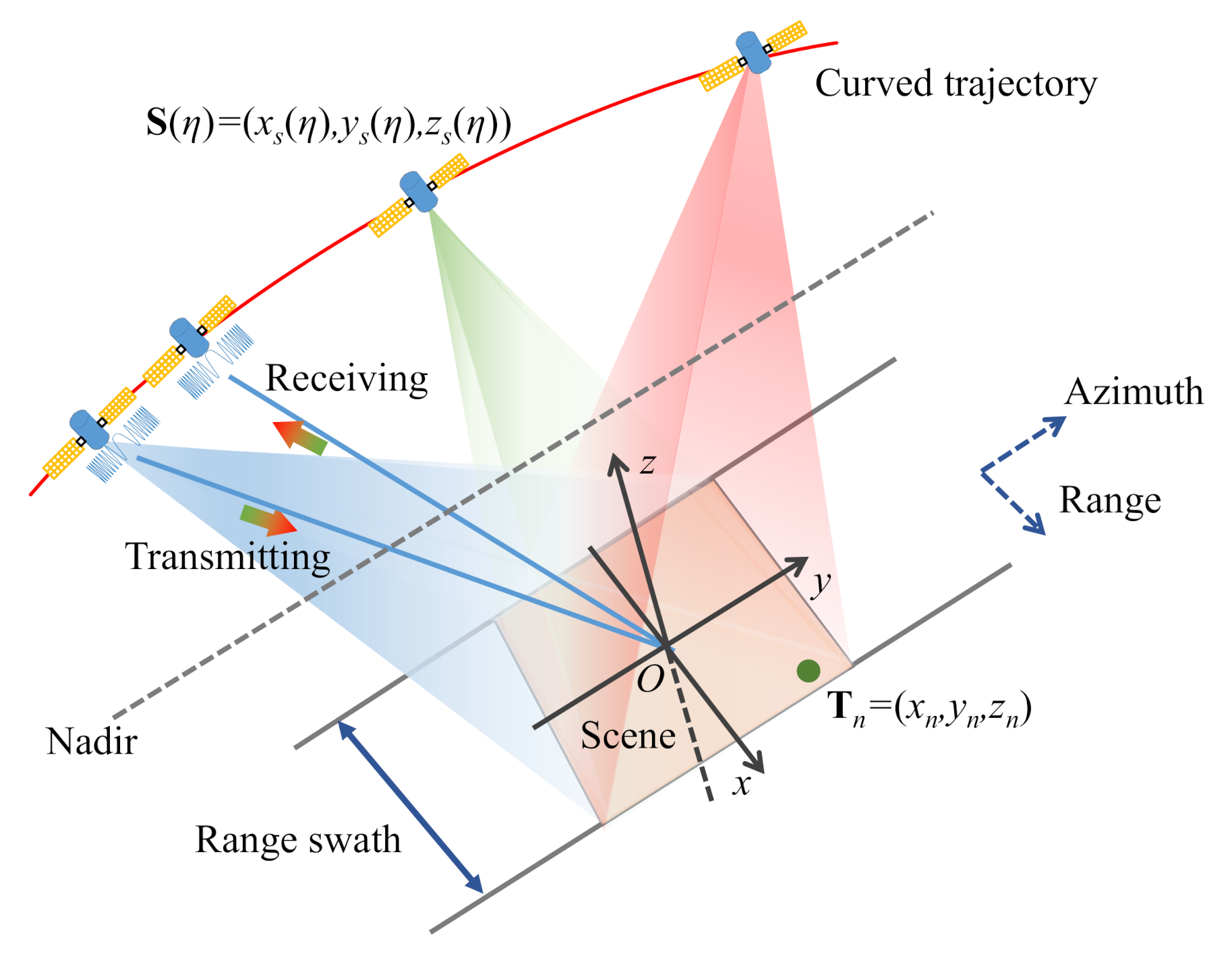
2.1. Echo Model of SAR
2.1.1. Traditional Echo Model
2.1.2. Problem
2.1.3. Correct Echo Model
2.1.4. Comparison between the Traditional Echo Model and the Correct Echo Model
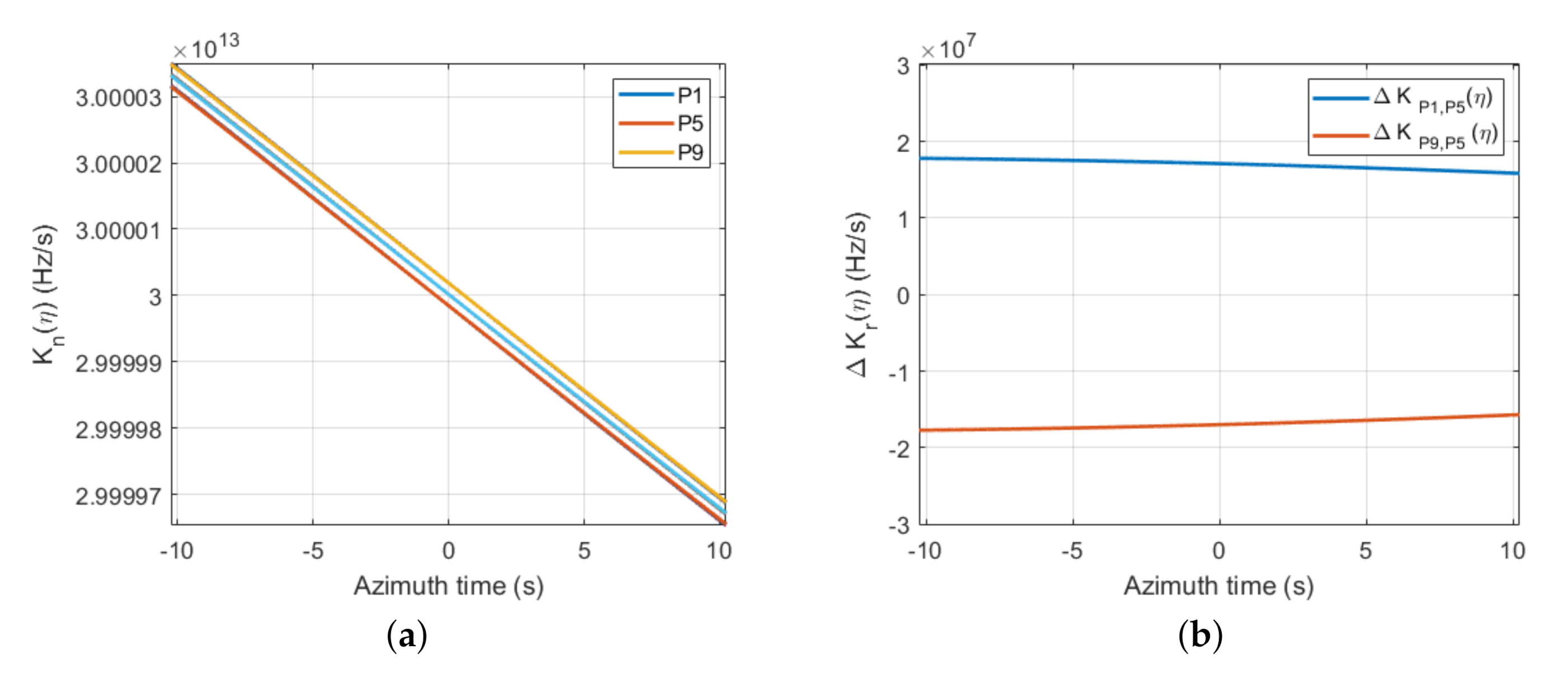
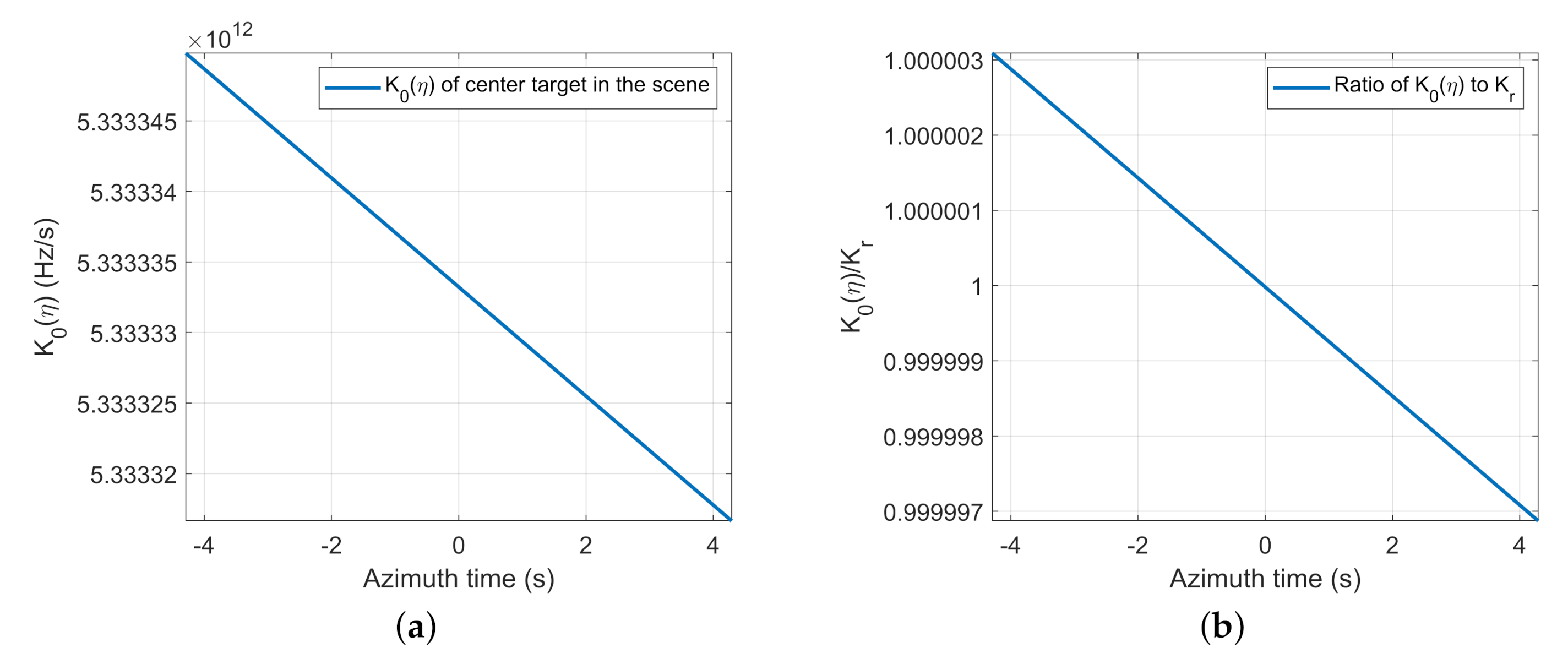
- A new range FM rate expression. can be regarded as an azimuth-time-varying FM rate in the correct echo model, while the range FM rate is constant in the traditional echo model.
- The position of the target after range compression is shifted. In the traditional echo model, the position of the target after range compression is . However, in the correct echo model, the peak position is .
- The azimuth phase is different. In the traditional echo model, the azimuth phase is . However, in the correct echo model, the azimuth phase is .
2.2. Modified Cartesian Factorized Backprojection Algorithm
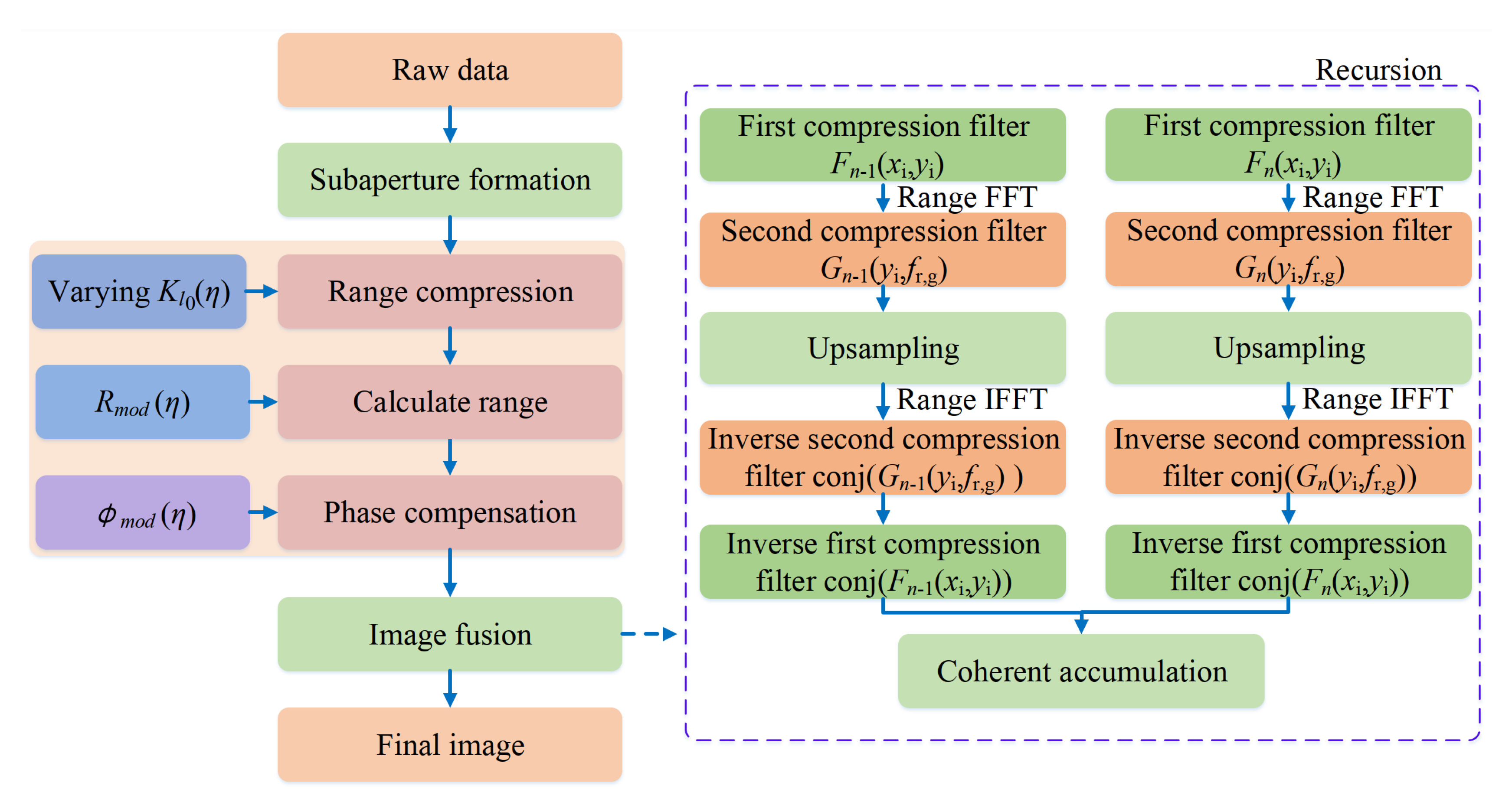
2.2.1. Processing Flow of the Modified CFBP Algorithm
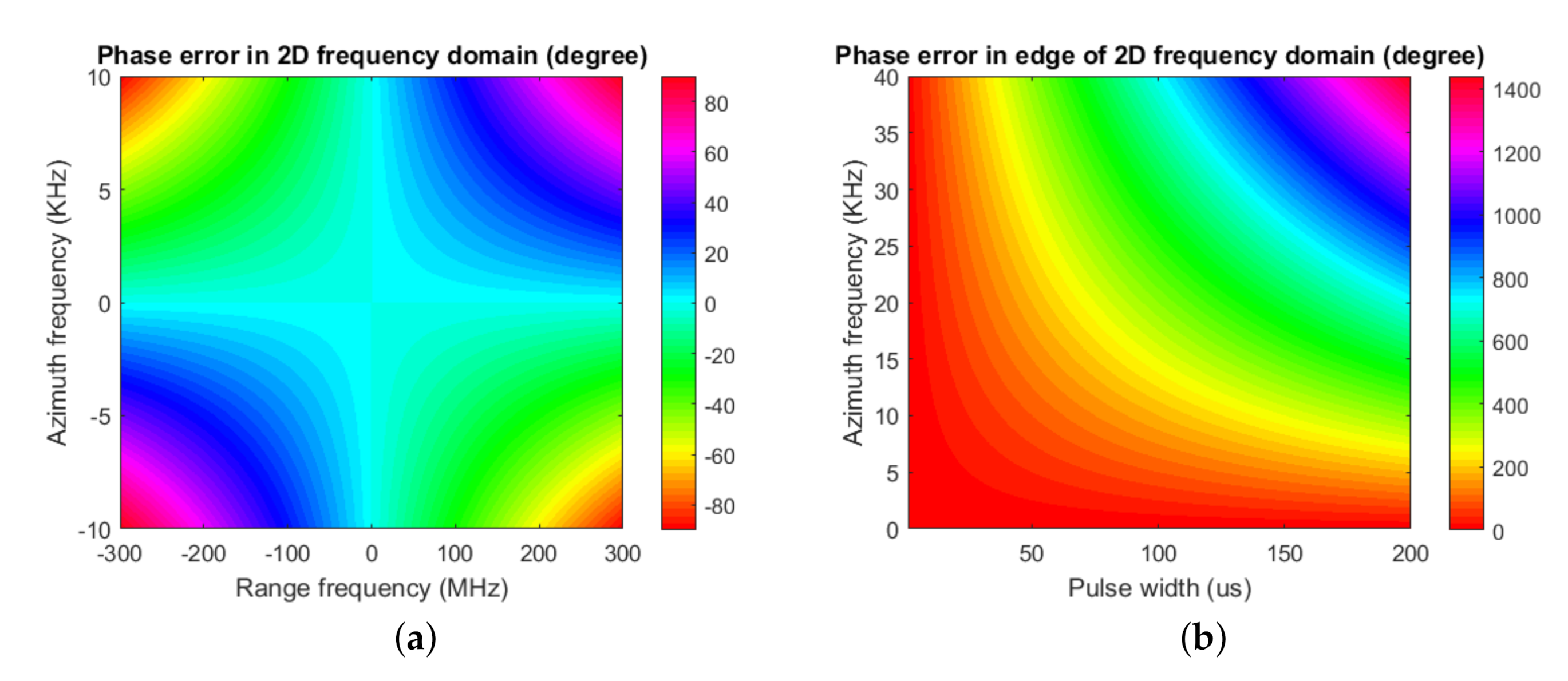
2.2.2. Derivation of the Error Due to Mismatch
2.2.3. Algorithm Steps
- Step 1
- Aperture division and subimage formation. The BPA is used for subimage formation.
- 1
- Range compression by a varying frequency modulation rate .
- 2
- The peak position in the compressed signal for target is .
- 3
- The peak position in the compressed signal for target is . The compensation phase is , where denotes the residual compensation phase due to mismatch.
- Step 2
- First compression filter step. It is operated in 2D time domain.
- Step 3
- Second compression filter step. It is operated in ground range frequency domain.
- Step 4
- Azimuth upsampling. Azimuth upsampling is operated in the azimuth frequency domain by using zero-padding method.
- Step 5
- Second compression filter recovery step. Multiply the conjugated second compression filter in the corresponding domain.
- Step 6
- First compression filter recovery step. Multiply the conjugated first compression filter in the corresponding domain.
- Step 7
- Coherent accumulation of subimage. Add up the subimage after upsampling for coherent accumulation.
- Step 8
- Recursion. Repeat the step3 to step8 until the final image with full resolution is obtained.
3. Results
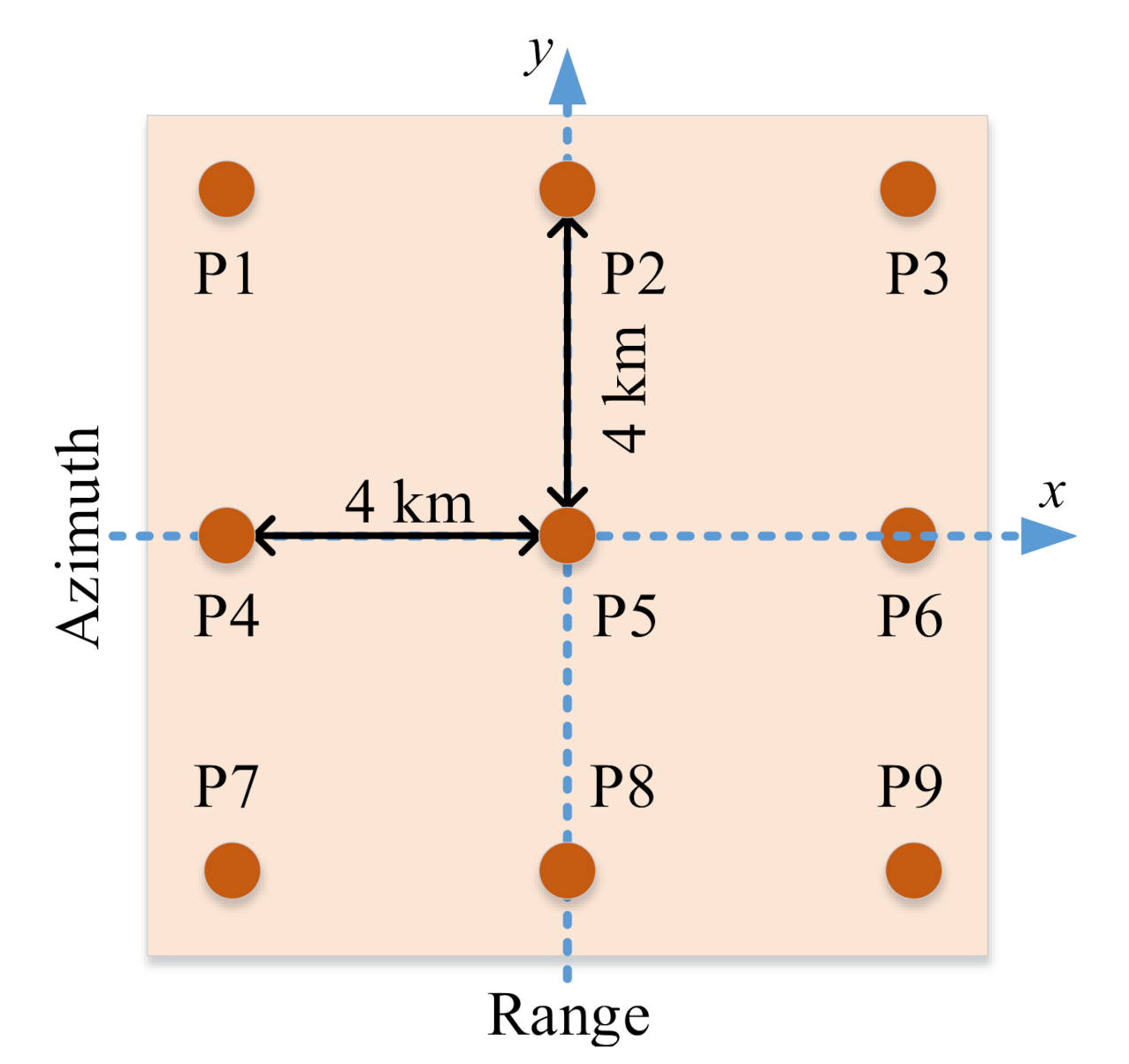
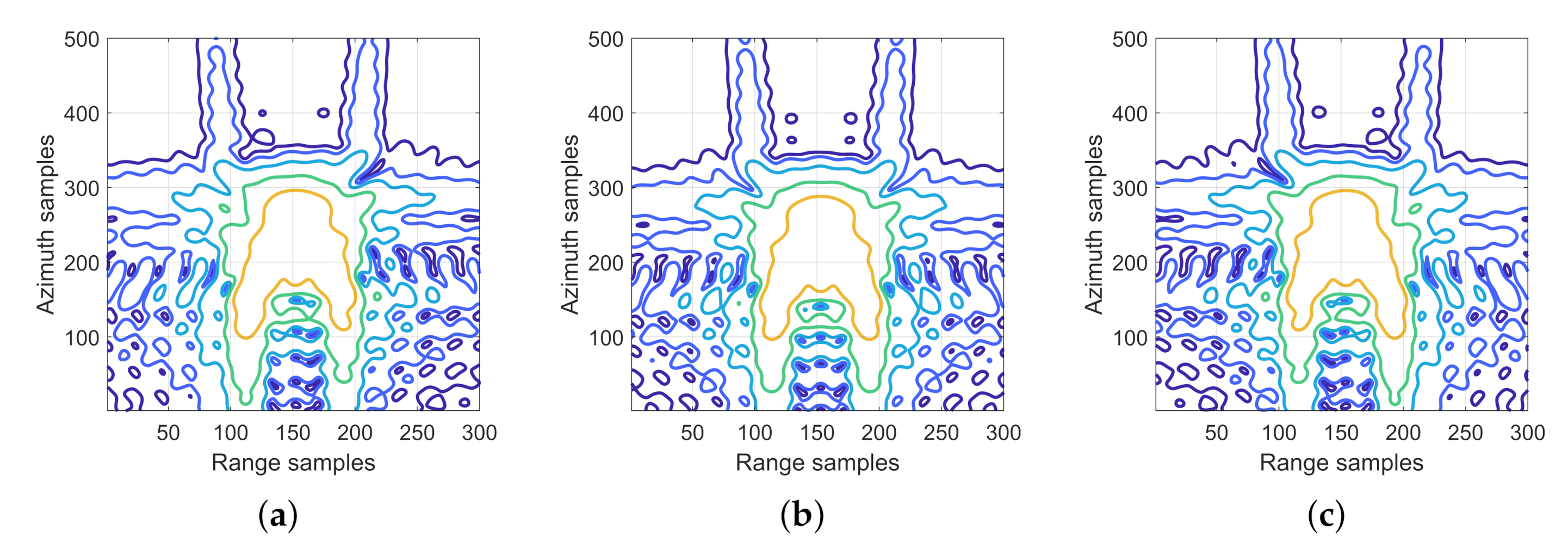
3.1. Simulation Experiment
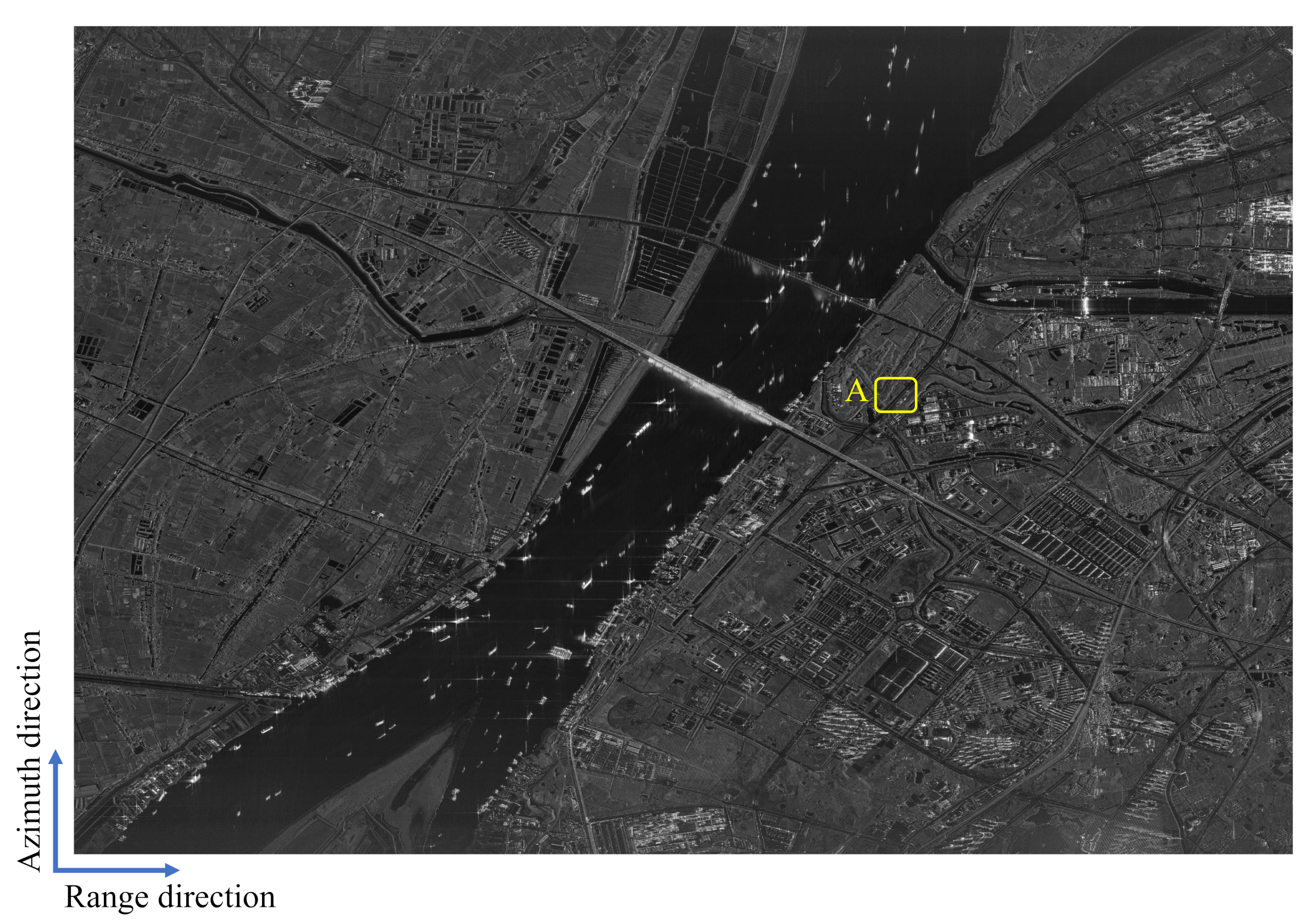
3.2. Real Data Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef] [Green Version]
- Jia, H.; Wang, Y.; Ge, D.; Deng, Y.; Wang, R. Improved offset tracking for predisaster deformation monitoring of the 2018 Jinsha River landslide (Tibet, China). Remote Sens. Environ. 2020, 247, 111899. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, Y.; Wang, W.; Liu, K.; Deng, Y.; Zhang, H.; Wang, Y.; Zhou, Y.; Wang, R. On the Frequency Dispersion in DBF SAR and Digital Scalloped Beamforming. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3619–3632. [Google Scholar] [CrossRef]
- Mittermayer, J.; Wollstadt, S.; Prats-Iraola, P.; Scheiber, R. The TerraSAR-X Staring Spotlight Mode Concept. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3695–3706. [Google Scholar] [CrossRef]
- Sun, J.; Yu, W.; Deng, Y. The SAR Payload Design and Performance for the GF-3 Mission. Sensors 2017, 17, 2419. [Google Scholar] [CrossRef] [Green Version]
- Lorusso, R.; Nicoletti, M.; Gallipoli, A.; Lor, V.A.; Milillo, G.; Lombardi, N.; Nirchio, F. Extension of Wavenumber Domain Focusing for spotlight COSMO-SkyMed SAR Data. Eur. J. Remote Sens. 2015, 48, 49–70. [Google Scholar] [CrossRef] [Green Version]
- Prats-Iraola, P.; Scheiber, R.; Rodriguez-Cassola, M.; Mittermayer, J.; Wollstadt, S.; Zan, F.D.; Brautigam, B.; Schwerdt, M.; Reigber, A.; Moreira, A. On the Processing of Very High Resolution Spaceborne SAR Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6003–6016. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Wang, R.; Deng, Y.; Pei, W.; Ning, L.; Yu, W.; Wei, W. Precise Calibration of Channel Imbalance for Very High Resolution SAR With Stepped Frequency. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4252–4261. [Google Scholar] [CrossRef]
- Ning, L.; Wang, R.; Deng, Y.; Yu, W.; Zhang, Z.; Liu, Y. Autofocus Correction of Residual RCM for VHR SAR Sensors With Light-Small Aircraft. IEEE Trans. Geosci. Remote Sens. 2017, 55, 441–452. [Google Scholar]
- Liang, D.; Zhang, H.; Fang, T.; Deng, Y.; Yu, W.; Zhang, L.; Fan, H. Processing of Very High Resolution GF-3 SAR Spotlight Data With Non-Start–Stop Model and Correction of Curved Orbit. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 2112–2122. [Google Scholar] [CrossRef]
- Lanari, R.; Tesauro, M.; Sansosti, E.; Fornaro, G. Spotlight SAR data focusing based on a two-step processing approach. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1993–2004. [Google Scholar] [CrossRef]
- Tsynkov, S. On the Use of Start-Stop Approximation for Spaceborne SAR Imaging. Siam J. Imaging Sci. 2009, 2, 646–669. [Google Scholar] [CrossRef] [Green Version]
- Yu, Z.; Wang, S.; Li, Z. An Imaging Compensation Algorithm for Spaceborne High-Resolution SAR Based on a Continuous Tangent Motion Model. Remote Sens. 2016, 8, 223. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Cassola, M.; Prats, P.; Krieger, G.; Moreira, A. Efficient Time-Domain Image Formation with Precise Topography Accommodation for General Bistatic SAR Configurations. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2949–2966. [Google Scholar] [CrossRef] [Green Version]
- Yuan, W.; Sun, G.C.; Yang, C.; Yang, J.; Xing, M.; Zheng, B. Processing of Very High Resolution Spaceborne Sliding Spotlight SAR Data Using Velocity Scaling. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1505–1518. [Google Scholar]
- Prats, P.; Scheiber, R.; Mittermayer, J.; Meta, A.; Moreira, A. Processing of Sliding Spotlight and TOPS SAR Data Using Baseband Azimuth Scaling. IEEE Trans. Geosci. Remote Sens. 2010, 48, 770–780. [Google Scholar] [CrossRef] [Green Version]
- Ribalta, A. Time-Domain Reconstruction Algorithms for FMCW-SAR. IEEE Geosci. Remote Sens. Lett. 2011, 8, 396–400. [Google Scholar] [CrossRef]
- Desai, M.D.; Jenkins, W.K. Convolution backprojection image reconstruction for spotlight mode synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 1992, 1, 505–517. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Ma, L.; Zhang, X. Streaming BP for Non-Linear Motion Compensation SAR Imaging Based on GPU. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2013, 6, 2035–2050. [Google Scholar]
- Tang, J.; Deng, Y.; Wang, R.; Zhao, S.; Li, N. High-resolution Slide Spotlight SAR Imaging by BP Algorithm and Heterogeneous Parallel Implementation. J. Radars 2017, 6, 368–375. [Google Scholar]
- Bisceglie, M.D.; Santo, M.D.; Galdi, C.; Lanari, R.; Ranaldo, N. Synthetic aperture radar processing with GPGPU. IEEE Signal Process. Mag. 2010, 27, 69–78. [Google Scholar] [CrossRef]
- Yegulalp, A.F. Fast backprojection algorithm for synthetic aperture radar. In Proceedings of the 1999 IEEE Radar Conference, Waltham, MA, USA, 22 April 1999; pp. 60–65. [Google Scholar]
- Ulander, L.M.H.; Hellsten, H.; Stenstrom, G. Synthetic aperture radar processing using fast factorized back-projection. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 760–776. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Tang, J.; Wang, R.; Deng, Y.; Wang, W.; Li, N. An Accelerated Backprojection Algorithm for Monostatic and Bistatic SAR Processing. Remote Sens. 2018, 10, 140. [Google Scholar] [CrossRef] [Green Version]
- Dong, Q.; Sun, G.; Yang, Z.; Guo, L.; Xing, M. Cartesian Factorized Backprojection Algorithm for High-Resolution Spotlight SAR Imaging. IEEE Sens. J. 2018, 18, 1160–1168. [Google Scholar] [CrossRef]
- Luo, Y.; Zhao, F.; Li, N.; Zhang, H. A Modified Cartesian Factorized Back-Projection Algorithm for Highly Squint Spotlight Synthetic Aperture Radar Imaging. IEEE Geosci. Remote Sens. Lett. 2019, 16, 902–906. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, L.; Zhao, L.; Wang, Y.; Zhou, H.; Chen, L.; Xing, M. A New Fast Factorized Back Projection Algorithm for Bistatic Forward-Looking SAR Imaging Based on Orthogonal Elliptical Polar Coordinate. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 1508–1520. [Google Scholar] [CrossRef]
- Shao, Y.F.; Wang, R.; Deng, Y.K.; Liu, Y.; Chen, R.; Liu, G.; Loffeld, O. Fast Backprojection Algorithm for Bistatic SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1080–1084. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H.; Qiao, Z.; Xu, Z. A Fast BP Algorithm With Wavenumber Spectrum Fusion for High-Resolution Spotlight SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1460–1464. [Google Scholar] [CrossRef]
- Frolind, P.; Ulander, L.M.H. Evaluation of angular interpolation kernels in fast back-projection SAR processing. IEE Proc. Radar Sonar Navig. 2006, 153, 243–249. [Google Scholar] [CrossRef]
- Dong, Q.; Yang, Z.; Sun, G.; Xing, M. Cartesian factorized backprojection algorithm for synthetic aperture radar. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016. [Google Scholar]
- Luo, Y.; Zhao, F.; Li, N.; Zhang, H. An Autofocus Cartesian Factorized Backprojection Algorithm for Spotlight Synthetic Aperture Radar Imaging. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1244–1248. [Google Scholar] [CrossRef]
- Chen, X.; Sun, G.; Xing, M.; Li, B.; Yang, J.; Bao, Z. Ground Cartesian Back-Projection Algorithm for High Squint Diving TOPS SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2020, 1–16. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital Signal Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Yan, L.; Xing, M.; Sun, G.; Lv, X.; Zheng, B.; Wen, H.; Wu, Y. Echo Model Analyses and Imaging Algorithm for High-Resolution SAR on High-Speed Platform. IEEE Trans. Geosci. Remote Sens. 2012, 50, 933–950. [Google Scholar]
- Zhang, Q.; Wu, J.; Qu, J.; Li, Z.; Huang, Y.; Yang, J. Echo Model Without Stop-and-Go Approximation for Bistatic SAR With Maneuvers. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1056–1060. [Google Scholar] [CrossRef]
- Zhang, F.; Li, G.; Li, W.; Hu, W.; Hu, Y. Accelerating Spaceborne SAR Imaging Using Multiple CPU/GPU Deep Collaborative Computing. Sensors 2016, 16, 494. [Google Scholar] [CrossRef] [PubMed] [Green Version]




| Model | Traditional Echo Model | Correct Echo Model |
|---|---|---|
| Range FM rate | ||
| Target position in range line | ||
| Azimuth compensation phase |
| Parameter | Value |
|---|---|
| Platform Height | 600 km |
| Eccentricity | 0.0011 |
| Inclination | 97.44 degrees |
| Semimajor axis | 6971 km |
| Argument of perigee | 78 degrees |
| Ascending node | 80 degrees |
| Incidence angle | 33.23 degrees |
| Parameter | Value |
|---|---|
| Carrier frequency | 9.6 GHz |
| Pulse width | 40 s |
| Range bandwidth | 1.2 GHz |
| Range sampling frequency | 1.4 GHz |
| Synthetic aperture time | 20.47 s |
| PRF | 6000 Hz |
| Scene extent | 8 km × 8 km |
| Targets | Range | Azimuth | ||||
|---|---|---|---|---|---|---|
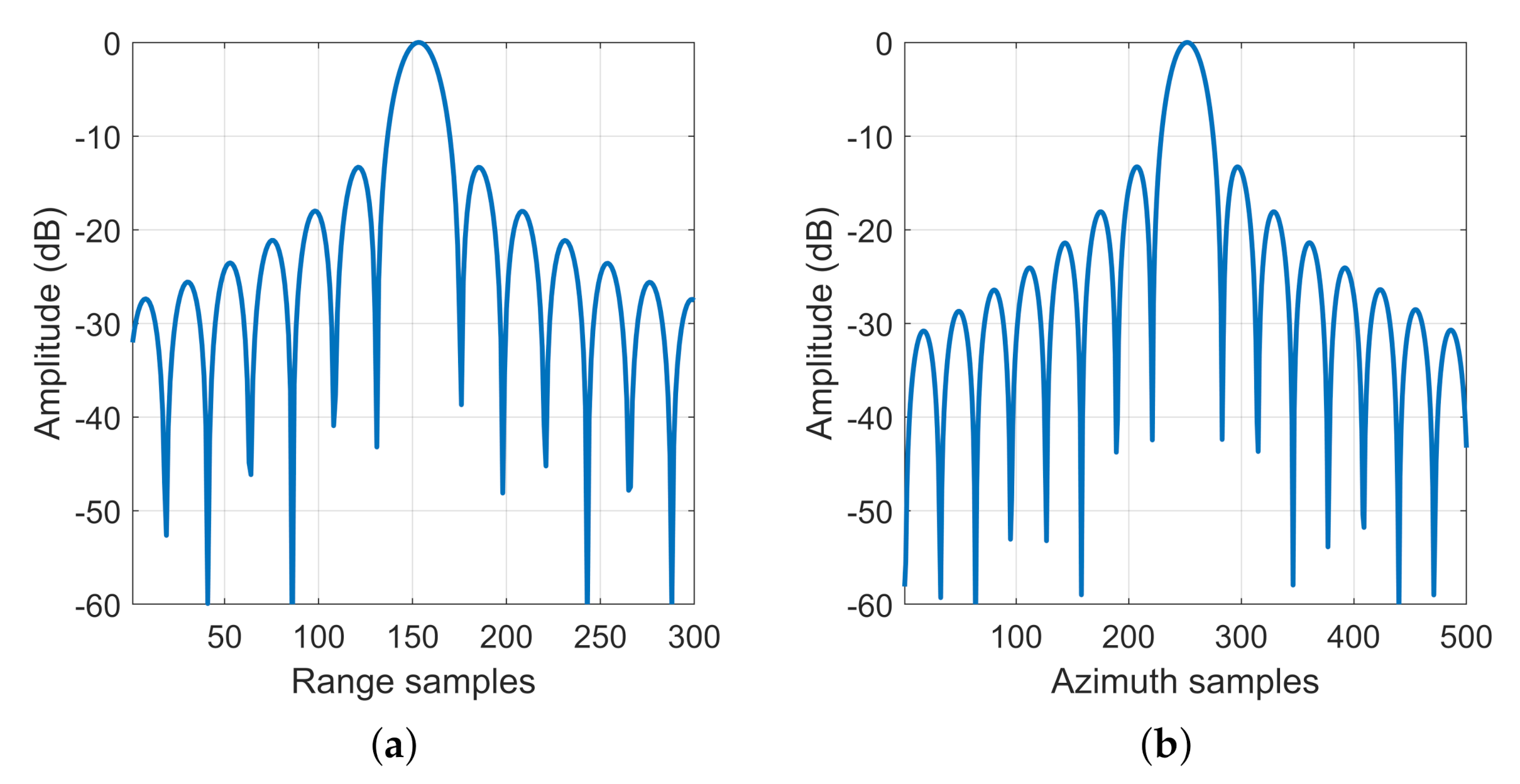
| IRW (m) | PSLR (dB) | ISLR (dB) | IRW (m) | PSLR (dB) | ISLR (dB) | |
| P1 | 0.2037 | −13.32 | −10.38 | 0.0634 | −13.28 | −10.54 |
| P2 | 0.2021 | −13.32 | −10.37 | 0.0636 | −13.28 | −10.54 |
| P3 | 0.2007 | −13.32 | −10.37 | 0.0638 | −13.28 | −10.54 |
| P4 | 0.2036 | −13.32 | −10.36 | 0.0634 | −13.27 | −10.54 |
| P5 | 0.2021 | −13.32 | −10.36 | 0.0636 | −13.27 | −10.54 |
| P6 | 0.2007 | −13.31 | −10.35 | 0.0638 | −13.27 | −10.54 |
| P7 | 0.2036 | −13.32 | −10.38 | 0.0634 | −13.28 | −10.54 |
| P8 | 0.2023 | −13.32 | −10.38 | 0.0636 | −13.28 | −10.54 |
| P9 | 0.2007 | −13.32 | −10.37 | 0.0638 | −13.27 | −10.54 |
| Target | Range | Azimuth | ||||
|---|---|---|---|---|---|---|
| IRW (m) | PSLR (dB) | ISLR (dB) | IRW (m) | PSLR (dB) | ISLR (dB) | |
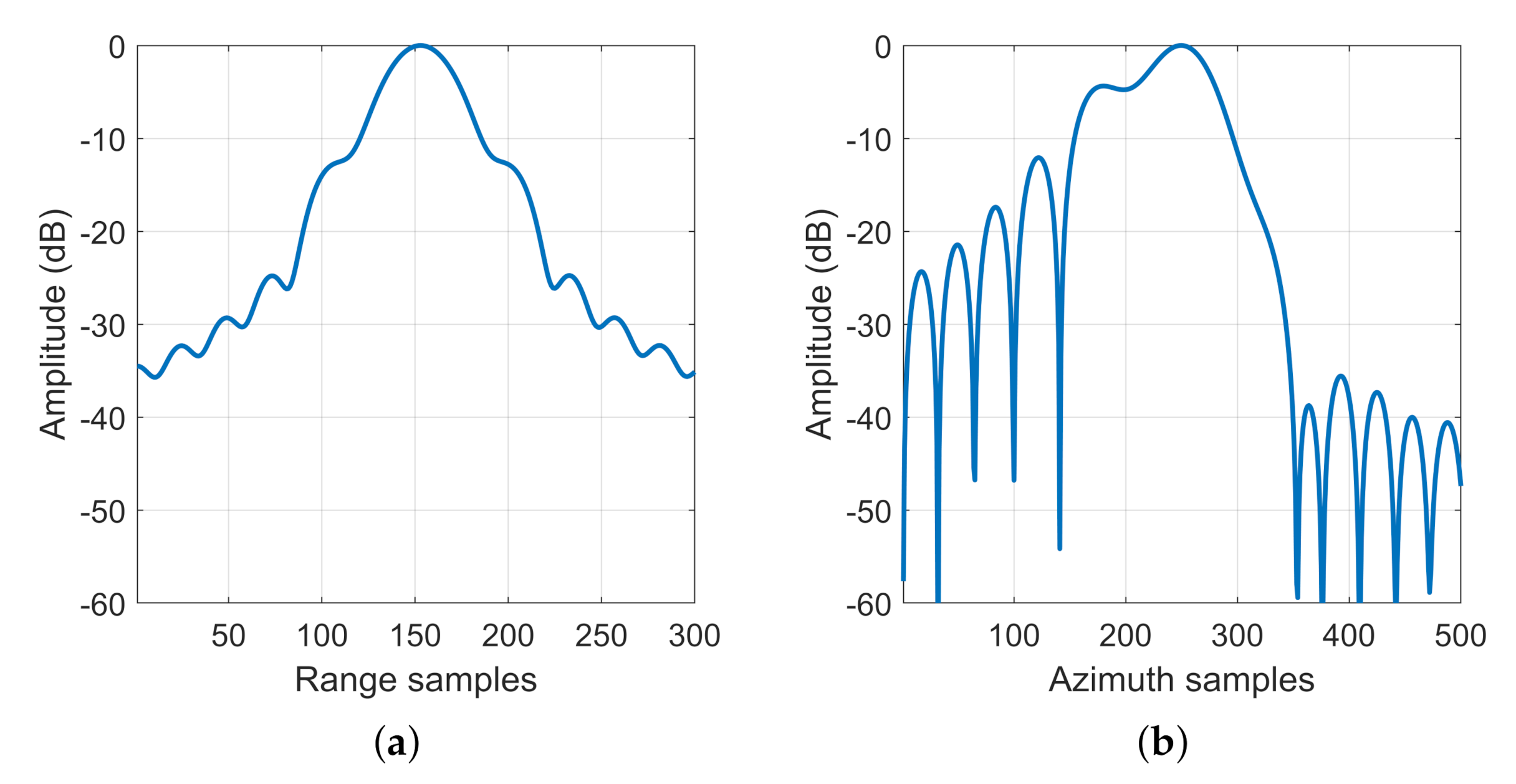
| P5 | 0.4889 | −4.9765 | −10.7928 | 0.1279 | −4.3672 | −5.7967 |
| Parameter | Value |
|---|---|
| Carrier frequency | 5.4 GHz |
| Azimuth steering range | ± |
| Look angle | 33.75 |
| Incidence angle | 38.51 |
| Range bandwidth | 240 MHz |
| Range sampling frequency | 266.67 MHz |
| Pulse duration | 45 s |
| PRF | 3742.80 Hz |
| Acquisition time | 8.58 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, D.; Zhang, H.; Fang, T.; Lin, H.; Liu, D.; Jia, X. A Modified Cartesian Factorized Backprojection Algorithm Integrating with Non-Start-Stop Model for High Resolution SAR Imaging. Remote Sens. 2020, 12, 3807. https://doi.org/10.3390/rs12223807
Liang D, Zhang H, Fang T, Lin H, Liu D, Jia X. A Modified Cartesian Factorized Backprojection Algorithm Integrating with Non-Start-Stop Model for High Resolution SAR Imaging. Remote Sensing. 2020; 12(22):3807. https://doi.org/10.3390/rs12223807
Chicago/Turabian StyleLiang, Da, Heng Zhang, Tingzhu Fang, Haoyu Lin, Dacheng Liu, and Xiaoxue Jia. 2020. "A Modified Cartesian Factorized Backprojection Algorithm Integrating with Non-Start-Stop Model for High Resolution SAR Imaging" Remote Sensing 12, no. 22: 3807. https://doi.org/10.3390/rs12223807
APA StyleLiang, D., Zhang, H., Fang, T., Lin, H., Liu, D., & Jia, X. (2020). A Modified Cartesian Factorized Backprojection Algorithm Integrating with Non-Start-Stop Model for High Resolution SAR Imaging. Remote Sensing, 12(22), 3807. https://doi.org/10.3390/rs12223807