Joint Delay-Doppler Estimation Performance in a Dual Source Context
Abstract
1. Introduction
1.1. Contributions
- A compact Fisher Information Matrix (FIM) for the general dual source narrowband CSM (i.e., where the Doppler effect on the band-limited baseband signal is not considered and amounts to a frequency shift) is provided in Section 3. This extends the work of [17,18] dealing with the single source narrowband CSM and completes the work of [28] in which the FIM is given for the specific case of a static, ground-based receiver, leading yo an identical Doppler effect for the two paths;
- The FIM is expressed in an easy to use form, based on the baseband signal samples;
- The formal connection with existing literature [28] and possible uses of the new CRB are discussed;
1.2. Notation
1.3. Organization
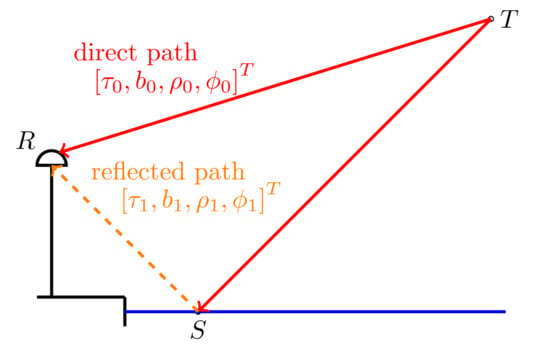
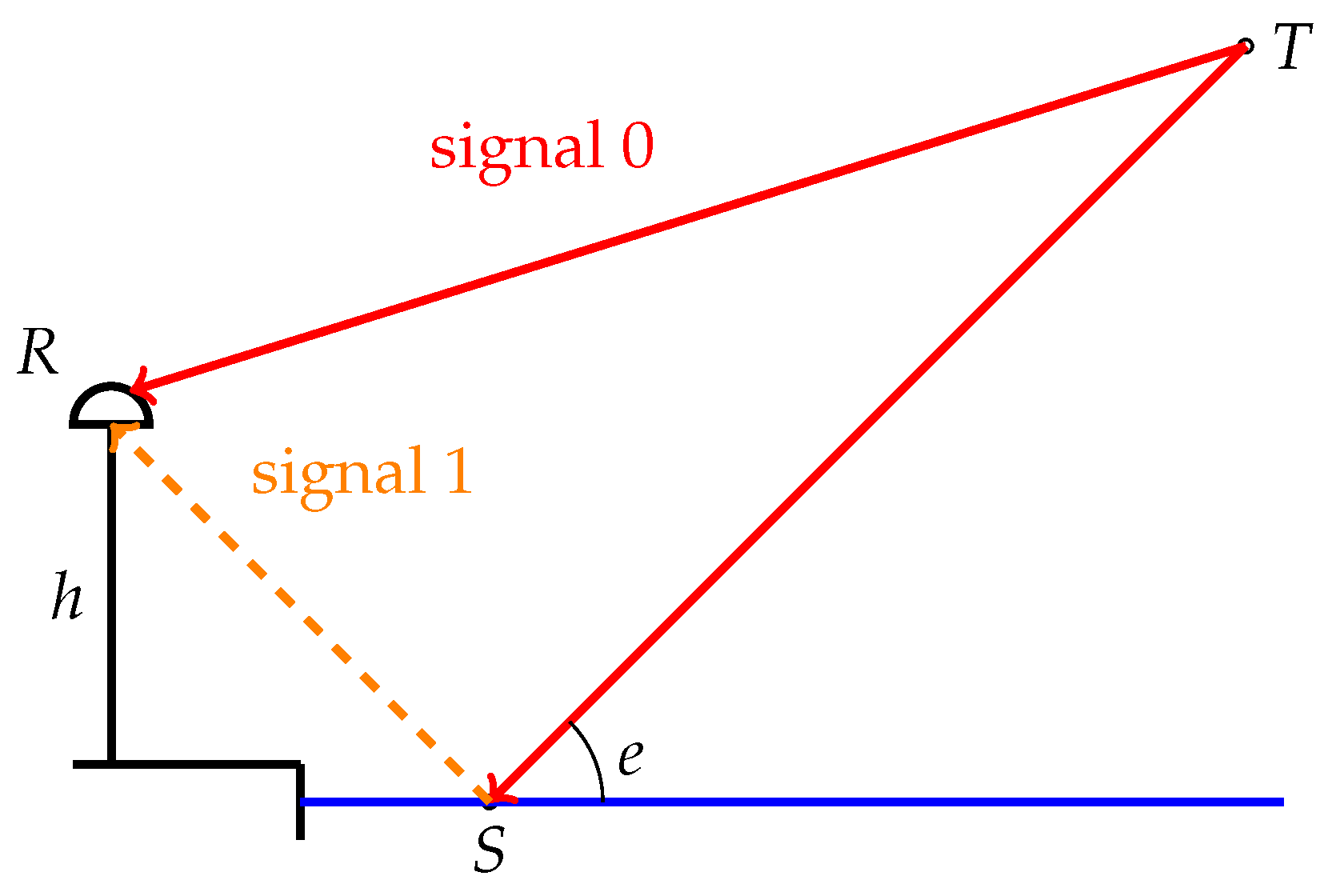
2. Signal Model
2.1. Single Antenna Receiver
2.2. Narrowband Signal Model
3. New Compact Dual Source CRB for Delay and Doppler Estimation with Band-Limited Signals
3.1. Problem Formulation
- .
- and correspond to the FIMs of the signals when they are totally decoupled. These matrices have been derived and studied in [16] without the Doppler frequency estimation, and in [17,18] for the general Gaussian CSM. The main results in [17,18] concerning the single source CSM FIM terms are summarized in Section 3.2.
- = characterizes the interference between both signals. The derivation of such FIM terms is given in Section 3.3.
3.2. Decoupled Fisher Information Matrix Terms
3.3. Interference Fisher Information Matrix Terms
4. Maximum Likelihood and CLEAN RELAX Estimators
4.1. Dual Source Conditional Maximum Likelihood Estimator
4.2. Sub-Optimal Estimator: CLEAN-RELAX
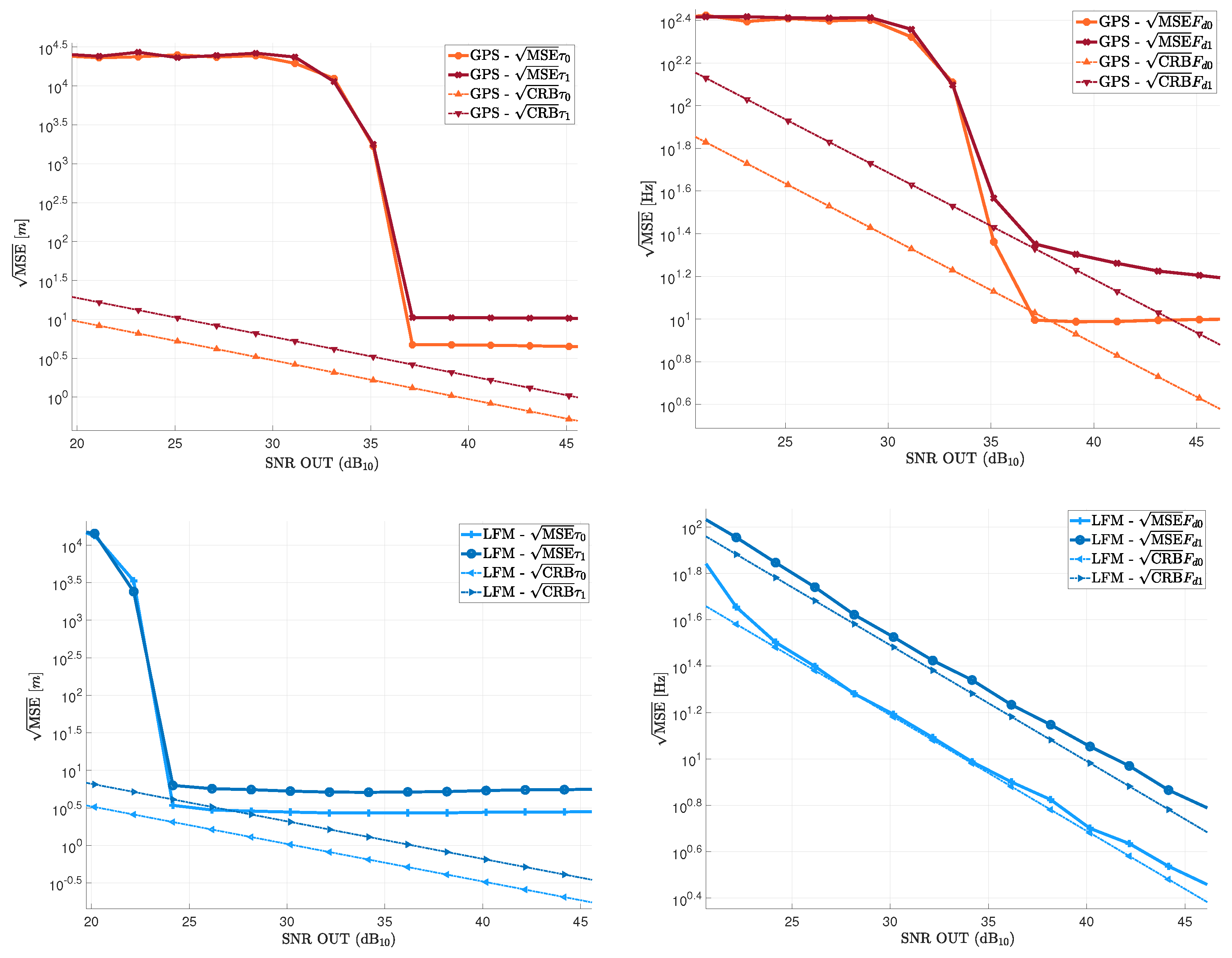
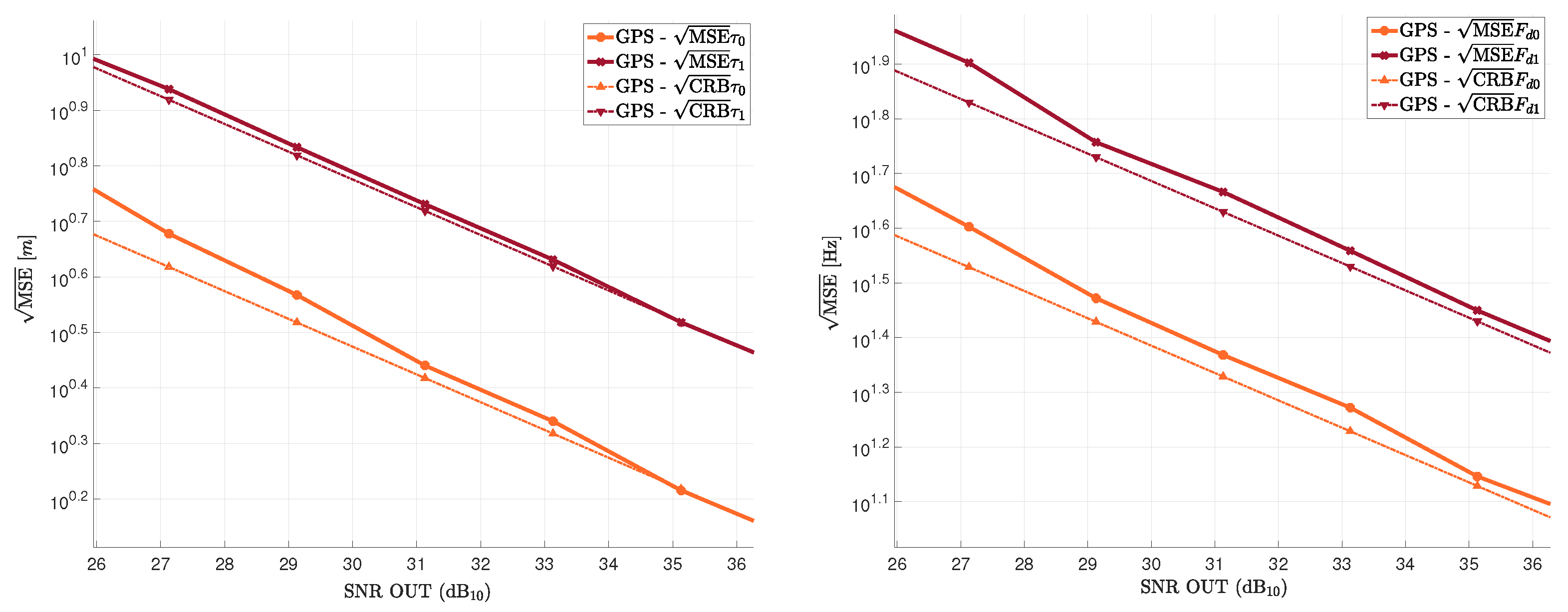
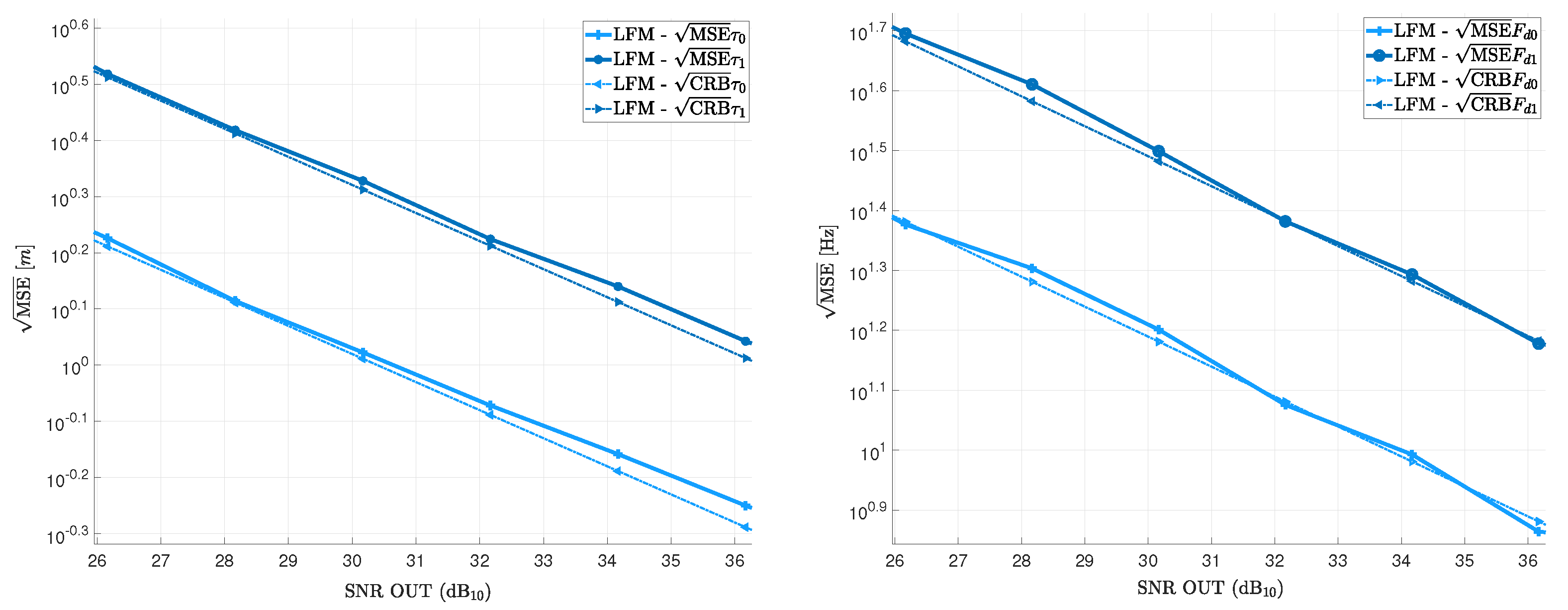
5. Validation and Discussion
5.1. Methodology
5.2. Results
5.2.1. Scenario (a): Larger than 1 Chip
5.2.2. Scenario (b): Smaller Than 1 chip
5.2.3. Scenario (c): smaller than 1 chip
6. Further Insights and Outlooks
6.1. Comparison with Existing Literature
6.2. Possible CRB Applications
- As a direct extension of the results presented in the previous Section 6.1, one could look for the different parameters that can be obtained from , and calculate a new CRB dedicated to these specific parameters. In [28], the study applied to the GNSS-R altimetry problem, investigates the receiver altitude and the complex ratio between the reflected and the direct amplitudes. A generalization of this method can easily be outlined as follows. The first step is to translate either the constraints or the new variables into a transform similarly to (29), then the general expression (31) yields the corresponding FIM. If it is simple enough, a matrix inversion might end up to a closed-form expression of the CRB.
- Another application could be the assessment of the impact the secondary signal has on the main signal’s parameters estimation. From the CRB expression it is indeed quite simple to extract the CRB for the time-delay estimation while there is no reflection, and the same CRB when the NLOS signals interfere with the LOS one. Such study may bring a new tool to characterize the signal robustness to multipath, being a key issue for instance in safety-critical GNSS applications, an ultimately drive the future generation of signal design.
- Again in the GNSS context, such CRBs can also be used to have an optimal performance assessment of the Carrier-to-Noise Density Ratio () estimation under multipath conditions. Notice that the is an important parameter used in several GNSS applications.
- Regarding precise positioning techniques such as real time kinematics (RTK), needed in modern applications, these CRBs may bring a valuable information on the impact that multipath may have on the final position estimate. Indeed, it is known that RTK solutions are not able to fix the carrier phase ambiguities under harsh propagation conditions such as strong multipath. This would extend the results presented in [17,18,35] to more realistic conditions.
- In the dual antenna GNSS-R context, the dual source CRB proposed in this contribution can be exploited in order to characterize the impact that an imperfect isolation between antennas may have on the final GNSS-R product. This may account for the reflected signal leaking into the upward antenna, or the LOS signal contaminating the downward one.
- Finally, a compact CRB expression can be exploited to do optimal signal design as suggested in [16]. As an example, we can study the case of the estimation of the receiver altitude (33). It was shown that the optimal signal can be linked to the first eigenvector of the matrix . The optimal CRB would then be given by:where is the largest eigenvalue of .
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CCF | Cross-Correlation Function |
| CMLE | Conditional Maximul Likelihood Estimator |
| CRB | Cramér Rao Bound |
| CRE | CLEAN RELAX Estimator |
| CSM | Conditional Signal Model |
| FIM | Fisher Information Matrix |
| GNSS | Global Navigation Satellite System |
| GNSS-R | GNSS Reflectometry |
| GPS | Global Positioning System |
| LFM | Linear Frequency Modulated |
| LOS | Line-Of-Sight |
| MEDLL | Multipath Mitigating Delay Lock Loop |
| MMT | Multipath Mitigation Technique |
| MSE | Mean Square Error |
| MVU | Minumum Variance Unbiased |
| NLOS | Non-Line-Of-Sight |
| Probability Density Function | |
| PSD | Power Spectral Density |
| RMSE | Root Mean Square Error |
| RTK | Real Time Kinematics |
| SNR | Signal-to-Noise Ratio |
Appendix A. Details of the Derivation of the Fisher Information Matrix
Appendix A.1. Prior Calculation on Fourier Transforms
Appendix A.2. Bounds Derivation
Appendix B. Details on the Constrained Fisher Information Matrix
References
- Van Trees, H.L. Part III: Radar-Sonar Signal Processing and Gaussian Signals in Noise. In Detection, Estimation, and Modulation Theory; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Chen, J.; Huang, Y.; Benesty, J. Time Delay Estimation. In Audio Signal Processing for Next-Generation Multimedia Communication Systems; Huang, Y., Benesty, J., Eds.; Springer: Boston, MA, USA, 2004; Chapter 8; pp. 197–227. [Google Scholar]
- Levy, B.C. Principles of Signal Detection and Parameter Estimation; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Mengali, U.; D’Andrea, A.N. Synchronization Techniques for Digital Receivers; Plenum Press: New York, NY, USA, 1997. [Google Scholar]
- Fernández-Prades, C.; Lo Presti, L.; Falletti, E. Satellite radiolocalization from GPS to GNSS and beyond: Novel technologies and applications for civil mass market. Proc. IEEE 2011, 99, 1882–1904. [Google Scholar] [CrossRef]
- Amin, M.G.; Closas, P.; Broumandan, A.; Volakis, J.L. Vulnerabilities, Threats, and Authentication in Satellite-based Navigation Systems [scanning the issue]. Proc. IEEE 2016, 104, 1169–1173. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Gleason, S.; Cardellach, E.; Camps, A. Tutorial on remote sensing using GNSS bistatic radar of opportunity. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–45. [Google Scholar] [CrossRef]
- Townsend, B.R.; Fenton, P.C.; Van Dierendonck, K.J.; Richard Van Nee, D.J. Performance Evaluation of the Multipath Estimating Delay Lock Loop. Navigation 1995, 42, 502–514. [Google Scholar] [CrossRef]
- Weill, L.R. Multipath Mitigation using Modernized GPS Signals: How Good Can it Get? In Proceedings of the 15th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2002), Portland, OR, USA, 24–27 September 2002; pp. 493–505. [Google Scholar]
- Fenton, P.C.; Jones, J. The Theory and Performance of NovAtel Inc.’s Vision Correlator. In Proceedings of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation, Long Beach, CA, USA, 13–16 September 2005; pp. 2178–2186. [Google Scholar]
- Lowe, S.T.; LaBrecque, J.L.; Zuffada, C.; Romans, L.J.; Young, L.E.; Hajj, G.A. First Spaceborne Observation of an Earth-reflected GPS Signal. Radio Sci. 2002, 37, 1–28. [Google Scholar] [CrossRef]
- Lestarquit, L.; Peyrezabes, M.; Darrozes, J.; Motte, E.; Roussel, N.; Wautelet, G.; Frappart, F.; Ramillien, G.; Biancale, R.; Zribi, M. Reflectometry with an Open-Source Software GNSS Receiver: Use Case with Carrier Phase Altimetry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4843–4853. [Google Scholar] [CrossRef]
- Treuhaft, R.; Lowe, S.; Zuffada, C.; Chao, Y. 2-cm GPS Altimetry over Crater Lake. Geophys. Res. Lett. 2001, 22, 4343–4346. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Larson, K.M.; Braun, J.J.; Small, E.E.; Gutmann, E.D.; Bilich, A.L. A Physical Model for GPS Multipath Caused by Land Reflections: Toward Bare Soil Moisture Retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 100–110. [Google Scholar] [CrossRef]
- Dogandzic, A.; Nehorai, A. Cramer-Rao Bounds for Estimating Range, Velocity, and Direction with an Active Array. IEEE Trans. Signal Process. 2001, 49, 1122–1137. [Google Scholar] [CrossRef]
- Das, P.; Vilà-Valls, J.; Chaumette, E.; Vincent, F.; Davain, L.; Bonnabel, S. On the Accuracy Limit of Time-delay Estimation with a Band-limited Signal. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 5282–5286. [Google Scholar]
- Medina, D.; Ortega, L.; Vilà-Valls, J.; Closas, P.; Vincent, F.; Chaumette, E. A New Compact CRB for Delay, Doppler and Phase Estimation—Application to GNSS SPP & RTK Performance Characterization. IET Radar Sonar Navig. 2020. [Google Scholar] [CrossRef]
- Das, P.; Vilà-Valls, J.; Vincent, F.; Davain, L.; Chaumette, E. A New Compact Delay, Doppler Stretch and Phase Estimation CRB with a Band-Limited Signal for Generic Remote Sensing Applications. Remote Sens. 2020, 12, 2913. [Google Scholar] [CrossRef]
- Bartov, A.; Messer, H. Lower Bound on the Achievable DSP Performance for Localizing Step-Like Continuous Signals in Noise. IEEE Trans. Signal Process. 1998, 46, 2195–2201. [Google Scholar] [CrossRef]
- Ricker, D.W. Echo Signal Processing; Kluwer Academic; Springer: New York, NY, USA, 2003. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Ottersten, B.; Viberg, M.; Stoica, P.; Nehorai, A. Exact and Large Sample Maximum Likelihood Techniques for Parameter Estimation and Detection in Array Processing. In Radar Array Processing; Haykin, S., Litva, J., Shepherd, T.J., Eds.; Springer: Heidelberg, Germany, 1993; Chapter 4; pp. 99–151. [Google Scholar]
- Yau, S.F.; Bresler, Y. A Compact Cramér-Rao Bound Expression for Parametric Estimation of Superimposed Signals. IEEE Trans. Signal Process. 1992, 40, 1226–1230. [Google Scholar] [CrossRef]
- Menni, T.; Chaumette, E.; Larzabal, P. Reparameterization and Constraints for CRB: Duality and a Major Inequality for System Analysis and Design in the Asymptotic Region. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 3545–3548. [Google Scholar]
- Zhao, T.; Huang, T. Cramer-Rao Lower Bounds for the Joint Delay-Doppler Estimation of an Extended Target. IEEE Trans. Signal Process. 2016, 64, 1562–1573. [Google Scholar] [CrossRef]
- Germain, O.; Ruffini, G. A Revisit to the GNSS-R Code Range Precision. arXiv 2006, arXiv:0606180. [Google Scholar]
- Camps, A.; Park, H.; Valencia i Domènech, E.; Pascual, D.; Martin, F.; Rius, A.; Ribo, S.; Benito, J.; Andrés-Beivide, A.; Saameno, P.; et al. Optimization and Performance Analysis of Interferometric GNSS-R Altimeters: Application to the PARIS IoD Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1436–1451. [Google Scholar] [CrossRef]
- Ribot, M.A.; Botteron, C.; Farine, P. Derivation of the Cramér-Rao Bound in the GNSS-Reflectometry Context for Static, Ground-Based Receivers in Scenarios with Coherent Reflection. Sensors 2016, 16, 2063. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. Performances Study of Conditional and Unconditional Direction of Arrival Estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1783–1795. [Google Scholar] [CrossRef]
- Menni, T.; Chaumette, E.; Larzabal, P.; Barbot, J.P. CRB for Active Radar. In Proceedings of the 2011 19th European Signal Processing Conference, Barcelona, Spain, 29 August–2 September 2011. [Google Scholar]
- Menni, T.; Galy, J.; Chaumette, E.; Larzabal, P. Versatility of Constrained CRB for System Analysis and Design. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1841–1863. [Google Scholar] [CrossRef]
- Vincent, F.; Besson, O.; Chaumette, E. Approximate Maximum Likelihood Direction of Arrival Estimation for Two Closely Spaced Sources. In Proceedings of the 2013 5th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), St. Martin, France, 15–18 December 2013; pp. 320–323. [Google Scholar]
- Vincent, F.; Besson, O.; Chaumette, E. Approximate Maximum Likelihood Estimation of Two Closely Spaced Sources. Signal Process. 2014, 97, 83–90. [Google Scholar] [CrossRef]
- Renaux, A.; Forster, P.; Chaumette, E.; Larzabal, P. On the High-SNR Conditional Maximum-Likelihood Estimator Full Statistical Characterization. IEEE Trans. Signal Process. 2006, 54, 4840–4843. [Google Scholar] [CrossRef]
- Ortega, L.; Medina, D.; Vilà-Valls, J.; Vincent, F.; Chaumette, E. Positioning Performance Limits of GNSS Meta-Signals and HO-BOC Signals. Sensors 2020, 20, 3586. [Google Scholar] [CrossRef] [PubMed]
- Capon, J. High-Resolution Frequency-Wavenumber Spectrum Analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple Emitter Location and Signal Parameter Estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. MUSIC, Maximum Likelihood and Cramer-Rao Bound. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing (ICASSP-88), New York, NY, USA, 11–14 April 1988; Volume 4, pp. 2296–2299. [Google Scholar]
- Ziskind, I.; Wax, M. Maximum Likelihood Localization of Multiple Sources by Alternating Projection. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1553–1560. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. Efficient mixed-spectrum estimation with applications to target feature extraction. IEEE Trans. Signal Process. 1996, 44, 281–295. [Google Scholar]
- Beckmann, P.; Spizzichino, A. The Scattering of Electromagnetic Waves From Rough Surfaces; Artech House: Norwood, MA, USA, 1987. [Google Scholar]
- Kaplan, E.; Hegarty, C. (Eds.) Understanding GPS: Principles and Applications, 2nd ed.; Artech House: Norwood, MA, USA, 2006. [Google Scholar]
- Van Trees, H.L. Part I: Detection Estimation and Linear Modulation Theory. In Detection, Estimation, and Modulation Theory; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Das, P.; Ortega, L.; Vilà-Valls, J.; Vincent, F.; Chaumette, E.; Davain, L. Performance Limits of GNSS Code-Based Precise Positioning: GPS, Galileo & Meta-Signals. Sensors 2020, 20, 2196. [Google Scholar] [CrossRef]
- U.S. Goverment. Interface Specification IS-GPS-200 Navstar GPS Space/Segment/Navigation User Interface. Available online: https://www.gps.gov/technical/icwg/IS-GPS-200K.pdf (accessed on 16 January 2020).
- Lehmann, E.L.; Casella, G. Theory of Point Estimation, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar]
- Hu, C.; Benson, C.; Park, H.; Camps, A.; Qiao, L.; Rizos, C. Detecting Targets above the Earth’s Surface Using GNSS-R Delay Doppler Maps: Results from TDS-1. Remote Sens. 2019, 11, 2327. [Google Scholar] [CrossRef]
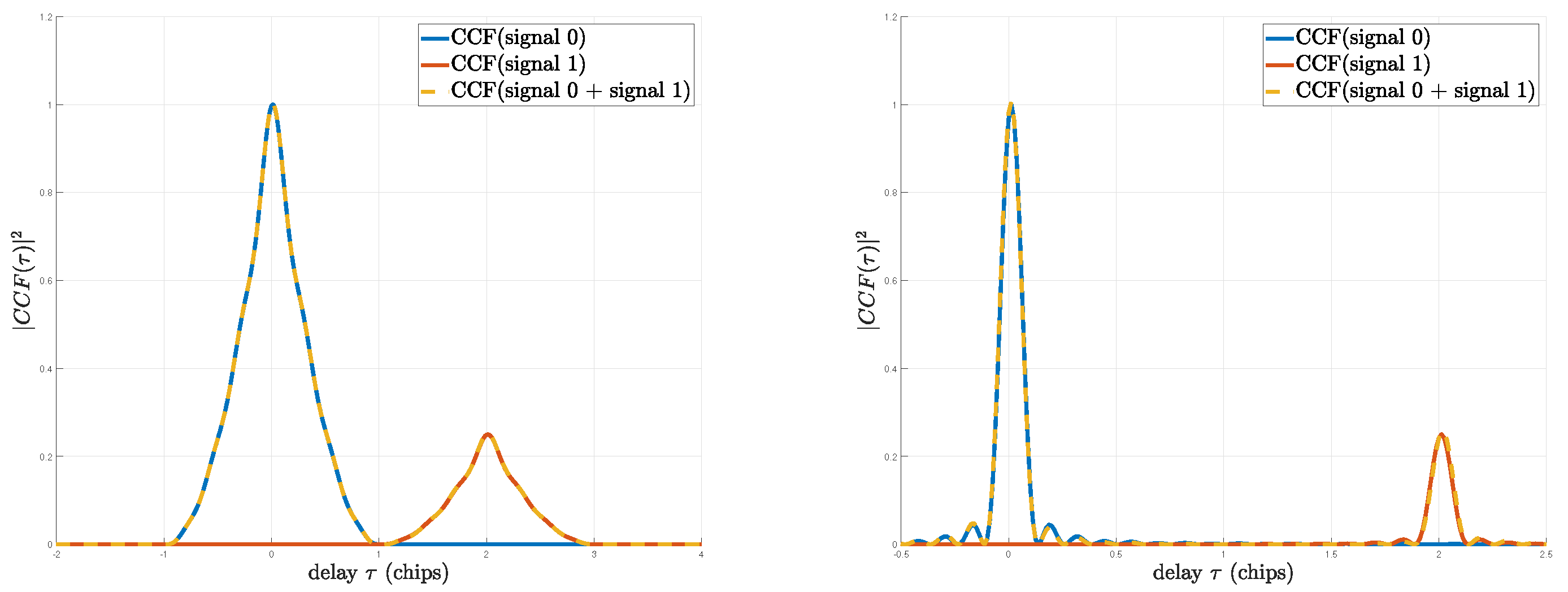
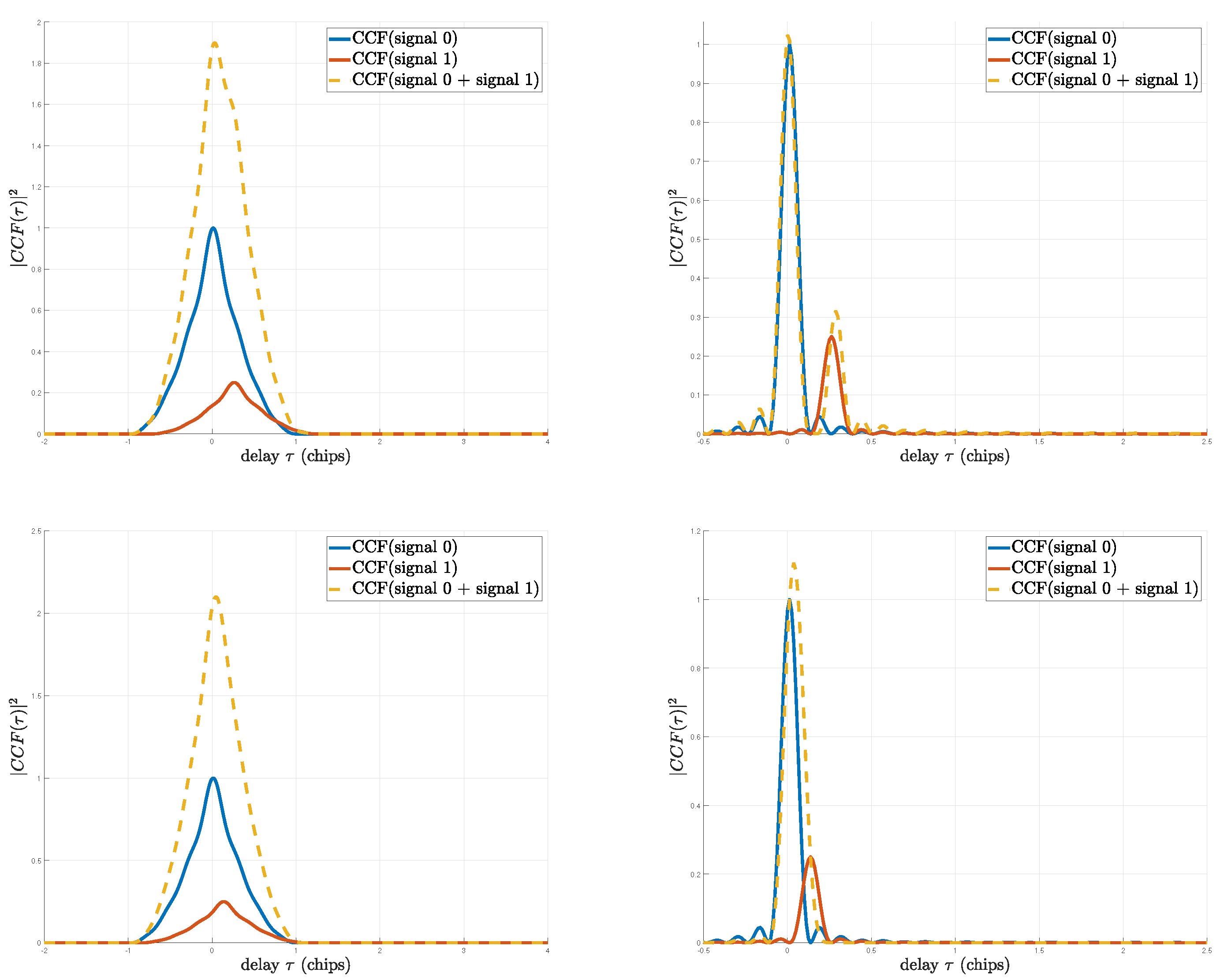


| Estimator | (MHz) | (L1 C/A Chips) | (m) | () | (Hz) | ||
|---|---|---|---|---|---|---|---|
| (a) | CRE | 8 | 2 | 600 | 0.5 | 15 | 20/50 |
| (b) | CRE | 8 | 1/4 | 75 | 0.5 | 15 | 20/50 |
| (c1) | CRE | 8 | 1/8 | 37.5 | 0.5 | 15 | 20/50 |
| (c2) | CMLE | 8 | 1/8 | 37.5 | 0.5 | 15 | 20/50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lubeigt, C.; Ortega, L.; Vilà-Valls, J.; Lestarquit, L.; Chaumette, E. Joint Delay-Doppler Estimation Performance in a Dual Source Context. Remote Sens. 2020, 12, 3894. https://doi.org/10.3390/rs12233894
Lubeigt C, Ortega L, Vilà-Valls J, Lestarquit L, Chaumette E. Joint Delay-Doppler Estimation Performance in a Dual Source Context. Remote Sensing. 2020; 12(23):3894. https://doi.org/10.3390/rs12233894
Chicago/Turabian StyleLubeigt, Corentin, Lorenzo Ortega, Jordi Vilà-Valls, Laurent Lestarquit, and Eric Chaumette. 2020. "Joint Delay-Doppler Estimation Performance in a Dual Source Context" Remote Sensing 12, no. 23: 3894. https://doi.org/10.3390/rs12233894
APA StyleLubeigt, C., Ortega, L., Vilà-Valls, J., Lestarquit, L., & Chaumette, E. (2020). Joint Delay-Doppler Estimation Performance in a Dual Source Context. Remote Sensing, 12(23), 3894. https://doi.org/10.3390/rs12233894