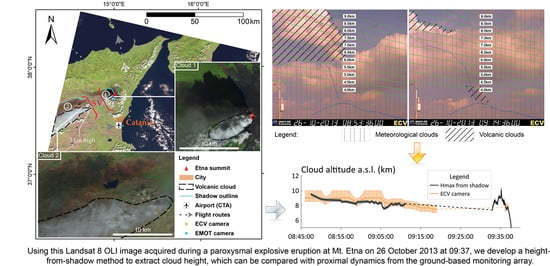
Plume Height Time-Series Retrieval Using Shadow in Single Spatial Resolution Satellite Images
Abstract
:1. Introduction
2. Case Study: OLI Imagery of the 25–26 October 2013 Fountaining at Etna
2.1. The 25–26 October 2013 Eruption
2.2. Data
3. Methodology
3.1. Height-from-Shadow Time Series from a Single High-Spatial Resolution Image
3.1.1. Sun–Cloud Geometric Relations
3.1.2. Viewing and Shadow Geometry
3.1.3. Height Calculations and Corrections
3.1.4. Error Calculation
3.1.5. Cloud Dispersal Velocity Calculation
3.1.6. Generation of Cloud Height Time Series
3.2. Cloud Height Validation
3.2.1. Cloud Height from the INGV-OE ECV Camera
3.2.2. Cloud Height from PEM
4. Results
4.1. Cloud Height Variation with Distance
4.2. Cloud Height Time Series
4.3. Comparison with PEM and ECV Camera
5. Discussion
5.1. Cloud Separation: Shut-Down in Activity?
5.2. Settling of Cloud Height to Neutral Buoyancy Level
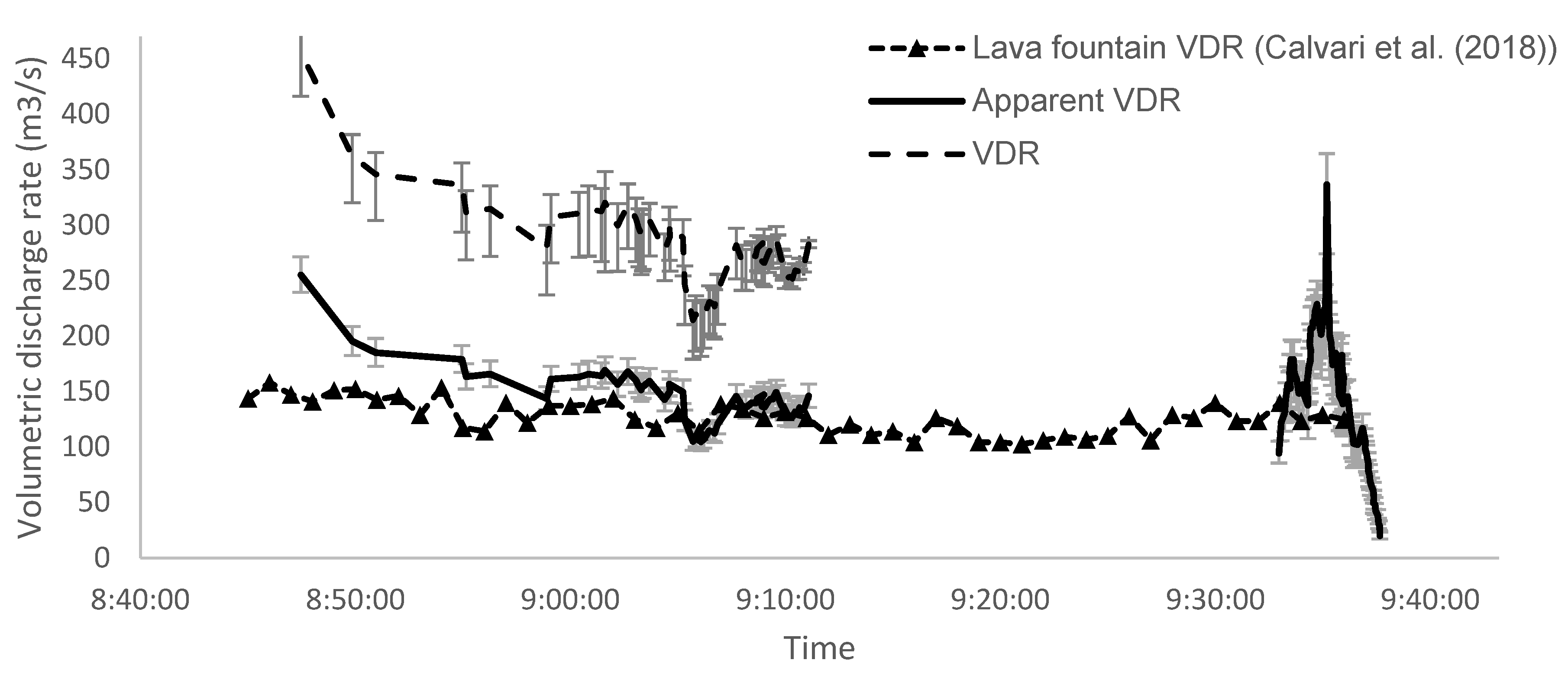
5.3. Mass Flux Fluctuation Effect
5.4. Wind Effects on the Plume above the Vent
5.5. Plume/Cloud Ascent and Dispersion Dynamics: Summary
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Casadevall, T.J. Volcanic Ash and Aviation Safety; Proceedings of the First International Symposium on Volcanic Ash and Aviation Safety; U.S. Geological Survey Bulletin: Washington, DC, USA, 1994.
- Kienle, J.; Shaw, G.E. Plume dynamics, thermal energy and long-distance transport of vulcanian eruption clouds from Augustine Volcano, Alaska. J. Volcanol. Geotherm. Res. 1979, 6, 139–164. [Google Scholar] [CrossRef]
- Hanstrum, B.N.; Watson, A.S. A case study of two eruptions of Mount Galunggung and an investigation of volcanic eruption cloud characteristics using remote sensing techniques. Autralian Meteorol. Mag. 1983, 31, 171–177. [Google Scholar]
- Aloisi, M.; D’Agostino, M.; Dean, K.G.; Mostaccio, A.; Neri, G. Satellite analysis and PUFF simulation of the eruptive cloud generated by the Mount Etna paroxysm of 22 July 1998. J. Geophys. Res. Solid Earth 2002, 107, ECV 9-1–ECV 9-12. [Google Scholar] [CrossRef]
- Guffanti, M.; Mayberry, G.C.; Casadevall, T.J.; Wunderman, R. Volcanic hazards to airports. Nat. Hazards 2009, 51, 287–302. [Google Scholar] [CrossRef]
- Alemanno, A. Governing Disasters—The Challenges of Emergency Risk Regulation; Edward Elgar Publishing Limited: Cheltenham, UK, 2011; ISBN 9780857935731. [Google Scholar]
- Oppenheimer, C. Volcanological applications of meteorological satellites. Int. J. Remote Sens. 1998, 19, 2829–2864. [Google Scholar] [CrossRef]
- Sparks, R.S.J.; Bursik, M.; Carey, S.; Gilbert, J.S.; Glaze, L.S.; Sigurdsson, H.; Woods, A.W. Volcanic Plumes; Wiley: Chichester, UK, 1997; ISBN 9780471939016. [Google Scholar]
- Bonadonna, C.; Folch, A.; Loughlin, S.; Puempel, H. Future developments in modelling and monitoring of volcanic ash clouds: Outcomes from the first IAVCEI-WMO workshop on Ash Dispersal Forecast and Civil Aviation. Bull. Volcanol. 2012, 74, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Newhall, C.G.; Self, S. The volcanic explosivity index (VEI) an estimate of explosive magnitude for historical volcanism. J. Geophys. Res. 1982, 87, 1231. [Google Scholar] [CrossRef]
- Francis, P.W. Infra-red techniques for volcano monitoring and prediction-A review. J. Geol. Soc. Lond. 1979, 136, 355–359. [Google Scholar] [CrossRef]
- Francis, P.W.; Oppenheimer, C. Applications of satellite remote sensing techniques to volcanology. In Understanding the Terrestrial Environment—The Role of Observation from Space; Paylor & Francis: London, UK, 1992; pp. 37–52. [Google Scholar]
- Francis, P.W.; Oppenheimer, C. Volcanoes, 2nd ed.; Oxford University Press: Oxford, UK, 2003; ISBN 9780199254699. [Google Scholar]
- Pyle, D.M. Sizes of Volcanic Eruptions. In The Encyclopedia of Volcanoes; Elsevier: London, UK, 2015; pp. 257–264. [Google Scholar]
- Mouginis-Mark, P.J.; Pieri, D.C.; Francis, P.W.; Wilson, L.; Self, S.; Rose, W.I.; Wood, C.A. Remote sensing of volcanos and volcanic terrains. EOS Trans. Am. Geophys. Union 1989, 70, 1567–1575. [Google Scholar] [CrossRef]
- Glaze, L.S.; Francis, P.W.; Self, S.; Rothery, D.A. The 16 September 1986 eruption of Lascar volcano, north Chile: Satellite investigations. Bull. Volcanol. 1989, 51, 149–160. [Google Scholar] [CrossRef]
- Glaze, L.S.; Wilson, L.; Mouginis-Mark, P.J. Volcanic eruption plume top topography and heights as determined from photoclinometric analysis of satellite data. J. Geophys. Res. Solid Earth 1999, 104, 2989–3001. [Google Scholar] [CrossRef]
- Woods, A.W.; Self, S. Thermal disequilibrium at the top of volcanic clouds and its effect on estimates of the column height. Nature 1992, 355, 628–630. [Google Scholar] [CrossRef]
- Holasek, R.E.; Self, S.; Woods, A.W. Satellite observations and interpretation of the 1991 Mount Pinatubo eruption plumes. J. Geophys. Res. B Solid Earth 1996, 101, 27635–27655. [Google Scholar] [CrossRef]
- Zakšek, K.; Hort, M.; Zaletelj, J.; Langmann, B. Monitoring volcanic ash cloud top height through simultaneous retrieval of optical data from polar orbiting and geostationary satellites. Atmos. Chem. Phys. 2013, 13, 2589–2606. [Google Scholar] [CrossRef] [Green Version]
- Marchese, F.; Falconieri, A.; Pergola, N.; Tramutoli, V. A retrospective analysis of the Shinmoedake (Japan) eruption of 26-27 January 2011 by means of Japanese geostationary satellite data. J. Volcanol. Geotherm. Res. 2014, 269, 1–13. [Google Scholar] [CrossRef]
- Patrick, M.R. Dynamics of Strombolian ash plumes from thermal video: Motion, morphology, and air entrainment. J. Geophys. Res. 2007, 112, B06202. [Google Scholar] [CrossRef]
- Carey, S.; Bursik, M. Volcanic Plumes. In The Encyclopedia of Volcanoes; Elsevier: London, UK, 2015; pp. 571–585. [Google Scholar]
- Bonaccorso, A.; Calvari, S. A new approach to investigate an eruptive paroxysmal sequence using camera and strainmeter networks: Lessons from the 3–5 December 2015 activity at Etna volcano. Earth Planet. Sci. Lett. 2017, 475, 231–241. [Google Scholar] [CrossRef]
- Carey, S.; Sparks, R.S.J. Quantitative models of the fallout and dispersal of tephra from volcanic eruption columns. Bull. Volcanol. 1986, 48, 109–125. [Google Scholar] [CrossRef]
- Slawson, P.R.; Csanady, G.T. On the mean path of buoyant, bent-over chimney plumes. J. Fluid Mech. 1967, 28, 311. [Google Scholar] [CrossRef]
- Andò, B.; Pecora, E. An advanced video-based system for monitoring active volcanoes. Comput. Geosci. 2006, 32, 85–91. [Google Scholar] [CrossRef]
- Calvari, S.; Cannavò, F.; Bonaccorso, A.; Spampinato, L.; Pellegrino, A.G. Paroxysmal Explosions, Lava Fountains and Ash Plumes at Etna Volcano: Eruptive Processes and Hazard Implications. Front. Earth Sci. 2018, 6. [Google Scholar] [CrossRef]
- Behncke, B.; Branca, S.; Corsaro, R.A.; De Beni, E.; Miraglia, L.; Proietti, C. The 2011–2012 summit activity of Mount Etna: Birth, growth and products of the new SE crater. J. Volcanol. Geotherm. Res. 2014, 270, 10–21. [Google Scholar] [CrossRef]
- De Beni, E.; Behncke, B.; Branca, S.; Nicolosi, I.; Carluccio, R.; D’Ajello Caracciolo, F.; Chiappini, M. The continuing story of Etna’s New Southeast Crater (2012–2014): Evolution and volume calculations based on field surveys and aerophotogrammetry. J. Volcanol. Geotherm. Res. 2015, 303, 175–186. [Google Scholar] [CrossRef]
- Coltelli, M.; Del Carlo, P.; Vezzoli, L. Discovery of a Plinian basaltic eruption of Roman age at Etna volcano, Italy. Geology 1998, 26, 1095. [Google Scholar] [CrossRef]
- Istituto Nazionale di Statistica-Roma, I. Demografia in Cifre. Available online: http://demo.istat.it/ (accessed on 1 October 2020).
- Vulpiani, G.; Ripepe, M.; Valade, S. Mass discharge rate retrieval combining weather radar and thermal camera observations. J. Geophys. Res. Solid Earth 2016, 121, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Del Carlo, P.; Vezzoli, L.; Coltelli, M. Last 100 ka tephrostratigraphic record of Mount Etna. GMS 2004, 143, 77–89. [Google Scholar]
- Corradini, S.; Guerrieri, L.; Lombardo, V.; Merucci, L.; Musacchio, M.; Prestifilippo, M.; Scollo, S.; Silvestri, M.; Spata, G.; Stelitano, D. Proximal Monitoring of the 2011–2015 Etna Lava Fountains Using MSG-SEVIRI Data. Geosciences 2018, 8, 140. [Google Scholar] [CrossRef] [Green Version]
- Greco, F.; Currenti, G.; Palano, M.; Pepe, A.; Pepe, S. Evidence of a shallow persistent magmatic reservoir from joint inversion of gravity and ground deformation data: The 25–26 October 2013 Etna lava fountaining event. Geophys. Res. Lett. 2016, 43, 3246–3253. [Google Scholar] [CrossRef] [Green Version]
- Andronico, D.; Behncke, B.; De Beni, E.; Cristaldi, A.; Scollo, S.; Lopez, M.; Lo Castro, M.D. Magma Budget From Lava and Tephra Volumes Erupted during the 25-26 October 2013 Lava Fountain at Mt Etna. Front. Earth Sci. 2018, 6. [Google Scholar] [CrossRef]
- De Michele, M.; Raucoules, D.; Corradini, S.; Merucci, L.; Salerno, G.; Sellitto, P.; Carboni, E. Volcanic cloud top height estimation using the plume elevation model procedure applied to orthorectified Landsat 8 data. test case: 26 October 2013 Mt. Etna eruption. Remote Sens. 2019, 11, 785. [Google Scholar] [CrossRef] [Green Version]
- Young, N.E.; Anderson, R.S.; Chignell, S.M.; Vorster, A.G.; Lawrence, R.; Evangelista, P.H. A survival guide to Landsat preprocessing. Ecology 2017, 98, 920–932. [Google Scholar] [CrossRef] [Green Version]
- Qiu, S.; He, B.; Zhu, Z.; Liao, Z.; Quan, X. Improving Fmask cloud and cloud shadow detection in mountainous area for Landsats 4–8 images. Remote Sens. Environ. 2017, 199, 107–119. [Google Scholar] [CrossRef]
- Dean, K.G.; Bowling, S.A.; Shaw, G.E.; Tanaka, H. Satellite analyses of movement and characteristics of the Redoubt Volcano plume, January 8, 1990. J. Volcanol. Geotherm. Res. 1994, 62, 339–352. [Google Scholar] [CrossRef]
- Holasek, R.E.; Self, S. GOES weather satellite observations and measurements of the May 18, 1980, Mount St. Helens eruption. J. Geophys. Res. Solid Earth 1995, 100, 8469–8487. [Google Scholar] [CrossRef]
- Kinoshita, K. Observation of flow and dispersion of volcanic clouds from Mt. Sakurajima. Atmos. Environ. 1996, 30, 2831–2837. [Google Scholar] [CrossRef]
- Denniss, A.M.; Harris, A.J.L.; Rothery, D.A.; Francis, P.W.; Carlton, R.W.T. Satellite observations of the April 1993 eruption of Lascar volcano. Int. J. Remote Sens. 1998, 19, 801–821. [Google Scholar] [CrossRef]
- Prata, A.J.; Grant, I.F. Retrieval of microphysical and morphological properties of volcanic ash plumes from satellite data: Application to Mt Ruapehu, New Zealand. Q. J. R. Meteorol. Soc. 2001, 127, 2153–2179. [Google Scholar] [CrossRef]
- Tupper, A.; Carn, S.A.; Davey, J.; Kamada, Y.; Potts, R.; Prata, F.; Tokuno, M. An evaluation of volcanic cloud detection techniques during recent significant eruptions in the western ‘Ring of Fire’. Remote Sens. Environ. 2004, 91, 27–46. [Google Scholar] [CrossRef] [Green Version]
- Iqbal, M. Sun–Earth Astronomical Relationships. In An Introduction to Solar Radiation; Elsevier: London, UK, 1983; pp. 1–28. ISBN 9780123737502. [Google Scholar]
- Harris, A.J.L. Thermal Remote Sensing of Active Volcanoes; Cambridge University Press: Cambridge, UK, 2013; ISBN 9781139029346. [Google Scholar]
- Mouginis-Mark, P.J.; Domergue-Schmidt, N. Acquisition of satellite data for volcano studies. Geophys. Monogr. Ser. 2000, 116, 9–24. [Google Scholar] [CrossRef]
- Markham, B.L. Characterization of the Landsat sensors’ spatial responses. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 864–875. [Google Scholar] [CrossRef]
- Oppenheimer, C.; Francis, P.W.; Rothery, D.A.; Carlton, R.W.T.; Glaze, L.S. Infrared image analysis of volcanic thermal features: Lascar Volcano, Chile, 1984-1992. J. Geophys. Res. 1993, 98, 4269–4286. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- Scollo, S.; Prestifilippo, M.; Pecora, E.; Corradini, S.; Merucci, L.; Spata, G.; Coltelli, M. Eruption column height estimation of the 2011-2013 Etna lava fountains. Ann. Geophys. 2014, 57. [Google Scholar] [CrossRef] [Green Version]
- Prata, A.J.; Turner, P.J. Cloud-top height determination using ATSR data. Remote Sens. Environ. 1997, 59, 1–13. [Google Scholar] [CrossRef]
- De Michele, M.; Raucoules, D.; Arason, Þ. Volcanic Plume Elevation Model and its velocity derived from Landsat 8. Remote Sens. Environ. 2016, 176, 219–224. [Google Scholar] [CrossRef]
- Bursik, M. Effect of wind on the rise height of volcanic plumes. Geophys. Res. Lett. 2001, 28, 3621–3624. [Google Scholar] [CrossRef] [Green Version]
- Mastin, L.G.; Guffanti, M.; Servranckx, R.; Webley, P.W.; Barsotti, S.; Dean, K.G.; Durant, A.; Ewert, J.W.; Neri, A.; Rose, W.I.; et al. A multidisciplinary effort to assign realistic source parameters to models of volcanic ash-cloud transport and dispersion during eruptions. J. Volcanol. Geotherm. Res. 2009, 186, 10–21. [Google Scholar] [CrossRef]
- Sellitto, P.; Di Sarra, A.; Corradini, S.; Boichu, M.; Herbin, H.; Dubuisson, P.; Sèze, G.; Meloni, D.; Monteleone, F.; Merucci, L.; et al. Synergistic use of Lagrangian dispersion and radiative transfer modelling with satellite and surface remote sensing measurements for the investigation of volcanic plumes: The Mount Etna eruption of 25-27 October 2013. Atmos. Chem. Phys. 2016, 16, 6841–6861. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, Y.J.; Koyaguchi, T. Effects of wind on entrainment efficiency in volcanic plumes. J. Geophys. Res. Solid Earth 2015, 120, 6122–6140. [Google Scholar] [CrossRef] [Green Version]
- Woodhouse, M.J.; Hogg, A.J.; Phillips, J.C.; Sparks, R.S.J. Interaction between volcanic plumes and wind during the 2010 Eyjafjallajökull eruption, Iceland. J. Geophys. Res. Solid Earth 2013, 118, 92–109. [Google Scholar] [CrossRef] [Green Version]
- Allard, P.; Burton, M.; Muré, F. Spectroscopic evidence for a lava fountain driven by previously accumulated magmatic gas. Nature 2005, 433, 407–410. [Google Scholar] [CrossRef]
- Costa, A.; Suzuki, Y.J.; Cerminara, M.; Devenish, B.J.; Ongaro, T.E.; Herzog, M.; Van Eaton, A.R.; Denby, L.C.; Bursik, M.; de’ Michieli Vitturi, M.; et al. Results of the eruptive column model inter-comparison study. J. Volcanol. Geotherm. Res. 2016, 326, 2–25. [Google Scholar] [CrossRef] [Green Version]
- Ramsey, M.S. Synergistic use of satellite thermal detection and science: A decadal perspective using ASTER. Geol. Soc. Lond. Spec. Publ. 2016, 426, 115–136. [Google Scholar] [CrossRef] [Green Version]











| Bands | Wavelength (μm) | Spatial Resolution (m) | Measure |
|---|---|---|---|
| Band 1—Coastal aerosol | 0.43–0.45 | 30 | TOA/SR |
| Band 2—Blue | 0.45–0.51 | 30 | TOA/SR |
| Band 3—Green | 0.53–0.59 | 30 | TOA/SR |
| Band 4—Red | 0.64–0.67 | 30 | TOA/SR |
| Band 5—NIR | 0.85–0.88 | 30 | TOA/SR |
| Band 6—SWIR 1 | 1.57–1.65 | 30 | TOA/SR |
| Band 7—SWIR 2 | 2.11–2.29 | 30 | TOA/SR |
| Band 8—Panchromatic | 0.50–0.68 | 15 | TOA |
| Band 9—Cirrus | 1.36–1.38 | 30 | TOA |
| Band 10—Thermal Infrared (TIRS) 1 | 10.6–11.19 | 100 | Temperature |
| Band 11—Thermal Infrared (TIRS) 2 | 11.50–12.51 | 100 | Temperature |
| Cloud 1 | Cloud 2 | |
|---|---|---|
| Cloud altitude error | Hmax error | Cloud altitude error |
| ±140 m | ±210 m | ±185 m |
| Time Range | Cloud Dispersal Velocity (m/s) (This Study) |
|---|---|
| 8:40–8:50 | 17.4 |
| 8:50–9:00 | 19.6 |
| 9:00–9:10 | 16.7 |
| 9:10–9:20 | 21.5 |
| 9:20–9:30 | 26.2 |
| 9:30–9:40 | 26.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pailot-Bonnétat, S.; Harris, A.J.L.; Calvari, S.; De Michele, M.; Gurioli, L. Plume Height Time-Series Retrieval Using Shadow in Single Spatial Resolution Satellite Images. Remote Sens. 2020, 12, 3951. https://doi.org/10.3390/rs12233951
Pailot-Bonnétat S, Harris AJL, Calvari S, De Michele M, Gurioli L. Plume Height Time-Series Retrieval Using Shadow in Single Spatial Resolution Satellite Images. Remote Sensing. 2020; 12(23):3951. https://doi.org/10.3390/rs12233951
Chicago/Turabian StylePailot-Bonnétat, Sophie, Andrew J. L. Harris, Sonia Calvari, Marcello De Michele, and Lucia Gurioli. 2020. "Plume Height Time-Series Retrieval Using Shadow in Single Spatial Resolution Satellite Images" Remote Sensing 12, no. 23: 3951. https://doi.org/10.3390/rs12233951
APA StylePailot-Bonnétat, S., Harris, A. J. L., Calvari, S., De Michele, M., & Gurioli, L. (2020). Plume Height Time-Series Retrieval Using Shadow in Single Spatial Resolution Satellite Images. Remote Sensing, 12(23), 3951. https://doi.org/10.3390/rs12233951