Shadow Detection and Restoration for Hyperspectral Images Based on Nonlinear Spectral Unmixing
Abstract
:1. Introduction
- –
- –
- –
- –
- –
- Shadow restoration may introduce spectral distortion in sunlit pixels.
- –
- –
2. Methodology
2.1. Shadowed Spectra Model
2.2. Nonlinear Mixture Model
2.3. Sunlit Factor Map
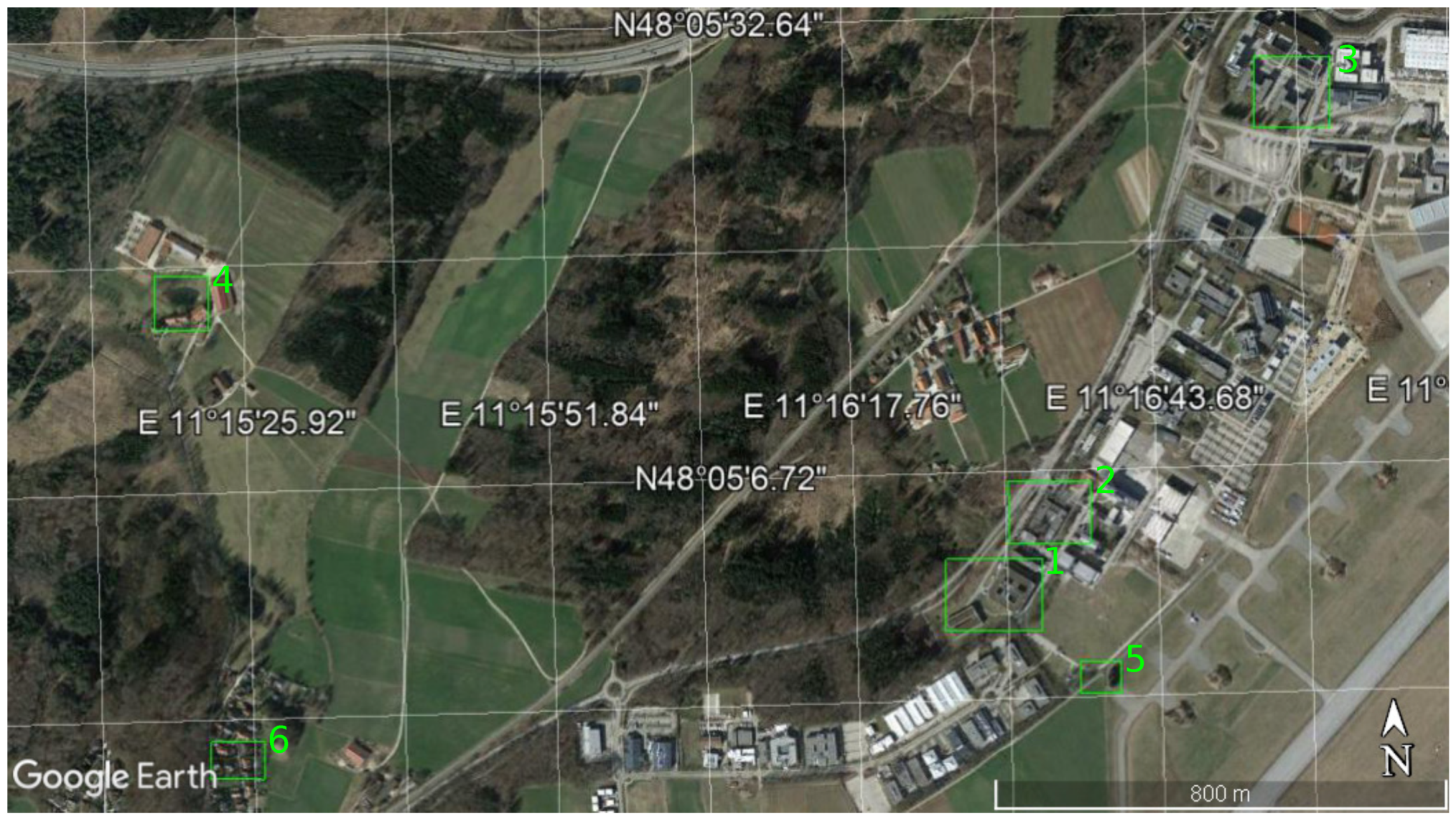
3. Dataset
4. Results
4.1. Reconstruction Error
4.2. Spectral Distance
4.3. Restoration and Classification Results
4.4. Sunlit Factor Map
4.5. The F Parameter
5. Discussion
5.1. Level of Automatism
5.2. Computational Cost
5.3. Benefits and Challenges
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shahtahmassebi, A.; Yang, N.; Wang, K.; Moore, N.; Shen, Z. Review of shadow detection and de-shadowing methods in remote sensing. Chin. Geogr. Sci. 2013, 23, 403–420. [Google Scholar] [CrossRef] [Green Version]
- Song, H.; Huang, B.; Zhang, K. Shadow detection and reconstruction in high-resolution satellite images via morphological filtering and example-based learning. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2545–2554. [Google Scholar] [CrossRef]
- Dare, P.M. Shadow analysis in high-resolution satellite imagery of urban areas. Photogramm. Eng. Remote Sens. 2005, 71, 169–177. [Google Scholar] [CrossRef] [Green Version]
- Ashton, E.A.; Wemett, B.D.; Leathers, R.A.; Downes, T.V. A novel method for illumination suppression in hyperspectral images. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XIV; International Society for Optics and Photonics: Orlando, FL, USA, 2008; Volume 6966, p. 69660C. [Google Scholar]
- Polder, G.; Gowen, A. The hype in spectral imaging. J. Spectr. Imaging 2020, 9. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef] [Green Version]
- Adeline, K.R.; Chen, M.; Briottet, X.; Pang, S.; Paparoditis, N. Shadow detection in very high spatial resolution aerial images: A comparative study. ISPRS J. Photogramm. Remote Sens. 2013, 80, 21–38. [Google Scholar] [CrossRef]
- Nagao, M.; Matsuyama, T.; Ikeda, Y. Region extraction and shape analysis in aerial photographs. Comput. Graph. Image Process. 1979, 10, 195–223. [Google Scholar] [CrossRef]
- Rüfenacht, D.; Fredembach, C.; Süsstrunk, S. Automatic and accurate shadow detection using near-infrared information. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 1672–1678. [Google Scholar] [CrossRef]
- Qiao, X.; Yuan, D.; Li, H. Urban shadow detection and classification using hyperspectral image. J. Indian Soc. Remote Sens. 2017, 45, 945–952. [Google Scholar] [CrossRef]
- Tsai, V.J. A comparative study on shadow compensation of color aerial images in invariant color models. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1661–1671. [Google Scholar] [CrossRef]
- Sarabandi, P.; Yamazaki, F.; Matsuoka, M.; Kiremidjian, A. Shadow detection and radiometric restoration in satellite high resolution images. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2004, Anchorage, AK, USA, 20–24 September 2004; Volume 6, pp. 3744–3747. [Google Scholar]
- Han, H.; Han, C.; Lan, T.; Huang, L.; Hu, C.; Xue, X. Automatic shadow detection for multispectral satellite remote sensing images in invariant color spaces. Appl. Sci. 2020, 10, 6467. [Google Scholar] [CrossRef]
- Nakajima, T.; Tao, G.; Yasuoka, Y. Simulated recovery of information in shadow areas on IKONOS image by combing ALS data. In Proceedings of the Asian conference on remote sensing (ACRS), Kathmandu, Nepal, 25–29 November 2002. [Google Scholar]
- Zhan, Q.; Shi, W.; Xiao, Y. Quantitative analysis of shadow effects in high-resolution images of urban areas. In Proceedings of the 3nd International Symposium on Remote Sensing and Data Fusion Over Urban Areas, Tempe, AZ, USA, 14–16 March 2005. [Google Scholar]
- Tolt, G.; Shimoni, M.; Ahlberg, J. A shadow detection method for remote sensing images using VHR hyperspectral and LIDAR data. In Proceedings of the 2011 IEEE international geoscience and remote sensing symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 4423–4426. [Google Scholar]
- Adler-Golden, S.M.; Matthew, M.W.; Anderson, G.P.; Felde, G.W.; Gardner, J.A. Algorithm for de-shadowing spectral imagery. In Imaging Spectrometry VIII; International Society for Optics and Photonics: Seattle, WA, USA, 2002; Volume 4816, pp. 203–210. [Google Scholar]
- Richter, R.; Müller, A. De-shadowing of satellite/airborne imagery. Int. J. Remote Sens. 2005, 26, 3137–3148. [Google Scholar] [CrossRef]
- Cameron, M.; Kumar, L. Diffuse skylight as a surrogate for shadow detection in high-resolution imagery acquired under clear sky conditions. Remote Sens. 2018, 10, 1185. [Google Scholar] [CrossRef] [Green Version]
- Levine, M.D.; Bhattacharyya, J. Removing shadows. Pattern Recognit. Lett. 2005, 26, 251–265. [Google Scholar] [CrossRef]
- Vicente, T.F.Y.; Hou, L.; Yu, C.P.; Hoai, M.; Samaras, D. Large-scale training of shadow detectors with noisily-annotated shadow examples. In European Conference on Computer Vision (ECCV); Springer: Amsterdam, The Netherlands, 2016; pp. 816–832. [Google Scholar]
- Nguyen, V.; Yago Vicente, T.F.; Zhao, M.; Hoai, M.; Samaras, D. Shadow detection with conditional generative adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4510–4518. [Google Scholar]
- Finlayson, G.D.; Hordley, S.D.; Lu, C.; Drew, M.S. On the removal of shadows from images. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 28, 59–68. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, G.; Vukomanovic, J.; Singh, K.K.; Liu, Y.; Holden, S.; Meentemeyer, R.K. Recurrent Shadow Attention Model (RSAM) for shadow removal in high-resolution urban land-cover mapping. Remote Sens. Environ. 2020, 247, 111945. [Google Scholar] [CrossRef]
- Finlayson, G.D.; Drew, M.S.; Lu, C. Entropy minimization for shadow removal. Int. J. Comput. Vis. 2009, 85, 35–57. [Google Scholar] [CrossRef] [Green Version]
- Arbel, E.; Hel-Or, H. Shadow removal using intensity surfaces and texture anchor points. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1202–1216. [Google Scholar] [CrossRef]
- Lorenzi, L.; Melgani, F.; Mercier, G. A complete processing chain for shadow detection and reconstruction in VHR images. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3440–3452. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Q.; Xiao, C. Shadow remover: Image shadow removal based on illumination recovering optimization. IEEE Trans. Image Process. 2015, 24, 4623–4636. [Google Scholar] [CrossRef]
- Xiao, Y.; Tsougenis, E.; Tang, C.K. Shadow removal from single RGB-D images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3011–3018. [Google Scholar]
- Khan, S.H.; Bennamoun, M.; Sohel, F.; Togneri, R. Automatic shadow detection and removal from a single image. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 431–446. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qu, L.; Tian, J.; He, S.; Tang, Y.; Lau, R.W. Deshadownet: A multi-context embedding deep network for shadow removal. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4067–4075. [Google Scholar]
- Kruse, F.A.; Lefkoff, A.; Boardman, J.; Heidebrecht, K.; Shapiro, A.; Barloon, P.; Goetz, A. The spectral image processing system (SIPS)-interactive visualization and analysis of imaging spectrometer data. In AIP Conference Proceedings; American Institute of Physics: Pasadena, CA, USA, 1993; Volume 283, pp. 192–201. [Google Scholar]
- Roussel, G.; Weber, C.; Ceamanos, X.; Briottet, X. A sun/shadow approach for the classification of hyperspectral data. In Proceedings of the 2016 8th Workshop on Hyperspectral Image and Signal Processing, Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016; pp. 1–5. [Google Scholar]
- Windrim, L.; Ramakrishnan, R.; Melkumyan, A.; Murphy, R.J. A physics-based deep learning approach to shadow invariant representations of hyperspectral images. IEEE Trans. Image Process. 2017, 27, 665–677. [Google Scholar] [CrossRef] [PubMed]
- Windrim, L.; Melkumyan, A.; Murphy, R.; Chlingaryan, A.; Nieto, J. Unsupervised feature learning for illumination robustness. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 4453–4457. [Google Scholar]
- Zhang, Q.; Pauca, V.P.; Plemmons, R.J.; Nikic, D.D. Detecting objects under shadows by fusion of hyperspectral and lidar data: A physical model approach. In Proceedings of the 2013 5th Workshop on Hyperspectral Image and Signal Processing, Evolution in Remote Sensing (WHISPERS), Gainesville, FL, USA, 25–28 June 2013; pp. 1–4. [Google Scholar]
- Friman, O.; Tolt, G.; Ahlberg, J. Illumination and shadow compensation of hyperspectral images using a digital surface model and non-linear least squares estimation. In Image and Signal Processing for Remote Sensing XVII; International Society for Optics and Photonics: Prague, Czech Republic, 2011; Volume 8180, p. 81800Q. [Google Scholar]
- Dobigeon, N.; Tourneret, J.Y.; Richard, C.; Bermudez, J.C.M.; McLaughlin, S.; Hero, A.O. Nonlinear unmixing of hyperspectral images: Models and algorithms. IEEE Signal Process. Mag. 2013, 31, 82–94. [Google Scholar] [CrossRef] [Green Version]
- Plaza, A.; Martínez, P.; Pérez, R.; Plaza, J. A quantitative and comparative analysis of endmember extraction algorithms from hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 650–663. [Google Scholar] [CrossRef]
- Yang, J.; He, Y.; Caspersen, J. Fully constrained linear spectral unmixing based global shadow compensation for high resolution satellite imagery of urban areas. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 88–98. [Google Scholar] [CrossRef]
- Nascimento, J.M.; Bioucas-Dias, J.M. Nonlinear mixture model for hyperspectral unmixing. In Image and Signal Processing for Remote Sensing XV; International Society for Optics and Photonics: Berlin, Germany, 2009; Volume 7477, p. 74770I. [Google Scholar]
- Omruuzun, F.; Baskurt, D.O.; Daglayan, H.; Cetin, Y.Y. Shadow removal from VNIR hyperspectral remote sensing imagery with endmember signature analysis. In Next-Generation Spectroscopic Technologies VIII; International Society for Optics and Photonics: Baltimore, MD, USA, 2015; Volume 9482, p. 94821F. [Google Scholar]
- Heylen, R.; Scheunders, P. A multilinear mixing model for nonlinear spectral unmixing. IEEE Trans. Geosci. Remote Sens. 2015, 54, 240–251. [Google Scholar] [CrossRef]
- Guo, R.; Dai, Q.; Hoiem, D. Single-image shadow detection and removal using paired regions. In CVPR 2011; IEEE: Providence, RI, USA, 2011; pp. 2033–2040. [Google Scholar]
- Mo, N.; Zhu, R.; Yan, L.; Zhao, Z. Deshadowing of urban airborne imagery based on object-oriented automatic shadow detection and regional matching compensation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 585–605. [Google Scholar] [CrossRef]
- Zhang, G.; Cerra, D.; Mueller, R. Towards the Spectral Restoration of Shadowed Areas in Hyperspectral Images Based on Nonlinear Unmixing. In Proceedings of the 2019 10th Workshop on Hyperspectral Imaging and Signal Processing, Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 September 2019; pp. 1–5. [Google Scholar]
- Zhang, G.; Cerra, D.; Mueller, R. Improving the classification in shadowed areas using nonlinear spectral unmixing. In Proceedings of the 2020 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Waikoloa Village, HI, USA, 16–26 July 2020. in press. [Google Scholar]
- Schott, J.R. Remote Sensing: The Image Chain Approach; Oxford University Press on Demand: New York, NY, USA, 2007. [Google Scholar]
- Heylen, R.; Parente, M.; Gader, P. A review of nonlinear hyperspectral unmixing methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1844–1868. [Google Scholar] [CrossRef]
- Fan, W.; Hu, B.; Miller, J.; Li, M. Comparative study between a new nonlinear model and common linear model for analysing laboratory simulated-forest hyperspectral data. Int. J. Remote Sens. 2009, 30, 2951–2962. [Google Scholar] [CrossRef]
- Slater, P.N.; Doyle, F.; Fritz, N.; Welch, R. Photographic systems for remote sensing. Man. Remote Sens. 1983, 1, 231–291. [Google Scholar]
- Bredies, K.; Kunisch, K.; Pock, T. Total generalized variation. SIAM J. Imaging Sci. 2010, 3, 492–526. [Google Scholar] [CrossRef]
- Köhler, C.H. Airborne imaging spectrometer hyspex. J. Large Scale Res. Facil. JLSRF 2016, 2, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Richter, R.; Schläpfer, D.; Müller, A. An automatic atmospheric correction algorithm for visible/NIR imagery. Int. J. Remote Sens. 2006, 27, 2077–2085. [Google Scholar] [CrossRef]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Borsoi, R.A.; Imbiriba, T.; Bermudez, J.C.M.; Richard, C.; Chanussot, J.; Drumetz, L.; Tourneret, J.Y.; Zare, A.; Jutten, C. Spectral Variability in Hyperspectral Data Unmixing: A Comprehensive Review. arXiv 2020, arXiv:2001.07307. [Google Scholar]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 6, 679–698. [Google Scholar] [CrossRef]
- Somers, B.; Zortea, M.; Plaza, A.; Asner, G.P. Automated extraction of image-based endmember bundles for improved spectral unmixing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 396–408. [Google Scholar] [CrossRef] [Green Version]
- Nascimento, J.M.; Dias, J.M. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef] [Green Version]
- Cun, X.; Pun, C.M.; Shi, C. Towards Ghost-Free Shadow Removal via Dual Hierarchical Aggregation Network and Shadow Matting GAN. In Proceedings of the AAAI, New York, NY, USA, 7–12 February 2020; pp. 10680–10687. [Google Scholar]












| Subset | Region | LMM | FAN | Proposed |
|---|---|---|---|---|
| 1 | sunlit regions | 0.113 | 0.083 | 0.077 |
| shadowed regions | 0.414 | 0.421 | 0.026 | |
| both | 0.191 | 0.171 | 0.064 | |
| 2 | sunlit regions | 0.088 | 0.077 | 0.071 |
| shadowed regions | 0.209 | 0.210 | 0.021 | |
| both | 0.114 | 0.106 | 0.060 | |
| 3 | sunlit regions | 0.092 | 0.090 | 0.081 |
| shadowed regions | 0.708 | 0.738 | 0.023 | |
| both | 0.290 | 0.298 | 0.062 | |
| 4 | sunlit regions | 0.059 | 0.044 | 0.039 |
| shadowed regions | 0.099 | 0.100 | 0.018 | |
| both | 0.064 | 0.052 | 0.037 | |
| 5 | sunlit regions | 0.088 | 0.079 | 0.063 |
| shadowed regions | 0.0685 | 0.732 | 0.030 | |
| both | 0.199 | 0.200 | 0.057 | |
| 6 | sunlit regions | 0.126 | 0.108 | 0.117 |
| shadowed regions | 0.156 | 0.158 | 0.025 | |
| both | 0.132 | 0.118 | 0.084 |
| Data | Input | Restored |
|---|---|---|
| subset 1 | OA = 73.472% K = 0.552 | OA = 95.366% K = 0.927 |
| subset 2 | OA = 82.203% K = 0.715 | OA = 93.553% K = 0.883 |
| subset 3 | OA = 55.0% K = 0.366 | OA = 93.939% K = 0.880 |
| subset 4 | OA = 84.495% K = 0.799 | OA = 95.138% K = 0.937 |
| subset 5 | OA = 80.340% K = 0.703 | OA = 90.170% K = 0.852 |
| subset 6 | OA = 85.373% K = 0.80 | OA = 93.284% K = 0.908 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Cerra, D.; Müller, R. Shadow Detection and Restoration for Hyperspectral Images Based on Nonlinear Spectral Unmixing. Remote Sens. 2020, 12, 3985. https://doi.org/10.3390/rs12233985
Zhang G, Cerra D, Müller R. Shadow Detection and Restoration for Hyperspectral Images Based on Nonlinear Spectral Unmixing. Remote Sensing. 2020; 12(23):3985. https://doi.org/10.3390/rs12233985
Chicago/Turabian StyleZhang, Guichen, Daniele Cerra, and Rupert Müller. 2020. "Shadow Detection and Restoration for Hyperspectral Images Based on Nonlinear Spectral Unmixing" Remote Sensing 12, no. 23: 3985. https://doi.org/10.3390/rs12233985
APA StyleZhang, G., Cerra, D., & Müller, R. (2020). Shadow Detection and Restoration for Hyperspectral Images Based on Nonlinear Spectral Unmixing. Remote Sensing, 12(23), 3985. https://doi.org/10.3390/rs12233985






